Advances in measuring lifespan in the yeast Saccharomyces cerevisiae

Abstract

Much research aimed at discovering the genetic bases of longevity focuses on the budding yeast Saccharomyces cerevisiae. Unfortunately, yeast researchers use a definition of longevity not applied to other species. We propose here a method that makes it possible to estimate for yeast the same measures of longevity calculated for other species. We also show that the conventional method (equating longevity with the number of offspring) is only an approximate measure of true chronological lifespan. Our method will allow results for yeast to be compared more correctly with those for other species.

Much research aimed at discovering the genetic bases of longevity focuses on the yeast Saccharomyces cerevisiae (1–7). Researchers hope that after identifying genes that promote longer life in yeast cells they may be able to spot analogous genes for more complex species, including humans. However, the assessment of longevity in yeast is conventionally based on definitions and assumptions not applied to other species, hindering comparisons. In this article we propose a method for calculating longevity in yeast on the same basis used for other species (8–10).

By far the most common measure of longevity reported in yeast studies is budding lifespan (3–7). This is the number of buds or daughter cells produced by a mother cell. To avoid the formation of colonies, and thus to ensure that the same cell is being followed throughout the experiment, buds or daughter cells are removed from the mother cell with a micromanipulator. This way of assessing longevity at the individual level has been used since the earliest studies ≈50 years ago (11), but it is a most unusual definition of longevity. It is, in fact, a measure of fertility rather than longevity.

In demographic terminology budding lifespan is a measure of the quantum of fertility. It will only be the same as true longevity (defined in time elapsed from birth) if certain assumptions are justified. In particular, this definition assumes that there is a directly proportional relationship between the number of buds and the time taken to produce them. Moreover, it also assumes that there is no postreproductive life. Conflating fertility and longevity into one measure in this way has potentially very serious implications. For example, it is logically impossible to tell whether a mutation that appears to increase longevity is in fact doing so. It may be increasing fertility, without increasing the length of life.

An alternative approach for studying the length of life for yeast cells is to use the definitions preferred for other species: reproductive lifespan and postreproductive lifespan. Reproductive lifespan is the length of time taken for a cell to produce the number of offspring reported in the budding lifespan, i.e., the time elapsed from birth to the appearance of the last daughter cell. Postreproductive lifespan is the time elapsed from the appearance of the last bud to the death of the cell. Reproductive lifespan can be calculated from the same experimental observations made for budding lifespan, reporting the time elapsed rather than the number of offspring (see Supporting Text, which is published as supporting information on the PNAS web site). However, estimating postreproductive lifespan requires a methodological innovation, as normal experimental methods do not directly observe death in all circumstances. To make this possible we incorporated a vital dye, Phloxine B, into the food on which the cells were kept. All cells absorb the dye, but metabolically active cells are able to pump it out and remain colorless. Dead cells are dyed: they passively incorporate the dye and thus show up as stained red. Phloxine B has been successfully used in studies of both budding and fission yeast, both on cells mounted for fluorescence microscopy (12) and added in the food to detect, for instance, temperature-sensitive colonies (13). In our experiment observations of single cells have been made with the dye incorporated in the food. By measuring elapsed time and using the dye, we are able to estimate both reproductive and postreproductive lifespan, rather than make assumptions about them, and by adding them together we can obtain overall lifespan.

The use of budding lifespan to describe longevity is so widespread in the literature that it is virtually taken for granted. However, no systematic set of experiments has been carried out to investigate its relationship to the definitions used for other species or to assess the validity of the assumptions that underlie the measure. The argument normally given in the literature for preferring budding lifespan as a definition of longevity is that true longevity (defined in time elapsed from birth) in yeast is strongly affected by environmental conditions; in particular, it is clearly temperature-dependent. Müller et al. (14) showed that whereas the length of life was sensitive to large changes in temperature (they compared cells kept at 10°C overnight with those kept at a constant 29°C), the average number of daughters born was more robust to such differences. However, the budding lifespan also can be affected by environmental changes, for example, by different food. Because environmental dependency is a characteristic of all cold-blooded organisms, including several used widely in the study of longevity, it is not clear to us why this should be a more important consideration for yeast than for other species. Moreover, temperature sensitivity is not a significant issue when experiments are carried out, as here, to compare strains of yeast experiencing the same environmental conditions. In sum, we think that the problems with the conventional budding lifespan definition of longevity outweigh its advantages.

In this article we assess the longevity of yeast cells during their exponential growth phase. Populations of yeast cells also can survive in a nondividing state called stationary phase (15). Cells enter stationary phase after having exhausted the available nutrients during their exponential growth. Cells that survive in stationary phase can exit it and divide again once food is provided. The measure of the lifespan for cells in stationary phase is conventionally referred to as “chronological” lifespan (16). The variable normally measured is the ability to resume division when food is provided. Only the cells able to exit stationary phase, divide, and form a colony in the presence of food are thus taken into account. The longer the cells spend in stationary phase the less likely they are to be able to exit it successfully. We have recently carried out a study of the relation between budding lifespan and chronological lifespan (3). We have shown that the inactivation of the Ras/cAMP/PKA pathway is able to increase both lifespans. In contrast, stress-resistance genes such as SODs, MSN2, MSN4, and RIM15 have opposite effects on budding and chronological lifespans.

Materials and Methods

Strains. We analyzed longevity in four haploid yeast strains. The strains were selected because they are known to have different lengths of average budding lifespan (5, 17) and because the mutation in CYR1 and the deletions in SCH9, MSN2, and MSN4 deactivate genes involved in similar pathways (refs. 17–19 and Supporting Text). The four strains reproduce with a normal generation time of ≈90 min at 30°C. For each strain we calculated the budding lifespan, reproductive lifespan, and post-reproductive lifespan.

The four strains studied were S288C (MATα mal gal2), EG103 (DBY746 MATα leu2–3, 112his3Δ1 trp1–289 ura3–52 GAL⁺), EG103cyr1 (DBY746 MATα leu2–3, 112his3Δ1 trp1–289 ura3–52 GAL⁺ cyr1::mTn), and EG103sch9msn2/4 (DBY746 MATα leu2–3, 112his3Δ1 trp1–289 ura3–52 GA L⁺ sch9Δ::URA3 msn2Δ::HIS3 msn4Δ::LEU2).

Experimental Methods. A sample of frozen cultures was streaked onto standard YPD (2% glucose, 2% peptone, 1% yeast extract) plates. After 3 days of incubation at 30°C, a single colony was sampled and cells were transferred to 40 ml of liquid YPD media where they were grown overnight (30°C and 200 rpm). One microliter of each culture was dropped at a specific place on the YPD plates in which Phloxine B (Sigma, ref. P2759) was added at 10 μg/ml at the time the YPD was prepared.

A few hours later, single cells were micromanipulated to defined places on the plates. After the production of the first daughter, the parental cell was removed and the daughter cell was followed for the total number of offspring. Plates were kept at 30°C and each cell was observed every 90 min. New daughter cells were removed and recorded. Plates were placed at 4°C overnight to avoid excessive budding (one daughter cell was usually grown overnight at that temperature). A cell was considered to be dead when appearing red because of the incorporation of the dye Phloxine B inside the cell. Phloxine B was the most suitable dye because it is detected under normal light, thus allowing us to see its incorporation during the normal course of the experiment, without further manipulating the cells.

On each plate, a total of 12 cells for each genotype were displayed. Four plates were followed in each experiment and two replicates were carried out. In fact, we studied a total of 376 experimental cells, rather than 384. Five cells failed to produce a daughter that would have been used as an experimental cell and three cells could not be followed for their entire lives because of technical problems.

Statistical Analyses. Of the 376 cells, only those that produced at least five daughters were included in the analyses. These comprised 100% of the cells for genotype S288C and EG103cyr1, 98.9% for EG103, and 80.9% for EG103sch9msn2/4. For each strain in each replicate we recorded and analyzed the budding, reproductive, and postreproductive lifespans. The two replicates were analyzed separately because they showed slightly different values for the variables means (Table 1). However, the statistical results were essentially the same for both replicates.

Table 1. Mean ± SEM for each genotype and each replicate of the budding, reproductive, and postreproductive lifespans.

	Budding lifespan		Reproductive lifespan		Postreproductive lifespan
Genotype	Replicate 1	Replicate 2	Replicate 1	Replicate 2	Replicate 1	Replicate 2
S288C	N = 46	N = 48	N = 46	N = 48	N = 46	N = 48
	29.96 ± 1.72	31.27 ± 1.80	62.29 ± 3.60	62.03 ± 3.84	6.52 ± 0.89	9.66 ± 1.71
EG103	N = 46	N = 47	N = 46	N = 47	N = 45	N = 47
	14.85 ± 0.71	20.62 ± 0.89	56.74 ± 4.29	67.02 ± 3.50	8.13 ± 1.34	10.18 ± 1.97
EG103cyr1	N = 46	N = 47	N = 46	N = 47	N = 44	N = 47
	20.13 ± 1.26	22.74 ± 1.25	70.83 ± 4.69	61.18 ± 3.78	11.80 ± 1.43	14.17 ± 1.58
EG103sch9 msn2/4	N = 33	N = 39	N = 33	N = 39	N = 33	N = 39
	10.00 ± 0.65	13.72 ± 1.00	41.91 ± 3.75	53.89 ± 4.09	11.77 ± 2.38	9.99 ± 1.65

Because only one daughter was usually produced overnight, we counted the 9 h spent at 4°C as 90 min, the normal observation frequency, to avoid exaggerating the length of life of cells spending several nights at 4°C. With this conversion, 1 day is 15 h long.

Budding and reproductive lifespans for both replicates and postreproductive lifespan for the second replicate were log-transformed to fit a normal distribution. Normality was assessed with Kolmogorov–Smirnov tests. We then used ANOVA on the lifespans to test the effect of genotype (fixed factor), plate (random factor), and their interaction. Bonferroni post hoc tests identified the specific origin of overall differences. Postreproductive lifespan data for the first replicate failed to fit a normal distribution, and Kruskal–Wallis tests were performed to assess the effect of genotype and plate on this variable, but this meant that the interaction term could not be estimated (Table 2). Pearson (parametric) or Spearman (nonparametric) correlation coefficients between the three variables were calculated at the individual level for each genotype (Table 3).

Table 2. Statistical analyses showing the effect of genotype, plate, and their interaction for each replicate on the budding, reproductive, and postreproductive lifespans.

	Budding lifespan		Reproductive lifespan		Postreproductive lifespan
Factor	Replicate 1	Replicate 2	Replicate 1	Replicate 2	Replicate 1	Replicate 2
Genotype	F(3, 9) = 135.66	F(3, 9) = 109.66	F(3, 9) = 15.53	F(3, 9) = 6.36	3 df X2 = 14.1	F(3, 9) = 4.15
	P < 0.0001	P < 0.0001	P < 0.001	P = 0.013	P = 0.003	P = 0.040
Plate	F(3, 155) = 1.32	F(3, 165) = 2.45	F(3, 154) = 0.11	F(3, 165) = 1.53	3 df X2 = 8.73	F(3, 165) = 0.71
	P = 0.269	P = 0.065	P = 0.957	P = 0.208	P = 0.033	P = 0.550
Genotype by plate	F(9, 155) = 0.40	F(9, 165) = 0.30	F(9, 154) = 0.56	F(9, 165) = 0.39	Not applicable	F(9, 165) = 1.00
	P = 0.934	P = 0.974	P = 0.826	P = 0.941	(see text)	P = 0.439

Table 3. Correlation coefficients for each genotype and replicate between the budding, reproductive, and postreproductive lifespans.

	Budding lifespan/reproductive lifespan		Budding lifespan/postreproductive lifespan		Reproductive lifespan/postreproductive lifespan
Genotype	Replicate 1	Replicate 2	Replicate 1	Replicate 2	Replicate 1	Replicate 2
S288C	N = 46	N = 48	N = 46	N = 48	N = 46	N = 48
	r2 = 0.79	r2 = 0.84	r2 = 0.0121	r2 = 0.009	r2 = 0.0025	r2 = 0.0144
	P < 0.0001	P < 0.0001	P = 0.485	P = 0.823	P = 0.743	P = 0.421
EG103	N = 46	N = 47	N = 45	N = 47	N = 45	N = 47
	r2 = 0.77	r2 = 0.74	r2 = 0.14	r2 = 0.0144	r2 = 0.09	r2 = 0.0081
	P < 0.0001	P < 0.0001	P = 0.009	P = 0.406	P = 0.048	P = 0.568
EG103cyr1	N = 45	N = 47	N = 44	N = 47	N = 44	N = 47
	r2 = 0.74	r2 = 0.88	r2 = 0.0196	r2 = 0.0441	r2 = 0.0064	r2 = 0.576
	P < 0.0001	P < 0.0001	P = 0.379	P = 0.159	P = 0.604	P = 0.102
EG103sch9 msn2/4	N = 33	N = 39	N = 33	N = 39	N = 33	N = 39
	r2 = 0.44	r2 = 0.53	r2 = 0.0324	r2 = 0.0121	r2 = 0.0144	r2 = 0.0081
	P < 0.0001	P < 0.0001	P = 0.305	P = 0.495	P = 0.497	P = 0.581

Survival curves were derived for each genotype from the budding lifespan and reproductive lifespan to compare the relation between the number of daughters and the time taken to produce those daughters. The survival curves indicate the number of experimental cells reaching the value x for the variable under study (N_x) divided by the total number of experimental cells for that genotype and replicate (N_o). Postreproductive survival was analyzed to know whether the decline in the number of living cells was strictly exponential (a test for randomness).

Results

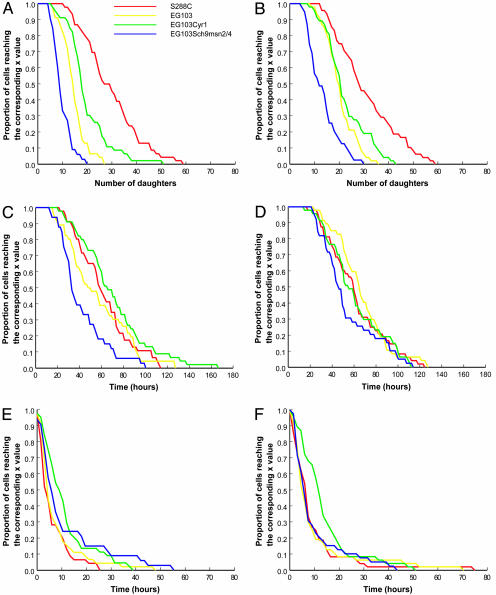
Fig. 1 presents survival curves for each sample, with each column of graphs corresponding to a replicate of the experiment. Fig. 1 A and B summarizes conventional budding lifespans, Fig. 1 C and D shows reproductive lifespans, and Fig. 1 E and F shows postreproductive lifespans.

Fig. 1.

Survival curves. (A, C, and E) Replicate 1. (B, D, and F) Replicate 2. (A and B) Budding lifespan. (C and D) Reproductive lifespan. (E and F) Postreproductive lifespan.

Fig. 1 A and B clearly shows that the four strains have different budding lifespans, with the rank order of the strains corresponding to expectations. S288C had the highest number of daughters, and, when compared with the control strain EG103, EG103cyr1 had more daughters and EG103sch9msn2/4 had fewer. The difference between EG103 and EG103cyr1 was less marked in the second replicate of the experiment.

As is clear in Fig. 1 C and D, when actual time elapsed is calculated the differences between the four strains change. The strain with the shortest budding lifespan, EG103sch9msn2/4, remains the shortest-lived, but the other three strains show less differentiation, and the strain with the longest budding lifespan does not show the longest reproductive lifespan. Statistical analysis indicates that the three longer-lived strains are indistinguishable in terms of reproductive lifespan. In other words, two strains with very different budding lifespans (for example, one of which produces 50% more daughter cells than another) can show no difference in lifespan measured in time rather than in generations. As Table 3 shows, there is a significant correlation between the two measures (r² is > 0.7 for three strains, but < 0.5 for the fourth), but there is also a substantial amount of variance in the reproductive lifespan that is not captured by the budding lifespan.

Fig. 1 E and F shows postreproductive lifespans. As expected, postreproductive lifespan is much shorter than the length of the reproductive life, but it is not zero (it can amount to as much as 10% of total lifespan), nor is it identical for all strains. Moreover, for three of the strains there is no statistical correlation between postreproductive lifespan and either budding lifespan or reproductive lifespan. Only for EG103 is there any significant correlation, and only in one of the two replicates is there significant correlation. The length of the post-reproductive lifespan ranged from zero (death at the time of budding the last daughter) to 75 h (based on a 15-h day). The distribution of the time between last budding and death differed between the genotypes and was not exponential. Both of these features suggest that postreproductive lifespan is not a purely random phenomenon. Causes of death in old yeast cells are not known. Budding lifespan is modulated by dozens of genes (1) and environmental changes such as caloric restriction (lower glucose concentration in the food) that increases budding lifespan (5). An increase in glucose concentration above the standard 2% also leads to a higher budding lifespan (20). Morphological and physiological changes with replicative age have been described (e.g., refs. 1 and 21), that could be possible explanations for the existence of a postreproductive lifespan in yeast (discussed in ref. 22). However, none of those changes have been shown to be a leading cause of death in yeast. The only known plausible cause of death is the induction of apoptosis (23, 24) because this phenomenon is known to directly lead to the death of the cell implementing an apoptotic process. We did not investigate potential causes of death in the present experiment.

Discussion

This article proposes two deceptively modest innovations to experimental procedures. These small changes seem small, but they have considerable potential for improving our understanding of the genetic basis of longevity in yeast. Our most important result is that budding lifespan is not an accurate predictor of reproductive lifespan. This finding indicates that unqualified use of budding lifespan as a measure of longevity is not justified. We also show that postreproductive lifespan differs between strains, undermining another assumption needed for budding lifespan to be a true indication of longevity.

It will be relatively straightforward for other researchers to carry out similar analyses to those reported here. The information needed to calculate reproductive lifespan should be found in the records of any experiment that reported budding lifespan. We hope, therefore, that the generality of our findings for other strains of yeast can be rapidly established by reference to this existing (but unreported) information. Estimating postreproductive lifespan for more strains will require additional experiments, but the methodological innovation of incorporating dye in the yeast's growing medium is not difficult to implement.