Evidence for self-cleaning in gecko setae

Abstract

A tokay gecko can cling to virtually any surface and support its body mass with a single toe by using the millions of keratinous setae on its toe pads. Each seta branches into hundreds of 200-nm spatulae that make intimate contact with a variety of surface profiles. We showed previously that the combined surface area of billions of spatulae maximizes van der Waals interactions to generate large adhesive and shear forces. Geckos are not known to groom their feet yet retain their stickiness for months between molts. How geckos manage to keep their feet clean while walking about with sticky toes has remained a puzzle until now. Although self-cleaning by water droplets occurs in plant and animal surfaces, no adhesive has been shown to self-clean. In the present study, we demonstrate that gecko setae are a self-cleaning adhesive. Geckos with dirty feet recovered their ability to cling to vertical surfaces after only a few steps. Self-cleaning occurred in arrays of setae isolated from the gecko. Contact mechanical models suggest that self-cleaning occurs by an energetic disequilibrium between the adhesive forces attracting a dirt particle to the substrate and those attracting the same particle to one or more spatulae. We propose that the property of self-cleaning is intrinsic to the setal nanostructure and therefore should be replicable in synthetic adhesive materials in the future.

Adhesive foot hairs, or setae, on the tokay gecko (Gekko gecko) are remarkably sticky: a single seta can generate up to 200 μN of force (1). Geckos use this adhesive to rapidly and repeatedly navigate a wide variety of surfaces (2, 3); they can even climb vertically on smooth surfaces at a speed >1 m/s (4). Locomotion with such a robust adhesive raises the following question: how do their feet stay clean (3)? Geckos neither groom their footpads, as do some beetles (5), nor secrete fluids that could remove adhering particles, as do certain ants (6), crickets (7), and tree frogs (8).

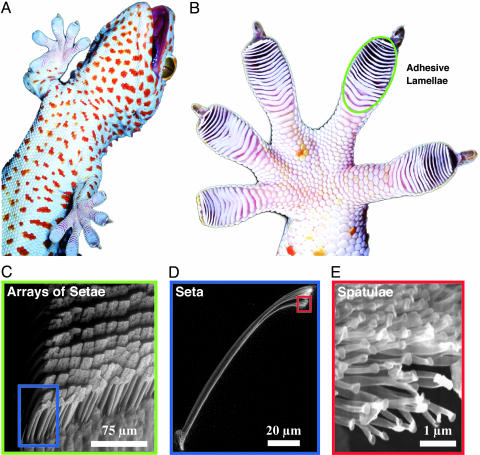
Setae occur in uniform arrays on overlapping lamellar pads at a density of 14,400 per mm² (Fig. 1C) (9). Each seta (Fig. 1D) is ≈110 μm in length and 5 μm in diameter (4, 10) and branches at the tip into 100–1,000 spatulae, which are ≈0.2 μm in length and maximal width (11) (Fig. 1E). Adhesion occurs when spatulae flatten against a substrate, and their cumulative spatula–substrate van der Waals interactions generate forces capable of supporting many times the animal's body weight (2, 3). To adhere, setae must be oriented properly and preloaded with a small perpendicular force and 5-μm rearward displacement (1). A single seta can resist 200 μN of force, or ≈10 atmospheres of stress (1 atmosphere = 101.3 kPa) (1). Particles encountered during locomotion seem likely to adhere with similar tenacity to the setal tips. Yet, casual observation (Fig. 1 B and C) shows that gecko feet and setae remain clean for periods of months between molt cycles but reveals little about the mechanism or time scale of the process.

Fig. 1.

Structural hierarchy of the gecko adhesive system. (A) Macrostructure: ventral view of a tokay gecko (G. gecko) climbing vertical glass. (B) Mesostructure: ventral view of the foot, with adhesive lamellae (scansors) visible as overlapping pads. Note the clean appearance of the adhesive surface. (C) Microstructure: proximal portion of a single lamella, with individual setae in an array visible. (D and E) Nanostructure: single seta with branched structure at upper right, terminating in hundreds of spatular tips.

We tested the hypothesis that, unlike conventional adhesives, gecko setae become cleaner with repeated use. We measured the effects of particulate contamination on the toes of live geckos and on isolated setal arrays to determine whether cleaning of setae occurs apart from the gecko. First, we measured shear force on clean glass for isolated setal arrays and whole live digits (multiple overlapping arrays) of tokay geckos. Next, we applied alumina-silica microspheres (2.5-μm mean radius) to the adhesive areas and measured shear force as we simulated steps on smooth glass. Microspheres applied to digits visibly completely covered adhesive areas, whereas we applied significantly fewer microspheres to isolated arrays with the goal of applying a single, diffuse layer of particles. For direct comparison of isolated array and live digit measurements, we define the recovery index, R(n) = (F_n - F_dirty)/(F_clean - F_dirty), representing the fraction of the initial loss in force that is recovered by step n.

Materials and Methods

Isolated Setal Array Force Measurements. Tokays regrow the setal layer approximately every 2 months. Intact setal arrays can be isolated without harm to the animal. We isolated setal arrays from five live, restrained, nonmolting tokay geckos and bonded them within 2 min to acetate strips (0.25 × 1.0 × 0.08 inch) with cyanoacrylate gel. Arrays were cured for 1 h before experimentation. To prepare the standardized dirt, we mixed 0.83 g of silica-alumina ceramic microspheres (2.5-μm mean radius; G-200 Zeeospheres, 3M Co.) in 35 ml of ethanol, dispersed 50-μl aliquots onto glass coverslips, creating an approximate monolayer of particles, and allowed them to air dry.

We measured shear forces for setal arrays by using a vertically mounted piezoelectric force sensor (Kistler 9207, Kistler Instrument, Winterthur, Switzerland) with a 2.5 × 2.5-cm glass slide for the force plate. The setal array was mounted in a rigid holder at a slight angle to the glass plate and preloaded into the surface with a set force of 24.5 mN, flexing the acetate and aligning the array parallel to the glass. Shear forces were measured by pulling the array downward. We programmed closed-loop dc servo motors (Newport, Irvine, CA) attached to a micromanipulator to automatically preload and pull each array at 3 mm/s. We compared force after dirtying with force before dirtying for the same array. For each array, 10 pulls were completed to characterize the clean force, F_c, and then we applied the microspheres and completed 5 additional pulls, each performed on a clean section of the force plate to avoid microsphere detritus. Size constraints of the force sensor prevented additional pulls on clean glass. Trials during which arrays broke or detached from the acetate were discarded. Real-time data accurate to 5 mN were collected and analyzed by using igor pro 4.0 (WaveMetrics, Lake Oswego, OR) and statview 5.6.1 (SAS Institute, Cary, NC) software.

Live Digit Force Measurements. Measuring whole-digit forces requires a larger surface than measuring array forces, so we constructed a single-axis force plate by attaching a 5 × 5 × 0.1524-cm slide of optically clear glass (VWR Scientific) to a vertically mounted single-axis force sensor (Vernier, Beaverton, OR). We calibrated the system and confirmed calibration by using test forces from 0.00981 to 9.81 N at the beginning and end of every set of trials.

We measured single-toe shear forces for three tokay geckos by manually isolating a single toe, placing it on the force plate, and touching it lightly to the substrate to ensure complete toe uncurling and to mimic the preload procedure necessary for setal attachment (1). Then, we pulled the foot downward until the toe detached from the glass. Digits adhered so strongly that clean measurements often involved peeling of the superficial layer of skin of the lamellae, so we used contralateral digits for clean and dirty measurements. It should be noted that clean foot force measurements quantify the maximum force that the outer layer of integument can withstand, not the maximum force of attachment by the setae. Shear force is strongly correlated with pad area (12), which differs among digits, so we standardized digit measurements by pad area. Force of attachment of clean toes on glass was measured for every digit on the left side of each animal. To clog the toe pads, we applied 0.20 g of silica-alumina ceramic microspheres dispersed on glass (G-200 Zeeospheres; 2.5-μm mean radius) to each digit, resulting in saturation of the adhesive areas. Measurements then were taken for the two right feet, allowing a number of steps ranging from 0 until the point at which shear force was substantially restored and increases in force between successive trials were small (up to 18 steps). Full strides were not used, because inducing the gecko to take a specified number of steps without otherwise disturbing its feet was not feasible. Digital hyperextension did not occur. Because the measurement itself was much like a step, we gently cleaned the soiled foot with compressed air and deionized water to dislodge and flush away clogging microspheres. We reclogged the same foot between successive trials instead of counting the measurement as a step itself. After each day of experiments, the gecko's feet were fully rehydrated and allowed to recover for 24 h. Real-time data accurate to 6 mN were collected in maclab/chart v.3.6.5 (A. D. Instruments, Milford, MA) at 40 Hz. Data were analyzed with commercial software (statview v5.6.1, SAS Instruments, and superanova, Abacus Concepts, Berkeley, CA). To obtain the toe pad areas, we scanned each gecko's foot on a flatbed scanner (Agfa Snapscan) and measured areas with commercial software (canvas 8, ACD Systems, Saanichton, BC, Canada).

Results and Discussion

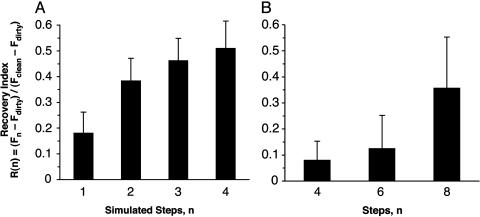
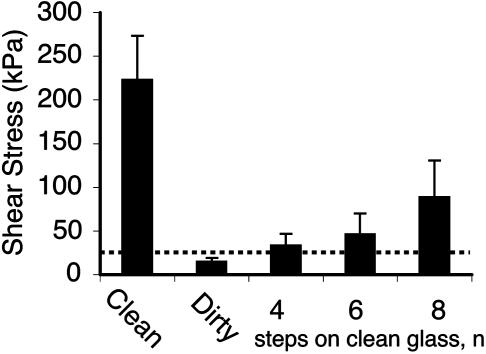
Experimental Support for the Self-Cleaning Hypothesis. After application of microspheres, arrays lost 59.95% (SD = 17.45%; n = 5 arrays; 30 measurements) of shear force. Four simulated steps on clean glass restored 51.00% (SD = 23.64%) of this functional loss (Fig. 2A). All arrays exhibited increasing force with increasing number of pulls after contact with microspheres, independent of force magnitude. For digits, force measured immediately after application of microspheres was below the sensitivity of the force sensor (F₀ < 6 mN); at two steps the loss of force was still 92.99% (SD = 3.40%; n = 3 geckos; 133 measurements), the value we used to represent the force of a dirty toe. After eight simulated steps, 35.65% (SD = 34.09%; n = 3 geckos; 133 measurements) of this loss was recovered, although each gecko recovered shear capacity at a different rate as indicated by the large SD (Fig. 2B). Average recovered digit force after eight steps was well over the force required for an animal to support its body mass (43 g) by a single digit (Fig. 3). Additionally, we visually examined dirty arrays by scanning electron microscopy and compared them with clean arrays to confirm self-cleaning (Fig. 4).

Fig. 2.

Recovery of force by self-cleaning, R(n) = (F_n - F_dirty)/(F_clean - F_dirty). (A) R(n) for isolated gecko setal arrays on glass after n simulated steps. (B) R(n) for digits of live geckos, standardized by adhesive area.

Fig. 3.

Mean shear stress in clean, dirty, and self-cleaned gecko digits. Dotted line indicates minimum shear stress required to support one gecko's body weight (43 g) by a single toe (area = 0.19 cm²). After clogging with >2.5-μm-radius microspheres, four steps on clean glass restored setal force to a level sufficient to support the gecko by a single toe.

Fig. 4.

Scanning electron micrographs of arrays. (A) Representative array after dirtying with microspheres. Arrow indicates a microsphere adhering to several spatulae. (B) Array from the same animal after five simulated steps. Microspheres are still present, but spatular surfaces are mostly clean. (Scale bars: 10 μm.)

These results show that microspheres interfere with attachment of gecko toes and in isolated arrays. Reproducing the seta–substrate interactions of a step significantly restored capacity to resist shear in both cases. Self-cleaning occurred in the toes of live geckos and did not require strides or extra toe movement to remove rapidly even copious amounts of microspheres. We conclude from the digit experiment that self-cleaning is a function of contact with a substrate and not simply a consequence of foot motion. Likewise, cleaning occurred in setal arrays apart from the gecko. We further conclude that self-cleaning is an inherent property of the setae; the “self” refers to the adhesive, not the animal.

The unique distally directed peeling motion of live gecko toes (digital hyperextension) during attachment and detachment (4) would seem to be a candidate for a cleaning mechanism. However, a rough calculation suggests that dynamics of the foot alone are not the primary mechanism of cleaning. With a step frequency of 30 Hz (4), assuming sinusoidal motion of a 1-cm digit, a 2.5-μm microsphere (mass = 1.6 × 10^-13 kg) adhering to the spatulae of the distalmost lamella on the 1-cm digit is acted on by an inertial force, F_i = 5.8 × 10^-11 N, >2 orders of magnitude smaller than the force of a single spatula (10^-8 N) (1, 13). While attached to N spatulae, the particle would experience an adhesive force of N × 10^-8 N. For the particle to be detached by inertia during foot placement, the acceleration required is at least a = N × 6 × 10⁴ m/s², or a = N × 6,000 × gravity, making detachment by macroscale foot movement unlikely. Stride elements such as digital hyperextension and lamellar positioning may aid the speed and effectiveness of the cleaning process, possibly by sliding or rolling particles and thereby easing detachment (14); however, we must consider substrate–particle interactions to explain the basic phenomenon.

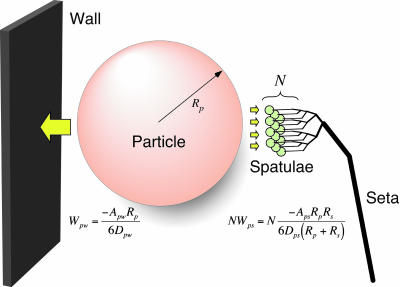
Models of Self-Cleaning. A single gecko spatula consists of a stalk with a thin, roughly triangular end, where the apex of the triangle connects the spatula to its stalk. Spatulae are ≈200 nm in length and width at the tip (10, 11) with thickness decreasing from ≈30 nm at the base to ≈10 nm at the tip (Fig. 1E). Empirical measurements of setal and spatular force (1, 2, 13) in combination with new theoretical results (15) suggest that relatively simple shapes can be used to model the contact mechanics of spatulae. First, we model spatulae as curved surfaces with approximately spherical geometry at the interface, and then as flexible strips. In each case, we compare the magnitude of attraction between a spherical dirt particle and a planar wall to the combined attraction of the same particle to a number of spatulae.

Spatulae as curved surfaces. The interaction energy between a spherical dirt particle and a planar wall is given by

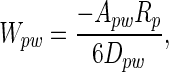[1]

where p and w refer to particle and wall, respectively; A is the Hamaker constant (typically ≈10^-19 J for van der Waals interactions in air); and D is the particle-to-wall distance (16). If we model the spatular surface as a spherical section, the interaction energy between a spherical dirt particle and a spatula (s) is given by the following equation (16):

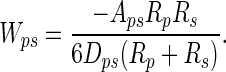[2]

When the system is in energetic equilibrium, equal energy is required to separate the particle from the wall and from the spatulae. Unless particles are very small (see below), many spatulae must be attached simultaneously to a single particle to balance W_pw. To predict the number of particle–spatula interactions (N) needed to achieve energetic equilibrium with the particle–wall interaction (Fig. 5), we take the ratio of the interaction energies,

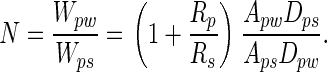[3]

In the case of N spatulae attached to each particle, approximately half of the particles will remain attached to the wall, and self-cleaning will occur with each step, assuming a clean substrate is encountered. If less than N spatulae are attached to each particle, self-cleaning will occur rapidly as a consequence of energetic disequilibrium; particles tend to remain attached to the wall rather than to the spatulae.

Fig. 5.

Model of interactions between N gecko spatulae of radius R_s, a spherical dirt particle of radius R_p, and a planar wall. Van der Waals interaction energies for the particle-spatula (W_ps) and particle-wall (W_pw) systems are shown. When N × W_ps = W_pw, equal energy is required to detach the particle from wall or N spatulae. Our results suggest that N is sufficiently great that self-cleaning results from energetic disequilibrium between the wall and the relatively few spatulae that can attach to a single particle.

In our study, R_p = 2.5 μm and R_s = 0.1 μm. Therefore,

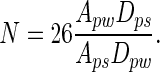[4]

This model suggests that >26 spatulae would need to be attached simultaneously to a single 2.5-μm-radius dirt particle in order for self-cleaning not to occur, assuming similar Hamaker constants and gap distances. Hamaker constants are unlikely to vary by more than a factor of 2 (16); if we take the worst case where A_ps = 2 A_pw, energetic equivalence occurs with 13 spatulae attached. Gap distance remains an unknown parameter in the model. Until measurements are available, we will assume that D_pw and D_ps have similar probability distributions, and thus can be assumed to be approximately equal.

If R_p < R_s, it follows from Eq. 3 that a particle of radius of <50 nm would result in W_pw < 1.5 W_ps, yielding N < 1.5. However, because it is unlikely that more than one spatula could attach to a 50-nm particle, we suggest that self-cleaning should occur for spherical spatulae interacting with spherical particles of all sizes. Spatulae as flexible strips. If we model spatulae as nanoscale strips of adhesive tape (13, 15, 17) that peel during detachment, the particle–spatula pulloff force is given by

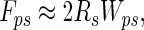[5]

where W_ps is the adhesion energy at the dirt particle–spatula interface, 2R_s is the width of the spatula (0.2 μm), and assuming negligible elastic energy storage (17). By using a value of W_ps typical for van der Waals interactions, 50 mJ/m² (16), F_ps is ≈10 nN, as also shown empirically by Huber et al. (13) and consistent with measurements of single setae (1).

The pulloff force of the dirt particle from a planar wall, by using the Johnson–Kendall–Roberts model (18), is

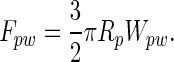[6]

By using a value of W_ps = W_ps of 50 mJ/m² (16), the pulloff force of a dirt particle with R_p = 2.5 μm is ≈590 nN. This result suggests that if spatulae act as flexible strips, >59 spatulae would need to be attached simultaneously to each 2.5-μm-radius particle to prevent self-cleaning. It follows from Eqs. 5 and 6 that as the diameter of the dirt particle approaches the width of the spatula, N approaches 3π/4 ≈ 2.4, suggesting again that self-cleaning can occur for spherical particles of all sizes.

Few spatulae adhere to each particle. Spatular density at the tips of the tokay setae in our sample was 3.79 per μm² (± 1.33 SD; n = 1,477). Therefore, the maximum number that could be attached to one hemisphere of radius 2.5 μm (39.3 μm² in surface area) is 149 spatulae, well above N for spherical or strip models. In reality, many fewer spatulae seem to be attached to a single microsphere (Fig. 4). This outcome is due to most particles remaining superficial to the spatular branches. The curvature of the particles relative to the roughly planar field of spatulae at the setal tip likely limits the number of spatulae that adhere to a single particle. Particles that are strongly impacted by the setal surfaces could become irreversibly attached to numerous spatulae. We observed some particles lodged between spatular branches and between setae (Fig. 4). The fate of particles trapped in interstices and their effect on setal function remains unknown.

Self-Cleaning: Lotus Effect and Gecko Effect. Roughness can make surfaces highly hydrophobic (19–21) and results in surfaces that are self-cleaning in the presence of water droplets. This microstructure-based resistance to soiling and facile cleaning by water is known as the lotus effect (22–24) and is observed for plants with microrough epicuticular wax layers, for nano-rough pilot whale skin (Globicephala melas) (25), and possibly for the feet of nonadhesive gecko species (e.g., Stenodactylus khobarensis) (26).

The phenomenon of self-cleaning in gecko setae is surprising because setae are adhesive and can self-clean when dry. Adhesion in gecko setae is a consequence of many divided contact points (spatulae) that deform to achieve intimate, high-density contact with the surface, whereas lotus-like surfaces remain slippery because their rough, and in some cases waxy, cuticle prevents intimate contact. Lotus-like surfaces require water as a cleaning agent (22–24), whereas self-cleaning in gecko setae may occur because it is energetically favorable for particles to be deposited on the surface rather than remain adhered to the spatulae.

Interestingly, one fundamental mechanism may underlie self-cleaning in gecko and lotus-like surfaces: Both gecko and lotus-like surfaces become cleaner after contamination for structural reasons; both possess a micro- or nano-rough topology that reduces adhesion with solid and liquid surfaces alike. Nonadhering setae should exhibit lotus-like wet self-cleaning characteristic of nonadhesive micro- or nano-rough surfaces. Nonadhered lamellar surfaces do appear to be highly nonwettable, with a water droplet contact angle of 160.9° (2). Thus, particles contacting the unloaded surface should wash away easily in the presence of water. However, it is not known how often geckos' feet become wet.

Conclusion

Our results confirm that isolated gecko setae self-clean and are consistent with adhesion models, implying that self-cleaning is an intrinsic property of arrays of setae. We showed that self-cleaning occurs even under extreme exposure to clogging particles. We predict that setal self-cleaning will depend strongly on particle and spatula size and spatula material properties. We hypothesize that key design principles for a passive, dry self-cleaning adhesive nanostructure are an array of spatulae (2) with the following properties: (i) surface area smaller than that of dirt particles, (ii) made of relatively hard, nontacky materials (27–29), and (iii) having low surface energy (γ, one-half the energy of cohesion).

Our models suggest that self-cleaning may in fact require γ of spatulae to be relatively low (equal to or less than that of the wall), perhaps constraining the spatula to be made of a hydrophobic material (16). For low values of W_ps, N may become greater than the number of spatulae that could possibly attach to a single particle. For example, if we take W_ps = 21 mJ/m², as measured by atomic force microscopy (13), and W_pw = 50 mJ/m², it follows from Eqs. 5 and 6 that >140 spatulae would be required to prevent self-cleaning of 2.5-μm-radius particles. Whereas decreasing γ would decrease the adhesion energy of each spatula, promoting self-cleaning may increase adhesion of the array as a whole by maximizing the number of uncontaminated spatulae.

Matting of adjacent setal stalks and adhesion of facing arrays have not been reported. Anti-self-adhesion properties may result from a principle similar to that of self-cleaning: It is unlikely that the number of spatula–spatula bonds will yield forces exceeding the forces acting to pull two facing arrays of setae apart. Resistance to matting also depends on additional factors such as γ and setal stiffness (30–32). If γ were to be increased by supplementing van der Waals forces with stronger intermolecular forces such as polar or H-bonding, it is likely that self-cleaning and anti-self-adhesion properties would be lost. Thus, the self-cleaning and anti-self conditions may represent a sweet spot in the evolutionary and engineering design spaces for adhesive nanostructures.