Abstract
Agent-based modeling is a technique currently used to simulate complex systems in computer science and social science. Here, we propose its application to the problem of molecular self-assembly. A system is allowed to evolve from a separated to an aggregated state following a combination of stochastic, deterministic, and adaptive rules. We consider the problem of packing rigid shapes on a lattice to verify that this algorithm produces more nearly optimal aggregates with less computational effort than comparable Monte Carlo simulations.
Keywords: agent-based simulation, molecular self-assembly, nanostructure prediction
Self-organization is one of the most fascinating phenomena in nature. It appears in such apparently disparate arenas as crystal growth, the regulation of metabolism, and dynamics of animal and human behavior (1–3). One of the great challenges in the field of complexity is the definition of the common patterns that make possible the emergence of order from apparently disordered systems. Although it is not proven that self-organization in apparently unrelated systems can be studied within a unique framework, many researchers are trying to identify new methods for interpretation of this aspect of complexity that allow a unified view. One example is given by the scale invariant networks that appear to offer a good perspective for many complex systems (4). Another possibility is the study of emergent phenomena through agent-based (AB) modeling. This developed, almost in parallel, in computer science (5–7) and social science (8–10) and has proved to be an excellent tool for the study of self-organizing computer programs, robots, and individuals. In this paper, after defining briefly the principles of AB modeling, we explore the possibility that such a modeling paradigm could be useful for the study of self-organizing chemical systems, complementing the currently used stochastic (Monte Carlo) or deterministic (molecular dynamics) methods.
Agent-Based Model of Molecular Self-Assembly
Background. An agent is a computer system that decides for itself (11, 12). After sensing the environment it takes decisions based on some rules. A typical example is a thermostat that switches on and off the heating after sensing the temperature. An intelligent agent is capable of “flexible” autonomous actions: (i) It interacts with other agents and its environment; (ii) its actions (rules) might change in time as a result of this interaction; and (iii) the agent shows goal-directed behavior (i.e., it takes the initiative to satisfy a goal). An AB simulation is a simulation with many intelligent agents interacting among themselves and with the environment. In a typical AB simulation of social behavior, the agents are the individuals that take rational decision based on their neighbors' decisions. Very interesting social phenomena have been recently investigated for example by Axelrod (13) (cooperation), Epstein (14) (social instability), and Helbing (15) (crowd modeling).
The great advantage of this modeling technique is that the emergent phenomena can be modeled through very simple rules governing the behavior of each agent. The global effect resulting from the interaction of the individuals is often unpredictable. Common features of the agent rules are as follows. (i) Nonlinearity: The rules have thresholds and if-then conditions. (ii) Locality: Some of the decisions are taken considering only the local environment and not the global average. (iii) Adaptation: The rules may change in time through processes of learning.
Rule-based models for physical systems, as alternatives to the traditional partial differential equation models, were recently suggested for several problems. In Cellular Automata (CA) modeling (16), the physical system is idealized as a discrete lattice whose cells can take a finite set of values. The equations of motion are replaced by rules that govern the discrete evolution of the lattice configuration, and in many cases, this method has provided an excellent description of complex phenomena. Famous examples include lattice gas automata (17–19), which were used for the description of complex phenomena in flow dynamics, and models for diffusion (20–22) and percolation (23) processes. AB modeling can be considered a generalization of CA where the model system is (in general) not required to be on a lattice and the rules can take any form including adaptive elements and goals-directed behavior. These models take advantage of the extreme simplification of the physical system and of the efficient computer implementation of rule-based models compared with differential equation models.
Application to Molecular Self-Assembly. A problem that arises very often and for which a general approach has not been devised is the following: Given N molecules, what is the lowest-energy organized structure that they can form? It is useful to recall the reasons that make this question very challenging and largely unanswered. The processes of self-organization occur on multiple time scales and involve motions of portions of the system of different sizes. For example, it is not generally possible to characterize the dynamics of molecular crystal growth without considering the conformational dynamics of the individual molecule. But the latter is usually faster than the diffusion processes involved in the former, and a deterministic approach like molecular dynamics (or simulated annealing) will only slowly lead to the correct structure because small integration times are required together with very long trajectory calculations. A different but related problem arises when these processes are modeled with stochastic methods such as Monte Carlo (MC). The random moves that allow the formation of small clusters of molecules from a disordered gas are usually inefficient for describing the fusion between small clusters of molecules and the formation of larger ordered domains. In an ideal simulation, smaller and larger portions of the system should be moved together (for a discussion of several techniques recently introduced to deal with these problems, see refs. 24–28).
Using an AB approach, the original question is modified as follows: Is it possible to devise a set of rules that let a system of N molecules evolve toward the lowest-energy ordered structure? Because this is an optimization problem, any method that leads to a better minimum is preferable. It is not necessary that the evolution follow a particular path on the potential surface (as in the deterministic methods) nor that the final distribution converge to some standard distribution (as in most stochastic methods). However, because it is not possible to build a set of rules completely de novo, it could be convenient to start from a well established method and introduce an additional set of rules that bypass the traditional bottlenecks. In this first attempt at AB modeling for self-assembly, we will start with a computational scheme that resembles the Metropolis MC simulation on a lattice. Then we introduce a few additional rules that avoid the limitations of the Metropolis algorithm and, through a population learning algorithm, speed up the formation of low-energy ordered structures.
We tried to devise a unique set of rules that leads any given system, defined by the interactions between its components, to the best self-assembled structure. Other researchers (29–31) are investigating instead the self-assembly of structures whose components are designed to assemble according to different sets of predefined rules. The most promising chemical systems of this kind are the two-dimensional arrays of “DNA tiles” (32) that could be, in principle, used to perform large-scale parallel computation.
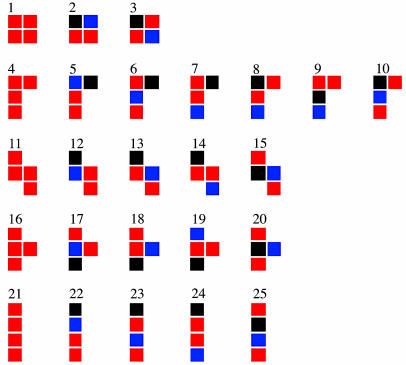
Model Systems. As a test-bed for the algorithm, we considered the problem of packing rigid shapes (models for rigid molecules) on a two-dimensional square lattice with periodic boundary conditions. All shapes were formed by four contiguous cells of one of the three cell types: neutral, positive, or negative. Cell interactions are nearest-neighbor only and obey Table 1. This table mimics van der Waals attraction between all cell types plus Coulombic repulsion/attraction between similarly/differently charged cells. To build a large unbiased set of shapes, we considered possible shapes made by four contiguous cells where two cells are neutral, one is positive, and one is negative, or where all four are neutral. The 25 possibilities, excluding those equivalent by symmetry, are shown in Fig. 1. We considered relatively small systems made by 40 particles on a 32 × 30 lattice.
Table 1. Cell interaction table for AB simulations (reduced units).
| Neutral | Positive | Negative | |
|---|---|---|---|
| Neutral | –1 | –1 | –1 |
| Positive | –1 | 9 | –11 |
| Negative | –1 | –11 | 9 |
Fig. 1.
The 25 primitive agents considered in this article. The colors represent the cell type: red, neutral; blue, positive; black, negative.
The Algorithm. We identify an agent with a molecule or a group of molecules. Initially each agent coincides with a rigid molecule (or shape); as the simulation proceeds, the agents change to represent stable portions of the system that can be considered locally minimized. Each agent, during the simulation, can undertake one of the following actions: (i) move to a new position on the lattice, (ii) merge with another agent, or (iii) split into two different agents (if formed by more than one inseparable component). Splitting is forbidden for each of the initial, primitive agents. The rules are such that the movement of an agent is decided stochastically, merging decisions are deterministic, and the decision to split one agent in two has elements of learning/adaptation.
(i) The move of each agent resembles a Metropolis MC algorithm, with multiple attempted moves. A set of M predefined moves, defined by a fixed set of allowed translations and rotations, is assessed. As an example, the simulations discussed in Results occur on a square lattice. The allowed moves are translations by a single lattice unit and rotations by multiples of 90°. For each move m the new potential energy Em is computed (Em = +∞ if the attempted move leads to an overlap with another agent). The actual move is selected among the attempted moves with probability
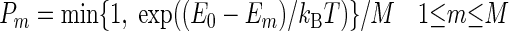 |
[1a] |
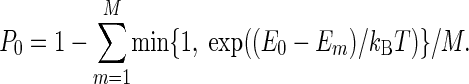 |
[1b] |
P0 is the probability to stay in the current configuration, and E0 is the potential energy before the move. T is a parameter that would correspond to the temperature of a canonical MC algorithm if we did not include merging and splitting, which do not obey detailed balance.
(ii) If none of the possible moves lowers the energy from the current position, and the algorithm chooses to keep the current configuration, an agent merges with the agent with which it has the largest attractive interaction. This merging introduces a major difference with respect to a conventional simulation because it allows the formation of clusters of molecules (the extended agents) that are then moved as a whole. In this way, the exploration of the system configuration is much faster because large and stable portions are moved globally. This move suite is in the spirit of previous Monte Carlo studies (24–28), which included cluster moves (but with different “bonding” criteria). The effect of nondeterministic “bonding” in Monte Carlo is considered in a companion paper (33).
(iii) Of course, not all of the agents formed by merging smaller agents are the best possible units for the self-assembly. If the number of initial molecules is sufficiently high, at least a group of molecules will find the best aggregation. We can make the rest of the agents “learn” of this best arrangement if we compare the energy of an agent made by several molecules with the energy of the most stable agents of equal or smaller size. In practice, we continuously update a list of the best (most negative) energy 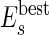 of all of the agents made by s molecules. An agent of energy En constructed from n molecules is split unless En satisfies the following equation§:
of all of the agents made by s molecules. An agent of energy En constructed from n molecules is split unless En satisfies the following equation§:
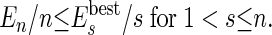 |
[2] |
Eq. 2 should be valid if the agent represents a stable portion of the system (e.g., a tetramer should be more stable than two dimers, etc.). In our algorithm, if a selected agent does not satisfy Eq. 2, it is split, because it is clear that there is at least one portion of the system where a better cluster of molecules has been formed. This approach is clearly a case of population learning, i.e., during the simulation, whenever an energetically good solution is found, all of the agents share this information and modify their actions. The way an agent (made by more than two molecules) can be split in two agents is not unique. Here, we compute the interaction of each molecule within an agent with all of the other molecules in the same agent. The molecule with the lowest interaction with the others (i.e., the most weakly bound) will be defined as a new agent, and all of the remaining molecules will be the other new agent. Other, more complicated choices did not improve the performance but might be considered for different systems.
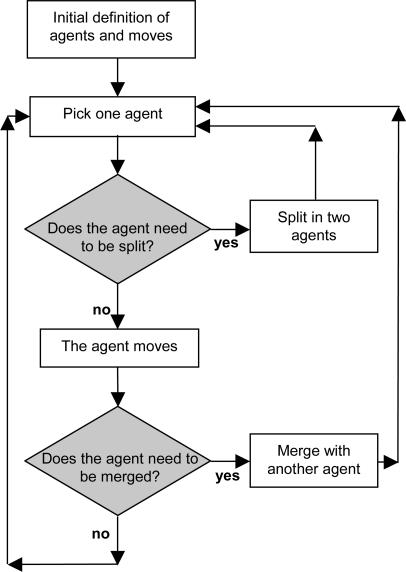
The overall algorithm takes the form outlined in Fig. 2: An agent is chosen; its energy is compared with the best energies of smaller and equally sized agents to determine whether it will split into two agents; if it does not split, a multiple-try Metropolis move is attempted; if the agent does not move, and all possible moves increase the total energy, the agent is merged with the one it interacts with most attractively. Overall, the difference with respect to a conventional Metropolis algorithm is given by the splitting and merging possibilities. They are not symmetrical: The splitting is done to keep the agent as the most stable unit of its size or smaller in the simulation and is an “intelligent” action in the sense that exploits the experience gained globally by the simulation; the merging is a purely deterministic choice done to escape from the impasse of having no available moves. One can set the maximum number of molecules that form an agent: If this number is set to one, the simulation proceeds as a normal Metropolis algorithm; in general it is possible to tune the degree of clustering by reducing the maximum number of molecules in one agent. We noted that it is better to slow down the formation of clusters at the beginning of the simulations, to avoid the formation of relatively unstable agents. We set our simulation so that the maximum number of molecules in one agent increases from one to a predefined value linearly during a simulation. It seems reasonable to set the maximum number of molecules in one agent to a number not much larger than the square root of the total number of molecules (we set this parameter to 9 in our example).
Fig. 2.
A flow-chart representation of the agent-based algorithm as implemented in this work.
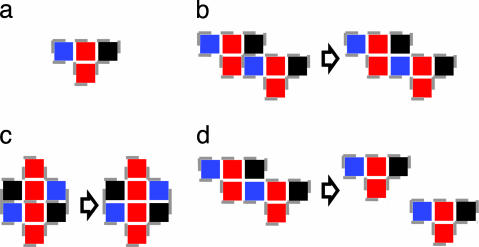
In Fig. 3, we sketched some typical actions occurring during a simulation that illustrate how this algorithm learns the building blocks of the assembled structure by trial and error. Differently from other stochastic algorithms, this one does remember the good solutions and propagates them through the system.
Fig. 3.
Typical steps of an AB simulation. (a) Initially, each shape is a primitive agent (an agent is delimited by the dashed gray line). (b) When two agents interact and do not find a move that lowers the energy, they merge into a unique agent (a dimer in this case). (c) The same can happen in another point of the lattice where a better dimer can be formed. (d) Because a better dimer has been formed, the dimer formed in b is split the next time it is moved.
Results
During the implementation and testing of this algorithm, the evolution of the system was monitored by inspection for all considered shapes. To evaluate the performance of the method, we ran 10 AB simulations of 15,000 steps for each of the primitive agents (shown in Fig. 1) and tabulated the average lowest energy encountered by the simulation (〈EAB〉). A similar quantity, 〈EMC〉, was computed from equally long Metropolis MC simulations (the same code produces a comparable MC simulation if the maximum number of molecules per agent is fixed to 1). The two averages are collected in Table 2 for all of the considered shapes. The quantity (〈EMC〉 - 〈EAB〉)/|EMC|〉 (also included in Table 2) expresses the relative improvement of the AB method with respect to the MC method.
Table 2. Average lowest-energy configuration found for different primitive agents with AB and MC methods.
| Shape | 〈EAB〉 | 〈EMC〉 | 〈EMC〉 – 〈EAB〉)/|〈EMC〉| |
|---|---|---|---|
| 1 | –515 ± 4 | –428 ± 6 | 0.204 ± 0.018 |
| 2 | –800 ± 14 | –749 ± 7 | 0.068 ± 0.021 |
| 3 | –1,051 ± 18 | –900 ± 24 | 0.168 ± 0.034 |
| 4 | –607 ± 7 | –495 ± 7 | 0.227 ± 0.019 |
| 5 | –829 ± 19 | –724 ± 10 | 0.145 ± 0.030 |
| 6 | –1,029 ± 21 | –929 ± 11 | 0.108 ± 0.026 |
| 7 | –1,080 ± 20 | –935 ± 9 | 0.155 ± 0.023 |
| 8 | –1,156 ± 22 | –972 ± 10 | 0.189 ± 0.025 |
| 9 | –886 ± 13 | –690 ± 11 | 0.283 ± 0.024 |
| 10 | –767 ± 17 | –719 ± 15 | 0.066 ± 0.032 |
| 11 | –595 ± 5 | –450 ± 5 | 0.322 ± 0.016 |
| 12 | –779 ± 18 | –719 ± 11 | 0.083 ± 0.029 |
| 13 | –974 ± 16 | –854 ± 11 | 0.141 ± 0.023 |
| 14 | –1,225 ± 13 | –981 ± 14 | 0.248 ± 0.020 |
| 15 | –827 ± 12 | –738 ± 12 | 0.120 ± 0.024 |
| 16 | –551 ± 7 | –462 ± 6 | 0.194 ± 0.020 |
| 17 | –809 ± 17 | –716 ± 11 | 0.130 ± 0.028 |
| 18 | –841 ± 10 | –814 ± 13 | 0.033 ± 0.021 |
| 19 | –1,118 ± 20 | –1,002 ± 8 | 0.115 ± 0.022 |
| 20 | –819 ± 19 | –722 ± 16 | 0.134 ± 0.034 |
| 21 | –790 ± 7 | –603 ± 8 | 0.309 ± 0.018 |
| 22 | –822 ± 20 | –741 ± 14 | 0.109 ± 0.033 |
| 23 | –1,446 ± 26 | –1,132 ± 20 | 0.278 ± 0.029 |
| 24 | –1,589 ± 25 | –1,275 ± 16 | 0.247 ± 0.024 |
| 25 | –1,039 ± 9 | –793 ± 9 | 0.310 ± 0.016 |
The numbering scheme for primitive agents is as shown in Fig. 1.
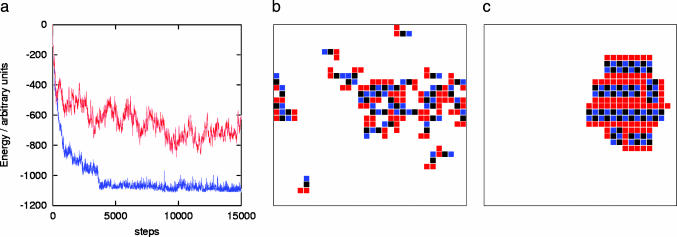
The AB method always outperformed the MC, and in more than one-half of the considered shapes, the structure found by the AB method has a total energy >15% lower than the corresponding MC. In these cases, the inspection of the final structures reveals that the AB simulation produced a more ordered and uniform structure. Fig. 4a, for example, shows the energy decrease during the simulation, comparing the Metropolis method and the AB simulation for one of the considered shapes. Fig. 4b shows the system configuration after 15,000 MC steps, and Fig. 4c shows the configuration after the same number of steps of the AB calculation. The improvement introduced by the AB simulation is striking in this and other cases.
Fig. 4.
Comparison of MC and AB simulations. (a) The energy decrease during 15,000 simulation steps for shape no. 9 (see Fig. 1). Red, MC simulation; blue, AB simulation. (b and c) The final configurations for MC and AB simulations, respectively.
One reason for the poorer performance of the MC algorithm is the inadequacy of the set of attempted moves. After the formation of smaller clusters of molecules, single-agent moves are almost always rejected. Formation of large clusters is entropically disfavored, a fact that is reflected in small proposal probabilities for aggregation beyond small clusters in Metropolis MC. On the other hand, escape from a cluster is energetically disfavored, resulting in small acceptance probabilities in Metropolis MC (26). A solution would be the definition of more complex moves, but those can be very complex and are ideally treated on a case-by-case basis. On the other hand, AB modeling does not depend on the particular molecule considered. We do not investigate here the relative importance of the learning aspect of the algorithm versus the improved set of moves.
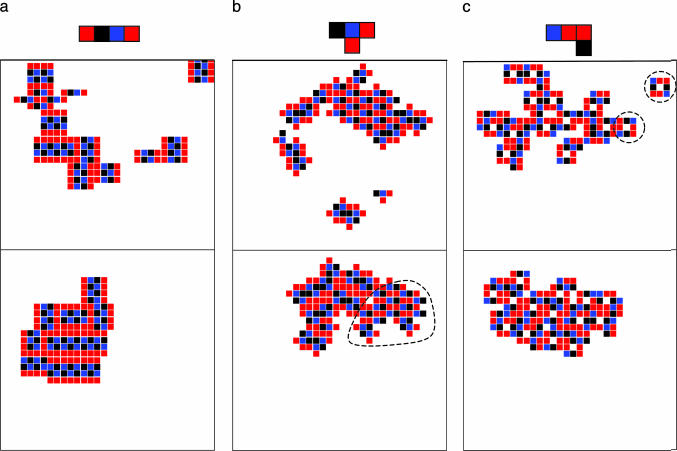
Beyond the identification of the most stable molecular arrangement, these simulations can be helpful for the study of several other aspects of the self-assembly process. Fig. 5a displays a snapshot of a simulation showing how the ordered regions are separated by grain boundaries. At the end of the simulation, the agents tend to coincide with the grains, and the simulation explores the grain–grain conformation and merging. In a few cases, we observed the coexistence of more than one ordered phase (Fig. 5b), suggesting that this technique might be useful for localizing nonequivalent minima. Importantly, the algorithm is very efficient in identifying the correct substructure that is responsible for the crystal growing process (see the example in Fig. 5c), demonstrating that this approach might also provide useful information on the mechanism of growth.
Fig. 5.
Several snapshots illustrating the formation of grain boundaries (a), the coexistence of different phases (minority phase circled) (b), and the identification of the building block for the growing process (circled) (c). (Upper) Some intermediate stage of the simulations. (Lower) The last snapshots of the simulation.
It should be noted that the algorithm in its present form could not lead to the most stable aggregate if the subunits that form the latter are not the most stable clusters. For the model systems considered here, characterized by short-range interactions, this event is very unlikely, but when the interaction range is very long (e.g., for salts or metals), this possibility should be taken into account. The possibility of forming the wrong building blocks can be systematically reduced by increasing the population size and performing an “equilibration,” i.e., a number of simulation steps where the merging is suppressed.
Conclusions
We have considered the application of agent-based modeling on the problem of molecular self-assembly. We have shown that it is possible to devise a combination of stochastic, deterministic, and adaptive rules that lead a disordered system to organize itself in an ordered low-energy configuration. We considered the problem of packing rigid shapes verifying that this approach can efficiently predict the structure of the self-organized structure. A key feature is that the algorithm, through the self-definition of the agents, defines the moves to be attempted and updates them as the simulation proceeds.
An important remaining question is the following: Is it possible to adapt the current algorithm so that the final distribution simulates the distribution of some thermodynamical ensemble? The preliminary answer is composite. There are two novelties in the presented algorithm: the definition of group moves, and the learning processes that affect the grouping. It is probably possible to bring the grouping component into the orthodoxy of the MC method (as done for example in ref. 33, employing data-augmentation techniques). Any learning component cannot be introduced into a purely stochastic method. Several researchers, however, are working on adaptive MC methods (34), i.e., stochastic methods that improve the quality of the attempted moves as the simulation converges to the limit distribution.
The concepts of intelligent merging and splitting can be used to extend simulation schemes different from MC and to perform off-lattice simulations of realistic systems. Many molecular modeling packages implement rigid-body motions, i.e., the user decides at the beginning of the simulation what portions of the system are rigid (i.e., the solvent molecules or some portions of a protein) and the dynamics/optimization/MC proceed treating that portions of the system as rigid bodies (35–37). One can use agent-based rules to define “on the fly” what portions of the system are rigid, changing the definition continuously as the simulation proceeds.
Acknowledgments
We are grateful for the support of the Department of Defense–Multidisciplinary University Research Initiative program and the National Nanotechnology Institute program of the National Science Foundation.
Author contributions: A.T., V.W., and M.A.R. designed research; A.T. and V.W. performed research; A.T., V.W., and M.A.R. analyzed data; and A.T., V.W., and M.A.R. wrote the paper.
Abbreviation: MC, Monte Carlo.
Footnotes
Alternatively, an agent can be split if its energy does not satisfy the less strict criterion 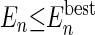 (i.e., the energy is compared only with the best energy of the agents of the same size).
(i.e., the energy is compared only with the best energy of the agents of the same size).
References
- 1.Pinpinelli, A. & Villain, J. (1999) Physics of Crystal Growth (Cambridge Univ. Press, Cambridge, U.K.).
- 2.Camazine, S., Deneubourg, J.-L., Franks, N. R., Theraulaz, G. & Bonabeau, E. (2003) Self-Organization in Biological Systems (Princeton Univ. Press, Princeton).
- 3.Krugman, P. R. (1996) The Self-Organizing Economy (Blackwell, Cambridge, MA).
- 4.Albert, R. & Barabasi, A.-L. (2002) Rev. Mod. Phys. 74, 47-97. [Google Scholar]
- 5.Bonabeau, E., Dorigo, M. & Theraulaz, G. (1999) Swarm Intelligence: From Natural to Artificial Systems (Oxford Univ. Press, New York).
- 6.Wooldridge, M. (2002) An Introduction to MultiAgent Systems (Wiley, Chichester, U.K.).
- 7.Weiss, G., ed. (2000) Multiagent Systems: A Modern Approach to Distributed Artificial Intelligence (MIT Press, Cambridge, MA).
- 8.Davidson, P. (2001) Lect. Notes Artif. Int. 1979, 97-107. [Google Scholar]
- 9.Bonabeau, E. (2002) Proc. Natl. Acad. Sci. USA 99, 7280-7287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Danielson, P. (2002) Proc. Natl. Acad. Sci. USA 99, 7237-7242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Holland, J. H. (1995) Hidden Order: How Adaptation Builds Complexity (Addison–Wesley, Reading, MA).
- 12.Russel, S. J. & Norvig, P. (2003) Artificial Intelligence: A Modern Approach (Prentice–Hall, Upper Saddle River, NJ).
- 13.Axelrod, R. (1997) The Complexity of Cooperation (Princeton Univ. Press, Princeton).
- 14.Epstein, E. M. (2002) Proc. Natl. Acad. Sci. USA 99, 7243-7250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Helbing, D., Farkas, I. & Vicsek, T. (2000) Nature 407, 487-490. [DOI] [PubMed] [Google Scholar]
- 16.Chopard, B. & Droz, M. (1998) Cellular Automata Modeling of Physical Systems (Cambridge Univ. Press, Cambridge, U.K.).
- 17.Frisch, U., Hasslacher, B. & Pomeau, Y. (1986) Phys. Rev. Lett. 56, 1505-1508. [DOI] [PubMed] [Google Scholar]
- 18.Wolfram, S. (1986) J. Stat. Phys. 45, 471-526. [Google Scholar]
- 19.Kadanoff, L. P., McNamara, G. R. & Zanetti, G. (1989) Phys. Rev. A 40, 4527-4541. [DOI] [PubMed] [Google Scholar]
- 20.Taleb, A., Chausse, A., Dymitrowska, M., Stafiej, J. & Badiali, J. P. (2004) J. Phys. Chem. B 108, 952-958. [Google Scholar]
- 21.Kier, L. B., Cheng, C. K. & Testa, B. (2003) J. Chem. Inf. Comput. Sci. 43, 255-258. [DOI] [PubMed] [Google Scholar]
- 22.Mao, L. Y., Harris, H. H. & Stine, K. J. (2002) J. Chem. Inf. Comput. Sci. 42, 1179-1184. [DOI] [PubMed] [Google Scholar]
- 23.Kier, L. B., Cheng, C. K. & Testa, B. (1999) J. Chem. Inf. Comput. Sci. 39, 326-332. [Google Scholar]
- 24.Tsangaris, D. M. & de Pablo, J. J. (1994) J. Chem. Phys. 101, 1477-1489. [Google Scholar]
- 25.Busch, N. A., Wertheim, M. S. & Yarmush, M. L. (1996) J. Chem. Phys. 104, 3962-3975. [Google Scholar]
- 26.Chen, B. & Siepmann, J. I. (2000) J. Phys. Chem. B 104, 8725-8734. [Google Scholar]
- 27.Wierzchowski, S. & Kofke, D. A. (2001) J. Chem. Phys. 114, 8752-8762. [Google Scholar]
- 28.Wu, D., Chandler, D. & Smit, B. (1992) J. Phys. Chem. 96, 4077-4083. [Google Scholar]
- 29.Winfree, E. (2000) J. Biomol. Struct. Dyn. 11, 263-270. [DOI] [PubMed] [Google Scholar]
- 30.Mao, C. D., LaBean, T. H., Reif, J. H. & Seeman, N. C. (2000) Nature 407, 493-496. [DOI] [PubMed] [Google Scholar]
- 31.Klavins, E., Ghrist, R. & Lipsky, D. (2003) Graph Grammars for Self Assembling Robotic Systems, http://sveiks.ee.washington.edu/papers/icra04-sa.pdf.
- 32.Seeman, N. C. (2003) Nature 421, 427-431. [DOI] [PubMed] [Google Scholar]
- 33.Troisi, A., Wong, V. & Ratner, M., J. Chem. Phys., in press.
- 34.Gilks, W. R., Roberts, R. O. & George, E. I. (1994) The Statistician 43, 179-189. [Google Scholar]
- 35.Ciccotti, G., Ferrario, M. & Ryckaert, J.-P. (1982) Mol. Phys. 47, 1253-1264. [Google Scholar]
- 36.Ikeguchi, M. (2004) J. Comput. Chem. 25, 529-541. [DOI] [PubMed] [Google Scholar]
- 37.Shinoda, W. & Mikami, M. (2003) J. Comput. Chem. 24, 920-930. [DOI] [PubMed] [Google Scholar]