Computational psychiatry as a bridge from neuroscience to clinical applications

Abstract

Translating advances in neuroscience into benefits for patients with mental illness presents enormous challenges because it involves both the most complex organ, the brain, and its interaction with a similarly complex environment. Dealing with such complexities demands powerful techniques. Computational psychiatry combines multiple levels and types of computation with multiple types of data in an effort to improve understanding, prediction and treatment of mental illness. Computational psychiatry, broadly defined, encompasses two complementary approaches: data driven and theory driven. Data-driven approaches apply machine-learning methods to high-dimensional data to improve classification of disease, predict treatment outcomes or improve treatment selection. These approaches are generally agnostic as to the underlying mechanisms. Theory-driven approaches, in contrast, use models that instantiate prior knowledge of, or explicit hypotheses about, such mechanisms, possibly at multiple levels of analysis and abstraction. We review recent advances in both approaches, with an emphasis on clinical applications, and highlight the utility of combining them.

The translation of advances in neuroscience into concrete improvements for patients suffering from mental illness has been slow. Part of the problem is the complexity of disease classification and outcome measurement in psychiatry¹. A broader reason, however, is the complexity of the problem: mental health depends not only on the function of the brain, the most complex of organs, but also on how that function relates to, influences, and is influenced by the individual’s environmental and experiential challenges. Understanding mental health, and its disruption, therefore relies on linking multiple interacting levels, from molecules to cells, circuits, cognition, behavior, and the physical and social environment.

One of the difficulties is that the mapping between these levels is not one-to-one. The same biological disturbance can affect several seemingly unrelated psychological functions and, conversely, different biological dysfunctions can produce similar psychological and even neural-circuit disturbances^2–4. Disturbances can arise independently in some levels without dysfunction in other levels. Low mood, for example, may affect social function independently of its particular biological cause. Mappings between health and biology also vary with external circumstances⁵. For example, neurobiologically determined emotion-regulation abilities may suffice for some environments, but produce mood disorders in others. The current age of big data, with the ability to acquire and manipulate extremely high-dimensional, multimodal data sets, including clinical, genetic, epigenetic, cognitive, neuroimaging and other data types^6,7, holds great promise to uncover these complex relations, but poses formidable data-analytic challenges. Here we argue that these theoretical and data-analytic challenges are insurmountable without powerful computational tools and the conceptual frameworks they provide. Computational psychiatry, conceived broadly, is therefore critical to the future of psychiatry and will likely have a central role in the rational development of treatments, nosologies and preventive strategies.

Computational psychiatry encompasses two approaches⁸: data-driven, theoretically agnostic data-analysis methods from machine learning (ML) broadly construed (including, but extending, standard statistical methods), and theory-driven models that mathematically specify mechanistically interpretable relations between variables (often including both observable variables and postulated, theoretically meaningful hidden variables). We review advances in both approaches, with an emphasis on clinical applications, and discuss how they can be combined. Further aspects of computational psychiatry have been reviewed in other general^9–12 and more specific reviews^8,13–16.

The blessing and curse of dimensionality

Very few individual signs, let alone symptoms, are sufficiently specific to identify underlying diseases. Depressed mood, for example, is insufficient for the diagnosis of major depressive disorder. The intuition behind classification schemes such as DSM¹⁷ and ICD¹⁸ is that the presence of additional features, such as anhedonia, fatigue, overeating and suicidal thoughts, increases specificity by identifying a group of people with a relatively worse outcome that requires intervention, and thereby sanctions the labels disorder or disease. This description proceeds in the absence of any understanding of the underlying biological (or environmental) pathology, and without any guarantee about an identifiable relationship between symptom clusters and biology. The hope is that biomarkers might provide additional information and either augment (stratify¹) or even (partially) replace¹⁹ symptoms.

Improving classification through the addition of features is in fact an important concept in ML, with blessings and curses. The ‘kernel trick’ consists of implicitly adding a large or infinite number of features²⁰. The blessing of dimensionality is that in this infinite-dimensional space any finite-sized data set can always be classified perfectly using a simple linear classifier (Fig. 1a–c). The resulting classification in the original space can be complex and nonlinear, particularly if the included (implicit) features are nonlinear or involve interactions or correlations between original data dimensions or features. Practically, this blessing can also be a curse, as it is always possible to perfectly distinguish n patients from m controls by using n + m − 1 features (Fig. 1d–g). As this is true for any outcome of interest and any features, it will perform well even on random noise (Fig. 1e–g) and overfit (Box 1), meaning that the results will generalize poorly to new data (for example, future subjects). The danger of overfitting decreases as the number of subjects, not number of measurements, increases, motivating larger studies and consortia pooling their efforts^6,7,21.

Figure 1.

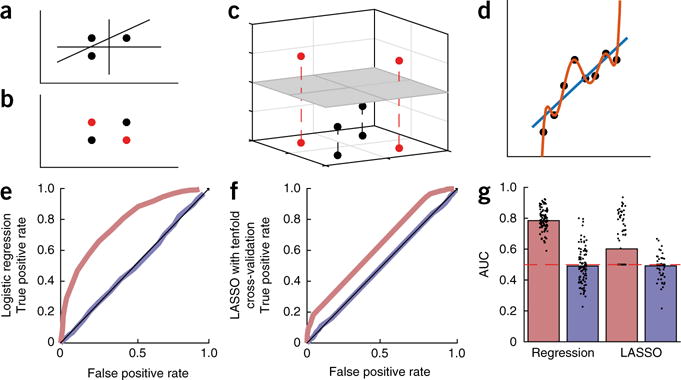
The blessing and curse of dimensionality. In rich data sets in psychiatry, the number of measured variables d per subject can substantially exceed the number of subjects. (a) When this occurs, subjects can always be separated linearly: up to d + 1 subjects can always be separated linearly into two classes if the data span a d-dimensional space. Three subjects can always be separated into two groups using a combination of two features. (b) For d + 2 (or more) subjects, linear separation is not always possible. (The subjects indicated by black points are not linearly separable from those indicated by red points.) (c) Such data can, however, be separated linearly if projected into a higher-dimensional space. Here, a third dimension was added to the two-dimensional data in b by calculating the absolute distance from the line through the black points, thereby making the two classes linearly separable, as shown by the gray two-dimensional plane. (d) A similar fact can be illustrated in regression: a d-order polynomial can always fit d + 1 points perfectly (red line), but it makes extreme predictions outside the range of observations and is extremely sensitive to noise, overfitting the training data. (e) Even when the features and classes are just random noise, performing regression in a high-dimensional space leads to misleadingly high performance¹⁴². The panel shows receiver operating characteristic (ROC)—the false positive against the true positive rate—for logistic regression applied to such random data. The red curve shows that logistic regression performs misleadingly well on the training data, with a high area under the ROC curve (AUC) (regression training data, g). Obviously, however, this is overfitting, as the data are random. Indeed, applying the resulting regression coefficients to unseen validation data not included in the training set, the predictions are random as they should be (blue line; regression validation data, g). (f) Using LASSO, a form of cross-validated regularized regression (Box 1), partially prevents overfitting (red line; LASSO training data, g). However, because the regularization parameter is fitted to the training data, even LASSO does not fully prevent overfitting: it is only when the LASSO parameters are tested on the validation data set that performance is correctly revealed to be at chance level (blue line; LASSO validation data, g).

Box 1. Dealing with overfitting.

Unsupervised dimensionality reduction

Overfitting tends to occur when the dimensionality of the data set (which is usually proportional to the number of variables) is excessively high relative to the size of the training set. A first approach to overfitting therefore focuses on reducing the number of variables: dimensionality reduction. This reduction can be done as a preprocessing step: variables that are highly related provide little independent information, and such redundancies can be identified and removed using general-purpose unsupervised methods, such as principal or independent component analysis, factor analysis or k-nearest neighbor143,144, or approaches specific to the data at hand145. Other ML techniques can subsequently be applied to the reduced data (Fig. 2).

Regularization

Performing dimensionality reduction as a preprocessing step has an important limitation: it is not tailored to the specific problem being solved (for example, prediction of a given outcome). Another approach is therefore to limit the number of variables selected by using regularization—for instance, by including a penalization term for too many predictors—in the prediction and classification algorithms themselves (Fig. 2). This approach is inherent in support vector machines, LASSO, elastic nets, stochastic discrimination approaches such as random forests146 and other variable-selection methods in multiple regression.

Bayesian model evidence

Bayesian approaches automatically penalize excessively complex models and are therefore an alternative to regularization. These approaches evaluate how well a model fits the data by using the model evidence, which averages the likelihood over all possible parameter settings, instead of using just the maximum-likelihood parameter set. The model evidence inherently penalizes excessively complex models; the intuition is that even though for the maximum-likelihood parameter set these models may have a very high likelihood (as a result of overfitting), they also allow a very wide range of other parameter settings that would produce very low likelihood. Appropriately complex models fare better, as they predict the data with higher probability across parameter settings147. For example, in Figure 1d, data was generated from a straight line with some noise added. Even though the model including higher order polynomials fits the data perfectly with a specific setting of parameters, the data would have very low likelihood under other parameter settings, making the model evidence low. A linear model will have somewhat lower likelihood for the maximum-likelihood parameter set (as it cannot overfit), but its model evidence will be larger because the likelihood of the data integrated across all parameter settings will be higher. The model evidence will therefore select the model with the appropriate complexity, preventing overfitting. The downsides of the Bayesian approach are that it does not provide absolute, but only relative, measures of model quality and that it is computationally demanding.

Cross-validation

The fundamental problem with overfitting is that it leads to poor predictions on new data. Cross-validation is a technique that estimates and minimizes this problem by splitting the data set into two subsets: a training data set, which is used to estimate the prediction parameters, and a validation data set, which is used to test how well those parameters predict ‘new’ data (Fig. 1). This procedure can provide an unbiased estimate of the expected error on new data148, but the variance of the estimator depends on the size of the data set. Splitting the data set into two subsets decreases the size of the training data set, which leads to loss of valuable examples that could be used to improve prediction. Note that cross-validation (for example, leave-one-out cross-validation) is often used in the training data to optimize aspects of the algorithm, and then the final held-out part of the data is referred to as validation set. It is critical to keep these apart.

Three broad approaches exist to cope with the curse of dimensionality. First, unsupervised methods can be used to perform dimensionality reduction before classification or regression (Fig. 2 and Box 1). Second, techniques such as regularization, Bayesian model selection and cross-validation can be used to select the most informative features for classification or regression²⁰, thereby integrating dimensionality reduction with the predictive task of interest (Fig. 2 and Box 1). Both of these approaches are entirely data driven (although Bayesian approaches allow the incorporation of prior knowledge). A third, radically different approach uses theory-driven models to extract theoretically meaningful parameters based on models of the underlying processes. These parameters can then be used as efficient, low-dimensional representations of the very high-dimensional data to which ML techniques for classification or regression can subsequently be applied (Fig. 2). For example, models of a variety of time-varying processes, such as learning²², multi-neuron recordings²³ and BOLD time series²⁴, can collapse long and seemingly complex time series into a few parameters characterizing the underlying dynamics. To the extent that the theory-driven models accurately portray or summarize the processes generating the data, they may improve the performance of ML algorithms beyond approaches that do not consider such generative mechanisms^13,24,25.

Figure 2.

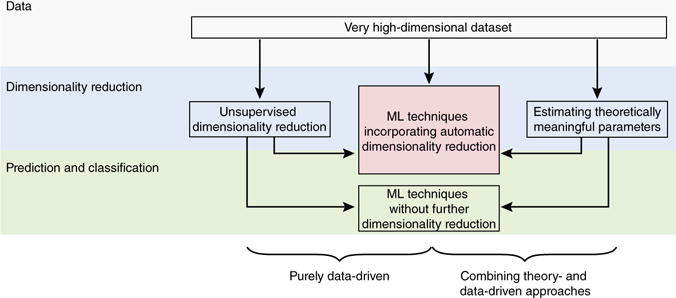
Exploiting and coping with high dimensionality in psychiatric data sets. Purely data-driven approaches (left and middle branches) and combinations of theory- and data-driven approaches (right branch) can be used to analyze large data sets to arrive at clinically useful applications. Dimensionality reduction is a key step to avoid overfitting. It can be performed as a preprocessing step using unsupervised methods before application of other ML techniques with or without further dimensionality reduction (left branch; Box 1); using ML techniques that automatically limit the number of variables for prediction; using regularization or Bayesian model selection (middle branch; Box 1); or using theory-driven models that in essence project the original high-dimensional data into a low-dimensional space of theoretically meaningful parameters, which can then be fed into ML algorithms that may or not further reduce dimensionality (right branch).

Data-driven approaches

ML approaches have been applied to several clinically relevant problems, including automatic diagnosis, prediction of treatment outcomes and longitudinal disease course, and treatment selection. We provide an overview of the central methodological features of these approaches and highlight some illustrative examples. Other recent reviews provide complementary information beyond the scope of this review^26,27.

Diagnostic classification

Most symptoms in the compendia of psychiatric classification are shared between two or more disorders²⁸. Current classification schemes attempt to improve diagnosis by requiring the presence of multiple symptoms^17,18. Unfortunately, individuals often still satisfy criteria for multiple disorders (co-morbidity²⁹) or do not fit any category clearly³⁰, the categorical thresholds do not separate clusters differing in illness burden³¹, and diagnostic reliability for some disorders is still problematic³².

A now substantial body of work has applied ML to automatically classify patients versus controls^26,27. The state of the art for using MRI data to distinguish schizophrenia from healthy controls was recently examined in a competition³³. The best entry reached an area under the curve (AUC) for classification of validation data of 0.89 (ref. 34), and a combination of the top approaches reached 0.93. The first three entries achieved similar performance despite using different techniques³⁵. There is nevertheless scope for further improvement through the integration of more modalities³⁶, or from algorithmic advances, for example, with deep belief networks³⁷ or other methods³⁸ that outperform more standard approaches on a variety of ML benchmarks^35,39,40. Similar accuracies have been reported for other disorders²⁷, and these results have been extended in several ways—for example, probabilistic classification approaches yield an estimate of how certain the classification is^34,35, and multi-class techniques deal with the clinically more relevant problem of distinguishing between diagnostic groups^27,41.

The fact that ML analyses of neuroimaging data can distinguish cases and controls suggests that, at least in these cases, the symptom clusters do map onto specific neurobiological substrates, despite diagnostic caveats and likely heterogeneity in disorders³². However, one cannot always identify the relevant neural substrates simply by inspecting the features used by the classifiers: these features are typically complex, counterintuitive and not meaningful in isolation, and cannot usually be collated across different ML techniques⁴². These approaches also have several limitations that would need to be overcome to make them practically useful. First, the comparison of cases to healthy controls might treat severity in a flawed manner^34,43: although severity exacerbates comorbidity and hence blurs diagnostic boundaries, it is also often used as a quantitative marker for degree of caseness, making an understanding of how to deal with severity and comorbidity critical⁴⁴. Second, existing binary or multi-class classification approaches usually treat comorbidity incorrectly by assuming that different diagnoses are mutually exclusive; addressing this limitation may require statistical schemes that allow for multiple labels for each individual (for example, see ref. 45) that are much more demanding computationally. Third, the extent to which these algorithms, which are typically trained on unambiguous cases, yield useful information for ambiguous cases, which are clinically more relevant, remains to be explored. Finally, these approaches may be fundamentally limited because they reify⁴⁶ symptom-based classification, although they could feasibly be used to refine them by subdividing existing classes¹.

Prediction of treatment response

The current limitations in nosology have led to a shift toward predicting inherently more valid and immediately useful variables such as relapse in alcoholism, suicide, longitudinal conversion in at-risk groups^47–52 and treatment response. The latter addresses a pressing need in psychiatry.

In depression, for example, although up to three quarters of patients will eventually respond to an antidepressant, two thirds require multiple treatment trials before responding⁵³. Several quantitative electroencephalography (qEEG) markers have each been found to predict pharmacological response in depression^54,55. However, a recent large-scale study, the International Study to Predict Optimized Treatment in Depression (ISPOT-D⁶), tempered hopes about several of these individual qEEG predictors^56–58. Some combinations of qEEG variables, such as cordance⁵⁹ or the antidepressant treatment response index⁶⁰, outperform individual predictors. The combination of qEEG features in a fully data-driven way promises better results: combined features yielded better prediction of treatment response (81% specificity, 95% sensitivity) than relying on any individual predictor (60% specificity, 86% sensitivity)⁶¹, although this sample size was too small to include a proper separate validation sample (Fig. 1).

Results from other modalities similarly highlight the usefulness of applying ML techniques for prediction using multiple features. For example, a reanalysis of data from STAR*D and COMED, two large trials in depression, suggested that a combination of supervised dimensionality reduction and multivariate classifiers yielded a cross-validated prediction of remission with an area under the curve (AUC; Fig. 1) of 0.66. The number needed to treat (NNT) was 14, meaning that applying the algorithm to 14 patients should result in one additional remission⁶². Similarly, although univariate cognitive markers acquired in ISPOT-D did not distinguish remitters from non-remitters^63,64, the multivariate pattern of task performance did predict response to the selective serotonin reuptake inhibitor (SSRI) escitalopram in a subgroup of patients⁶⁴. Multivariate structural MRI analyses also improved the identification of patients unlikely to respond, beyond the level achieved using individual markers⁶⁵. As these examples illustrate, ML techniques can lead to improvements in treatment-response prediction. In addition to these combinations of features in modalities, it seems likely that a combination of features across multiple modalities would lead to even further performance improvements.

Treatment selection

The most relevant question for practitioners is not necessarily whether a given treatment will work, but rather which of several possible treatments (or treatment combinations in the age of polypharmacy) will work best for a given patient. Theoretically, multiclass classifications can be cast in terms of multiple binary classifications⁶⁶. Practically, however, it presents additional challenges: it may not be feasible to perform different tests (for example, neuroimaging, genetics, etc.) for each treatment option, so, ideally, the same set of tests should be used to distinguish responses to multiple treatments. Furthermore, if different tests, or even different ML algorithms for the same tests, are used for different treatments, these predictions may not be directly comparable and hence not facilitate choice between treatments.

Nevertheless, studies have started to address this question using data from trials in which subjects were randomized to multiple treatment arms, by looking for interactions between treatments and relevant variables in multiple regression. This has shown that being married and employed and having had more life events and more failed antidepressant trials predicted relatively better response to cognitive-behavioral therapy (CBT) over antidepressants, whereas comorbid personality disorders favored response to antidepressants over CBT⁶⁷. The improvement that could be expected through allocating each patient to the ideal treatment was a further reduction of 3.6 points on the Hamilton Rating Scale for Depression beyond the reduction obtainable using standard treatment selection, a clinically significant effect⁶⁸. Similar approaches to the ISPOT-D data yielded predictions for remission with escitalopram in individuals with poor cognitive function with a NNT of 3.8, meaning that assigning patients in this group to escitalopram on the basis of their cognitive performance pattern led to remission in one additional patient for every four evaluated⁶⁴. One study⁶³ was able to make individual response predictions that were strong enough to guide treatment choice in the majority of patients, resulting in NNTs of 2–5.

Steps toward using ML applied to neuroimaging data for treatment selection are being made. One group⁶⁹ used a univariate marker, amygdala responses to subliminal facial emotion stimuli, to predict overall responses to SSRIs and serotonin-noradrenaline reuptake inhibitors (SNRI) and differential responses to SNRIs versus SSRIs. Another group showed that increased insula activity related to better response to CBT, but worse response to escitalopram. The effect size was large, although predictive power was not examined⁷⁰. As in the case of treatment-response prediction, it seems likely that treatment-selection approaches will also benefit from including multiple variables from various modalities.

To the best of our knowledge, only one study has thus far attempted to validate the clinical utility of an automatic treatment-selection algorithm in a randomized clinical trial⁷¹, with tantalizingly promising results. This study used a proprietary algorithm constructed from a reference database of EEGs from over 1,800 subjects with within-subject information about response to multiple treatment attempts (about 17,000 treatment attempts in total). The algorithm extracts 74 features from the EEG of each patient to predict the most likely successful medication for depression. Notably, the automatic algorithm significantly outperformed clinical selection (Fig. 3). One caveat is that the medications prescribed in the two arms differed substantially, and the improvement in the automatic-selection arm might not have arisen purely through better targeting of the medications, but rather through using more monoamine oxidase inhibitors and stimulants (although stimulants have generally fared poorly in the treatment of depression⁷²).

Figure 3.

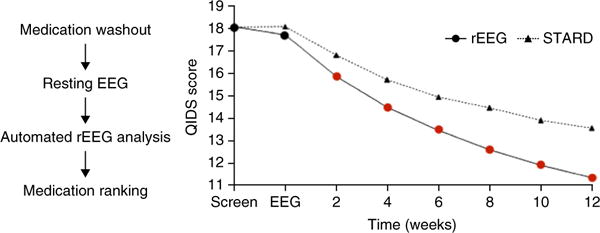
Using EEG measures for treatment selection in depression improves treatment response. Left, reference EEG (rEEG) procedure. After withdrawing all medications, a rEEG was performed. This was submitted for online automated analysis involving 74 biomarkers and a comparison to a large reference database of EEG measures linked to longitudinal treatment outcomes. Finally, a medication ranking was returned. Right, in a 12-site trial, patients were randomized to treatment selection via an optimized clinical protocol (based on STAR*D) or rEEG. The rEEG-based selection led to improved treatment response relative to the optimized clinical protocol after 2 weeks (red dots), and this effect grew stronger over 12 weeks. These results suggest that biological measures can improve treatment selection in depression. Adapted with permission from ref. 71.

Understanding relations between symptoms

Limitations of current diagnostic schemes have been mentioned above and are discussed elsewhere^1,32,73. An alternative framework that provides insight into patterns of co-occurrence and sequential expression of symptoms comes from descriptions of symptoms as networks, where, rather than being considered as expressions of an underlying latent variable (a given disorder), symptoms are viewed as entities in their own right with direct relationships to other symptoms. Sleep disturbances, for example, typically cause fatigue; their co-occurrence might therefore be a result of their direct causal interaction rather than, say, underlying depression⁷⁴. Indeed, computational modeling of the symptoms that appear earliest before, and remain longest after, depressive episodes—hopelessness and poor self-esteem⁷⁵—suggests that they might drive features such as anhedonia and lack of motivation⁷⁶.

Network analyses of the descriptions in the DSM itself have shown that the symptom overlap across DSM diagnoses by itself recapitulates many key features of empirically observed comorbidity patterns and reveal one dominant cluster with a small-world topology²⁸ (Fig. 4): a few symptoms strongly mediate between other symptoms (having high betweenness and centrality) with short ‘paths’ from one symptom to another. Strong coherence between many symptoms has been argued to reflect a general psychopathology factor p, capturing concurrent and sequential comorbidity patterns in a manner akin to how the factor g of general intelligence captures covariance between multiple cognitive abilities⁴⁴.

Figure 4.

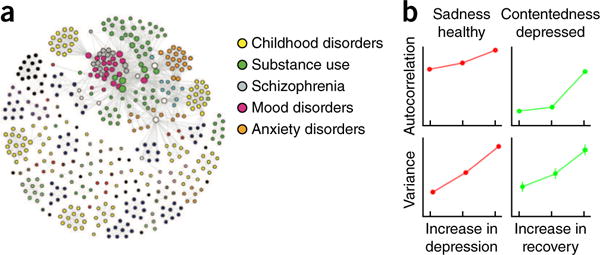
Networks of symptoms. (a) Network of symptoms in DSM-IV. Two symptoms have a link if they belong to a common diagnostic category. There is a large, strongly connected cluster containing 48% of the symptoms. Overall, the network has small-world characteristics, with the average path length between two symptoms being only 2.6. Adapted with permission from ref. 28. (b) Autocorrelations and variance, two signs of critical slowing down, increase before a phase transition in dynamic networks. Prior to a transition from a healthy state to depression, negative emotions such as sadness show increasing variance and temporal autocorrelation. Prior to a transition from depression to a remitted state, this is observed in positive emotions, such as contentedness. Adapted with permission from ref. 81.

Dynamic network analyses that examined the temporal occurrence patterns of symptoms over days (assessed, for example, using experience-sampling methods⁷⁷) revealed frequent loops of mutually reinforcing symptoms that could potentially stabilize each other^78–80. Indeed, before transitions between non-depressed and depressed states, or vice-versa, symptoms show increased variance and increased autocorrelations⁸¹. These are signs of so-called critical slowing down, which are indicative of a transition from a stable state to another stable state in dynamical systems. Indeed, residual subthreshold symptom variation is known to be a risk factor for relapse and may relate to the variance identified here^82,83.

Dispensing entirely with latent variables is questionable in the long run, as symptoms do reflect multiple underlying variables. Network analyses could be integrated with other levels of analyses (for example, genetics, neural-circuit function, etc.) using graphical models²⁰. These provide a probabilistic generalization of network descriptions that can include hidden as well as observed variables and can incorporate complex relationships between variables at different levels, potentially forming a bridge to more mechanistic models.

Theory-driven approaches

We now turn to theory-driven models. Unlike data-driven approaches, these models encapsulate a theoretical, often mechanistic, understanding of the phenomena at hand. Their descriptions at theoretically independent⁸⁴, but practically linked, levels provide powerful tools for integration. Models can be classified in many different ways; here, we will distinguish between synthetic, algorithmic and optimal models.

Synthetic models, exemplified by biophysically detailed models, may be the most intuitive ‘model building’ exercises. They are informed by data from multiple sources relevant to the particular system(s) of interest (for example, a neural system, its modulation by specific neurotransmitters, etc.) and explore the interaction between these factors through simulations and mathematical analysis. These models often bridge different levels of analysis and can be used deductively to infer the likely consequences of known or suspected causes (for example, what effect a change in the concentration of a given neurotransmitter will have on neural-circuit dynamics or behavior) or abductively to try to infer the likely causes for a known consequence (for example, what type of disturbance in the concentration of certain neurotransmitters could give rise to observed neural-circuit or behavioral disturbances)⁹. These models can have many different parameters that are constrained by a broad scientific literature. They are validated by qualitatively examining their predictions, which may include multiple levels of analysis (for example, neural activity and behavior).

Algorithmic models, exemplified here by reinforcement learning (RL) models, are usually simpler. Validation typically occurs through quantitative statistical means (for example, model-comparison and model-selection techniques) that assess whether the data warrants the features and complexities embodied in each model (for example, see ref. 85). They contain a comparatively small number of parameters, whose values can be estimated for individual subjects by fitting the models to the data. These parameters, which represent theoretically meaningful constructs, can then be compared across groups, correlated with symptom severity, etc⁹. These models are particularly useful as tools for measuring hidden variables and processes that are difficult or impossible to measure directly.

Optimal (Bayesian) models attempt to link observed behavior to the Bayes-optimal solution of a problem. This is particularly revealing when that optimum is unique, as it can be used to show whether subjects can solve a task and whether they have done so in a particular experimental instance. Bayesian decision theory broadly provides three routes to psychopathology⁸⁶: solving the wrong problem correctly (for example, consistently prioritizing alcohol intake over health), solving the correct problem wrongly (for example, using alcohol to ‘treat’ emotional problems), and solving the correct problem correctly, but in an unfortunate environment or after unfortunate prior experiences (for example, having persecutive worries after persecutory experiences).

The distinction between these model types can be blurry. For example, a biophysically realistic model of the basal ganglia may have an algorithmic-like RL component to calculate prediction errors. Furthermore, the different model types can sometimes profitably be used in concerted fashion. For example, by approximating a detailed neural model with a more abstract algorithmic model to allow quantitative estimation of parameters from subject data⁸⁷. This approach also allows one to refine the details of one level of description constrained by the other. For example, detailed basal-ganglia models distinguish between opponent direct and indirect pathways that differentially process dopaminergic reinforcement signals. Incorporating this feature in more abstract models allows one to formally analyze its consequences for a variety of behaviors across a wide range of parameters. It also facilitates the quantitative fitting of behavioral data, and formulating normative accounts for how adding this opponency is helpful beyond classical algorithmic models⁸⁸. Finally, it should also be noted that Bayesian techniques can be applied to all three types of models for fitting, validation and other purposes, that is, non-Bayesian models can also be fit using Bayesian techniques.

Biophysically realistic neural-network models

Synthetic, biophysically realistic neural-network models have been used to link biological abnormalities in psychiatric disorders to their neurodynamical and behavioral consequences. One class of models that has led to important insights in psychiatry includes cortical pyramidal neurons, connected recurrently, and GABAergic interneurons; these models can form stable ‘bumps’ of activity that maintain information online. Reducing NMDA receptor density on inhibitory interneurons as found in schizophrenia⁸⁹ led to weaker and broader attractor states (Fig. 5a) that were more sensitive to disruption by inputs close to the bump, suggesting that working memory in schizophrenia should be particularly sensitive to distractors similar to the items held in working memory⁹⁰. A different use of this model to integrate across levels has been to relate NMDA receptor density to BOLD signals. Ketamine induces symptoms of psychosis⁹¹ and abolishes the negative relationship between the resting-state default mode and task-related modes⁹². A model that incorporated two populations of neurons representing the default-mode and task-positive networks was only able to capture this disruption when NMDA receptor function on GABAergic interneurons (and not on pyramidal neurons) was reduced⁹².

Figure 5.

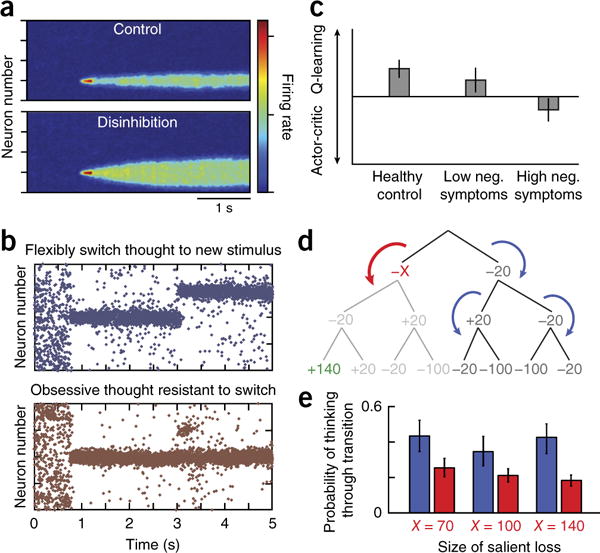
Theory-driven biophysical and RL approaches. (a) Insights into working-memory disturbances in schizophrenia. Reducing NMDA currents on inhibitory interneurons leads to overall disinhibition and broadens the bump representation of a stimulus in working memory (compare top versus bottom), making it more susceptible to distractors, especially those that activate neighboring neurons. Adapted with permission from ref. 90. (b) Insights into obsessive-compulsive disorder. Both lowering serotonin levels and increasing glutamatergic levels renders activity patterns excessively stable, such that when a new cluster of neurons is stimulated, activity does not shift to the new location, as would be expected (top, normal response), but rather remains ‘stuck’ in the previous location (bottom). Adapted with permission from ref. 2. (c) Negative symptoms in schizophrenia are related to a failure to represent expected values. In an instrumental-learning task, healthy controls and patients with schizophrenia with low levels of negative symptoms learned according to a reinforcement-learning algorithm that explicitly represents the expected value of each state-action pair (Q-learning), whereas patients with schizophrenia with high levels of negative symptoms learned according to an algorithm that learns preferences without such explicit representations (actor-critic). Adapted with permission from ref. 101. (d) Examining the processes that guide goal-directed evaluations. Shown is a decision tree corresponding to a sequence of three binary choices, where each choice leads to a gain or loss indicated by the numbers. A RL model was fitted to choices and contained two key parameters, representing the probability of continuing thinking when encountering a large salient loss (red arrow, −X) or when encountering other outcomes (blue arrows). (e) Subjects were far less likely to continue evaluating a branch after encountering a salient loss (red bars) than after other outcomes, for a variety of salient loss sizes. Adapted with permission from ref. 132.

This class of attractor models has also been used to explore the effects of glutamatergic and serotonergic disturbances in obsessive-compulsive disorder (OCD)². Both decreased serotonin and increased glutamate, two suspected abnormalities in OCD, led to the development of strong and persistent activity patterns toward which the network tended to and from which it had difficulty escaping—a possible neurodynamic substrate for obsessions (Fig. 5b). Of note, the model suggested that these neurodynamic disturbances can be alleviated by increasing serotonin levels independently of whether the underlying cause is low levels of serotonin or high levels of glutamate. The model also included specific serotonin receptor types: 5HT2A blockade ameliorated the neurodynamical abnormalities, suggesting one explanation for why treatment augmentation with atypical antipsychotics can be beneficial.

A similar integration from synaptic properties to high-level function was achieved with biologically detailed models of the cortico-striato-thalamic loops^93,94. As reviewed previously, these models explain various aspects of Parkinson’s disease, Tourette’s syndrome, schizophrenia and addiction^9,87.

In short, where detailed knowledge of the structure and function of relevant circuits exists, synthetic models often allow an understanding of causally complex and even distant relations between levels of analysis (for example, from synaptic alterations to behavior). Such models represent a critical tool to link biological details to symptoms. Biophysically detailed models can also be reduced to extract the core nonlinear dynamical components⁹⁵ and make it amenable to detailed mathematical analysis using stability or perturbation analyses. It should be noted, however, that even detailed biophysical models typically involve substantial simplification, and conclusions are restricted to the levels of analysis included in the model. What is, for instance, captured by an alteration in the parameter supposed to reflect NMDA receptor density could be a result of other biological and emergent factors of the system.

Biophysical models have also been successfully applied to neurological conditions⁹⁵, such as epilepsy, with strong, identifiable neurophysiological correlates that can be modeled in their own right. The absence of known strong correlates in psychiatry makes it difficult to model them in their own right and instead requires them to be related to symptoms either theoretically, as in the examples discussed here, or empirically, as in data-driven approaches.

Algorithmic reinforcement learning models

RL encompasses a set of algorithms to infer policies that optimize long-run returns⁹⁶ and thus has been applied extensively to issues of affect, motivation and emotional decision-making. Practically, RL models typically consist of two components: an RL algorithm putatively capturing the internal learning and evaluation processes, and a link function relating the results of the internal evaluations to choice^3,97. This allows them to assign a probability to each individual participant’s choice in an experiment and give statistically detailed accounts of learning and behavior. Although they do not tend to be biophysically detailed, they have characterized multiple aspects of neural activity and behavior⁹⁸. The most prominent example is so-called ‘model-free’ (MF) temporal prediction errors that compare expected to obtained reinforcement. These appear to be reported by phasic dopaminergic activity⁹⁹. Here, we describe several uses of these models in psychiatry.

Reward sensitivity is altered in many psychiatric circumstances. However, when analyzing behavior, variations in reward sensitivity are often difficult to distinguish from variations in other processes, particularly those of MF learning. When RL models were fitted to data to disentangle them, anhedonia in depression related specifically to a loss of reward sensitivity in a manner distinct from that of dopaminergic manipulations affecting learning²². Similar approaches have facilitated more precise measurements of the sensitivity to irrelevant valued stimuli, which predicts relapse in alcoholism⁵¹ and the naturalistic course of depression¹⁰⁰, to relate negative symptoms to a shift in learning strategy away from representing expected values (Fig. 5c)¹⁰¹. In schizophrenia, RL has been used to examine aberrant learning¹⁰² and to show that ventral striatal hypofunction persists even when quantitatively controlling for differences in reward sensitivity and learning strategy¹⁰³.

A second important direction has been the examination of two algorithms for choice valuation that were initially thought to act in parallel and to compete for behavioral expression^104,105. Resource-costly prospective ‘model-based’ (MB) systems simulate the future on the basis of an internal model of the world, are thought to capture goal-directed actions and rely on cognitive and limbic cortico-striato-thalamo-cortical (CSTC) loops. Resource-light MF systems conversely learn values by iteratively updating them with prediction errors through experience, and are thought to capture habits and rely on sensorimotor CSTC loops^98,105–108. As most¹⁰⁹ addictive substances release dopamine, they may boost dopaminergic prediction-error learning¹¹⁰ (but see ref. 111) and speed up the establishment of drug-related habits¹¹². Indeed, animals that rely more on prediction-error learning are more prone to addiction^113–115, with parallel findings of a shift from MB to MF choices emerging in humans^116–118. A similar argument has been made for a shift toward MF actions in OCD based on the idea that compulsions in OCD and compulsive drug use share some features^117,119,120. However, tonic dopamine promotes MB rather than MF decisions^121,122, questioning its role in shifting competition from MB to MF valuation in addiction. An alternative to a competitive account between MB and MF is a more integrated one where the goals driving MB evaluations are provided by MF processes¹²³, for instance by more abstract plans in anterior CSTC circuits being reinforced by dopaminergic signals¹²⁴. This would account for the prominent goal-seeking features of drug addiction¹²⁵. Finally, the shifts from MB to MF across disorders have often been a result of reductions in the MB component, rather than more prominent MF components, both neurally^117,120 and behaviorally^117,116 (but see ref. 116), raising the possibility that the MB to MF shift is a result of nonspecific impairments in executive function^126,127 or stress¹²⁸ affecting resources for MB computations.

Indeed, a re-emerging RL direction explicitly addresses the effect of resource constraints and bounded rationality^15,129. These may provide paths toward normative accounts of how MB and MF systems interact, with the MB system only being engaged when the resource costs are outweighed by the potential additional gains¹³⁰. Furthermore, given that full MB evaluation is prohibitively costly, they have to be partial, with profound consequences for the resulting valuations: if important potential outcomes are not included in the evaluation, the results can differ vastly and the glass will go from half full to half empty. The regulation of internal valuation strategies may be related to cognitive aspects of emotion regulation^15,131. RL modeling has started to identified specific aspects of these processes, such as a role for aversive outcomes in guiding resource allocation process^132,133 (Fig. 5d,e).

Bayesian models

Bayes-optimal modeling approaches can be used to better understand the nature of problems and their solutions. For example, conditioning models that use gradual acquisition of associations fail to capture standard extinction phenomena that result from the fact that extinction generally involves new learning rather than unlearning. The correct statistical description of extinction procedures is that there is a latent variable, the experiment phase, that causes sudden switches in the association between stimulus and outcome. Using models that allow for the learning of such latent variables provides a better account of standard extinction phenomena¹³⁴ and predicts that stable unlearning can in fact occur as long as there is no obvious sudden switch, which was verified experimentally¹³⁵. One important aspect of Bayesian models more generally is their emphasis on the representation and use of uncertainty. These have been used to show that the statistics of aversive experiences have important, but sometimes neglected, roles in several other processes, from familiarity in fear conditioning¹³⁶ to learned helplessness and depression⁷⁶.

Optimal models can also be used to ask whether a given symptom relates to suboptimal inference. For example, individuals with high trait anxiety are unable to optimally update how volatile an aversive environment is, whereas low-anxiety controls exhibit close to Bayes-optimum behavior¹³⁷. Finally, Bayesian models can also be used for applied purposes. For example, a Bayesian model of stop-signal task performance¹³⁸ differentiated occasional stimulant users with good and poor long-term outcomes and provided regressors for fMRI analyses that allowed longitudinal prediction²⁵; classical analyses failed to achieve either.

Combining theory- and data-driven approaches

Studies aimed at developing clinically useful applications have tended to use theoretically agnostic ML approaches, whereas studies aimed at increasing understanding of disorders have tended to use theory-driven mechanistic approaches. Theory-driven approaches depend, of course, on the extent to which prior knowledge, mechanistic understanding, and appropriate assessments of such mechanisms (for example, via suitable tasks or physiological measurements) are available. When such enabling factors are present, however, some preliminary studies suggest that the combined use of theory-driven and ML approaches can be advantageous even from an applied viewpoint. If the mechanistic theory is sufficiently accurate, theory-driven approaches allow the estimation of features specifically relevant to the disorder. In other words, theory-driven approaches use prior knowledge to massively reduce the dimensionality of the data set by ‘projecting’ it to the space of a few relevant parameters. ML approaches can then work on this lower-dimensional data set with increased efficiency and reliability (Fig. 2). Figure 6 shows a simulation of this intuitive effect: applying a classifier to data produced by a generative model performs worse than applying it to the model parameters recovered from that data.

Figure 6.

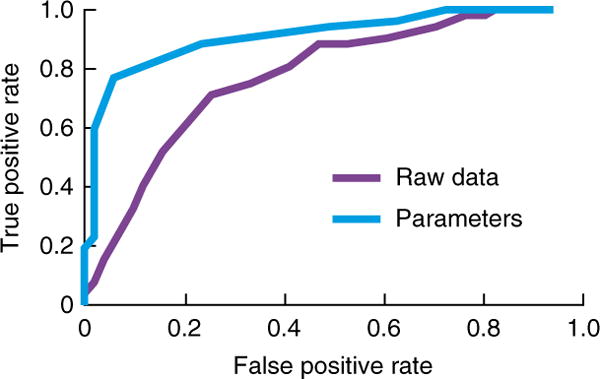
Mechanistic models yield parameters that can be used as features to improve ML performance. A classifier trained on estimated parameters of a model fitted to simulated behavioral data (light blue curve, AUC 0.87) performed better than when trained on the raw data directly (purple curve, AUC 0.74). Data for 200 subjects with Gaussian distributed parameters were simulated from a simple MF RL model with time-varying action reinforcements. Subjects were separated into two groups based on only one parameter (the learning rate). The data set was split into two, with half of the subjects used for training a classifier and the other half for validation. Two classifiers were trained, with one trained on the raw behavioral data, and the other on the parameters estimated by fitting a RL model. The ROC curve is shown for performance on the validation set.

A proof-of-concept study illustrating this approach built on prior work showing that the drift-diffusion model’s (DDM’s) decision threshold—the amount of evidence required in favor of one option over another before committing to a choice—is partly controlled by communication between frontal cortex and the subthalamic nucleus (STN)¹³⁹. Impulsive behaviors that result from reduced decision thresholds are observed in patients with Parkinson’s disease treated with STN deep brain stimulation (DBS) and are linked to disruption of normal communication between frontal cortex and STN¹⁴⁰. One study used ML methods applied to EEG and behavioral data to classify patients into those on versus off DBS¹². Classification was better when using fitted DDM parameters than when using the raw data; moreover, as suggested by the prior mechanistic work, the most informative parameters for classification were the decision threshold and its modulation by frontal cortical activity. Similar improvements were found using model parameters for classifying presymptomatic Huntington’s patients versus controls and separating patients that were closer versus further from exhibiting symptoms¹⁴¹. Using model-based assessments has also enhanced classification and subtyping of schizophrenia patients²⁴ and the aforementioned prospective prediction of stimulant abuse²⁵.

Conclusion

We have outlined multiple fronts on which computational psychiatry is likely to substantially advance psychiatry. Data-driven approaches have started to bear some fruit for clinically relevant problems, such as improving classification, predicting treatment response and aiding treatment selection. These approaches, however, are limited in their ability to capture the complexities of interacting variables in and across multiple levels. Theory-driven modeling efforts, on the other hand, have yielded key insights at many levels of analysis concerning the processes underlying specific disorders, but for the most part have yet to be applied to clinical problems. We have highlighted why and how the combination of theory- and data-driven approaches can be especially powerful and have described some initial, but promising, attempts at such integration. A shift in focus across both approaches from understanding or predicting current disease categories toward transdiagnostic approaches and the prediction of imminently practical and valid variables, such as treatment outcomes, appears to be very promising.

Computational tools have a number of limitations. Most obviously, they require substantial expertise and are frequently opaque to the non-expert. One challenge for the field is hence how to stimulate fruitful exchange between clinicians, experimentalists, trialists and theorists. This might be helped by a stronger focus on establishing utility by actively pursuing computational approaches in clinical trials. In addition, computational tools are not a panacea and are not released from the requirements of independent replication. However, the increasing popularity of open-source code and databases will facilitate such replications and the establishment and extension of (clinically) robust methods. Overall, the interaction between theorists and clinicians promises many opportunities and ultimately better outcomes for patients.