The active force–length relationship is invisible during extensive eccentric contractions in skinned skeletal muscle fibres

Abstract

In contrast to experimentally observed progressive forces in eccentric contractions, cross-bridge and sliding-filament theories of muscle contraction predict that varying myofilament overlap will lead to increases and decreases in active force during eccentric contractions. Non-cross-bridge contributions potentially explain the progressive total forces. However, it is not clear whether underlying abrupt changes in the slope of the nonlinear force–length relationship are visible in long isokinetic stretches, and in which proportion cross-bridges and non-cross-bridges contribute to muscle force. Here, we show that maximally activated single skinned rat muscle fibres behave (almost across the entire working range) like linear springs. The force slope is about three times the maximum isometric force per optimal length. Cross-bridge and non-cross-bridge contributions to the muscle force were investigated using an actomyosin inhibitor. The experiments revealed a nonlinear progressive contribution of non-cross-bridge forces and suggest a nonlinear cross-bridge contribution similar to the active force–length relationship (though with increased optimal length and maximum isometric force). The linear muscle behaviour might significantly reduce the control effort. Moreover, the observed slight increase in slope with initial length is in accordance with current models attributing the non-cross-bridge force to titin.

1. Background

Muscle force production depends on the arrangement of fibres within the muscle, the contraction velocity, the fibre length, the activation, and the muscle contraction history [1–4]. The variability in the function of skeletal muscles during movements [5,6] requires concentric (active and shortening), isometric (active and at constant length), and eccentric (active and lengthening) contractions as well as combinations thereof. Muscles activated during eccentric movements can serve as shock absorbers, energy stores, and struts, e.g. to stabilize posture, decelerate, or prepare reutilization of stored energy for power enhancement [5,7]. However, processes underlying lengthening contractions on the molecular level remain unclear (see Nomenclature table in the electronic supplementary material).

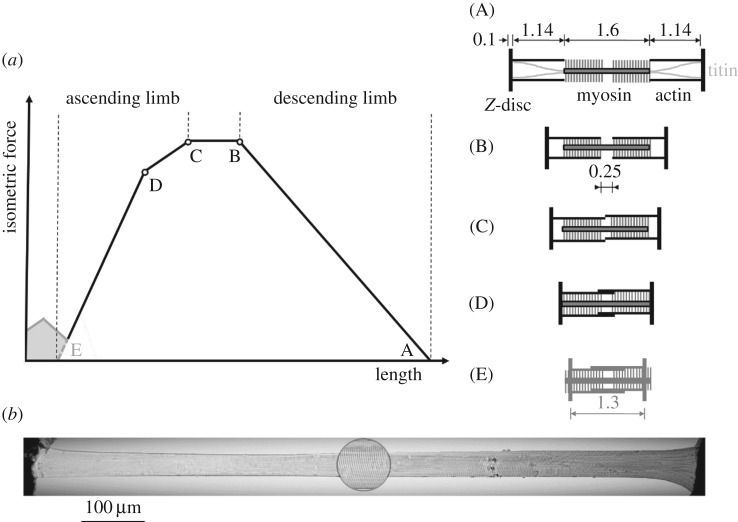
A novel, physiological model of fibre contraction [8] extends the well-accepted mechanisms of active force production in sarcomeres—the sliding filament [9,10] and cross-bridge theories [11]—to short sarcomere lengths (figure 1a, range left of D). However, these theories fail spectacularly when predicting the isometric muscle force after an active eccentric contraction, for example [13]. While titin, a non-cross-bridge structure connecting the myosin filaments to the Z-disc (figure 1a, top right schematic), is suggested to be a key player in explaining the differences between predictions and experiments [14–17], there is still debate and an incomplete understanding with regard to the underlying force-producing mechanisms [17–21].

Figure 1.

Force–length relationship (FLR) and EDL muscle fibre. (a) The active isometric FLR can be directly explained with actin and myosin filament overlap [4]. Qualitative changes in overlap (see corresponding sarcomere configuration schematics (A)–(E) to the right) lead to slope changes of the FLR (indicated with open circles at lengths B, C, D). Forces in the range below D (including the force hump [12] left of E for very short sarcomere lengths, illustrated by the grey area) can be explained with myosin filament sliding through the Z-disc [8]. (b) Representative picture of a permeabilized single muscle fibre of a rat EDL muscle at optimal sarcomere length L_S0 = 2.5 µm in relaxed state. Only fibres with a homogeneous sarcomere pattern, without any lesions or damage were analysed. The photomicrograph was captured with a 20 × objective under bright-field illumination. The spot (×500 magnification) shows the striation pattern.

Many studies have reported a linear rise in tension for moderate muscle lengthening that is independent of contraction speed for whole muscles [22–24], across muscle fibre bundles [25,26], down to intact single fibres [18]. These findings agree with the idea of a passive, spring-like contribution of, for example, titin to total muscle force. However, because a muscle's active force depends on myofilament overlap that leads to clearly visible pronounced slope changes of the active isometric force–length relationship (FLR)—especially at the fibre level (figure 1a, [4])—these different slopes and particularly the slope changes (marked with open circles in figure 1a) should be reflected in sufficiently long isokinetic lengthening contractions. The currently reported linear force rise in lengthening contractions might have resulted from performing experiments on limited FLR regions of constant slope. Only one very long eccentric ramp comprising different slope regions of the FLR showing an unexpected linear force rise during the complete stretch has been reported [23].

This group stretched a degraded whole muscle–tendon complex from 30% below to 40% above optimum fibre length. Such a linear behaviour deviates from the behaviour of classic muscle models, and it could simplify the control of muscles during locomotion. Some doubts remain as to whether this behaviour is a genuine property of the contractile machinery of the muscle or is a result of degradation, three-dimensional muscle deformation, or interaction with elasticities outside of the fibre. Therefore, measurements at the muscle fibre level with extensive magnitudes of stretch seem suitable to clarify this.

To better understand the underlying mechanisms of force production in lengthening contractions, it is useful to characterize the cross-bridge and non-cross-bridge contributions. A systematic limitation of cross-bridge force has been achieved by applying various amounts of the strong actomyosin-inhibitor 2,3-butanedione monoxime (BDM, see table 1 in the electronic supplementary material for a list of symbols and abbreviations) to the activation solution [27–29]. BDM acts at the myofibrillar level directly and reversibly on the myosin heads [30]. A reduction in myosin ATPase slows the phosphate release and suppresses cross-bridge attachment even at low BDM concentrations (less than 1 mM, mM represents mmol l⁻¹) [28,30,31]. Accompanied with reduced shortening speed and suppressed isometric tension, the entire contractile apparatus is inhibited [27,28]. This presumably allows a study of force effects that is nearly independent of cross-bridges when comparing forces obtained with and without BDM.

The aim of this study was to investigate whether slope changes in the FLR (figure 1a) would be visible in force traces of lengthening contractions of activated fibres as expected considering the sliding filament and cross-bridge theories [4,32]. A second goal was to separate cross-bridge and non-cross-bridge contributions to total muscle fibre force. To achieve these goals, in vitro isokinetic stretch experiments of maximally activated single skinned fibres from rat extensor digitorum longus (EDL) muscles were performed with extensive magnitudes of stretch comprising different characteristic ranges of the FLR. To separate forces, cross-bridge contributions were increasingly suppressed using BDM. We tested the hypothesis that the superposition of cross-bridge forces—in accordance with classic theories of contraction—and non-cross-bridge forces yield total fibre forces in eccentric contractions.

2. Methods

(a). Fibre preparation

Muscle fibres were extracted from five freshly killed female Wistar rats (8–10 months, 300–350 g, cage-sedentary, 12 h : 12 h light : dark cycle, housing-temperature: 22°C) provided by another animal study that was approved according to Section 8 of the German animal protection law (Tierschutzgesetz, BGBl I 1972, 1277). The applicants of the approved animal experiment study had no objection against the extraction of muscle fibres from dead rats. Their results were not impaired by the extraction of muscle fibres.

The muscle fibres were obtained from EDL muscles from both hind limbs (in total 10 muscles from five rats). The EDL is a predominantly fast skeletal muscle with a fibre type distribution of approximately 75% of type 2B fibres [33]. Eight to 10 small fibre bundles (length: 5–10 mm, width: 0.5–1 mm) were immediately dissected from the medial region of each EDL muscle under a stereomicroscope. For the mechanical experiments, the skinned muscle fibres were prepared according to the protocol of Goldmann & Simmons [34].

Briefly, fibre bundles were permeabilized at 4°C in a skinning solution (table 1). The demembranated fibre bundles were stored at −20°C in a storage solution (skinning solution made up in 50% glycerol) (table 1) and used within six weeks. On the day of the experiment, small segments of the skinned fibre bundles were dissected and used to prepare several single fibres (1.5–2 mm long) in storage solution on a temperature-controlled stage at 4–6°C. Thereafter, the fibre extremities were loosely clamped by aluminium foil ‘T-clips’ (Institute of Applied Physics, Ultrafast Optics, Jena, Germany), in accordance with Ford et al. [35]. Afterwards, the fibres were treated with relaxing solution (table 1) containing Triton X-100 (1% v/v) for 1–2 min at 4°C to ensure complete removal of internal membranes without affecting the contractile apparatus [36,37].

Table 1.

Solution compositions. All concentrations are in mmol l⁻¹, except glycerol (v/v) and creatine phosphokinase. TES, N-tris[hydroxymethyl]methyl-2-aminoethanesulphonic acid; ATP, adenosine 5′- triphosphate disodium salt hydrate; EGTA, ethylene glycol-bis(2-aminoethylether)-N,N,N′,N′-tetraacetic acid; CP, N-[Imino(phosphonoamino) methyl]-N-methylglycine; GLH, glutathione; HDTA, 1,6 diaminohexane-N,N,N′,N′-tetraacetic acid; KP, potassium propionate; IMID, imidazole; PMSF, phenylmethanesulfonyl fluoride, 10 µM transepoxysuccinyl-l-leucylamido-(4-guanidino)butane (E-64) and 20 µg ml⁻¹ leupeptin. pH (adjusted with KOH) was 7.1 at 12°C. The ionic strength was 190 mM. CK was obtained from Roche (Mannheim, Germany); all other chemicals from Sigma (St Louis, MO, USA).

solution compositions
	TES	MgCl2	Na2ATP	EGTA	Na2CP	GLH	HDTA	CaEGTA	CK (U ml−1)
relaxing	100	7.70	5.44	25	19.11	10	—	—	400–500
preactivating	100	6.93	5.45	0.1	19.49	10	24.9	—	400–500
activating	100	6.76	5.46	—	19.49	10	—	25	400–500
	KP	MgCl2	Na2ATP	EGTA	IMID	GLH	PMSF	Glycerol	CK (U ml−1)
skinning	170	2.5	2.5	5	10	—	0.2		—
storage	170	2.5	2.5	5	10	10	0.2	50%	—

(b). Experimental set-up

The fibre clip unit was mounted in an Aurora 600A permeabilized fibre test apparatus positioned on the x–y moving stage of an inverted microscope (Nikon Eclipse Ti-S). The test apparatus consisted of a temperature-controlled stage with seven wells (160 µl) and a single large chamber (200 µl) for multiple solutions, which were moved horizontally by a stepper motor. This large chamber was filled with a relaxing solution (table 1), and the clips were attached via stainless steel wire hooks to a force transducer (Aurora Scientific 403a, force range: 5 mN, force resolution: 0.1 µN) and a high-speed length controller (Aurora Scientific 322 C-I, max. force: 100 mN, length signal resolution: 0.5 µm). The attachment unit of the hook and clip was free of clearance and was rigid. This ensured optimal horizontal alignment between the fibre and transducer lever. The fibre ends were cross-linked [38] with a drop of rigor solution containing 8% (v/v) glutaraldehyde and 5% (w/v) toluidine blue [39] to minimize sarcomere length inhomogeneity and to improve stability and mechanical performance. The fixed fibre-part was determined by visualizing the toluidine blue.

Thereafter, the sarcomere length (L_S), measured in the central segment of the fibre (figure 1b), was set to 2.5 ± 0.05 µm which is the optimal sarcomere length (L_S0) for maximal isometric force (F_im) development [40]. The corresponding fibre length was defined as the individual optimal fibre length (L₀). The fibre width (w) and height (h) were measured in approximately 0.1 mm intervals over the entire length with a 40× ELWD dry-objective (NA 0.60, Nikon) and a 10× eyepiece. The mean L₀ was 0.73 ± 0.24 mm, the fibre cross-sectional area was determined assuming an elliptical cross-section (πhw/4) and was 5 017 ± 1 400 µm². For visualization of the striation pattern and for accurate, dynamic tracking of L_S changes, a high-speed video system (Aurora Scientific, 901B) was used in combination with a 20 × ELWD dry-objective (NA 0.40, Nikon) and an accessory lens (2.5×, Nikon).

(c). Experimental protocol

All skinned fibre experiments were conducted at a constant temperature of 12°C ± 0.1°C. At 12°C, the fibres proved very stable and able to withstand active lengthening protocols over an extended period of time as well as prolonged activations [41–43]. Each fibre was activated by calcium diffusion in the presence of ATP. The fibre was immersed in preactivating solution for 60 s for equilibration and afterwards in an activating solution (pCa = 4.5, free Ca²⁺ is sufficient to produce maximum force [44]). This offered maximal activation that was characterized by a rapid rise in force until a plateau (defined as a change in force of less than 1% over a period of 1 s, achieved approx. 5 s after activation) was reached. Then, the fibre was stretched. Subsequently, fibres were immersed in relaxing solution for at least 450 s.

Eccentric ramps comprised three blocks of repeated experiments. First, fibres (five rats, six fibres each) were actively stretched in randomized order from three different initial fibre lengths L_i (0.7, 0.85, and 1.0 L₀) with constant stretch amplitudes of 0.45 L₀ to corresponding end lengths L_e (1.15, 1.3, and 1.45 L₀). Second, fibres (six fibres of one rat, four fibres of two other rats each) were stretched in activating solution with varying concentrations (0, 2, 5, and 10 mM) of BDM in randomized order from L_i of 0.85 and 1.0 L₀ to corresponding L_e of 1.3 and 1.45 L₀, respectively. Third, a subset of the fibres from the first and second blocks of experiments as well as additional fibres were stretched in prolonged ramps from 0.7 L₀ to 1.45 L₀.

To ensure structural and mechanical integrity of fibres in the experiments, the following criteria were applied to discard fibres: (i) isometric force in reference contractions was decreased by more than 10%, (ii) abnormal behaviour of force traces, evidenced by artefacts, oscillations, or abrupt flattening was noted, and (iii) lesions, ruptures, or fibre contortion were identified visually. This procedure resulted in at least two valid experiments per rat in eccentric ramps of the first block starting at 0.7 L₀ and at least three valid experiments per rat in all other experimental conditions.

All stretches were performed at a velocity of 11% maximum shortening velocity (v_max). The v_max was defined as 2.25 L₀ s⁻¹, an average value of maximum unloaded shortening velocity of EDL muscles from young (three to six months, v_max = 2.47 ± 0.90 L₀ s⁻¹) and old (22–24 months, v_max = 2.00 ± 0.66 L₀ s⁻¹) female Wistar rats determined at 12°C in a previous study by Degens et al. [45].

The ‘cycling-protocol’ by Brenner [46] was used to conserve the structural and mechanical properties in maximally activated fibres over an extended period of time as well as to reduce sarcomere inhomogeneities. For calculating force degradation, isometric reference contractions at L₀ were performed before and after the ramp experiments. In eccentric contraction experiments, the isometric force in successive activations decreased at an average rate of 1.80% per activation.

(d). Data processing and statistics

The length and force signals from the transducers were recorded at 1 000 Hz with an A/D interface (604A, Aurora Scientific, Canada). Real-time software (600A, Aurora Scientific) was used for data acquisition. Force values were divided by individual F_im, fibre length data divided by L₀ and the force–length traces were cut after the bump (100 ms after beginning the eccentric ramps). For the first block of experiments, a linear regression model was used to estimate the slope of the force–length trace and the corresponding coefficient of determination of each eccentric ramp. Each rat's force–length slope (first block of experiments) and the force–length data using BDM (second block of experiments) were analysed using Gaussian linear mixed effect models accounting for repeated measurements per rat and per fibre. In addition, rat-specific variances of data were allowed (using the nlme package of the statistics software system R [47,48]).

To assess the effect of initial length on the slope of the force–length traces, an intercept-only model was compared with a model accounting for starting length as a factor using a likelihood-ratio test. To assess the nonlinearity of the force–length traces during eccentric ramps for different BDM concentrations, a hierarchical series of models incorporating linear and quadratic length effects, BDM concentration as a factor and their interactions was compared with likelihood-ratio tests. In both cases, assumptions were checked by plotting standardized residuals. For graphical display, all data are expressed as mean ± standard deviation (s.d.) across all valid experiments.

(e). Solutions

Table 1 describes the solutions. The concentrations of components were calculated with the computer program of Millar & Homsher [44]. Cysteine and cysteine/serine protease inhibitors (trans-epoxysuccinil-l-leucylamido-(4-guanidino) butane, E-64, 10 mM; leupeptin, 20 μg ml⁻¹) were added to all solutions to preserve lattice proteins and thus sarcomere homogeneity [36].

(f). Calculations of cross-bridge and non-cross-bridge forces

Two methods (A and B) were used to separate cross-bridge and non-cross-bridge forces during lengthening contractions from the experimental data. Both assume that cross-bridges produce a constant average force during isokinetic stretch after an initial equilibration of cross-bridge distributions [11,49]. The factor f_v corresponding to the applied constant stretch velocity was estimated to be 1.1 from figure 2a by drawing a line through the linear part of the eccentric force of the ramp starting at the plateau of the FLR and taking the intercept value similar to Roots et al. [26]. Because the contribution of all cross-bridges depends on filament overlap only, this contribution should resemble the FLR scaled by f_v during stretch. Moreover, BDM suppresses only a fraction f_XB of cross-bridges (this was assessed by comparing the initial isometric force with and without BDM); it reached 94% in the case of 10 mM BDM.

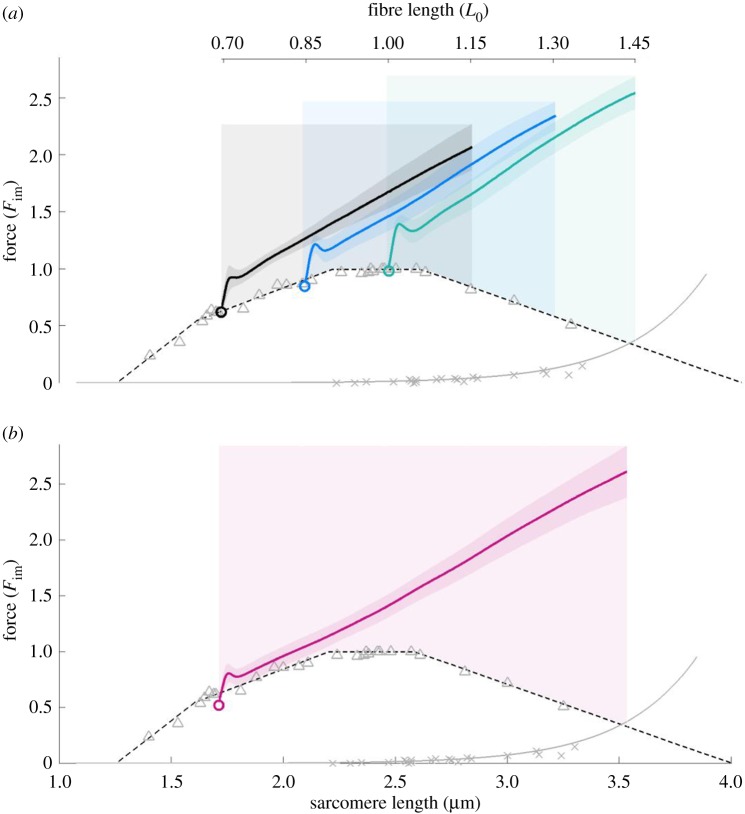
Figure 2.

The mean ± s.d. of force–length traces of eccentric isokinetic contractions. Solid black, blue, and green lines indicate the means. The shaded regions around the solid lines indicate the corresponding s.d. during active stretching. (a) Eccentric ramps show a small bump followed by a linear force increase. The small bump after initiation of the stretch could be due to short range stiffness [50] and passive properties of the fibre such as inertia or viscosity [35]. Eccentric ramps starting from 0.7, 0.85, and 1.0 L₀ comprise 17, 24, and 24 experiments, respectively. (b) Extensive ramps with stretch amplitude of 0.75 L₀ also show a linear force increase. Extensive ramps comprise 18 valid experiments. The stretch velocity is 11% v_max in all ramps. The force is normalized to maximum isometric force (F_im) and length to optimal fibre length (L₀). Isometric pre-stimulation is not shown. Crosses and triangles indicate measurements of passive and active isometric fibre forces, respectively. For comparison, the active isometric sarcomere FLR (dashed line) and passive sarcomere force–length data (solid grey line) of fast single skinned fibres from EDL muscles, reported by Stephenson & Williams [40] and Stephenson [51], are shown. Comparison of statistical linear mixed effect models accounting for repeated measurements (see table 2, Methods section) revealed a significant increase in slope with initial length.

Method A assumes that the active force during stretching is suppressed by BDM percentagewise like the isometric force. Furthermore, in methods A and B, we assumed that BDM does not affect the passive force and that the FLR is valid during stretching, respectively. Hence, for method A, the difference between control force (figure 3, black solid line) and BDM-suppressed force (figure 3, solid coloured lines) was divided by f_v and f_XB to obtain the normalized, isometric force (figure 3, coloured dashed lines). This can be compared with the FLR. In method B, the difference between control force and FLR multiplied with f_v (figure 4, blue dashed line) was calculated to obtain the expected non-cross-bridge force that can be compared with the measured 10 mM BDM suppressed force.

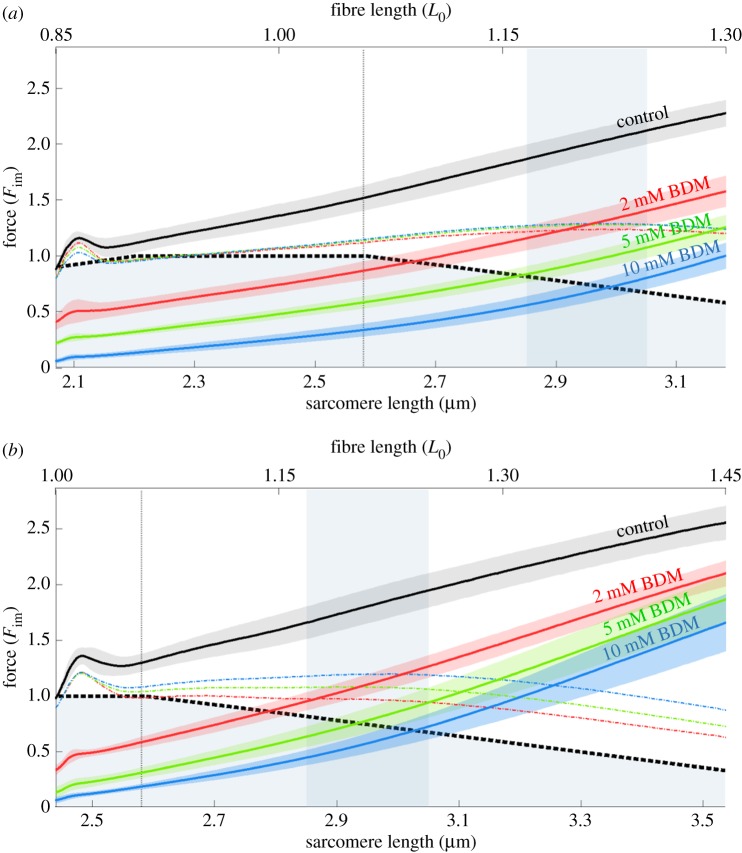
Figure 3.

Force–length traces of eccentric isokinetic contractions at different BDM concentrations. Mean (solid black line) and s.d. (shaded regions around solid lines) of control contractions (without BDM, black solid line) and contractions with increasing concentrations of BDM (2, 5, 10 mM, coloured solid lines) with stretch velocity of 11% v_max and initial fibre lengths of 0.85 L₀ (a) and 1.0 L₀ (b), respectively. Eccentric experiments comprised 14 valid experiments for each concentration of BDM. Coloured dashed lines represent scaled isometric cross-bridge forces underlying the ramp contractions (method A, see §2f), which can be compared with the isometric FLR. Shaded rectangular areas indicate rightward-shifted plateau-region of FLR during eccentric contractions. Comparison of hierarchical statistical models (see table 2 and Methods section) revealed increasing progressive nonlinearity with increasing BDM concentration.

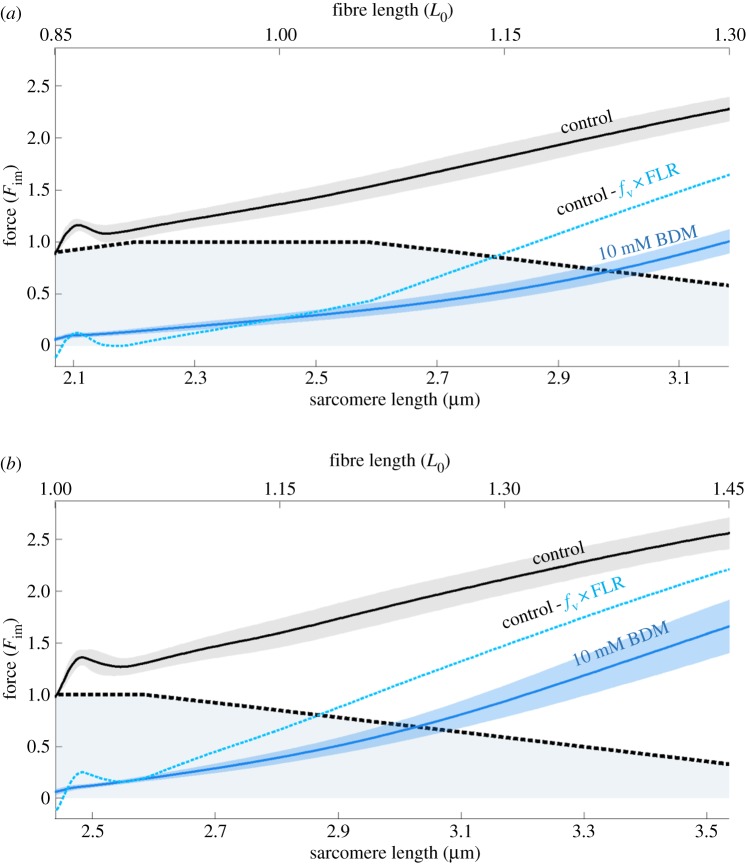
Figure 4.

Comparison of theoretical and experimental non-cross-bridge force traces during eccentric contractions. Blue solid lines indicate depressed force responses (around 94% cross-bridges abolished) due to 10 mM BDM application (mean (solid lines) ± s.d. (shaded regions around solid lines) of 14 valid experiments) for eccentric ramps with stretch velocity of 11% v_max and initial fibre lengths of 0.85 L₀ (a) and 1.0 L₀ (b), respectively. The blue dashed lines are expected to have non-cross-bridge forces (method B, see §2f) assuming a valid isometric FLR (black dashed lines) during eccentric contraction.

3. Results

Neither the force–length traces of the isokinetic eccentric ramps starting from different initial lengths (figure 2a) nor those of the long isokinetic eccentric ramps (figure 2b) reflected the slope changes of the underlying FLR. In contrast, linear regression models fitted the linear force–length traces remarkably well (mean coefficient of determination of 0.99). This is in stark contrast to classic theories of muscle contraction. According to these theories, forces during isokinetic eccentric stretching resemble a scaled version of the FLR (ignoring the passive forces, which only start at long lengths, cf. figure 2).

(a). Slope increases slightly with initial length in isokinetic eccentric ramp experiments

A slight increase in stiffness for longer initial lengths is seen (figure 2a, black versus green line). Statistical analyses yielded significantly different estimated slopes (table 2, model 1c) of 2.82, 3.02, and 3.15 F_im L₀⁻¹ for initial lengths of 0.70, 0.85, and 1.0 L₀, respectively. Stretching the fibre by 0.45 L₀ from each initial length resulted in a force increase by about 1.5 F_im. Thus, for eccentric contractions starting at L₀ (figure 2a, green line), eccentric forces of 2.5 F_im were observed in the descending limb of the FLR. This clearly exceeded the maximum active forces produced by cross-bridges at these lengths according to the sliding filament and cross-bridge theories.

Table 2.

Hierarchical statistical model comparisons. The likelihood-ratio statistics and p-values for subsequent model comparisons. To determine the effect of starting length on the slope of eccentric ramps (cf. figure 2a), we tested if the slope differs from 0 (models 1a versus 1b) and if the slope changes with starting length by considering initial length as a factor (models 1b versus 1c). To check for a nonlinear effect of BDM on force in eccentric ramps (cf. figure 3), data were tested for a nonlinear effect in force by adding a quadratic length effect to the model (models 2a versus 2b). It was then tested for improvement by adding BDM levels (model 2b versus 2c) and finally for interactions between BDM and length effects (models 2c versus 2d).

experiments	model	model name	d.f.	likelihood-ratio	p-value
block 1 (slopes)	slope ∼ −1	1a	6
	slope ∼ 1	1b	7	32.2	<0.0001
	slope ∼ 1 + as.factor(initlength)	1c	9	6.9	0.0311
block 2 Li = 0.85 L0 (BDM)	force ∼ 1 + length	2a	7
	force ∼ 1 + length × BDM	2b	13	350 806.2	<0.0001
	force ∼ 1 + length × BDM + (length2)	2c	14	23 514.6	<0.0001
	force ∼ 1 + (length + (length2)) × BDM	2d	17	4 609.5	<0.0001
block 2 Li = 1 L0 (BDM)	force ∼ 1 + length	2a	7
	force ∼ 1 + length × BDM	2b	13	290 509.6	<0.0001
	force ∼ 1 + length × BDM + (length2)	2c	14	6 832.7	<0.0001
	force ∼ 1 + (length + (length2)) × BDM	2d	17	9 219.8	<0.0001

(b). Determination of the effects of cross-bridge kinetics on eccentric force generation

Increasing BDM concentrations (2, 5, and 10 mM) decreased the maximum isometric forces to 0.33, 0.13, and 0.06 F_im at L₀, respectively (figure 3b). A similar suppression of cross-bridge forces was observed for 0.85 L₀ (figure 3a). Accordingly, forces during and at the end of the stretch decreased with increasing BDM concentrations (figure 3, solid coloured lines). Interestingly, in contrast to the linear behaviour in the control experiments (figure 3, solid black line, without BDM), increasing BDM increased the nonlinearity of the force response (figure 3, coloured solid lines). In accordance with this, the estimated quadratic coefficients in model 2d (table 2) describing the progressive nonlinear effect of force increased from 1.05 to 1.17 to 1.74 to 2.79 for ramps starting at 0.85 L₀ and from −1.2 to 2.6 to 4.1 to 5.5 for ramps starting at 1 L₀, respectively, for 0 to 2 to 5 to 10 mM BDM concentration.

To investigate the cross-bridge contributions (method A), BDM-suppressed forces (figure 3, coloured solid lines) were subtracted from the total forces of control ramps (figure 3, black lines) and then divided by f_v and f_XB. The resulting normalized isometric forces (figure 3, coloured dashed lines) reach about 1.2 F_im in their plateau region (figure 3, indicated by blue vertical bars). Assuming that this plateau results from the underlying FLR, one of the most intriguing results of this investigation is the remarkable rightward-shift by approximately 15% (to between 2.85 and 3.05 µm sarcomere length) during active stretching versus the plateau region of the classic FLR. Finally, our BDM results indicate that both the cross-bridge and non-cross-bridge components contribute nonlinearly to force production, and their forces sum up to a linear force-response of activated muscle in extensive stretch contractions.

4. Discussion

The most surprising result of this study is the absence of changes in the eccentric force slope, while the underlying FLR does have slope changes. In contrast, in classic muscle models, i.e. models that incorporate the sliding filament and cross-bridge theories, the corresponding slope changes are clearly visible during stretch simulations because their predicted force represents a scaled FLR in isokinetic eccentric contractions. Experimental observations of linear force responses during stretching in the muscle fibres imply the following: (i) the physiology of eccentric muscle contraction is not completely understood, (ii) muscle models must be adapted and/or changed to represent muscle behaviour, and (iii) there may be advantages of positive stiffness of actuators (in vivo or in technics) with respect to control.

To date, eccentric force potentiation remains a matter of debate [21,52,53]. Only a limited number of existing ideas can potentially explain strongly increased forces during and after prolonged stretching. Some have speculated that the classic cross-bridge dynamics [11] may be modified during eccentric contractions [54] that could not be validated in experiments thus far [55]. Alternatively, titin—a non-cross-bridge, semi-active structure—might contribute to the enhanced force-response during active stretch contractions, especially in the range of the descending limb of the FLR [13,15,16,53,56]. Combining a linear non-cross-bridge contribution with the idea that the isometrically determined FLR is not valid in eccentric contractions, Till et al. [20] offered a model with constant, linear slope of force in eccentric contractions on the FLR's ascending limb (figure 1a). They assumed that the myosin filament is compressed at short sarcomere lengths corresponding to the steep part of the ascending limb of the FLR, and that it retains its length in eccentric contractions. Additional assumptions were required to extend the resulting linear behaviour to other regions of the FLR. However, there are several strong arguments against myosin compression [8]. To approach the physiological mechanisms, it is important to separate cross-bridge and non-cross-bridge contributions to total muscle force.

The calculated normalized and isometric force (method A; figure 3, coloured dashed lines) shows distinct deviations from the typical FLR (figure 3, black dashed line). Its plateau region is rightward-shifted by approximately 15% L₀ for starting lengths of 0.85 and 1.0 L₀; the plateau value is slightly increased. An arbitrarily higher f_v value of 1.3 applied during normalization would decrease the maximal isometric force of the coloured dashed lines in figure 3 to a mean 1.0 F_im; however, the differences between the coloured dashed lines remain. Consequently, the sum of classical FLR and non-cross-bridge forces deviates from the experimental total force-response that is characterized by linearity. With the assumptions of method A, there are multiple and non-exclusive possible causes for this linearity. These include the alteration of the cross-bridge cycle during stretch, non-percentagewise effects of BDM on cross-bridge forces during stretch, or even altered myofilament overlap.

While the compliance of the myofilaments (figure 1a, actin and myosin filaments) is low (less than 1% in active muscle at maximum isometric force) and their compliance accounts for about 70% of total active sarcomere compliance [57,58], the Z-discs (figure 1a) may still play an important role in explaining a rightward-shift of the plateau of the calculated normalized, isometric force (figure 3, coloured dashed lines). In our contractions, forces exceeded the maximal isometric forces by up to 150% (figure 3, black solid lines). Vertebrate muscle Z-discs transmit the forces between sarcomeres via a varying number of α-actinin-layers [59]. Z-discs in fast-twitch fibred muscles transmit these forces via a lower number of α-actinins. This may result in increased serial compliance—narrow Z-discs in fast muscles are more prone to distortions and axial shifts of the myofilaments compared with Z-discs of slow muscles, which might be more rigid and able to maintain their structure [60].

If these α-actinins are subjected to a very high force, they may show increased compliance or even popping of some domains. In this case, the Z-disc is in series to titin and the myofilaments, which would lead to a rightward-shift of the plateau region [61] of the FLR. Moreover, when accounting for this serial elasticity in calculations, the deviations between the FLR and the calculated, normalized isometric force would even increase [61]. However, this remains highly speculative because to the best of our knowledge, the behaviour of the Z-discs in longitudinal direction under high forces has not yet been investigated.

The calculated non-cross-bridge force (method B; figure 4, blue dashed lines) is higher than its experimental counterpart (figure 4, blue solid lines), although this counterpart contains about 6% active cross-bridges. Hence, under the assumptions of method B, BDM suppresses the non-cross-bridge force. Evidence is accumulating that the non-cross-bridge force production during active stretching is associated with titin and titin–actin binding [13,16,62–64]. To date, a conclusive understanding of the mechanism(s) of actin–titin binding is still lacking [63]. Likewise, systematic studies of the effects of BDM on non-contractile proteins (e.g. titin or troponin) are missing. Hence, there is room for speculation. Recently, troponin C-depleted active myofibrils were reported to produce forces exceeding the passive force by only a small amount relative to active fibres [64]. Troponin C depletion means that no myosin binding sites are available on actin. This supports the myosin binding site-dependent [16] or force-dependent [15] titin–actin binding. There are contradictory reports as to whether and how BDM influences the ability of non-cross-bridge force production in eccentric contractions [29,64,65]. In our experiments, deviations of coloured dashed lines from theoretical sarcomere FLR increased with increasing BDM concentration (especially in figure 3b), suggesting an effect of BDM on non-cross-bridge forces. Concluding, these considerations remain speculative and require further study.

While skinned EDL fibres can operate robustly at 12°C [41–43], they produce only about half the isometric force as at physiological temperature [66,67]. Moreover, peak isometric force, time to peak force, and maximal shortening velocity decrease linearly with temperature. Thus, under physiological conditions, the cross-bridge contributions in ramps will be roughly twice as high. A reduced number of available binding sites might cause the decrease in isometric forces [68]. Depending on the so far unclear mechanism of titin–actin binding [63], such a reduction in available binding sites might hamper the ability of fibres to produce non-cross-bridge force in eccentric contractions [15,16]. Further studies are required to clarify whether non-cross-bridge contributions to force also scale with temperature.

The observed linear elastic behaviour (according to Hooke's law) of muscle during large stretches regardless of the (even negative) slope of the underlying FLR might also stimulate interest in biologists and roboticists investigating locomotion. Because of the important uses of compliance in locomotion [69], the concept of series elastic actuators mimicking muscles has been introduced [70] and applied in the last decades [71] in robotics. What might have seemed to be a simplistic approach, namely to represent muscle behaviour by means of motors in series with springs, may actually represent observed muscle behaviour during stretch very well. For example, if the resting length of the motor spring is set to a fixed length and locked in a robotic leg before touchdown, the response of the spring to the subsequent stretch in the loading phase mimics that of a fully activated muscle in our experiments. This finding adds not only to the credibility of robotic models employing series elastic actuators as tools to understand biological motion, for example, when investigating and demonstrating simple control strategies like, for example, switching of resting lengths [72,73], but also to the interpretation of neuro-muscle-mechanical models investigating control in locomotion using classic muscle models [74].

5. Conclusion

The results support the idea of a cumulative mechanism that combines nonlinear cross-bridge and non-cross-bridge effects to result in a linear force-response during muscle lengthening contractions. This linear muscle behaviour potentially facilitates control in biological locomotion. Our approach does not clearly separate non-cross-bridge and cross-bridge contributions because BDM seems to affect the non-cross-bridge and cross-bridge force. Accordingly, alternative inhibitors should be considered for further studies attempting to separate cross-bridge and non-cross-bridge contributions [75,76].

Authors' contributions

A.T., C.R., and T.S. developed the ideas, analysed the data, and drafted the manuscript. A.T. performed the experiments. J.S. performed the statistical analyses. All authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

We received no funding for this study.