Multisensory Integration Uses a Real-Time Unisensory–Multisensory Transform

Abstract

The manner in which the brain integrates different sensory inputs to facilitate perception and behavior has been the subject of numerous speculations. By examining multisensory neurons in cat superior colliculus, the present study demonstrated that two operational principles are sufficient to understand how this remarkable result is achieved: (1) unisensory signals are integrated continuously and in real time as soon as they arrive at their common target neuron and (2) the resultant multisensory computation is modified in shape and timing by a delayed, calibrating inhibition. These principles were tested for descriptive sufficiency by embedding them in a neurocomputational model and using it to predict a neuron's moment-by-moment multisensory response given only knowledge of its responses to the individual modality-specific component cues. The predictions proved to be highly accurate, reliable, and unbiased and were, in most cases, not statistically distinguishable from the neuron's actual instantaneous multisensory response at any phase throughout its entire duration. The model was also able to explain why different multisensory products are often observed in different neurons at different time points, as well as the higher-order properties of multisensory integration, such as the dependency of multisensory products on the temporal alignment of crossmodal cues. These observations not only reveal this fundamental integrative operation, but also identify quantitatively the multisensory transform used by each neuron. As a result, they provide a means of comparing the integrative profiles among neurons and evaluating how they are affected by changes in intrinsic or extrinsic factors.

SIGNIFICANCE STATEMENT Multisensory integration is the process by which the brain combines information from multiple sensory sources (e.g., vision and audition) to maximize an organism's ability to identify and respond to environmental stimuli. The actual transformative process by which the neural products of multisensory integration are achieved is poorly understood. By focusing on the millisecond-by-millisecond differences between a neuron's unisensory component responses and its integrated multisensory response, it was found that this multisensory transform can be described by two basic principles: unisensory information is integrated in real time and the multisensory response is shaped by calibrating inhibition. It is now possible to use these principles to predict a neuron's multisensory response accurately armed only with knowledge of its unisensory responses.

Introduction

Multisensory neurons in the superior colliculus (SC) enhance their sensory processing by synthesizing information from multiple senses. For example, when visual and auditory signals are in spatiotemporal concordance, as they would be when derived from the same event, they elicit enhanced responses (Stein et al., 1975; Meredith and Stein, 1983; Stein and Meredith, 1993; Miller et al., 2015). The originating event is then more robustly detected and localized (Stein et al., 1989; Wilkinson et al., 1996; Burnett et al., 2004, 2007; Gingras et al., 2009). The brain develops this capability for “multisensory integration” by acquiring experience with crossmodal signals early in life (Wallace and Stein, 1997; Wallace et al., 2006; Stein et al., 2009, 2014; Xu et al., 2012, 2014, 2015, Yu et al., 2010, 2013; see also Stein, 2012; Rowland et al., 2014; Felch et al., 2016). In the absence of these antecedent experiences and the changes that they induce in the underlying neural circuitry, the net response to concordant crossmodal stimuli is no more robust than to the most effective individual component stimulus; that is, the neuron's “default” multisensory computation reflects a maximizing or averaging of those unisensory inputs (Jiang et al., 2006; Alvarado et al., 2008; Stein et al., 2014).

The postnatal acquisition of this capacity, its nonlinear scaling, and its functional utility have attracted the attention of many (Ernst and Banks, 2002; Anastasio and Patton, 2003; Alais and Burr, 2004; Colonius and Diederich, 2004; Ma et al., 2006; Rowland et al., 2007a; Morgan et al., 2008; Bürck et al., 2010; Ohshiro et al., 2011; Cuppini et al., 2012), but its biological bases remain poorly understood. In part, this is because efforts to understand this process have focused on the generalized, “canonical” relationship between net multisensory and unisensory response magnitudes. These are abstract quantities calculated by averaging the responses (i.e., impulse counts) of many neurons over long temporal windows and are therefore not a direct indicator of the actual multisensory transform as it occurs on a moment-by-moment basis and as individual neurons communicate their multisensory products to their downstream targets. It merely reflects aggregate relationships quantified in an empirically convenient fashion. It is also sufficiently abstract as to be reproducible by any number of “biologically plausible” models. However, because they are based on these abstract, averaged quantities, such proposals are loosely constrained, have limited predictability, and fail to take into account the inherent variation in multisensory products among neurons at different times. A comprehensive analysis of the statistical properties and dynamic features of the multisensory computation is needed to understand the actual operating constraints of the biological mechanism.

The present effort sought to do just that. The operating principles of the multisensory transform were inferred from empirical data gathered here and, to determine whether they fully described this transform, they were put to a stringent test: predicting the actual moment-by-moment multisensory responses of individual neurons given only knowledge of each neuron's response to its modality-specific component stimuli. This was accomplished by embedding the principles in a simple neurocomputational model: the continuous-time multisensory model (CTMM; Fig. 1). Despite being highly constrained by a small number of relatively inflexible parameters (and even when fixing those parameters across the population), the model proved to be highly accurate and precise in predicting the moment-by-moment multisensory responses. Therefore, it demonstrated that these operating principles provided a complete description of the multisensory transform as it operates in real time. Although this approach was developed for describing SC multisensory integration, the principles identified here are likely to be common among neurons throughout the nervous system.

Figure 1.

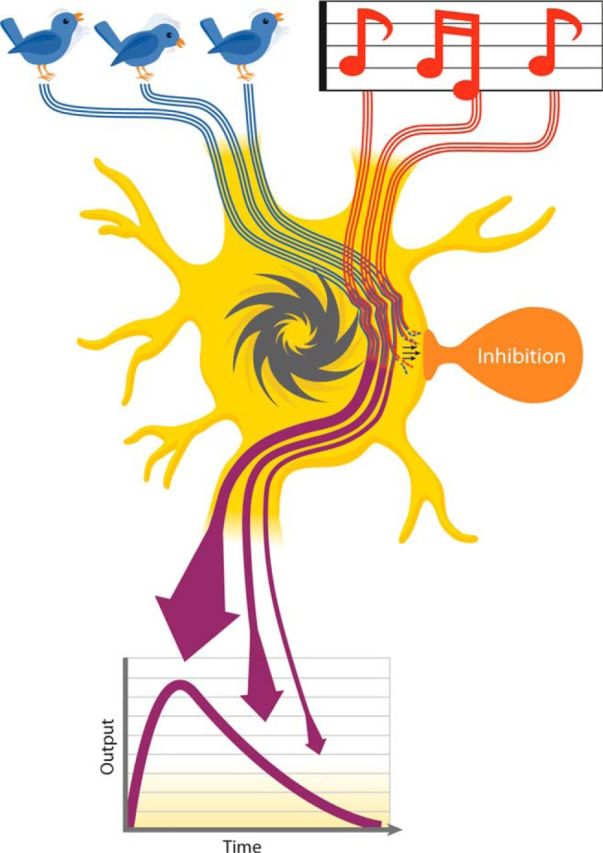
CTMM schematic. Visual (bird) and auditory (accompanying song) inputs (top) are integrated continuously as they arrive at their common target neuron (middle). The multisensory input drives the neuron's impulse generator (dark gray ratchet) to produce its multisensory outputs (purple arrows). Note that the moment-by-moment integrated multisensory products (firing rate) are plotted graphically as “output” (bottom) and decrease over time. This is due to the influence of a delayed calibrating inhibition (shown in orange, middle), which disproportionately suppresses later portions of the response.

Materials and Methods

Electrophysiology

Protocols were in accordance with the National Institutes of Health's Guide for the Care and Use of Laboratory Animals, Ed 8. They were approved by the Animal Care and Use Committee of Wake Forest School of Medicine, an Association for the Assessment and Accreditation of Laboratory Animal Care International-accredited institution. Two male cats were used in this study. Some samples from a previously acquired dataset (Miller et al., 2015) were also added to the present analysis.

Surgical procedures

Each animal was anesthetized and tranquilized with ketamine hydrochloride (25–30 mg/kg, IM) and acepromazine maleate (0.1 mg/kg, IM). It was then transported to the surgical preparation room, where it was given prophylactic antibiotics (5 mg/kg enrofloxacin, IM) and analgesics (0.01 mg/kg buprenorphine, IM) and intubated. It was then transferred to the surgical suite. Deep anesthesia was induced and maintained (1.5–3.0% inhaled isoflurane) and the animal was placed in a stereotaxic frame. During the surgery, expired CO₂, oxygen saturation, blood pressure, and heart rate were monitored with a vital signs monitor (VetSpecs VSM7) and body temperature was maintained with a hot water heating pad. A craniotomy was made dorsal to the SC and covered with a stainless steel recording cylinder (McHaffie and Stein, 1983), which was secured to the skull with stainless steel screws and dental acrylic. The skin was sutured closed around the implant, the anesthetic discontinued, and the animal was allowed to recover. When mobility was regained, the animal was returned to its home pen and given analgesics (2 mg/kg ketoprofen, IM, once per day; 0.01 mg/kg buprenorphine, IM, twice per day) for up to 3 d.

Recording procedures

After a minimum of 7 d of recovery, weekly experimental recording sessions began. In each session, the animal was anesthetized and tranquilized with ketamine hydrochloride (20 mg/kg, IM) and acepromazine maleate (0.1 mg/kg IM), intubated, artificially respired, and secured to a stereotaxic frame in a recumbent position by attaching two head posts to a recording chamber, which ensures that no wounds or pressure points were introduced. Respiratory rate and volume were adjusted to keep the end-tidal CO₂ at ∼4.0%. Expiratory CO₂, heart rate, and blood pressure were monitored continuously to assess and, if necessary, adjust, the depth of anesthesia. Neuromuscular blockade was induced with an injection of rocuronium bromide (0.7 mg/kg, IV) to preclude movement artifacts and to fix the orientations of the eyes and ears. Contact lenses were placed on the eyes to prevent corneal drying and focus them on the tangent plane where LEDs were positioned. Anesthesia, neuromuscular blockade, and hydration were maintained by intravenous infusion of ketamine hydrochloride (5 mg/kg/h), rocuronium bromide (1–3 mg/kg/h), and 5% dextrose in sterile saline (2–4 ml/h). Body temperature was maintained at 37–38°C using a hot water pad.

A glass-coated tungsten electrode (1–3 MΩ impedance at 1 kHz) was lowered manually with an electrode manipulator to the surface of the SC and then advanced by hydraulic microdrive to search for single neurons in its multisensory (i.e., intermediate and deep) layers. The neural data were sampled at ∼24 kHz, band-pass filtered between 500 and 7000 Hz, and spike-sorted online and offline using a Tucker-Davis Technologies recording system and OpenSorter software. When a visual–auditory neuron was isolated (amplitude 4 or more SDs above background), its visual and auditory receptive fields (RFs) were mapped manually using white LEDs and broadband noise bursts. These stimuli were generated from a grid of LEDs and speakers ∼60 cm from the animal's head.

Testing stimuli were presented at the approximate center of each RF. Stimulus intensities were adjusted to evoke weak, but reliable, responses from each neuron for each stimulus modality. Only neurons that were reliably responsive to both visual and auditory cues individually were included in the study. This required that each unisensory response was at least 1 impulse/trial above the spontaneous activity and that this difference was statistically significant (t test, α = 0.05). Stimuli for testing included a visual stimulus alone (V, 75 ms duration white LED flash), an auditory stimulus alone [A, 75 ms broadband (0.1–20 kHz) noise with a square-wave envelope], and their crossmodal combinations at varying stimulus onset asynchronies (SOAs). From these, 3 SOAs were chosen: V0A (simultaneous), V25A (auditory lagging visual by 25 ms), and V50A. These SOAs were chosen because they represent the range over which integration is most robust (Miller et al., 2015) and are characteristic of external events occurring within a reasonable range (i.e., 17 m) of the animal. Furthermore, although the overall magnitudes of multisensory products at the population level tend to be quite similar at these different SOAs (Miller et al., 2015), they can be quite variable within individual neurons (Fig. 2). This is because the shapes of the multisensory responses (and alignments of the unisensory inputs) vary substantially. Therefore, they provide an effective means of evaluating how moment-by-moment changes in unisensory relationships affect their multisensory transform independent of substantial changes in their net products. At the end of a recording session, the animal was injected with ∼50 ml of saline subcutaneously to ensure postoperative hydration. Anesthesia and neuromuscular blockade were terminated and, when the animal was demonstrably able to breathe without assistance, it was removed from the head-holder, extubated, and monitored until ambulatory. Once ambulatory, it was returned to its home pen.

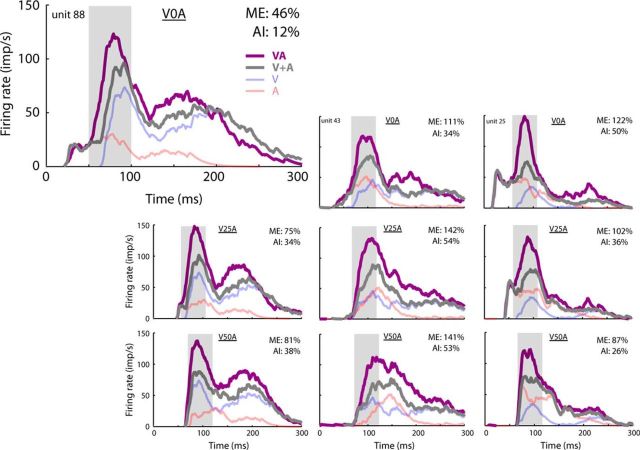
Figure 2.

Variation in multisensory products across neurons and SOAs. In these three exemplar neurons (left to right), the relationship between the timing of the visual and auditory inputs and their synthesized multisensory product was examined. Three SOAs were used with the visual stimulus preceding the auditory: 0 ms (V0A, top), 25 ms (V25A, middle), and 50 ms (V50A, bottom). In each of the panels, the unisensory response spike density functions (V and A) were plotted, as were their arithmetic sum (V + A) and the actual multisensory response they yielded in combination (VA). Note that even the smallest change in the relative timing of the crossmodal component stimuli altered the alignment of their inputs substantially and changed the magnitude of their integrated product significantly (i.e., ME and AI). In each case, the enhanced product was greatest during the period of the IRE (gray shading; Rowland et al., 2007a). Together, these observations suggest that crossmodal inputs are synthesized in real time, but that the scale of the multisensory products that they generate changes during the course of the response.

Data analysis

Analyses were divided into two sections. The first analyzed the empirical data to reveal the operational principles of the moment-by-moment multisensory transform. The second embedded these principles within a neurocomputational model (CTMM) and tested whether they could be used to predict accurately the moment-by-moment multisensory responses of any given neuron. This provided a means of determining the sufficiency and completeness of the empirically derived principles to describe the multisensory transform.

Evaluation of the multisensory transform.

The computations underlying the SC multisensory response (i.e., the manner in which various unisensory inputs are combined to evoke a multisensory discharge train) are typically inaccessible to direct probes. However, the operational principles of the moment-by-moment multisensory transform can be inferred from the overt responses of the neuron to modality-specific cues presented individually (i.e., its unisensory responses) and in combination (i.e., its multisensory response). This is because the impulse generator of the SC neuron that transforms its inputs to its outputs (i.e., its responses) is reasonably assumed to be source agnostic; that is, it is a transform that is consistently applied to all inputs regardless of whether they are unisensory or multisensory. Consistently applied transforms do not alter the statistical relationships between variables (Howell, 2014). Therefore, the relationships between the moment-by-moment unisensory and multisensory responses reflect, on the other side of the impulse generator, relationships between the moment-by-moment unisensory inputs and their multisensory synthesis (i.e., the multisensory transform).

Accordingly, the basic objective was to quantify the relationships between the unisensory and multisensory responses at a high temporal resolution (“moment-by-moment,” operationally: 1 ms resolution) relative to stimulus onset. These comparisons required shifting each of the recorded unisensory responses to align stimulus onsets with those in the matching multisensory condition. For example, in comparisons involving the V0A (i.e., simultaneous) crossmodal condition, the multisensory response at t = 60 ms after stimulus onset was compared with the sum of the unisensory visual and auditory responses at t = 60 ms. In comparisons involving the V50A crossmodal condition, in which the auditory stimulus was delayed by 50 ms relative to the visual stimulus, the multisensory response at t = 60 ms was compared with the sum of the unisensory visual response at t = 60 ms and the unisensory auditory response (recorded on the auditory-alone trials) at t = 10 ms.

For population analyses, samples were grouped by SOA condition and synchronized to the “estimated time of convergence” (ETOC). The ETOC was an estimate of when inputs from both the visual (V) and auditory (A) modalities first converged onto their target neuron in the crossmodal stimulus condition, and thus when the multisensory transform could begin. To find this time, the two unisensory response latencies (LV and LA) were added to the two stimulus onset times (SV and SA) and the maximum of these two sums was identified as follows: ETOC = max(SV + LV, SA + LA).

To obtain quantitative measures of “instantaneous” response efficacy, the binary impulse raster matrices (1 ms resolution) for each response were converted to spike density functions by convolving each trial with a narrow Gaussian kernel [N(0.8 ms)] and calculating mean and variance across trials. Response onsets and offsets (relative to stimulus onset) were calculated from each impulse raster using a three-step geometric method (Rowland et al., 2007b). This method identifies response onsets and offsets by finding the timing of “hooks” in the cumulative impulse count function, which indicate changes in the firing rate. In addition, a linear splining technique was applied to each response trace (slope at time t estimated as the slope of a line connecting the mean spike density function at t − 10 ms and t + 10 ms) to generate an estimate of its “instantaneous” slope.

Correlation-based analyses of the timing of multisensory and unisensory responses were conducted to determine whether their dynamics were time locked. A temporal correlation between each mean multisensory response and the summed unisensory responses (Fig. 3) was calculated as the R² between firing rate traces paired by time step (1 ms resolution). Because conventional statistical thresholds require that observations be independent and identically distributed (invalid for data sampled on adjacent time steps), a randomization and resampling procedure was used to evaluate the statistical significance of this R² value. The sampling distribution of R² expected if the multisensory and summed unisensory responses were uncorrelated was calculated by repeatedly (10,000 times): (1) randomizing the times of the impulses in the multisensory impulse raster, (2) calculating the resultant spike density function, and (3) calculating the R² between the now-randomized multisensory and unisensory spike density functions as before (i.e., paired by time step). The proportion of this distribution of these R² values that was greater than the actual R² value was used to estimate the p-value for this correlation. A second analysis correlated the multisensory and summed unisensory responses at each time step across the neurons sampled. To accomplish this, samples were grouped by SOA and synchronized by the ETOC. Then, at each time step, R² was computed between the multisensory and summed unisensory firing rates for the population of neurons studied. Statistical significance was determined using conventional standards (i.e., α = 0.05). Identical analyses were applied to the estimated instantaneous slopes of the multisensory and unisensory responses. A third analysis calculated the cross-correlation coefficients between the multisensory and summed unisensory responses at multiple temporal lags (5 ms intervals) to determine whether their dynamics were time locked.

Figure 3.

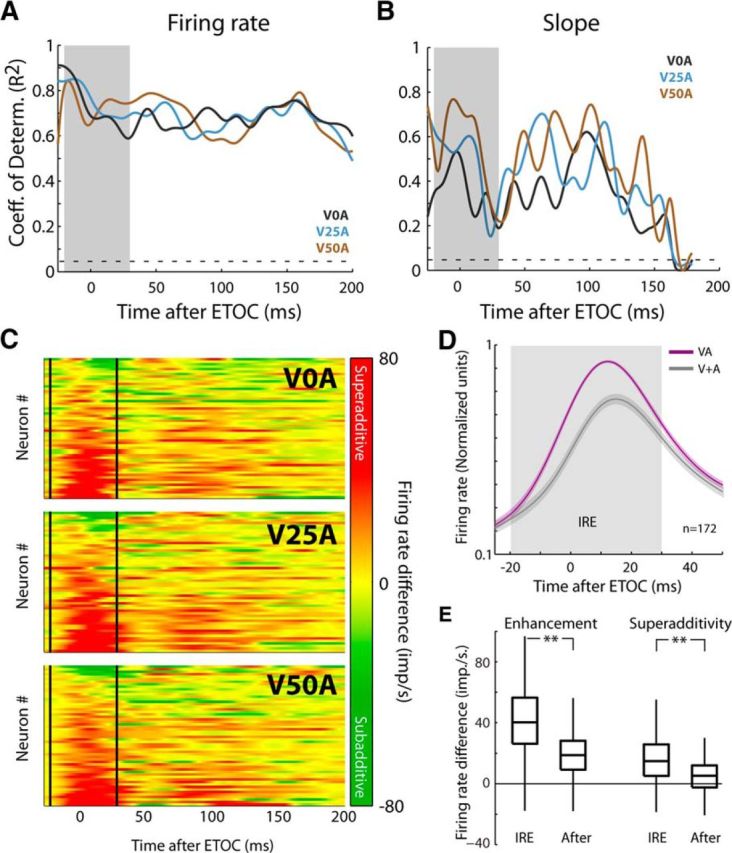
Population differences between multisensory response and additive prediction. A, Samples were grouped by SOA and synchronized by ETOC. The unisensory–multisensory correlation was then assessed within each of the 3 groups (V0A, V25A, and V50A). The coefficient of determination (R²) was significant and high throughout the duration of the multisensory response (the gray shading indicates the region of the IRE). The dashed line indicates the threshold for significance (R² = 0.045). B, Significant (albeit diminished) correlations were also observed within each cohort between the moment-by-moment slopes of the multisensory and summed unisensory responses. The dashed line indicates the threshold for significance (R² = 0.045). C, Heat maps for the 3 SOAs for all neurons (each row is a neuron) illustrate the consistency of the IRE across neurons and SOAs (delineated by solid vertical lines). They also illustrate the transition in the magnitude of the multisensory products, which are heavily superadditive (red) during the IRE but change to more additive (yellow) and subadditive (green), thereafter. D, Normalized, averaged multisensory (VA) and summed unisensory (V + A) responses within, and immediately after the IRE (gray shading) were plotted. As shown in the heat map, the superadditive enhancement was largely confined to the IRE. E, Comparisons of the average firing rate differences between the multisensory and best unisensory component responses (multisensory enhancement) and between the multisensory and summed unisensory responses (superadditivity) demonstrated that both were significantly (p < 0.001) greater within, than after, the IRE. Box-and-whisker plots indicate median, interquartile range, and range.

To examine trends in the multisensory/unisensory magnitude difference (Fig. 3), the multisensory and summed unisensory response traces were aligned and subtracted directly from one another. The amplitude of the resulting difference trace (which indicated nonlinearity in the multisensory product) was assessed within different windows of time (t tests). This often exposed a phenomenon referred to as the “initial response enhancement” (IRE; see Rowland et al., 2007b). Multisensory amplification was further quantified by calculating the proportionate difference between the mean total multisensory response magnitude (#impulses) and either the largest associated unisensory response magnitude (“multisensory enhancement,” ME) or the sum of the unisensory response magnitudes (“additivity index,” AI) (Meredith and Stein, 1983) as follows:

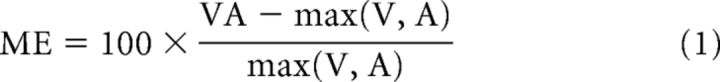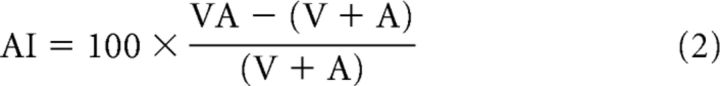All response magnitudes were corrected for levels of spontaneous activity as in earlier studies (Alvarado et al., 2009). ME and AI were calculated for the entire response and also within two windows, one representing the early window of multisensory interaction which contained the IRE (ETOC − 20 ms to ETOC + 30 ms) and the other the remaining portion of the response. The deviation of ME and AI from zero and differences between them across these windows of time were evaluated statistically using t tests (Fig. 3). It is important to note that each of these empirical analyses was conducted on each neuron in the sample to identify their common principles.

CTMM.

The principles inferred from the empirical analyses above were tested for validity and completeness by embedding them in a neurocomputational model (the CTMM) and evaluating whether this model could predict accurately and reliably the multisensory response of a given neuron in an unbiased fashion given only knowledge of the associated unisensory responses of the neuron (Fig. 1). The model was designed to be the simplest and most direct implementation of the principles of the multisensory transform identified above and its use here parallels other statistical regressions. For example, just as a simple linear regression between two variables is used to support a (linear) model mapping from variable X to variable Y according to some free parameters (slope and intercept), here, a (nonlinear) model (the CTMM) maps from unisensory responses to multisensory responses according to some internal parameters (n = 3). In both cases, the validity and completeness of the model is supported when the mapping errors are small and unpatterned.

A leaky integrate-and-fire single neuron model (I/F) is the simplest model of a neuronal impulse generator. The output impulse train of a model I/F neuron, R(t), produced by a continuous “net input signal,” I(t), and stochastic zero-mean Gaussian-distributed “noise input,” N(0, σ), is determined by a membrane potential, V(t), with time constant τ and a rule that clamps V(t) to rest (0) for some refractory period (1 ms) after it exceeds an arbitrarily defined threshold of V(t) > 1 as follows:

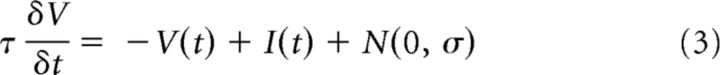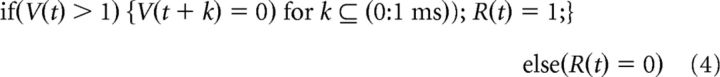The “noise input,” N(0, σ), represents random fluctuations of input and is randomly sampled on each moment in time. Equations 3 and 4 were simulated numerically from an initial condition to produce an output impulse train in response to any arbitrary input, I(t). It was then simulated many (10,000) times from randomly selected initial conditions, V(0) ∈ [0,1], and the resulting impulse raster convolved with a narrow Gaussian kernel, N(0, 8 ms), and averaged across trials to estimate a mean response S to arbitrary input I. This is referred to as the “forward model transform”: S = M(I|τ, σ). The prediction for the multisensory response S_VA is generated from I_VA, which is calculated from the responses of the neuron to the modality-specific components using an equation with three components:

The first two components represent the input from the individual modalities (I_V and I_A) combined according to the simplest possible rule: summation. Due to the way that they are estimated (see below), I_V and I_A already account for both excitatory and inhibitory influences. The third component (H_VA) is a delayed, “calibrating” inhibition in the multisensory condition that is in addition to the inhibition already captured by the unisensory inputs. Here, “calibrating” means that its magnitude is dependent on the strength of the preceding response and it has the effect of forcing the higher activity levels associated with the multisensory response back to baseline.

To maintain conceptual parallels with other regression techniques and to mitigate concerns of overfitting, a simple formula for its a priori calculation is provided based only on the observed unisensory responses (i.e., without knowledge of the multisensory response). This formula was constructed to offset amplification in the multisensory response and includes a low-pass filtering convolution to introduce a delay as follows:

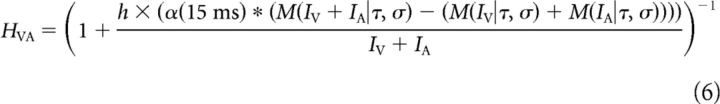In Equation 6, α represents an α function with a rate parameter of 15 ms that delays and smooths the predictive error calculation in the numerator (* denotes the operation of convolution). It scales with the amplification of the multisensory response. Parameter h controls the strength of this inhibitory component. Equations 3–6 represent a complete system for predicting the multisensory response given estimated unisensory inputs I_V and I_A and according to parameters τ, σ, and h. They are simulated numerically with temporal resolution Δt = 0.1 ms using the solution of Equation 3 under the assumption that input is approximately constant within a time step (Koch and Segev, 2003, Chapter 9).

Conceptually, the unisensory inputs are estimated by applying the inverse model transform to the overt unisensory spike density functions as follows:

This is accomplished numerically by applying an iterative algorithm to the recorded unisensory spike density functions. In generic form, this algorithm infers input I(t) from observed spike density function FR(t) according to parameters τ and σ.

The algorithm is predicated on the idea that the instantaneous firing rate of a neuron depends not only on the instantaneous input magnitude, but also on its recent history. Therefore, it begins with an initial estimate of input magnitude. It then moves forward in time, estimating at each subsequent time step the most likely input value that would produce the observed firing rate. To estimate the initial input magnitude (I_spont), the algorithm starts with an assumption that the spontaneous firing rate is constant (as measured −100 to 0 ms before stimulus onset). I_spont is identified as the constant input magnitude that will produce the observed “output” firing rate FR_spont of the neuron. Operationally, I_spont is calculated by simulating Equations 3–4 for different levels of constant input and identifying a value that produces an average firing rate within 0.2 impulses/s of FR_spont. Then, at each future time step T after stimulus onset, I(T) is initially assigned value I(T − 1). Equations 3–4 are simulated from t = −100 to t = T 10,000 times and the mean value of the firing rate of the model at time T, S(T), is calculated. I(T) is then raised or lowered based on whether the mean S(T) underpredicts or overpredicts the actual firing rate, FR(T) and the simulations are rerun. When the mean of S(T) is within 1% or 0.5 impulses/s of FR(T), then the value of I(T) is fixed and the algorithm advances to time step T + 1 (note that this involves only unisensory responses).

Applying this procedure to the unisensory visual and auditory responses derives the unisensory input traces I_V(t) and I_A(t) for each value of τ and σ. Equations 3–6 were then simulated 10,000 times with random initial conditions to derive a model-predicted multisensory response trace based only on the unisensory responses for each combination of parameters used in this study. Ideal or “optimal” values of the model parameters for each sample (Table 1) were identified as those minimizing the mean sum-of-squares difference between the model-predicted and actual multisensory response trace over the entire response duration.

Table 1.

List of parameters of the CTM model, a description of what each represents, and the range of their optimal values

Parameter name	Description	Optimal range
τ	Time constant controlling the speed with which the model reacts to changing input	5–10 ms
σ	Random fluctuations of input	1.5–2.5
h	Strength of delayed, calibrating inhibition	0.0064–0.0128

Evaluation of the CTMM.

The model was evaluated for accuracy, reliability, and bias. Accuracy was assessed by comparing, on a neuron-by-neuron and moment-by-moment basis, the model-predicted firing rate to the mean firing rate of the actual multisensory response normalized by the SE (the error t-score). For an individual sample, if a model prediction was within the central 95% of this distribution it was considered to be “practically equivalent.” Reliability was assessed by the SE of the distribution of error t-scores at each moment in time. Bias (i.e., whether a model consistently overpredicted or underpredicted) was determined at each time step by calculating whether the model-predicted response was greater than (scored as +1), lesser than (−1), or equal to (within 10%) the actual multisensory response (0). These scores were averaged across neurons at each time step.

Successful prediction of the moment-by-moment dynamics of the multisensory response should, in principle, also mean successful prediction of net or total response metrics (e.g., total response magnitude) and thus any higher-order features based on them: ME, AI, and sensitivity of the multisensory response magnitude to SOA for individual samples. This was evaluated by correlating the values calculated for individual samples with the model predictions of them.

In addition, the performance of the CTMM was compared with that of several referent models in which various CTMM components were “broken” or removed. These comparisons provided a way of evaluating the relative importance of the manipulated CTMM parameters. Principal among these other referents was an “additive” model formed by summing the unisensory responses. This represented a referent in which integration took place in real time, but did not contain any of the nonlinear components of the CTMM. CTMM performance was also evaluated against another referent model in which only the delayed, calibrating inhibition was removed. Other referent models that were used for comparison involved fixing one or more of the CTMM parameters in a sensitivity analysis using a Bayesian information criterion (BIC) (Kass and Raftery, 1995). The final analysis determined whether the CTMM parameters optimally fit for different neurons could be used to explain the observed variation among their multisensory responses.

Results

Overview

The responses of individual visual-auditory multisensory SC neurons (n = 86) were recorded and analyzed to determine each neuron's moment-by-moment unisensory-to-multisensory transform. These 86 neurons were tested at three SOAs each, yielding 258 multisensory responses. Of these 258 responses, 172 (67%) exhibited multisensory integration, defined here by multisensory enhancement (the multisensory response was significantly greater than the largest unisensory response). These 172 samples were used for the majority of analyses, which revealed two operating principles of the multisensory transform: (1) unisensory inputs are integrated continuously and in “real time” (i.e., virtually instantaneously) and (2) there is a delayed, calibrating inhibition. To determine whether these principles represented a sufficient and complete description of the multisensory transform, they were then embedded into the neurocomputational model (CTMM) as described in the Materials and Methods, which used the unisensory visual and auditory responses of a neuron to predict its moment-by-moment multisensory response. Finally, the model was used to explain observed variation in multisensory products.

Empirical analyses

Each of the neurons was studied with a battery of randomly interleaved tests that included the component stimuli individually and their spatially concordant crossmodal combination at three different ecologically common SOAs: synchronous (V0A), visual 25 ms before auditory (V25A), and 50 ms before auditory (V50A). The unisensory response latencies (visual = 68 ± 10 ms, auditory = 22 ± 8 ms, mean ± SD) and magnitudes (visual = 6.3 ± 4.3 impulses/trial, auditory = 4.8 ± 3.4 impulses/trial) and estimates of the net ME (105 ± 98%) and AI (36 ± 46%) were all consistent with previous reports (Stein et al., 1973a, 1973b; Stanford et al., 2005; Yu et al., 2009; Pluta et al., 2011).

The fundamental operating principles of the moment-by-moment multisensory transform were immediately evident from inspection of the unisensory and multisensory responses (spike density functions; see Materials and Methods) of several representative exemplars (Fig. 2). First, when responses were aligned by stimulus onset, there was a strong correlation between the dynamics of the summed unisensory and multisensory responses: when the former rose or fell, there were similar changes in the latter even though their magnitudes differed, suggesting that the unisensory inputs were being synthesized immediately upon arrival at the target neuron. This observation may seem somewhat counterintuitive for two reasons. First, multisensory integration is known to depend on descending inputs from association cortex (Wallace and Stein, 1994; Jiang et al., 2001; Alvarado et al., 2009; Yu et al., 2013), which, by being multiple synapses downstream from primary tectopetal sources, would be expected to introduce a delay in the emergence of this transform (Cuppini et al., 2010). Second, its immediacy would not be expected if that transform required intrinsic SC circuit dynamics for processing (Deneve et al., 2001). Indeed, the enhancement visible in the multisensory response was largest near the ETOC (producing the IRE; Rowland et al., 2007b), but rapidly diminished thereafter. Although there are several ways to interpret the post-IRE downward trend (see Discussion), the most plausible is that it is due to a delayed inhibitory influence.

These two operational principles were robustly represented in the population. Across the entire response window, significant correlations (see Materials and Methods) were identified between the magnitudes and slopes of the mean multisensory and associated summed unisensory responses for virtually every sample (100% of magnitude correlations and 99.4% of slope correlations were significant). In a second analysis involving comparing the moment-by-moment responses pooled over samples grouped by SOA, significant (p < 0.05) correlations in response magnitude were evident at all time steps after the ETOC (Fig. 3A) and these did not change significantly at different stages of the response. Significant (p < 0.05) correlations in the slopes of the responses were also identified throughout, but these diminished as responses became less robust and more variable late in the discharge train, dropping below significant correlation at 165–169 ms after ETOC. There was also high consistency in the results at the different SOAs, so that no significant differences in any of these metrics were noted across SOA groups. A cross-correlational analysis compared the multisensory and summed unisensory responses. Presumably because multisensory responses are speeded relative to their unisensory counterparts (Rowland et al., 2007b), the maximum temporal correlation was identified when the summed unisensory responses were shifted earlier in time by ∼15–20 ms. This finding is consistent with a model in which the SC neuron integrates inputs as soon as they arrive, even when they are subthreshold, and converts them to output using standard mechanisms for action potential generation. Taken together, these observations reveal that the multisensory and unisensory response traces are reliable, that multisensory responses are not de novo quantities with arbitrary dynamics, and, most importantly, that the multisensory transform synthesizes unisensory inputs without delay.

The difference in magnitude between the multisensory and summed unisensory responses was greatest around the ETOC where the IRE was largest (85% of samples were net superadditive during the IRE; Fig. 3C). This feature was consistent across neurons despite variation among the temporal profiles of unisensory responses, did not depend on SOA, and remained robust at the population level (Fig. 3D). Within the IRE, the average (median) raw multisensory response enhancement was 40 impulses/s and 15 impulses/s above the sum of the unisensory responses (Fig. 3E). After the IRE, this dropped to 19 and 5 impulses/s, respectively. This trend is consistent with the influence of a delayed, calibrating inhibition.

These two operational principles (real-time integration and delayed, calibrating inhibition) alone proved to be sufficient to understand the multisensory transform. This was established quantitatively using the simplest possible neurocomputational model (CTMM; see Materials and Methods) that would encompass these principles. The model was then used to predict each individual moment-by-moment multisensory response given only knowledge of the associated unisensory responses.

CTMM evaluation

The CTMM predictions are shown in Figure 4 for a highly representative neuronal exemplar tested at multiple SOAs (Fig. 4A,B), as well as for neurons with more idiosyncratic response profiles (Fig. 4C). In all cases, the CTMM was highly accurate in predicting the temporal dynamics of the multisensory response. Therefore, it also predicted the total magnitude of each response accurately, and thus the net enhancement of the response (ME and AI), as well as variations in its magnitude at different SOAs.

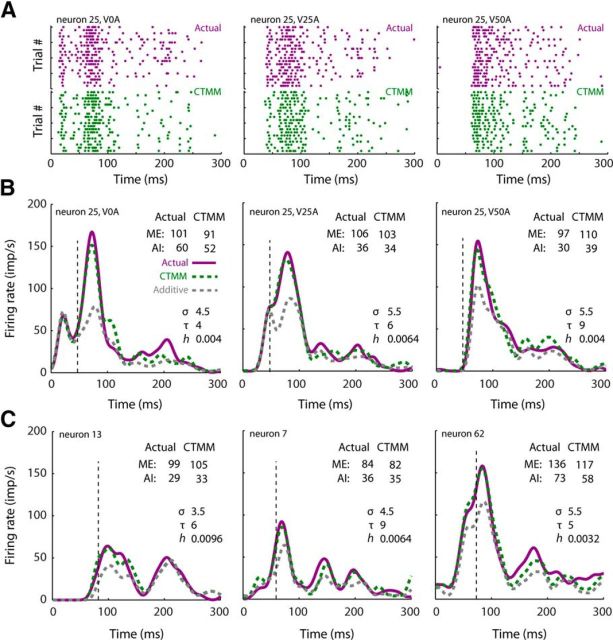
Figure 4.

CTMM accuracy at the single neuron level. A, Actual response rasters (purple) are plotted along with model output (green) for a representative neuron at three SOAs. Each dot represents an action potential and each row of dots represents a response of the neuron to a single crossmodal presentation. Twenty trials are plotted for both actual responses and model output, although more were collected/produced. B, Actual multisensory responses (purple) and model responses (green) of the same exemplar neuron as in A plotted in spike density function form. Multisensory responses were matched by the predicted response at each SOA, whereas the additive prediction (dashed gray) had very poor performance near the ETOC (vertical line), when the most robust integration was taking place (i.e., the IRE). Note that model accuracy was high for both total ME and AI. C, Model accuracy remained high even for neurons with atypical response profiles.

The CTMM had low error scores (mean error t-score = 1.1 ± 0.9) throughout the response window, but error was lowest (0.9 ± 0.7) around the ETOC, when the strongest multisensory products were observed (Fig. 5A). The foil additive model behaved quite differently: its error was not only higher throughout the response, but particularly high around the ETOC (mean error t-score = 2.3 ± 1.4), when the integration process was most productive. As shown in Figure 5B, the CTMM-predicted multisensory responses were often statistically indistinguishable from the actual multisensory responses, with 85% of them being practically equivalent around the ETOC and 78% practically equivalent across the entire response (versus 46% and 61% for the additive model). Furthermore, the small CTMM errors were generally unbiased (Fig. 5C), even around the ETOC (−0.01 versus −0.53 for the additive model) and the CTMM was equally accurate for all response efficacies, whereas the additive model errors were especially high when responses were weak (Fig. 5D).

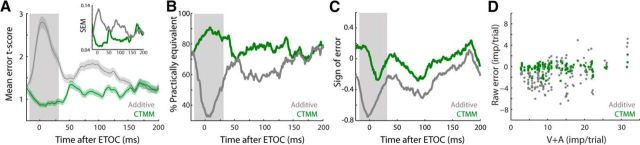
Figure 5.

CTMM accuracy at the population level. A, Mean error t-score (across neurons) at each moment in time after the ETOC was quantified as a t-score (a larger score is worse). The CTMM error (green) is much lower than that of the additive prediction (gray) throughout the multisensory response, but particularly within the IRE (gray box), where multisensory enhancement was greatest. A, Inset, SEM t-score for the CTMM was also lower than that of the additive model throughout most of the response, indicating that CTMM more precisely captured the variation within the population. B, Percentage of CTMM predictions (green) and additive predictions (gray) across the population that are “practically equivalent” (i.e., not statistically distinguishable) from the actual multisensory response at each moment in time. Note the high effectiveness of the CTMM predictions, especially during the IRE, where the performance of the additive model is particularly poor. C, Bias of the CTMM (green) and additive prediction (gray) at each moment in time indicate when either model prediction of the multisensory response was consistently too high (positive) or too low (negative). The CTMM predictions varied around 0. However, the additive model underestimated the magnitude of the multisensory response significantly during the IRE. D, By regressing the total error of each model's predictions against the sum of the total unisensory magnitudes, a pattern of errors was noted for the additive prediction (gray) that changed as the magnitude of the multisensory response changed. Such a pattern of errors was not present in the CTMM predictions.

Because the CTMM could predict the moment-by-moment firing rate of the multisensory response reliably, it could also predict its total response magnitude reliably (R² = 0.98). Therefore, it could also predict the traditional quantified products of multisensory integration reliably [ME (R² = 0.91) and AI (R² = 0.89); Fig. 6A] and could also predict the tuning of these products to SOA in individual neurons accurately (Fig. 6B) (Rowland et al., 2007b; Miller et al., 2015).

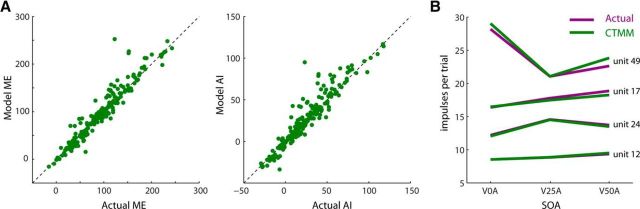
Figure 6.

CTMM is highly accurate in predicting the secondary (“higher-order”) features of multisensory integration. A, As a consequence of having predicted the moment-by-moment multisensory response accurately, the CTMM also predicted the total response magnitude accurately and thus such traditionally quantified derived metrics of multisensory integration as ME (left) and AI (right). Each point in these plots represents a different sample, with the line of unity indicating an exact match between the CTMM and the empirical data. B, CTMM also predicted accurately the temporal tuning of the multisensory products in each neuron at each SOA tested, as illustrated by these four exemplars with different SOA-tuning preferences.

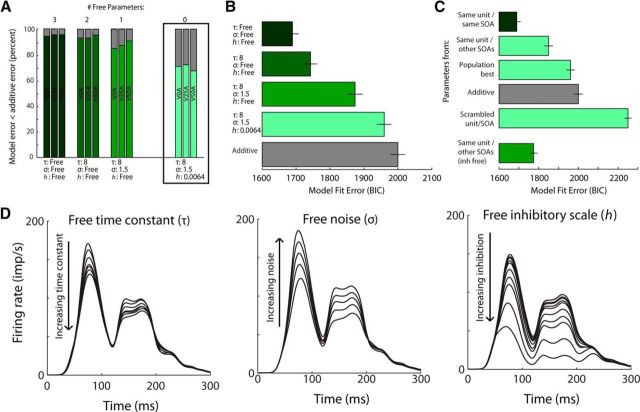
The accuracy of the CTMM was, of course, best when all three model parameters were selected optimally for each sample (BIC = 1689 ± 19; see Materials and Methods). However, τ could be fixed to its population-optimal value (8 ms) and there was only a minor increase in mean error (BIC = 1743 ± 19) across the population. However, even when all parameters were fixed to their population-optimal values (τ = 8 ms, σ = 1.5, h = 0.0016), the CTMM was still significantly more accurate (BIC = 1960 ± 21) than the additive model (BIC = 2000 ± 22) (Fig. 7B). In this circumstance, the CTMM outperformed the additive model 75% of the time in the region around the ETOC and 70% of the time overall (Fig. 7A), revealing the importance of its nonlinear components.

Figure 7.

Parameter sensitivity. A, Fixing various numbers of free parameters (3, 2, 1, 0) shows that, even with no free parameters, the CTMM is better at predicting the multisensory response than an additive prediction for ∼70% of neurons and this is true regardless of SOA. B, BIC error is similarly better than for the additive model regardless of the number of free parameters. All bars differ significantly from each other [paired t test, p < 0.005. BIC = n * ln(RSS/n) + k * ln(n)]. C, Fixing all parameters based on the best parameters found using the same neuron but at a different SOA (second bar) was far better than simply using the best parameters for the overall population (third bar) or choosing the parameters from a random unit/SOA (fifth bar). Using the tau and noise parameters from the same unit/other SOA and allowing only the inhibition scale to vary freely further reduced the error. All bars differ significantly (paired t test, p < 0.005). D, Exemplar neuron demonstrating the impact of changing the three parameters within our tested range: τ (left), σ (middle), and h (right). Note how changing each of the parameters primarily affects the magnitude and actually has a relatively small impact on the shape of the model output, particularly at the beginning of the multisensory response (IRE).

The importance of the delayed inhibitory component of the CTMM was further assessed by comparing its performance with another foil model, one identical to the CTMM but lacking the delayed inhibitory component (i.e., setting parameter h to zero). This reduced model exhibited a BIC of 1863 ± 22, substantially worse than the intact CTMM.

The model parameters were also found to represent consistent and predictable features of a given neuron's multisensory integration capabilities. This was tested by using best-fit parameters for a neuron at a particular SOA and then testing those parameters for the same neuron at a different SOA. If the parameters represent actual features of a neuron's multisensory integration capabilities, then this should produce a more accurate prediction than if the parameters are instead taken from a randomly chosen neuron. Indeed, this was found to be true; using the best parameters from the same neuron but at a different SOA produced an average BIC error of 1849 ± 22 (Fig. 7C, second bar), whereas using the best parameters from a randomly chosen neuron produced an average BIC error of 2250 ± 17 (Fig. 7C, fifth bar). This indicated that the optimal parameters for a given multisensory response were not arbitrary, but were a highly predictable feature of each neuron. The impact of different parameter variations on the model output is shown in an exemplar in Figure 7D. Notably, the enhancement early in the response window (i.e., during the IRE) was less sensitive to these parameters than were later portions.

Using the CTMM to predict new relationships

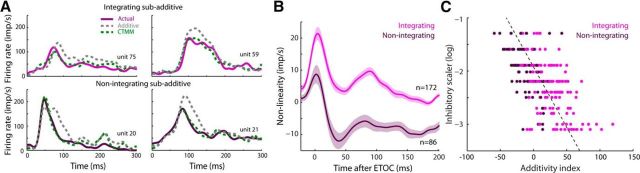
One long-standing puzzle is how so-called “nonintegrating” SC neurons can be responsive to inputs from multiple sensory modalities and yet be unable to produce enhanced responses to their combined inputs (cf. Stein and Meredith, 1993; exemplars in Fig. 8A). In other words, how can two independent excitatory inputs yield a response that is no more robust than one of them alone? One possibility is that, at the time of testing these neurons, the visual and auditory input traces were mismatched in some way so as to preclude facilitatory interactions. Another possibility is that these neurons lack some critical internal multisensory machinery. Interestingly, the CTMM predicts the multisensory responses of integrating (n = 172) and nonintegrating (n = 86) samples with approximately equal accuracy (t test, p = 0.12). This was initially surprising given that one of the premises of the model is the linear real-time synthesis of the crossmodal inputs. However, examination of the temporal profiles of enhancement (i.e., the “nonlinearity” or difference between actual response and additive estimate) in integrating and nonintegrating samples revealed very similar patterns, except that the nonintegrating samples exhibited what could be interpreted as much larger suppressions later in the response (Fig. 8B). Consistent with this, nonintegrating samples were found to be fit optimally by larger values of the parameter h (Fig. 8C). The mean fit h parameter value for integrating samples was 0.009 ± 0.011 (mean ± SD) and for nonintegrating samples was 0.017 ± 0.015. (Mann–Whitney U, p < 0.001). This suggests that interneuronal variability in the amount of inhibition (or sensitivity to it) within the SC may be principally responsible for variation in the products of a multisensory response. This observation challenges the common notion that integrating and nonintegrating neurons are engaged in fundamentally dissimilar behaviors and computations. Rather, the CTMM reveals that neurons typically categorized as “integrating” or “nonintegrating” exist along a continuum of enhancement as predicted by the optimal h parameter. Whether the same results would be obtained for nonintegrating SC neurons in different populations in which they constitute the majority of samples (e.g., neonatal animals, those raised in the darkness or in omnidirectional noise, or those with compromised cortical inputs; Wallace and Stein, 2000; Yu et al., 2010; Xu et al., 2014) is currently unknown.

Figure 8.

CTMM explains variations in enhancement magnitude among neurons. A, Four atypical exemplar neurons are shown: the top two show subadditive multisensory enhancement and the bottom two show no multisensory enhancement. Nevertheless, both groups show similar trends, although with more subadditivity in the nonintegrating samples. Conventions are the same as in Figure 5. B, These similarities are also apparent at the level of the population of integrating or nonintegrating neurons. The most apparent difference between integrating and nonintegrating samples appears to be the stronger delayed inhibition in the latter. C, Magnitude of the CTMM inhibitory scaling parameter (h, y-axis) was highly predictive of the neuron's integration capabilities as measured by the AI (the higher the h factor, the lower the AI). Also shown is the best fit line (dashed) to the relationship.

Discussion

In 1952, Hodgkin and Huxley derived a nonlinear, continuous-time model of action potential generation from careful study of the statistical principles of this phenomenon in the squid giant axon. That study provided a framework for studying and predicting neuronal behavior. It was followed by a number of other influential works in which the basic biophysical properties of individual neurons, inferred from empirical study, were then tested for their completeness via forward simulation (Churchland and Sejnowski, 1992; Rieke, 1997; Koch, 1999; Dayan and Abbott, 2001; Gerstner and Kistler, 2002; Koch and Segev, 2003). The present study attempted to continue in that spirit with the objective of predicting the products of multisensory integration. Two basic principles of the individual SC neuron's multisensory transform proved to be essential for this purpose: (1) crossmodal inputs (visual and auditory) are synthesized continuously in real time as they converge on their common target neuron and (2) later portions of the multisensory response are reduced by a delayed, calibrating inhibition. These principles governing the underlying biological process were exposed via statistical analysis of neural responses to the presentation of visual and auditory cues individually and in combination. To ensure that these two principles were sufficient to describe the multisensory transform accurately and completely, they were embedded within a simple neurocomputational model (CTMM), which was used to predict the actual magnitude and timing of a neuron's moment-by-moment multisensory (visual–auditory) response based only on its two unisensory responses.

The predictions of the CTMM proved to be highly accurate, producing the typical response profile in which the transform yields superadditive products during the early phase of unisensory input convergence and then gradually transitions to additive products thereafter. Indeed, most of its predictions were practically equivalent to the empirically observed responses. The CTMM was consistently accurate for neurons with differently shaped response profiles, as well as for responses obtained from different SOAs from the same neuron. The few predictive errors that were observed were small and unbiased. On this basis, it was concluded that the identified principles capture the most reliable aspects of the multisensory transform; that is, they constitute a sufficient description of the underlying biological process. It is important to note that the CTMM only uses the strength and timing of the unisensory responses in making predictions about multisensory products. This is consistent with the empirical literature suggesting that these factors are the principal determinants of a multisensory product. Although other stimulus and organismic features (Meredith et al., 1987; Wallace and Stein, 1997; Wallace et al., 1998; Kadunce et al., 2001; Miller et al., 2015) have thus far been found to have little influence over this process, the possibility that other factors than those explored here could also have an impact cannot yet be excluded.

The current approach derives the structure of the CTMM directly from elemental neural response properties. By doing so, it avoids the need to speculate about which of many possibilities are actually at work. It also goes beyond reproducing general relationships between the averages of unisensory and multisensory responses across large populations of neurons to reproducing the moment-by-moment yield of the multisensory transform in each individual neuron. This, of course, also allows for more global predictions of net multisensory magnitude of a response (i.e., the proportional enhancement of the multisensory response relative to the unisensory responses) and the sensitivity of this enhancement to other factors such as the SOA. In short, the CTMM can be used to predict how a neuron will respond to any combination of visual and auditory cues at any SOA and (presumably) under any environmental condition based only on its unisensory responses. Further, it can also be used as a tool to parameterize the transform implemented by each neuron and compare it across different neurons, cohorts, and manipulations.

As a specific demonstration of how the predictive power of the CTMM can be used as a tool in data analysis, it was used here to understand how so-called “nonintegrating” neurons could be responsive to multiple sensory modalities yet fail to produce a net enhanced response to their combination. The responses of these neurons were predicted with the same accuracy as were those of integrating neurons. The only difference was higher values for h, the parameter controlling the strength of the delayed inhibitory dynamic. This result suggested that these neurons have the same basic capabilities as their counterparts, but for unknown reasons are more strongly affected by delayed inhibition.

The delayed inhibitory component is an abstract entity here and does not have a 1:1 relationship with any single biological aspect, but it is likely to be dependent upon preceding portions of the (multisensory) response, as is common among neurons elsewhere in the brain. In many cases (e.g., olfactory cortex and visual cortex), principal neurons are reciprocally connected with local inhibitory circuits that enforce a homeostatic “reset” to baseline activity levels after sensory-processing events (Francis et al., 1994; Koch and Davis, 1994; Ren et al., 2007). However, it is also possible that the mechanism of delayed inhibition represents a more local effect, one dependent on adapting ionic channels within the multisensory SC neuron's membrane (Brette and Gerstner, 2005).

It is important to note that, in the current analysis, the visual and auditory inputs are each considered as singular inputs even though they are known to derive from a number of sources (Edwards et al., 1979) and may play different roles. For example, the anterior ectosylvian sulcus is known to provide a major input to the SC and to play a critical role in SC multisensory integration (Wallace and Stein, 1994; Wilkinson et al., 1996; Jiang et al., 2001, 2006). Each of the other inputs to the SC may contribute in their own way to the strength and timing of multisensory integration, but how these various inputs operate within the current context remains to be determined. However, the model does assume that the input channels are independent and have a net excitatory influence. In its current form, it makes no predictions about responses to other stimulus conditions (e.g., multiple cues from within the same modality), but it can be extended to do so.

It is also important to note the ubiquity of the superadditive computation observed here. This shows that SC multisensory integration is not, as has been previously considered, a minor phenomenon limited to a few samples or specific conditions, thereby limiting its behavioral role (Holmes and Spence, 2005; Fetsch et al., 2013). The presence of superadditive computations around the ETOC is a highly characteristic feature of integrated SC multisensory responses, being seen in nearly all such neurons under all conditions (Fig. 3). However, this IRE (Rowland et al., 2007b) is not limited to the time at which the visual and auditory inputs first converge on their common target neuron and initiate activity, but continues for some time (e.g., 40 ms) thereafter, when the unisensory inputs are already superthreshold. Therefore, it not only represents the period of greatest enhancement, but also encompasses the most active phase of the multisensory response. Additive computations, in contrast, are mostly observed in the response's declining phases. The timing of these superadditive and additive computations in this structure also has important functional implications. Given that SC-mediated behavioral responses (e.g., saccades) are often initiated 80–180 ms after stimulus onset (Fischer and Boch, 1983; Sparks et al., 2000), the IRE may be the response phase most important for SC-mediated behavioral decisions (Rowland et al., 2007b). The additive/subadditive computations that take place later in the multisensory response as the result of the calibrating inhibition may have little to do with these immediate decisions and reactions, but may support later-occurring processing aims or provide a resetting mechanism.

In sum, the present observations reveal the underlying mechanism by which neurons integrate information across the senses on a moment-by-moment basis and suggest that the biophysical mechanisms underlying this process are likely to be much simpler than previously thought (Anastasio and Patton, 2003; Rowland et al., 2007a; Cuppini et al., 2010). The CTMM explains not just the general relationship between canonical multisensory and unisensory responses, but also the observed variation in the actual outcomes of multisensory integration over time and across neurons. Therefore, it can be a useful tool moving forward by quantitatively parameterizing the multisensory transform implemented and has been used here to suggest a resolution to a long-standing puzzle in the field regarding “nonintegrating” multisensory SC neurons. It seems reasonable to expect that this approach will be effective with multisensory neurons in other areas of the brain and with other sensory modality combinations, but this remains to be determined.