Summary
The medial entorhinal cortex (mEC) has been identified as a hub for spatial information processing by the discovery of grid, border, and head-direction cells. Here we find that in addition to these well characterized classes, nearly all of the remaining two thirds of mEC cells can be categorized as spatially selective. We refer to these cells as non-grid spatial cells and confirmed that their spatial firing patterns were unrelated to running speed and highly reproducible within the same environment. However, in response to manipulations of environmental features, such as box shape or box color, non-grid spatial cells completely reorganized their spatial firing patterns. At the same time, grid cells retained their spatial alignment and predominantly responded with redistributed firing rates across their grid fields. Thus, mEC contains a joint representation of both spatial and environmental feature content, with specialized cell types showing different types of integrated coding of multimodal information.
Introduction
The medial entorhinal cortex (mEC) is specialized for spatial information processing with many neurons in the superficial layers displaying spatially and directionally selective firing (Hafting et al., 2005; Sargolini et al., 2006; Solstad et al., 2008). Among mEC cell types, grid cells show the most well defined spatial firing fields and, similar to place fields in the hippocampus (O’Keefe and Nadel, 1978), the spatial firing locations of these fields are reliably reproduced when animals repeatedly explore the same environment (Hafting et al., 2005). Moreover, grid cells respond to exploration of distinct environments with profound shifting of their spatial firing patterns and, concurrently, orthogonal hippocampal place cell maps are formed (‘global remapping’) (Fyhn et al., 2007; Leutgeb et al., 2005). The parallel reorganization of activity patterns between mEC and hippocampus (Fyhn et al., 2007; Hargreaves et al., 2007) suggests that grid and place cells each provide a stable spatial representation of a particular environment, but reconfigure their spatial firing to distinguish between environments at distinct locations (Buzsaki and Moser, 2013; O’Keefe and Nadel, 1978). In addition, aspects of an experience other than the location, such as timing, reward contingencies, or the appearance of an environment, are also discriminated by neuronal activity in mEC (Kraus et al., 2015; Lipton et al., 2007; Marozzi et al., 2015; Quirk et al., 1992).
When examining the different types of spatial and non-spatial coding in mEC, past work has largely focused on the cell population as a whole, on anatomically defined cell types such as layer II stellate and pyramidal cells, or on only grid cells. For the entire mEC cell population the reorganization of firing patterns is generally more pronounced in response to larger differences [with the exception of layer II pyramidal cells (Kitamura et al., 2015)], but more limited in response to minor differences between environments (Hargreaves et al., 2007; Keene et al., 2016; Kitamura et al., 2015; Perez-Escobar et al., 2016). This pattern is consistent with findings from only grid cells, for which large contextual changes elicit distinct spatial firing patterns and for which more minor manipulations of environmental features, such as the shape of its exterior or the color of its walls, do not alter the spatial firing patterns (Fyhn et al., 2007). Yet, less is known about the responses of non-grid mEC cells to manipulations of environments. It is feasible that non-grid cells show major reorganization along with the realignment of grid cells, but only minor responses when the grid pattern is stable. In the latter case, discrimination between environmental features could thus be predominantly performed by the hippocampus in response to lateral entorhinal cortex (lEC) input (Lu et al., 2013). Alternatively, it is possible that mEC cells other than grid cells contribute to distinguishing between environmental features. To examine this possibility, we performed single-unit recordings from the superficial layers of dorsal mEC without biasing our sampling for a particular cell type. By subsequently classifying all recorded entorhinal cells and analyzing cell classes separately, we could identify whether feature discrimination was performed by distributed mEC networks, irrespective of functional cell type, or whether spatial location information and environmental feature information were preferentially represented by particular functional cell types.
Results
Nearly all mEC cells expressed reliable spatial firing patterns in the open field
Using 10-min sessions of random foraging, we sorted all recorded mEC cells (n = 345 cells in 7 rats; Figure S1) into distinct functional cell classes including grid, border, non-grid spatial (reliable spatial firing but not in a grid pattern or along a border), pure head direction (HD; heading modulated firing but no spatial firing), and non-spatial cells (otherwise uncategorized). For mEC recordings, classification has previously been performed by first calculating descriptive values for each cell class (grid score, border score, spatial information, HD mean resultant length) and by then comparing the values to those calculated from the shuffled data of all recorded mEC cells pooled together (Figure S2A) (Barry et al., 2012; Bjerknes et al., 2015; Boccara et al., 2010; Koenig et al., 2011; Kropff et al., 2015; Krupic et al., 2015; Langston et al., 2010; Latuske et al., 2015; Perez-Escobar et al., 2016; Stensola et al., 2012; Tang et al., 2014; Wills et al., 2010; Winter et al., 2015; Zhang et al., 2013). However, pooling shuffled data across all cells fails to account for the firing statistics of individual cells, most notably the relationship between a cell’s firing rate and its spatial information (Figure S2B) (Rolls et al., 1997). Thus, to consider the characteristics of individual cells and more closely follow methods that have been used to define hippocampal place cells as spatially precise and consistent (Aghajan et al., 2015; Lee et al., 2015; Muller et al., 1987), we generated shuffled data for each cell independently. For identifying cells as spatial we then required that a cell’s spatial information as well as its correlation between the first and second halves of a recording session were both above the 95th percentile of the corresponding measurements taken from the same cell’s shuffled data. Using these criteria, a large majority (~95 %) of mEC cells was classified as spatial (Figure 1A), including numerous cells which would previously have been identified as non-spatial (Figure S2C). The proportions of cells with specialized spatial firing patterns were comparable to previous reports (grid cells: 17.7 %; border cells: 9.3 %) (Kropff et al., 2015; Latuske et al., 2015; Tang et al., 2014; Zhang et al., 2013) (Figure S2D), but also included a substantial fraction of spatial cells (67.5 %) that lacked any grid or border pattern. We refer to the latter type as non-grid spatial cells (Figure 1B, C and Table S1) and confirmed that their spatial firing patterns did not arise from systematic variation in running speed. First, all non-grid spatial cells remained classified as non-grid spatial when using firing rate maps that excluded periods of low running speed (< 5 cm/s). Second, we found no relation between running speed patterns and cells’ firing rate patterns (Figure S1).
Figure 1. Approximately 95 % of cells in mEC superficial layers were identified as spatial.
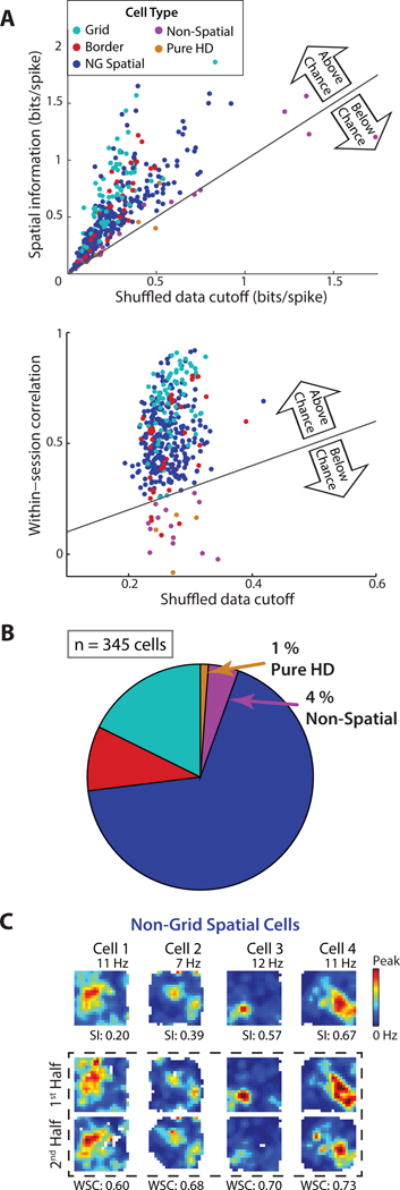
(A) Each cell’s spatial information (top) and within-session spatial correlation (bottom) is plotted against the respective 95th percentile value from the same cell’s shuffled data (‘cutoff’). Approximately 95 % of mEC cells were above the cutoffs for both spatial information and spatial correlation. (B) Of the spatial cells, 17.7 % had significant grid scores and 9.3 % had significant border scores. The remaining 67.5 % did not have either of these specialized firing patterns and are thus referred to as ‘non-grid spatial cells’. (C) Rate maps of four cells that were identified as non-grid spatial. Firing rates are color-coded according to the scale bar on the right. For each rate map, the peak rate is noted above and the spatial information (SI) value is noted below. In the box marked by the stippled line, rate maps from the four cells are shown separately for the first and second half of the 10-min behavioral session. The within-session correlation (WSC) between the two half-session rate maps is noted below each pair of rate maps. See Figure S1 for histology and cluster quality metrics and Figure S2 for comparison to previously used classification criteria for mEC cells. Table S1 shows that all cell types were identified in similar proportions across animals.
Grid alignment remained stable for manipulations of environment shape or color
Given that non-grid spatial cells were the most numerous cell type in mEC, we sought to determine whether they responded coherently with or distinctly from grid cells to manipulations of box shape, box color, and box location. We began by reproducing previously reported results for grid cells which showed retained grid alignment across manipulations of environmental features (i.e., box shape and box color), but major shifts across different box locations (Fyhn et al., 2007; Hafting et al., 2005). Our experiments thus repeated these paradigms (Figure 2A). For the shape-change manipulation, recordings consisted of four 10-min sessions during which rats randomly foraged in an enclosure that remained at a fixed location within a room. Using flexible walls, the enclosure was shaped as a circle during two sessions and as a square during two sessions. For the color-change manipulation, recordings were performed in a second, different room using a square enclosure. The enclosure again remained at a fixed location within the room, and its walls were black for two sessions and white for two sessions. Because the shape-change and color-change manipulations were performed in separate rooms, cells that were recorded in both rooms were used to evaluate the response of mEC cells to changes in box location.
Figure 2. For manipulations of box shape or box color, grid cell maps showed only minor shifts in their spatial location, but substantial redistributions of firing rates.
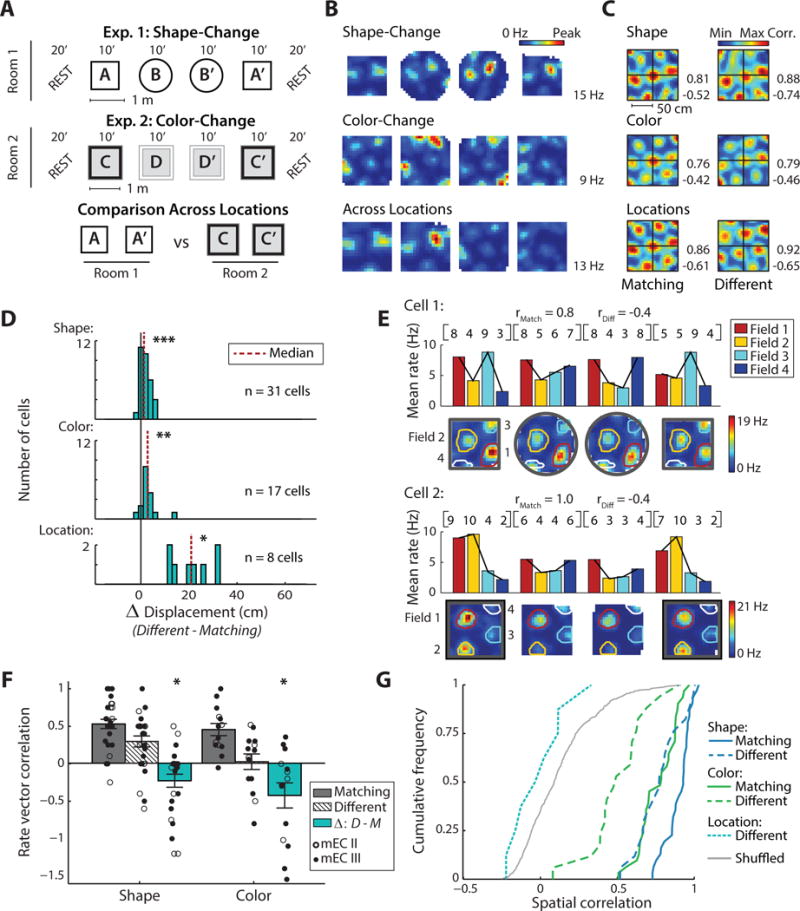
(A) Schematic of the experimental paradigms. (B) Firing rate maps of an example grid cell that was recorded across all conditions. The peak rate of the cell across each set of four sessions is indicated to the right. (C) To measure the spatial stability between sessions, spatial cross-correlations were computed for the rate maps of each grid cell. For the example cell in (B), spatial cross-correlation maps are shown across matching conditions (left column) and across different shapes (right, top), colors (right, middle), and locations (right, bottom). Cross-correlation matrices are scaled from the minimum to the maximum correlation coefficient (noted to the right, blue to red). The displacement of the central peak from the origin measures the extent of the shift in the grid pattern. (D) Displacement from the origin when manipulating box shape, color, or location. For each comparison, the shift between repetitions of matching conditions was subtracted from the shift between sessions in different conditions (Δ displacement). Grid cells exhibited a significant displacement for shape, color, and location changes (Wilcoxon signed-rank matching vs different shape: z = 3.8, p < 0.001; different color: z = 3.3, p < 0.01; different location: z = 2.5, p < 0.05), although the median increase was only 1.3 cm for the shape change and 2.8 cm for the color change. (E) To further evaluate the overall firing profile of grid fields, we considered coordinated rate changes across grid fields and, for each grid cell, generated firing rate vectors (RVs) in which each element is the mean rate of a grid field. Rate maps and the resulting RVs (row vectors and bar graphs) are shown for two example grid cells in the shape-change and color-change paradigms. The average Spearman correlation of RVs across matching and different conditions is noted for both examples. Note that the vector is similar between matching conditions but changes across different conditions. (F) For grid cells with at least three fields (shape: n = 27; color: n = 14), rate vector correlation coefficients between matching environments and different environments are shown, along with the mean ± SEM. In addition, the Δ between the correlation coefficient in matching and different environments is plotted. RVs are more correlated between matching boxes compared to boxes with different shapes or different colors (Wilcoxon signed-rank matching vs different shape: z = −2.4, p < 0.05; different color: z = −2.0, p < 0.05). (G) Cumulative density functions (CDFs) of the spatial correlation between pairs of grid cell rate maps. Pairs were from recordings of the same cell in either matching or in different environments, and cell identity was permutated to generate chance correlations. Compared to correlations between rate maps in matching environments, spatial correlations decreased in response to manipulations of environment shape or color (Wilcoxon signed-rank matching vs different shape: z = −4.7, p < 0.001; different color: z = −3.6, p < 0.001). When comparing across different locations, spatial correlations were not different from shuffled values (Mann-Whitney U different location vs shuffled: z = −1.4, n.s.). * p < 0.05, ** p < 0.01, *** p < 0.001. See Figure S3 for corresponding data from individual animals and Figure S4 for corresponding hippocampal CA1 place cell data.
We first confirmed that ensembles of grid cells retained stable spatial maps within the shape-change and color-change paradigms. For each rat and paradigm we generated the population vector (PV) for the set of recorded grid cells (shape-change: 2–7 grid cells from 6 rats; color-change: 2–21 grid cells from 3 rats) and calculated the PV cross-correlation between pairs of sessions. For the color-change paradigm in 1 additional rat, only one grid cell was recorded, and we thus used the cell’s spatial cross-correlation. In the resulting correlation matrices, the displacement of the most central peak from the origin was used to measure the spatial alignment of the grid patterns (Figure S3A, B). As previously reported for feature manipulations (Fyhn et al., 2007), the spatial firing of grid cell ensembles remained stable across manipulations of either box shape or color in the majority of rats (shape-change: 6 of 6 rats; color-change: 3 of 4 rats).
Because we were specifically interested in mEC firing patterns under conditions when the spatial coding of grid cells remained stable, we further analyzed individual grid cells from datasets with stable grid maps (Figure 2B). We calculated spatial cross-correlations for each cell separately and again measured the displacement of the central peak (Figure 2C). As a baseline for the analysis across different box features or locations, we compared repeated recording sessions in matching environments. Across sessions in matching environments, grid cell displacement was minor (median displacement: 2.4 cm and 2.6 cm for matching box shape and color, respectively). Across different box shapes or box colors, we detected a small increase in displacement relative to matching conditions (median increase: 1.3 cm and 2.8 cm, p < 0.001 and p < 0.01, respectively; Figure 2D). These increases were well below those that were detected across environments located in different rooms (median increase: 20.9 cm; Kruskal-Wallis comparing box shape, color, and location: Chi-square (2) = 21.1, p < 0.001; post-hoc location vs shape, p < 0.001; location vs color p < 0.01).
Manipulations of box shape or color resulted in a firing rate redistribution across grid fields
While we observed only minimal changes in the spatial firing patterns of grid cells in response to our manipulations, it is possible that the environmental change is instead represented by grid fields using a distributed rate code. Consistent with previous reports, we found only minor fluctuations in the firing rates within individual grid fields (Figure S3C) as opposed to the large rate changes characteristic of place fields (Fyhn et al., 2007; Leutgeb et al., 2005; Perez-Escobar et al., 2016). Yet, small differences in firing rates of individual grid nodes could be indicative of a coordinated rate redistribution across the fields of individual grid cells. We therefore performed two analyses that are well suited to detect rate differences across multiple firing fields. First, we calculated the mean firing rate within each grid field and entered these values into a rate vector for each grid cell and each 10-min session. By comparing the rate vectors across sessions (Figure 2E, F), we confirmed that the firing rates of a cell’s grid fields were similar between sessions in matching box shapes or colors (median Spearman’s rank correlation: 0.50 and 0.43 respectively). However, when comparing across different box shapes or colors we found a significantly lower correlation of grid rate vectors (median correlation: 0.40 and 0.13; both p < 0.05 vs matching; Figure 2F), indicating that grid cell rate patterns became redistributed, in particular for manipulations of environment color where the correlation across different conditions was at chance levels (Mann-Whitney U different color vs shuffled field identity: z = 1.22, n.s.). Second, we evaluated the overall similarity of the spatial maps of grid cells by calculating the spatial correlation between rate maps (Figure 2G). Although spatial correlation has frequently been used for confirming the spatial stability of cells’ firing patterns, it is also highly sensitive to a redistribution of firing rates across multiple fields. For grid cells, spatial correlations were high between repeated recordings with matching box shapes or colors (median spatial correlation: 0.85 and 0.70 respectively), but lower across different box shapes or colors (median correlation: 0.72 and 0.42 respectively; both p < 0.001 vs matching), again indicating that grid cell firing rates became redistributed in response to feature manipulations.
Non-grid spatial cells responded to feature manipulations with pronounced changes in their spatial firing patterns
After establishing that grid cells showed relatively stable spatial firing patterns along with a rate redistribution across grid fields, we proceeded to test whether non-grid spatial cells would show corresponding responses to feature manipulations (Figure 3A–E). Non-grid spatial cells were defined based on stable spatial firing within a 10-min behavioral session (see Figure 1). We therefore expected that their spatial firing would also be reproducible over repeated 10-min recording sessions in matching environments. To confirm reproducible firing, we calculated the cross-correlation displacement and the spatial correlation between rate maps of each cell. For matching box shapes or colors we found that cross-correlation displacements were small (median displacement: 4.4 cm and 4.7 cm respectively) and that spatial correlations were high (median spatial correlation: 0.62 and 0.62 respectively). The firing patterns of mEC non-grid spatial cells were therefore reliable across repeated exploration of the same environment, though measurably below the values for grid cells (Mann-Whitney U grid vs non-grid spatial cells, displacement across matching shapes: z = −4.5, p < 0.001; colors: z = −3.2, p < 0.01; spatial correlation across matching shapes: z = −6.5, p < 0.001; colors: z = −2.4, p < 0.05).
Figure 3. For manipulations of box shape or box color, non-grid spatial cells exhibited profound changes in their spatial firing patterns.
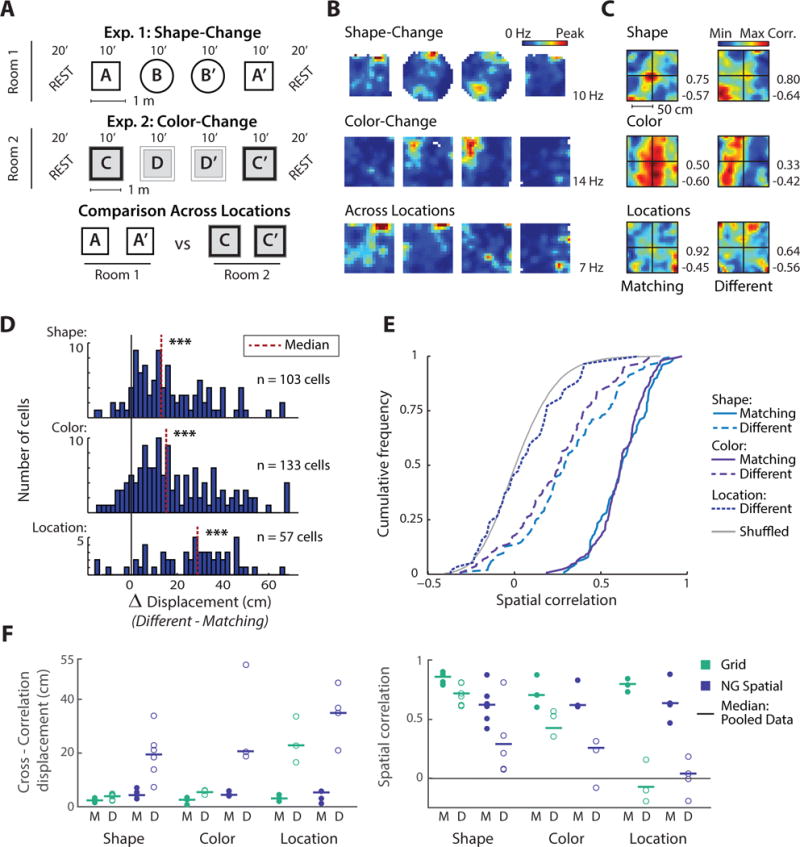
(A) Schematic of the experimental paradigms (redrawn from Figure 2). (B) Firing rate maps of an example non-grid spatial cell across all three conditions. (C) Spatial cross-correlation maps for the example cell in (B) indicate that the predominant firing has shifted to a different location. (D) Displacement of the cross-correlation central peak for manipulations of box shape, color, or location (Δ displacement between different and matching conditions). Manipulations of box shape or box color resulted in pronounced shifts in the predominant firing location (matching vs different shape: median displacement increase of 13.1 cm, Wilcoxon signed-rank, z = 8.1, p < 0.001; different color: median increase of 15.3 cm, z = 9.1, p < 0.001), but which was less than the more complete reorganization of the spatial maps across different locations (matching vs different location: median increase of 28.9 cm, z = 5.6, p < 0.001). (E) CDFs of the spatial correlation between pairs of rate maps. Pairs were from recordings of the same cell in either matching or in different environments, and cell identity was permutated to generate chance correlations. Spatial correlations decreased in response to manipulations of environment shape or color (Wilcoxon signed-rank matching vs different shape: z = −8.7, p < 0.001; different color: z = −10.0, p < 0.001) but less than across different locations where correspondence between maps was not different from shuffled values (Mann-Whitney U different location vs shuffled: z = 1.0, n.s.). (F) Comparison of the median cross-correlation displacement (left) and the median spatial correlation (right) between grid cells and non-grid spatial cells. Horizontal lines: medians of all cells; circles: medians of individual animals for matching (M, filled) and different conditions (D, open). *** p < 0.001. See Figure S4 for corresponding hippocampal place cell data.
We then examined the consistency of the firing patterns of non-grid spatial cells across different environment shapes or colors. Compared to sessions in matching conditions, non-grid spatial cells showed a median increase in displacement of 13.1 cm and 15.3 cm for shape and color change respectively (both p < 0.001 vs matching) indicating a profound change in spatial firing location, but not reaching the level of displacement observed across rooms (median increase: 28.9 cm; Kruskal-Wallis comparing box shape, color, and location: Chi-square (2) = 11.9, p < 0.01; post-hoc location vs shape, p < 0.01; location vs color p < 0.05). Measuring the spatial correlation yielded corresponding results with much lower correlations across different box shapes or colors (median spatial correlation: 0.29 and 0.26, respectively) compared to matching conditions (both p < 0.001). In fact, the degree of change elicited by feature manipulations was so substantial that response magnitudes overlapped with those produced by changing locations, limiting the ability of an ROC analysis to discriminate between these two highly distinct manipulations (Figure S3D).
Responses were consistent across animals and in simultaneous recordings of grid and non-grid spatial cells
After finding in our full dataset that manipulations of environmental shape or color resulted in largely stable grid cell maps, but a pronounced reorganization of the firing patterns of non-grid spatial cells, we examined whether this pattern could also be observed in individual animals and in simultaneous recordings of grid and non-grid spatial cells. We found that grid cells responded less than non-grid spatial cells to feature manipulations in each subject (Figure 3F) and found that the differences between cell types were comparable to the full data set when only analyzing simultaneously recorded ensembles of grid and non-grid spatial cells (Figure 4, Table S2). Furthermore, differences between grid and non-grid cells were also apparent when analyzing either layer II or III separately (Figure S1E). Taken together, the distinct responses of mEC grid and non-grid spatial cells to manipulations of environmental features occurred consistently across animals and in both superficial cell layers.
Figure 4. Analysis of only simultaneous recordings of grid and non-grid spatial cells confirmed the results from the full dataset.
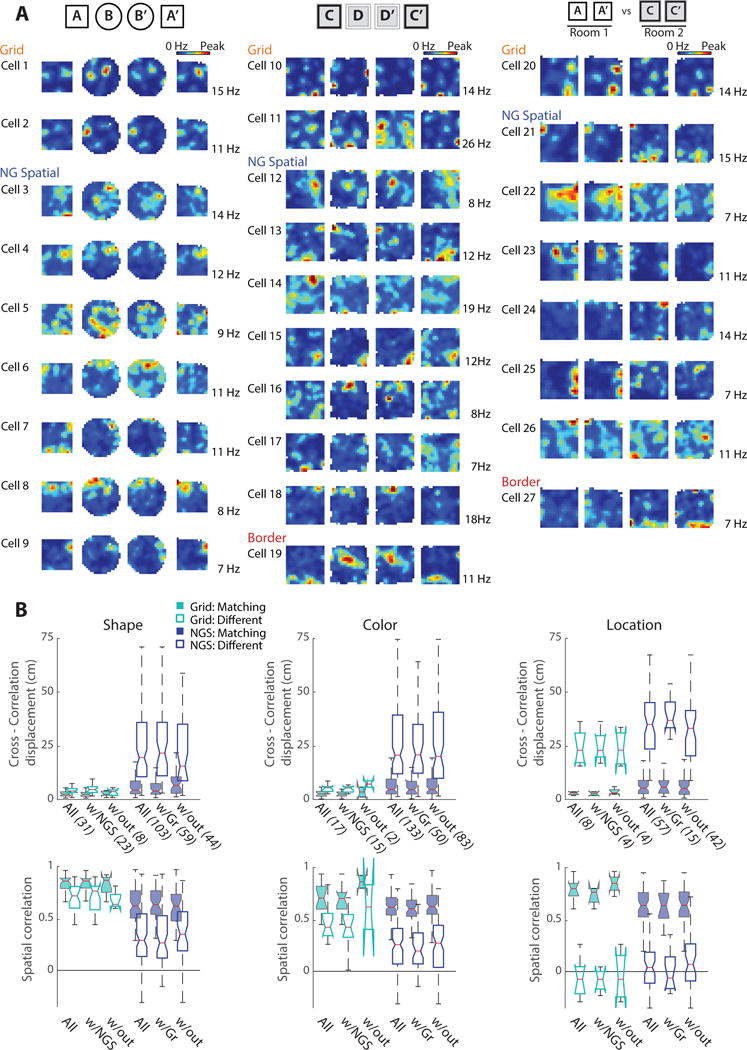
Across all sessions, 38 of 48 grid cells were recorded with non-grid spatial cells (NGS) and 109 of 236 NGS cells were recorded with grid cells. (A) Rate maps of simultaneously recorded cell ensembles during manipulations of environment shape (left), color (middle), and location (right). Different ensembles are presented for each of the three manipulations. (B) Cross-correlation displacement (top row) and spatial correlation (bottom row) of subsets of grid and NGS cells across matching or different box shapes (left), colors (middle), and locations (right). Data are first presented for all recorded grid and NGS cells (All, same data as in Figs. 2 and 3) and then divided into subsets: grid cells with at least one NGS cell (w/NGS), NGS cells with at least one grid cell (w/Gr), and either cell type recorded simultaneously without cells from the opposing category (w/out). For each subset, the number of cells is noted in parenthesis. See Table S2 for additional quantification of simultaneous recordings of grid and non-grid spatial cells.
Discussion
In comprehensive recordings from mEC superficial layers, we found that ~95 % of mEC cells exhibited spatial firing patterns. Of these spatially selective cells, ~20 % were grid cells and ~10 % were border cells, while the remaining two thirds (‘non-grid spatial cells’) had less specialized, yet consistent spatial firing patterns. The classification of a much larger proportion of mEC cells as spatial compared to previous reports is based on applying criteria that have been widely used for hippocampal place cells. As for hippocampus (Aghajan et al., 2015; Lee et al., 2015), we shuffled the spiking data of each individual mEC cell to generate cell-specific cutoffs that account for the variability of an animal’s behavior as well as the spiking statistics of individual cells. After identifying a major proportion of mEC non-grid cells as spatial, we asked whether these cells responded in parallel to grid cells to manipulations of environmental features. While grid cells predominantly exhibited a firing rate redistribution across spatially stable grid fields, non-grid spatial cells underwent a profound reorganization of their spatial firing patterns in response to the same environmental manipulations. The qualitative difference in the response pattern between grid and non-grid spatial cells also makes it unlikely that a sizeable fraction of non-grid spatial cells are in fact single fields of grid cells at a larger spacing. Grid fields would be expected to have stable spatial firing fields across our recording conditions, contrary to our findings for non-grid spatial cells. In addition, recordings of grid and non-grid spatial cells were highly intermixed along the dorso-ventral axis. Our experiments therefore identified mEC cell-type selective response patterns, which have not been observed in previous studies that either evaluated only grid cells, did not distinguish between functional cell types, or reported changes that were consistent across mEC cell types (Fyhn et al., 2007; Hargreaves et al., 2007; Keene et al., 2016; Kitamura et al., 2015; Lipton et al., 2007; Marozzi et al., 2015; Perez-Escobar et al., 2016; Quirk et al., 1992).
Notably, the response pattern that we describe for grid cells resembles the mechanism by which place cell reorganization represents environmental features. In the hippocampus, firing rates are modulated while the spatial locations of place fields remain fixed in response to changes in environment shape or color (‘rate remapping’) (Anderson and Jeffery, 2003; Leutgeb et al., 2005). We confirmed that hippocampal cells showed rate modulation while their spatial firing was stable using the same experimental paradigms in which spatial firing patterns of grid cells were retained (10 rats in our laboratory, including one rat with simultaneous recordings of hippocampal and mEC cells; Figure S4). The stability of spatial firing patterns of grid cells and place cells in these conditions is in contrast to substantially reorganized spatial firing patterns of mEC non-grid spatial cells. Such reorganization of spatial firing of non-grid cells in response to cue manipulations illustrates that spatially distinct patterns are used to represent more than just allocentric space. Related joint coding of environmental features by combined spatial and rate responses has also been reported for hippocampal place cell populations, where it is referred to as partial remapping (Quirk et al., 1990). While we found a similar coding scheme for mEC, our findings differ from the hippocampal data in that the type of response (spatial or rate) to a manipulation is dependent on functional cell type (non-grid or grid).
Furthermore, we show that integration of feature and spatial coding occurs within mEC and that mEC cells can serve as a source for the emergence of feature coding by the hippocampus, in addition to direct inputs from lEC (Deshmukh, 2014; Knierim et al., 2006; Renno-Costa et al., 2010). LEC lesions were found to produce a 30 % impairment in hippocampal rate coding (Lu et al., 2013), which indicates that remaining entorhinal inputs may provide a major contribution to rate coding. Although our data are thus consistent with the general notion that hippocampal coding patterns emerge from joint inputs from the two EC divisions (Eichenbaum et al., 2012; Keene et al., 2016; Knierim et al., 2014), they also show that joint representations of spatial and feature information are already present in the mEC inputs to hippocampus. Information streams could thus be integrated in parallel within hippocampus and mEC indicating that the rodent mEC is not predominantly specialized for only spatial or sequence representations (Buzsaki and Moser, 2013; Kraus et al., 2015), but may instead show similar integration of multimodal coding features as the primate entorhinal cortex (Bellgowan et al., 2009; Killian et al., 2012; Quian Quiroga et al., 2009; Wirth et al., 2003).
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources may be directed to, and will be fulfilled by the Lead Contact, Dr. Jill K. Leutgeb (jleutgeb@ucsd.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Data from the dorsal medial entorhinal cortex (mEC) were collected from seven adult male, experimentally naïve, Long Evans rats (Rats A–G) with a preoperative weight of 300–400 g. In one rat (Rat G), mEC data were collected simultaneous with data from the hippocampal CA1 region. In an additional group of three rats (Rats H–J), tetrodes were aimed at mEC and hippocampus but only hippocampal CA1 cells were successfully recorded. In one rat (Rat J), a cannula was also directed at the medial septal area (MSA) for use in a different study, however all data included here were collected prior to any drug infusions. Rats were housed individually and maintained on a 12-h light/dark schedule with lights off at 7:00 am. All behavioral testing occurred during the dark phase and was performed in dim light in dedicated behavioral testing rooms within the laboratory. All experimental procedures were performed as approved by the Institutional Animal Care and Use Committee at the University of California, San Diego and according to National Institutes of Health and institutional guidelines.
METHOD DETAILS
Surgery
At the time of surgery, rats were anesthetized with isoflurane (1.5–2.5 % in O2) and buprenorphine (0.02 mg/kg, S.C.) was administered as an analgesic. A craniotomy was drilled above the right mEC exposing the transverse sinus. A ‘hyperdrive’ consisting of 14 independently movable tetrodes was implanted 0.5–1.0 mm anterior to the transverse sinus and 4.6–5.2 mm lateral to the midline. In rats G–J, half of the tetrodes were directed towards mEC with the remaining tetrodes directed towards the right hippocampus, and implanted at approximately 4.2 mm posterior and 3.2 mm lateral to bregma, at an angle of approximately 15° anterior. Tetrodes were constructed from 17 μm platinum-iridium (90/10 %) wire and were plated with a 1.5 % platinum solution to lower impedances to 125–325 kΩ at 1 kHz prior to surgery. In rat J, a stainless steel guide cannula (23 gauge), was directed to the MSA and implanted at 0.6 mm anterior and 1.1 mm lateral to bregma, 4.3 mm ventral to dura, at an angle of 10° lateral (Koenig et al., 2011). The guide cannula was filled with a stainless steel dummy wire (32 gauge) that extended 0.5 mm beyond the cannula.
Behavioral procedures
After one week of recovery from surgery, rats were partially food-deprived to 85 % of free feeding weight and trained to forage for randomly scattered cereal crumbs in an open field enclosure with flexible black walls that could be shaped either as a square (80 × 80 cm) or as a 16-sided polygon (50 cm radius, referred to as a ‘circle’). A polarizing white cue card (20 cm wide) was placed on one interior wall. Seven rats (rats D–J) also foraged in a larger square enclosure (100 × 100 cm), located in a second room, with reversible walls colored black on one side and white on the other. A polarizing black and white checkerboard pattern (25 cm wide) was placed on the interior of one wall. Environments were always centered in the same place in the room, and the position of the cue card was kept constant. The recording system, experimenter, and all other external cues within the room were readily visible to the rats.
Rats were trained in blocks of four 10-minute sessions. In the smaller enclosure with flexible walls the box shape was manipulated. Two sessions were conducted with the enclosure shaped as a square and two sessions with the enclosure shaped as a circle (‘shape-change paradigm’). For three rats (rats A–C) the order of squares and circles was varied randomly in each block of four sessions and two training blocks of the box shape-change paradigm were conducted each day, separated by six hours. When single units were recorded in both blocks, they were only analyzed for the block in which a larger number of well-isolated clusters were identified. For the remaining seven rats (rats D–J), each block of four sessions was ordered in an ABB’A’ design, with the identity of the first session randomized for each block. In addition, these seven rats (rats D–J) were also trained in a second paradigm, the color-change paradigm. The box appearance was manipulated by conducting two sessions with four black walls facing the inside of the box and two sessions with four white walls facing the inside of the box. The rats that were trained in both paradigms would often perform two blocks in a single day, one in each paradigm. The order of paradigms varied from day to day. As the two paradigms were conducted in different rooms, a comparison across the two was used to evaluate the effect of changing box location. Each of the training paradigms was flanked by 20-minute sleep periods, and rats were given five minutes between sessions to rest in a pot away from the foraging enclosure. Between sessions the floor of the enclosure was cleaned with water. Prior to any electrophysiological recordings, all enclosures were made highly familiar over at least six training days, and rats performing both paradigms had approximately equal exposure to each. Behavioral procedures while recording mEC units were identical to training procedures.
Recordings and single unit identification
Following surgery, tetrodes were gradually advanced towards the superficial layers of mEC. One tetrode remained in the visual cortex and was used as a reference for all recordings. A second tetrode was rapidly advanced through the brain to identify the beginning of mEC, which was marked by the presence of clear theta oscillations in the local field potential (LFP) and strong theta modulation in unit activity. The same tetrode was later advanced through mEC to identify the transition from layer II to layer I, marked by a clear inversion of the phase of LFP theta. The remaining 12 tetrodes were advanced 25 to 160 μm per day through mEC to record single unit activity. Recordings were performed when well-isolated cells could be observed. At the end of each day of recording, tetrodes were advanced so as to avoid multiple recordings of the same cell. All advancements of tetrodes and recordings were performed blind to cell identity, ensuring an unbiased sampling of the functional cell types within mEC. We continued to record units and to advance tetrodes through mEC until all tetrodes reached layer I. MEC data were collected over 3–12 recording days (mean: 7.1) per animal for the shape-change paradigm and 7–16 recording days (mean: 10.5) per animal for the color-change paradigm. For rats G–J, one of the tetrodes that were implanted above hippocampus remained in the cortex to serve as a local reference. The remaining tetrodes were advanced to the CA1 cell layer. Recordings began when well-isolated cells were simultaneously observed in mEC and CA1. All analyzed CA1 data were collected on a single recording day for each rat.
For recording spikes and local field potentials, hyperdrives were connected through a multichannel, head-mounted preamplifier to a digital Neuralynx recording system. Unit activity was amplified and band-pass filtered between 0.6 kHz and 6 kHz. Spike waveforms above a trigger threshold (35–55 μV) were time-stamped and digitized at 32 kHz for 1 ms. Continuous LFP was recorded from each tetrode, filtered between 0.1 Hz and 900 Hz, and sampled at 2000 Hz. Position data of a red and a green LED located on either side of the head-mounted preamplifier were tracked at 30 Hz by a video camera mounted above the experimental area to determine the rat’s x-y position and head-direction.
Spike sorting was manually performed offline using a customized version of MClust (Redish, A.D. MClust. http://redishlab.neuroscience.umn.edu/MClust/MClust.html) (Mankin et al., 2012). Sleep periods before and after behavioral sessions were used to ensure stability of recorded cells. Only clusters that were deemed by the experimenter as well separated were included in analysis. To quantify the quality of analyzed clusters we calculated the L-Ratio and isolation distance of each (Schmitzer-Torbert et al., 2005). While we did not establish an exclusion threshold for either metric, others have set minimum isolation distances of 5 or 10 cm (Newman and Hasselmo, 2014; Perez-Escobar et al., 2016). Of those clusters that we accepted for analysis, 99.5 % had isolation distances of at least 10 cm. Putative interneurons were identified and removed from the data set based on an average firing rate above 10 Hz and a peak to valley ratio of the average spike waveform below 1.
Histological analysis of tetrode locations
At the completion of all experiments, rats were given an overdose of sodium pentobarbital and were perfused transcardially with saline and 4 % formaldehyde. Brains were extracted and post fixed for 24 hours before being transferred to a 30 % sucrose solution and allowed to sink. Sagital sections (40 μm) were cut on a freezing microtome and sections through the right mEC and hippocampus were mounted on slides and stained with cresyl violet. Tetrode trajectories through mEC or hippocampus were determined through 3D reconstruction of the sectioned tissue. Based on records of the systematic movement of tetrodes through the brain and the trajectory information, complemented by records of LFP profiles, tetrode locations on each recording day were assigned to either the deep or superficial layers of mEC and to a dorsoventral distance from the parasubiculum border. Any recordings from the deep mEC layers or from the pre- or parasubiculum were removed from the dataset. Along the dorsoventral axis, recording locations of mEC grid and non-grid cells were intermixed with numerous instances of simultaneous recordings of grid and non-grid spatial cells on the same tetrode (69 grid and 71 non-grid spatial cells across 55 recordings). In each rat we also identified the most ventral recording location with an identified grid cell and found that over 85% of the data was recorded from more dorsal regions of mEC. This anatomical intermixing, coupled with the discretized increase in grid spacing from dorsal to ventral (Stensola et al., 2012), suggests that no more than a minor fraction of non-grid spatial cells could be grid cells with spacing large enough to exceed our detection limits.
Data Analysis
Rate maps
We constructed firing rate maps in the standard manner by summing the total number of spikes that occurred in a given location bin (5 × 5 cm), dividing by the total amount of time that the rat occupied the bin, and smoothing with a 5 × 5 bin Gaussian filter with a standard deviation of approximately 1 bin (Koenig et al., 2011):
[0.0025 0.0125 0.0200 0.0125 0.0025;
0.0125 0.0625 0.1000 0.0625 0.0125;
0.0200 0.1000 0.1600 0.1000 0.0200;
0.0125 0.0625 0.1000 0.0625 0.0125;
0.0025 0.0125 0.0200 0.0125 0.0025].
Bins that were never within a distance of less than 2.5 cm from the tracked path or with total occupancy of less than 150 ms were regarded as unvisited and were not included in the rate map. To control for possible influences of stationary periods, rate maps were also constructed with periods below a minimum running speed of 5 cm/s excluded. The selection of only high running speed epochs did not result in the reclassification of any mEC cells. Furthermore, the spatial correlation between unthresholded and thresholded maps was high (median correlation: > 0.96), and spatial information values of thresholded maps were 6.8% higher than for unthresholded maps. Thus, we retained the maps with the more conservative estimate of spatial information (i.e., the untresholded maps) for all subsequent analyses. Unless otherwise noted, rate maps for a given cell are shown scaled to the peak firing rate across all four sessions in a recording block. To avoid errors associated with low sampling, cells with a peak rate below 2 Hz in all bins of the four sessions of a block were considered ‘silent’ and excluded from subsequent analysis (5 of 59 hippocampal cells from the shape-change paradigm and 7 of 69 hippocampal cells from the color-change paradigm).
Speed maps
To identify any local variations in the average running speed we constructed speed maps for each behavioral session. Speed maps were calculated corresponding to rate maps, except that running speed values within each bin were summed and divided by the time spent in each bin.
Firing field boundaries
Firing field boundaries for mEC grid cells and hippocampal place cells were calculated by first generating a reference map for the four sessions of a recording block. The reference map was built by averaging the rate maps of the four 10-min sessions. For recordings from the shape-change paradigm, only the area common to the two shapes (80 × 80 cm) was used to build the reference map. The minimum peak rate to identify a field was 2 Hz for grid cells and 1 Hz for place cells, with a minimum field size of 250 cm2. A lower minimum peak rate was used for place cells to correct for the fact that some place fields are active in one environmental condition but silent in another, yielding a reduced average firing rate in the reference map (Leutgeb et al., 2005). Starting from the peak bin, field bounds were defined on the reference map by building contours iteratively outwards until a threshold value of 0.3 times that peak rate was reached. If any peaks above the minimum rate remained, the procedure was repeated. For cells with multiple fields, contours were then recalculated simultaneously for all fields, and the edge of each field was defined as the contour at which the threshold value was reached or where two fields met, whichever came first. These field boundaries from the reference map were then applied to each of the four sessions, and firing statistics were calculated for each identified field in each session. For each field, the mean field rate was taken as the average of all in-field bin rates and the field center was taken as the center of mass (COM) of all firing within the field bound.
Spatial correlation, rate overlap, and population vector correlation
We calculated the spatial similarity between two rate maps (or between a rate map and a speed map) using Pearson’s correlation between the firing rates of bins at corresponding locations. Any bins that were unvisited in either map were excluded from the calculation. Firing rate overlap was calculated for each grid or place field as: where R1 is the mean in-field firing rate from map 1 and R2 is the mean in-field firing rate from map 2.
For population vector (PV) correlations, the rate maps of individual cells were stacked into a three-dimensional matrix in which the x and y axes correspond to spatial location in the environment, and the z axis corresponds to cell identity (Leutgeb et al., 2005). PV correlations were then obtained by calculating, for each x-y location, the Pearson correlation coefficient for firing rates along the z-dimension between pairs of sessions. The correlation coefficients of all spatial bins were then averaged to estimate the population vector correlation for a pair-wise comparison between sessions.
Spatial cross-correlation and population vector cross-correlation
To generate a spatial cross-correlation matrix we calculated the spatial correlation between two rate maps while shifting one of the maps in the x and y directions for all the combinations of x-y offsets to generate a matrix of correlation values. When evaluating cell ensembles, a population vector (PV) cross-correlation was performed in which the entire ensemble was shifted together and a PV correlation was calculated for each x-y offset. For grid cells, ensembles were composed of all grid cells recorded within a single animal. For place cells, ensembles were composed of place cell data pooled across all animals. If an ensemble contained only a single cell a spatial cross-correlation was performed. For displacement calculations, the cross-correlation matrix was normalized to the maximal correlation value and peaks were identified as described above for firing fields, using a minimum peak value of 0.8, a threshold of 0.3, and a minimum size of 250 cm2. From the identified cross-correlation peaks, map displacement was calculated as the offset of COM of the central most peak from the origin (Fyhn et al., 2007). Whenever displaying PV cross-correlations the total number of cells in the ensemble is noted. If the number of cells is not given adjacent to a cross-correlation matrix, the cross-correlation was performed on the rate maps of a single cell.
Comparisons across sessions
For each manipulation (shape, color, or location) we evaluated the effect on mEC cells relative to a baseline value obtained by taking the corresponding measurements across repeated recordings in matching boxes. For each block of four sessions (ABB′A′), we compared each condition to its repetition (A to A′, B to B′), and averaged the resulting values to yield a single baseline measurement. To measure the effect of shape and color manipulations, we compared across the two pairs of non-adjacent, contrasting conditions (A to B′, B to A′), and then averaged these values to yield a single measurement for the effect of the manipulation. For all analyses, rate maps were only compared if at least one of the two maps had a peak rate of at least 2 Hz. For the shape-change paradigm, only the area common to both shapes (80 × 80 cm) was used for calculations. For comparisons of boxes across locations, the square environment from the shape-change paradigm and the black environment from the color-change paradigm were used. Since the color-change box was larger, only the central 80 × 80 cm was used for calculations. As a control for any effects of removing edge firing, an alternative comparison was also made in which rate maps from the color change box were shrunk to 80 × 80 cm in order to maintain firing throughout. Shrinking maps yielded comparable results to cutting out the central 80 × 80 cm so the cutout method was used in all analysis so as to maintain proper spacing of grid fields. When comparing across locations, all rate maps from a given animal were rotated in 90° steps between rooms to determine which rotation of the population yielded the highest average spatial correlation across all cells. For each animal, the ideal rotation across the two rooms was then applied to all rate maps for all analysis between rooms. To determine chance level spatial correlation across distinct box locations, cell identities were permutated such that the rate map of each cell was correlated against the rate map of every other cell, but never against itself. Chance distributions were generated independently for each cell classification (i.e. grid cell rate maps were only permuted with those of other grid cells).
ROC discrimination
To compare the degree of change produced by environmental manipulations to that produced by moving across distinct locations we performed a discrimination between changes in shape vs location and between changes in color vs location using receiver operating characteristics analysis (ROC). Analyses were performed in Matlab (2015b) using the built in functions ‘patternnet’ and ‘roc’. For each ROC, the area under the curve (accuracy) and d’ metric were used to evaluate discrimination quality. To account for stochasticity in training the neural network, ROC was performed 100 times for each comparison and the median accuracy value was used.
Grid score and spatial auto-correlation
To identify grid cells we evaluated the degree of sixfold rotational symmetry in each cell’s spatial auto-correlation by calculating a grid score as described previously (Koenig et al., 2011). For each cell, we calculated rate maps as above (Data analysis: Rate Maps) but based on a bin size of 2.5 cm. To then generate the spatial auto-correlation matrix we used the same procedure as for the spatial cross-correlation, but now shifted each cell’s rate map with respect to itself. From this spatial auto-correlation matrix an annulus that contained the first hexagon of peaks around the center, but excluded the central peak, was extracted. The average correlation value of bins in the annulus was then taken at each angle from the center (i.e., along a ‘ray’). These values were rotated in 30 degree steps and correlated to the un-rotated average values. If six-fold symmetry exists, the correlations at 30, 90, and 150 degrees are expected to be low while the correlations at 60 and 120 degrees are expected to be high. A cell’s grid score was thus taken as the average difference between the latter and former sets of correlation values.
Border score
To identify border cells we calculated a border score for each rate map, which is a measure of the proportion of firing localized to the edges of an environment as compared to the firing within the middle of the environment (Solstad et al., 2008). We identified firing fields as described above (Data analysis: Firing field boundaries) using a minimum firing rate of 2 Hz, a threshold value of 0.3 times the peak field rate, and a minimum field size of 250 cm2. We then determined the proportion of each wall that was adjacent to a firing field and the value CM was taken as the maximal extent of a single field along any wall. The mean firing distance dm was calculated as the average distance to the nearest wall of each bin in the map, weighted by its firing rate and normalized by half of the length of the shortest side of the environment to obtain a fraction between 0 and 1. Border score was calculated as: , and ranged from −1 for cells with central firing to 1 for cells with firing aligned to walls. Any rate map in which a firing field could not be identified was not assigned a border score.
Spatial information score
To identify cells as spatial we calculated the spatial information per spike for each firing rate map as: , where i indexes the spatial bins, Pi is the probability of occupancy in each bin, Ri is the mean firing rate in each bin, and R is the mean firing rate across the spatial map (Skaggs et al., 1993). For calculating spatial information of speed maps, the mean running speed was substituted for the mean firing rate.
Within-session correlation
As a secondary metric for identifying cells as spatial we determined the reliability of spatial firing of each cell by calculating a within-session correlation. For each cell in each session, the 10-mins of trajectory and spiking data was cut in half into the first 5 minutes and the second 5 minutes. Firing rate maps were then generated independently for each half of the behavioral session and the two half-session rate maps were correlated. Within-session correlations for speed maps were calculated using identical procedures.
Head-direction mean resultant length
To identify head-direction cells we calculated the mean resultant length (MRL) of the polar plot generated by comparing cell spiking to angular direction of the animal’s head. Using angular bins with one degree resolution, the number of spikes was divided by the amount of time spent at each bin. These values were used to generate polar plots from which the mean angle and MRL of head-direction modulated firing were calculated.
Speed score
To identify cells with speed-related firing rates, we calculated a speed score for each cell. As previously described (Kropff et al., 2015), the speed score for each cell was the Pearson’s correlation between the instantaneous running speed and the instantaneous firing rate. Instantaneous running speed was calculated for each camera frame by passing trajectory data through a Kalman filter. Instantaneous firing rate was calculated across all frames in a session by summing the number of spikes that occurred between subsequent frames, dividing by the time between frames, and smoothing with a 250-ms wide Gaussian filter with a standard deviation of 90-ms. Periods below an instantaneous running speed of 2 cm/sec and in the top 5 % of running speeds were excluded from the correlation. Cells with a speed score above 0.15 or below −0.15 were selected as highly speed modulated.
Shuffled distributions
To generate shuffled distributions we drew a single random value from a uniform distribution between 20 and 580 seconds. For each cell in each session we added this value to the timestamp of each individual spike. This shuffling procedure serves to dissociate neuronal spiking from x-y position while maintaining any variation in the animal’s behavior and any internal spiking statistics. As such, any biases associated with either will be retained in the shuffled data and accounted for. Spike times exceeding the total duration of a session (~600 sec) were wrapped around to the beginning of the session. We then constructed firing rate maps based on the shuffled spike times, and calculated grid scores, border scores, spatial information scores, within-session correlations, and head-direction MRLs as described above. Shuffling was repeated 1000 times for each cell in each session. For the historical, pooled shuffling method of cell identification, the values for each type of score (grid, border, spatial information, and head direction MRL) were pooled over all recordings of all cells to generate each of the score’s shuffled distribution (Langston et al., 2010; Wills et al., 2010). To account for differences in environment size, data were pooled independently for the shape-change and color-change paradigms. The 95th percentile of each score’s distribution was taken as the cutoff for the metric and was applied to all cells. For the pooled shuffling method, only information score was used for determining the identity of non-grid spatial cells. Note that this method for identifying mEC cells was only used in Figure S2D. For the single-cell method of cell identification, shuffled values were not pooled across all cells but instead the 95th percentile cutoff for each type of score (grid, border, spatial information, within-session correlation, and head direction MRL) was taken from the distribution of 1000 scores that were obtained from the same cell’s shuffled data (see also Figure S2). The single-cell shuffling procedure was used for cell classification throughout the manuscript, with the exception of Figure S2D.
Cell type identification
For each cell we first defined cell identity in each session hierarchically from grid > border > non-grid spatial > head-direction > non-spatial if the corresponding firing metric was above its respective ‘cutoff score’. Thus, if a cell’s grid score was above the grid score cutoff it was identified as a grid cell for the session. Otherwise, its border score was compared to the border score cutoff and so on until the cell was classified, or it passed no cutoff values and was identified as a non-spatial cell. For identification of non-grid spatial cells, a twofold criterion was used in which both the cell’s spatial information and its within-session correlation had to pass their respective cutoff scores. Note that as a result of the hierarchy, the classification of ‘head-direction’ signifies a pure head-direction cell (Pure HD), that is, a cell with head-direction specific firing but no conjunctive representation of space (grid, border, or non-grid spatial). We then determined the overall classification for each cell as the category to which the majority of 10-min sessions were assigned. In the event of a tie (e.g. border cell classification in two sessions and non-grid spatial cell classification in two sessions), cells were assigned as grid > border > non-grid spatial > head-direction > non-spatial. The majority classification was then used for all recordings of a given cell (i.e., a ‘grid cell’ was classified as a ‘grid cell’ in every recording session of the same cell). For cells recorded in both the shape-change and color-change paradigms, all eight sessions were considered for classification.
Rate vector comparisons
To compare the firing rate profile of grid fields of a grid cell we determined the mean firing rate of each identified field and collected these values into a vector. The correspondence between fields was maintained across all four sessions in a given block. For grid cells with at least 3 fields, rate vectors were then compared across sessions using Spearman’s rank correlation. To compare rate vectors to chance, shuffled firing rate vectors were generated by permuting grid fields across all grid cells such that rate vectors of each grid cell were populated by randomly selected firing rates from the entire population of mean field rates.
Excluded Data
We sought to evaluate the response of mEC cells to manipulations associated with hippocampal rate remapping (Fyhn et al., 2007; Leutgeb et al., 2005; Lu et al., 2013; Mankin et al., 2012), specifically looking at the behavior of non-grid cells when the grid map remained stable. In one rat we recorded no grid cells during the shape-change paradigm. In another rat the shift in the spatial firing pattern of grid cells during the color-change paradigm was identified as an outlier from the other recordings during manipulations of environmental features based on Tukey’s test for outliers. The PV displacement for this rat exceeded a distance of 3*IQR beyond the third quartile of the data set. As we were not able to verify for either of these cases that the grid map remained stable, we excluded these data from analysis of the effects of manipulations of environmental features (Rat D in shape-change: 0 grid cells and 31 non-grid cells; Rat F in color-change: 21 grid cells and 40 non-grid cells).
QUANTIFICATION AND STATISTICAL ANALYSIS
Evaluation of the effects of box shape, box color, or box location manipulations were made by comparing the effects of each manipulation vs repeated recordings in matching conditions using the Wilcoxon signed-rank test. Spatial correlations across locations were compared to chance distributions using a Mann-Whitney U test. Comparison across mEC cell types (Grid vs Border vs Non-Grid Spatial) or between box manipulations (Shape vs Color vs Location) were made using the Kruskal-Wallis test with Tukey’s honestly significant difference (HSD) criterion for post-hoc analysis. If only two cell types were compared, a Mann-Whitney U test was used. Comparison between ensemble averages and the pooled data set were made using a Mann-Whitney U test. Evaluation of the differences between cells with high and low isolation distances and between mEC layer II and layer III subpopulations was made using a Mann-Whitney U test. For statistical comparisons n represents the number of mEC cells, except when evaluating the firing rate of individual grid or place fields where n represents the number of fields. Data centers are presented as medians or as means ± SEM when noted in the figure legend. Statistical comparisons were significant at p < 0.05 for two tailed distributions.
DATA AND SOFTWARE AVAILABILITY
MClust software is freely available from A.D. Redish at: http://redishlab.neuroscience.umn.edu/MClust/MClust.html
ADDITIONAL RESOURCES
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Biological Samples | ||
| Chemicals, Peptides, and Recombinant Proteins | ||
| Isoflurane | MWI | Cat #: NDC 13985-528-60 |
| Buprenorphine | MWI | Cat #: 29308 |
| Plantinic acid for platinum plating | Sigma-Aldrich | Cat #: 206083; CAS 18497-13-7 |
| Sodium pentobarbital | MWI | Cat #: 15199 |
| Formaldehyde | EMD | Cat #: FX-0415-4; CAS 50-00-0 |
| Cresyl violet | EMD | Cat #: M-19012; CAS 10510-54-0 |
| Critical Commercial Assays | ||
| Deposited Data | ||
| Experimental Models: Cell Lines | ||
| Experimental Models: Organisms/Strains | ||
| Long Evans rats | Charles River Labs | RRID: RGD_2308852 |
| Recombinant DNA | ||
| Sequence-Based Reagents | ||
| Software and Algorithms | ||
| MClust | A.D. Redish | http://redishlab.neuroscience.umn.edu/MClust/MClust.html |
| Matlab v 2015b | Mathworks | RRID: SCR_001622 |
| Other | ||
| Hyperdrive | Custom built; Designed by B McNaughton | US Patent: US5928143 A |
| Platinum-Iridium tetrode wire | California fine wire company | Cat #: CFW0011873 |
| Freezing microtome | Leica | Model: SM 2000R |
| Digital Neuralynx recording system | Neuralynx | Model: Digital Lynx SX |
Supplementary Material
Acknowledgments
We thank B. Boublil and M. Wong for technical assistance. Research was supported by National Institute of Health grants MH-100349, MH-102841, the Whitehall Foundation 20130571, and a Walter F. Heiligenberg Professorship to J.K.L, and National Institute of Health grants MH-100354, NS-084324, and NS-086947 to S.L.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
The authors declare no competing financial interests.
Author Contributions
G.W.D., S.L. and J.K.L. designed research, G.W.D. and O.J.H. collected data, G.W.D. analyzed data, and G.W.D., S.L., and J.K.L. wrote the manuscript.
References
- Aghajan ZM, Acharya L, Moore JJ, Cushman JD, Vuong C, Mehta MR. Impaired spatial selectivity and intact phase precession in two-dimensional virtual reality. Nat Neurosci. 2015;18:121–128. doi: 10.1038/nn.3884. [DOI] [PubMed] [Google Scholar]
- Anderson MI, Jeffery KJ. Heterogeneous modulation of place cell firing by changes in context. J Neurosci. 2003;23:8827–8835. doi: 10.1523/JNEUROSCI.23-26-08827.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barry C, Ginzberg LL, O’Keefe J, Burgess N. Grid cell firing patterns signal environmental novelty by expansion. Proc Natl Acad Sci U S A. 2012;109:17687–17692. doi: 10.1073/pnas.1209918109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bellgowan PS, Buffalo EA, Bodurka J, Martin A. Lateralized spatial and object memory encoding in entorhinal and perirhinal cortices. Learn Mem. 2009;16:433–438. doi: 10.1101/lm.1357309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bjerknes TL, Langston RF, Kruge IU, Moser EI, Moser MB. Coherence among head direction cells before eye opening in rat pups. Curr Biol. 2015;25:103–108. doi: 10.1016/j.cub.2014.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boccara CN, Sargolini F, Thoresen VH, Solstad T, Witter MP, Moser EI, Moser MB. Grid cells in pre- and parasubiculum. Nat Neurosci. 2010;13:987–994. doi: 10.1038/nn.2602. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, Moser EI. Memory, navigation and theta rhythm in the hippocampal-entorhinal system. Nat Neurosci. 2013;16:130–138. doi: 10.1038/nn.3304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshmukh SS. Spatial and Nonspatial Representations in the Lateral Entorhinal Cortex. In: Derdikman D, Knierim JJ, editors. Space, Time and Memory in the Hippocampal Formation. Vienna: Springer Vienna; 2014. pp. 127–152. [Google Scholar]
- Eichenbaum H, Sauvage M, Fortin N, Komorowski R, Lipton P. Towards a functional organization of episodic memory in the medial temporal lobe. Neurosci Biobehav Rev. 2012;36:1597–1608. doi: 10.1016/j.neubiorev.2011.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fyhn M, Hafting T, Treves A, Moser MB, Moser EI. Hippocampal remapping and grid realignment in entorhinal cortex. Nature. 2007;446:190–194. doi: 10.1038/nature05601. [DOI] [PubMed] [Google Scholar]
- Hafting T, Fyhn M, Molden S, Moser MB, Moser EI. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
- Hargreaves EL, Yoganarasimha D, Knierim JJ. Cohesiveness of spatial and directional representations recorded from neural ensembles in the anterior thalamus, parasubiculum, medial entorhinal cortex, and hippocampus. Hippocampus. 2007;17:826–841. doi: 10.1002/hipo.20316. [DOI] [PubMed] [Google Scholar]
- Keene CS, Bladon J, McKenzie S, Liu CD, O’Keefe J, Eichenbaum H. Complementary Functional Organization of Neuronal Activity Patterns in the Perirhinal, Lateral Entorhinal, and Medial Entorhinal Cortices. J Neurosci. 2016;36:3660–3675. doi: 10.1523/JNEUROSCI.4368-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killian NJ, Jutras MJ, Buffalo EA. A map of visual space in the primate entorhinal cortex. Nature. 2012;491:761–764. doi: 10.1038/nature11587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitamura T, Sun C, Martin J, Kitch LJ, Schnitzer MJ, Tonegawa S. Entorhinal Cortical Ocean Cells Encode Specific Contexts and Drive Context-Specific Fear Memory. Neuron. 2015;87:1317–1331. doi: 10.1016/j.neuron.2015.08.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knierim JJ, Lee I, Hargreaves EL. Hippocampal place cells: parallel input streams, subregional processing, and implications for episodic memory. Hippocampus. 2006;16:755–764. doi: 10.1002/hipo.20203. [DOI] [PubMed] [Google Scholar]
- Knierim JJ, Neunuebel JP, Deshmukh SS. Functional correlates of the lateral and medial entorhinal cortex: objects, path integration and local-global reference frames. Philos Trans R Soc Lond B Biol Sci. 2014;369:20130369. doi: 10.1098/rstb.2013.0369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koenig J, Linder AN, Leutgeb JK, Leutgeb S. The spatial periodicity of grid cells is not sustained during reduced theta oscillations. Science. 2011;332:592–595. doi: 10.1126/science.1201685. [DOI] [PubMed] [Google Scholar]
- Kraus BJ, Brandon MP, Robinson RJ, 2nd, Connerney MA, Hasselmo ME, Eichenbaum H. During Running in Place, Grid Cells Integrate Elapsed Time and Distance Run. Neuron. 2015;88:578–589. doi: 10.1016/j.neuron.2015.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kropff E, Carmichael JE, Moser MB, Moser EI. Speed cells in the medial entorhinal cortex. Nature. 2015;523:419–424. doi: 10.1038/nature14622. [DOI] [PubMed] [Google Scholar]
- Krupic J, Bauza M, Burton S, Barry C, O’Keefe J. Grid cell symmetry is shaped by environmental geometry. Nature. 2015;518:232–235. doi: 10.1038/nature14153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langston RF, Ainge JA, Couey JJ, Canto CB, Bjerknes TL, Witter MP, Moser EI, Moser MB. Development of the spatial representation system in the rat. Science. 2010;328:1576–1580. doi: 10.1126/science.1188210. [DOI] [PubMed] [Google Scholar]
- Latuske P, Toader O, Allen K. Interspike Intervals Reveal Functionally Distinct Cell Populations in the Medial Entorhinal Cortex. J Neurosci. 2015;35:10963–10976. doi: 10.1523/JNEUROSCI.0276-15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee H, Wang C, Deshmukh SS, Knierim JJ. Neural Population Evidence of Functional Heterogeneity along the CA3 Transverse Axis: Pattern Completion versus Pattern Separation. Neuron. 2015;87:1093–1105. doi: 10.1016/j.neuron.2015.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leutgeb S, Leutgeb JK, Barnes CA, Moser EI, McNaughton BL, Moser MB. Independent codes for spatial and episodic memory in hippocampal neuronal ensembles. Science. 2005;309:619–623. doi: 10.1126/science.1114037. [DOI] [PubMed] [Google Scholar]
- Lipton PA, White JA, Eichenbaum H. Disambiguation of overlapping experiences by neurons in the medial entorhinal cortex. J Neurosci. 2007;27:5787–5795. doi: 10.1523/JNEUROSCI.1063-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu L, Leutgeb JK, Tsao A, Henriksen EJ, Leutgeb S, Barnes CA, Witter MP, Moser MB, Moser EI. Impaired hippocampal rate coding after lesions of the lateral entorhinal cortex. Nat Neurosci. 2013;16:1085–1093. doi: 10.1038/nn.3462. [DOI] [PubMed] [Google Scholar]
- Mankin EA, Sparks FT, Slayyeh B, Sutherland RJ, Leutgeb S, Leutgeb JK. Neuronal code for extended time in the hippocampus. Proc Natl Acad Sci U S A. 2012;109:19462–19467. doi: 10.1073/pnas.1214107109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marozzi E, Ginzberg LL, Alenda A, Jeffery KJ. Purely Translational Realignment in Grid Cell Firing Patterns Following Nonmetric Context Change. Cereb Cortex. 2015;25:4619–4627. doi: 10.1093/cercor/bhv120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller RU, Kubie JL, Ranck JB., Jr Spatial firing patterns of hippocampal complex-spike cells in a fixed environment. J Neurosci. 1987;7:1935–1950. doi: 10.1523/JNEUROSCI.07-07-01935.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman EL, Hasselmo ME. Grid cell firing properties vary as a function of theta phase locking preferences in the rat medial entorhinal cortex. Front Syst Neurosci. 2014;8:193. doi: 10.3389/fnsys.2014.00193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Keefe J, Nadel L. The hippocampus as a cognitive map. Oxford: Clarendon Press); 1978. [Google Scholar]
- Perez-Escobar JA, Kornienko O, Latuske P, Kohler L, Allen K. Visual landmarks sharpen grid cell metric and confer context specificity to neurons of the medial entorhinal cortex. Elife. 2016;5 doi: 10.7554/eLife.16937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quian Quiroga R, Kraskov A, Koch C, Fried I. Explicit encoding of multimodal percepts by single neurons in the human brain. Curr Biol. 2009;19:1308–1313. doi: 10.1016/j.cub.2009.06.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quirk GJ, Muller RU, Kubie JL. The firing of hippocampal place cells in the dark depends on the rat’s recent experience. J Neurosci. 1990;10:2008–2017. doi: 10.1523/JNEUROSCI.10-06-02008.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quirk GJ, Muller RU, Kubie JL, Ranck JB., Jr The positional firing properties of medial entorhinal neurons: description and comparison with hippocampal place cells. J Neurosci. 1992;12:1945–1963. doi: 10.1523/JNEUROSCI.12-05-01945.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renno-Costa C, Lisman JE, Verschure PF. The mechanism of rate remapping in the dentate gyrus. Neuron. 2010;68:1051–1058. doi: 10.1016/j.neuron.2010.11.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rolls ET, Treves A, Tovee MJ, Panzeri S. Information in the neuronal representation of individual stimuli in the primate temporal visual cortex. J Comput Neurosci. 1997;4:309–333. doi: 10.1023/a:1008899916425. [DOI] [PubMed] [Google Scholar]
- Sargolini F, Fyhn M, Hafting T, McNaughton BL, Witter MP, Moser MB, Moser EI. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science. 2006;312:758–762. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]
- Schmitzer-Torbert N, Jackson J, Henze D, Harris K, Redish AD. Quantitative measures of cluster quality for use in extracellular recordings. Neuroscience. 2005;131:1–11. doi: 10.1016/j.neuroscience.2004.09.066. [DOI] [PubMed] [Google Scholar]
- Skaggs WE, McNaughton BL, Gothard KM, Markus EJ. An information-theoretic approach to deciphering the hippocampal code. Advances in Neural Information Processing Systems. 1993;5:1030–1037. [Google Scholar]
- Solstad T, Boccara CN, Kropff E, Moser MB, Moser EI. Representation of geometric borders in the entorhinal cortex. Science. 2008;322:1865–1868. doi: 10.1126/science.1166466. [DOI] [PubMed] [Google Scholar]
- Stensola H, Stensola T, Solstad T, Froland K, Moser MB, Moser EI. The entorhinal grid map is discretized. Nature. 2012;492:72–78. doi: 10.1038/nature11649. [DOI] [PubMed] [Google Scholar]
- Tang Q, Burgalossi A, Ebbesen CL, Ray S, Naumann R, Schmidt H, Spicher D, Brecht M. Pyramidal and stellate cell specificity of grid and border representations in layer 2 of medial entorhinal cortex. Neuron. 2014;84:1191–1197. doi: 10.1016/j.neuron.2014.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Strien NM, Cappaert NL, Witter MP. The anatomy of memory: an interactive overview of the parahippocampal-hippocampal network. Nat Rev Neurosci. 2009;10:272–282. doi: 10.1038/nrn2614. [DOI] [PubMed] [Google Scholar]
- Wills TJ, Cacucci F, Burgess N, O’Keefe J. Development of the hippocampal cognitive map in preweanling rats. Science. 2010;328:1573–1576. doi: 10.1126/science.1188224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winter SS, Mehlman ML, Clark BJ, Taube JS. Passive Transport Disrupts Grid Signals in the Parahippocampal Cortex. Curr Biol. 2015;25:2493–2502. doi: 10.1016/j.cub.2015.08.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wirth S, Yanike M, Frank LM, Smith AC, Brown EN, Suzuki WA. Single neurons in the monkey hippocampus and learning of new associations. Science. 2003;300:1578–1581. doi: 10.1126/science.1084324. [DOI] [PubMed] [Google Scholar]
- Zhang SJ, Ye J, Miao C, Tsao A, Cerniauskas I, Ledergerber D, Moser MB, Moser EI. Optogenetic dissection of entorhinal-hippocampal functional connectivity. Science. 2013;340:1232627. doi: 10.1126/science.1232627. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


