Abstract
Mapping the complex heterogeneity of vascular tissue in the brain is important for understanding cerebrovascular disease. In this translational study, we build on previous work using vessel architectural imaging (VAI) and present a theoretical framework for determining cerebral vascular function and heterogeneity from dynamic susceptibility contrast magnetic resonance imaging (MRI). Our tissue model covers realistic structural architectures for vessel branching and orientations, as well as a range of hemodynamic scenarios for blood flow, capillary transit times and oxygenation. In a typical image voxel, our findings show that the apparent MRI relaxation rates are independent of the mean vessel orientation and that the vortex area, a VAI-based parameter, is determined by the relative oxygen saturation level and the vessel branching of the tissue. Finally, in both simulated and patient data, we show that the relative distributions of the vortex area parameter as a function of capillary transit times show unique characteristics in normal-appearing white and gray matter tissue, whereas tumour-voxels in comparison display a heterogeneous distribution. Collectively, our study presents a comprehensive framework that may serve as a roadmap for in vivo and per-voxel determination of vascular status and heterogeneity in cerebral tissue.
Keywords: DSC-MRI, glioma, tumour heterogeneity, vascular modelling, vessel architectural imaging
Introduction
Magnetic resonance imaging (MRI) is the modality of choice in a range of brain disorders, including tumours, stroke and neurodegenerative disorders. Although structural MRI can provide useful information about the disease, it is inadequate for detecting clinical relevant properties of cerebrovascular function.1 In contrast, dynamic susceptibility contrast (DSC) MRI is designed specifically for this purpose to assess cerebral perfusion and blood volume.2 These measures are complemented by dual-echo techniques, where gradient echo and spin echo acquisitions are performed simultaneously to estimate tissue vessel calibres3–6 and vessel density.7 The methodology and more details of these techniques have thoroughly been reviewed elsewhere.8–10
More recently, vessel architectural imaging (VAI) has emerged as a new MRI-based paradigm for in vivo assessment of microvascular architecture and oxygen saturation status. VAI relies on a hysteresis effect – a relative shift in the shape and peak position of the relaxation rate curves from the gradient echo and spin echo signals.5 By introducing a tissue model with a vascular network consisting of arteries, capillaries and veins where the vessel types vary in size, oxygen saturation levels and concentration-time curves, it was shown that this hysteresis effect reflects the underlying microvascular and hemodynamic properties of the tissue.11,12 In the brain, this information has proved value for glioma grading11,13 and response-evaluation of anti-angiogenic therapy in patients with recurrent12 and newly diagnosed glioblastomas.14 Because of the complex relation between the MRI signal response and the underlying vascular and hemodynamic characteristics of the tissue, we hypothesize that VAI holds the key to decipher this heterogeneity and that a comprehensive theoretical framework may serve as a roadmap for in vivo and per-voxel determination of vascular status.15,16
To this end, we here reappraise current theoretical models for VAI to cover realistic scenarios for the vascular heterogeneity of an image voxel by including information on vessel generation branching, vessel orientation relative to the main magnetic field and branching angles, as well as capillary transit times. Our goal is to determine the corresponding effects on the MRI properties of blood volume, vessel calibre and oxygenation status. In a typical image voxel, our findings indicate that the apparent MRI relaxation rates are independent of the mean vessel orientation in both gray matter-like and white matter-like structures, and that the vortex area, a VAI-based parameter, is proportional to the relative oxygen saturation level and the vessel branching of the tissue. Finally, in both simulated and patient data, we show that the relative distributions of the vortex area parameter as a function of capillary transit times show unique characteristics in normal-appearing white- and gray matter tissue, whereas tumour-voxels in comparison display a heterogeneous distribution.
Methods
Simulation model
Monte Carlo simulations of intravascular magnetic susceptibility perturbations were conducted to obtain relaxation rate curves from spin echo and gradient echo signals. The general theory behind the signal simulations has been previously described.3,6 In summary, cylinders with a given radius (R), diffusion coefficient (D) and susceptibility difference between intra- and extravascular space (Δχ) were randomly distributed to fill a given volume fraction of the simulation space. If a given cylinder overlapped with one of the other cylinders already placed in the simulation space, a new position was generated until no overlapping occured. The Monte Carlo simulation was performed for N = 5000 protons, where a new distribution of cylinders was generated for each proton. The protons were initially placed in the origin of the simulation space and the accumulated phase () was calculated after each step of the protons’ random walk, , where γ is the gyromagnetic ratio, Δt is the time step in the random walk and ΔB is the magnetic field at the protons location given by
| (1) |
where is the angle of the kth cylinder relative to the main magnetic field, () is the polar coordinates of the proton in the orthogonal plane and Nk is the number of cylinders. The top line () and bottom line () is the contribution from extravascular and intravascular space, respectively. The susceptibility difference is the sum of contributions from deoxygenated blood and contrast agent concentration:
| (2) |
where (=4π = 1.54 × 10−6 in SI units) is the susceptibility difference between fully oxygenated and fully deoxygenated blood17 with haematocrit level set to Hct = 0.45, is the fraction of deoxygenated blood, (=0.34 × 10−6 mM−1) is the molar susceptibility of Gadolinium and [Gd] is the concentration of Gadolinium in the vessel.
The signal intensity is then calculated by
| (3) |
where N is the number of protons. The resulting change in the relaxation rate is given as
Δ denotes the change in relaxation rate from gradient echo (ΔR2*) and spin echo (ΔR2) acquisitions.
The tissue concentration for each vessel generation () is calculated based on an arterial input function (AIF) obtained from Jsim (National Simulation Resource Physiome initiative).18 The vessels are approximated as cylindrical pipes with laminar flow. The transport function, i.e. the frequency function for transit times within each vessel, is thus given by
| (5) |
where t0 is the smallest transit time through the vessel (see Supplementary Methods). The mean transit time for a single vessel due to its flow profile becomes . The time-concentration curve for vessel generation k, i.e. all vessels within the same branching level of the vessel tree, is given by
| (6) |
where = AIF and * denotes convolution. The tissue concentration, , can then be calculated
| (7) |
where f is the fractional flow ( and R(t) is the residual function, .
The tissue concentration curves of each vessel generation were then coupled with the corresponding relaxation rate results obtained by the Monte Carlo simulations. The total spin echo and gradient echo relaxation rate curves were calculated by a weighted sum of the relaxation rate curves from each vessel generation.
| (8) |
where wk is the fraction of the total blood volume made up from vessel generation k.
Vessel orientation distributions
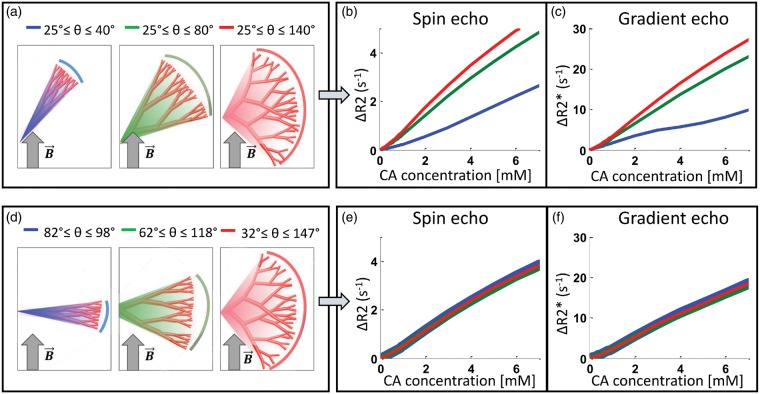
As given in equation (1), the magnetic field perturbations are affected by the orientation of the vessels with respect to the main magnetic field. To investigate the effect of vessel orientation distribution on the signal response, we first performed simulations where the orientation of the vessels were randomly chosen from an interval of angles ranging from 25° to 40°, 25° to 80° and 25° to 140°, giving a mean vessel orientation of 32.5°, 52.5° and 82.5°, respectively (see Figure 2(a)). Next, we performed simulations using the same interval ranges, but the mean vessel orientation was fixed at 90°, i.e. with interval of angles ranging from 82.5° to 97.5°, 67.5° to 112.5° and 32.5° to 147.5° (see Figure 2(d)). All angles are relative to the main magnetic field.
Figure 2.
The effects of vessel orientation distribution on the concentration dependence of the relaxation rates. When vessel orientations are randomly chosen within an interval with minimum angle set to 25° (a) both ΔR2 and ΔR2* increases with branching angle heterogeneity (b,c). However, if the mean vessel orientation is set perpendicular to the main magnetic field (d), the relaxation rates become independent of branching angle heterogeneity (e,f).
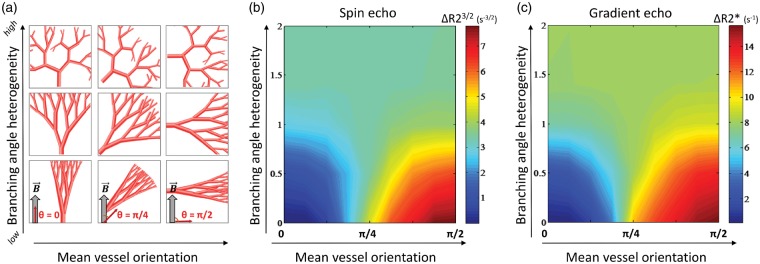
To estimate the effects of the vessel orientation distribution, we assessed the MR response to vessel branching angles randomly chosen from a Gaussian distribution with mean vessel orientations (µθ) ranging from 0 to π/2, and branching heterogeneity (defined here as the standard deviation, ) from 0 to 2 in both white matter- and gray matter-like branching structures.
Capillary transit time heterogeneity (CTTH) and oxygenation
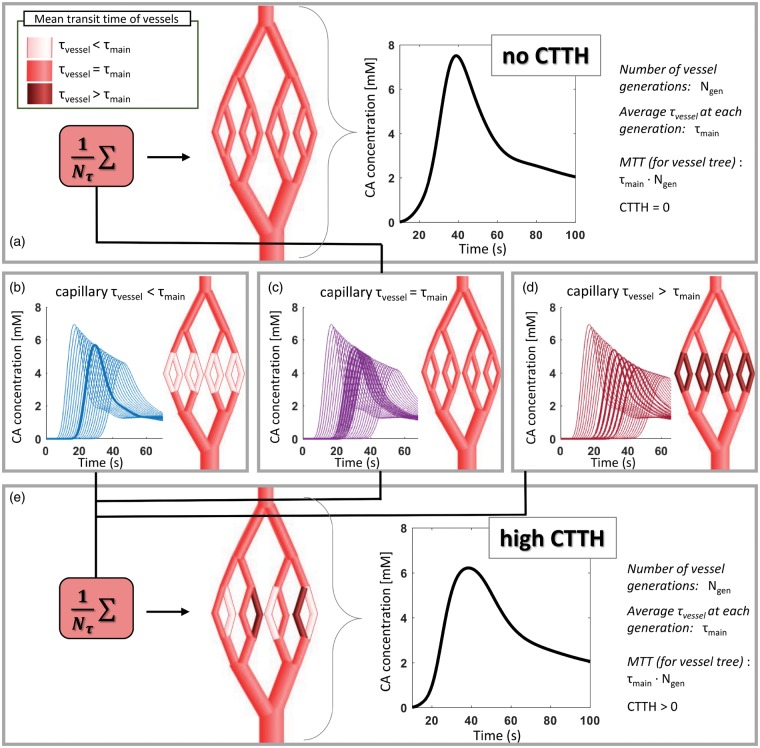
To assess the effect of transit time distribution on the capillary level, simulations of vessel trees with various capillary mean transit times (i.e. , cf. equation (5)) were performed and combined to mimic realistic vessel scenarios as shown in Figure 1.
Figure 1.
Schematic representation of implementation of CTTH into the vascular model. To obtain a simulated vessel network with CTTH = 0 (top panel (a)), all vessels in the vessel tree have the same mean transit time (), indicated by the same shade of red in the illustrated vessel tree. The resulting concentration time curve for the whole vessel tree is shown in the graph. To obtain CTTH > 0, several vessel trees are generated where in arteries and veins remain constant at , whereas on the capillary levels becomes shorter (shown in light red in (b)) or longer (shown in dark red in (d)) compared to The corresponding concentration time curves for each vessel generation are shown in (b) to (d), where the curves from capillary generations are highlighted with thicker lines. Note that the graphs in (b) to (d) display concentration time curves from vessel trees with vessel generations, whereas the illustrated vessel trees contain only = 8. The vessel trees are then combined with equal weight (=1/, where is number of vessel trees with different capillary , here shown for = 3), as shown in bottom panel (e). The concentration time curve for the resulting vessel tree with high CTTH is shown in the graph (bottom right), where the peak of the curve is wider and lower compared to that of the concentration time curve with no CTTH. Note that the concentration time-curves in (a) and (e) is for illustration only and not used in the simulation as such, as the signal response for each vessel generation is calculated before they are combined.
For all simulations, the mean transit times in arteries and veins were kept constant and set to
| (9) |
where MTT is mean transit time for the whole vessel network in the simulated voxel and is the number of vessel generations within the voxel. To obtain transit time heterogeneity on the capillary level, vessel trees with various were generated with
| (10) |
where Δt = 0.1 s and is the number of different for a given CTTH. The vessel trees with different were then combined with equal weight (=1/), so that the mean of for each vessel generation becomes (see Figure 1). CTTH is defined as the standard deviation of :
| (11) |
Minimum was set to 0.05 s, hence maximum , and consequently maximum obtainable CTTH, decreases for lower MTT.
For validation of the CTTH-implementation in the model, simulations were performed with a range of CTTH across various MTT. We then compared the simulated CTTH, i.e. the standard deviation of the average transit times as given in equation (11), and the measured CTTH, which is given by the standard deviation of the estimated transport function of the simulated voxel19 as described below (equation (12)). As the simulated CTTH is only dependent on the distribution of capillary transit times, whereas the measured CTTH is dependent on the distribution of transit times in the whole vessel tree – which includes the flow profile of all vessels (equation 5) – it is expected that the simulated CTTH is considerably lower than the measured CTTH. Similarly, simulated MTT of the voxel was compared with the measured MTT, given by the mean of the transport function.
To evaluate the combined effects of transit time distributions and oxygenation, simulations were performed with different levels of oxygen saturation (SO2) at the venous side, starting at the first vessel generation of capillaries. Arterial SO2 was set to 93%, while capillary- and venous SO2 varied from 93% (no consumption) to 0% (anoxic conditions).
Branching structure of the vascular network
The vascular network was modelled by a vessel tree structure consisting of arteries, capillaries and veins.11 For generation of vessel structures associated with white matter, each vessel on the arterial side branches into two equally sized daughter vessels. The process of bifurcation is repeated until the daughter vessels reach the minimum size of capillaries, which is set to = 2.3 µm. The process is then reversed so that two smaller vessels merge into one on the venous side. The radii of the vessels follow Murray’s law, so that the radius is changed by a factor 21/3 at each generation.20 On the venous side, the radii are scaled with a factor of 1.5 to the corresponding vessel generation on the arterial side to account for veins generally being larger than arteries.21,22
In addition, a separate vessel tree were modelled to mimic the branching structure found in cortical gray matter.22 Here, the arterial vessels split into one larger and one smaller vessel, where the radius of the smaller vessel is set to half the size of the parent vessel. The smaller one branches into two equally sized vessels, as described above, while the larger one continues to branch asymmetrically into one large and one small vessel.
MR acquisitions
Subject data included five patients imaged before first-time surgery and subsequent diagnosed with a glioblastoma (Supplementary Table 1). The study was approved by our Institutional Review Board (ref: LOOPS) and the Regional Committee for Medical and Health Research Ethics (ref: 2013/1033). All patients signed a consent form before being included in the study.
All scans were performed with an Ingenia 3T Philips system (Philips Healthcare, The Netherlands, Software release: 5.1.7). The MRI protocol included: 3D T1-weighted images, pre- and post-contrast agent injection (TR/TE = 5.2/2.3 ms; reconstructed voxel size = 0.5 × 0.5 × 0.5 mm3; matrix size = 512:512); T2-weighted (FLAIR) images (TR = 4800/325 ms, voxel size = 0.49 × 0.49 × 1.0 mm3; matrix size = 512:512); inversion recovery Look Locker echo-planer imaging (TE = 18.7 ms, inversion time interval = 200 ms, 12 inversion times, flip angle = 4°, voxel size = 1.8 × 1.8 × 5.0 mm3); diffusion tensor images (B-values = 0 and 800 s/mm2, 15 directions, TR/TE = 9676/60 ms, voxel size = 2.5 × 2.5 × 2.5 mm3) and a gradient-echo, spin-echo DSC perfusion image series (GyroTools LLC, Zürich, Switzerland) with TR = 1500 ms, TE = 25/105 ms, voxel size = 1.8 × 1.8 × 5.0 mm3, where a 0.1 mmol/kg dose of contrast (Gadovist, Bayer Pharma AG, Germany) was injected.
MR post-processing
Binary maps of white matter and gray matter (excluding regions of tumour and oedema) were obtained from Look-Locker acquisitions using the FRASIER method with slice selective inversions.23 By fitting the observed signal to a linear combination of three exponential functions representing T1-relaxation of white matter, gray matter and CSF, fractional maps of the different brain tissues regions were obtained. Binary maps were generated by selecting voxels with fractional volume above 0.85 for white matter and above 0.70 for gray matter, respectively.
DSC-perfusion analysis was performed in nordicICE (NordicNeuroLab AS, Norway). Based on the contrast-enhanced first-pass of the data, CBV- and MTT-maps were created by standard SVD deconvolution with automatically detected AIF and corrected for contrast agent extravasation.24 The leakage correction is performed based on the method proposed by Boxerman et al.,25 where the extravascular effects of both T1- and T2*-relaxation time reduction are estimated and corrected for.
VAI analysis was performed as previously described.12 In short, relaxation rate curves for gradient- and spin-echo were obtained from DSC images, leakage-corrected and fitted to a gamma-variate curve. The corresponding voxel-level parametric plot of the pair-wise gradient- and spin-echo temporal data points form a vortex, which is characterized by its long axis, slope of a linear fit, the direction of the temporal vortex propagation and the area of the loop. All parameters were normalized to mean values of normal appearing white matter.
In our study, to assess the true effect on vortex area and because we examine the properties of tissue at selected intervals of CBV-values only, we used the area of the vortex directly instead of the proposed corrected vortex area12 that also compensate for the CBV dependency of the tissue.
In addition, voxel-wise CTTH measurements were performed as follows19: The transport function, h(t), obtained from the time derivative of the residual function, R(t), is fitted to a gamma distribution characterized by α and β:
| (12) |
CTTH and MTT are then given by the standard deviation and the mean of the gamma distribution, respectively: and MTT = αβ.
Results
Effect of branching angle heterogeneity dependent on the mean vessel orientation
Our findings show that the effect of branching angle heterogeneity depends on the distribution of vessel orientations. When the branching angle heterogeneity increases by extending the maximum angle in the interval of vessel orientations, the relaxation rates increases, in accordance with the findings of Semmineh et al.26 (Figure 2(a) to (c)). However, with the same branching angle heterogeneity, but with the mean vessel orientation fixed perpendicular to the main magnetic field (), the relaxation rates become independent of the branching angle heterogeneity (Figure 2(d) to (f)).
More specifically, as seen in Figure 3(a) to (c), higher branching angle heterogeneity causes a relative increase in ΔR2(*) when the mean vessel orientation < π/4, while we see a relative decline in ΔR2(*) when the mean vessel orientation > π/4. In addition, the simulations show that for low branching angle heterogeneity, the relaxation rates consistently increase as the mean vessel orientation increases. Figure 3 displays the results from white matter-like branching structures, and similar results were found in gray matter-like structures as shown in Supplementary Figure 1.
Figure 3.
The effects of vessel orientation distributions on the relaxation rates. Illustrations of white matter-like vessel trees (a) with increasing mean vessel orientation relative to the main magnetic field (left to right) and increasing branching angle heterogeneity (bottom to top). The resulting relaxation rates from spin echo (b) and gradient echo (c) are independent of mean vessel orientation when branching angle heterogeneity is high (σ > 1). With lower branching angle heterogeneity (σ < 1), the relaxation rates increase when mean vessel orientation approaches π/2.
Our main finding is that in capillary-dominated tissue structures with high branching angle heterogeneity – a likely scenario within the typical size of an image voxel – the relaxation rates are independent of the mean vessel orientation. However, please note that in voxels containing large feeding arteries or draining veins, the assumption of high branching angle heterogeneity is likely not to hold and other relaxation effects will dominate, i.e. intravascular relaxation with red blood cells as main perturbers.
Vortex area as a measure of oxygenation is modified by MTT and CTTH
In concordance with previous findings,19 our simulations show that the implementation of varying CTTH and MTT in our vascular model leads to corresponding changes in relaxation rate curves (Supplementary Figure 2A-B).
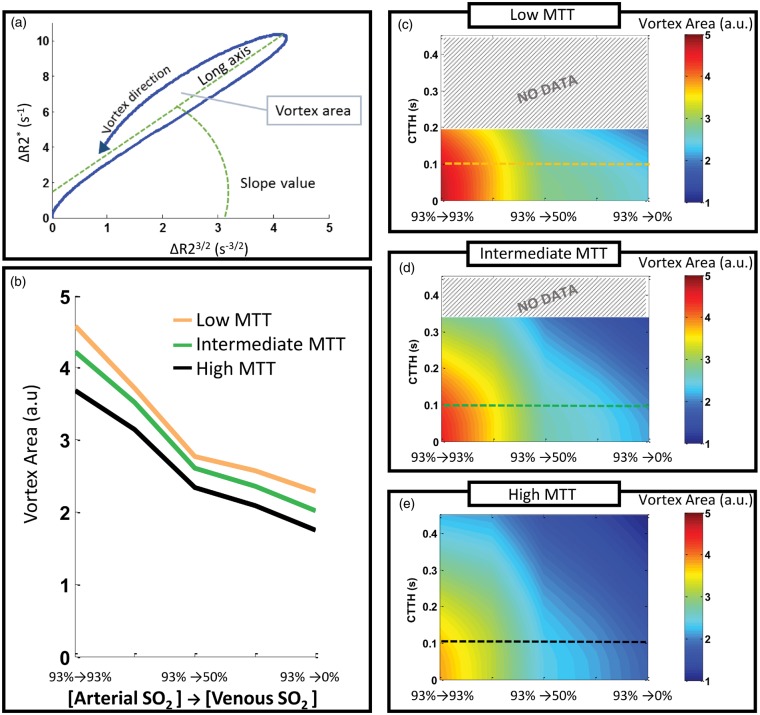
VAI simulations using our vascular model show that the vortex area decreases markedly when the artery-to-venule ΔSO2 increases (Figure 4(a)). However, the vortex area is also affected by both MTT and CTTH, in that for a given ΔSO2-level, the vortex area increases for lower MTT and lower CTTH. The combined effects of ΔSO2, MTT and CTTH on vortex area are shown in Figure 4(b) to (d). The long axis of the vortex also decreases as MTT and CTTH increases, while the other VAI-parameters were not affected by varying MTT and CTTH (Supplementary Figure 3A-B). Besides the apparent change in vortex area, varying ΔSO2 produced insignificant changes in the other VAI-parameters (Supplementary Figure 3C).
Figure 4.
Vortex area for varying CTTH, MTT and ΔSO2-levels. A parametric plot of the gradient echo and spin echo relaxation rate curves forms a vessel vortex curve and is characterized by the vortex direction, long axis, slope value and the vortex area (a). The vortex area decreases as the ΔSO2 increases (b) and can thus indicate the oxygenation status of the tissue. However, the vortex area is modified by the MTT and CTTH in the vessel system. The combined effects of CTTH and ΔSO2 on vortex area are shown for low MTT (c), intermediate MTT (d) and high MTT (e). Coloured lines in (c–e) correspond to the coloured lines in (b). Low CTTH and low MTT produces higher vortex area values than high CTTH and long MTT, and must be accounted for to obtain an accurate estimation of the SO2-level. No data for upper values of CTTH in (c) and (d), as maximum CTTH is dependent on MTT.
Our main finding is that even in a heterogeneous and highly realistic vascular model, the vortex area is proportional to ΔSO2. However, it should be noted that for a precise estimation of ΔSO2 at the voxel level, the effects of MTT and CTTH probably needs to be taken into account.
Determining cerebral vascular function and heterogeneity in patient data
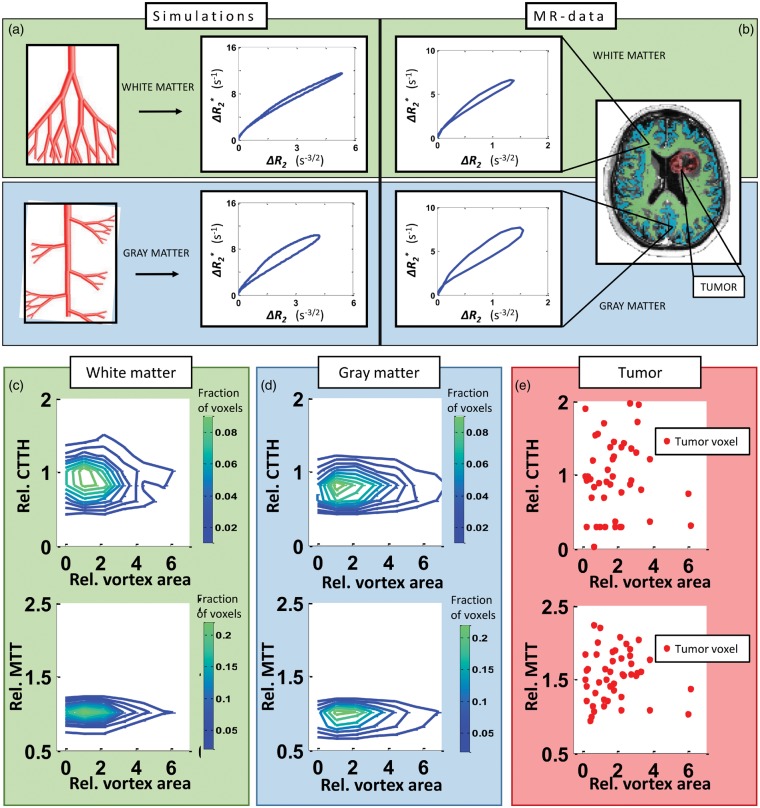
Our simulations show that an asymmetrical branching structure, which mimics cortical gray matter vasculature, produces VAI signatures of larger vortex areas compared to that of the symmetrical branching structure typically associated with white matter (Figure 5(a)). Our vessel model indicates that the vortex area in gray matter is larger than that of white matter by a factor of 2.15. This is in accordance with what we find in our patient data (Figure 5(b)), where the mean ratios of gray matter to white matter vortex area in healthy tissue were 1.76, 2.15, 2.25, 2.34 and 2.54, respectively, in voxels from the binary tissue masks with relative CBV-values ranging from 0.9 to 1.1 to match the volume fraction of the simulations.
Figure 5.
Vortex area-distribution in tissue types. (a) Simulations of vessel branching associated with white matter produces vortices with a relative small area (top row), compared to vessel branching mimicking gray matter, which gives vortices with a larger area (bottom row). The same GM to WM ratio of the vortex area is found in patient data. (b) A typical vortex from a white matter-voxel (top row) and from a gray matter-voxel (bottom row) is shown. WM- and GM-voxels are identified from maps as shown in MR-image (right) generated from Look-Locker acquisitions. Distribution of relative CTTH-values (top row) and relative MTT-values (bottom row) across relative vortex area in white matter (c), gray matter (d) and tumour (e) in voxels with relative CBV-values from 1.6 to 2.0, in a glioblastoma patient. Green (blue) contour lines denote higher (lower) fraction of voxels. Red dots correspond to single voxels in tumour region identified from contrast enhanced T1-weighted MRI.
Moreover, we here show representative data of the relative distributions of vortex area as a function of CTTH and MTT, respectively, in normal-appearing white matter (Figure 5(c)) and gray matter (Figure 5(d)) in a patient with a glioblastoma. In general, the vortex areas are shifted towards higher values in gray matter compared to those of white matter, indicating different branching structure and potentially different ΔSO2 levels of the two tissue types. We here also show example data from the tumour region of the same patient (Figure 5(e)). Compared to the corresponding values in normal-appearing tissue, voxels in the contrast enhanced tumour region display a heterogeneous and wide range of MTT and CTTH-values across the vortex area levels.
Discussion
For assessment of brain tumours and other cerebrovascular diseases, attaining information about the heterogeneous vascular tissue is essential. The results presented in our study outline the effects of a range of hemodynamic scenarios on the observed DSC-MRI response, and VAI in particular. By extending available theoretical vascular models to also include systems that account for vessel generation structure and branching, vessel orientation, capillary transit times and oxygenation level, we are able to map how the different microvascular characteristics influence the VAI-parameters. In short, we find that the observed MRI relaxation rates are independent of the mean vessel orientation in a typical capillary-dominated image voxel for both gray matter-like and white matter-like structures, and that the VAI-based vortex area is influenced by the relative oxygen saturation level and the branching structure of the tissue. We demonstrate a high concordance between the synthetic and human data, and we postulate that our work may serve as a roadmap for in vivo and per-voxel determination of vascular function and heterogeneity in the clinical setting by generating a database of VAI-derived parameters (including conventional DSC-parameters and CTTH) linked to a wide range of vascular characteristics.15,16
Semmineh et al.26 showed that relaxation rates increased with higher branching angle heterogeneity. In their setup, the increased heterogeneity also increased the mean vessel orientation, making it difficult to separate the effects of branching angle heterogeneity from the effects of vessel orientation. To address this issue, we show that the relaxation rate increases when a larger proportion of the vessels are oriented perpendicular to the main magnetic field (i.e. θ = π/2), because the extravascular magnetic field perturbation is proportional to sin2θ, as given in equation (1). Nonetheless, the dependency of the MRI relaxation rates to the mean vessel orientation appears relevant for low vessel branching angle heterogeneity only. For high branching angle heterogeneity, our data suggest the relaxation rates are independent of the mean vessel orientation. Due to the relatively large voxel size in DSC imaging (>1–2 mm3), it is reasonable to assume that the vessels within a given voxel do not align in any specific direction. Although the orientation of a given branching vessel will be limited based on the orientation of the parent vessel, a voxel in a DSC image will contain numerous vessel trees aligned in different orientations. The vessel orientation distribution within a voxel can thus be approximated by a uniform random distribution. However, using the theoretical framework presented in our study, any potential differences in the direction of the vessel architecture between frontal, occipital, lateral and temporal lobes may be investigated in future studies.
Moreover, our simulations indicate that the vortex area obtained with VAI could serve as an apparent indicator of the relative oxygen saturation level of the tissue. MRI-based voxel-wise measurements of oxygenation status have also been performed by blood oxygen level dependent (BOLD)-techniques, with promising results in rat models and human subjects.27–30 Future studies with both BOLD and VAI should be conducted to compare and validate the oxygenation measurements derived from these techniques. BOLD-based measurements require either fitting the signal to a complex model function27 – making the estimations subject to uncertainties due to the inherent low SNR – or an independent estimation of CBV28,30 (e.g. from DSC). In contrast, with the VAI-technique, all the relevant parameters are derived from the same acquisition.
In our simulation model, the oxygen saturation level changes sharply from the last arteriole to the first capillary. A more physiologically accurate representation would include a gradual change of the oxygen level across several vessel generations. However, our simulations have shown that this has marginal effect on the signal response. Xu et al.11 used a model approach with random vessel orientation and showed that, excluding the effects of varying ΔSO2, the shape of the vessel vortex was affected by varying MTT. In our tissue model, the vortex area was found proportional to ΔSO2 in a size-dependent matter. This is in concordance with previous reports, where poor hemodynamic flow was associated with higher relative vortex area values in patients with newly diagnosed14 and recurrent glioblastomas,12 indicating poor oxygen delivery and consumption.
Jespersen et al.31 have recently shown that the maximum oxygen extraction fraction from the capillaries is dependent on CTTH, and that CTTH can be measured using DSC MRI,19 assuming that the distribution of transit times in a DSC-voxel stems from capillaries only. Therefore, for quantitative estimation of oxygen saturation levels, both our data and previous reports suggests that the effects of capillary transit times (i.e. MTT and CTTH) should be taken into consideration when trying to estimate reliable measurements of oxygen saturation levels. However, while estimates of MTT and CTTH may provide information about the maximum oxygen extraction fraction,31,32 they do not provide information about the actual oxygen level in the tissue. To this end, our data indicate that combining measurements of VAI-based vortex area with CTTH and MTT have the potential to return a more robust assessment of the oxygenation status in the tissue.
While the measured CTTH in our study scaled with the simulated CTTH, the measured CTTH cannot approach zero even when simulated CTTH is set to zero because our vessel model includes vessels with a flow profile, i.e. a distribution of transit times at each vessel generation. How much CTTH will affect the shape of the transport function – and thus the accuracy of the measured CTTH – is likely to be dependent on the fractional volume of capillaries relative to the fractional volume of arterioles and venules in a given DSC-voxel. Finally, our simulations show that vortex area in tissues with branching structure similar to those found in gray matter is higher than that of white matter. This indicates that the higher vortex area found in normal-appearing gray matter in our patient data is due to the complexity of the branching structure and not due to unrealistic low oxygen consumption rates.33 This highlights the importance of mapping out the relevant contributions to vortex area to be able to determine the underlying physiological properties of the tissue. This could be especially relevant in tumour, where abnormal branching of the vessels, as well as abnormal oxygen levels are likely to occur. In addition, the tumour vasculature often deviates from that of the healthy brain in terms of permeability, vessel calibre and tortuosity, which may affect the signal response and thus impede the estimation of the parameters. Due to the complex interaction between microvascular and hemodynamic characteristic of the tissue and the signal response, it is difficult to assign a relative change in a single parameter to a single change in tissue characteristic. To this end, we believe that a fingerprinting approach could help reveal the underlying physiological mechanism responsible for a VAI-response on a per-voxel basis.15,16
A challenge with synthetic tissue models, in general, is the use of certain assumptions in order to achieve a realistic representation of the system while maintaining a manageable level of complexity. Here, we have made the assumption of randomly oriented vessels within a voxel. Because the orientation of the downstream vessel branching is limited by the orientation of its upstream parent vessel, vessels within a given vessel tree will to some extend be aligned along a certain direction34 (= mean vessel orientation) relative to the main magnetic field. We assume, however, that the effect of randomly oriented vessel trees, with vessels aligned around a certain direction, return the same effect as that of randomly oriented vessel. The branching structure of the vessel tree, with either symmetrical or asymmetrical branching of vessels, is also a simplification of the cerebral vasculature. Moreover, for implementation of CTTH, we assumed a uniform distribution of capillary transit times centred around a given . An evaluation of how accurate our choice of distribution is a realistic representation of actual capillary transit times is challenging since, in our model, transit times are distributed within each vessel, as well as across different capillaries. The resulting transport function for all vessel has the form of a gamma distribution, in accordance with models previous used.19,35 However, in our model, the standard deviation of the transport function (i.e. the measured CTTH) is not a direct measurement of the standard deviation of the capillary transit times (i.e. the simulated CTTH), due to the effect of transit time distribution across all vessels in the system. The simulated MTT for the whole voxel are in general higher than MTT-values reported from DSC.36 Simulating shorter transit times would extensively increase the computational power needed, as the convolution steps (see equations (6) and (7)) demand higher temporal resolution, and thus significantly increase the memory use of the arrays involved.
In conclusion, by re-evaluating and extending current theoretical models for DSC-MRI and VAI, we have simulated realistic scenarios of vascular heterogeneity, including vessel orientation distributions, vessel generation branching and capillary transit times. Our findings show that VAI analysis, in combination with CTTH-measurements, can reveal information about microvascular tissue characteristics, including branching structure and oxygenation status. Collectively, our study presents a comprehensive framework that may serve as a roadmap for in vivo and per-voxel determination of vascular status and heterogeneity in cerebral tissue.
Supplementary Material
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: Norwegian Cancer Society Grant 3434180, South-Eastern Norway Regional Health Authority Grant 2013069.
Declaration of conflicting interests
The author(s) declared the following potential conflicts of interest with respect to the research, authorship, and/or publication of this article: KEE: Intellectual property rights; NordicNeuroLab AS, Bergen, Norway. AB: Intellectual property rights; NordicNeuroLab AS, Bergen, Norway. Board Member; NordicNeuroLab AS, Bergen, Norway. All other authors declare that they have no conflict of interest.
Authors’ contributions
I.D. wrote the manuscript. F.C. provided the technical setup for the dual-echo sequence. T.R.M., E.V.M, G.L. and S.A.V. acquired all the MRI data. I.D. and A.B. performed the MatLab simulations. I.D. and K.E.E analysed and interpreted the simulations and human data. I.D., A.B., S.A.V, G.L., F.C., T.R.M., E.V.M and K.E.E. revised the manuscript critically. I.D., A.B., S.A.V, G.L., F.C., T.R.M., E.V.M and K.E.E. approved the final version of the manuscript.
Supplementary material
Supplementary material for this paper can be found at the journal website: http://journals.sagepub.com/home/jcb
References
- 1.Viallon M, Cuvinciuc V, Delattre B, et al. State-of-the-art MRI techniques in neuroradiology: principles, pitfalls, and clinical applications. Neuroradiology 2015; 57: 441–467. [DOI] [PubMed] [Google Scholar]
- 2.Covarrubias DJ, Rosen BR, Lev MH. Dynamic magnetic resonance perfusion imaging of brain tumors. Oncologist 2004; 9: 528–537. [DOI] [PubMed] [Google Scholar]
- 3.Weisskoff RM, Zuo CS, Boxerman JL, et al. Microscopic susceptibility variation and transverse relaxation: theory and experiment. Magn Reson Med 1994; 31: 601–610. [DOI] [PubMed] [Google Scholar]
- 4.Tropres I, Grimault S, Vaeth A, et al. Vessel size imaging. Magn Reson Med 2001; 45: 397–408. [DOI] [PubMed] [Google Scholar]
- 5.Kiselev VG, Strecker R, Ziyeh S, et al. Vessel size imaging in humans. Magn Reson Med 2005; 53: 553–563. [DOI] [PubMed] [Google Scholar]
- 6.Boxerman JL, Hamberg LM, Rosen BR, et al. MR contrast due to intravascular magnetic susceptibility perturbations. Magn Reson Med 1995; 34: 555–566. [DOI] [PubMed] [Google Scholar]
- 7.Jensen JH, Chandra R. MR imaging of microvasculature. Magn Reson Med 2000; 44: 224–230. [DOI] [PubMed] [Google Scholar]
- 8.Barbier EL, Lamalle L, Decorps M. Methodology of brain perfusion imaging. J Magn Reson Imaging 2001; 13: 496–520. [DOI] [PubMed] [Google Scholar]
- 9.Tropres I, Pannetier N, Grand S, et al. Imaging the microvessel caliber and density: Principles and applications of microvascular MRI. Magn Reson Med 2015; 73: 325–341. [DOI] [PubMed] [Google Scholar]
- 10.Emblem KE, Farrar CT, Gerstner ER, et al. Vessel caliber–a potential MRI biomarker of tumour response in clinical trials. Nat Rev Clin Oncol 2014; 11: 566–584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Xu C, Kiselev VG, Moller HE, et al. Dynamic hysteresis between gradient echo and spin echo attenuations in dynamic susceptibility contrast imaging. Magn Reson Med 2013; 69: 981–991. [DOI] [PubMed] [Google Scholar]
- 12.Emblem KE, Mouridsen K, Bjornerud A, et al. Vessel architectural imaging identifies cancer patient responders to anti-angiogenic therapy. Nat Med 2013; 19: 1178–1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Stadlbauer A, Zimmermann M, Heinz G, et al. Magnetic resonance imaging biomarkers for clinical routine assessment of microvascular architecture in glioma. J Cereb Blood Flow Metab 2017; 37: 632–643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Batchelor TT, Gerstner ER, Emblem KE, et al. Improved tumor oxygenation and survival in glioblastoma patients who show increased blood perfusion after cediranib and chemoradiation. Proc Natl Acad Sci U S A 2013; 110: 19059–19064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature 2013; 495: 187–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Christen T, Pannetier NA, Ni WW, et al. MR vascular fingerprinting: A new approach to compute cerebral blood volume, mean vessel radius, and oxygenation maps in the human brain. Neuroimage 2014; 89: 262–270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Jain V, Abdulmalik O, Propert KJ, et al. Investigating the magnetic susceptibility properties of fresh human blood for noninvasive oxygen saturation quantification. Magn Reson Med 2012; 68: 863–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Barboriak DP, MacFall JR, Viglianti BL, et al. Comparison of three physiologically-based pharmacokinetic models for the prediction of contrast agent distribution measured by dynamic MR imaging. J Magn Reson Imaging 2008; 27: 1388–1398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mouridsen K, Hansen MB, Ostergaard L, et al. Reliable estimation of capillary transit time distributions using DSC-MRI. J Cereb Blood Flow Metab 2014; 34: 1511–1521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Murray CD. The physiological principle of minimum work applied to the angle of branching of arteries. J Gen Physiol 1926; 9: 835–841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kaplan HA. Arteries and veins of the human brain. Electroencephal Clin Neurophysiol 1970; 28: 330–331. [Google Scholar]
- 22.Reina-De La Torre F, Rodriguez-Baeza A, Sahuquillo-Barris J. Morphological characteristics and distribution pattern of the arterial vessels in human cerebral cortex: a scanning electron microscope study. Anat Rec 1998; 251: 87–96. [DOI] [PubMed] [Google Scholar]
- 23.Shin W, Geng X, Gu H, et al. Automated brain tissue segmentation based on fractional signal mapping from inversion recovery Look-Locker acquisition. Neuroimage 2010; 52: 1347–1354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bjornerud A, Emblem KE. A fully automated method for quantitative cerebral hemodynamic analysis using DSC-MRI. J Cereb Blood Flow Metab 2010; 30: 1066–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Boxerman JL, Schmainda KM, Weisskoff RM. Relative cerebral blood volume maps corrected for contrast agent extravasation significantly correlate with glioma tumor grade, whereas uncorrected maps do not. AJNR Am J Neuroradiol 2006; 27: 859–867. [PMC free article] [PubMed] [Google Scholar]
- 26.Semmineh NB, Xu J, Boxerman JL, et al. An efficient computational approach to characterize DSC-MRI signals arising from three-dimensional heterogeneous tissue structures. PLoS One 2014; 9: e84764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.He X, Yablonskiy DA. Quantitative BOLD: mapping of human cerebral deoxygenated blood volume and oxygen extraction fraction: default state. Magn Reson Med 2007; 57: 115–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Christen T, Lemasson B, Pannetier N, et al. Evaluation of a quantitative blood oxygenation level-dependent (qBOLD) approach to map local blood oxygen saturation. NMR Biomed 2011; 24: 393–403. [DOI] [PubMed] [Google Scholar]
- 29.He X, Zhu M, Yablonskiy DA. Validation of oxygen extraction fraction measurement by qBOLD technique. Magn Reson Med 2008; 60: 882–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Toth V, Forschler A, Hirsch NM, et al. MR-based hypoxia measures in human glioma. J Neurooncol 2013; 115: 197–207. [DOI] [PubMed] [Google Scholar]
- 31.Jespersen SN, Ostergaard L. The roles of cerebral blood flow, capillary transit time heterogeneity, and oxygen tension in brain oxygenation and metabolism. J Cereb Blood Flow Metab 2012; 32: 264–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tietze A, Mouridsen K, Lassen-Ramshad Y, et al. Perfusion MRI derived indices of microvascular shunting and flow control correlate with tumor grade and outcome in patients with cerebral glioma. PLoS One 2015; 10: e0123044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhu XH, Chen W. In vivo17O MRS imaging - Quantitative assessment of regional oxygen consumption and perfusion rates in living brain. Anal Biochem. Epub ahead of print 26 August 2016. DOI: 10.1016/j.ab.2016.08.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Adam JA. Blood vessel branching: Beyond the standard calculus problem. Math Mag 2011; 84: 196–207. [Google Scholar]
- 35.Buxton RB, Frank LR. A model for the coupling between cerebral blood flow and oxygen metabolism during neural stimulation. J Cereb Blood Flow Metab 1997; 17: 64–72. [DOI] [PubMed] [Google Scholar]
- 36.Helenius J, Perkio J, Soinne L, et al. Cerebral hemodynamics in a healthy population measured by dynamic susceptibility contrast MR imaging. Acta Radiol 2003; 44: 538–546. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.