Compaction of Duplex Nucleic Acids upon Native Electrospray Mass Spectrometry

Abstract

We report on the fate of nucleic acids conformation in the gas phase as sampled using native mass spectrometry coupled to ion mobility spectrometry. On the basis of several successful reports for proteins and their complexes, the technique has become popular in structural biology, and the conformation survival becomes more and more taken for granted. Surprisingly, we found that DNA and RNA duplexes, at the electrospray charge states naturally obtained from native solution conditions (≥100 mM aqueous NH₄OAc), are significantly more compact in the gas phase compared to the canonical solution structures. The compaction is observed for all duplex sizes (gas-phase structures are more compact than canonical B-helices by ∼20% for 12-bp, and by up to ∼30% for 36-bp duplexes), and for DNA and RNA alike. Molecular modeling (density functional calculations on small helices, semiempirical calculations on up to 12-bp, and molecular dynamics on up to 36-bp duplexes) demonstrates that the compaction is due to phosphate group self-solvation prevailing over Coulomb repulsion. Molecular dynamics simulations starting from solution structures do not reproduce the experimental compaction. To be experimentally relevant, molecular dynamics sampling should reflect the progressive structural rearrangements occurring during desolvation. For nucleic acid duplexes, the compaction observed for low charge states results from novel phosphate–phosphate hydrogen bonds formed across both grooves at the very late stages of electrospray.

Short abstract

Electrospray ionization is widely used in mass spectrometry. But to what extent is the solution structure conserved in the gas phase? Using ion mobility, we demonstrate that DNA duplexes are much more compact in the gas phase than in solution.

Introduction

Besides genetic information storage, nucleic acids perform pivotal regulatory functions in living organisms.¹ Conformational changes are key to these regulation mechanisms, whether at the DNA level (e.g., particular structures in gene promoters)² or at the RNA level (e.g., riboswitches).³ There is thus a need for new experimental approaches enabling one to detect and characterize the different ensembles of conformation simultaneously present in solution. “Native” electrospray ionization mass spectrometry (ESI-MS) helps to decipher the complexation equilibria.⁴⁻⁷ “Native MS” means that the solution conditions must be compatible with electrospray ionization, yet allow the system to fold in the same way as it would in physiological conditions.⁸ The typical solution condition for native MS is aqueous ammonium acetate (neutral pH, no organic cosolvent). Also, the mass spectrometer must be operated in “soft” conditions, meaning that the internal energy imparted to the ions must be just enough to desolvate the biomolecules and strip nonspecific ionic adducts, but not too high so as not to disrupt the complexes before they reach the mass analyzer.

Ion mobility spectrometry (IMS) further enables characterization of the shape of each complex separated by mass, based on the electrophoretic mobility of the ions in a buffer gas.⁹ Coupled to ion mobility spectrometry (IMS), native mass spectrometry thus makes it possible to reveal the topology of mutli-protein complexes,¹⁰ conformational changes upon ligand binding,¹¹⁻¹³ or the architecture of synthetic supramolecular assemblies.¹⁴ But before native ESI-IMS-MS can be applied to characterize nucleic acids conformations in solution, it is essential to understand to what extent the different types of DNA/RNA secondary structures are preserved, or affected, by the transition from the solution to the gas phase.

Tandem mass spectrometry¹⁵⁻¹⁸ experiments have shown that the kinetic stability of gas-phase DNA duplexes was correlated with the fraction of guanine–cytosine (GC) base pairs and with the base pair ordering. This suggested that Watson–Crick (WC) hydrogen bonding and base stacking were at least partially maintained in the gas phase. Infrared multiphoton dissociation spectroscopy on duplexes and single strands suggested that GC bases are engaged in hydrogen bonds in the gas-phase duplexes, although no such evidence was found for AT base pairs.¹⁹ Early molecular dynamics (MD) validated this view: although (12-mer)₂^6– and (16-mer)₂^8– duplexes were distorted in the gas phase, most WC H-bonding and stacking interactions were preserved, particularly in GC-rich regions.²⁰

The Bowers group further explored the gas-phase structure of DNA duplexes by IMS.^21,22 By comparing the experimental collision cross section (CCS) of d(GC)_n duplexes with those obtained on duplexes relaxed by short (5 ns) MD, they showed that the gas-phase structures resemble an A-helix for the short duplexes (8—16-mer) and a B-helix for longer ones (>18-mer). However, those experiments had been performed on the relatively high charge states (1 negative charge per 2 base pairs) obtained from solution conditions (49:49:2 mixture of H₂O/MeOH/NH₄OH) differing markedly from those typically used in native MS. Here we show that, at the lower charge states typically obtained from native MS conditions (100—150 mM NH₄OAc in 100% H₂O, pH = 7), the gas-phase conformations are significantly more compact than expected for B- or A-helices. We investigated the physical origin of this gas-phase compaction by molecular modeling.

Results and Discussion

DNA Duplexes in Their Predominant Native Charge State Are More Compact than a Canonical B-Helix

The sequences studied here were designed based on the Dickerson-Drew dodecamer,²³ here noted 12-d₆₆ indicating the number of base pairs (12), the nucleotide type (i.e., d for DNA and r for RNA), and the GC base pair percentage content (66%) as a subscript. This notation was used throughout the text. DNA or RNA duplexes were prepared by annealing in aqueous ammonium acetate and analyzed using drift tube ion mobility in helium (see methods and Supporting Information Section S1). In aqueous NH₄OAc, RNA sequences fold into the A-form, and DNA sequences fold into the B-form (according to the circular dichroism²⁴ spectra in Supporting Information Figure S2).

When sprayed from aqueous 100 mM NH₄OAc, the major charge state of 12-bp duplexes is 5– (Figure S3). This may seem at odds with the solution charge of the nucleic acid alone, which is 22–. One should however keep in mind that an atmosphere of counterions surrounds nucleic acids in solution.²⁵ If counterions were not present, the electrostatic repulsion between strands would amount to hundreds of kT, and double helices would not exist. The effective charge state of nucleic acids in solution is hard to define: bulk solutions being electrically neutral, the net charge of a duplex depends on which distance from the nucleic acid atoms one places the boundary. Molecular dynamics simulations on 18-bp B-DNA duplexes²⁶ showed that neutrality is reached at an average distance of 24 Å from the center of the helix, and that 76% neutralization (a threshold defined by Manning’s counterion condensation model²⁷) is reached at 18 Å. Electrospray droplets are however not neutral, and the final charge states could reflect the thickness of the layer of solvent and counterions surrounding the nucleic acid in the final droplets.

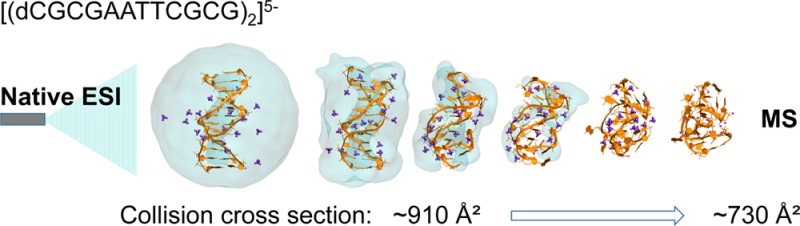
The ^DTCCS_He distributions for the 5– duplexes without ammonium ions bound and in the softest ion transfer conditions are shown in Figure 1A (full results in Supporting Figure S4). These distributions suggest more compact structures than those of canonical B- or A-forms (Table 2). Upon pre-IMS activation, the CCS distribution of 12-d₃₃ is unchanged, 12-d₆₆ is losing the high-CCS peak to the profit of the low-CCS peak, and the entire distribution of 12-d₁₀₀ is shifting toward lower CCS (from 730 Å down to ∼705 Ų, see Supporting Information Figure S5). At low pre-IMS activation, duplexes^5– with ammonium adducts are also detected. The CCS of these ions is similar to that of the bare duplexes, but for 12-d₆₆ the higher-CCS peak is more abundant—see Supporting Figure S6). The peak center values obtained for soft and harsh conditions are listed in Table 2. Charge states 4– and 6– are also detected in aqueous NH₄OAc. The duplex CCS distributions are highly charge-state dependent (see Supplementary Figure S4): charge states 4– and 5– are similarly compact, whereas charge state 6– has a ∼20% larger CCS. Charge state 7–, obtained for 12-d₆₆ and 12-d₁₀₀ by adding the “supercharging” agent sulfolane,²⁸ has a >30% larger CCS. The duplex CCS distributions are significantly broader than those of the tetramolecular G-quadruplex [dTG₄T]₄ (in black in Figure 1A, and Supplementary Figure S4), a rigid structure with the same number of bases. This indicates that a greater conformational space is explored in the gas phase by nucleic acid duplexes compared to the G-quadruplex,¹⁸ and that gas-phase duplexes consist of an ensemble of conformations not fully interconverting on the time scale of the mobility separation (10–30 ms).

Figure 1.

(A) Experimental ^DTCCS_He distribution measured under soft native conditions for the 12-bp DNA duplexes (green: (12-d₃₃)^5–, blue: (12-d₆₆)^5–, red: (12-d₁₀₀)^5–; see Table 1 for full sequences) and the rigid G-quadruplex ([d(TG₄T)]₄)^5– (black). (B–E) Calculated CCS distributions for molecular models generated by (B) gas-phase MD of the B-helices, (C) gas-phase MD of the A-helices, (D) T-REMD simulations on B-helices using distributed charges (note that most of the population of (12-d₃₃)^5– duplex dissociated during simulations), and (E) MD following a restrained minimization forcing H-bond formation between the phosphate groups across both grooves of a B-helix. The final MD structures of each duplex model, created with VMD software,²⁹ are shown for (12-d₆₆)^5– on the same scale (see Supporting Figure S11 for a magnification).

Table 2. Collision Cross Section Values in Helium (CCS_He) of 12-bp Duplexes, Experimental and Calculated Prior and Subsequent to PM7 Optimization, Unbiased MD, T-REMD (DC Model; Results with LC Model Are Not Listed Because They Depend on the Chosen Locations—See Text), and Unbiased MD on the Helix Zipped by Restrained Minimization^a.

		CALCCCSHe (Å2)
		B-helix				A-helix				zipped helix
	DTCCSHe (Å2)	canonical	PM7	MD	T-REMD (DC)	canonical	PM7	MD	T-REMD (DC)	MD
[12-d33]5–	soft/harsh: 760	918	914	954 ± 18	780 ± 24	900	861	826 ± 11		759 ± 12
[12-d66]5	soft: 735/803	903	831	881 ± 6	770 ± 15	893	942	886 ± 10		752 ± 10
	harsh: 735
[12-d100]5–	soft: 730	908	838	953 ± 8	771 ± 14	892	869	774 ± 6		711 ± 9
	harsh: 705
[12-r33]5–						944	938		741 ± 21
[12-r66]5–	soft/harsh: 725					945	902		747 ± 18
[12-r100]5–	soft: 735					940	896		743 ± 11
	harsh: 695

^aErrors reported for MD are the standard deviation on the different structures along the trajectory.

MD Trajectories, DFT, and Semiempirical Optimizations Reveal Phosphate–Phosphate Hydrogen Bond Formation

To find out which three-dimensional structures are compatible with the experimental CCS values of the 12-bp^5– duplexes, we first carried out unbiased MD simulations directly from B- and A-helix structures, stripped of the solvent. The two possibilities to reduce the total charge to −5 (major charge state) are the localized charges (LC) and distributed charges (DC) models.²⁰ With the DC model, the net charge of each phosphate group is reduced so that the total charge of the duplex is −5. With the LC model, protons are added on 17 out of the 22 phosphate groups. LC and DC gave similar results upon unbiased MD of duplexes,²⁰ so here only the LC model was tested extensively.

Figure 1B,C shows representative CCS distributions. All such simulations give CCS values significantly larger than the experimental ones. Independent trajectories, started from different conformations and with different sets of localized charges, confirmed this result (Supporting Figure S8). The experimental CCS values of the duplexes^6– are nonetheless compatible with the simulated A- and B-helices, and duplexes^7– are compatible with B-helices. This does not necessarily mean that the gas-phase conformations of 6– and 7– charge states are A- and B-helices, but it helps to understand conclusions previously derived solely based on more densely charged duplexes.^21,22

When starting from the B-form, MD simulations always show spontaneous hydrogen bond formation between phosphate groups situated on each side of the minor groove (Supporting Information Movie S1 and Figure S9). This causes the “zipping” of the minor groove. The structures are stable up to 1 μs (Figure S9), but too elongated compared to the duplexes^5– experimental data (compare Figure 1B with 1A). In simulations starting from the A-helix, zipping occurs as well, but this time across the major groove (Supporting Figure S10). In the gas phase, the closest protonated phosphate groups therefore tend to form hydrogen bonds that did not exist in solution. However, this kind of simulation does not reproduce the experiments.

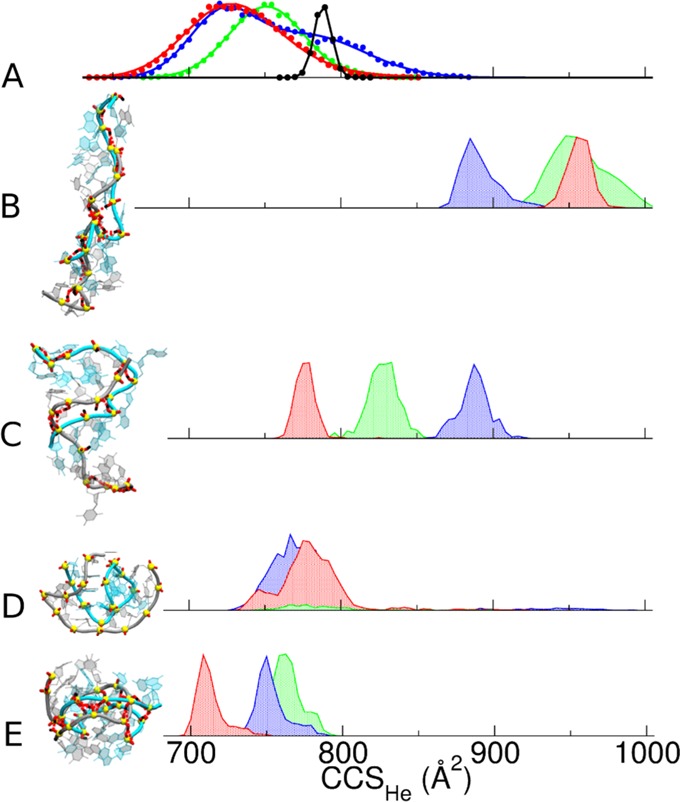
To check for possible artifacts due to using classical force fields to represent macromolecules in the gas phase, we also studied B-duplexes at the density functional theory (DFT) and semiempirical (SE) levels. Upon DFT optimization of 7-bp to 10-bp duplexes, phosphate groups form new H-bonds and close the minor groove as well (Figure 2 and Supporting Figure S12). WC H-bonds base stacking are well preserved,^30,31 and the helix compresses along its longitudinal axis (Figure 2C) and the ^CALCCCS_He of the DFT optimized structure is smaller than that of the canonical helix.

Figure 2.

DFT optimization of the 10-bp duplex^4–: (A) new hydrogen bonds formed between phosphate groups across the minor groove; (B) superposition of the sugar–phosphate backbones of the canonical B-helix (green) and optimized duplex (red); (C) superposition of the base pairs of the canonical B-helix (green) and optimized duplex (red).

For SE calculations, we first validated that the PM7 method best reproduces the DFT results (Supporting Figure S13). The CCS values obtained after PM7 optimization are summarized in Table 2 for all [12-bp duplexes]^5– (A- and B-form for DNA and A-form for RNA). Upon PM7 optimization, the duplex [12-d₆₆]^5– undergoes minor groove zipping, while WC H-bonds and base pair stacking interactions are preserved (Figure S14). The compaction compared to the solution structure is only ∼8%, still far from the experimental value.

Thus, starting from naked canonical structures, neither geometry optimization nor unbiased MD trajectories lead the system toward the experimentally observed conformational ensemble. So, either the sampling is incomplete (simulated and experimental time scales differ), or the starting structures, obtained by desolvating and charging the duplexes all at once, inadequately reflect the electrospray droplet desolvation and declustering.

Temperature Replica Exchange MD (T-REMD) Exploration of Gas-Phase Conformational Landscapes Do Not Converge to the Experimental Structure

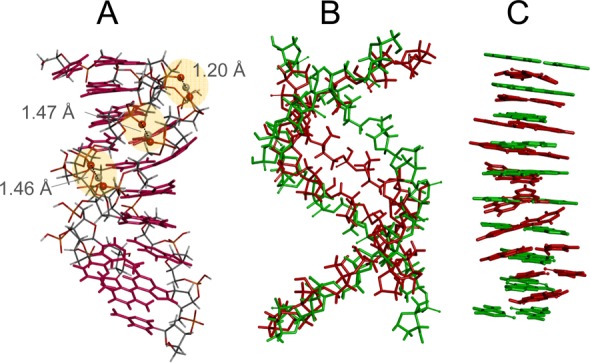
To enhance sampling, we carried out T-REMD simulations on the 12-bp duplexes^5– starting from their canonical structures. Because temperature replica exchange MD (T-REMD) simulations on gas-phase duplexes have never been attempted before, LC and DC models were both tested for T-REMD. DNA and RNA results, including representative snapshots, total hydrogen bonding, WC hydrogen bonding and stacking³² occupancies, are summarized in Supporting Information Section S7 (Figures S15—S25). For RNA, the theoretical CCS distributions, both with the DC and LC models, match with the experimental ones (Figures S16 and S19). However, the hydrogen bonding and stacking patterns (Figures S20—S22) always become scrambled in the gas phase. For DNA, the T-REMD results depend more critically on the charge location model: ^CALCCCS_He values agree with the experiments for the DC model (Figure 1D) and for some LC models (Figure 3).

Figure 3.

T-REMD on 12-bp DNA duplexes^5– with localized charges (LC). (A) [12-d₆₆]^5–, (B–C) [12-d₁₀₀]^5– with different LC models. The location of negatively charged phosphates is shown by the beads on the representative snapshot structure. The experimental ^DTCCS_He distribution and calculated one (shade) are overlaid. The fractional WC H-bond occupancies are shown on the right: the bases of each strand are numbered from 5′ to 3′, and perfect base pair matching is therefore indicated by a diagonal from top left to bottom right.

With the DC model, the CCS values are closer to the experimental ones, yet still significantly too large for 12-d₁₀₀^5–. The GC base pairs are mostly preserved (Figure S37), but the duplex 12-d₃₃^5– is mostly melted (separated into single strands; see Figure S15). DC models lack the explicit protons and therefore cannot form phosphate–phosphate hydrogen bonds. As a result, the strands can dissociate upon T-REMD. The rate of strand dissociation occurrence ranks 12-d₃₃ > 12-d₆₆ > 12-d₁₀₀ (Supporting Figure S15), in line with the relative gas-phase kinetic stabilities in tandem mass spectrometry.¹⁵⁻¹⁸

When LC models are used, the T-REMD final structures depend significantly on the choice of charge location (Figure S18, S20—S22). For example, for [12-d₁₀₀]^5–, a first model (Figure 3B) gives CCS values matching well with the experiment, but has lost most WC H-bonds, whereas a second model (Figure 3C) preserves WC H-bonds but its CCS values are much larger than the experimental ones (the representative structure resembles those obtained with unbiased simulations starting from the B-form).

In summary, the T-REMD results do not account simultaneously for the preservation of GC base pairs and the experimental collision cross sections. Yet they teach us that the duplex^5– conformations are closer to a compact globular shape than to the helices obtained by unbiased MD trajectories and suggest that sampling problems are at least partially responsible for the lack of agreement between simulation and experimental CCSs.

Progressive Duplex Desolvation Leads to Experimentally Relevant Structures

All simulations presented to this point, and nearly all previous simulations, are assuming an instantaneous transfer of the duplex from solution to the gas phase. But in practice, desolvation and declustering proceed gradually during the experiment. Consta and co-workers³³ modeled the desolvation process of duplex dA₁₁·dT₁₁ at the atomistic level in a water droplet containing Na⁺ and Cl^–, and found that the duplex collapses inside the droplet when the Na⁺ cations are numerous enough to interact with the phosphates and reduce the size of both grooves. Interestingly, the resulting charge density is similar to that observed experimentally from native conditions. It is therefore likely that the DNA duplexes are desolvated via the charged residue model^34,35 and that the compaction results from the association of NH₄⁺ cations to both minor and major groove before full desolvation. As a result, the starting structure for gas phase simulations might be quite different from the canonical A- or B-helices. Because electrostatic interactions prevail, the gas phase conformational space is very stiff, and an incorrect starting structure can significantly bias the entire trajectory.

Here we simulated the desolvation of duplex 12-d₆₆ placed in a droplet containing ∼2400 water molecules and 17 NH₄⁺ (net charge = −5). When the simulation at 350 K reaches 39.5 ns, 87 water molecules remain on the duplex together with the 17 NH₄⁺ cations. The simulation was pursued for 50 ns at 450 K, to allow this ultrastable inner solvation shell of water molecules to evaporate. The ammonium ions sticking to the duplex are mainly located close to phosphate groups, often in-between them. Several trajectories (see 4–, 5–, and 6– charge states in Supporting Information Section S8; Figures S26—S31) lead to a chain of ammonium ions in the minor groove. For the 5– charge state, ammonium ions are more distributed across both grooves, and thus upon evaporation both grooves get narrower to enable phosphate–ammonium–phosphate salt bridges to form. Accordingly, the CCS value diminishes (Figure 4).

Figure 4.

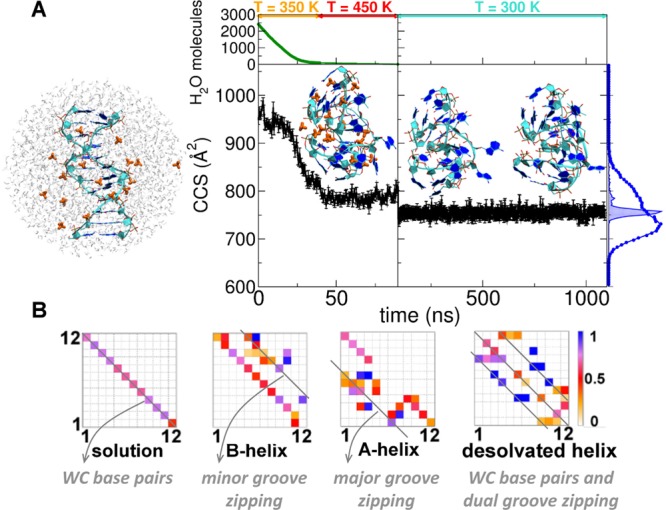
(A) ^CALCCCS_He evolution during the desolvation of the 12-d₆₆ droplet with −5 net charge. At the top the simulation temperatures are shown along the related trajectory portions. The initial, intermediate, and final structures are shown with DNA strands in cyan, bases aromatic rings in blue, and NH₄⁺ cations in orange. On the right the [12-d₆₆]^5-DTCCS_He distribution (blue circles) is superimposed on the ^CALCCCS_He (blue area) one. (B) H-bond occupancies of the desolvated helix (right), compared to Watson–Crick H-bond occupancies of a B-helix in solution (left), and to gas-phase B- or A-helices upon unbiased MD in the gas phase (middle). In the B-helix, extra H-bonds form between phosphates across the minor groove; in the A-helix, across the major groove, and in the desolvated helix, across both grooves.

Classical MD cannot model proton transfer, but if water evaporation is almost complete before the proton transfers start, then the structures generated by gradual desolvation are good candidates for modeling the electrosprayed structures. Also, ammonium ion positioning upon desolvation could predict which phosphate groups will share a proton and form hydrogen bonds after complete declustering.

To simulate the eventual ammonia loss, we arbitrarily transferred a proton from each ammonium ion to its closest phosphate oxygen. The resulting desolvated and declustered duplex (12-d₆₆)^5– is stable over 1-μs MD at 300 K (Figure 4). The total hydrogen bond occupancy reveals additional contacts across both grooves. Remarkably, the CCS value now matches the experimental one, and at the same time, the generated structure keeps partial memory of the WC base pairs (at least, preserving mostly the GC ones), in line with CID and IRMPD results.

In summary, progressive desolvation, allowing the duplex to form phosphate-phosphate hydrogen bonds across both grooves, can account simultaneously for the experimental compactness and for partial preservation of GC base pairs. In contrast, upon unbiased MD or structure optimization (DFT or SE), only the phosphate groups that were the closest in the starting structure (across the minor and major groove for B- and A-helices, respectively) could mate.

Longer Duplexes, DNA and RNA Alike, Undergo Compaction When Electrosprayed from Aqueous Solutions of Physiological Ionic Strength

Past studies on GC-rich DNA duplexes, with one charge every two base pairs, had suggested that A-helices predominate from 8-bp on, and that B-helices are preserved from 18-bp on.^21,22 To ascertain whether the compaction of lower charge states is a general phenomenon, we measured 12-bp to 36-bp DNA and RNA duplexes, from native solutions, either 100% aqueous or containing sulfolane. The tested duplexes included multiples of d₆₆, r₆₆, d₁₀₀, and r₁₀₀, and the DNA duplexes listed as potential CCS calibrants by the Fabris group.³⁶ The results are shown in Figure 5 (experimental values in Supporting Table S3).

Figure 5.

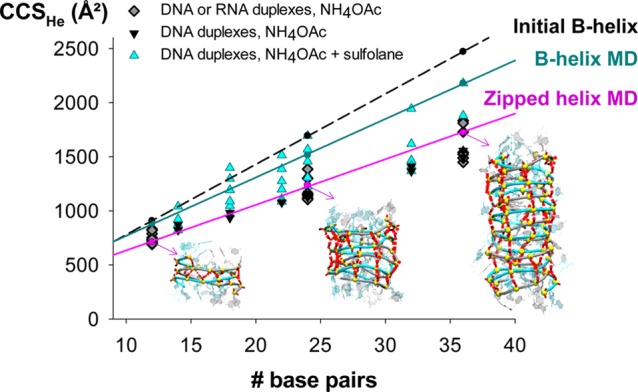
Comparison between experimental and calculated CCS_He of 12-bp to 36-bp duplexes. DNA and RNA sequences were either derived from 12-d/r_66/100 (diamonds, see Tables 2 and S3) or were identical to the DNA duplexes studied by Lippens et al.³⁶ (triangles, see Table S3). When measured at the charge states obtained from aqueous 100-mM NH₄OAc (black and dark gray), collision cross section values match with MD on the zipped helix (restrained minimization followed by MD). DNA duplexes at higher charge states produced by sulfolane addition adopt more extended conformations (cyan), which match better with MD simulations on B-helices.

We found that DNA and RNA duplexes have very similar gas-phase CCS values, although their helix types differ in solution (B vs A). The theoretical CCS values obtained with unbiased in vacuo MD directly from the solution B-helix are overlaid (B-helix MD trend line in Figure 5). They match only some of the high charge states produced in the presence of sulfolane. However, the low charge states produced from purely aqueous NH₄OAc solutions are significantly more compact.

To reproduce the dual-groove closing of longer duplexes while avoiding computationally costly desolvation simulations, we opted for biased exploration. We used restrained minimization and imposed distance constraints based on our knowledge that compact structures can be formed thanks to hydrogen bonds between phosphates across both grooves. Distance restraints were imposed using a harmonic potential between the hydrogen atom of neutral phosphates belonging to one strand and the oxygen atom of mating phosphates belonging to the other strand (Supporting Information Section S10, Figures S32—S34, and Movie S2 for a 12-bp duplex). The systems were minimized in vacuo, and then all restraints were removed prior to 1-μs gas phase MD.

For 12-bp duplexes, the resulting CCS distributions agree with the experiment, with the strongest compaction for 12-d₁₀₀ (Figure 1E). Applying the same procedure starting from an A-helix however did not lead to similarly low CCS values (Supporting Figure S35). The doubly groove-zipped helices obtained by restrained minimization generally keep WC hydrogen bonds less well than those obtained by desolvation (Supporting Figure S36—S38), but still reflect the solution trend, with the 12-d₁₀₀ preserving the highest fraction of hydrogen bonds. The advantage of the procedure is to reproduce the phosphate–phosphate H-bond pattern of the desolvated helices (two diagonals for zipping across both grooves, plus the central diagonal indicating preserved base pairs, Figure S36). We then applied restrained minimization to the longer (24-bp and 36-bp) helices (Supporting Figures S39—S40). Whatever the duplex length, the experimental CCS values obtained for low charge states (Figure 5) match better with these zipped helices than with the canonical structures or with the helices relaxed by long unbiased gas-phase MD.

Conclusions

In summary, at the charge states produced by electrospray from ≥100 mM aqueous ammonium acetate (traditional “native” solution conditions), double-stranded nucleic acids undergo a significant compaction in gas phase compared to the structure in solution. Unbiased molecular dynamics of B-helix or A-helix structures directly transposed from solution to the gas phase fails to reproduce the experimental results. This is due to several reasons: (i) only the phosphate groups closest to one another can pair to form hydrogen bonds on the simulation time scale, (ii) the starting structure is unrealistic and (iii) sampling in unbiased MD simulations is intrinsically limited. In the case of T-REMD, depending on the initial choice of charge location, the final structures either did not have any memory of the solution structure, or resembled those obtained by unbiased MD. T-REMD can help to solve the sampling effect (the question of the maximum internal temperature reached in the experiments remaining open), but not the problem that original charge locations might be incorrect.

Gradual desolvation generates more realistic starting structures for gas phase simulations. Conformational transitions occurring during dehydration cannot be ignored because they guide the entire sampling, within a particularly stiff conformational landscape in the case of nucleic acids. The conformationally restrained duplexes remain stable upon unbiased MD: once formed, they stay locked at room temperature. The broadness of the experimental CCS distributions therefore indicates a distribution of coexisting—but not interconverting—conformations, wherein each would have a slightly different phosphate-phosphate hydrogen bond network.

Our results highlight a key difference between nucleic acids and proteins in native mass spectrometry. Globular proteins can rearrange by relaxing their side chains³⁷ and undergo minimal salt bridge rearrangement.³⁸ Briefly optimized structures often have CCS values matching well with the experiments.^35,39−41 Fabris and co-workers have recently underlined the difficulties in transposing to DNA the MD and CCS calculation protocols traditionally used for proteins.³⁶ As a way out they proposed to calibrate all traveling wave IMS data using short MD simulation results, but our study shows why this approach would lead to a misrepresentation of nucleic acid structures in the gas phase.

DNA and RNA double helices are more compact in the gas phase than in solution, due mostly to new phosphate–phosphate interactions. At the low charge states produced from ammonium acetate, the Coulomb repulsion is not sufficient to keep the phosphate groups apart. They rearrange by self-solvation, cause major rearrangements of the backbone, and lead to a significant compaction (>20%) compared to the starting structure. Yet, they are metastable conformations keeping some memory of the solution structure.

Methods

Electrospray Ion Mobility Spectrometry

DNA and RNA duplexes were prepared by annealing their corresponding single-strands (purchased from Eurogentec, Seraing, Belgium, with RPcartridge-Gold purification) in aqueous 100 mM NH₄OAc. When sprayed at 10 μM duplex, the major charge states are 4– for the 10-bp, 5– for the 12-bp, 7– for the 24-bp, 8– and 9– for the 36-bp duplexes. Higher charge states were generated by adding 0.2% to 0.75% sulfolane to the solution. ESI-IMS-MS experiments were recorded on an Agilent 6560 IMS-Q-TOF, with the drift tube operated in helium (Supporting Information Section S1). The arrival time distributions were fitted by Gaussian peaks and the CCS values of the center of each peak were determined by the stepped-field method. For visualization, we converted the arrival time distributions into CCS distributions (see Supporting Information).

Gas-Phase Simulations

The starting structures of the duplexes were built with the Nucleic Acid Builder (NAB) software,⁴² both for the A-form (DNA and RNA) and the B-form (DNA). Table 1 lists the main sequences and levels of theory used here. For 12-d₃₃, 12-d₆₆, 12-d₁₀₀ (B-helix), and 12-r₆₆ (A-helix), we first carried out MD simulations in water. Then all water molecules and counterions were removed at once, before each 1-μs gas-phase simulation. The two possibilities to reduce the total charge to −5 (major charge state) are the localized charges (LC) and distributed charges (DC) models.²⁰ With the LC model, protons are added on 17 out of the 22 phosphate groups. Among the 26 334 possible protonation schemes, we selected a few low-energy ones based on single point molecular mechanics calculations. With the DC model, the net charge of each phosphate group is reduced so that the total charge of the duplex is −5.

Table 1. Size, Name, and Sequences of the Duplexes under Study, and Outline of Calculations.

size	theoretical levels of study for each size	name	sequence
10 bp	DFT (M06-2X - 4-31G(d))	10-bp	dCGCGGGCCCG·dCGGGCCCGCG
	semiempirical (PM7)
12 bp	semiempirical (PM7)	12-d33	(dCGTAAATTTACG)2
	MD from different starting structures (1 μs each)	12-d66	(dCGCGAATTCGCG)2
	T-REMD (1 μs × 18 replicas)	12-d100	(dCGCGGGCCCGCG)2
		12-r33	(rCGUAAAUUUACG)2
		12-r66	(rCGCGAAUUCGCG)2
		12-r100	(rCGCGGGCCCGCG)2
24/36 bp	MD on B-helix (0.25 μs)	Concatenations of the 12-bp duplexes above. See Supporting Information Section S9.
	MD on zipped helix (0.5 μs)

Solution and gas phase MD simulations were carried out with the MPI-versions of modules pmemd and sander, respectively, of the Amber12 suite of programs,⁴³ implementing parmBSC1 force field⁴⁴ for DNA and parmBSC0 force field + χ_OL3 correction^45,46 for RNA. The electrostatic interactions were calculated with the particle mesh Ewald algorithm⁴⁷ (real-space cutoff = 10 Å) in solution and direct Coulomb summation (no cutoff) in gas phase. All 12-bp duplexes were subjected gas phase T-REMD⁴⁸ (1 μs × 18 replicas) with temperature values from 300.00 to 633.94 K, chosen with predictor from Patriksson et al.⁴⁹ (average successful exchange rate of ca. 30%). Short duplexes (7—10 bp) were optimized at DFT level,⁵⁰ with the M06-2X⁵¹ functional including the dispersion correction GD3.⁵² The basis set was 6-31G(d,p) for the 7—9-bp duplexes (see Supporting Information) and 4–31G(d) for the 10-bp duplex. Duplexes up to 12-bp were also studied at the semiempirical (SE) level with MOPAC,⁵³ using different methods⁵⁴ (further details in Supporting Information). Hydrogen bond and stacking analysis was performed for all simulations as detailed in the Supporting Information Section S4.

Simulation of Desolvation and Proton Transfer

Starting from equilibrated MD simulations in solution, we cut droplets of ca. 2400 water molecules (radius ∼25 Å) containing the duplex 12-d₆₆, and 16, 17, and 18 NH₄⁺ cations to give a total net charge of −6, −5, and −4, respectively. The droplets were then subjected to gas-phase MD simulations following Konermann’s protocol.⁵⁵ Briefly, the trajectories were propagated by 500 ps chunks at constant temperature (350 K). To accelerate the evaporation, at the beginning of each chunk the initial velocities were reassigned according to the Boltzmann distribution at T = 350 K. At the end of each chunk, we stripped out all water molecules farther than 60 Å from the N6 atom of the 18^th residue adenine (which is approximately in the center of the duplex). A further 50 ns chunk at T = 450 K helped the last “sticky” water molecules to evaporate. In total, 12 independent trajectories were obtained (four at each charge state, 4–, 5–, and 6−). We then localized the charges (LC model) as follows: on the ultimate conformation of every trajectory a proton from each NH₄⁺ cation was transferred to the closest phosphate oxygen atom, and ammonia is removed. The resulting duplexes were then subjected to 1-μs unbiased MD.

CCS Calculations

The collision cross section (CCS) is calculated using the EHSSrot code⁵⁶ with the atom parametrization of Siu et al.,⁵⁷ a combination that is both accurate and efficient for calculating the CCS of nucleic acids in the gas phase.⁵⁸ The CCS is calculated for snapshots every 0.5 ns in each MD trajectory.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.7b00084.

• Experimental procedures including reconstruction of the CCS distributions, detailed computational procedures, ESI-IMS-MS supplementary results, circular dichroism results, full modeling results by in vacuo QM optimization, MD, T-REMD, and MD following restrained minimization, structural analysis, supplementary results on longer duplexes, full list of authors for references 43 and 50, and additional references (PDF)

• Movie S1: minor groove zipping upon MD of a 12-bp B-helix (AVI)

• Movie S2: dual groove zipping imposed by restrained minimization on a 12-bp B-helix (AVI)

The authors declare no competing financial interest.