Photonic-plasmonic hybrid single-molecule nanosensor measures the effect of fluorescent labels on DNA-protein dynamics

Probing the interaction between single molecules with a label-free nanosensor reveals labeling effects in fluorescence approaches.

Abstract

Current methods to study molecular interactions require labeling the subject molecules with fluorescent reporters. However, the effect of the fluorescent reporters on molecular dynamics has not been quantified because of a lack of alternative methods. We develop a hybrid photonic-plasmonic antenna-in-a-nanocavity single-molecule biosensor to study DNA-protein dynamics without using fluorescent labels. Our results indicate that the fluorescein and fluorescent protein labels decrease the interaction between a single DNA and a protein due to weakened electrostatic interaction. Although the study is performed on the DNA-XPA system, the conclusion has a general implication that the traditional fluorescent labeling methods might be misestimating the molecular interactions.

INTRODUCTION

DNA repair is a fundamental process that provides chemical stability for life (1). The xeroderma pigmentosum (XP) gene–encoded protein, XPA, is a zinc finger protein that recognizes damaged DNAs (2, 3). First discovered with biochemical assays (4, 5), interactions between XPAs and damaged DNAs are further explored with fluorescent labeling methods (6, 7). Despite the widely known concern that fluorescent reporters have potential influence on molecular dynamics, fluorescent labeling continues to be used as a general and powerful method for studying the dynamics of nonfluorescent molecules. Recent ensemble measurements indicate that one of the most widely used labels, fluorescein isothiocyanate (FITC), changes the dynamics of polymers (8) and glycan-binding proteins (9) at the ensemble level. Theoretical analysis also indicates that the addition of labels, such as FITC, significantly changes the protein absorption on a surface (10). Here, we demonstrate unperturbed real-time measurement of DNA-XPA interactions at the single-molecule level using a hybrid photonic-plasmonic antenna-in-a-nanocavity system. Our antenna-in-a-nanocavity single-molecule biosensor reveals that FITC and green fluorescent protein (GFP), the most widely used fluorescent reporters, decrease the interaction between DNAs and XPAs by 3 and 18 times, respectively, due to weakened electrostatic interactions.

Detecting single molecules without fluorescent labels has been the long-term goal in the field of nanobiotechnology. Recently, label-free microphotonic and nanophotonic technologies have achieved detection of single nanoparticles (11–15), single proteins (16–22), single DNAs (23, 24), and recently, single ions (25). Compared to nanoelectronic and nanomechanical sensors, nanophotonic sensors are more immune to biological noise and solution ionic strength, thus becoming an appealing tool to study biochemical processes under physiological conditions. However, multiple challenges remain to be solved to establish a new method to study single-molecule biophysical interactions and biochemical reactions. First, significant improvement in sensitivity is needed to identify single-molecule binding events. Fast acquisition needs to be achieved to capture the kinetics of the binding processes. Long-term stability is required to collect a large number of binding events for statistical analysis. Here, we demonstrate that the antenna-in-a-nanocavity hybrid system improves the detection figure of merit Q/V (Q, quality factor; V, mode volume) (see table S1) by an order of magnitude over previous label-free single-molecule nanosensors. Millisecond time resolution is achieved in the current system, with the possibility to be extended to the microsecond regime. Multiple binding events are collected in a single measurement.

RESULTS

Photonic-plasmonic hybrid antenna-in-a-nanocavity

The current system is implemented on the silicon-on-insulator (SOI) platform fabricated with complementary metal-oxide semiconductor (CMOS) compatible processes and is integrated with a microfluidic chip, as illustrated in Fig. 1A. The photonic chip (Fig. 1B) consists of sensing units, waveguides, and input/output coupling components (26, 27). The key sensing unit is an antenna-in-a-nanocavity, as shown in Fig. 1C. The antenna here is a gold nanoparticle, which confines photons in a deep subwavelength mode volume (V = 3.5 × 10⁻⁴λ³) while keeping a high quality factor (Q = 8.2 × 10³ in buffer solution) in the hybrid system. To study DNA-XPA interaction, XPA proteins are immobilized to a self-assembled monolayer of alkanethiols on the gold nanoparticle (see Fig. 1D and Materials and Methods). During the binding experiment, DNA molecules are delivered to the biosensor through microfluidic channels at a concentration below the binding affinity to avoid simultaneous multiple binding events. The DNA-XPA binding event will induce a resonance shift of the antenna-in-a-nanocavity system due to a reactive back action from the DNA molecule when it enters the mode area, a so-called reactive sensing mechanism demonstrated by Vollmer et al. (28, 29). In an antenna-in-a-nanocavity hybrid system, photons are trapped within the ultrasmall mode volume for a time that is five orders of magnitude longer than a single pass (Qλ/L_eff ~ 10⁵, where L_eff is the characteristic size of the nanoparticle). Therefore, the reactive back action of molecules to the trapped photons is significantly enhanced. The binding signal (that is, resonance shift) is inversely proportional to the normalized mode volume (Ṽ = V/λ³), whereas the ability to discern the minimum resonance shift is proportional to the Q-factor. η relates to the decrease in the resonance shift when the analyte molecule is not accessible to the maximum field location. Therefore, we compare the dimensionless parameter Qη/Ṽ among different micro-nano systems (20–23, 30–41) in Fig. 1E (table S1): Whispering-gallery mode (WGM) resonators have ultrahigh Q; however, they have large V at the same time. Plasmonic nanocavities have ultrasmall V, but their Q is low. Photonic crystal nanocavities have both high Q and small V, but Q/V is on par with WGM and plasmonic cavities. Our antenna-in-a-nanocavity system is a hybrid of both ultrasmall V from plasmonics and high Q from the one-dimensional photonic crystal nanobeam cavities, offering simultaneously ultrasmall V and high Q. The enhancement in Q/V brings the sensitivity to the single-molecule level with high signal fidelity.

Fig. 1. Photonic-plasmonic hybrid antenna-in-a-nanocavity.

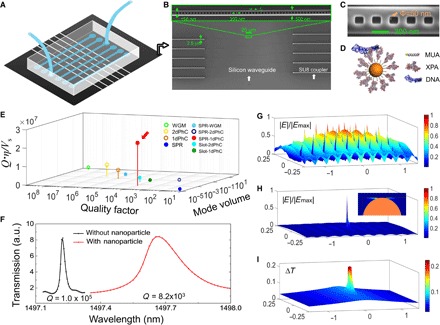
(A) Illustration of the biosensing system, consisting of a silicon photonic chip for biosensing and a polydimethylsiloxane (PDMS) microfluidic chip for sample delivery. (B) Scanning electron microscope image (SEM) of the silicon photonic chip shows the multiplexed photonic crystal nanobeam cavities (zoomed SEM inset) connected by waveguiding components to the edge of the chip for input/output coupling. (C) SEM image of the photonic crystal nanobeam cavity, with a single 50-nm-diameter gold particle located in the central grating of the nanocavity, thus forming an antenna-in-a-nanocavity architecture. (D) Illustration of the biofunctionalized gold nanoparticle. XPA proteins are immobilized to a self-assembled monolayer of 11-mercaptoundecanoic acid (11-MUA) on gold and interact with a double-stranded DNA (dsDNA). (E) Dimensionless factor Qη/$\tilde{\mathit{V}}$ is compared among different microphotonic and nanophotonic systems (for details, see table S1). Solid and hollow circles denote measurements performed in liquid and air, respectively. Our antenna-in-a-nanocavity system is indicated by the red arrow. PhC, photonic crystal cavity; SPR, surface plasmon resonance. (F) Resonance shift of 440 pm and Q-factor drop from 10⁵ to 8.2 × 10³ are the indications of trapping a gold nanoparticle. a.u., arbitrary units. (G) Electromagnetic field distribution of a bare photonic crystal nanobeam cavity without the gold nanoparticle. The cavity mode spans at wavelength cubed scale. (H) Electromagnetic field distribution of the antenna-in-a-nanocavity system. The hybrid mode is strongly localized in the gap region at the nanoparticle-silicon interface. Inset shows the zoomed-in field distribution at the gold nanoparticle (orange hemisphere). (I) Temperature increase distribution. The maximum temperature rise is ~0.2°C under the experimental condition: a power of 5 μW through the silicon waveguide.

To construct the antenna-in-a-nanocavity system, the photonic crystal nanocavities, silicon waveguides, and polymer couplers are first fabricated using a two-step electron beam (ebeam) lithography (see Materials and Methods). The photonic crystal nanocavity alone has a mode volume of V_nanocavity = 0.1 λ³ (Fig. 1G). Thus, cavity photons build up a strong electromagnetic field associated with a large gradient force, which can be used to attract a nanoantenna (that is, a gold nanoparticle in the present work) to its field maximum, thus forming an antenna-in-a-nanocavity system. Trapping gold nanoparticles has been demonstrated in photonic crystal nanocavities by different groups including us (42–44). The trapping is achieved by delivering the gold nanoparticles to the vicinity of the photonic crystal nanocavity through a microfluidic channel while scanning the laser at its resonance. The maximum field intensity accessible to the gold nanoparticle is located at the corners of the gratings. Once the nanoparticle is pulled to the field maximum, it sticks to the corner wall of the photonic crystal nanobeam cavity, as shown in Fig. 1C. The trapping event is indicated by a discrete resonance jump to the longer wavelength (by ~440 pm) and a drop in the Q-factor (from 1.0 × 10⁵ to 8.2 × 10³), as shown in Fig. 1F (setup shown in fig. S1). In the presence of the gold nanoparticle, the cavity photons excite collective oscillations of the surface electrons of the gold nanoparticle, creating a strong electromagnetic field at the gap between the nanoparticle and the silicon side wall (Fig. 1H). The cavity photons become polaritons, leading to a further reduced mode volume of the antenna-in-a-nanocavity hybrid system (V = 3.5 × 10⁻⁴λ³). This significant reduction in mode volume increases the resonance shift by ~280 times from a bare photonic crystal nanobeam cavity. In the present case, the cavity photons are detuned from the surface plasmon resonance of the gold nanoparticle antenna; thus, heating effect is reduced. Another ~20-fold enhancement could be achieved (on top of 280) if probe photons are at the antenna resonance. However, temperature rise will increase by a factor of ~500 due to resonant enhancement of electron ohmic loss; thus, input power level needs to be significantly reduced to avoid excess temperature increase (fig. S2). As we show below, the nonresonant driving regime already provides a high signal-to-noise ratio for single-molecule measurement while maintaining the temperature increase below 0.2°C (Fig. 1I).

Immobilize molecules on the gold surface

A self-assembled monolayer of 11-mercaptoundecanoic acid (11-MUA) can be formed on the gold surface due to strong thiol-gold interaction and hydrophobic stabilization (45). Next, a layer of XPA proteins can be immobilized to the 11-MUA layer using amine reaction to the lysine residues on XPA. To estimate how the surface charge on gold might affect DNA-XPA interaction, we first characterize the zeta potentials (DelsaNano, Beckman Coulter) of gold nanoparticles, MUA-gold nanoparticles, and XPA-MUA-gold nanoparticles in the standard binding buffer [20 mM Hepes, 75 mM KCl, 5 mM MgCl₂, and 100 μM dithiothreitol (pH ~7)]. All of the colloidal dispersions have low zeta potentials (gold, 2.8 mV; MUA-gold, 5.0 mV; XPA-MUA-gold, −5.8 mV). The zeta potential of the DNA molecules is 2.6 mV (ZETA-check, Particle Metrix). These small values are consistent with the short debye length (~1 nm) in the standard binding buffer (ionic strength, ~0.1 M), which also indicates that it is essential to use freshly prepared nanoparticles. Thus, the ionic screening effectively attenuates the electrical forces from the surface charges on the DNA-XPA interaction.

We also investigate potential charge transfer process from gold to XPA using density functional theory (DFT). Because of the high computational cost of DFT, we only include the lysine (Lys) residue of XPA in our simulation. Free Lys-MUA complex and Lys-MUA conjugated to the gold surface (Au) are calculated. The partial density of states (PDOS) of Lys-MUA and Lys-MUA-Au are compared in Fig. 2 (A and B). The Fermi level shifts to a lower energy because of gold, whereas the PDOS are barely affected by gold. The energy diagram (Fig. 2C) shows that an energy gap of ~2.2 eV exists from the highest occupied molecular orbital (HOMO) of MUA (~1.2 eV from HOMO of lysine). Therefore, the charge transfer probability from Au to Lys is very low at room temperature (0.03 eV). The probe photons (1500 nm; 0.8 eV) for the resonance shift measurements are also not enough to excite the charge transfer. The electron density plots of HOMOs for Lys-MUA and Lys-MUA-Au are shown in Fig. 2 (D and E). Thus, the alkyl chain of 11-MUA serves as an insulating layer to block potential charge transfer from gold to XPA.

Fig. 2. No charge transfer from gold to molecule.

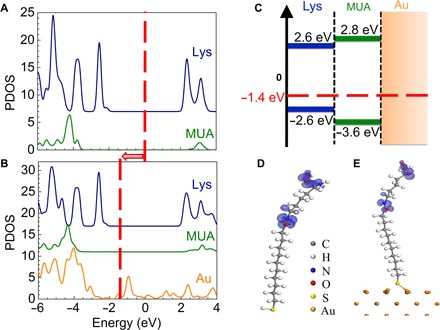
(A and B) PDOS of Lys-MUA (A) and Lys-MUA-Au (B) solved using DFT (see Materials and Methods). Red dashed line indicates the Fermi level, which shifts to lower energy in the presence of gold. (C) Energy diagram near the Fermi level for Lys-MUA-Au. The HOMOs and LUMOs (lowest unoccupied molecular orbitals) are shown. The Fermi level (red dashed line) is 2.2 eV above HOMO state of MUA. (D and E) Electron density of HOMO for Lys-MUA (D) and Lys-MUA-Au (E).

Single-molecule study on DNA-XPA interaction

We first demonstrate real-time detection of single-molecule DNA-XPA binding events. We inject 10 nM mismatched double-stranded DNA (dsDNA) in the standard binding buffer solution (20 mM Hepes, 75 mM KCl, 5 mM MgCl₂, and 100 μM dithiothreitol) and continuously monitor the resonance wavelength of the hybrid antenna-in-a-nanocavity system. Discrete resonance jumps of about 1 pm are seen in Fig. 3A. The red curves are obtained by a step fitting algorithm (see Materials and Methods and figs. S3 and S4) (46, 47). The resonance jumps to the longer wavelengths correspond to the binding events of the dsDNA to XPA, whereas those to shorter wavelengths correspond to the dissociation of the dsDNA from XPA (zoom in Fig. 3B). In the control experiment, we replace the mismatched dsDNA with normal dsDNA. As shown in Fig. 3 (C and D), we observe far fewer binding events with significantly shorter residence time on the binding state. We extract the association constant (k_on) and dissociation constant (k_off) by fitting the binding event histogram to an exponential function (fig. S5) and obtain k_on = 0.20 ± 0.04 nM⁻¹ s⁻¹ and k_off = 5.0 ± 1.1 s⁻¹ for the mismatched dsDNA and XPA (17). Electrostatic interaction has been proposed to be the dominant interaction between DNAs and proteins (48). We carry out molecular dynamics (MD) simulation to calculate the surface potential of the mismatched and normal dsDNAs (see Materials and Methods). As shown in Fig. 3 (E and F), a mismatched dsDNA has significantly higher surface potential than a normal dsDNA. An abnormal twist appears at the mismatched site, which results in a slightly bent configuration. A highly concentrated negative surface potential is identified in the vicinity of the mismatched position, which could strongly interact with the positive motif on the XPA protein (Fig. 3G).

Fig. 3. Single-molecule DNA-XPA dynamics.

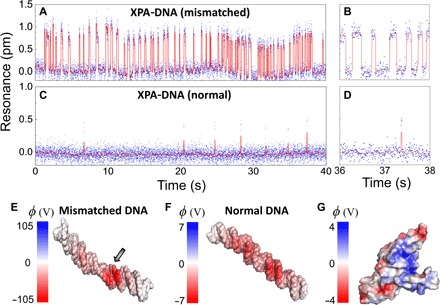
(A and B) Real-time binding dynamics of the mismatched dsDNA and XPA in the standard binding buffer, measured by tracking the resonances of the antenna-in-a-nanocavity system. The dsDNA concentration in the microfluidic channel is 10 nM. The binding kinetics are fitted from the event histogram (fig. S5): k_on = 0.20 ± 0.04 nM⁻¹ s⁻¹ and k_off = 5.0 ± 1.1 s⁻¹. (C and D) Resonance signals tracked in real time for the normal dsDNA and XPA as control. The mismatched dsDNA exhibits much longer residence time on the binding state than the normal dsDNA. (E to G) The solvent-accessible surface potential (φ = k_BT/e) of a mismatched dsDNA (E), a normal dsDNA (F), and an XPA protein (G) obtained from MD simulation. Mismatched dsDNA has a significantly higher surface potential, with an abnormal twist at the mismatched site (indicated by the arrow). Blue-colored regions on the XPA protein are positively charged domains, which bind to the negatively charged dsDNA.

Next, we change the ionic strength of the solution and compare the maximum surface potentials obtained from the MD simulation and from the k_off values measured from the experiment. The standard binding buffer condition is diluted by 95 times to obtain an ionic strength of 1 mM. KCl concentration alone is increased by five times (that is, 375 mM) to obtain an ionic strength of 405 mM. KCl concentration alone is increased by 10 times (that is, 750 mM) to obtain an ionic strength of 790 mM. Real-time resonance measurements at different ionic strengths are shown in Fig. 4 (A to D). At low ionic strength, the dsDNA binds more frequently and interacts more strongly to XPA. At high ionic strength, the ions in the solution screen the electrostatic potential of both dsDNA and XPA, which weakens DNA-XPA interaction. As shown in Fig. 4E, the extracted dissociation rate increases as the ionic strength increases, and both MD simulation and experiment results agree well over a range of seven orders of magnitude. This is consistent with the hypothesis that electrostatic interaction dominates the DNA-XPA dissociation dynamics. Last, we also change the DNA concentrations (fig. S6, A to C) and measure DNA-XPA dynamics. The number of binding events increases as the concentration increases, and the event rate scales linearly with the DNA concentration (fig. S6D).

Fig. 4. DNA-XPA dynamics at different ionic strengths.

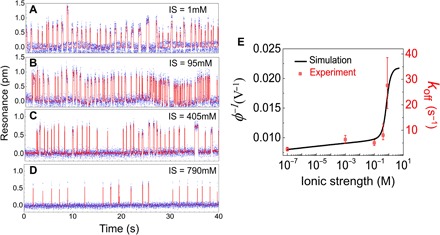
(A to D) Real-time binding dynamics of the mismatched dsDNA and XPA, measured at different ionic strengths (IS). The dsDNA concentration in the microfluidic channel is 10 nM for all. (E) k_off values obtained at different ionic strengths are consistent with the surface potentials calculated from MD simulation over a range of 7 logs.

Fluorescent labels change DNA-XPA dynamics

Now, we use the antenna-in-a-nanocavity single-molecule biosensor to study how labels (FITC and GFP) affect molecular interactions. Fluorophores (for example, FITC and GFP) can be tagged either to XPA or to DNA (or both). We note that XPA has many potential reaction sites for fluorescent labeling. To minimize the perturbation induced by labels, we tag fluorophores to the DNA 5′-ends (see Materials and Methods). The real-time binding events of XPA and FITC-labeled dsDNA molecules are shown in Fig. 5 (A and B). The surface potential of a FITC-labeled dsDNA is obtained from the MD simulation (Fig. 5C). Similarly, measurements on the GFP-labeled dsDNA and XPA interaction are shown in Fig. 5 (D and E). Comparing Figs. 3A, 5A, and 5D, it is evident that residence time on the binding state is reduced for the labeled dsDNA. The perturbation of GFP to dsDNA is greater than that of FITC to dsDNA. The association rate constants (k_on) for each case are statistically analyzed from the binding event histograms and summarized in Fig. 5G. It shows that the labeled dsDNA stays longer on the nonbinding states. We measure the diffusion constants in the ensemble of unlabeled dsDNAs, FITC-labeled dsDNAs, and GFP-labeled dsDNAs using the dynamic light scattering method (NANO-flex, Particle Metrix). The association constants (k_on) match well with diffusion constants for unlabeled and FITC-labeled dsDNA. It agrees reasonably well with GFP-labeled dsDNA, the discrepancy of which comes from the contribution from the short-range electrostatic interaction as dsDNA comes to the vicinity of XPA. The GFP labels decrease the genuine interaction between dsDNA and XPA, resulting in a slightly increased k_on value. This indicates that the unbinding states are free diffusion states until the dsDNAs come in close vicinity to XPA. On the other hand, the dissociation constants (k_off) agree well with the perturbed surface potentials of the dsDNA molecules by FITC and GFP (Fig. 5H). This indicates that decreased electrostatic interactions between XPA and DNA molecules result in increased k_off. The binding affinity (k_d = k_off/k_on = 68.7 nM) we obtained for the FITC-labeled DNA-XPA interaction agrees well with the literature value (49, 50). We also compare the observed resonance shifts with the molecular weights of dsDNA, FITC-dsDNA, and GFP-dsDNA. The labeling process conjugates two FITC or GFP molecules to each dsDNA, which scales very well with experiment (Fig. 5I). Thus, no simultaneous multiple binding events or aggregations occur during the kinetic measurement. Nevertheless, we note that our current sensitivity cannot discriminate unlabeled DNA and FITC-DNA. Together, FITC and GFP change the binding affinity of DNA-XPA interactions up to 3 and 18 times, respectively, due to decreased free diffusion rate and weakened electrostatic interaction.

Fig. 5. Fluorescent labeling weakens DNA-XPA interaction.

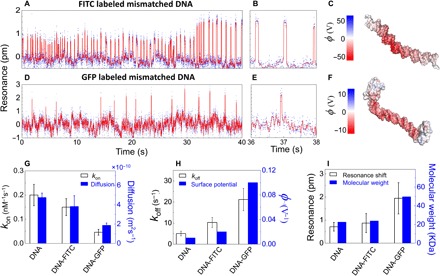
(A and B) Real-time binding dynamics of the FITC-labeled mismatched dsDNA and XPA under the standard binding buffer condition, measured from the resonance shifts of the antenna-in-a-nanocavity. The dsDNA concentration in the microfluidic channel is 10 nM. The binding rates are fitted from the event histogram: k_on = 0.15 ± 0.04 nM⁻¹ s⁻¹ and k_off = 10.3 ± 2.4 s⁻¹. (D to F) Real-time data for single GFP-labeled dsDNA and XPA protein in the standard buffer (D and E). DNA concentration, 10 nM; k_on = 0.05 ± 0.01 nM⁻¹ s⁻¹; k_off = 21.3 ± 5.3 s⁻¹. (C and F) The solvent-accessible surface potentials (φ = k_BT/e) of a FITC-labeled mismatched dsDNA (C) and GFP-labeled mismatched dsDNA (F). (G) k_on values obtained from the resonance shift measurements scale well with the diffusion constants obtained from the dynamic light scattering ensemble measurements, indicating that the association rates are limited by the diffusion process. (H) k_off values obtained from the resonance shift measurements agree well with the surface potentials obtained from MD simulations, indicating that fluorescent labels redistribute the surface charges and decrease the electrostatic interactions. (I) Resonance shifts agree well with the molecular masses of the DNA, FITC-DNA, and GFP-DNA complexes, indicating no simultaneous multimolecule binding events or aggregations.

DISCUSSION

The hybrid antenna-in-a-nanocavity single-molecule biosensor has several unique advantages. First, traditional fluorescent labeling methods cannot measure fast dynamics due to low photon counts from single or few fluorophores. They cannot collect binding events for long periods of time because of fluorophore photobleaching. The current design uses resonantly trapped photons to probe molecular interactions; thus, it is not limited by low photon counts or photobleaching. Second, the current technique does not need any fluorescent labels. Hence, the measurement is genuinely reflecting the molecular dynamics. It does not require balanced concentration or close proximity of labels to the subject molecules, as is strictly required in the fluorescent resonance energy transfer measurements. Third, our current implementation has a time resolution at the millisecond scale, limited by the laser scanning process, but fast enough to study DNA-DNA interactions and DNA-protein interactions. Using a large-bandwidth piezo external cavity laser or implementing a closed-loop laser frequency locking scheme will improve the time resolution to the microsecond scale. Last, current characterization on the DNA-protein interaction indicates that traditional fluorescent-based methods might affect the molecular interactions in general cases. Therefore, the antenna-in-a-nanocavity is a uniquely suitable tool to study fast dynamic processes unperturbed by fluorescent labels.

Furthermore, the CMOS-compatible fabrication process allows the integration of electronic components (for example, detectors, light sources, and a temperature control unit) on the same chip. The gold nanoantenna provides a stable and well-characterized surface for biochemical functionalization. The chemical specificity allows targeted functionalization on the gold nanoantenna (but not on the silicon waveguide), where the optical field is maximized. In the present case, the self-assembled 11-MUA monolayer avoids charge transfers from gold and minimizes the steric effect to the immobilized proteins. In practical drug discovery, many targets are membrane receptors, such as heterotrimeric guanine nucleotide–binding protein–coupled receptors and ion channels. Thus, molecules can be immobilized on the lipid bilayers functionalized on the gold surface to better reproduce their native states (51).

The effect of fluorescent labels has been evaluated using SPR ensemble measurements (52, 53). Compared to the ensemble methods, a single-molecule label-free approach offers some unique capabilities: In ensemble methods, interpreting binding kinetics (for example, SPR binding data) is frequently carried out by assuming a one-step interaction in a one-site binding model. Sometimes, two-site binding models are applied if a single set of k_on and k_off parameters does not produce good fitting. However, information on the potentially multiple binding domains and conformational states is obscured. In the single-molecule analysis, k_on and k_off are obtained separately from the event statistics of free (unbinding) states and binding states (thus, less fitting parameters), whereas the single or multiple binding steps are revealed in the binding step curve. In the ensemble model, slow dissociation processes from targets are usually challenging to fit due to increased noise when fewer proteins are left on the ligands. However, in drug discovery, information on k_off is more valuable than k_on, and slow dissociation rates are desirable (54). Therefore, single-molecule measurements have better accuracy, in particular, for k_off. A single-molecule approach also requires much lower sample consumption because it often works below the binding affinity concentration (to avoid simultaneous multiple binding events), whereas ensemble measurements require higher concentration above the affinity value because of a lack of sensitivity. These features collectively make the current system an appealing option for next-generation single-molecule drug discovery.

MATERIALS AND METHODS

Photonic crystal nanocavity design, fabrication, and characterization

The photonic crystal nanobeam cavity consisted of a series of rectangular gratings along a 500-nm-wide, 220-nm-thick waveguide. The distance between two neighboring gratings was fixed at 300 nm, and the width of each cuboid was fixed at 150 nm. The lengths of the cuboids (l_x) were linearly tapered from 165 to 105 nm from the middle of the nanobeam cavity to both its ends, in a total of 25 gratings, l_x(i) = 165 − 60 × (i − 1)/(25 − 1). This tapering geometry was optimized to create a hyperbolic potential for telecom photons, thus confining the optical energy to the middle of the structure with a Gaussian energy distribution (26, 27). The silicon waveguides had the same width as the photonic crystal nanobeam cavities. They were tapered at the end from 500 to 100 nm, penetrating into the SU8 polymer couplers. The SU8 waveguide had a dimension of 2.5 μm by 2.5 μm. The role of this SU8 polymer coupler is to couple light on and off the chip to a tapered optical fiber (OZ Optics).

The device was fabricated on an SOI wafer with a 220-nm silicon device layer and a 2-μm buried oxide layer. A square chip (1 cm by 1 cm) was diced from the wafer and cleaned by piranha solution (3:1 96% sulfuric acid and 30% hydrogen peroxide) for 10 min. It was then rinsed three times with deionized water, each time for 1 min, and then blow-dried with nitrogen gas. Hydrogen silsesquioxane (XR-1451-002, Dow Corning) negative-tone ebeam resist was spun at 4000 rpm for 40 s. The designed patterns were written using 125-keV ebeam lithography (ELS-F125, Elionix) at a current of 300 pA with the optimal dosage at around 1200 μC/cm². Tetramethylammonium hydroxide solution (25%) was then used to develop the ebeam resist for 20 s and rinsed by deionized water gently for 25 s four times. Next, inductively coupled plasma–reactive ion etching was used to transfer the ebeam pattern to the silicon layer. The etching process was performed with C4F8/SF6 chemistry for 1 min. The ebeam resist layer was then removed with a 7:1 buffered oxide etchant. The polymer coupler waveguides were fabricated by a second ebeam lithography step with two alignment markers. First, the chip was spin-coated with negative photoresist (SU8 2002, MicroChem) at 2000 rpm for 40 s, which generated an ~2.5-μm-thick SU8 layer. It was then soft-baked at 95°C for 1 min. Alignment markers that were fabricated during the first ebeam process were used to align the SU8 waveguides to the silicon waveguide. A current of 100 pA with a dosage of 15 μC/cm² was found to be optimal. After ebeam exposure, the wafer was postbaked at 65°C for 1 min and at 95°C for 1 min. The chip was then developed with the SU8 developer (MicroChem) at room temperature for 1 min and rinsed with isopropyl alcohol (IPA) twice, for 30 s each time. The chip was then hard-baked at 180°C for 30 min.

The device was characterized in a home-built fiber-coupled setup (fig. S1A). A tunable telecom laser (Santec) was scanned from 1480 to 1520 nm with a built-in motor. A typical transmission spectrum of the device is shown in fig. S1B. Once the resonance is detected, a function generator (HP) drives the piezo (not the motor) that fine-modulates the laser frequency for a range of 100 pm around its resonance. Tapered optical fiber was used to couple light onto the chip and collect light from the chip. Polarization control unit was implemented to filter out unwanted polarizations. The modulating signal and the output signal from the tapered fiber were recorded with a data acquisition system (NI-6258, National Instrument).

DNA sample preparation

All normal dsDNA, mismatched dsDNA, and amino-modified mismatched dsDNA samples in this study were purchased from Sigma-Aldrich. The sequences of normal dsDNA are as follows: 5′-CTTCTTCTGGTCTTCTCTTCCTTCTTCTTCTCTTCTGGTC-3′ and 3′-GAAGAAGACCAGAAGAGAAGGAAGAAGAAGAGAAGACCAG-5′. The sequences of mismatched dsDNA are as follows: 5′-CTTCTTCTGGTCTTCTCTTCCTTCTTCTTCTCTTCTGGTC-3′ and 3′-GAAGAAGACCAGAAGAGACCTTAGAAGAAGAGAAGACCAG-5′. Amino-modified dsDNA were used to further conjugate FITC-NHS-ester and GFP proteins on the 5′-end: 5′-amino-C3-CTTCTTCTGGTCTTCTCTTCCTTCTTCTTCTCTTCTGGTC-3′ and 3′-GAAGAAGACCAGAAGAGACCTTAGAAGAAGAGAAGACCAG-C3-amino-5′.

To label FITC to the DNA molecules, 5 μl of 10 mM fresh FITC-NHS-ester (Life Technologies) was mixed with 100 μl of 50 μM activated amino-C3-DNA solution at room temperature for 2 hours. To label GFP to DNA molecules, 50 μl of 10 μM GFP (NanoLight Technology) was first mixed with 50 μl of 1 mM N-hydroxysuccinimide (NHS; Sigma-Aldrich) and 1 mM N-(3-dimethylamin-opropyl)-N′-ethylcarbodiimide (EDC; Sigma-Aldrich) at room temperature for 15 min. Five microliters of 1 mM 2-mercaptoethanol (Sigma-Aldrich) was then added to quench EDC. After modification, 100 μl of 5 μM GFP was mixed with 100 μl of 0.5 μM activated amino-C3-DNA at room temperature for 2 hours. PD SpinTrap G-25 desalt column (GE Healthcare) was used to remove low–molecular weight compounds (unreacted fluorophores) from all samples. After all these preparations, the sample was diluted in the standard binding buffer (20 mM Hepes, 75 mM KCl, 5 mM MgCl₂, and 100 μM dithiothreitol) to a final concentration of 10 nM. Deuterium oxide (99.9%; heavy water) was used instead of deionized water to minimize the absorption of the laser at telecom wavelength. This standard binding buffer (ionic strength, 95 mM) was used in the following measurements: mismatched dsDNA (Fig. 3, A and B), normal dsDNA (Fig. 3, C and D), FITC-labeled mismatched dsDNA (Fig. 5, A and B), and GFP-labeled mismatched dsDNA (Fig. 5, D and E).

Gold nanoparticle surface functionalization

One milliliter of the 50-nm gold nanoparticle stock solution (Nanopartz) was mixed with 100 μl of 20 mM 11-MUA (Sigma-Aldrich) in ethanol. The mixture was sonicated at 55°C for 90 min and kept at room temperature overnight. These nanoparticles were centrifuged at 5500 rcf (relative centrifugal force) for 10 min and redispersed in 1 ml deionized water to remove excess 11-MUA. Then, 100 μl of 10 μM XPA (Novus Biologicals) was mixed with 10 μl of 1 mM EDC, 1 mM NHS, and 100 μl of the above functionalized nanoparticle solution at room temperature for 2 hours. To trap a single nanoparticle in the photonic crystal cavity, nanoparticles were diluted from 3.9 × 10⁷ particles/μl (stock solution) in heavy water to about 500 particles/μl. The nanoparticles were flowed into the microfluidic channel with a flow rate of 1 μl/min. When a single gold nanoparticle was trapped, we observed a discrete resonance shift of 440 pm, and the Q-factor dropped from 1.0 × 10⁵ to 8.2 × 10³ (Fig. 1F).

Microfluidic channel fabrication

The microfluidic channels were made by replica molding of a photolithographically defined SU8 structure with PDMS. First, a 4-inch silicon wafer was cleaned by piranha solution (3:1 96% sulfuric acid and 30% hydrogen peroxide) for 10 min. It was then rinsed with deionized water for 1 min three times and then blow-dried with nitrogen gas and baked at 180°C for 5 min. After the wafer cooled down, it was spin-coated with negative photoresist (SU8 2050, MicroChem) at 2500 rpm for 40 s, which generated an ~50-μm-thick SU8 layer. It was then soft-baked at 65°C for 2 min and then at 95°C for 6 min. The designed structures on the mask (100 μm × 50 μm × 2 mm channels with 0.3-mm-diameter inlet and outlet) were then transferred to the wafer using photolithography at 180 mJ/cm² (SUSS MicroTec). After exposure, the wafer was postbaked at 95°C for 2 min. The wafer was then developed with SU8 developer (MicroChem) at room temperature for 2 min and rinsed with IPA twice, for 1 min each time. It was then hard-baked at 180°C for 30 min. Next, the PDMS base (sylgard 184 silicone elastomer, Dow Corning) and the curing agent (Dow Corning) were mixed thoroughly at a 10:1 ratio by weight. The mixture was poured into the plastic petri dish that contained the wafer with SU8 structures. It was degassed in a vacuum chamber until no bubbles were present. It was then incubated in an oven at 70°C for 3 hours. The PDMS microfluidic channels were then rinsed in ethanol for 3 min and cut into individual pieces, followed by oxygen plasma cleaning at 20 sccm (standard cubic centimeter per minute), 0.5 torr, and 100 W for 1 min. The PDMS microfluidic channels were aligned and stamped with the silicon chip under a home-built microscope and cured in an oven at 70°C for 2 hours.

Step fitting algorithm

The real-time resonance data were subtracted by a ninth order polynomial fit to remove the resonance drift due to temperature fluctuations and mechanical drifts, generating a relatively flat base line (fig. S3). This process does not affect the identification of molecular binding events because the baseline drifts are slow events and do not exhibit step behavior.

A Steps and Bumps tool kit developed by Little et al. (46) was used to extract discrete state dynamics. This tool kit was developed especially for step-filtering of time series with autocorrelated noise in single-molecule time traces. We used the L1-PWC-ARP method provided in the tool kit. The starting point of this algorithm is the classical autoregressive smoothing filter. The noisy trace of the measurement signal can be generated by a recursive equation θ_{t + 1} = aθ_t + ε_t, where θ is the trace, a is the feedback constant, and ε is the white noise process. The goal of the filtering process was to find the best approximation m_t, observing only θ. The problem can usually be solved by minimizing the sum of residual white noise squared for the full time range t. Another method uses brute force to test every possible combination of m_t (55). This is quite expensive computationally and requires full knowledge of θ. Using the theory developed by Strong and Chan (47), Little et al. (46) proposed a new way to solve the fitting problem. The step-smoothness constraint could be replaced by a penalizing term that is proportional to the sum of absolute differences between m_t. In detail, the following optimization of negative log-posterior cost function with respect to m_t is established, $\text{NLP} ={\displaystyle \sum _{\mathit{t}=\mathit{P}+1}^{\mathit{T}}}{({\mathrm{\theta }}_{\mathit{t}}-{\displaystyle \sum _{\mathit{i}=1}^{\mathit{P}}}({\mathit{a}}_{\mathit{i}}{\mathrm{\theta }}_{\mathit{t}-\mathit{i}}-{\mathit{m}}_{\mathit{t}}))}^2+\mathrm{\gamma }{\displaystyle \sum _{\mathit{t}=2}^{\mathit{T}}}|{\mathit{m}}_{\mathit{t}}-{\mathit{m}}_{\mathit{t}-1}|$, where γ is the regularization (penalty) term. The implicit model is the first sum term (47). This model includes the linear, general Gaussian, and discrete time stochastic dynamics. A simplified model would be a = 0, which is good enough for most applications. The algorithm could also be used for further investigation of complicated processes, such as that with the molecular motor without much modification.

The only parameter in the fitting process was the regularization term γ. In fig. S4 (A to E), the fitting results were compared from different regularization terms in the range γ = 0.0004 to 0.4. It was obvious that the γ = 0.0004 result was underfitted and the γ = 0.4 result was overfitted. To identify the best value for γ, we showed the fitting results of k_off as a function of γ in fig. S4F. Owing to the high signal-to-noise ratio of our data (the binding and nonbinding states are well separated in histogram), the fitting results were not sensitive to the regularization term in the range of γ = 0.01 to 0.1. The tool kit can estimate the best regularization term (γ) according to the difference between m and θ. γ usually falls in the range 0.01 to 0.04.

Once the binding events were identified, an event histogram was made (fig. S5). The single-molecule binding association and dissociation constants were obtained by fitting the event histogram with exponential equation (17).

Density functional theory

DFT calculations were performed with the plane-wave pseudopotential code CASTEP (56). The default ultrasoft pseudopotentials were used with a cutoff energy of 350 eV with the Perdew-Burke-Ernzerhof–style generalized gradient approximation exchange-correlation functional. The gold (100) surface was used to simulate the surface of a gold nanoparticle. A gold slab of four layers was used with a vacuum layer of 4 nm to stop the image interaction. The supercell used is 2 nm × 2 nm for the (100) surface with one 11-MUA molecule. Considering the large supercell, only the Γ-point was used for reciprocal space integration. The geometry was relaxed until the residual force was less than 0.01 eV/Å. The van der Waals force was included using the Tkatchenko-Scheffler scheme (57).

MD simulation

Both normal and mismatched dsDNA models were generated by the online version of Nucleic Acid Builder. The hydrogen ions were added to model the protonation state at pH 7. The structure of FITC was taken from the crystal structure 4FAB from the Protein Data Bank (PDB). Note that the FITC ordered from Sigma-Aldrich is slightly different from the 4FAB structure because several atoms are modified to strengthen the fluorescence. The GFP structure was taken from the crystal structure 4GFP from the PDB. The structures of FITC and GFP were relaxed in the solution by Nanoscale Molecular Dynamics (NAMD) and visualized in Visual Molecular Dynamics (VMD) with the Chemistry Harvard Macromolecular Mechanics (CHARMM) force field. NAMD was developed by the Theoretical and Computational Biophysics Group in the Beckman Institute for Advanced Science and Technology at the University of Illinois at Urbana-Champaign (58). The total charge of FITC and GFP were calculated to be two electrons and eight electrons, respectively. Both FITC and GFP were manually added to dsDNA at both 5′-ends in PyMOL. Several C atoms were added to avoid the clashing of dsDNA with FITC and GFP. The dsDNA was then dissolved in KCl TIP3P water solution with different ionic strengths in VMD by the plugin of cionize (coulombic ionize) and solvated automatically. More Cl ions were added to neutralize the dsDNA model. The water box was set to be 35 nm × 35 nm × 250 nm under periodic boundary conditions. Other ions, such as Na and Mg, were tested, and the results were similar. The whole system was then relaxed in NAMD with a constant number of particles, constant pressure, and constant temperature (NPT) ensemble for 2 ns until the system reached equilibrium. The total energy was first minimized for 2000 steps. Then, MD with time step of 2 fs was performed for 1,000,000 time steps.

The XPA structure was taken from the 1XPA structure in the PDB. The hydrogen ions were added to model the protonation state at pH 7. The structure was then relaxed with NAMD with the CHARMM force field in KCl solution at the same ionic strength as DNA. The periodic boundary condition was used with a water box of 35 nm × 35 nm × 250 nm. The structure was first minimized for 2000 steps and then relaxed in NPT ensemble with MD for 2 ns to reach the equilibrium.

The molecular electrostatic potential grids were calculated for each DNA with PDB2PQR 2.1 on Opal and Adaptive Poisson-Boltzmann Solver (APBS) 1.3. The simulation temperature was set to 298 K. The ionic strengths were changed according to the experimental values. We used the default definition for the solute-solvent boundary. CHARMM force field was used, and the pH was set to 7. The potential grids for DNA were set to 129 × 129 × 353, centered on the geometric center of the DNA. The results were visualized in PyMOL by APBS plugin. The solvent-accessible surface potentials are shown in Fig. 3E (mismatched unlabeled dsDNA), Fig. 3F (normal unlabeled dsDNA), Fig. 3G (XPA), Fig. 5C (mismatched FITC-labeled dsDNA), and Fig. 5F (mismatched GFP-labeled dsDNA).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/5/e1602991/DC1

Supplementary Text

fig. S1. Cavity resonance measurement setup.

fig. S2. Electrostatic calculation of nanoplasmonic enhancement.

fig. S3. Baseline drift.

fig. S4. Step fitting algorithm.

fig. S5. k_on and k_off fitting.

fig. S6. Concentration dependence of DNA-XPA interaction.

table S1. Comparison of Q-factors and mode volumes (V).

References (59–69)