The Müller-Lyer illusion explained by the statistics of image–source relationships

Abstract

The Müller-Lyer effect, the apparent difference in the length of a line as the result of its adornment with arrowheads or arrow tails, is the best known and most controversial of the classical geometrical illusions. By sampling a range-image database of natural scenes, we show that the perceptual effects elicited by the MüllerLyer stimulus and its major variants are correctly predicted by the probability distributions of the possible physical sources underlying the relevant retinal images. These results support the conclusion that the Müller-Lyer illusion is a manifestation of the probabilistic strategy of visual processing that has evolved to contend with the uncertain provenance of retinal stimuli.

The standard Müller-Lyer stimulus (Fig. 1A) has been the subject of hundreds of studies since its introduction in the late 19th century (1). The perceptual effect is that two identical straight lines appear different in length when they are terminated, respectively, with “arrowheads” that extend inward or “arrow tails” that extend outward with respect to the “shaft.” Although there is considerable variation in the reported magnitude of the effect (presumably due to the different experimental conditions in various studies), the line terminated by the arrowheads always appears shorter than same line terminated by arrow tails (2–8).

Fig. 1.

Müller-Lyer stimuli. (A) The standard Müller-Lyer stimulus. (B) Variation in which the arrowheads and tails are replaced by squares. Despite this substitution, the illusory effect remains. (C) Variant in which the central shafts are missing. (D) The Müller-Lyer effect is also elicited by a figure comprising only dots.

Rationalizing this illusion has been made especially difficult by persistence of the effect when the identical lines are terminated with a variety of other adornments (9), a fact that undermines intuitive explanations based on what arrowheads and tails might signify. In Fig. 1B, for instance, the same perceptual discrepancy is generated when identical lines are terminated by outward and inward squares. A further obstacle for any simple explanation of the Müller-Lyer effect is that neither the shaft (Fig. 1C) nor continuous lines (Fig. 1D) is needed to elicit a misperception of the relevant spatial interval. Although the effects produced by these several variants have not been quantitatively compared, there is a general agreement that the shaft or the corresponding interval in the “outward” figure always appears longer than its counterpart in the “inward” figure. As a result, there has been much controversy about the genesis of the Müller-Lyer effect (6, 10–20), which still has no generally accepted explanation (21, 22).

Here we test the hypothesis that the standard Müller-Lyer effect and its variants are a result of the fundamentally probabilistic strategy of visual processing that contends with inverse optics problem. Any geometrical stimulus (or indeed any visual stimulus) can have been generated by many different real-world sources (23–27), presenting a quandary to observers whose survival depends on appropriate visually guided behavior. A plausible solution would be to generate visual percepts predicated on the probability distributions of the physical sources of retinal images. In these terms, the identical shafts or intervals in Müller-Lyer stimuli appear different in length because the probability distributions of the real-world sources of the lines or intervals, given the contexts provided by the arrowheads or arrow tails, are in fact different. To test this idea, we determined the physical sources of the standard Müller-Lyer stimulus and its variants in a range-image database that specified the distance and direction of every point in these natural scenes.

Methods

The range-image database of natural scenes is described in refs. 26 and 27. In keeping with the general approach used to identify the physical sources of lines and angles in these studies, we sampled the range images for sets of pixels whose positions matched the geometrical configurations of the Müller-Lyer stimuli tested.

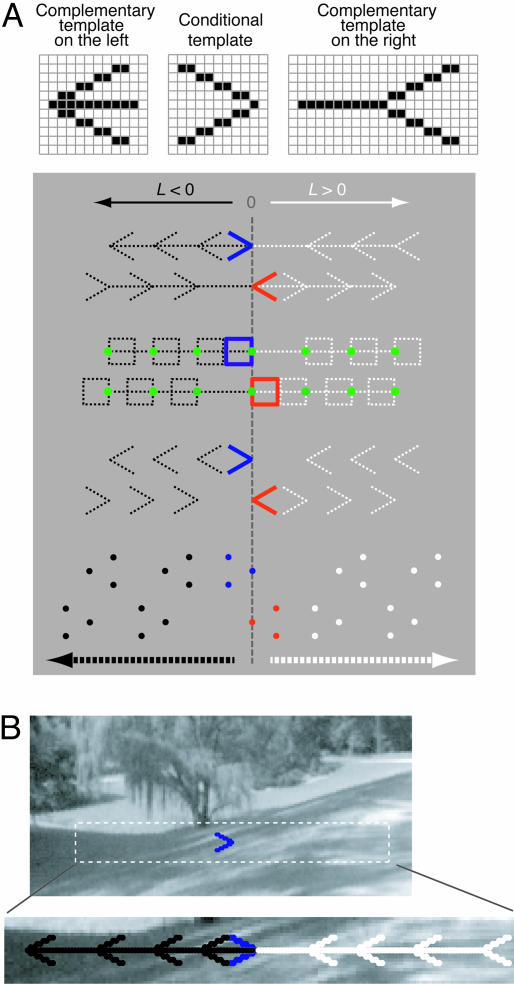
Fig. 2A shows examples of the geometrical templates used to identify the physical sources of different components of MüllerLyer stimuli. As a first step, a template was applied to the images to identify areas of the scenes containing the physical sources of one of the pair of adornments in a Müller-Lyer figure (i.e., an arrowhead, an arrow tail, or the equivalent in the Müller-Lyer variants). As indicated in Fig. 2B, the set of pixels underlying the template was then screened to determine whether the physical points corresponding to each straight line in the template formed a geometrically defined straight line in 3D space. If this criterion was met, the points were accepted as a valid sample of the physical source of what we subsequently refer to as the “conditional adornment.”

Fig. 2.

Sampling the range image database. (A Upper) The pixels in an image are diagrammatically represented by the grid squares; the black pixels show examples of the templates for sampling different elements of the standard Müller-Lyer figure. (A Lower) Each row illustrates a conditional template (blue or red) used in the first step of the sampling procedure, and a series of complementary templates (black or white) applied to the image as a next step (only a few examples in the series actually applied are shown). The green dots indicate the reference edge of a square adornment; L is the length of the central shaft or interval. (B) The sampling procedure applied to a typical image. The blue template indicates a conditional adornment sample that met the geometrical criterion described in Methods; a series of complementary templates was then overlaid at successively greater distances from the conditional adornment, as indicated in Lower.

After identifying a valid physical source of the conditional adornment, the same region of the scene was examined for the occurrence of the other components of the Müller-Lyer figure. For this purpose a series of templates complementary to the template for the conditional adornment was sequentially overlaid on the image (see Fig. 2 A). For a standard Müller-Lyer figure, the complementary templates comprised a shaft of increasing length and an arrow adornment configured as the mirror reflection of the conditional adornment. For the Müller-Lyer variant with squares, the complementary templates comprised a square with a shaft of increasing length attached to either the left or the right edge of the square. In the case of the variants without a shaft, or comprising only dots, the complementary template was simply a mirror reflection of the conditional template. This second step thus identifies the “complementary adornment” and the shaft or interval between the two adornments.

The length of the shaft (or the corresponding interval between the two adornments) was varied incrementally from –128 to 128 pixels (negative values indicating that the complementary template was to the left of the conditional adornment and positive values to the right). Thus as the complementary template shifted from the left to the right of the conditional adornment, the overall configuration of the stimulus formed by these two components was reversed (see Fig. 2). As above, the physical points corresponding to each straight line in the complementary template were also evaluated to see whether they formed a straight line in 3D space. If this further criterion was met, the sample was counted as a valid physical source of the Müller-Lyer figure in the configuration specified by the combination of the conditional and complementary templates.

This general procedure for sampling the Müller-Lyer configurations shown in Fig. 1 was repeated for each of the ≈10⁶ 2D image projections generated from the 3D scenes. We then counted the total number of valid samples of physical sources identified by each combination of conditional and complementary templates. These numbers, when expressed as a function of the length of the shaft or interval between the two adornments in each stimulus configuration, yielded a frequency distribution of the physical sources of Müller-Lyer figures of varying shaft (or interval length). Normalization of these frequency distributions gave the corresponding probability distributions.

Results

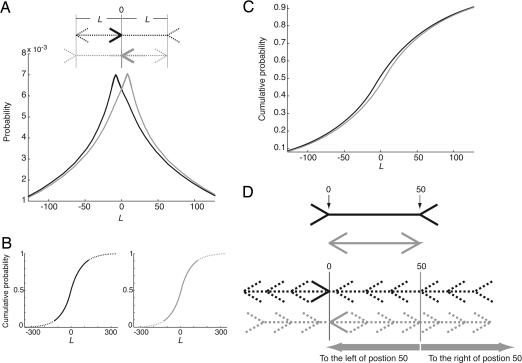
Analysis of the Standard Müller-Lyer Stimulus. Fig. 3A shows the probability distributions of the physical sources of the standard Müller-Lyer stimulus in Fig. 1 A with varying shaft lengths derived from the database of fully natural scenes (i.e., scenes with few if any human artifacts). The distribution indicated in black was derived by sampling with templates in which the apex of the conditional adornment pointed to the right; the distribution in gray was derived by using a conditional adornment whose apex pointed to the left (Fig. 3A Inset). Length of the shaft or corresponding interval in a Müller-Lyer stimulus (L) is given by the relative positions of the apices of the conditional and complementary adornments, negative values of L meaning the complementary adornment is on the left and positive values indicating the complementary adornment is on the right. Thus, the left half of the distribution indicated in black (where L < 0) represents shafts adorned with arrowheads, whereas the right half (where L > 0) represents shafts with arrow tails. The opposite is true for the distribution shown in gray. As evident in the figure, there is a systematic difference between these two probability functions. In relation to the point at which L = 0, the mode of the black distribution is shifted to the left, whereas the mode of the gray distribution is shifted to the right. Furthermore, for each value of L < 0, the distribution represented in black has a higher probability than the distribution in gray, whereas the opposite is true for all of the values of L > 0.

Fig. 3.

Statistical analysis of the fully natural scenes in the range-image database for the standard Müller-Lyer stimulus. (A) Probability distributions of the physical sources of Müller-Lyer figures with various shaft lengths (L, in pixels), given the presence of a conditional adornment with its apex pointing either to the right (black) or to the left (gray). In the diagram above, the conditional adornments are indicated by solid lines and the complementary components by dotted lines. (B) The cumulative probability distributions derived from the probability distributions in A. The dotted parts of the curves were computed by extrapolation. (C) Superimposition of the two functions in B.(D) Examples of two shafts 50 pixels in length, one adorned with arrow tails and the other with arrowheads (Upper). The left adornments are arbitrarily designated the conditional adornments and are indicated by solid lines at position 0 (Lower). Given each of these conditional adornments, the probability distributions shown in A–C indicate that the complementary adornment and shaft (dotted lines) can occur at different positions with varying probabilities. The summed probability of occurrence of all possible complementary adornments to the left of position 50 is greater when the fins of the conditional adornment extend to the left of position 0 (black) than when they extend to the right (gray), and conversely. This statistical fact means that a complementary adornment at position 50, given a conditional adornment extending to the left of position 0, is further to the right in the empirical range of possible positions for complementary adornments than is a complementary adornment at position 50, given a conditional adornment extending to the right of position 0.

These differences between the two distributions can also be compared in the corresponding cumulative probability distribution functions (Fig. 3 B and C). The cumulative probability value for a given shaft length l is the summed probability of occurrence of the physical sources of Müller-Lyer figures with shaft lengths less than or equal to l. Graphically, the cumulative probability equals the area underneath the curve of probability distributions such as those in Fig. 3A and to the left of the point where L = l. As is apparent in Fig. 3C, for any given shaft length, the cumulative probability derived from the probability distribution in black in Fig. 3A is always somewhat greater than the cumulative probability derived from the probability distribution in gray. This statistical difference means that the summed probability of occurrence of the physical sources of Müller-Lyer figures whose complementary adornment is to the left of position l, given the presence at position 0 of an arrow adornment whose apex points to the right, will always be greater than the same cumulative probability in the presence of an arrow adornment pointing to the left.

Perceptual Implications. To understand the perceptual implications of the differences between the two probability distributions in Fig. 3 A–C, consider, as an example, two identical shafts 50 pixels in length, one adorned with arrow tails and the other with arrowheads (Fig. 3D). Imagine taking one of the adornments on each shaft, the one on the left for instance, as the conditional adornment, defining the position of its apex as 0 (the same argument of course applies if the right adornment is selected). The complementary adornments are thus at position 50. Given the conditional adornment in the arrow-tails configuration in Fig. 3D (black), the summed probability of occurrence of the physical sources of complementary adornments whose positions are to the left of position 50 is greater than the comparable summed probability given the conditional adornment in the arrowheads configuration (gray). Conversely, the summed probability of occurrence of the physical sources of complementary adornments located to the right of position 50, given the conditional adornment in the arrow-tails configuration, is less than the comparable summed probability given the conditional adornment in the arrowheads configuration.

These differences in the cumulative probabilities of the stimulus sources mean that the complementary adornment that actually occurred at position 50 in the arrow-tails configuration lies further to the right in the empirical range of possible positions of complementary adornments than does the complementary adornment at position 50 in the arrowheads configuration. If the perceptions of the Müller-Lyer stimulus in Fig. 3D are determined by these probabilities, the complementary adornment in the arrow-tails configuration should appear further separated from the conditional adornment than the interval between the complementary adornment and the conditional adornment in the arrowheads configuration. Thus the shaft connecting the two adornments in the arrow-tails configuration should be seen as longer than the same line in the arrowheads configuration. The same reasoning can be generalized to Müller-Lyer stimuli with any shaft length, meaning that a shaft adorned with arrow tails should always look longer than the same shaft adorned with arrowheads. These predictions are, of course, consistent with the percepts elicited by the standard Müller-Lyer stimulus.

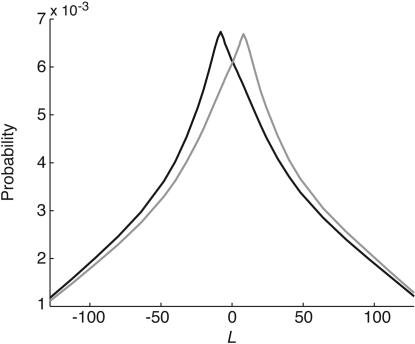
Statistics Derived from Different Types of Scenes. The results presented so far were derived from the set of fully natural scenes in the database, which is presumably the most important visual environment in the evolution of human perception. We also carried out the same analyses on the scenes in the database that include human constructions because the more rectilinear structure of man-made environments has sometimes been considered a factor contributing to the Müller-Lyer effect (see Discussion). The probability distribution of the physical sources of the standard Müller-Lyer stimulus derived from this type of environments is shown in Fig. 4. There is no obvious difference among the results obtained from these different types of scenes.

Fig. 4.

Probability distributions of the physical sources of the standard Müller-Lyer stimulus derived from scenes that contain human constructions.

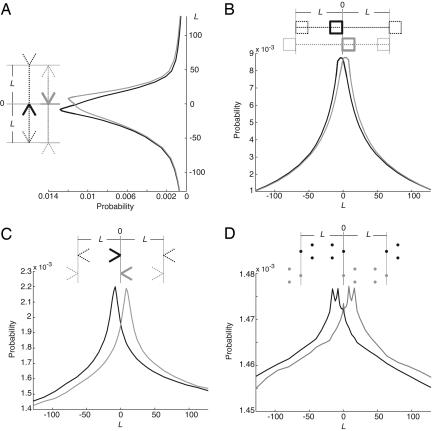
Variants of the Müller-Lyer Stimulus. Finally, we examined several variants of the standard Müller-Lyer stimulus that elicit the same perceptual effect, including the Müller-Lyer stimulus oriented vertically, identical shafts adorned with squares rather than arrows, standard arrow adornments without shafts and configurations comprising dots only (see Fig. 1 B–D). The probability distributions of the physical sources of these variants are shown in Fig. 5. In each case, the probability distributions derived in the context of different adornments differ in a manner similar to the differences between the probability distributions illustrated in Fig. 3, thus explaining the similar perceptual consequences of each of these variations.

Fig. 5.

Probability distributions of the physical sources of the major Müller-Lyer variants. (A) Standard Müller-Lyer stimulus oriented vertically. (B) Müller-Lyer variant with square adornments. (C) Variant with no shafts. (D) Variant comprising only dots.

Physical Basis for Differences Among the Observed Probability Distributions. The physical basis for the observed differences among the probability distributions of the sources of Müller-Lyer stimuli can be understood in the following terms. Because straight lines in the physical world are typically parts of geometrically planar surface patches, the presence of the physical source of a conditional adornment comprising straight lines typically signifies the presence of a plane at that location in 3D space. Given this fact, the probability of occurrence of the physical source of the complementary component of a Müller-Lyer stimulus will decrease as the interval between the two adornments increases. The reason is that as the complementary adornment becomes further removed from the conditional adornment, the physical points corresponding to the complementary component are less likely to lie in the same plane as the physical source of the conditional adornment. Thus, in the presence of the typical physical source of a conditional adornment whose fins extend to the left of a starting position, the physical points corresponding to the complementary component are less likely to be found in the plane of the conditional adornment when moving away to the right from that starting point than when moving away to the left (Fig. 7, which is published as supporting information on the PNAS web site). The opposite is true in the presence of a conditional adornment extending to the right of the starting position. This statistical difference in the occurrence of the physical sources of the complementary component of the stimulus, given the presence of a physical source of different conditional adornments, is presumably the basis for the different probability distributions of the physical sources of the various Müller-Lyer figures considered here.

Discussion

We have tested the hypothesis that the perceptual effects elicited by the Müller-Lyer stimulus and its major variants are the consequence of a fundamentally probabilistic strategy of visual perception. The results reported support this explanation: The anomalous percepts associated with the identical lines or intervals in Müller-Lyer stimuli can, in every geometrical variation examined, be explained by the statistical relationships of the stimulus elements and their possible physical sources.

Generating perceptions of Müller-Lyer (or other) geometrical stimuli according to the probability distributions of their physical sources is advantageous in that the relative similarities and differences among physical objects in the 3D world are preserved in perception, and thus ensuring behavioral responses have the best chance of contending successfully with retinal projections whose sources are inherently uncertain. Although the discrepancies between the physical measurements of a stimulus and the percepts they elicit may seem “maladaptive” on the face of it, this probabilistic strategy allows routinely successful behavior in typical visual environments (28).

Geometrical configurations of Müller-Lyer stimuli are not the only factor that determines the perceptions of shaft length in these figures; altering other features of the stimuli, contrast or color for instance, can also affect perceived geometry (e.g., refs. 21 and 29). Rationalizing these further effects would require taking into account the influence of additional parameters that affect the probability distributions of the physical sources of the relevant stimuli, such as illumination and surface reflectance. To assess these further influences one would need a natural scene database that included information about these further properties of stimulus sources in typical visual environments.

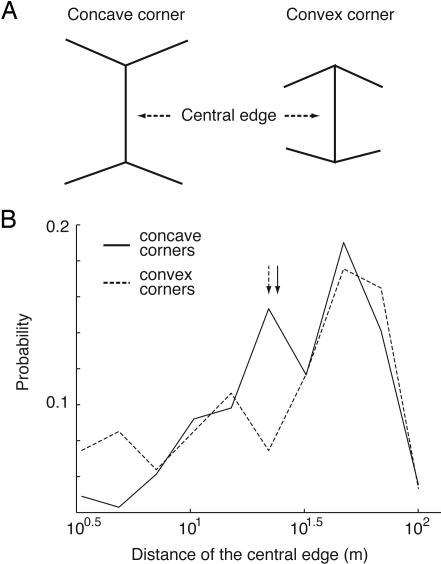
Previous Explanations of the Müller-Lyer Effect. Of the many previously suggested explanations of the Müller-Lyer illusion, the most often cited account is Gregory's proposal that the stimulus with arrow tails signifies a concave corner in the 3D world, whereas the configuration with arrowheads signifies a convex corner, the central shaft corresponding to the central edge of the two types of corners (refs. 14 and 15 and Fig. 6A). Because, on average, the central edge of concave corners was presumed to be further from an observer than the central edge of convex corners, the central shaft of the Müller-Lyer figure with arrow tails would, in this interpretation, appear longer as a “compensation” for the different distances of the 3D corners they represent.

Fig. 6.

Statistical analysis of concave and convex corners. (A) Diagram of these two types of 3D corners. (B) Probability distributions of the distance from the image plane of the central edges of concave and convex corners in the range image database. Arrows indicate the mean values of the two distributions.

This explanation has been rejected by some investigators because it does not explain the effects elicited by the Müller-Lyer variants illustrated in Figs. 1 B–D (22). It was nonetheless of interest to examine the merits of this influential idea directly. Accordingly, we identified all of the 3D corners in the image database by visual inspection and measured the distance to the central edges of the corners. Although only a small number of samples were obtained (≈200 for concave and convex corners, respectively), we found no significant difference between the probability distributions of the distance from the image plane to the central edges of concave and convex corners (Fig. 6B). Thus, although Gregory's intuition about the empirical significance of the Müller-Lyer stimulus points in the right general direction (i.e., an explanation based on past experience with the sources of such stimuli), convex and concave corners contribute little if anything to the Müller-Lyer effect.

Other suggested explanations of the Müller-Lyer illusion that have received significant attention over the years are the eye-movement theory (reviewed in ref. 30) and the assimilation theory (18, 31). The eye-movement theory claimed that the misperception of the central shaft arises from the different extents of eye movements needed to view a figure adorned with arrow tails compared to a figure with arrowheads. This older proposal has been generally dismissed because the illusion persists in the absence of eye movements (10, 32). The assimilation theory argues that the length of the central shaft is misperceived because the visual system cannot successfully isolate parts from wholes. In this scenario, the central shaft of the figure with arrow tails is seen as longer because the stimulus is, in its totality, longer. This explanation is contradicted, however, by a large group of geometrical illusions known as size contrast effects, in which a target embedded in a large surrounding component appears smaller than the same target in a small surround. In fact, such size contrast effects can be explained by using the same probabilistic framework that forms the basis of the present study (33).

Conclusion. The results summarized here further support the hypothesis that visual perception is a fundamentally probabilistic process that has evolved to contend with the inherent ambiguity of information in retinal stimuli. The otherwise puzzling perceptual effects of the standard Müller-Lyer stimulus and several variants that have been especially difficult to explain evidently arise because visual percepts are generated in a way that reflects the statistical relationship between retinal images and their real-world sources.