admixturegraph: an R package for admixture graph manipulation and fitting

Abstract

Summary

Admixture graphs generalize phylogenetic trees by allowing genetic lineages to merge as well as split. In this paper we present the R package admixturegraph containing tools for building and visualizing admixture graphs, for fitting graph parameters to genetic data, for visualizing goodness of fit and for evaluating the relative goodness of fit between different graphs.

Availability and Implementation

GitHub: https://github.com/mailund/admixture_graph and CRAN: https://cran.r-project.org/web/packages/admixturegraph.

1 Introduction

The relationship between populations is not always a simple tree. In addition to the splitting events, where an ancestral population split into two or more isolated groups, admixture events can merge two or more populations. Admixture graphs are extensions of phylogenetic trees that allow such merging events.

Inference of admixture graphs has not received the same attention as phylogenetic trees, but a number of methods have recently been developed for fitting genetic data to graphs and for using heuristics or brute-force search approaches to finding best-fitting graphs qpgraph (Castelo and Roberato, 2006), TreeMix (Pickrell and Pritchard, 2012), AdmixTools (Patterson et al., 2012; Zhao and Patterson, 2016), MixMapper (Lipson et al., 2013). These methods model the genetic relationship between populations as a graph where observed populations are represented as leaves, inner nodes represent ancestral populations, and edges represent the genetic drift separating an ancestral population from a descendent population. Without admixture events, the structure is simply a tree, but when the ancestry of the populations contain admixture, the graph contains nodes with more than one parent.

The graph describes the genetic drift within populations and the correlation of drift between populations. Data is usually summarized in some form studying patterns of allele frequency correlations across populations. In the TreeMix method by Pickrell and Pritchard (2012) data is thus represented as the covariance matrix of genetic drift while the AdmixTools software by Patterson et al. (2012) summarizes patterns of drift through so-called f-statistics. Given a graph topology together with edge lengths and admixture proportions the expected drift patterns can be computed and a likelihood derived and parameters of the graph can be inferred.

In this paper we describe the R package admixturegraph. This package contains functionality for:

• constructing and visualizing admixture graphs

• fitting graph parameters and visualizing the goodness-of-fit

• computing Bayes factors between graphs for comparing them

• exploring the space of graph topologies to find the best fitting graphs

For comparison, qpgraph and AdmixTools work on a user specified admixture graph, and MixMapper and TreeMix use a sequential heuristic building new admixture events based on the previous ones. The package admixturegraph can be used either for brute-force search on the graph topologies or for a heuristic approach generalizing the sequential one, building more complicated admixture graphs from a selected set of well performing simpler admixture graphs (as the sequential approach is not guaranteed to converge towards the best fitting admixture graphs). The package does not automatically infer an admixture graph from the data.

The R package does not add functionality that cannot be found in existing software, but by providing an R interface to working interactively with admixture graphs, fitting and visualizing the goodness of fit of graphs, we believe that we make admixture graphs more accessible to users.

2 Features

The admixturegraph R package provides a framework for constructing and analysing admixture graphs and evaluating their fit to genetic data summarized as f-statistics (Patterson et al., 2012).

2.1 Constructing and visualizing admixture graphs

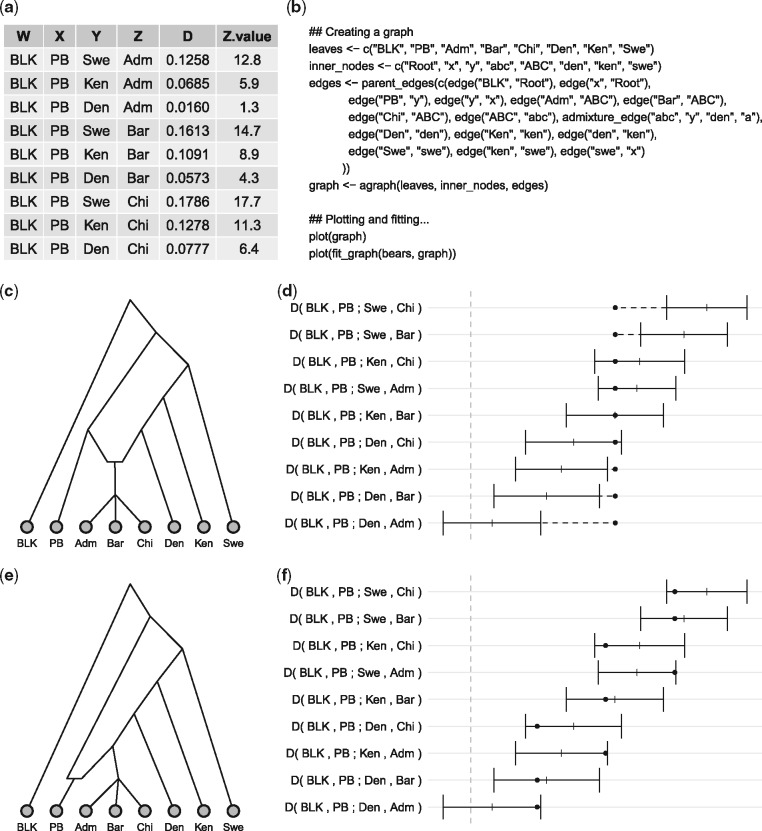
Admixture graphs are constructed using R functions specifying the nodes and edges and naming the admixture proportion parameters. Figure 1a shows a toy example dataset, adapted from Cahill et al. (2013), consisting of one black bear (BLK), one polar bear (PB) and a number of brown bear samples. Figure 1b shows example code for constructing an admixture graph that models that the ABC-bears (Adm, Bar, Chi) are admixed between polar bears and brown bears as suggested by Cahill et al. (2013). Figure 1e shows an alternative where polar bears are admixed (see Lan et al., 2016, https://dx.doi.org/10.1101/047498).

Fig. 1.

(a) Example data in the form of D statistics (equivalent to f₄ statistics. (b) Example of graph construction and plotting code. (c) and (e) Examples of admixture graphs. (d) and (f) Goodness-of-fit of the graphs in (b) and (d)

Unlike visualizing trees, which are always planar graphs, it is not trivial to present graphs in a visually pleasing way. We have therefore implemented heuristics for laying out graphs for plotting while providing a number of options for overruling the heuristics to customize plots. Examples of plotted graphs are shown in c and e.

2.2 Fitting graph parameters and visualizing fits

For fitting graph parameters to data, the data should be collected in an R data frame or equivalent (see package documentation for details on the expected format). The fitting procedure first extracts from the graph topology a set of equations for the expected values of each f-statistics in the data. These are linear equations on edge lengths and polynomials on admixture proportions. From the observed data and this set of equations, the likelihood of parameters can be computed and maximized. The likelihood used is

$$\det {(2\pi S)}^{-1/2}\hspace{0.17em}\text{exp}\hspace{0.17em}(-L/2)\hspace{0.17em},$$

where

$$L={(F-f)}^t{\Sigma }^{-1}(F-f)\hspace{0.17em},$$

f is the vector of observed statistics, F is the vector of statistics predicted by the graph topology and parameters, and Σ is the covariance matrix of the observed statistics f, which is either given by the user or replaced by a proxy of the identity or a diagonal matrix constructed from Z-scores given by AdmixTools for instance. The maximizing procedure used alternates between solving the linear problem on edge lengths, which can be optimized analytically, and the polynomial problem on admixture proportions, which is solved using numerical optimization.

Once we have fitted a graph to data we can visualize the goodness-of-fit by plotting the expected statistics against the observed statistics (see Fig. 1d and f where shows the fit of the two graphs in c and e). The genetic data is shown as observations with error bars (black lines) while the expected values are shown as solid dots.

2.3 Posterior distributions and graph comparisons

Fitting graph parameters to data provides a maximum likelihood point-estimate. To obtain confidence intervals for parameters, one can use a blocked jackknife or bootstrap procedure as in (Patterson et al., 2012) but the admixturegraph package also provides an alternative in the form of a Markov Chain Monte Carlo (MCMC) procedure for sampling from the posterior distribution of joint parameters.

Comparing the fit of two different graphs is not straight forward since graphs can have very different numbers of parameters and are usually not nested models. Instead we propose to use Bayes factors—the ration of the likelihood of one graph over another—to compare models. To do this it is necessary to integrate out the graph parameters and obtain a likelihood for a topology alone. To estimate this integral we use the MCMC to obtain samples from the posterior likelihood and use these in an importance sampler procedure to compute the graph likelihood.

2.4 Exploring the space of graph topologies

While we can compare the fit of different graph topologies to data, there are no known algorithms for inferring the optimal graph topology. Instead the package implements a few functions for brute force exploration of topologies and heuristics for extending topologies.

The set of all possible graphs, even when limited to one or two admixture events, grows super-exponentially in the number of leaves and it is generally not computationally feasible to explore this set exhaustively. Still, we give graph libraries for searching through all possible topologies with not too many leaves and admixture events. For larger graphs we provide functions for exploring all possible graphs that can be reached from a given graph by adding one extra admixture event or by adding one additional leaf. However, the best fitting admixture graphs are not necessarily extensions of best fitting smaller graphs, so we recommend that users not only expand the best smaller graph but a selected few best of them.

3 Conclusion

We have presented an R package for exploring and fitting admixture graphs. The package provides functionality for constructing and visualizing admixture graphs, for fitting graph parameters to genetic data, for visualizing goodness-of-fit, and for comparing the quality of fits between non-nested graph models. While the package does not contain algorithms for automatically inferring optimal graph topologies, it does provide functionality for exploring the space of possible topologies.

Funding

This research was funded by the Danish Council for Independent Research, Sapere Aude grant 12-125062.

Conflict of Interest: none declared.