Hierarchical sets: analyzing pangenome structure through scalable set visualizations

Abstract

Motivation

The increase in available microbial genome sequences has resulted in an increase in the size of the pangenomes being analyzed. Current pangenome visualizations are not intended for the pangenome sizes possible today and new approaches are necessary in order to convert the increase in available information to increase in knowledge. As the pangenome data structure is essentially a collection of sets we explore the potential for scalable set visualization as a tool for pangenome analysis.

Results

We present a new hierarchical clustering algorithm based on set arithmetics that optimizes the intersection sizes along the branches. The intersection and union sizes along the hierarchy are visualized using a composite dendrogram and icicle plot, which, in pangenome context, shows the evolution of pangenome and core size along the evolutionary hierarchy. Outlying elements, i.e. elements whose presence pattern do not correspond with the hierarchy, can be visualized using hierarchical edge bundles. When applied to pangenome data this plot shows putative horizontal gene transfers between the genomes and can highlight relationships between genomes that is not represented by the hierarchy. We illustrate the utility of hierarchical sets by applying it to a pangenome based on 113 Escherichia and Shigella genomes and find it provides a powerful addition to pangenome analysis.

Availability and Implementation

The described clustering algorithm and visualizations are implemented in the hierarchicalSets R package available from CRAN (https://cran.r-project.org/web/packages/hierarchicalSets)

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Pangenome analysis is concerned with the investigation of multiple bacterial genomes whose genes have been grouped according to similarity. A pangenome is thus defined as a set of gene groups containing members from one or more genomes. Figure 1 shows the general structure of a pangenome as visualized by a presence/absence matrix. Gene groups are often classified by their ubiquity in the genomes making up the pangenome. Core gene groups are present in all genomes, accessory gene groups are present in more than one, but not all genomes and singleton gene groups are only present in one genome. This classification of gene groups gives a broad overview of the heterogeneity of the pangenome through the number of core gene groups and total gene groups, but is also used to pinpoint the nature of the genes within each group. Core genes are likely genes that define the unique traits of the genomes under investigation, while accessory genes are disposable genes that define more specialized behavior. Singleton genes can be strain specific genes, pseudogenes, or annotation errors. As is evident from Figure 1, there are clear overlaps between the nomenclature associated with pangenome data and that of set algebra, where genomes can be considered sets and gene groups elements in these sets. Furthermore, intersection and core size, as well as pangenome and union size, are equivalent.

Fig. 1.

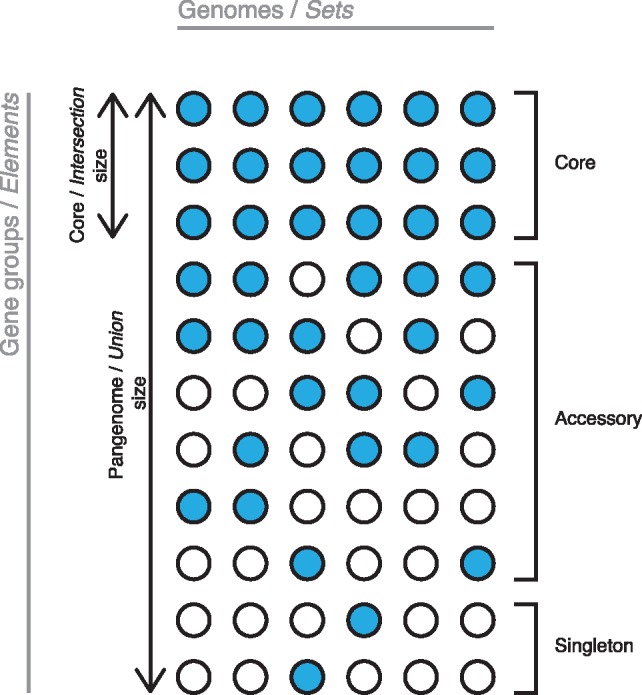
Overview of the nature of pangenome data and the nomenclature associated with it. Equivalent set algebra terms are shown in italic. Columns define genomes and rows gene groups. A filled circle indicates the presence of a member of the respective gene group in the genome while an empty circle indicates absence

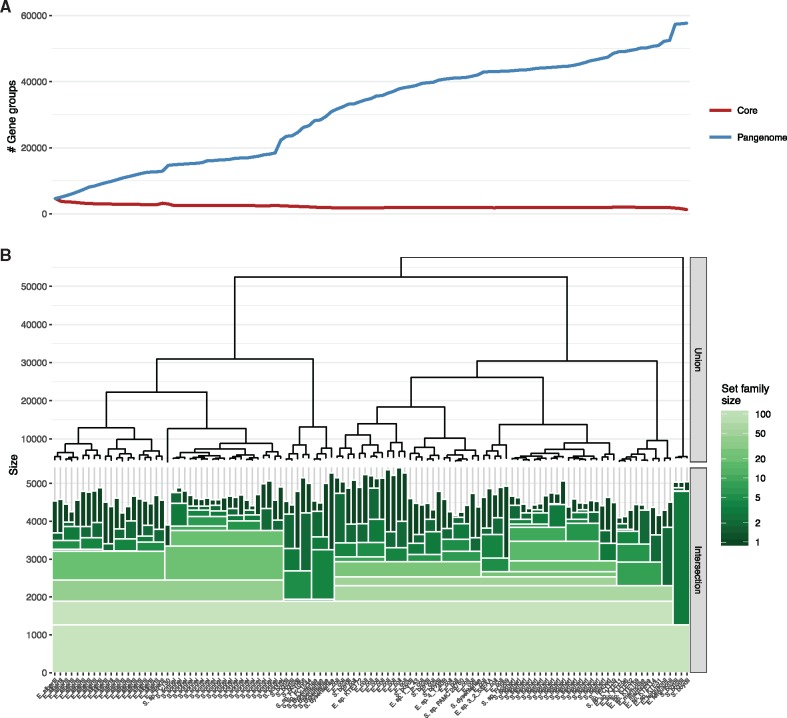
The first published pangenome covered eight strains of Streptococcus agalactiae (Tettelin et al., 2005), reflecting the number of available genome sequences for that species at the time. The number of genomes included in pangenome analyses has since increased along with the increased availability of sequenced bacterial genomes and now contains 100s or 1000s of genomes (Jun et al., 2014; Kaas et al., 2011; Land et al., 2015; Leekitcharoenphon et al., 2016; Méric et al., 2013; Snipen and Ussery, 2012) resulting in >10 000 gene groups. A main concern when evaluating the result of pangenome analyses is how the pangenome and core size change as genomes are added to the pangenome. Sudden drops in core size or jumps in pangenome size indicate the addition of a genome deviating strongly from the genomes already present in the pangenome. The standard approach to show this evolution in pangenome and core size is through a simple line-plot as shown in Figure 3A (De Maayer et al., 2014; Lukjancenko et al., 2010; Smokvina et al., 2012). This approach has considerable drawbacks as the shape of the line is determined by the order in which genomes are added. Although it is possible to define a progression of genomes that ensures that similar genomes follow each other, changes between genomes will still be obscured by the level of heterogeneity between the genomes that comes before it. The extreme case is a pangenome without any core gene groups. At some point along the line-plot the core line will drop to zero and any difference between genomes that follows this point will be invisible. The set nature of pangenome data could offer a better way of visualizing the change in core and pangenome size without imposing a specific order to the genomes. Set algebra has been used sparingly in pangenome visualizations. GenoSets (Cain et al., 2012) and PanViz (Pedersen et al., 2017) both apply set arithmetic to create visual queries for gene group subsets. Apart from query construction though, set algebra is largely unexplored when it comes to visualizing the relational structure between genomes. Although visualizing relations between large numbers of sets is difficult due to the combinatorial explosion of possible set combinations, different visualization techniques have been developed to show intersection sizes between sets in a scalable manner, such as, UpSet (Lex et al., 2014) and Radial Sets (Alsallakh et al., 2013). These techniques do not scale to the number of sets that is exposed in contemporary pangenomes though and are thus a poor fit for investigating all but the smallest pangenomes.

Fig. 3.

(A) A standard pangenome line plot showing the evolution in pangenome and core sizes as genomes are added to the pangenome. A soft core of 95% is used for calculating the core size. The order in which the genomes are added is determined by the ordering from the hierarchical set clustering visualized in B and A and B are thus sharing the x-axis. (B) Intersection and union sizes at the branch points in a hierarchical set clustering with t = 0.95, visualized as an icicle plot for the intersections and a dendrogram for the unions. The intersection size of each set family is encoded to the height of the bar and the size of the set family is encoded to the color of the bar. The area of each rectangle is thus proportional to the number of sets it represents and the increase in intersection size relative to the next branch point

Here, we present a new approach to set analysis and visualization called Hierarchical Sets that works particularly well on large structured collections of sets such as pangenomes. Hierarchical Sets limits the comparisons between sets to branch points of a hierarchical clustering. In that way it achieves good scalability at the expense of not showing direct comparisons between very dissimilar sets. Although the focus in this paper is on the use of Hierarchical Sets in pangenome visualization, the technique can be applied equally well to other problems involving large numbers of sets.

2 Data

The data set used for the examples is a pangenome based on 54 Escherichia and 59 Shigella genomes. The genomes were selected by retrieving all genomes from the two genera in the NCBI Assembly database that had either ‘Scaffold’ or ‘Complete Genome’ status. Genomes that deviated >25% from the median genome length for its species were removed and at most 15 genomes from each species were selected. The pangenome was created using FindMyFriends (Pedersen, 2015) with default parameters and consists of 57,664 gene groups classified into 23 core groups, 29 132 accessory groups and 28 509 singleton groups. As such the genome selection is a compromise between species coverage and sequence quality. Escherichia is a genus dominated by E.coli but consisting of seven species in total (Gaastra et al., 2014). Shigella is a genus often considered to be genetically indistinct from E.coli (Lukjancenko et al., 2010; Ogura et al., 2009; Pupo et al., 2000; Sims and Kim, 2011) as it often clusters within E.coli in genome based analyses.

3 Algorithm

Existing approaches for hierarchical clustering of sets or pangenomes usually follows a conversion of the data into a distance matrix followed by an agglomerative clustering. For pangenomes several distance measures have been used, e.g. binary (Richards et al., 2014), Jaccard (Kuenne et al., 2013) or Manhattan distance (Jacobsen et al., 2011) as well as several clustering algorithms, such as, average (Karlsson et al., 2011) or single linkage (Tettelin et al., 2005). These approaches have several drawbacks when it comes to interpreting the results in a set algebraic context. The reliance of a conversion to a distance matrix makes the clustering extremely sensitive to the choice of clustering algorithm as the clustering is no longer based on the original data. Furthermore, it implies that a distance exists for some combinations of sets which might not make sense if two groups of sets are fully independent (no intersecting elements). The consequence of the former is that the result of standard hierarchical clusterings can be hard to translate back to features of the set data, while the latter results in all sets are being merged into a final cluster even though there might not be any similarity between all sets in the analysis. To address these shortcomings we introduce a new agglomerative hierarchical clustering approach for sets that works directly with the set data itself, by means of a set family homogeneity measure defined below. The clustering happens through the following steps:

1. Let each set in the analysis define their own set family of size 1.

2. For each pair of set families calculate the homogeneity, λ, of the combined set family.

3. Choose the pair that exhibit the highest λ (on ties choose the pair with the smallest union) and let the pair define a new set family.

4. Repeat 2–3 until all available set family pairs have λ = 0 or all sets have been joined in a single set family.

Note that this approach specifically terminates the clustering before all sets have been combined to a single cluster if the remaining clusters have no pairwise homogeneity.

3.1 Set family homogeneity and heterogeneity measure

Similarity between two sets is often measured using Jaccard similarity defined as the size of their intersection divided by the size of their union. The similarity between two sets can also be thought of as the homogeneity of a set family consisting of the two sets. The Jaccard similarity can then be generalized to a measure of set family homogeneity for set families of any size by dividing the total intersection size with the total union size. Formally, for a set family A, the set family homogeneity λ is defined by:

$$\lambda (A)=\frac{|\cap (A)|}{|\cup (A)|}$$

In the case of pangenomes, the data is often incomplete as there is a chance to miss genes during sequencing, de novo assembly, and annotation. Therefore, core size can be underestimated and it is a custom to loosen the requirement for gene groups to be considered core by requiring the fraction of genomes represented in a core group to be above a fixed threshold (such as 0.95). The set family homogeneity definition can be modified to accommodate this practice by introducing a parameter $t\in [0,1]$

that defines the ratio threshold for an element to be considered part of the intersection (t = 1 will result in the standard intersection definition). The set family homogeneity subject to t can thus be defined as:

$$\lambda {(A)}_t=\frac{{\sum }_{i=1}^n\frac{{\sum }_{j=1}^m{A}_{i,j}}{m}\ge t}{|\cup (A)|}$$

where A is the set family, n is the universe size, m is the number of sets in the family, and t a value between 0 and 1. $A_{i,j}$ is 1 if element i is present in set j and 0 otherwise. Similar to the Jaccard similarity the set family homogeneity is bound between 0 and 1 ($\lambda \in [0,1]$). Conversely, the set family heterogeneity is defined as:

$$\lambda \prime {(A)}_t=\lambda {(A)}_t^{-1}-1$$

And it follows that $\lambda \prime \in [0,\infty ]$. This definition makes $\lambda \prime$ undefined for set families with λ = 0, which is sensible as the heterogeneity of a collection with no homogeneity must be undefined.

4 Results

4.1 Visualizing set family heterogeneity

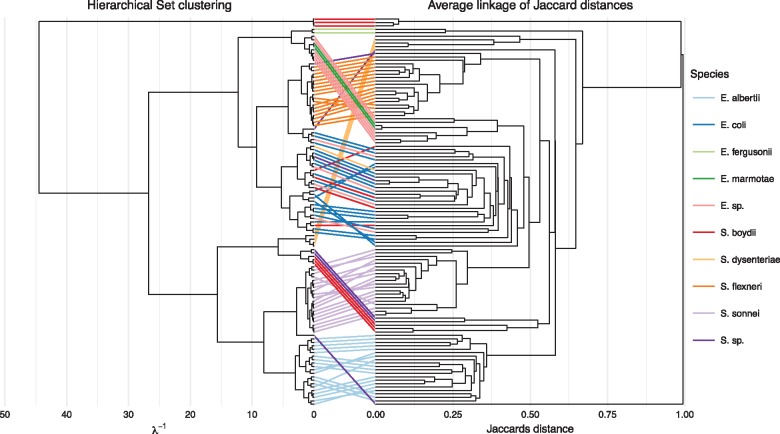
An obvious way to present the result of the clustering is through the use of a dendrogram. By encoding the height of the branch points to $\lambda \prime$, the dendrogram will illustrate how the heterogeneity increases as set families are combined. This dendrogram encoding is particularly good at identifying clusters of highly homogeneous sets as well as independent clusters (Fig. 2).

Fig. 2.

Comparison of hierarchical set clustering and complete linkage clustering based on Jaccard distance as performed on a pangenome based on 54 Escherichia and 59 Shigella strains. A colored link joins the same strains between the two clusterings with the color denoting the species. Unnamed species have been combined in the E.sp. and S.sp. groups. Both dendrograms have been sorted to best match the order in the other, so as to limit crossing of the links

It is apparent that Hierarchical Sets clustering makes different choices than average linkage applied to Jaccard distances. Although there is general agreement at the species level, there are some differences in the clustering within each species as well as major differences in how the clustering is defined between the species. Further, the interpretation of the x-axis differs substantially. Although $\lambda \prime$can clearly be interpreted as the ratio of intersection to union for the sets contained in each branch point, average linkage shows the average distance (here Jaccard distance) between all pairs of sets between the joining clusters. Average linkage can tend to created top-heavy dendrograms in combination with Jaccard distance since addition of smaller clusters to larger ones does relatively little to the average distance. The end result of this is a dendrogram where clusters are difficult to visually separate and where the overall structure of the clustering is less apparent. Hierarchical Sets generally provides a more balanced dendrogram as $\lambda \prime$ tend to increases at a larger rate as larger and larger clusters are joined. This means that the clustering structure is apparent at all levels of the hierarchy providing better overview.

4.2 Visualizing intersection and union sizes

Often in set analysis there is an interest in the intersection sizes of the different combinations of sets. For a number of sets, n, the number of possible set families are $2^n-1$, resulting in $10e33$ possible set families for the 113 sets used as example in this paper. This combinatorial explosion has made it difficult to visualize intersection sizes for large numbers of sets. The Hierarchical Sets clustering offers a way to decrease the number of set families by only considering set families at branch points. The intersection sizes of each branch point can be visualized while preserving the hierarchical layout by using an inverted icicle plot with bar height encoded to intersection size (Fig. 3B, bottom). The plot can be envisioned as a stack of blocks where the height of the stack denotes the total value and the height of the block denotes the contribution of that single block

Based on this plot a lot of information can be decoded. The intersection size of the different set families defined by the branch points are shown as the absolute height of the stacks while the drop in intersection size is shown as the height of each block. To improve visual separation of the blocks, their fill color is encoded to the number of the sets represented by the family. This type of plot can show relational structure between the different sets: Dark, narrow bars starting close to the x-axis (e.g. rightmost S.boydii cluster in Fig. 3B) represent sets having little overlap with the rest of the sets, while light and wide bars represent larger collections of sets showing large overlaps. The near absence of single-width bars (e.g. Escherichia marmotae in Fig. 3B) indicates near-similar sets and the absolute height of each single-width bar shows the total size of each set.

In the same way as intersection at each branch point can be shown, so can the union. In contrast to the intersection, the union decreases as you approach the leaves of the hierarchy, making a dendrogram a better choice for this (Fig. 3B, top). Although the union dendrogram would extend naturally from the top of the bars in the icicle plot, as the union and intersection of a single set are equal, the range of union sizes often vary substantially from that of intersection sizes (in this case almost tenfold). Thus, it is a better choice to plot them in separate plots, but stacked so that they share the x-axis. The addition of the union dendrogram reinforces the hierarchical nature of the data as well as providing the means to assess the homogeneity of the different clusters.

4.3 Visualizing deviations from hierarchy

Imposing a hierarchy on a dataset is likely to distort the data as complete adherence to a hierarchical structure is rare. In the case of a hierarchical set analysis, deviations from the hierarchy materialize as elements shared by two sets, but not by all sets in their common set family (Fig. 4). More formally outlying elements $\widehat{x}$ can be defined as

$$\widehat{x}\in \cap (A,B)\wedge \widehat{x}\notin \cap (C_{A,B})$$

Fig. 4.

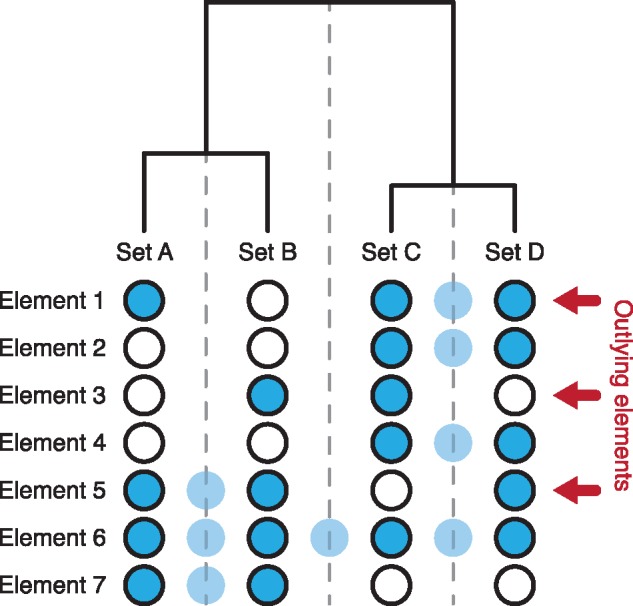
Definition of outlying elements: set A–D are sets defined by the presence of elements 1–7. Blue filled circles indicate presence while empty circles indicate absence. The shaded circles on the dashed lines show the set family intersection of the families defined by the clustering. The red arrows show outlying elements, i.e. elements that are shared by two sets but not shared by all sets in their common set family

Where A and B are sets and $C_{A,B}$ the smallest set family containing A and B derived from the hierarchical clustering.

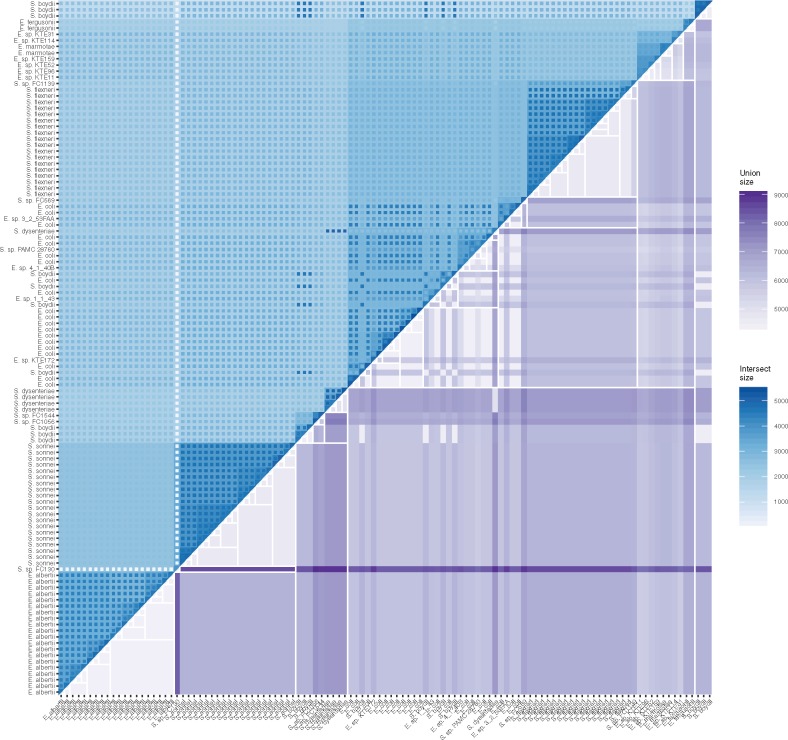
The concept of outlying elements is important since Hierarchical Sets purposefully limits the amount of information it shows in order to achieve scalability. Assessing the magnitude and structure of outlying elements provides a way to investigate how well the imposed hierarchy matches the underlying data and whether certain pairs or clusters of sets have been separated despite large overlaps. Visualizations of outlying elements can be either set- or element centric, depending on whether the focus is on how pairs of sets deviate from the hierarchy or on the individual elements that make up the deviation. Showing statistics on pairs of sets can be done effectively using a heatmap. By overlaying both hierarchy information and pair information in the same way as done by dendrogramix (Blanch et al., 2015), it is possible to get a matrix plot that both shows the intersection at each branch point, as well as the intersection and union size of each set pair. The contrasts between the branch point intersections and the set pair intersections are thus indicative of the amount of deviation from the hierarchy that each pair of sets exhibit (see Fig. 5).

Fig. 5.

A dendrogramix inspired heatmap showing pairwise intersection and union sizes. The hierarchical clustering has been overlaid with white lines on top of the union sizes while the set family intersection size for each cluster has been indicated as a backdrop color below the pairwise intersections. The contrast between the set family intersection sizes and the pairwise intersection size is indicative of how well the hierarchy describe the relationship between the two sets

An alternative way to show connections between leaves in a hierarchical clustering is by using hierarchical edge bundling (Holten, 2006). To avoid overplotting, edges can be filtered by weight (number of outlying elements), in order to only show the strongest deviations from the structure (Fig. 6).

Fig. 6.

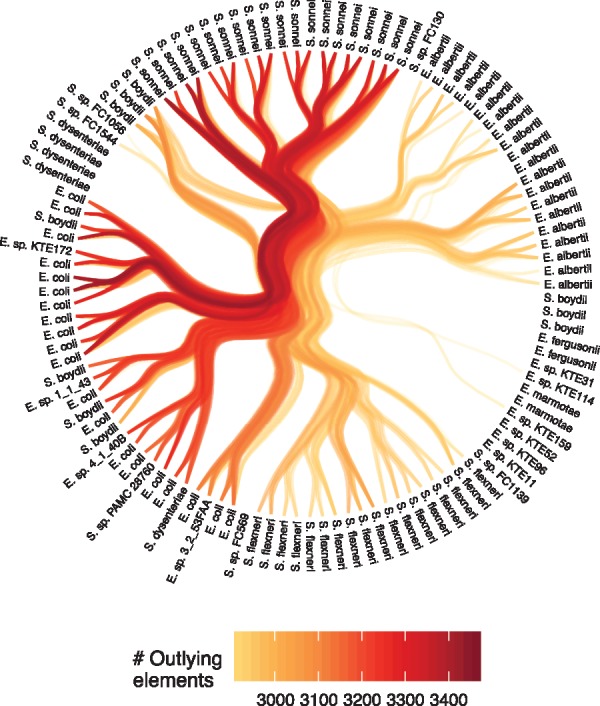
Hierarchical edge bundling showing the 15% strongest deviations from the hierarchy defined by a hierarchical set analysis (measured in number of outlying elements). Color is mapped to number of outlying elements

The elements themselves can be investigated as well, based on the outlying elements approach outlined earlier. Counting the number of times each element appears as outlying will give an indication of each elements propensity to not conform with the hierarchy. As the number of times an element can appear as an outlier is governed by the number of times it appears in a set, these two values can be shown in a scatter plot (see Supplementary Fig. S1) to quickly identify elements exhibiting unexpectedly high or low deviation. In Supplementary Figure S1 it can be seen that there are two bands of elements positioned below the main band indicating that while the elements are prevalent in the sets, they only deviate in a subset of the clusters.

5 Discussion

We have presented a new approach to hierarchical clustering of set data, a range of scalable visualizations that builds on top of the clustering, and an outlier definition for elements based on the clustering. Hierarchical Set analysis optimizes intersection size at each branch point, making it easier to reason about the clustering and, as a consequence, the visualizations. Hierarchical Set analysis is particularly well-suited for pangenome analysis as pangenome data often consists of a large number of sets with a clear hierarchical structure due to the evolutionary nature of genomes.

5.1 Pangenome evolution

In the context of pangenomes the intersection is equivalent to the core, while the union equates the pangenome. As such there is strong similarity between Figure 3A and B as they both try to convey the same type of information (i.e. the change in pangenome and core size as additional genomes are added). The main difference is that Figure 3B shows the core and pangenome sizes along a hierarchy instead of along a linear progression as in Figure 3A. The benefit of the hierarchical sets approach is that evolutionary features are not obscured. The line-plot hardly shows any change in core size in the last half of the plot despite the fact that this group of genomes are just as diverse as the first half. Further, the pangenome size evolution is not able to show the introduction of new species very clearly after the first appearance of S.boydii. In addition, Figure 3B also conveys the hierarchical structure of the pangenome, information that is very relevant when evaluating core and pangenome sizes of different subsets of the pangenome. Based on Figure 3B it is obvious that three sets (the rightmost S.boydii strains) deviate strongly from rest of the sets while showing high internal overlap. It is also easy to quickly compare the sizes of these three sets with the sizes of sets supposedly related to them (the other S.boydii) and determine that they are consistently larger. Large set families with many shared elements (e.g. Escherichia albertii and Shigella sonnei) are easily visible and clearly distinguishable from set families with a more heterogeneous composition (the central E.coli dominated cluster. Large jumps in intersection sizes and/or union sizes can, in the same way as in the line-plot, be interpreted as possible merging of species, but in Figure 3B these jumps are not masked by the heterogeneity of the species to the left removing the bias for a small subset of the samples.)

5.2 Deviations from the hierarchy

There is a clear similarity between the Hierarchical Sets based heatmap visualization (Fig. 5) and the BLAST matrices often used to show similarities between genomes in a pangenome, e.g. Figure 3 in Lukjancenko et al. (2012). The Hierarchical Sets heatmap provides additional information though, allowing for both an assessment of the pairwise similarities as well as deviation between the pairwise similarity and the similarity defined by their common ancestor. The deviation, defined as outlying elements in the context of Hierarchical Sets, has a clear analogy in gene deletion and horizontal gene transfer events. Such events results in distributions of gene groups not governed by the evolutionary hierarchy of the genomes itself but more related to shared environment. These events can be of just as much interest as the hierarchical structure itself. Detecting structure in where these events occur, in relation to the evolutionary hierarchy, can help researchers detect strong cross-talk between evolutionary unrelated organisms. In contrast to the heatmap approach used in Figure 5, hierarchical edge bundles puts focus on larger structures in the deviation, while obscuring the single pairwise values due to overplotting e.g. the high number of outlying elements between the E. coli and the S.sonnei cluster. The use of negative space also draws attention to clusters that lacks outlying elements (e.g. Shigella dysenteria) and single sets that shares some outlying elements within a group of sets that do not (e.g. E. sp. KTE159 and E. sp. KTE114).

5.3 Deviating gene groups

Looking into the diverging elements themselves and the number of times elements appear as outliers can guide researchers looking into mobile elements. The elements appearing as outliers constitute rows of the presence/absence matrix not conforming to the hierarchical structure. Extracting these rows and performing a second Hierarchical Sets analysis based on them will reveal the second most dominant structure in the dataset. Conceptually, this is equivalent to a principal component analysis (PCA) where components gradually diminish in explanatory power as they focus on structures not captured by the components before them. In an evolutionary context the main hierarchy revealed by Hierarchical Sets analysis is likely related (but not necessary identical) to the evolutionary tree of the genomes under investigation, while a secondary hierarchy based on outlying elements could reveal structures pertaining to increased strain interactions such as ecological niches. It is possible to continue creating sub-hierarchies based on outlying elements, but as with PCA the likelihood of beginning to model noise will increase with each step.

5.4 Escherichia and Shigella through hierarchical sets

Based on the figures provided in this article, it is possible to get a good overview of the Escherichia and Shigella pangenome. The first observation is that the two species are not clearly separated (Figs 2 and 3B). These results are not supportive of the notion that Shigella is part of E.coli specifically (Lukjancenko et al., 2010; Ogura et al., 2009; Pupo et al., 2000; Sims and Kim, 2011) it supports recent findings that Shigella spp. and Escherichia spp. are species within the same genus (Zuo et al., 2013). At a soft core threshold of 95% the core sizes for almost all included species are around 3000 (Fig. 3B). E.albertii, S.sonnei and Shigella flexneri appears to be very well defined species with relatively little internal difference, whereas E.coli shows much more variation in the core sizes of the internal subclusters. This difference is also pronounced in the heatmap representation in Figure 5 in both the upper and lower triangle. Figure 5 also shows that while S.boydii strains are scattered throughout the clustering they retain a large pairwise overlap. S.boydii is the most heterogeneous of the Shigella species (Feng et al., 2004) and these results indicate that they have a complicated relationship with the rest of the Shigella/Escherichia species. Although a subset of S.boydii strains shares a larger core with other species than with other S.boydii strains it is difficult to determine whether S.boydii should be split up or whether the defining traits of the species are simply encoded in a relatively small part of the genome, leaving a large variable portion of genes that can be interchanged with other species. A similar pattern can be found in S.dysenteriae where a single strain is placed outside the main cluster but retains a large pairwise overlap with the other strains from its species. It is important to emphasize that the scattering of the S.boydii and S.dysenteriae species is not a unique artifact of the Hierarchical Sets clustering as the same pattern is found using Jaccard distance and average linkage (Fig. 2). Although existence of large numbers of outlying elements between strains is interesting, so is the opposite. Escherichia fergusonii show almost no outlying elements with any of the other strains included in the pangenome, indicating a very stable and well-defined genome. E.albertii and S.sonnei shows an interesting relationship in that each species cluster is very well defined and that the two species, despite being closely related, have almost no outlying elements between their strains (Fig. 5). S.sonnei is a clonal species thought to have developed recently in Europe (Holt et al., 2012), whereas E.albertii has only recently been classified (Ooka et al., 2015) and have a less described lineage. It could be hypothesized based on the Hierarchical Sets results that these two species have evolved recently from a common ancestor and have lacked contact and exchange of genetic material since delineation.

S. sp. FC130 represents a challenge for the use of a soft core, both generally as well as when performing Hierarchical Set clustering. In the case of large and very homogeneous clusters such as the S.sonnei cluster the inclusion of a very distantly related genome will give almost no penalty as the core will remain unchanged. This problem is uniquely present when using a soft threshold in situations where both large homogeneous clusters and single, outlying sets are present and is easily identified with Figure 5. Still, work should be done to ensure that these situations are captured during clustering and penalized.

6 Implementation and availability

The described clustering algorithm as well as the different visualizations are implemented in the hierarchicalSets R package and available for free (GPLv2 license) on all major platforms through CRAN (R Core Team, 2016) as well as on https://github.com/thomasp85/hierarchicalSets. hierarchicalSets takes as input either a presence–absence matrix with sets as columns and elements as rows, or a list of sets defined by their elements. For use in pangenome analysis, hierarchicalSets can work directly with the the data structures defined in the FindMyFriends package (Pedersen, 2015). hierarchicalSets uses common, memory efficient R data-structures and the clustering algorithm is written in C ++ for speed, and has been tested on set collection up to 3800 sets with a universe size of 5.5 million.

7 Conclusion

Pangenome analyses continue to increase in scope, and visualization approaches that gracefully handle this increased complexity are paramount to extract knowledge from the results. Recent advances in pangenome analysis algorithms have facilitated the creation of pangenomes spanning thousands of genomes, covering the full bacterial domain and current visualization techniques do not adequately support such large and heterogeneous pangenomes. Based on the overlap between common set arithmetics and pangenome summaries, different approaches to scalable set visualization has been explored in order to address the challenges posed by large pangenome datasets. This article presents a new range of set visualization approaches well-suited to large collections of structured sets, such as genomes in a pangenome. All presented visualizations are centered around a new hierarchical clustering technique, called Hierarchical Sets, that optimizes the intersection size along the branch points. Based on this clustering it is possible to create scalable visualizations of intersection and union sizes (core and pangenome size), as well as visualizing elements (gene groups) that deviate from the overall structure of the data. We show the utility of hierarchical sets in pangenome analysis by applying it to a pangenome based on 113 genomes from the Shigella and Escherichia genera. The visualizations clearly showed how the different species under investigation differed in homogeneity and confirmed that the two genera should be merged, while also pointing towards interesting evolutionary relationships that should be further investigated. The visualizations presented here do not rely on interactions in order to communicate their message, making them easy to incorporate into composite visualization frameworks or directly augment with interactivity. Although Hierarchical Sets has been developed for the purpose of visualizing pangenome data, the approach is agnostic to the underlying data type, and it could potentially be applied to other large-scale set visualization problems, especially set data with a clear hierarchical interpretation.