Abstract
We report on the formation and ionization of cesium and C60Cs clusters in superfluid helium nanodroplets. Size distributions of positively and negatively charged (C60)mCsn± ions have been measured for m ≤ 7, n ≤ 12. Reproducible intensity anomalies are observed in high-resolution mass spectra. For both charge states, (C60)mCs3± and (C60)mCs5± are particularly abundant, with little dependence on the value of m. Distributions of bare cesium cluster ions also indicate enhanced stability of Cs3± and Cs5±, in agreement with theoretical predictions. These findings contrast with earlier reports on highly Cs-doped cationic fullerene aggregates which showed enhanced stability of C60Cs6 building blocks attributed to charge transfer. The dependence of the (C60)mCs3– anion yield on electron energy shows a resonance that, surprisingly, oscillates in strength as m increases from 1 to 6.
1. Introduction
Since the successful development of methods to synthesize fullerenes in macroscopic quantities, the properties of metal-doped fullerene solids and their potential applications have been studied. Early experiments on fullerides doped with alkali (A) metals revealed metal–insulator transitions1 and the appearance of superconductivity in potassium-doped fullerides below Tc = 18 K.2 Various crystal structures form depending on the dopant concentration which may be as large as 12:1 in Li12C60.3,4 Superconductivity, however, is restricted to the A3C60 fulleride salts in which the alkalis transfer their valence electrons to the lowest unoccupied triply degenerate molecular orbital of t1u symmetry, resulting in a half-filled conduction band of C60. The superconducting transition temperature in binary A1B2C60 fulleride salts (A, B = alkali metal) was found to correlate with the lattice parameter.4 Indeed, the highest transition temperature of any alkali-doped fulleride has been reported for Cs3C60 which is an insulator at ambient pressure but becomes superconducting below Tc = 38 K at elevated pressure without changing its body-centered cubic structure.5−7
In a recent report we presented ion abundances of (C60)mCsn+ cations prepared in the gas phase by electron ionization of helium nanodroplets doped with C60 and Cs.8 A key finding was that (C60)mCsn+ ions (m ≤ 6) are particularly abundant if they contain n = 6m + 1 cesium atoms; (C60)mCsn2+ dications were abundant (with the exception of (C60)4Csn2+) if n = 6m + 2. By and large these results were consistent with earlier photoionization experiments by Martin and co-workers involving potassium and rubidium which indicated that up to six alkali metal atoms per C60 transfer their valence electrons into the t1u orbital, resulting in particularly stable C60A6 building blocks.9,10 One or two additional alkali ions are needed to provide the net charge of the mono- and dications, respectively.
C60 powder is, in fact, known to react rapidly with liquid alkalis to form the body-centered cubic C60A6 phase.11 Evidence for C60A6 building blocks also appeared in abundance distributions of (C60)mNan+ (m ≤ 10) and (C60)mNan2+ (m ≤ 5),8 consistent with reports by Martin and co-workers for m ≤ 3 9,10 and photodissociation data reported by Pellarin et al. for m ≤ 2.12
Interestingly, the photodissociation experiments by Pellarin et al. revealed another pattern, namely, enhanced abundance of C60Na3+ and (C60)2Na5+.12 The authors noticed that these species marked the onset of cluster ion distributions in spectra reported by Martin and co-workers9 and proposed the existence of stable C60Na2 units in which the fullerenes are covalently bonded through a [2 + 2] cycloaddition. Similar onsets at C60A3+ and (C60)2A5+ with A = K or Rb were noticed in photodissociation experiments by Kappes and co-workers.13 For C60 trimers, however, Kappes and co-workers reported that (C60)3A8+ (A = K, Rb) formed the onset13 whereas Martin et al. identified (C60)3Na7+ as onset.9
A different experimental approach was pursued by Kern and co-workers who heated neutral C60-potassium clusters in helium gas.14,15 The preferred composition of clusters containing four or fewer C60 that survived at 900 K for about 1 ms was (C60K2)m.
In the present work we have doped helium nanodroplets with much smaller amounts of cesium than in our previous experiments, resulting in ions containing as many as 10 C60 and between 1 and about 12 Cs atoms. Furthermore, we investigate cations as well as anions. A surprising finding is a pronounced maximum in the abundance of (C60)mCs3± cations and anions for all values of m except for C60Csn– whose abundance declines very rapidly with increasing n. Another, weaker anomaly appears at (C60)mCs5±. The fact that these anomalies are independent of m and the charge state might suggest that they are due to particularly stable cesium cluster ions that are favored irrespective of the number of fullerenes. We observe, indeed, corresponding anomalies at n = 3 and 5 in abundance distributions of neat Csn+ and Csn–, consistent with theoretical predictions that these ions are particularly stable.16,17 However, in the literature we find no support for the proposed presence of stable alkali trimer and pentamer units in neutral or charged (C60)mAn. We also report the dependence of the abundance of (C60)mCs3– anions on the electron energy which shows an intriguing alternating pattern as m increases.
2. Experiment and Data Analysis
For the C60Cs experiment neutral helium nanodroplets were produced by expanding helium (Messer, purity 99.9999%) at a stagnation pressure of 20 bar through a 5 μm nozzle, cooled by a closed-cycle refrigerator to 9.3 K, into a vacuum chamber (base pressure about 2 × 10–6 Pa). For the measurements of neat cesium anions the cryostat temperature was lowered to 8.8 K. At these temperatures helium nanodroplets contain an average number of 4 × 105 and 1.2 × 106 helium atoms, respectively.18 The resulting supersonic beam was skimmed by a 0.8 mm conical skimmer and traversed a 20 cm long pickup region consisting of two differentially pumped pickup chambers. C60 (MER, purity 99.9%) was vaporized in a resistively heated oven in the first chamber; metallic cesium (Sigma-Aldrich, purity 99.95%) was vaporized in the second chamber. The temperatures of the ovens were varied in order to obtain the optimal experimental conditions for formation of complexes containing several C60 molecules and up to ∼10 cesium atoms.
The beam emerging from the dual pickup cell was collimated and crossed by an electron beam in a Nier-type ion source. For cations the energy was 89 eV; for anions the energy was varied between 0 and 35 eV in increments of 0.05 eV. However, distributions shown in this work use increments of 0.35 eV in order to reduce statistical scatter. The ions were accelerated into the extraction region of a reflectron time-of-flight mass spectrometer (Tofwerk AG, model HTOF) with a mass resolution Δm/m = 1/5000 (Δm = full-width at half-maximum). The base pressure in the mass spectrometer was 10–5 Pa. Ions were extracted at 90° into the field-free region of the spectrometer by a pulsed voltage. At the end of the field-free region they entered a two-stage reflectron which reflected them toward a microchannel plate detector operated in single ion counting mode. Additional experimental details have been provided elsewhere.19
Mass spectra were evaluated by means of a custom-designed software.20 The routine includes automatic fitting of a custom peak shape to the mass peaks and subtraction of background by fitting a spline to the background level of the raw data. It explicitly considers the presence of Hen+, a variety of impurity ions (e.g., OHC60+), and isotopic patterns. The abundance of ions with a specific composition (specific values of m and n) is derived by a matrix method.
3. Experimental Results
Abundanpce distributions of (C60)mCsn+ cations containing up to seven C60 are displayed in Figure 1. The staggered distributions have been individually normalized; their baselines and corresponding m values are indicated along the ordinate on the right. Error bars are plotted if they exceed the size of the symbols. For m = 1 we observe a steep drop in the abundance after n = 3; for larger m values n = 3 forms a local maximum. This maximum persists up to m = 10 (not shown), the largest value for which statistically significant data exist. A weaker local maximum is observed at n = 5, especially for m = 2, 3, and 4.
Figure 1.
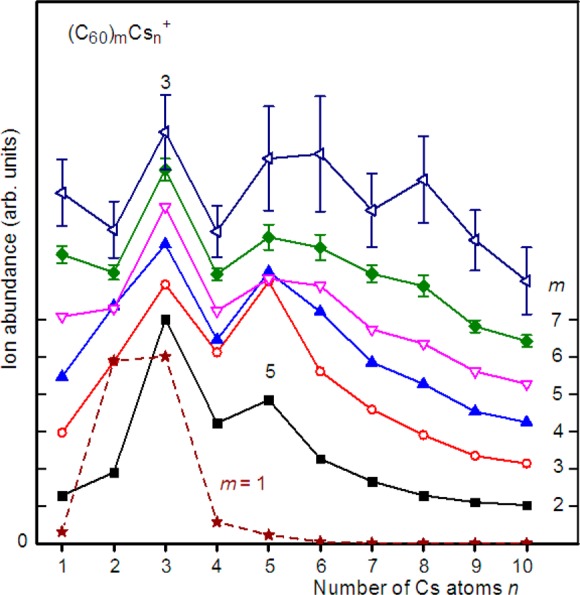
Abundance distributions of (C60)mCsn+, m ≤ 7. The distributions are individually normalized for each value of m and vertically offset (staggered); baselines are indicated on the ordinates. Error bars are not shown when they are smaller than the symbol size. Maxima or abrupt drops occur at n = 3 and 5 for all but the largest m values.
We did not notice these features in our previous report on heavily coated C60 cluster cations, but close inspection of Figure 1 in that report reveals a steep rise in the ion abundance of (C60)mCsn+ from n = 4 to 5 followed by a plateau, for m = 2, 3, and 4.8 The abundance of ions with n ≤ 4 was simply too small to discern any anomalies.
Figure 2 presents staggered abundance distributions of (C60)mCsn– anions formed by electron attachment at 13 eV, for m ≤ 7. They are surprisingly similar to those of cations, with (C60)mCs3– forming local maxima or, for m = 2 and 3, featuring abrupt drops. Secondary maxima appear at n = 5 for 2 ≤ m ≤ 6. The abundance of C60Csn– decreases very rapidly with n; the presence or absence of anomalies at n = 3 and 5 cannot be assessed.
Figure 2.
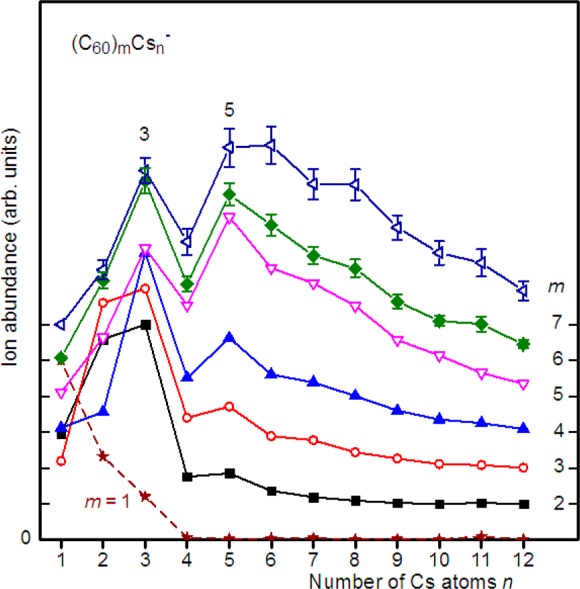
Staggered, normalized abundance distributions of (C60)mCsn– for m ≤ 7, recorded with an electron energy of 13 eV. Error bars are omitted if they are smaller than the symbol size. Maxima or abrupt drops occur at n = 3 and 5 for 2 ≤ m ≤ 6.
Distributions of neat cesium cluster ions Csn± are presented in Figure 3a. Data were extracted from mass spectra recorded without C60 doping. For Csn+, similar distributions were deduced from droplets co-doped with C60 but the yield of Csn– was very weak in the presence of C60. We cannot offer a compelling explanation for this difference. A logarithmic scale was chosen for the ordinate because the abundance of cations and anions decreases rapidly with n. Anions display strong maxima at n = 3 and 5. Cs3– is nearly 4 times more abundant than Cs2–; Cs5– is 5 times more abundant than Cs4–. The most pronounced anomaly in the distribution of cations occurs at Cs9+; less pronounced drops appear at Cs3+ and Cs5+. It is worth mentioning that abundance distributions of Csn+ extracted from a liquid-metal ion source show the same anomalies but the contrast is much larger, roughly 1:10 for the abundance ratio of Csn+1+ versus Csn+, for n = 3, 5, 9.21 The contrast ratio depends on instrumental factors such as the time window during which hot cluster ions are allowed to evaporate and whether or not ions produced by unimolecular dissociation after acceleration are detected or rejected.
Figure 3.
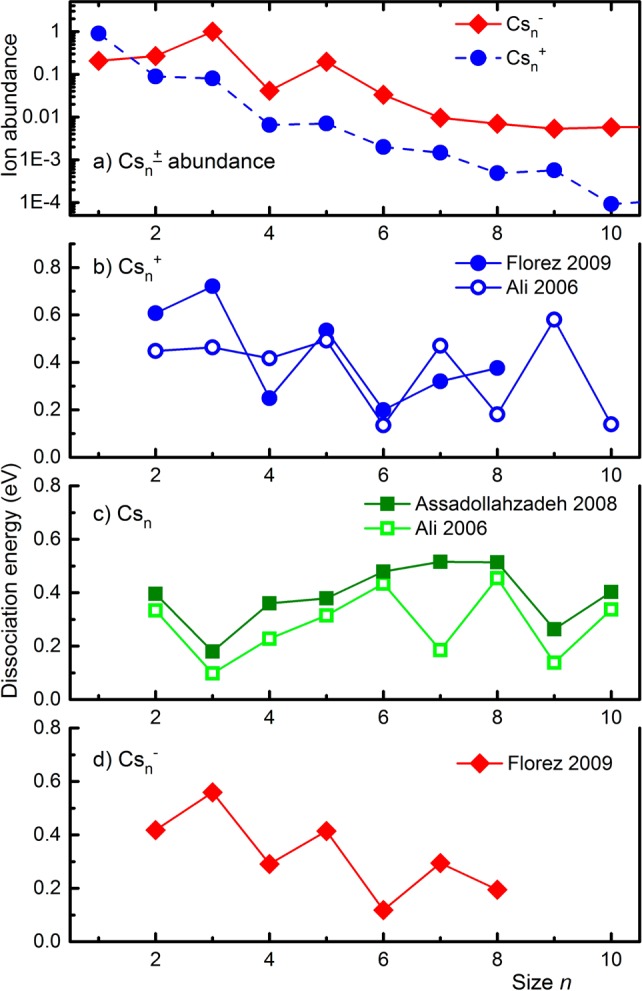
(a) Semilogarithmic abundance distributions of Csn– and Csn+. Error bars are smaller than the symbol size. Data were obtained from droplets doped with Cs but not C60. (b–d) Theoretical dissociation energies of cesium cluster cations, neutrals, and anions, deduced from published total binding energies.16,17,25
The dependence of the (C60)mCs3– ion abundance on the electron energy is displayed in Figure 4a for 1 ≤ m ≤ 7. We selected this ion series (with n = 3) because of its prominent appearance in Figure 2. The staggered distributions are normalized; baselines and values of m are indicated along the ordinate. Surprisingly, the patterns alternate with increasing m. Ions with odd values of m feature a broad maximum that gradually shifts from 10 eV for m = 1 to 15 eV for m = 5; ions with even m feature an even broader maximum around 23 eV. For m = 7 and larger (not shown), the distributions become rather similar, exhibiting a maximum between 15 and 20 eV.
Figure 4.
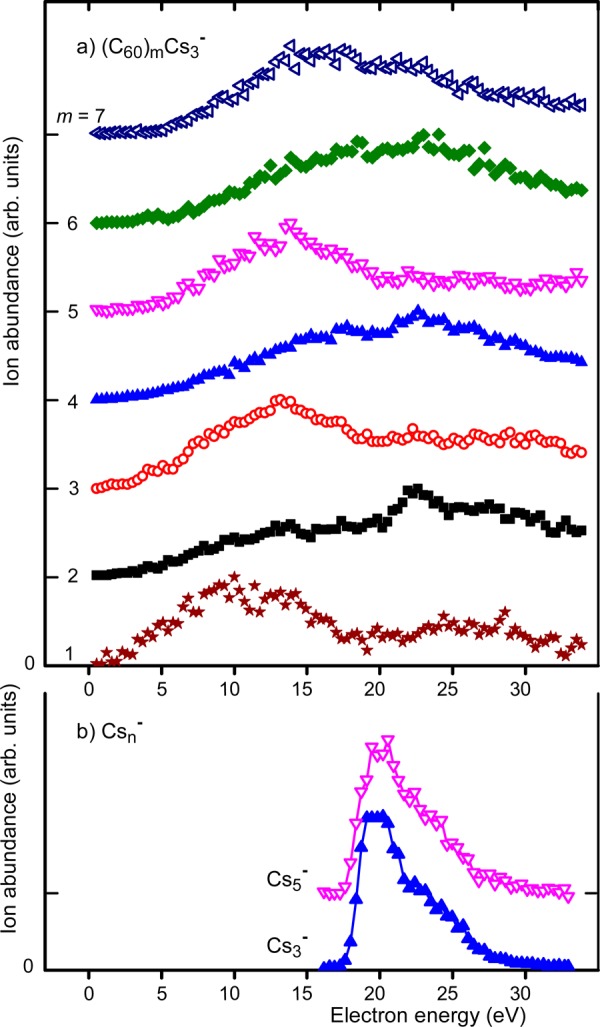
Dependence of the anion abundance on electron energy, for (C60)mCs3– with m ≤ 7 (a) and Cs3– and Cs5– (b). Data are normalized and staggered; individual baselines are indicated along the ordinate. Statistical uncertainties may be inferred from the scatter. Data in panel b were measured in the absence of C60-doping.
The energy dependences of Cs3– and Cs5– are shown (staggered and normalized) in Figure 4b. They feature an abrupt onset at 18.5 ± 0.5 eV. They are virtually identical but in marked contrast to those of (C60)mCs3–. Note that the Csn– data were recorded in experiments that did not involve co-doping with C60.
4. Discussion
In a recent report we had measured abundance distributions of (C60)mCsn+ cations containing up to six C60 and several dozen Cs.8 Local maxima in the ion abundance suggested that ions with n = 6m + 1 are particularly stable.22 The findings were consistent with earlier research by Martin and co-workers on potassium- and rubidium-doped fullerene aggregates; the authors suggested the presence of C60A6 building blocks in which the alkali metal atoms transfer their valence electrons to the 3-fold degenerate lowest unoccupied orbital (t1u) of the fullerene, forming essentially ionic bonds.9,10 Subsequent theoretical studies of sodium and potassium adsorbed on C60 have supported this interpretation.13,15,23,24 Further support for the model comes from a shift of the anomalies to n = 6m + 2 for (C60)mCsn2+ dications and to n = 6m + 3 for X(C60)mCsn+ where X = H2O or CO2.8
The results in the present study pertain to much weaker doping, i.e., smaller values of n; they cannot possibly reveal the existence of C60A6 building blocks. Instead, from observation of particularly abundant (C60)mCs3± and, to a lesser degree, (C60)mCs5± ions, either positively or negatively charged, one might conclude that Cs3± and Cs5± ions are particularly stable entities that form irrespective of the environment. Note that the prominence of Cs3± and Cs5± could also be augmented by particularly weak binding in Cs4± and Cs6±.
This interpreation is apparently supported by the enhanced ion abundances of bare Cs3± and Cs5± cluster ions; see Figure 3a, as well as theoretical studies of these species. Ali et al. have used density functional theory (DFT) to determine the structure and electronic properties (including ionization energies and electron affinities) of Csn+ and Csn, n ≤ 10. Dissociaton energies Dn, deduced from plots showing computed total energies in Ali’s work16 are plotted in Figure 3b and Figure 3c for cationic and neutral clusters, respectively.
Florez et al. also applied DFT to compute total energies of Csn+, Csn, and Csn–, n ≤ 8.17 Dissociation energies derived from their graphs are displayed in Figure 3b, Figure 3c, and Figure 3d, respectively. Also included in Figure 3c are dissociation energies computed for neutral Csn, n ≤ 20, by Assadollahzadeh et al.25 Several other theoretical studies of neutral Csn have focused on much larger clusters;26,27 those results are not included in Figure 3.
Dissocation energies derived from Florez’s work17 reveal that Cs3± and Cs5± enjoy enhanced stability. The enhanced stability of Cs3+ does not appear in Ali’s work16 which has been criticized by Florez et al. for using an extremely small basis set and neglecting relativistic effects.17 Within the spherical jellium approximation Cs3+ has enhanced stability because it features a closed s shell.28 The computed high stability of Cs3– is supported by photoelectron spectra which show that its vertical detachment energy is nearly twice that of Cs2–.29
We note in passing that the anomaly in the abundance and computed stability of Cs9+ (Figure 3a and Figure 3b) is expected within the spherical jellium model because this ion would have a closed 1s21p6 configuration.28 However, a corresponding anomaly for anions, at Cs7–, is not reflected in the ion abundance (Figure 3a) and only weakly in the computed stability (Figure 3d).
However, the hypothesis of intact Cs3 and Cs5 entities in C60 aggregates of either charge state finds little support from other investigations of neutral or charged C60-alkali complexes. One should emphasize though that previous work mostly pertains to the lighter alkalis (A = Li, Na, K) and that their properties are still debated.30
One topic of interest has been the nature of bonding which is dominantly ionic.31 Rayane et al. have computed the susceptibility and electric dipole moment of C60 complexed with one alkali atom.32 For Cs, Rb, and K the Mulliken charge on the alkali is very close to +1.00e but it decreases to about 0.90e for Na and 0.70e for Li. Qualitatively the same decreasing trend has been reported by other researchers for Li, Na, K.23,24,31,33
For C60 doped with multiple alkalis, however, charge transfer decreases with increasing n, thus decreasing the Coulombic repulsion between the ions.13,15,23,34,35 Furthermore, the above-mentioned trend reverses and charge transfer gradually increases from K to Li.36,37
Another topic of interest has been the energetically preferred adsorption site of a single alkali. Density functional theory studies find that Na and K alkali atoms preferentially adsorb at a hexagonal site33,38,39 (note that some studies mentioned here refer to charged complexes). For C60Li, however, the hexagonal and pentagonal sites are nearly isoenergetic.23,40,41 C60-lithium complexes have received the greatest attention because of their potential application as a lightweight medium for hydrogen storage,42,43 but their properties do not seem to be characteristic of C60 complexed with heavier alkalis; they will not be considered any further in this discussion.
The topic of greatest relevance to the present work is the structure and stability of C60 dressed with several alkali atoms. Theoretical studies reveal a delicate balance between Coulomb repulsion between atomic ions favoring uniform (homogeneous) coverage and metallic bonding favoring island formation, i.e., segregation.44 Conflicting results have been found for C60Nan. On the basis of mass spectra and photoelectron spectra of C60Nan–, n ≤ 12, Palpant et al. have concluded that sodium forms stable trimers on the fullerene surface.35,45 Their conclusion is supported by a DFT study of C60Nan– by Wang et al.,30 although these authors find another preferred motif, a tetrahedral Na4. For n = 4, 6, 7, 9 the ground state structure consists of a single three-dimensional sodium cluster, while for n = 5 and 8 two isolated clusters form on opposite sides of the fullerene.30
Researchers at the University of Lyon have measured the electric susceptibility of neutral C60Nan in a molecular beam deflection experiment.32,46,47 Strong deflection was attributed to complete segregation, i.e., formation of a single sodium droplet for all values of n. In later work though, supported by DFT studies, it was concluded that the first 8 sodium atoms spread uniformly over the C60 surface.38,48,49 In a subsequent DFT study Rabilloud concluded that up to 12 sodium atoms prefer to form distinct tetrahedral islands.33
The relevance of results pertaining to C60-sodium complexes for the interpretation of our C60-cesium data may be questioned, but work on heavier alkalis is scarce. In a DFT study of C60K12 Rabilloud finds the same preference for distinct tetrahedral clusters as for C60Na12.37
The appearance of electronic shell structure in abundance distributions of C60+ heavily coated with cesium10,50 has stimulated a few theoretical studies of this core–shell system,51,52 but they are of little relevance to the present discussion.
Our group has recently investigated adsorption of hydrogen on neutral and cationic C60Cs.53 DFT calculations including empirical dispersion correction and harmonic vibrational zero-point corrections resulted in dissociation energies of 0.793 eV for C60Cs+. In another DFT study we have concluded that the lowest energy configuration of neutral C60Cs2 consists of two Cs atoms located on opposite sites of C60.54
The various studies summarized above provide no support for the hypothesis of stable Cs3± and Cs5± entities; we therefore seek an alternative explanation. As mentioned in the Introduction, Pellarin et al. reported evidence for particularly stable C60Na3+ and (C60)2Na5+ based on mass spectrometric expereriments in which C60-sodium complexes were deliberately heated by the ionizing laser.12 The authors pointed out that related features appeared in mass spectra reported by Martin’s group in form of abrupt onsets at C60Na3+, (C60)2Na5+, and (C60)3Na7+.9,10 Those experiments also involved deliberately heating and fragmenting the cations.
Pellarin et al. conjectured that (C60)2Na5+ and (C60)3Na7+ might dissociate by losing a C60Na2 unit. Although this reaction could not be experimentally observed, the hypothesis of stable C60A2 units has been beautifully confirmed by Kern and co-workers for A = potassium.14,15 The researchers thermalized neutral C60-potassium clusters for about 1 ms in hot helium gas; the clusters were then softly ionized by one-photon ionization. At temperatures of 900 K they observed abundance distributions that sharply peaked at (C60K2)m for m ≤ 4. Their DFT calculations of C60Kn and (C60)2Kn at finite temperatures revealed that (C60)2K4 is, indeed, thermodynamically most stable among all (C60)2Kn species for n ≤ 6. The authors emphasized that (C60K2)m owe their superior stability to their high entropy rather than to closure of any electronic or geometric shells.14
The computed ground state structure of C60K2 features two alkali atoms at opposite hexagonal sites, whereas that of (C60)2K4 consists of a C60 dimer with the four alkali atoms wrapped around its waiste. This configuration is also favored when atoms or molecules are physisorbed on (C60)2,55 but Coulomb repulsion between adsorbed alkali cations tends to destabilize it. In fact, the most stable geometries computed for (C60)2K5 and (C60)2K6 have two K atoms at opposite sites of the (C60)2 dumbbell axis.15
The computational results for C60K2 and (C60K2)2 provide little guidance as to the structures of (C60K2)3 and (C60K2)4 and the reason for their superior thermodynamic stability. Where are the cesium atoms located in clusters containing more than two C60? Do the three cesium atoms in the magic (C60)mCs3+ (m ≥ 2) prefer sites that are separated as far as possible, as computed for C60K2,15 or do they cluster in groove sites as computed for (C60K2)2?
And why do not we observe an anomaly at the presumably magic (C60)3Cs7+? Perhaps, one may argue that the low cesium concentration in our experiments renders the observation of this ion impossible and the prominence of (C60)mCs3± and (C60)mCs5± is owed to the well-known odd–even effect in the stability of alkali clusters.15,28,56 A look at Figure 1 makes this explanation unconvincing; the falloff in the ion abundance beyond the magic (C60)3Cs5+ is gradual and smooth.
We can think of two factors that might cause the differences between our data and previous reports: (i) differences between cesium and its lighter and smaller cousins and (ii) differences in the way by which aggregates are synthesized and ionized. In previous studies, aggregates were formed in gas-phase collisions between C60 and alkali atoms (sometimes brought into the gas phase by laser ablation) and subsequently ionized by photons.9,10,12−15,34,35,45 In the present study as well as our earlier work8 aggregates were synthesized in helium droplets and ionized by electrons. In many cases mass spectra resulting from these different approaches are very similar.57,58 Cesium, however, is exceptional because it is extremely heliophobic. Superfluid helium does not wet bulk cesium;59 even large neutral cesium clusters will not be solvated by helium nanodroplets but rather remain on the surface.60
The situation changes, though, in the presence of other solutes that are highly polarizable. Recently we could show that neutral C60 or C60 aggregates embedded in a droplet will pull neutral cesium clusters into the droplet by a harpooning mechanism, the only exception being atomic cesium. Although not discussed in that work, it seems likely that atomic cesium will be pulled into the droplet once a C60An aggregate has formed because the electric polarizability of C60An is an order of magnitude larger than that of C60.47,48 If a Cs dimer but not a Cs atom would be pulled into a droplet containing a C60Csn aggregate, an interesting odd–even effect would appear where C60-doped helium droplets containing n Cs atoms would consist of solvated (C60)mCsn if n is even but solvated (C60)mCsn–1 plus a Cs atom on the surface if n is odd.
Perhaps the most intriguing and hardest to explain feature in our data is the peculiar pattern in the energy dependence of (C60)mCs3– anions which alternates with increasing m; see Figure 4. The spectrum of C60Cs3– with its main maximum around 10 eV is not unlike those of C60– and (C60)2– obtained from C60-doped helium nanodroplets which feature a broad maximum around 5–10 eV plus a weaker one at about 25 eV.61 The spectra of (C60)2Cs3– and (C60)4Cs3–, however, are missing the 10 eV resonance. If the (C60)m aggregates were van der Waals bound, this odd–even effect would be difficult to explain. But are they? Pellarin et al. have proposed that the fullerenes are covalently bonded through a [2 + 2] cycloaddition.12 They did not explain how that reaction would be initiated but dimerization of fullerenes in (C60)m may provide a clue toward the observed odd–even effect.
5. Conclusion
Electron ionization of helium droplets doped with C60 and cesium results in mass spectra that consistenly feature maxima in the abundance of positively and negatively charged (C60)mCs3± and (C60)mCs5± for a range of m values. This also holds true for m = 0, i.e., for bare cesium ions. The most straightforward explanation, the presence of highly stable Cs3± and Cs5± clusters, is not supported by previous work involving complexes of C60 with lighter alkalis. The features are reminiscent of features in cationic spectra of C60 complexed with lighter alkalis (A) which point to particularly stable C60A2 building blocks,9,10,12−15 but we do not observe a corresponding enhancement of the abundance for (C60)3Cs7± or (C60)4Cs9±. Also, it is not clear why anions should show the same “magic numbers” as cations. Perhaps the most puzzling finding is a pattern in the energy dependence of (C60)mCs3– that alternates with increasing m. Odd–even effects are well-known for monovalent metal clusters but not for presumably van der Waals bound C60 aggregates. Further experiments are needed, preferably involving lighter alkalis that are more amenable to high-level theoretical investigations.
Acknowledgments
This work was supported by the Austrian Science Fund, Wien (FWF Projects I978, M1908, and P26635).
The authors declare no competing financial interest.
References
- Haddon R. C.; Hebard A. F.; Rosseinsky M. J.; Murphy D. W.; Duclos S. J.; Lyons K. B.; Miller B.; Rosamilia J. M.; Fleming R. M.; Kortan A. R.; et al. Conducting Films of C60 and C70 by Alkali-Metal Doping. Nature 1991, 350, 320–322. 10.1038/350320a0. [DOI] [Google Scholar]
- Hebard A. F.; Rosseinsky M. J.; Haddon R. C.; Murphy D. W.; Glarum S. H.; Palstra T. T. M.; Ramirez A. P.; Kortan A. R. Superconductivity at 18 K in Potassium-Doped C60. Nature 1991, 350, 600–601. 10.1038/350600a0. [DOI] [Google Scholar]
- Fleming R. M.; Ramirez A. P.; Rosseinsky M. J.; Murphy D. W.; Haddon R. C.; Zahurak S. M.; Makhija A. V. Relation of Structure and Superconducting Transition Temperatures in A3C60. Nature 1991, 352, 787–788. 10.1038/352787a0. [DOI] [Google Scholar]
- Margadonna S.; Prassides K. Recent Advances in Fullerene Superconductivity. J. Solid State Chem. 2002, 168, 639–652. 10.1006/jssc.2002.9762. [DOI] [Google Scholar]
- Palstra T. T. M.; Zhou O.; Iwasa Y.; Sulewski P. E.; Fleming R. M.; Zegarski B. R. Superconductivity at 40 K in Cesium Doped C60. Solid State Commun. 1995, 93, 327–330. 10.1016/0038-1098(94)00787-X. [DOI] [Google Scholar]
- Ganin A. Y.; Takabayashi Y.; Khimyak Y. Z.; Margadonna S.; Tamai A.; Rosseinsky M. J.; Prassides K. Bulk Superconductivity at 38 K in a Molecular System. Nat. Mater. 2008, 7, 367–371. 10.1038/nmat2179. [DOI] [PubMed] [Google Scholar]
- Ganin A. Y.; Takabayashi Y.; Jeglic P.; Arcon D.; Potocnik A.; Baker P. J.; Ohishi Y.; McDonald M. T.; Tzirakis M. D.; McLennan A.; et al. Polymorphism Control of Superconductivity and Magnetism in Cs3C60 Close to the Mott Transition. Nature 2010, 466, 221–U93. 10.1038/nature09120. [DOI] [PubMed] [Google Scholar]
- Harnisch M.; Daxner M.; Scheier P.; Echt O. Adsorption of Sodium and Cesium on Aggregates of C60. Eur. Phys. J. D 2016, 70, 192. 10.1140/epjd/e2016-70438-4. [DOI] [Google Scholar]
- Martin T. P.; Malinowski N.; Zimmermann U.; Näher U.; Schaber H. Metal-Coated Fullerene Molecules and Clusters. J. Chem. Phys. 1993, 99, 4210–4212. 10.1063/1.466118. [DOI] [Google Scholar]
- Zimmermann U.; Malinowski N.; Burkhardt A.; Martin T. P. Metal-Coated Fullerenes. Carbon 1995, 33, 995–1006. 10.1016/0008-6223(95)00028-C. [DOI] [Google Scholar]
- Chen H. S.; Kortan A. R.; Haddon R. C.; Kopylov N. Formation Energy of Alkali Metal-Doped Fullerite Compounds A6C60. J. Phys. Chem. 1993, 97, 3088–3090. 10.1021/j100115a004. [DOI] [Google Scholar]
- Pellarin M.; Cottancin E.; Lerme J.; Vialle J. L.; Broyer M.; Tournus F.; Masenelli B.; Melinon P. Photodissociation and Photoionization of Sodium Coated C60 Clusters. Eur. Phys. J. D 2003, 25, 31–40. 10.1140/epjd/e2003-00216-4. [DOI] [Google Scholar]
- Weis P.; Beck R. D.; Bräuchle G.; Kappes M. M. Properties of Size and Composition Selected Gas Phase Alkali Fulleride Clusters. J. Chem. Phys. 1994, 100, 5684–5695. 10.1063/1.467134. [DOI] [Google Scholar]
- Enders A.; Malinowski N.; Ievlev D.; Zurek E.; Autschbach J.; Kern K. Magic Alkali-Fullerene Compound Clusters of Extreme Thermal Stability. J. Chem. Phys. 2006, 125, 191102. 10.1063/1.2400027. [DOI] [PubMed] [Google Scholar]
- Zurek E.; Autschbach J.; Malinowski N.; Enders A.; Kern K. Experimental and Theoretical Investigations of the Thermodynamic Stability of Ba-C60 and K-C60 Compound Clusters. ACS Nano 2008, 2, 1000–1014. 10.1021/nn800022d. [DOI] [PubMed] [Google Scholar]
- Ali M.; Maity D. K.; Das D.; Mukherjee T. Geometrical and Electronic Properties of Neutral and Charged Cesium Clusters Csn (n = 2–10): A Theoretical Study. J. Chem. Phys. 2006, 124, 024325. 10.1063/1.2158988. [DOI] [PubMed] [Google Scholar]
- Florez E.; Fuentealba P. A Theoretical Study of Alkali Metal Atomic Clusters: From Lin to Csn (n = 2–8). Int. J. Quantum Chem. 2009, 109, 1080–1093. 10.1002/qua.21906. [DOI] [Google Scholar]
- Gomez L. F.; Loginov E.; Sliter R.; Vilesov A. F. Sizes of Large He Droplets. J. Chem. Phys. 2011, 135, 154201. 10.1063/1.3650235. [DOI] [PubMed] [Google Scholar]
- Schöbel H.; Bartl P.; Leidlmair C.; Daxner M.; Zöttl S.; Denifl S.; Märk T. D.; Scheier P.; Spångberg D.; Mauracher A.; et al. Sequential Penning Ionization: Harvesting Energy with Ions. Phys. Rev. Lett. 2010, 105, 243402. 10.1103/PhysRevLett.105.243402. [DOI] [PubMed] [Google Scholar]
- Ralser S.; Postler J.; Harnisch M.; Ellis A. M.; Scheier P. Extracting Cluster Distributions from Mass Spectra: Isotopefit. Int. J. Mass Spectrom. 2015, 379, 194–199. 10.1016/j.ijms.2015.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhaskar N. D.; Klimcak C. M.; Cook R. A. Electronic-Shell-Structure Effects in Csn+. Phys. Rev. B: Condens. Matter Mater. Phys. 1990, 42, 9147–9150. 10.1103/PhysRevB.42.9147. [DOI] [PubMed] [Google Scholar]
- Vibrationally excited ions that feature energetically facile dissociation channels (low dissociation energies Dn) are less likely to survive on the time scale of mass spectrometric analysis than strongly bound ions. Thus the maxima and abrupt drops in the abundance distributions reveal ions that are exceptionally stable with respect to monomer loss, relative to the next larger cluster. The method by which neutral precursors are formed may have some effect on the overall distribution of the ions but not on local anomalies.
- Hamamoto N.; Jitsukawa J.; Satoko C. Electronic and Geometric Properties of Alkali-C60 Molecules. Eur. Phys. J. D 2002, 19, 211–221. 10.1140/epjd/e20020072. [DOI] [Google Scholar]
- Chandrakumar K. R. S.; Ghosh S. K. Alkali-Metal-Induced Enhancement of Hydrogen Adsorption in C60 Fullerene: An Ab Initio Study. Nano Lett. 2008, 8, 13–19. 10.1021/nl071456i. [DOI] [PubMed] [Google Scholar]
- Assadollahzadeh B.; Thierfelder C.; Schwerdtfeger P. From Clusters to the Solid State: Global Minimum Structures for Cesium Clusters Csn (n = 2–20, ∞) and Their Electronic Properties. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 78, 245423. 10.1103/PhysRevB.78.245423. [DOI] [Google Scholar]
- Mananes A.; Alonso J. A.; Lammers U.; Borstel G. Inhomogeneous Contraction of Interatomic Distances in Metallic Clusters - Calculations for Csn and OCsn. Phys. Rev. B: Condens. Matter Mater. Phys. 1991, 44, 7273–7282. 10.1103/PhysRevB.44.7273. [DOI] [PubMed] [Google Scholar]
- Aguado A. Discovery of Magnetic Superatoms and Assessment of Van Der Waals Dispersion Effects in Csn Clusters. J. Phys. Chem. C 2012, 116, 6841–6851. 10.1021/jp2119179. [DOI] [Google Scholar]
- De Heer W. A. The Physics of Simple Metal Clusters: Experimental Aspects and Simple Models. Rev. Mod. Phys. 1993, 65, 611–676. 10.1103/RevModPhys.65.611. [DOI] [Google Scholar]
- McHugh K. M.; Eaton J. G.; Lee G. H.; Sarkas H. W.; Kidder L. H.; Snodgrass J. T.; Manaa M. R.; Bowen K. H. Photoelectron Spectra of the Alkali Metal Cluster Anions: Nan=2-5-, Kn=2-7-, Rbn=2-3-, and Csn=2-3-. J. Chem. Phys. 1989, 91, 3792–3793. 10.1063/1.456861. [DOI] [Google Scholar]
- Wang H. B.; Li S. J.; Xiu S. L.; Gong L.; Chen G.; Mizuseki H.; Kawazoe Y. Insight into the Vertical Detachment Energy Oscillation of NanC60- Clusters. J. Chem. Phys. 2012, 136, 174314. 10.1063/1.4712219. [DOI] [PubMed] [Google Scholar]
- Robledo M.; Aguirre N. F.; Diaz-Tendero S.; Martin F.; Alcami M. Bonding in Exohedral Metal-Fullerene Cationic Complexes. RSC Adv. 2014, 4, 53010–53020. 10.1039/C4RA10776D. [DOI] [Google Scholar]
- Rayane D.; Allouche A. R.; Antoine R.; Compagnon I.; Broyer M.; Dugourd P. Susceptibility and Electric Dipole in Metal C60 Compounds. Eur. Phys. J. D 2003, 24, 9–13. 10.1140/epjd/e2003-00134-5. [DOI] [Google Scholar]
- Rabilloud F. Structure and Electronic Properties of Alkali-C60 Nanoclusters. J. Phys. Chem. A 2010, 114, 7241–7247. 10.1021/jp103124w. [DOI] [PubMed] [Google Scholar]
- Wang L. S.; Cheshnovsky O.; Smalley R. E.; Carpenter J. P.; Hwu S. J. Electronic Structure of KxC60- in the Gas Phase. J. Chem. Phys. 1992, 96, 4028–4031. 10.1063/1.461853. [DOI] [Google Scholar]
- Palpant B.; Negishi Y.; Sanekata M.; Miyajima K.; Nagao S.; Judai K.; Rayner D. M.; Simard B.; Hackett P. A.; Nakajima A.; et al. Electronic and Geometric Properties of Exohedral Sodium- and Gold-Fullerenes. J. Chem. Phys. 2001, 114, 8459–8466. 10.1063/1.1366641. [DOI] [Google Scholar]
- Östling D.; Rosen A. Electronic Structure and Optical Properties of Bare and Li, Na, K and Ca Coated C60 Molecules. Chem. Phys. Lett. 1997, 281, 352–359. 10.1016/S0009-2614(97)01252-9. [DOI] [Google Scholar]
- Rabilloud F. Electronic and Geometric Properties of Exohedral Potassium-Fullerenes. Comput. Theor. Chem. 2011, 964, 213–217. 10.1016/j.comptc.2010.12.023. [DOI] [Google Scholar]
- Roques J.; Calvo F.; Spiegelman F.; Mijoule C. Wetting-to-Nonwetting Transition in Metal-Coated C60. Phys. Rev. Lett. 2003, 90, 075505. 10.1103/PhysRevLett.90.075505. [DOI] [PubMed] [Google Scholar]
- Robledo M.; Martin F.; Alcami M.; Diaz-Tendero S. Exohedral Interaction in Cationic Lithium Metallofullerenes. Theor. Chem. Acc. 2013, 132, 1346. 10.1007/s00214-013-1346-8. [DOI] [Google Scholar]
- Sun Q.; Wang Q.; Jena P. Functionalized Heterofullerenes for Hydrogen Storage. Appl. Phys. Lett. 2009, 94, 013111. 10.1063/1.3058678. [DOI] [Google Scholar]
- Wang Q.; Jena P. Density Functional Theory Study of the Interaction of Hydrogen with Li6C60. J. Phys. Chem. Lett. 2012, 3, 1084–1088. 10.1021/jz3002037. [DOI] [PubMed] [Google Scholar]
- Venkataramanan N. S.; Mizuseki H.; Kawazoe Y. Hydrogen Storage on Nanofullerene Cages. Nano 2009, 4, 253–263. 10.1142/S1793292009001733. [DOI] [Google Scholar]
- Teprovich J. A.; Wellons M. S.; Lascola R.; Hwang S. J.; Ward P. A.; Compton R. N.; Zidan R. Synthesis and Characterization of a Lithium-Doped Fullerane (LixC60Hy) for Reversible Hydrogen Storage. Nano Lett. 2012, 12, 582–589. 10.1021/nl203045v. [DOI] [PubMed] [Google Scholar]
- Karamanis P.; Pouchan C. Fullerene-C60 in Contact with Alkali Metal Clusters: Prototype Nano-Objects of Enhanced First Hyperpolarizabilities. J. Phys. Chem. C 2012, 116, 11808–11819. 10.1021/jp3026573. [DOI] [Google Scholar]
- Palpant B.; Otake A.; Hayakawa F.; Negishi Y.; Lee G. H.; Nakajima A.; Kaya K. Photoelectron Spectroscopy of Sodium-Coated C60 and C70 Cluster Anions. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 60, 4509–4512. 10.1103/PhysRevB.60.4509. [DOI] [Google Scholar]
- Antoine R.; Rayane D.; Benichou E.; Dugourd P.; Broyer M. Electric Dipole Moment and Charge Transfer in Alkali-C60 Molecules. Eur. Phys. J. D 2000, 12, 147–151. 10.1007/s100530070051. [DOI] [Google Scholar]
- Dugourd P.; Antoine R.; Rayane D.; Compagnon I.; Broyer M. Enhanced Electric Polarizability in Metal C60 Compounds: Formation of a Sodium Droplet on C60. J. Chem. Phys. 2001, 114, 1970–1973. 10.1063/1.1344885. [DOI] [Google Scholar]
- Roques J.; Calvo F.; Spiegelman F.; Mijoule C. Nucleation of a Sodium Droplet on C60. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 68, 205412. 10.1103/PhysRevB.68.205412. [DOI] [Google Scholar]
- Rabilloud F.; Antoine R.; Broyer M.; Compagnon I.; Dugourd P.; Rayane D.; Calvo F.; Spiegelman F. Electric Dipoles and Susceptibilities of Alkali Clusters/Fullerene Complexes: Experiments and Simulations. J. Phys. Chem. C 2007, 111, 17795–17803. 10.1021/jp071126m. [DOI] [Google Scholar]
- Springborg M.; Satpathy S.; Malinowski N.; Zimmermann U.; Martin T. P. Electronic Shell Structure and Relative Abundances of Cesium-Coated C60. Phys. Rev. Lett. 1996, 77, 1127–1130. 10.1103/PhysRevLett.77.1127. [DOI] [PubMed] [Google Scholar]
- Springborg M. Electronic Properties, Stability, and Length Scales of Csn Clusters. J. Phys.: Condens. Matter 1999, 11, 1–18. 10.1088/0953-8984/11/1/002. [DOI] [Google Scholar]
- Mierzynski P.; Pomorski K. Shell Structure of Cesium Layer Covering the C60 Fullerene Core. Eur. Phys. J. D 2002, 21, 311–314. 10.1140/epjd/e2002-00210-4. [DOI] [Google Scholar]
- Kaiser A.; Renzler M.; Kranabetter L.; Schwärzler M.; Parajuli R.; Echt O.; Scheier P.. On Enhanced Hydrogen Adsorption on Alkali (Cesium) Doped C60 and Effects of the Quantum Nature of the H2 Molecule on Physisorption Energies. Int. J. Hydrogen Energy, in press. [Google Scholar]
- Renzler M.; Daxner M.; Kranabetter L.; Kaiser A.; Hauser A. W.; Ernst W. E.; Lindinger A.; Zillich R.; Scheier P.; Ellis A. M. Communication: Dopant-Induced Solvation of Alkalis in Liquid Helium Nanodroplets. J. Chem. Phys. 2016, 145, 181101. 10.1063/1.4967405. [DOI] [PubMed] [Google Scholar]
- Echt O.; Kaiser A.; Zöttl S.; Mauracher A.; Denifl S.; Scheier P. Adsorption of Polar and Non-Polar Molecules on Isolated Cationic C60, C70, and Their Aggregates. ChemPlusChem 2013, 78, 910–920. 10.1002/cplu.201300198. [DOI] [PubMed] [Google Scholar]
- Brack M. The Physics of Simple Metal-Clusters - Self-Consistent Jellium Model and Semiclassical Approaches. Rev. Mod. Phys. 1993, 65, 677–732. 10.1103/RevModPhys.65.677. [DOI] [Google Scholar]
- Ferreira da Silva F.; Bartl P.; Denifl S.; Echt O.; Märk T. D.; Scheier P. Argon Clusters Embedded in Helium Nanodroplets. Phys. Chem. Chem. Phys. 2009, 11, 9791–9797. 10.1039/b913175b. [DOI] [PubMed] [Google Scholar]
- Schöbel H.; Bartl P.; Leidlmair C.; Denifl S.; Echt O.; Märk T. D.; Scheier P. High-Resolution Mass Spectrometric Study of Pure Helium Droplets, and Droplets Doped with Krypton. Eur. Phys. J. D 2011, 63, 209–214. 10.1140/epjd/e2011-10619-1. [DOI] [Google Scholar]
- Ross D.; Rutledge J. E.; Taborek P. Superfluid Droplets on a Solid Surface. Science 1997, 278, 664–666. 10.1126/science.278.5338.664. [DOI] [Google Scholar]
- Theisen M.; Lackner F.; Ernst W. E. Cs Atoms on Helium Nanodroplets and the Immersion of Cs+ into the Nanodroplet. J. Chem. Phys. 2011, 135, 074306. 10.1063/1.3624840. [DOI] [PubMed] [Google Scholar]
- Jaksch S.; Mähr I.; Denifl S.; Bacher A.; Echt O.; Märk T. D.; Scheier P. Electron Attachment to Doped Helium Droplets: C60, (C60)2, and C60D2O Anions. Eur. Phys. J. D 2009, 52, 91–94. 10.1140/epjd/e2008-00252-6. [DOI] [Google Scholar]


