Simulation study of Hemodynamic in Bifurcations for Cerebral Arteriovenous Malformation using Electrical Analogy

Abstract

Background and Objective:

Cerebral Arteriovenous Malformation (CAVM) hemodynamic is disease condition, results changes in the flow and pressure level in cerebral blood vessels. Measuring flow and pressure without catheter intervention along the vessel is big challenge due to vessel bifurcations/complex bifurcations in Arteriovenous Malformation patients. The vessel geometry in CAVM patients are complex, composed of varying diameters, lengths, and bifurcations of various angles. The variations in the vessel diameter and bifurcation angle complicate the measurement and analysis of blood flow features invasively or non-invasively.

Methods:

In this paper, we proposed a lumped model for the bifurcation for symmetrical and asymmetrical networks in CAVM patients. The models are created using MATLAB Simulation software for various bifurcation angles. Each bifurcation angle created using electrical network- RLC. The segmentation and pre-processing of bifurcation vessels are implemented using adaptive segmentation. The proposed network address clinicians problem by measuring hemodynamic non-invasively. The method is applicable for any types of bifurcation networks with different bifurcation angles in CAVM patients.

Results:

In this work, we constructed a mathematical model, measured hemodynamic for 23 patients (actual and simulated cases) with 60 vessel bifurcation angles variations. The results indicate that comparisons evidenced highly significant correlations between values computed by the lumped model and simulated mechanical model for both networks with p < 0.0001. A P value of less than 0.05 considered statistically significant.

Conclusion:

In this paper, we have modelled different bifurcation types and automatically display pressure and flow non-invasively at different node and at different angles of bifurcation in the complex vessel with help of bifurcation parameters, using lumped parameter model. We have simulated for different bifurcation angles and diameters of vessel for various imaging modality and model extend for different organs. This will help clinicians to measure haemodynamic parameters noninvasively at various bifurcations, where even catheter cannot be reached.

Introduction

In a normal brain, the blood flow is from arteries to veins through a capillary bed. In the case of Cerebral Arteriovenous Malformation (CAVM) condition, the normal blood flow is affected and there arteries are directly connected to veins without a capillary bed, forming a tangle of abnormal blood vessels. The central part of the malformation consisting of tangled abnormal vessels is called ‘Nidus’ [1]. There is very low pressure in the AVM; hence, a large amount of blood drawn into this. This causes lot of pressure built up in the blood vessels, especially in the veins. The risk of rupturing of the veins draining the malformation is high because veins cannot handle as much blood pressure as that of arteries. The need for modelling is to help Doctors to take preventive steps and for early diagnosis for the risk of rupture and treatment planning for the AVM patients.

Figure 1 shows the AVM complex structure, which is very difficult and challenging to model bifurcations [2]. The researchers analysed vessels bifurcation for various organs based on the mechanical property of the blood flows, but some clinical parameters for modelling are not considered [3]. Hoogstraten studied the bifurcation angle and bifurcation analysis based on the radius and length of the vessel, but not considered angle variations [4]. The author Goubergrits investigated vessel geometry modelling for the carotid artery, to analyse various geometric parameters using mechanical modelling [5]. In another study, the author Malve, analysed modelling of asymmetrical network, based on the Womersley numbers [6]. The literature shows symmetrical network modelling is available for the coronary artery, to model LAD and LCX based on the lumped parameter model [7]. The researchers studied various lumped network model for the analysis, concentrating on the calculation of the bifurcation angle [8]. Ghasemalizadeh et.al, [9] analysed on the anatomical model for the blood flow in heart, the limitation is that the major assumptions included in the blood flow model concern the pressure radius relationship, the radial velocity profile, and pressure loss at vessel bifurcations. Gijsen et al. [10] have produced a preliminary model, which indicates that blood vessel movement may have a significant effect on coronary blood flow. The author Smith [11] has analysed on the anatomical model for the blood flow in heart, the limitation is that the major assumptions included in the blood flow model concern the pressure radius relationship, the radial velocity profile, and pressure loss at vessel bifurcations. Milan et al. [12] have produced a preliminary model, which indicates that blood vessel movement may have a significant effect on coronary blood flow. The effect of vessel movement limited by mechanical parameters in the mechanical model by determining the flow profile using, vessel movement relative to blood flow velocity.

Figure1.

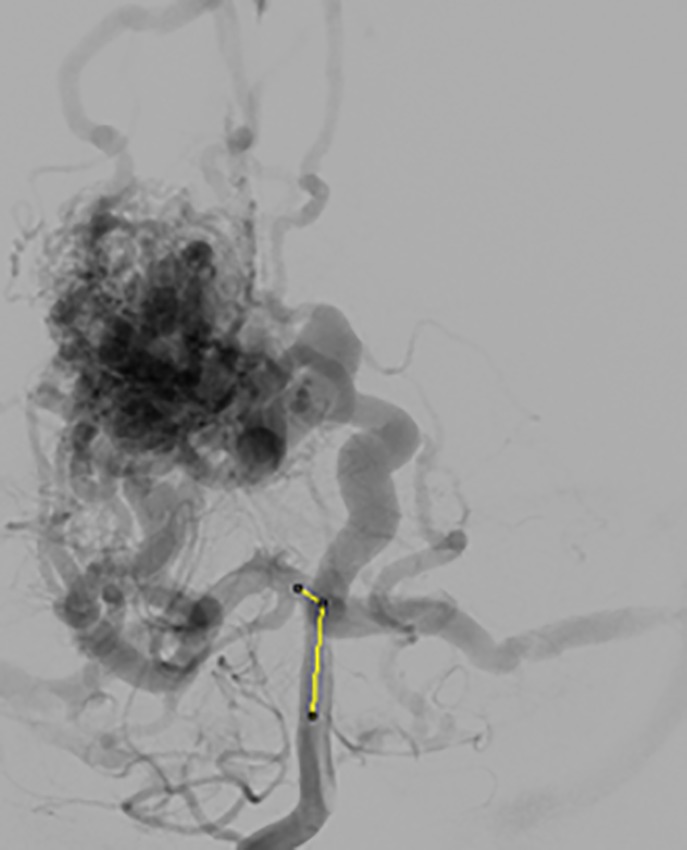
AVM Complex Structure

The author Murray [13], has showed that, ratio of the bifurcating vessel diameter (d1/d2) ratio changes (increases/decreases) when the bifurcation angle varies. In literature, there exist relationship between the bifurcation angle and ratio of the diameters, i.e. bifurcation angle is inversely proportional to the change in the branch diameter ratio. However, there is no direct relationship between angle and lumped model networks as per the literature. The proposed model addresses the above limitations with creation of direct relationship with bifurcation angle, diameter and pressure measurement using electrical network. In this paper, we proposed the modelling for the segment of the bifurcation by navigating through the complex vessels. The bifurcation is combination of asymmetric and symmetric bifurcation based on the clinical parameters of the blood vessels and model output based on the segmented vessels.

Material and Methods

The methodology used to implement the bifurcation model for the blood vessel are as follows:

Pre-processing

The input image used is 2D/3D image of various imaging modality like Digital subtraction Angiography (DSA) and 3D-Rotational Angiogram [14]. The image is pre-processed using fast fourier transform (FFT) and image enhancement and smoothing filters applied to the image is performed, that helps to find the accurate distance and length of the vessels. [15-16].

Segmentation

The pre-processed image segmented using OTSU segmentation for drawn ROI (region of interest) [17-19]. We have segmented bifurcation vessels near NIDUS for various frames based on adaptive segmentation [20]. The segmented bifurcation vessel diameters, length and bifurcation angles are calculated.

Electrical Model

The electrical model is based on the model was based on the principle of electrical networks -Kirchhoff’s voltage law (KVL) as shown in Table 1. Lumped models are equivalent to simple electrical networks, where blood pressure represented by voltage and blood flow by amperage of the electrical current through the network. The formation of lumped model using R-L-C elements is constructed using Windkessel model [21-22]. The three-element Windkessel model used to represent the pressure-blood flow relationship of regional circulation helps to capture the dynamics of the cerebral circulation.

Table 1.

Electrical Analogy

Electrical Analogy	Mechanical Analogy
Current	Flow
Potential	Pressure
Capacitance	Young Modulus
Resistance	Poiseuille Coefficient
Charge	Area

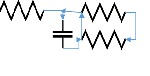
The lumped parameter model derived from electrical circuit analogies where current (I) represents blood flow (cm³/s) and voltage (v) represents pressure (mmHg). Resistances (R, ohms) represent vascular resistances; capacitor (C, microfarads) represents volume compliance of the vessels that allows them to store significant amounts of blood. Windkessel models have advantages over other parametric models that they provide a simple model structure in terms of individual elements (R, C) of its electrically analogous circuit, facilitating the extraction and interpretation of physiological changes from the dynamic variation of each element. The diameter and length variation determines design of network formation such as R-R, R-L, R-C, RLC combinations. This helps to simulate the exact vessel and bifurcation modelling construction [23]. The electrical network updated according the diameter and length of the vessel bifurcations [24] as shown in Table 2. The electrical network created based on the vessel diameter and length, the equations 1 and 2 are formed by applying KVL for RLC and RC is as follows:

Table 2.

Electrical Network components variations

Symmetric Network Formation
Bifurcation angle	d1/d2 ratio	D0 (cm)	d1 (cm)	d2 (cm)	Network for d0	Network for d1	Network for d2	Combination of Networks
Original Input
75	1	2	1	1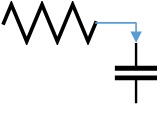
Simulated Input’
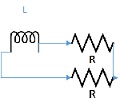
45	3	2	3	3
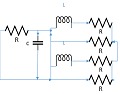105	0.5	2	2	2
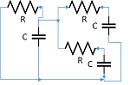Asymmetric Network Formation
Bifurcation angle	d1/d2 ratio	D0 (cm)	d1 (cm)	d2 (cm)	Network for d0	Network for d1	Network for d2	Combination of Networks
Original Input
75	1	2	1	1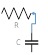
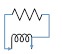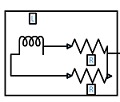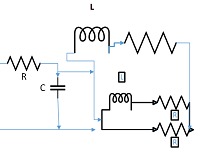Simulated Input
45	3	2	3	1
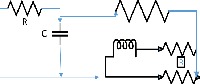105	2	2	1	0.5
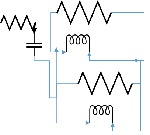10	2.5	2	5	2
Bifurcation angle	d1/d2 ratio	D0 (cm)	d1 (cm)	d2 (cm)	Network for d0	Network for d1	Network for d2	Combination of Networks
150	9	2	9	1
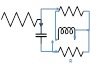180	0.11	2	1	9
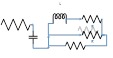90	0.33	2	2	6
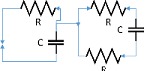135	2.5	2	10	4

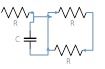$\mathrm{vi}\left(t\right)=\mathrm{RI}\left(t\right)+L\frac{\mathrm{di}}{\mathrm{dt}}+\frac{1}{c}\int \mathrm{dt}$ (1)

$\mathrm{vi}\left(t\right)=\mathrm{RC}\frac{\mathrm{dv}}{\mathrm{dt}}+\mathrm{LC}\frac{dv2}{dt2}+V0\left(t\right)$ (2)

The equations are solved using ode-4 Runge-Kutta method [25-26].

Results

The lumped model implemented using MATLAB -SIMULINK. The input pressure at feeding arteries simulated using electrical parameters and the results are validated using Mechanical outputs [27]. The clinical parameters are converted to voltage and current, simulated with RLC networks, the part of the vessel analysis implementation by electrical network is shown in Figure 2. We have simulated for the symmetrical and asymmetrical Bifurcation angles variation in the Vessels and our analysis shows that electrical network varied for different bifurcation angles that help to determine the pressure and flow parameters of AVM hemodynamic non-invasively. The simulated angles are as per the bifurcation angles of the various locations of cerebral vasculature bending angles. The simulation performed for various signal combinations like square, pulse and simulated pressure waveforms [28-29].

Figure2.

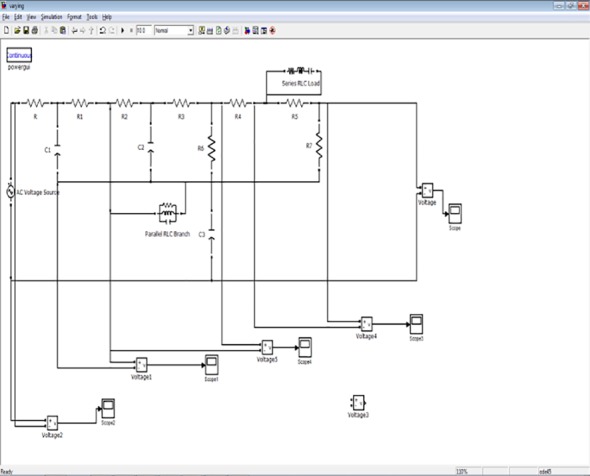
Implementation of Bifurcation Angle

Asymmetric Network

The bifurcation analysis for the asymmetric network based on the nodes unequal diameter ratio and angle variations. The bifurcation model changed based on the diameters length and ratio as well as on the angles between the parent and child branch. The ratio differences have a huge impact, which affects the electrical network of the bifurcation model. Figure 3 shows the asymmetrical network of cerebral AVM vessel structure. It shows vessels P1 as the parent vessels, which bifurcate to vessels into various child branches - P2, P3, and P4. The P4 branch in turn bifurcates to sub-branch as P5 vessel. For each vessel the diameter and length is calculated and angle between the parent and child branch is calculated. The electrical network simulated for each vessel using vessel diameter, length and angles between the parent and child vessel. The complete network created for the given vessel by parallel combination of T and PI network of vessels networks- ((P1 + || (P2 ||P3 || (P4 || P5)). The measured diameter for Vessel P1 is 0.93cm and corresponding network elements are RL with values R-6.17, L-2.5, Vessel P2 is of diameter 1.19cm, and its corresponding network is RL with values, R-1.8, L-1.89. The measurements of Vessel P3 & P4 are 0.87cm &0.36 cm, with its corresponding network RL values, R-6.3; L-2.94; R-96.59 L-8.571 respectively. Table 3 denotes the results of node pressure measurements for various signal combinations.

Figure3.

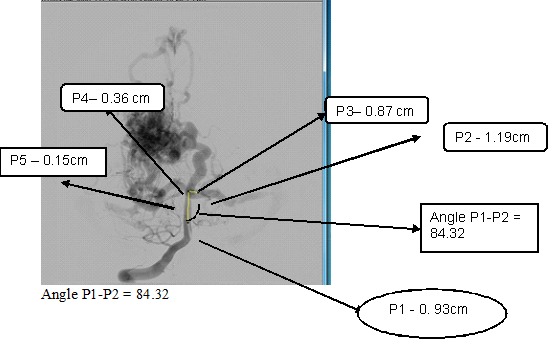
Asymmetrical network of cerebral AVM vessel structure

Table 3.

Results of node pressure measurements for Asymmetrical networks using various signal combinations

Input voltage	P1- Node	P2- Node	P3- Node	P4- Node	P5- Node
0.6	0.55	0.5	0.53	0.49	0.42
	Mechanical -0.52	Mechanical -0.48	Mechanical -0.5	Mechanical -0.467	Mechanical -0.389
	Accuracy -5 %	Accuracy -4 %	Accuracy -5.6 %	Accuracy -4.6 %	Accuracy -7.3 %
1.5	1.34	1.3	1.32	1.27	1.21
	Mechanical -1.3	Mechanical -1.23	Mechanical -1.278	Mechanical -1.223	Mechanical -1.1
	Accuracy -3 %	Accuracy -5.3 %	Accuracy - 3.1 %	Accuracy - 3.7 %	Accuracy - 9 %
2.0	1.8	1.7	1.72	1.68	1.6
	Mechanical -1.7	Mechanical -1.58	Mechanical -1.62	Mechanical -1.6	Mechanical -1.49
	Accuracy - 5.5 %	Accuracy - 7 %	Accuracy - 5.8 %	Accuracy - 5 %	Accuracy - 6.8 %
0.4	0.3	0.25	0.27	0.23	0.19
	Mechanical -0.21	Mechanical -0.2	Mechanical -0.257	Mechanical -0.217	Mechanical -0.172
	Accuracy - 3 %	Accuracy -2 %	Accuracy - 1.02%	Accuracy - 5.6%	Accuracy - 9.4%
2.2	2.1	1.92	1.98	1.94	1.77 (small branch)
	mechanical(2.02)	mechanical(1.89)	(mechanical - 1.958)	(mechanical - 1.898)	(mechanical -1.54)
	accuracy -3.8%	accuracy -1.5%	Accuracy-1.11 %	Accuracy-2.1 %	Accuracy -9.4 %
1.2	1.08	1.04	1.07	1.01	0.97
	mechanical(1.02)	mechanical(1)	mechanical(1.03)	mechanical(0.98)	mechanical(0.90)
	accuracy -5.5%	accuracy -3.8%	accuracy -3.7%	accuracy -3.1%	accuracy -7.2%
1.1	0.99	0.95	0.98	0.94	0.895
	mechanical(0.96)	mechanical(0.92)	mechanical(0.94)	mechanical(0.90)	mechanical(0.836)
	accuracy -3.0%	accuracy -3.15%	accuracy -4.0%	accuracy -4.2%	accuracy -6.5%
0.8	0.76	0.72	0.73	0.71	0.63
	mechanical(0.746)	mechanical(0.702)	mechanical(0.71)	mechanical(0.689)	mechanical(0.601)
	accuracy -3.9%	accuracy -2.5%	accuracy -2.8%	accuracy -2.9%	accuracy -6.8%
1.0	0.95	0.93	0.91	0.88	0.815
	mechanical(0.935)	mechanical(0.911)	mechanical(0.892)	mechanical(0.852)	mechanical(0.756)
	accuracy -1.5%	accuracy -1.0%	accuracy -2.0%	accuracy -3.1%	accuracy -7.2%
1.4	1.25	1.2	1.23	1.20	1.13
	mechanical(1.23)	mechanical(1.189)	mechanical(1.204)	mechanical (1.75%)	mechanical(0.66)
	accuracy -1.6%	accuracy -1%	accuracy -2.11%	accuracy -2.11%	accuracy -4.2%
0.7	0.65	0.6	0.62	0.58	0.53
	mechanical(0.63)	mechanical(0.581)	mechanical(0.596)	mechanical(0.556)	mechanical(0.496)
	accuracy -3.07%	accuracy -3.16%	accuracy -3.8%	accuracy -4.1%	accuracy -6.4%

Symmetric Networks

The symmetrical networks are networks that have branch angles are equal and of same diameter. The symmetric bifurcation model created based on the diameters length and ratio as well as on the angles between the parent and child branch. Figure 4 shows the symmetrical network of cerebral AVM vessel structure. The results of node pressure measurements for various input signal combinations for symmetrical networks shown in Table 4. For simulation purpose, we change the bifurcation angle of 75 to 45 degrees (decrement of angle), results in the increase in the diameter ratio, results change in electrical network, and leads to change pressure variations for each part of the bifurcation angle change.

Figure4.

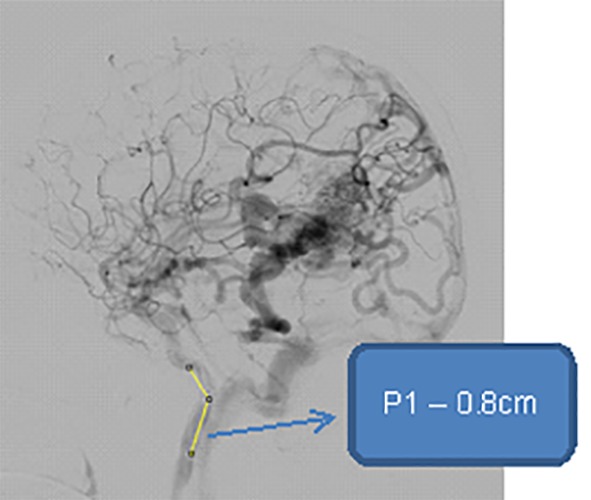
Symmetrical Network showing Parent vessel - P1, vessel diameter - 0.8cm

Table 4.

Results of node pressure measurements for Symmetrical networks using various signal combinations

Input voltage	P1 - Node output	P2 - Node output	P3 - Node output
0.6	0.55	0.51	0.51
	Mechanical -0.52	Mechanical -0.49	Mechanical -0.49
	Accuracy -5 %	Accuracy -4.08 %	Accuracy -4.08 %
1.5	1.34	1.3	1.3
	Mechanical -1.3	Mechanical -1.24	Mechanical -1.24
	Accuracy -3 %	Accuracy -4.6 %	Accuracy -4.6 %
2.0	1.8	1.74	1.74
	Mechanical -1.7	Mechanical -1.68	Mechanical -1.68
	Accuracy - 5.5 %	Accuracy - 3.4 %	Accuracy - 3.4 %
0.4	0.3	0.25	0.25
	Mechanical -0.21	Mechanical -0.21	Mechanical -0.21
	Accuracy - 3 %	Accuracy -1.9 %	Accuracy -1.9%
2.2	2.1	1.92	1.92
	mechanical(2.02)	mechanical(1.9)	mechanical(1.9)
	accuracy -3.8%	accuracy -1.04%	accuracy -1.04%
1.2	1.1	1.07	1.07
	mechanical(1.02)	mechanical(1.01)	mechanical(1.01)
	accuracy -5.5%	accuracy -5.6%	accuracy -5.6%
1.1	0.99	0.95	0.95
	mechanical(0.96)	mechanical(0.9)	mechanical(0.9)
	accuracy -3.0%	accuracy -5.12%	accuracy -5.12%
0.8	0.76	0.70	0.70
	mechanical(0.746)	mechanical(0.66)	mechanical(0.66)
	accuracy -3.9%	accuracy -5.7%	accuracy -5.7%
1.0	0.95	0.73	0.73
	mechanical(0.935)	mechanical(0.701)	mechanical(0.701)
	accuracy -1.5%	accuracy -3.9%	accuracy -3.9%
1.4	1.25	1.2	1.2
	mechanical(1.23)	mechanical(1.149)	mechanical(1.149)
	accuracy -1.6%	accuracy -3.5%	accuracy -3.5%
0.7	0.65	0.6	0.6
	mechanical(0.63)	mechanical(0.571)	mechanical(0.571)
	accuracy -3.07%	accuracy -5%	accuracy -5%

Statistics

The electrical model validated with clinical outputs supported by the Clinicians, the pressure values at bifurcations nodes validated with model outputs as voltages. We have also validated our results with mechanical simulation using ANSYS FLUENT v12 software for various simulated inputs. Data expressed as mean +/- standard error of the mean (SEM). Correlations between values derived from the new method and the classical methods were evaluated using least squares and systematic bias was calculated as the mean of the difference between values derived from each method. The accuracy of the identification of parameters evaluated using the difference of 1-R2. (R2 is the square of the multiple correlation coefficient of the regression). Changes in hemodynamic were evaluated by a repeated-measures analysis of variance. A P value of less than 0.05 considered statistically significant. Accuracy in percentage across various node outputs for various signal combinations for asymmetric networks and symmetric networks are examined.

Discussion

The development and integration of a CAVM complex vessel is a challenging task. The vessels have lot of complex geometry structures with different types of bifurcations inside in asymmetric/symmetrical networks. The proposed model helps to simulate the physiologic and hemodynamic variations of the CAVM patients. 23 CAVM patients are analysed using our simulated model with 60 bifurcations of symmetrical and asymmetrical networks. The pressure and flow parameters are measured for four bifurcation nodes for each cases, totally 60 measurements are validated with clinical /mechanical simulation. The results are validated with clinical invasive measurements and through the mechanical simulation. The accuracy of the results is shown in Table 4. All statistical analyses were performed using SPSS for Windows (SPSS Inc., Chicago), version 17 [30]. We have also simulated the bifurcation analysis for symmetrical and asymmetrical network using the various signal combinations as input source to replicate the actual clinical scenarios of pressure variations in CAVM patients by simulated pressure waveforms and by mixing of the signals.

In the asymmetrical network analysis, the accuracy analysis shows that observation is that for the small vessel diameter less than 1cm, the node pressure measurements has the deviation is in the range of 5-10%, and for the vessel diameter more than 1.5 cm, the analysis is that deviation is the range below 5%. Similarly, for the symmetrical networks, the same behaviour is observed. We have simulated for various bifurcation branches of one to five child nodes from parent nodes. Our results shows bifurcation branch pressure measurements of 60 branching vessels with node outputs for 30 input signal combinations. The hemodynamic measurements are calculated non-invasively at each bifurcation of the vessels, which is the unique advantage of bifurcation modelling, where even catheter cannot navigate to find pressure at various small branches or bifurcations.

Conclusion

In this paper, we have proposed Bifurcation modelling of the AVM based on the mathematical model to define bifurcation analysis in a vessel structure of symmetrical and asymmetrical bifurcation networks and further assess its role. We have provided a rigorous approach for electric circuits whose physical constants (R, L and C), are parameterized on the standard length of the vessel using normal in order to recover correct values for pressure or flow-rate at Bifurcations for AVM patients. The Bifurcation angles simulated for various types of networks and pressure measurements are calculated non-invasively for symmetrical and asymmetrical networks. With the help of the clinical data, we are able to validate our results with invasive measurement and with the simulated Mechanical results as cross-validation analysis. 23 AVM patients were studied with evaluation of 60 bifurcation vessels locations as node point of symmetrical and asymmetrical networks, the node measurements were evaluated with accuracy of 93%, and computed p-value is smaller than the significance level 0.05. Our study acts as a natural link between simulation and clinical scenario. Such an integrative approach should possibly lead to a comprehensive understanding of the regulatory and management of cerebral neurovascular abnormality analysis. Our accuracy analysis shows that observation is that for the small vessel diameter less than 1cm, the node pressure measurements has the deviation is in the range of 5-10%, and for the vessel diameter more than 1,5 cm, the analysis is that deviation is the range below 5%. From a medical viewpoint, it provides us new insight into the role of haemodynamic analysis on the neurovascular vessel analysis. This work can be extended to develop more complex geometric bifurcations vessels analysis of the various parts of CAVM. In summary, a novel approach to determining access flow and pressure measurements by non-invasively at various bifurcation nodes and the feasibility of determining access volume flow independent of access geometry is examined.