The first multiplication atom-bond connectivity index of molecular structures in drugs

Abstract

In the field of medicine, there are a large number of new drugs synthesis every year. Before entering the clinical stage, it needs a lot of work on drug testing of the various properties. Due to the lack of a large number of laboratory technician, laboratory equipment and reagents, the drug testing of many biochemical properties are not completed. Theoretical medicine provides a theoretical way for medical researchers to obtain the pharmaceutical properties of compounds by calculation tricks. In this paper, the first multiplication atom-bond connectivity index of several common drugs structure are studied, and the accurate expressions are determined. These theoretical conclusions provide practical guiding significance for pharmaceutical engineering.

1. Introduction

The increasing emergence of disease and the more and more mature medicine technology stimulate the development of newly invented drugs every year. As a result, it proposed the need to determine the pharmacological, chemical and biological features of these new drugs in experiments (Halim and Phang, 2017). On the other hand, it also threw us the tough work and make the relevant research much more headache. To be detailed, qualified and adequate reagents equipment and assisted researchers are necessary in the measurement for the performances and the side effects of the existing drugs (Mustafa et al., 2017). However, the equipment for the measurement of the biochemical properties is a tough problem in poor areas like some parts in South America, Africa and Southeast Asia. What should be glad is that the connection between chemical and pharmacodynamics characteristics of drugs and their molecular structures is found by researchers before (Feng et al., 2016, Xie et al., 2016, Tao et al., 2016). Concerning the definition of the topological indices, the indicators of these drug molecular structures are calculated. As a result, it’s turned out to be efficient to make clear the medicinal properties and it can guarantee the well going of medicine and chemical experiments. In other word, the methods on topological index computation can help to get the available biological and medical information of new drugs without the support of chemical experiment hardware (Liu et al., 2016, Iftakhar et al., 2015, Sarfraz et al., 2016). Consequently, it is proved to be suitable to be used in poor parts of the world.

In the below, let G = $(V(G)\text{,}E(G))$ be a molecular graph with vertex set $V(G)$ and edge set $E(G)$, then we can look upon a topological index as a map f: G $\to {\mathbb{R}}^{+}$. Several degree-based or distance-based indices like Randic index, Wiener index, harmonic index, PI index, sum connectivity index and others are borrowed here. Moreover, there are some mention-able contributions on distance-based and degree-based indices of special molecular structures and they can be referred to Harishchandra and Ramane (2016), Gao et al., 2016a, Gao et al., 2016b, Gao et al., 2016c, Gao et al., 2016d, Gao et al. (2017a), Gao and Siddiqui (2017), Gao and Wang, 2015, Gao and Wang, 2016 and Gao et al. (2017b).

The atom-bond connectivity index (shortly, ABC index) is defined by Estrada et al. (1998) as

$${\mathit{ABC}}_1(G)={\displaystyle \sum _{\mathit{uv}\in E(G)}}\sqrt{\frac{d(u)+d(v)-2}{d(u)d(v)}}\text{.}$$

Very recently, Kulli (2016) defined the first multiplicative atom-bond connectivity index which stated as

$${\mathit{ABC}}_1\text{II}(G)={\displaystyle \prod _{\mathit{uv}\in E(G)}}\sqrt{\frac{d(u)+d(v)-2}{d(u)d(v)}}\text{.}$$

Many papers contributed to different kinds of atom-bond connectivity indices. Farahani, 2013a, Farahani, 2013b determined the fourth atom-bond connectivity index of circumcoronene series of benzenoid. Goubko et al. (2015) presented an example to show the contradiction on the main result of previous work. Ahmadi and Sadeghimehr (2010) computed the atom bond connectivity index of some graphs and an infinite class of nanostar dendrimers. Husin et al. (2013) obtained the atom bond connectivity index of two families of nanostar dendrimers. Dehghan-Zadeh and Ashrafi (2014) studied the atom-bond connectivity index of quasi-tree graphs. Dehghan-Zadeh et al. (2014) determined the upper bound of atom-bond connectivity index in the class of tetracyclic graphs. Farahani, 2013a, Farahani, 2013b yielded the fourth atom-bond connectivity index of V-phenylenic nanotubes and nanotori. Dimitrov (2013) researched the efficient computation trick of trees with smallest atom-bond connectivity index. Ashrafi et al. (2015) raised the upper bound of atom-bond connectivity index of cactus graphs with fixed vertex number. Das et al. (2012) established the Upper bounds and Nordhaus-Gaddum type results for atom bond connectivity index.

The past forty years have witnessed the prosperity of the research on computation of degree-based and distance-based indices for certain special drug molecular structure. Despite the disagreements and conflicts on index computation of molecular graphs, the relevant research has made great progresses, but still leaving space for us to keep forward. Moreover, as widespread and critical drug structures, the applications of alkene, cycloalkenes, dendrimers, benzenoid systems and phenylenes are frequently found in chemical, medical, biological and pharmaceutical engineering. Therefore, a further discussion is needed to calculate the drug structures (Chen et al., 2016, Nawaz et al., 2017, Rashid et al., 2017).

The main contribution in this work is threefold: (1) the first multiplicative atom-bond connectivity index of alkene and cycloalkenes is obtained; (2) the expressions of the first multiplicative atom-bond connectivity index of special dendrimers are raised; (3) the formula of the first multiplicative atom-bond connectivity index of benzenoid systems and phenylenes is also obtained and analyzed.

2. Main results and proofs

In the below, the minimum and maximum degree of G are denoted by $\delta (G)$ and $\mathrm{\Delta }(G)$. Edge set E(G) and vertex set V (G) are categorized into the following items:

• •for any i with $\delta (G)⩽i⩽\mathrm{\Delta }(G)\text{,}\text{let}{D}_i=\{u\in V(G)|d(v)=i\}\text{and}{d}_i=|D_i|$
• •for any i, j satisfy $\delta (G)\mathit{lesi}\text{,}j⩽\mathrm{\Delta }(G)\text{,}\text{let}{E}_{i\text{,}j}=\{e=\mathit{uv}\in E(G)|d(u)=i\text{,}\text{and}d(v)=j\}\text{and}{n}_{\mathit{ij}}=|E_{i\text{,}j}|$.

2.1. The first multiplicative atom-bond connectivity index of alkene and cycloalkenes

In this part, we discuss the structure on alkene and cycloalkenes which are widely used in medicine and pharmaceutical engineering. Some applications on alkene and cycloalkenes can refer to Dziechciejewski et al., 2015, Babaee et al., 2012, Sysoiev et al., 2012, Tsarev et al., 2010, and Wilson et al. (2007).

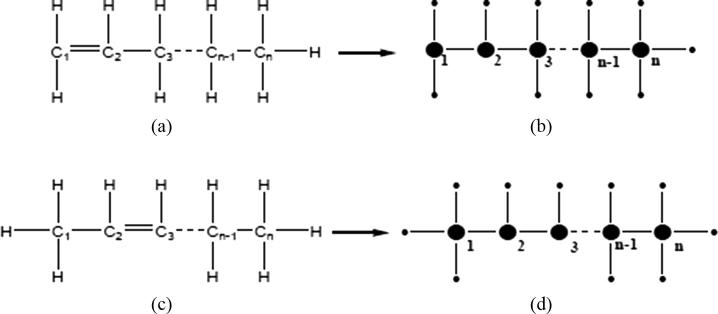
As an unsaturated hydrocarbon with at least one carbon-carbon double bond, an alkene is composed of two hydrogen atoms less than the relevant alkane which has the same number of carbon atoms, with general formula $C_n{H}_{2n}$. The smallest alkene is ethylene ($C_2{H}_4$). Only a dobell bond between any two atoms of carbon is used to build the multiplicative ABC index for alkene, and in the index the numbers of covalent bonds are 4 for carbon and 1 for hydrogen (see Fig. 1).

Theorem 1

Let $n⩾3$ be an integer. The first multiplicative atom-bond connectivity index of molecular structure in Fig. 1 associated with alkenes C_nH_2n is

$${\mathit{ABC}}_1\text{II}(G)=\left\{\begin{array}{c}\frac{2}{3}\sqrt{\frac{5}{12}}{\left(\sqrt{\frac{2}{3}}\right)}^3{\left(\frac{\sqrt{6}}{4}\right)}^{n-3}{\left(\frac{\sqrt{3}}{2}\right)}^{2n-3}\text{,}\text{if}n⩾3\text{and}G=b\hfill \\ \frac{2}{3}{\left(\sqrt{\frac{5}{12}}\right)}^2{\left(\sqrt{\frac{2}{3}}\right)}^2{\left(\frac{\sqrt{6}}{4}\right)}^{n-4}{\left(\frac{\sqrt{3}}{2}\right)}^{2n-2}\text{,}\text{if}n⩾4\text{and}G=d\hfill \end{array}\right)\text{.}$$

Proof of Theorem 1

We present its proof by using mathematical induction and considering the following two cases.

• •The molecular structure is described as Fig.1(b).

If $n=3$, then the molecular structure is associated with alkene $C_3{H}_6$ and its first multiplicative atom-bond connectivity index is

$${\mathit{ABC}}_1\mathit{II}(G)=\sqrt{\frac{3+3-2}{3·3}}\sqrt{\frac{3+4-2}{3·4}}{\left(\sqrt{\frac{3+1-2}{1·3}}\right)}^3{\left(\sqrt{\frac{4+1-2}{1·4}}\right)}^3\text{.}$$

Thus, the result is true when $n=3$. We assume that the results is correct for $n=k$, i.e., the first multiplicative atom-bond connectivity index of the molecular structure G associated with alkene $C_k{H}_{2k}$ is

$${\mathit{ABC}}_1\text{II}(G)=\frac{2}{3}\sqrt{\frac{5}{12}}{\left(\sqrt{\frac{2}{3}}\right)}^3{\left(\frac{\sqrt{6}}{4}\right)}^{k-3}{\left(\frac{\sqrt{3}}{2}\right)}^{2k-3}\text{.}$$

Let $C_i$ be the carbon vertex at the i-th position and e be the edge incident vertex k of this molecular structure with vertex corresponding to the end hydrogen vertex. Furterhmore, let $G_1$ be the molecular structure obtained from G by deleting the edge e, and $G_2$ be the molecular structure yielded by connecting the k-th vertex in $G_1$ with the center vertex of $K_{1\text{,}3}$. Hence, $G_2$ is the molecular structure G associated with alkene $C_{k+1}{H}_{2k+2}$, and

$${\mathit{ABC}}_1\mathit{II}(G_2)=\frac{{\mathit{ABC}}_1\mathit{II}(G)}{\sqrt{\frac{4+1-2}{4}}}{\left(\sqrt{\frac{4+1-2}{4}}\right)}^3\sqrt{\frac{4+4-2}{16}}=\frac{2}{3}\sqrt{\frac{5}{12}}{\left(\sqrt{\frac{2}{3}}\right)}^3{\left(\frac{\sqrt{6}}{4}\right)}^{k-3}{\left(\frac{\sqrt{3}}{2}\right)}^{2k-3}\times {\left(\sqrt{\frac{4+1-2}{4}}\right)}^2\sqrt{\frac{4+4-2}{16}}=\frac{2}{3}\sqrt{\frac{5}{12}}{\left(\sqrt{\frac{2}{3}}\right)}^3{\left(\frac{\sqrt{6}}{4}\right)}^{k-2}{\left(\frac{\sqrt{3}}{2}\right)}^{2k-1}\text{.}$$

Thus, the result is correct when $n=k+1$.

• •The molecular structure is described in Fig.1(d).

We can deduce the desired conclusion in terms of the tricks presented in the above case.

All the alkenes that own 4 or more carbon atoms display structural isomerism. Even though there are lots in common among structural isomers, they share different structural formulas. Therefore, one molecular formula could be drawn from the different structural formulas. To illustrate, the following two different molecules can share the same formula $C_4{H}_8$. These can be named 1-butene and 2-methylpropene respectively (see Fig. 2). □

Fig. 1.

(a) and (c) denote the molecular structure of alkenes $C_n{H}_{2n}$; (b) and (d) denote the molecular graph associated with chemical compound of alkenes $C_n{H}_{2n}$.

Fig. 2.

Molecular structure of butene and methylpropene.

Structural isomers share the common molecular formula but different structural expression, so that the multiplicative atom bond connectivity index of isomers of alkenes shares the same general formula in Theorem 1 (Safi et al., 2015, Razali and Said, 2017). As a result, the same numbers of carbon and hydrogen atoms are also the same in isomers of alkenes and the same degree of vertices are in the same number of edges.

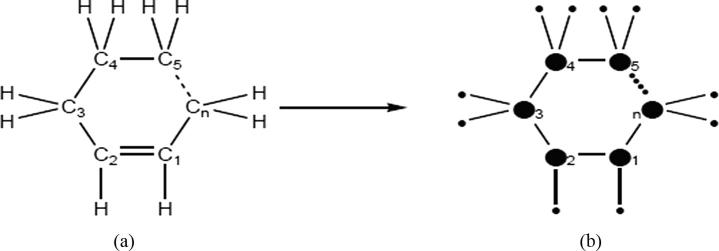
Cycloalkenes (also called a cycloolefin) is a type of alkene hydrocarbon with a closed ring of carbon atoms. The Greek prefix cyclo- represents round here. If the ends of a carbon chain are connected one with one, the molecule becomes cyclic or round, and then there is no difference between alkenes and other carbon chains (see Fig. 3).

Theorem 2

Let $n⩾3$ be an integer. The first multiplicative atom-bond connectivity index of molecular structure in Fig.3(b) associated with alkenes $C_n^H$ is

$${\mathit{ABC}}_1\text{II}(G)=\frac{2}{3}{\left(\sqrt{\frac{5}{12}}\right)}^2{\left(\sqrt{\frac{2}{3}}\right)}^2{\left(\frac{\sqrt{3}}{2}\right)}^{2n-4}{\left(\frac{\sqrt{6}}{4}\right)}^{n-3}\text{.}$$

Proof of Theorem 2

We present its proof by using mathematical induction. Let $G_n$ be the molelcular strcture associated with $C_n^H$.

If $n=3$, then the molecular structure is associated with alkene $C_3^H$ and its first multiplicative atom-bond connectivity index is

$${\mathit{ABC}}_1\text{II}(G_3)=\frac{2}{3}{\left(\sqrt{\frac{5}{12}}\right)}^2{\left(\sqrt{\frac{2}{3}}\right)}^2{\left(\frac{\sqrt{3}}{2}\right)}^2\text{.}$$

Thus, the result is true when $n=3$. We assume that the results are correct for $n=k$, i.e., the first multiplicative atom-bond connectivity index of the molecular structure $G_k$ associated with alkene $C_k^H$ is

$${\mathit{ABC}}_1\mathit{II}(G_k)=\frac{2}{3}{\left(\sqrt{\frac{5}{12}}\right)}^2{\left(\sqrt{\frac{2}{3}}\right)}^2{\left(\frac{\sqrt{3}}{2}\right)}^{2k-4}{\left(\frac{\sqrt{6}}{4}\right)}^{k-3}\text{.}$$

Let e be the edge connecting the 1-th vertex with k-th vertex, G′ be the molecular structure obtained from $G_k$ by deleting the edge e, and G″ be the molecular structure yielded by connecting G′ and $K_{1\text{,}4}$ (with $x_1$ has degree 4, $x_2\sim x_5$ has degree 1) using the following way:

$x_1$ = k+1-th vertex in G′; $x_2$ = 1-th vertex in G′; $x_3$ = k-th vertex in G′.

Hence, G″ is the molecular structure $G_{k+1}$ associated with alkene $C_{k+1}^H$, and

$${\mathit{ABC}}_1\text{II}(G_{k+1})=\frac{{\mathit{ABC}}_1\mathit{II}(G_k)}{\sqrt{\frac{4+3-2}{12}}}\sqrt{\frac{4+3-2}{12}}\sqrt{\frac{4+4-2}{16}}{\left(\sqrt{\frac{1+4-2}{4}}\right)}^2=\frac{2}{3}{\left(\sqrt{\frac{5}{12}}\right)}^2{\left(\sqrt{\frac{2}{3}}\right)}^2{\left(\frac{\sqrt{3}}{2}\right)}^{2k-4}{\left(\frac{\sqrt{6}}{4}\right)}^{k-3}\times \sqrt{\frac{4+4-2}{16}}{\left(\sqrt{\frac{1+4-2}{4}}\right)}^2=\frac{2}{3}{\left(\sqrt{\frac{5}{12}}\right)}^2{\left(\sqrt{\frac{2}{3}}\right)}^2{\left(\frac{\sqrt{3}}{2}\right)}^{2k-2}{\left(\frac{\sqrt{6}}{4}\right)}^{k-2}\text{.}$$

Thus, the result is correct when $n=k+1$. □

Fig. 3.

(a) Structure of cycloalkenes $C_n^H$ and its molecular graph expression.

2.2. The first multiplicative atom-bond connectivity index of dendrimers

In this subsection, we determine the first multiplicative atom-bond connectivity index of dendrimers which is widely appeared in the drug structures. More medicine engineering applications on different kinds of dendrimers can be referred in Cevik et al., 2016, Heredero-Bermejo et al., 2016, Heredero-Bermejo et al., 2015, Worley et al., 2016, Vacas-Cordoba et al., 2016, Rivero-Buceta et al., 2015, Ozcan and Sezginturk, 2015, Gothwal et al., 2015, and Sepulveda-Crespo et al. (2015). In Theorem 3–Theorem 6, we assume n be the growth stages.

Theorem 3

The first multiplicative atom-bond connectivity index of nano-star ${\mathit{NS}}_2[n]$ is

$${\mathit{ABC}}_1\text{II}({\mathit{NS}}_2[n])=\frac{2}{3}{\left(\frac{\sqrt{2}}{2}\right)}^{18·2^n-6}\text{.}$$

Proof of Theorem 3

The molecular structure of ${\mathit{NS}}_2[n]$ is stated in Fig.4: By analyzing the structure of ${\mathit{NS}}_2[n]\text{,}$we ensure that the edge set $E({\mathit{NS}}_2[n])$ can be divided into three partitions:

• •$E_{2\text{,}2}=\{e=\mathit{uv}\in E(G)|d(u)=d(v)=2\}\text{and}{n}_{22}=6·2^n+2$;
• •$E_{2\text{,}3}=\{e=\mathit{uv}\in E(G)|d(u)=2\mathit{and}d(v)=3\}\text{and}{n}_{23}=12·2^n-8$;
• •$E_{3\text{,}3}=\{e=\mathit{uv}\in E(G)|d(u)=d(v)=3\}\text{and}{n}_{33}=1$ .

Hence, by means of the definitions of first multiplicative atom-bond connectivity index, we get the desired result. □

Theorem 4

The first multiplicative atom-bond connectivity index of nano-star ${\mathit{NS}}_3[n]$ is

$${\mathit{ABC}}_1\text{II}({\mathit{NS}}_3[n])={\left(\frac{2}{3}\right)}^{3·2^n-3}{\left(\frac{\sqrt{2}}{2}\right)}^{18·2^n-12}\text{.}$$

Proof of Theorem 4

The molecular structure of ${\mathit{NS}}_3[n]$ is stated in Fig.5. By analyzing the structure of ${\mathit{NS}}_3[n]\text{,}$ we ensure that the edge set $E({\mathit{NS}}_3[n])$ can be divided into three partitions:

• •$E_{2\text{,}2}=\{e=\mathit{uv}\in E(G)|d(u)=d(v)=2\}\text{and}{n}_{22}=6·2^n$;
• •$E_{2\text{,}3}=\{e=\mathit{uv}\in E(G)|d(u)=2\text{and}d(v)=3\}\text{and}{n}_{23}=12·2^n-12$;
• •$E_{3\text{,}3}=\{e=\mathit{uv}\in E(G)|d(u)=d(v)=3\}\text{and}{n}_{33}=3·2^n-3$ .

Thus, in terms of the definitions of first multiplicative atom-bond connectivity index, we infer the desired result. □

Theorem 5

The first multiplicative atom-bond connectivity index of polyphenylene dendrimer $D_4[n]$ is

$${\mathit{ABC}}_1\text{II}(D_4[n])={\left(\sqrt{\frac{5}{12}}\right)}^4{\left(\frac{2}{3}\right)}^{36·2^n-36}{\left(\frac{\sqrt{2}}{2}\right)}^{104·2^n-80}\text{.}$$

Proof of Theorem 5

The kernel and an example of $D_4[n]$ are presented in Figs. 6 and 7, respectively. By analyzing the structure of $D_4[n]$, we ensure that the edge set $E(D_4[n])$ can be divided into four partitions:

• •$E_{2\text{,}2}=\{e=\mathit{uv}\in E(G)|d(u)=d(v)=2\}\text{and}{n}_{22}=56·2^n-40$
• •$E_{2\text{,}3}=\{e=\mathit{uv}\in E(G)|d(u)=2\text{and}d(v)=3\}\text{and}{n}_{23}=48·2^n-40$;
• •$E_{3\text{,}3}=\{e=\mathit{uv}\in E(G)|d(u)=d(v)=3\}\text{and}{n}_{33}=36·2^n-36$;
• •$E_{3\text{,}3}=\{e=\mathit{uv}\in E(G)|d(u)=3\text{and}d(v)=4\}\text{and}{n}_{34}=4$.

Therefore, in light of the definitions of first multiplicative atom-bond connectivity index, we yield the result in Theorem 5. □

Theorem 6

The first multiplicative atom-bond connectivity index of polyphenylene dendrimer $D_2[n]$ is

$${\mathit{ABC}}_1\text{II}(D_2[n])={\left(\frac{2}{3}\right)}^{36·2^n-35}{\left(\frac{\sqrt{2}}{2}\right)}^{104·2^n-92}\text{.}$$

Proof of Theorem 6

The kernel and an example of $D_2[n]$ are presented in Figs. 8 and 9, respectively.By analyzing the structure of $D_2[n]$, we ensure that the edge set $E(D_2[n])$ can be divided into three partitions:

• •$E_{2\text{,}2}=\{e=\mathit{uv}\in E(G)|d(u)=d(v)=2\}\text{and}{n}_{22}=56·2^n-48$;
• •$E_{2\text{,}3}=\{e=\mathit{uv}\in E(G)|d(u)=2\text{and}d(v)=3\}\text{and}{n}_{23}=48·2^n-44$;
• •$E_{3\text{,}3}=\{e=\mathit{uv}\in E(G)|d(u)=d(v)=3\}\text{and}{n}_{33}=36·2^n-35$.

Therefore, using the definitions of the first multiplicative atom-bond connectivity index, we deduce the result. □

Fig. 4.

The basic molecular structure of ${\mathit{NS}}_2[n]$.

Fig. 5.

The basic molecular structure of ${\mathit{NS}}_3[n]$.

Fig. 6.

The kernel of $D_4[n]$.

Fig. 7.

The molecular struture of $D_4[n]$ with 2 growth stages.

Fig. 8.

The kernel of $D_2[n]$.

Fig. 9.

The molecular struture of $D_2[n]$ with 3 growth stages.

2.3. The first multiplicative atom-bond connectivity index of benzenoid systems and phenylenes

First, we introduce some notations of benzenoid systems and phenylenes:

• •r the number of inlets;
• •B the number of simple bays;
• •C the number of coves;
• •F the number of fjords;
• •f the number of fissures;
• •L the number of lagoons;
• •b the number of regions.

It’s necessary to mention that bays, coves, fjords, fissures and lagoons are structural characteristics of the perimeter of the benzenoid systems and they are important in their theory. For the description of examples, please refer to Fig. 10.

Fig. 10.

Some kinds of inlets in the perimeter of a benzenoid system.

Then if we assume r be the sum of inlets on the perimeters of a benzenoid system represented just now, we can obtain $b=B+2C+3F+4L$ and $r=B+C+F+f+L$.

Phenylenes are a kind of chemical compounds and the carbon atoms form 6- and 4-membered cycles in it. Every 4-membered cycle(=square) is next to two disjoint 6-membered cycles(=hexagons), and no two hexagons are found to be next to each other. The hexagonal squeeze of the respective phenylene, a catacondensed hexagonal system (which may be jammed), is obtained by eliminating, and “squeezing out” the squares from a phenylene (Yine et al., 2015, Shareef et al., 2017). Obviously, a phenylene (PH) is corresponding to its hexagonal squeeze (HS), for they share the same number (h) of hexagons. Moreover, a phenylene with h hexagons own $h-1$ squares. The number of vertices of pH and HS are $6h$ and $4h+2$, respectively; The number of edges of pH and HS are $8h-2$ and $5h+1$, respectively. For description of the example of phenylene and its hexagonal squeeze, please refer to Fig. 11.

Fig. 11.

A phenylene PH and its hexagonal squeeze HS.

As for the example of phenylenes, a fissure, bay, cove, fjord, and lagoon are considered as the benzenoid systems. A fissure (resp. a bay, cove, fjord, or lagoon) is corresponding to a sequence of four (resp, six, eight, ten, and twelve) consecutive vertices on the perimeter, and the first and the last of it are 2 degree vertices and the rest are 3 degree vertices.

Several contributions and engineering applications on benzenoid systems and phenylenes can refer to Cruz et al., 2013, Dias, 2010, Smirnova et al., 2017, Koyama et al., 2017, Nguyen et al., 2017, Abdulkarim et al., 2016, Rai et al., 2016, Selter et al., 2016, and Raju et al. (2016). Now, the main conclusions in this part are stated as follows.

Theorem 7

The first multiplicative atom-bond connectivity index of benzenoid system S with n vertices, h hexagons and r inlets is

$${\mathit{ABC}}_1\text{II}(S)={\left(\frac{2}{3}\right)}^{3h-r-3}{\left(\frac{\sqrt{2}}{2}\right)}^{n-2h+r+2}\text{.}$$

Proof of Theorem 7

Clearly, the edge set $E(S)$ can be divided into three partitions:

• •$E_{2\text{,}2}=\{e=\mathit{uv}\in E(G)|d(u)=d(v)=2\}\text{and}{n}_{22}=n-2h-r+2$;
• •$E_{2\text{,}3}=\{e=\mathit{uv}\in E(G)|d(u)=2\text{and}d(v)=3\}\text{and}{n}_{23}=2r$;
• •$E_{3\text{,}3}=\{e=\mathit{uv}\in E(G)|d(u)=d(v)=3\}\text{and}{n}_{33}=3h-r-3$.

By simple calculation, we infer the desired result. □

Theorem 8

The first multiplicative atom-bond connectivity index of phenylene PH with h hexagons and r inlets is

$${\mathit{ABC}}_1\text{II}(\mathit{PH})={\left(\frac{2}{3}\right)}^{6h-r-6}{\left(\frac{\sqrt{2}}{2}\right)}^{2h+r+4}$$

Proof of Theorem 8

Obviously, the edge set $E(\mathit{PH})$ can be divided into three partitions:

• •$E_{2\text{,}2}=\{e=\mathit{uv}\in E(G)|d(u)=d(v)=2\}\text{and}{n}_{22}=2h-r+4$;
• •$E_{2\text{,}3}=\{e=\mathit{uv}\in E(G)|d(u)=2\text{and}d(v)=3\}\text{and}{n}_{23}=2r$;
• •$E_{3\text{,}3}=\{e=\mathit{uv}\in E(G)|d(u)=d(v)=3\}\text{and}{n}_{33}=6h-r-6$.

By simple calculation, we infer the desired result. □

3. Conclusion

This paper proposed the multiplicative atom-bond connectivity index of alkene, cycloalkenes, dendrimers, benzenoid systems and phenylenes by analyzing certain molecular structural, degree computation and mathematical derivation. The conclusion also demonstrate the wide and promising application prospect in medical and pharmacy engineering.

Conflict of interests

The authors declare that there is no conflict of interests regarding the publication of this paper.