Significance
Recent works have hinted at an ability of cells to respond in the exact same manner to a fold change in the input stimulus. The property is thought to allow cells to function properly regardless of changes in the absolute concentrations of signaling molecules. Despite its general importance, however, evidence has remained scarce. The present work demonstrated that, in the social amoeba Dictyostelium, a response to cell–cell communication molecules is fold-change dependent and that this property is tightly linked to the condition that allows them to oscillate collectively, and thus to organize into a multicellular form. Such properties may be of importance for robustness of other developmental systems where oscillatory signaling plays a pivotal role in defining multicellular organization.
Keywords: fold-change detection, oscillations, collective behavior, Dictyostelium, robustness
Abstract
Cell–cell signaling is subject to variability in the extracellular volume, cell number, and dilution that potentially increase uncertainty in the absolute concentrations of the extracellular signaling molecules. To direct cell aggregation, the social amoebae Dictyostelium discoideum collectively give rise to oscillations and waves of cyclic adenosine 3′,5′-monophosphate (cAMP) under a wide range of cell density. To date, the systems-level mechanism underlying the robustness is unclear. By using quantitative live-cell imaging, here we show that the magnitude of the cAMP relay response of individual cells is determined by fold change in the extracellular cAMP concentrations. The range of cell density and exogenous cAMP concentrations that support oscillations at the population level agrees well with conditions that support a large fold-change–dependent response at the single-cell level. Mathematical analysis suggests that invariance of the oscillations to density transformation is a natural outcome of combining secrete-and-sense systems with a fold-change detection mechanism.
Cell–cell signaling lies at the basis of development and maintenance of multicellular forms of life. Extracellular signals are often subject to greater fluctuations in the size of extracellular space and the number of cells (Fig. 1A), not to mention nonspecific binding to other molecules, degradation, and dilution. These factors introduce an uncertainty to the detectable number of extracellular ligand molecules, thus posing a threat to the fidelity of cell–cell communication. One of the means by which cells could cope with such uncertainties is to base their behavioral decisions on temporal changes in the extracellular signals. Persistent stimuli are often ignored while their changes in time elicit transient responses—a property collectively called adaptation (1–3). Recent studies have highlighted cellular response whose magnitude appears to be dictated by the fold change in the input stimuli—a property referred to as “fold-change detection” (FCD) (4, 5). In bacterial chemotaxis, cells respond adaptively to a fold change in chemoattractant concentration (6) so that their search patterns depend only on the spatial profiles of the chemoattractant irrespective of its absolute level. Fold-change dependence is also implied in eukaryotic chemotactic response (7, 8) as well as cell fate control and gene regulation in Xenopus embryo (9), Drosophila imaginal disk (10), and mammalian cells (11). These studies have shed light on the role of FCD for a simple unidirectional signal transduction from an extracellular ligand-receptor interaction (input) to a cellular response (output). However, cell–cell signaling and multicellular systems as a whole often use secretion and sensing of the same molecules (12), whereby the output is fed back to the responding cell itself in addition to the neighboring cells, thus forming a complex bidirectional signal transduction system. The consequence of equipping such systems with an adaptive response and FCD is so far unaddressed.
Fig. 1.
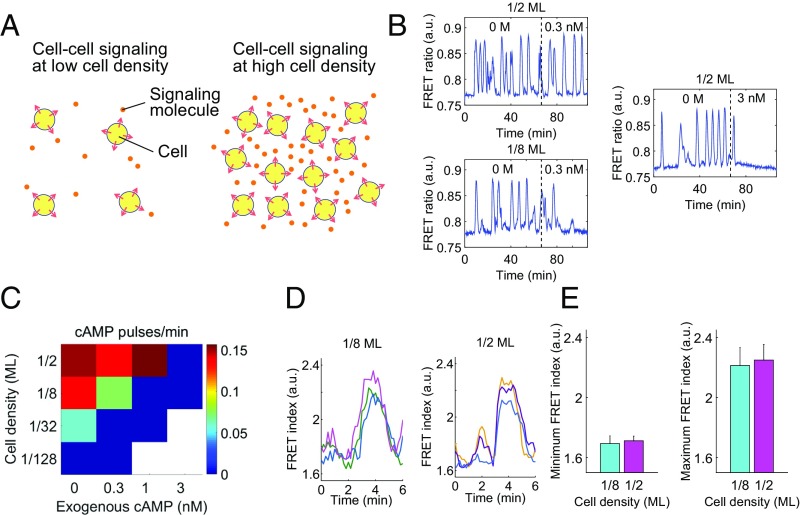
Dependency of the cAMP oscillations on cell density and the background concentrations of extracellular cAMP. (A) A schematic illustrating how variability in cell density introduces uncertainties in the concentration of diffusive signaling molecules. (B) Representative time series from Epac1camps (59)-expressing cells (24) before and after application of exogenous cAMP (0.3 nM, 3 nM). Exogenous cAMP (0.3 nM) extinguished oscillations at a low cell density (1/8 ML), whereas almost no clear effect was observed at a high cell density (1/2 ML). (C) A phase diagram of the mean pulse frequency as a function of cell density and exogenous cAMP. At high cell densities, the oscillations were relatively insensitive to exogenous cAMP. Squares represent three to six independent measurements of a 2-h duration (n = 4, 4, 3, and 3 for 1/2 ML from Left to Right; n = 8, 4, 3, and 3 for 1/8 ML; n = 4, 3, and 3 for 1/32 ML; n = 3 and 3 for 1/128 ML). (D) Representative time series of the FRET index (Epac1camps/AX4 cells) obtained from individual cells oscillating in a population of 1/8 monolayer (ML) (Left) and 1/2 ML cell density; perfusion rate, 1.5 mL/min. Colors indicate different cells. (E) The average of minimum (Left) and maximum (Right) FRET index. Error bars represent SD (n = 21 for 1/8 ML and n = 19 for 1/8 ML).
Oscillations of extracellular cAMP that dictate aggregation of the social amoebae Dictyostelium discoideum is a prime example of robust collective behaviors in cell populations. Under starvation, cells synthesize and secrete cAMP, which stimulates other cells in the vicinity to induce further synthesis and secretion of cAMP—a process called “cAMP relay” (13). After prolonged exposure to cAMP, the rise in extracellular cAMP level ceases due to inactivation of adenylyl cyclase (14). As extracellular cAMP level is lowered by degradation, the cells exit from the state of reduced responsivity over the course of several minutes (15, 16), and hence the extracellular cAMP level once again starts to elevate. This tendency for the extracellular cAMP level to rise when it is lowered, and to be lowered when it is raised, essentially renders extracellular cAMP level unstable and oscillatory. The emerging oscillatory waves of extracellular cAMP in the cell population provide a temporal guidance cue for directional cell migration (17, 18). Both cAMP oscillations and cell aggregation are known to occur at a wide range of cell densities spanning at least two to three orders of magnitude (19–22). Cells lacking the cAMP-synthesizing enzyme adenylyl cyclase ACA when ectopically forced to differentiate cannot form aggregates unless they are allowed to randomly collide and form cell clusters at high cell densities (23), indicating that robust cell aggregation depends on intercellular cAMP signaling. Recent live-cell imaging studies have elucidated an input–output relation of the cAMP relay response at the single-cell level resolution (16, 24–26). Although these analyses have implied a role played by the stochastic cAMP relay response at low basal concentrations of extracellular cAMP (∼100 pM) in initiating the synchronized pulses, how they could take place robustly in a wide range of cell densities is yet poorly understood.
Results
Density Dependence of the Oscillations.
To gain insights on the concentration range of intracellular and extracellular cAMP that supports oscillations, we revisited the cAMP dynamics quantitatively by live-cell imaging of cells expressing the cAMP probe Epac1camps (24) combined with a corrected quantification of the fluorescence resonance energy transfer (FRET) efficiency (27) (“FRET index”; Fig. S1 and SI Materials and Methods). Collective cAMP oscillations occur spontaneously in cell populations continuously perfused with buffer solution at a moderate flow rate (1.5 mL/min), where extracellular cAMP breakdown by secreted phosphodiesterase (PDE) in vivo is effectively emulated by dilution (24, 28). First, we tested the effect of adding cAMP in the perfusion flow (hereafter refer to as “exogenous cAMP”), which adds on top of endogenously synthesized and secreted cAMP present in the extracellular space. For 0.3 nM exogenous cAMP, the oscillations persisted at a relatively high cell density [1/2 monolayer (ML); 1 ML ≡ 6.6 × 103 cells per mm2] (Fig. 1B, Left Upper); however, they were extinguished at a lower cell density (1/8 ML) (Fig. 1B, Left Lower). If we assume cAMP to be the single dominant extracellular factor that dictates the dynamics of cytosolic cAMP, then the results suggest that the concentrations of extracellular cAMP were different under these conditions. Indeed, when the high-cell density cells (1/2 ML) were supplied with higher exogenous cAMP, the oscillations were also extinguished (Fig. 1B, Right). Systematic analysis of the occurrence of synchronized pulses at various cell densities and exogenous cAMP concentrations showed that the oscillations were more easily suppressed at low cell densities (Fig. 1C; vertical axis) and by high exogenous cAMP concentrations (Fig. 1C; horizontal axis). On the other hand, the minimum and the maximum of the FRET indices measured at the single-cell level during the cAMP oscillations at low and high cell densities (Fig. 1D; 1/2 ML and 1/8 ML) were indistinguishable (Fig. 1E), suggesting that the range of cytosolic cAMP concentration during the oscillations does not depend strongly on the cell density. To summarize, the oscillatory range of extracellular cAMP level depends on the cell density and thus is more easily masked by exogenous cAMP at low cell densities, whereas that of the cytosolic cAMP is unchanged.
Fig. S1.
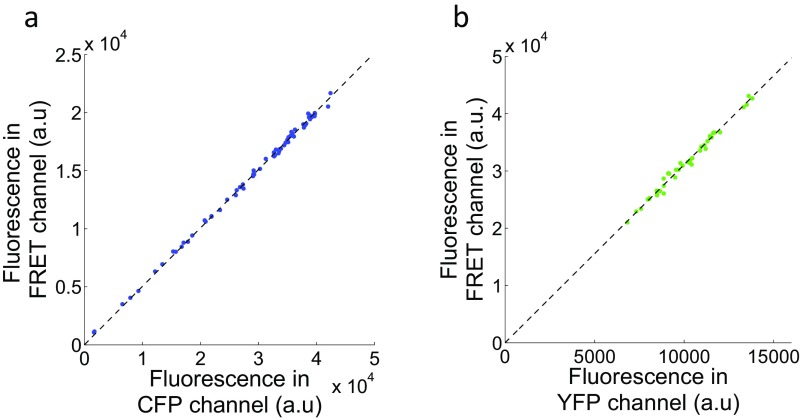
Determination of the coefficients to correct for channel cross talk and cross-excitation. (A) Plots of the background-subtracted mean fluorescence intensities in the CFP and FRET channels obtained from CFP-expressing cells excited with 435-nm light. Dots represent measurements from individual cells. The dashed line marks the least-squares regression line (IFRET = 0.5ICFP). (B) YFP-expressing cells were excited with 435-nm light and 500-nm light for YFP channel, and the mean fluorescence intensities were plotted after background correction. The least-squares regression line is represented by the dashed line (IFRET = 3.1IYFP).
Rescaled Response Sensitivity.
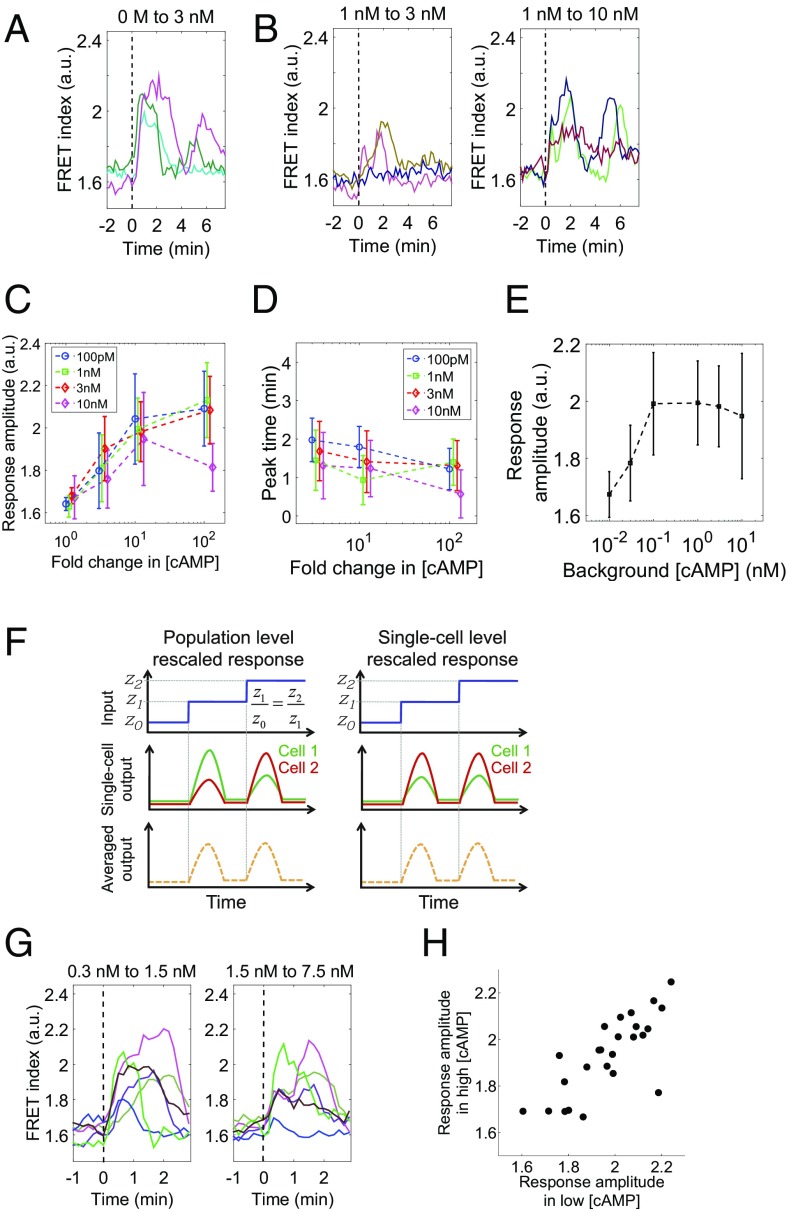
What exact concentration and magnitude change in the extracellular cAMP are required to sustain the collective oscillations? Before and during the early stage of cell aggregation, the basal level of extracellular cAMP slowly builds up and is estimated to reach around 10 nM or less (29, 30), which is near the Kd of the membrane-bound G-protein–coupled receptor CAR1. To see the effect of background concentrations of extracellular cAMP in this range, we measured single-cell level cAMP relay responses in well-isolated cells (<10−3 ML) (24) that were first primed with a fixed concentration of cAMP (0.1, 1, 3, and 10 nM) for about 40 min to let the initial response attenuate before elevating the cAMP level in a step-like manner (Materials and Methods). Note that, in contrast to the population-level oscillation experiments described in the previous section, here, care was taken so that cAMP secreted by the cells becomes negligible (24); extracellular buffer was rapidly diluted by fast perfusion (4–8 mL/s; Materials and Methods), cells were plated at low cell densities (see Materials and Methods), and a cell was chosen for observation after confirming that there is no other cell within the surrounding area of ∼0.3-mm radius. Fig. 2A shows reference time courses of the cAMP relay response to a step increase in the extracellular cAMP concentration from 0 to 3 nM, a nonprimed stimulus condition that elicits a maximum amplitude response as measured by the FRET signal (24). The level of cytosolic cAMP reached the maximum at 2–3 min after the stimulus application followed by secondary peaks that slowly attenuated in close agreement with a previous study (24). Under primed conditions, the response to 3 nM on top of 1 nM extracellular cAMP was markedly reduced in both initial and secondary peak amplitude (Fig. 2B, Left), whereas elevation from 1 to 10 nM induced a large magnitude response (Fig. 2B, Right) comparable to that observed under nonpriming conditions.
Fig. 2.
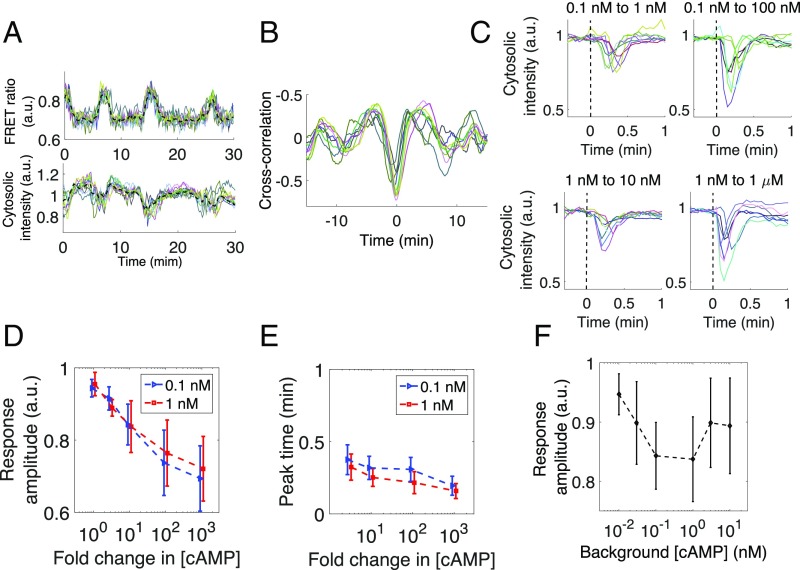
The cAMP relay response at the single-cell level obeys fold-change detection. (A and B) The concentration of perfused cAMP was changed from 0 to 3 nM (A), 1 to 3 nM (B; Left), and 1 to 10 nM (B, Right). The dotted lines indicate the time of stimulus switch. Colors indicate different cells. (C and D) The peak amplitude (C) and the response time (D) of the response; priming concentrations, 0.1 nM (blue), 1 nM (green), 3 nM (red), and 10 nM (magenta) cAMP. The vertical axis: the maximum FRET index during the 4 min after the input change (C) and the time it took for the FRET index to reach the initial peak (D). Dots and error bars indicate the mean and SD (n = 11, 16, 16, and 15 for 1-, 3-, 10-, and 100-fold change from 100 pM, respectively. In the same way, n = 13, 23, 15, and 16 for 1 nM; n = 11, 13, 11, and 14 for 3 nM; n = 16, 7, 10, and 9 for 10 nM). (E) The amplitude of the response to 10-fold increase in the extracellular cAMP concentration. Error bars indicate SD (n = 10, 14, 16, 15, 11, and 10 for 10−2, 3 × 10−2, 0.1, 1, 3, and 10 nM, respectively). (F) Two possible scenarios for the curves in C. (Left) The response sensitivity is heterogeneous and not rescaled at the single-cell level. (Right) The response sensitivity rescales at the single-cell level. (G) Representative responses to sequential fivefold step inputs from 0.3 to 1.5 nM (Left), and then from 1.5 to 7.5 nM (Right). Colors are mapped to identify individual cells consistently in two panels. Cells were kept at 1.5 nM cAMP for 15 min before the second increment. (H) A scatter plot of the response amplitude to two incremental step inputs; correlation coefficient, 0.68 (n = 25).
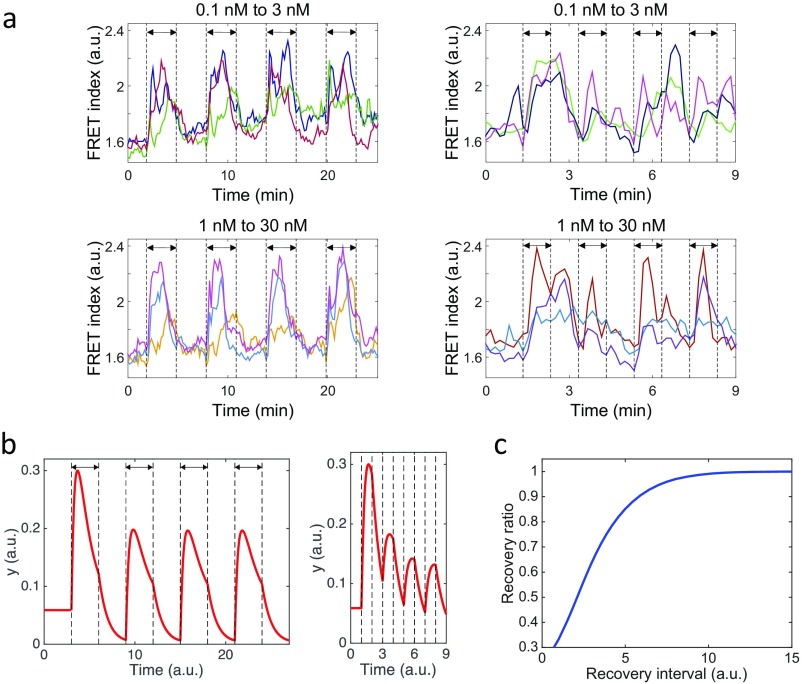
Next, we quantified the initial peak amplitude 2–3 min after the stimulus increase. This serves as the primary measure of the strength of the relay response underlying the collective oscillations, because the secondary peaks were not observed when the level of extracellular cAMP was elevated only for a few minutes (24) (Fig. S2A) as is the case during the collective oscillations. Fig. 2C plots the index as a function of fold increase in extracellular cAMP concentration for four priming concentrations tested. For priming concentrations below 10 nM (0.1, 1, and 3 nM), the plots collapsed on a single curve, indicating that, within this concentration range, the single major determinant of the peak amplitude of the cAMP relay response is the fold change in the extracellular cAMP concentration. The peak FRET index observed during the relay response was half-maximal at about a 3-fold increase in the extracellular cAMP concentration and levels off at about a 10-fold increase. The time at which the initial peak reached the maximum value showed almost no dependency on the background level of extracellular cAMP (Fig. 2D). Moreover, the amplitude of the response to a fold change of 10 was more or less constant between 0.1 and 10 nM background concentrations (Fig. 2E), suggesting that the rescaling property holds for two orders of magnitude. The same rescaling property was also observed when the step-stimulus was repeated (Fig. S2A).
Fig. S2.
cAMP signaling response to periodic stimuli of different absolute concentrations and refractoriness in the cAMP relay response. (A) The cytosolic cAMP dynamics in isolated cells stimulated with a fold change of 30 [0.1–3 nM (Upper) and 1–30 nM (Lower)] at a 6-min (Left) or 2-min period (Right). Double arrows indicate the time windows of elevated stimulus. (B) Numerical simulations of the FCD model (Eq. 3; equations for x and y) for periodic stimuli of 30-fold change z = 0.1 and z = 3. Parameters are the same as in Fig. 5. Double arrows indicate the time window of elevated z (=3). The stimulus period is T = 6 (Left) and T = 2 (Right). For the initial conditions, x and y are set at the steady state for z = 0.1. (C) The deadaptation curve of the model. z was initially set to 1.0, and x and y were allowed to reach the steady state. z was lowered to 0.1 for the time duration indicated in the horizontal axis before setting it back to 1.0. The vertical axis represents values of y normalized by its maximum.
One should note that an apparent fold-change dependence in the population-averaged response (Fig. 2C) should not be readily equated with a fold-change detection at the single-cell level. For example, cell–cell variability in the response sensitivity alone in the absence of FCD could deceptively bring about a similar response curve after averaging (Fig. 2F, Left). In principle, whether or not rescaling holds at the level of individual cell (Fig. 2F, Right) should be tested by measuring the response to fold-change stimulus numerous times in single cells. However, this is not feasible due to phototoxicity and also because cells differentiate in the timescale of hours. Instead, we measured the response to two incremental steps with a fold change of 5 (0.3, 1.5, and 7.5 nM cAMP). Fig. 2G shows representative time series of single-cell level responses. Those cells that show weak response in the initial increment also tend to show weak response in the second increment. Likewise, cells with large response were consistent in two incremental stimuli. Despite a large cell–cell variability in the amplitude, the variability was spread along a linear slope in the scatter plot (Fig. 2H). In other words, the amplitudes of the response to the consecutive inputs were highly correlated in each individual cells. The results indicate that the fold-change dependence is a single-cell level property.
During cell aggregation of Dictyostelium discoideum, synchronous emission of cAMP gives rise to periodic traveling waves of extracellular cAMP, and thus the level of extracellular cAMP is oscillating (29). In this respect, the spatially uniform and temporally abrupt stimulus used in the above section deviates from the naturally occurring one. In general, a response to a step stimulus may not necessarily have the same propensity as that for a slowly varying stimulus. Moreover, directional migration is induced by a traveling-wave stimulus (17, 18) and thus may affect the cAMP relay owing to a large overlap in the signal transduction network (16, 31, 32). To test relevance of the fold-change response property for natural cAMP wave, we used a microfluidics lighthouse (33)—a gradient-generating platform capable of delivering traveling-wave stimulus of various amplitude, frequencies, and speed. Using this device, we applied 6-min period cAMP stimuli to cells in the region of interest (Fig. 3A; dotted square) in the form of spatially symmetric bell-shaped gradient that measures ∼500 μm from the trough to the peak and traversed at a speed of ∼2–3 × 102 μm/min (Fig. 3 A and B), which closely follows the estimated parameters of natural cAMP waves (34). The flow is slow and does not bias directionality of cell migration (33), and there is no apparent shear-induced effect on the level of cytosolic cAMP (Fig. 3C). Fig. 3 D–F shows representative responses of well-isolated cells to repetitive wave stimulus with fold increase/decrease of 30 for background concentration of 0.1, 1.0, and 3.0 nM extracellular cAMP. In all three conditions, albeit cell–cell variability, the concentration of cytosolic cAMP in individual cells oscillated in phase with that of extracellular cAMP whose peak time showed delay of ∼10–40 s. The peak FRET index was on average almost constant under these conditions (Fig. 3G), confirming that the magnitude of single-cell level response to traveling-wave stimulus is fold-change dependent.
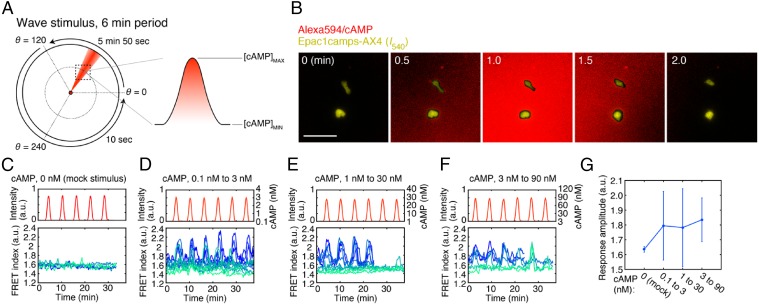
Fig. 3.
The cAMP relay response to traveling-wave stimuli. (A) Application of a traveling-wave stimulus using the lighthouse device (33). A schematic of generating periodically rotating waves at 6-min period (Left). Due to diffusion, a bell-shaped gradient forms perpendicular to the flow of buffer solution containing high concentration of cAMP (red). The orientation of the stimulus flow was varied at the rate of 0.34°/s anticlockwise from θ = 0° to 120°, thereby allowing a bell-shaped gradient to traverse the observation area (dotted square). For the remaining region from θ = 120° to 360°, the rotation was fast-forwarded by switching the direction discretely in two steps from 120° to 240°, and then 240° to 360° (33). Alexa Fluor 594 was included in the stimulus solution to estimate the spread of cAMP. For each run of experimental observation, the rotation was cycled four to six times. (B) Merged confocal images of the stimulus profile (red; Alexa) and Epac1camps/AX4cells [yellow; YFP (I540nm) channel] during a wave passage. (Scale bar, 50 µm.) (C–F) cAMP response to the wave stimulus. cAMP concentrations: mock (C; n = 5 cells), 0.1–3 nM (D; n = 12 cells), 1–30 nM (E; n = 10 cells), and 3–90 nM (F; n = 6 cells). Temporal profiles of the wave stimulus (Upper) and individual cell responses (Lower; graded blue green colors indicate different cells). Buffer solution containing Alexa Fluor 594 without cAMP was used for the mock control (C). cAMP concentrations were estimated from the fluorescence intensity of the Alexa dye (D–F). (G) The average peak FRET index. Error bars indicate SDs.
The cAMP relay response is mediated by complex signaling cascades downstream of G-protein–coupled receptors that are yet to be fully revealed (31, 35). Binding of extracellular cAMP to the receptor activates small GTPase Ras, which then activates phosphoinositide 3-kinase (PI3K) to elevate phosphatidylinositol-(3,4,5)-triphosphate (PIP3) at the plasma membrane (36). PIP3 serves as a docking site for a pleckstrin homology (PH) domain-containing protein cytosolic regulator of adenylyl cyclase (CRAC) that is essential for the activation of adenylyl cyclase ACA (37, 38). These activation processes are counteracted by deactivation of Ras by RasGAP (39) and conversion from PIP3 to PIP2 by phosphatase PTEN (40). Less is known about adaptation of ACA besides the fact that it depends on receptor phosphorylation (41) and PI3K (16, 38). Semirescaling of the response sensitivity has been reported at the level of Ras activation (42), which appears “FCD-like” after population averaging (7, 8).
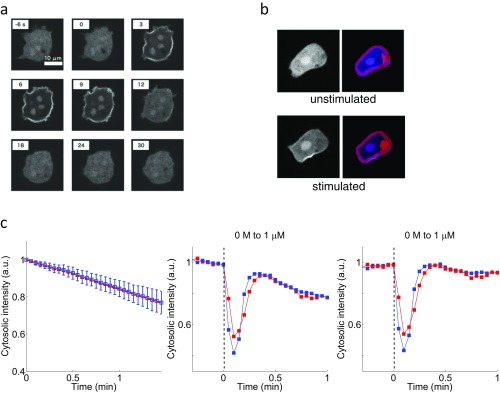
To gain further insights into how the rescaling property is embedded at an event closely upstream of ACA, we measured membrane translocation of PH domain of CRAC (37) fused to RFP (PHCRAC-RFP) (43) (Materials and Methods; Fig. S3). In the perfused cell populations, the FRET index and PHCRAC-RFP translocation oscillated in phase at the single-cell level (Fig. 4A and Movie S1) with delay of no more than 1 min as evident by the cross-correlation analysis (Fig. 4B). In isolated cells exposed to rapid step stimuli (50% exchange of extracellular solution in less than 10 s), the correlation between the membrane translocation of PHCRAC-RFP and the cAMP relay response at the single-cell level was less apparent. The transient translocation of PHCRAC-RFP from the cytosol to the plasma membrane occurred within 10–20 s after the stimulus elevation, which is in contrast to the cAMP relay response that took close to 2 min to reach its peak. Fig. 4C shows the time course of PHCRAC-RFP translocation in isolated cells at different priming concentrations (Materials and Methods). Similar to the cAMP relay response, for 0.1 and 1 nM priming concentrations of cAMP, the degree of membrane translocation of PHCRAC-RFP exhibited a fold-change dependency (Fig. 4D). The time it took for the response to reach its peak also appeared almost identical (Fig. 4E) with a slight decline at a higher fold stimuli as has been noted for Ras activation (7). Rescaling of the response sensitivity was observed in a somewhat narrower range of the background cAMP concentrations (∼0.1–1 nM) (Fig. 4F) compared with that of the cAMP relay response (∼0.1–10 nM) (Fig. 2E). On average, there was decrease in the degree of PHCRAC-RFP translocation at priming concentrations higher than 1 nM. These results suggest that information regarding fold change in the extracellular cAMP concentration is encoded and transduced, at least partially, by the degree of membrane translocation of CRAC.
Fig. S3.
Quantification of the response in the ACA activating pathway. (A) Snapshots of confocal images showing translocation of PHCRAC-RFP to the plasma membrane. The cell was stimulated in a perfusion chamber with spatially homogeneous 1 μM extracellular cAMP at t = 0 s. (B) Analysis of fluorescence images of PHCRAC-RFP. Representative images before (“unstimulated”) and after stimulation (“stimulated”) (t = 6 s) with 1 μM cAMP. The plasma membrane (magenta), nucleus, and other fluorescent objects (purple) and nonfluorescent objects (red) were detected by image analysis to obtain a median value of fluorescence intensities of the cytosolic region (blue) (SI Materials and Methods). (C) Independent measurements of PHCRAC-RFP–expressing cells under no stimulus for the estimation of the rate of photobleaching (Left). Blue squares and bars (Left) indicate the mean and the SD of time series data (n = 27 cells). The red dotted line (Left) is the least-square fit (ICytosol = −0.16t + 1). The normalized cytosolic fluorescence intensity (SI Materials and Methods) (Middle) was corrected by using the estimated rate of photobleaching (Right) (Middle and Right). Two cells are represented by red and blue (Middle and Right).
Fig. 4.
Rescaling of the response sensitivity in an ACA activating pathway. (A) Simultaneous measurements of cytosolic cAMP (Upper) and PHCRAC-RFP (Lower) (Epac1camps/PHCRAC-RFP/AX4 cells; 1/2 ML density). Representative data taken from cells chosen randomly from a field of view (n = 10). Colored lines indicate single-cell data, and the black line represents the average. (B) Cross-correlations for single-cell data. (C) Representative time courses of PHCRAC-RFP membrane translocation after a 10-fold (Left) or 103-fold (Right) increase in the extracellular cAMP concentration. Colors indicate different cells. (D and E) The amplitude (D) and the response time (E) of PHCRAC-RFP membrane translocation after an increase in the extracellular cAMP concentrations from 0.1 and 1 nM. Error bars represent SD (n = 21, 18, 30, 31, and 28 for 1-, 3-, 10-, 100-, and 1,000-fold change from 0.1 nM, respectively. Likewise, n = 18, 19, 28, 46, and 30 for 1 nM). The minimum cytosolic fluorescence intensity for the first 1 min after the input change (D; vertical axis). The time it took for the cytosolic intensity to reach the minimum value (E). (F) The response amplitude to 10-fold increase in extracellular cAMP. Mean and SD are shown (n = 18, 22, 30, 28, and 17 for 10−2, 3 × 10−2, 0.1, 1, 3, and 10 nM, respectively).
Scale Invariance of FCD-Based Signaling.
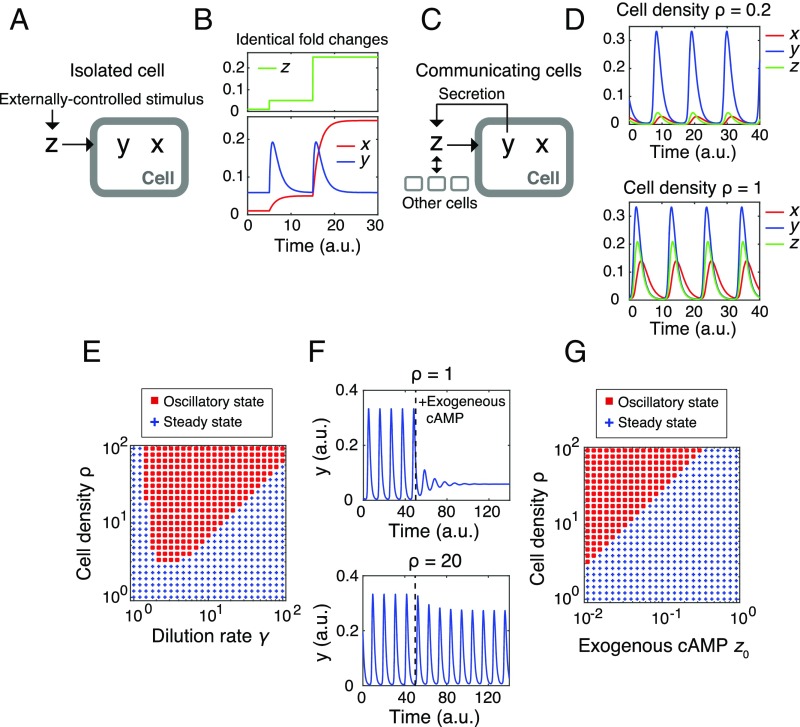
How are the input–output properties revealed at the single-cell level related to the oscillatory behavior at the population level? Let us formulate a secrete-and-sense system where the output “y” is determined by the input signal “z”; conversely, the input z is determined by the response y. To this end, we shall first describe a ligand-induced response by a two-variable system , where intracellular and extracellular cAMP are represented by y and z, respectively (Fig. 5A). Here, x is an internal variable required for adaptation. Mathematically, the system obeys FCD when the functions f and g satisfy a condition:
| [1] |
with an appropriate transformation function ϕ and an arbitrary scaling factor p (>0) (5) (SI Equations). Under this constraint, the variable y responds in an identical manner to two incremental p-fold increase in the input z (Fig. 5B). By introducing a third equation that describes the dynamics of extracellular cAMP z in a perfusion chamber (13, 24), we arrive at a closed-loop system (Fig. 5C):
| [2] |
where ρ, kt, and γ represent the cell density, the secretion rate, and the dilution rate, respectively. The extracellular cAMP z affects the dynamics of the cells—that is, the subsystem x and y; hence the system describes “sensing and secretion” of the same molecules (12, 44).
Fig. 5.
Density robustness is a basic property of a secrete-and-sense system consisting of FCD elements. (A and B) A reaction scheme (A, “Isolated Cell”) and the characteristic behaviors (B) of an FCD system. The time evolution of y and x are described by functions f and g that together constitutes a FCD system (A). Simulated time course of x and y (B, Lower) to incremental increase in z (B, Upper). (C and D) A Schematic diagram of a closed-loop secrete-and-sense system (C, “Communicating cells”) and results from model simulations (Eq. 3) for low (Upper) and high (Lower) cell densities. Here, x and y follow the same reaction scheme as in A except that y is secreted, and thus transformed to z to further stimulate the cells. (E) A phase diagram of the system (Eq. 3) with a lower detection limit. Oscillatory (red squares) and static [blue plus sign (+)] states. (F) Results from numerical simulations of a modified model (Eq. 3 with dz/dt = ρkty – γ(z − z0)). (G) A phase diagram of the system (the model in D) as a function of cell density ρ and the exogenous cAMP level z0. Red squares and blue plus signs (+) indicate oscillatory and static states, respectively. The parameters were τ = 1.5, n = 2, K = 4, kt = 2, and γ = 3, unless otherwise indicated.
From the above mathematical formulation, it is readily shown that Eq. 2 are invariant under a transformation; that is, (see Supporting Information for proof). The scale invariance ensures that, although extracellular cAMP (z) scales with the cell density, the intracellular cAMP y, regardless of whether it is a fixed constant or dynamically changing variable, remains unaffected by density transformation . Because the invariance derives simply by requiring the FCD condition (Eq. 1) for the response dynamics (Eq. 2; equations for x and y), and combining them with the secretion/dilution dynamics (Eq. 2; the equation for z), it can be said that the robustness of the cAMP oscillations to variation in cell density is a natural outcome of the observed response-rescaling property of the constituent cells. Note that, for the sake of clarity, the above derivation assumed that the response functions f(x, y; z) and g(x, y; z) are the same in all cells. The conclusion holds when there is cell–cell variability (SI Equations; Eqs. S6 and S7).
Scale Invariance of the cAMP Oscillations.
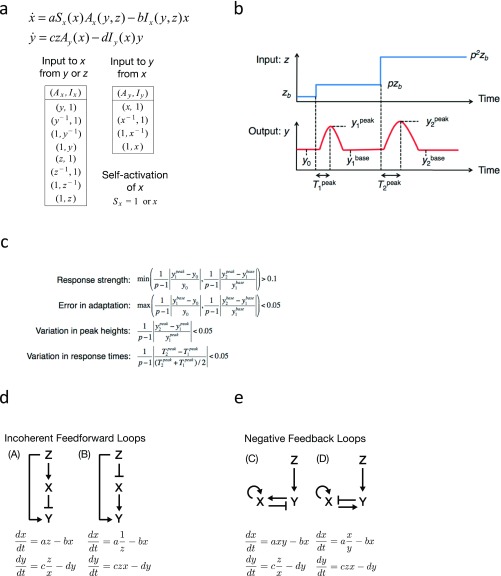
To obtain networks that exhibit adaptive response that obeys FCD, which could then be combined with the equation for z (Eq. 2 and Fig. 5C), a computational search for minimal networks with two nodes and three links (3, 45, 46) was performed (Fig. S4 A–C). Four networks were identified: two “incoherent feedforward loop” type (Fig. S4D) and two negative-feedback loops type (Fig. S4E), which are consistent with recent analytical search of a topology space (46). The basic network models could be slightly modified to take into account the nonlinear input–output relation of the cAMP relay response (Fig. 2C) while preserving the network topology and the FCD property (SI Equations). Although details of the response can be compared to further constrain the network topology (26, 47–49), the present aim is rather to understand the general outcome of incorporating FCD in a secrete-and-sense system. Qualitative features detailed below were conserved in all four selected network types (Fig. S5). For brevity of presentation, a feedforward-type network,
| [3] |
is described below (SI Equations, model [A″]). Parameters τ, n, and K are positive constants. The feedforward network depicts receptor-mediated signals that induce both fast activation and slow terminating reactions (1) and is compatible with adaptation and deadaptation of adenylyl cyclase that depend strictly on elevation and lowering of the extracellular cAMP level, respectively. Earlier mathematical models of cAMP relay (50, 51) as well as chemotaxis models that describe conversion between GTP-bound and GDP-bound form of Ras (42) also have this network topology.
Fig. S4.
Computational search for minimal FCD models. (A) The equations used for the computational search, which describe a network of two nodes and three links. a, b, c, and d are positive parameters (Upper). The list of the explored sets of functions (Ax, Ix), (Ay, Iy) and Sx are shown (Lower). (B) A schematic diagram of two incremental step stimuli used to evaluate model candidates; zb → pzb → p2zb (zb = 0.1, p = 10). The interval time between the two stimuli was 500, which was large enough to allow the systems to relax to the steady state. (C) Criteria for the model selection. The first two criteria “response strength” and “error in adaptation” ensure that the output respond to input change transiently but return to the prestimulus level. The other two criteria “variation in peak heights” and “variation in response times” ensure that the first and second responses are similar in shape. (D and E) The network diagram of the selected models with an incoherent feedforward topology (model [A] and [B]) (D) and a negative-feedback type (models [C] and [D]) (E).
Fig. S5.
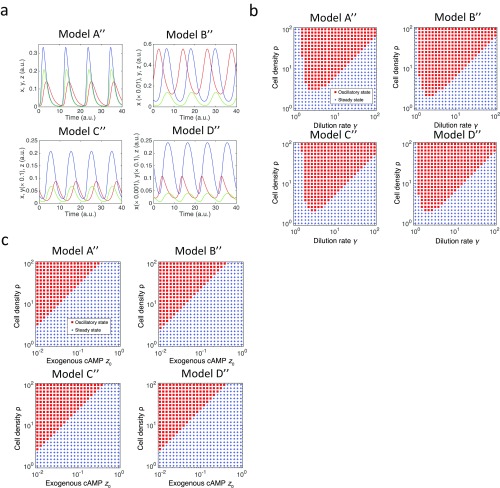
Robustness of the oscillations to variations in cell density does not depend on the detail of the FCD models. (A) Numerical solutions of the models (SI Equations, [A″]–[D″]). Red, blue, and green lines represent variables x, y, and z, respectively. Model [A″]: τ = 1.5, n = 2, K = 4, ρkt = 2, and γ = 3 (Upper Left). Model [B″]: τ = 2, n = 2, K = 2.5, ρkt = 0.75, and γ = 3 (Upper Right). Model [C″]: τ = 3, n = 2, α = 2.5, ρkt = 0.1, and γ = 3 (Lower Left). Model [D″]: τ = 1.7, n = 2, α = 3, ρkt = 0.05, and γ = 3 (Lower Right). (B) Phase diagrams plotted as a function of the dilution rate γ and the cell density ρ; oscillatory (red) and static (red) solutions for models [A″]–[D″]. The parameters were the same as in A except that z on the right-hand side of the equations for x and y were replaced by z + δ with δ = 0.01. (C) Phase diagrams plotted as a function of the cell density ρ and the exogenous stimuli z0 where the governing equation for z was . Oscillatory (red) and static (blue) solutions for models [A″]–[D″]. The parameters were the same as in A.
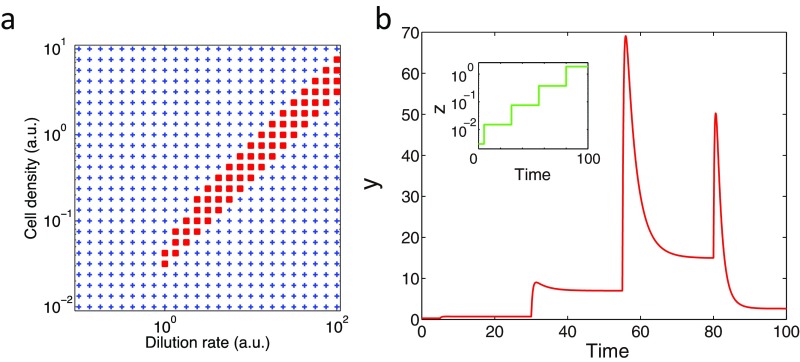
With an appropriate choice of parameter values, the system (Eq. 3) exhibited oscillations (Fig. 5D). The oscillatory solution in the present model (Eq. 3), especially the level of intracellular cAMP y, is insensitive to the value of (Fig. 5B) owing to the scale invariance resulting from the FCD property. This feature is in marked contrast with earlier models (50, 51) where oscillations were observed only in a narrow range of cell density (less than one order of magnitude) irrespective of the dilution rate γ [for model (50), see Fig. S6]. With further inclusion of lower detection limit by replacing z by on the right-hand side of the equations for x and y (Eq. 3), where is a positive constant parameter (SI Equations), we see that the lower limit of cell density that supports collective oscillations becomes a monotonically increasing function of the dilution rate (Fig. 5E)—in agreement with earlier experimental data (figure 2B in ref. 24).
Fig. S6.
Oscillations in M&G model require fine-tuning of cell density. (A) A phase diagram as a function of γ (dilution rate) and ρ (cell density) (red: oscillatory; blue: static state). M&G model was numerically integrated for time steps long enough (from t = 0 to 30,000) to remove the effect of the initial state before the variable y was evaluated by V = 2(ymax − ymin)/(ymax + ymin). The criterion used for oscillations was V > 0.1 (see SI Equations for the details). (B) The time evolution of the intracellular cAMP level in M&G model. Beginning from the steady state, sequential fivefold increases in the stimuli were provided (Inset). Parameters are adopted from ref. 50; k1 = 0.036, k2 = 0.666, L1 = 10, L2 = 0.005, c = 10, α = 3, λ = 0.01, θ = 0.01, ε = 1, q = 4,000, σ = 0.6, ki = 1.7, and kt = 0.9.
The most important suggestion of the present model is that the range of extracellular cAMP level that confers fully periodic collective oscillations should be dictated by the operation range of FCD. Such a view is supported from the estimates of the extracellular cAMP concentration at various cell densities. Under typical experimental parameters, owing to the high dilution rate (γ ∼ 6 min−1 in the present study) compared with the timescale of intracellular cAMP dynamics (∼1/7 min−1), the concentration of extracellular cAMP (z) can be estimated by applying quasi–steady-state approximation (SI Equations). At cell densities of 1/2 and 1/8 ML, where population of cells exhibited cAMP oscillations at a constant high frequency (Fig. 1C) (24), the estimated basal concentrations of extracellular cAMP are 0.72 nM for 1/2 ML and 0.18 nM for 1/8 ML, which are well within the FCD range (Fig. 2E; ≥0.1 nM). At 1/32 and 1/128 ML where populations showed sporadic or no oscillation, the estimated extracellular cAMP are 0.05 nM for 1/32 ML and 0.01 nM for 1/128 ML, which lie at the border or outside the FCD range (Fig. 2E; <0.1 nM). Thus, the conditions that support full-amplitude ∼7-min period oscillations agree well with the FCD range.
The critical relation between FCD and the oscillatory conditions is also vindicated by the suppression of oscillations in the presence of exogenous cAMP and/or at low cell densities as demonstrated experimentally (Fig. 1 B and C) as well as in the numerical simulations (Fig. 5F). Here, the model equations were extended to include the influx of exogenous cAMP (z0) by rewriting the equation for z as , which now violates the condition for scale invariance. The phase diagram in the parameter space (z0, ρ) obtained numerically shows a linear slope that demarcates the oscillatory and nonoscillatory domains (Fig. 5G), which closely resembles the phase diagram obtained experimentally (Fig. 1C). The feature of the phase diagram can be understood by the fold-change responsiveness of the constituent cells as follows. Under no exogenous cAMP, the estimated fold change in the extracellular cAMP level during the oscillations is zpeak(ρ)/zbasal(ρ), where zpeak and zbasal are the peak and basal concentrations of extracellular cAMP, respectively, both of which increase as a function of cell density (SI Equations). Conversely, in the presence of exogenous cAMP, the estimate would be Az (ρ, z0) = (zpeak(ρ) + z0)/(zbasal(ρ) + z0). Because Az is a decreasing function of z0 and increasing function of ρ, at higher concentrations of exogenous cAMP and/or at lower cell densities, the response becomes small and less likely to sustain oscillations. Our single-cell data (Fig. 2C) indicate that the change in the level of extracellular cAMP should be greater than ∼10-fold; otherwise, the response amplitude was markedly diminished, and there were no population-level oscillations. Consistent with such a view, the values of Az for conditions that supported the oscillations were always higher than those in the nonoscillatory conditions and the border between the two domains was at Az ∼ 10 (Table S1). These results suggest that the secrete-and-sense system that consists of FCD elements captures the essence of the density dependence of the oscillations.
Table S1.
Estimated ratio change in the extracellular cAMP level in the presence of exogenous cAMP; Az = (zpeak + z0)/(zbasal + z0)
| z0 = 0, nM | z0 = 0.3, nM | z0 = 1, nM | z0 = 3, nM | |
| 1/2 ML | 30.0 | 21.5 | 13.1 | 6.6 |
| 1/8 ML | 30.0 | 11.9 | 5.4 | 2.6 |
| 1/32 ML | 30.0 | 4.8 | 2.2 | 1.4 |
Oscillatory (in boldface) and nonoscillatory (in regular font) states experimentally determined (Fig. 1C) are shown.
SI Materials and Methods
FRET Index Calculations.
FRET efficiency between the CFP and the YFP moiety in the cAMP sensor Epac1camps is a monotonically decreasing function of cAMP concentration (59). Cells are typically illuminated with 435-nm light, and the ratio of fluorescent intensities at 485 and 540 nm (“FRET ratio”) serves as a convenient measure of relative changes in the cytosolic cAMP level in individual and populations of Dictyostelium cells (24, 26). However, the simple ratiometry contains a channel cross talk and cross-excitation, thus not ideally suited for detailed quantification and cell-to-cell comparisons. The cross talk results from spectral overlaps between CFP and YFP emission. Cross-excitation refers to fluorescence from YFP excited by 435-nm light that is intended to target CFP. The degree of data distortion depends on the expression level of the sensor protein, which is variable between the cells, and the optical setup used.
The measured signals were corrected for the non-FRET components essentially as described earlier (27, 60, 61). In brief, the coefficient for spectral bleed-through (α) in our optical setup was determined by first obtaining fluorescence images from AX4 cells expressing untagged CFP. Here, the CFP-expressing cells were excited with 435-nm light and the single-cell fluorescence intensities in the “CFP-channel” (460–510 nm) and the “FRET channels” (515–560 nm) were obtained. The average background fluorescence intensities obtained from pixels outside the cells were subtracted before calculating the coefficient (Fig. S1A). Next, the coefficient for the cross-excitation (β) was obtained by illuminating AX4 cells expressing untagged YFP with 435- or 500-nm light and recording the average fluorescence intensities in the FRET channel (515–560 nm) for 435-nm excitation and the “YFP-channel” (515–560 nm) for 500-nm excitation. After background correction, the fluorescence intensity in the FRET channel was divided by YFP channel to obtain the ratio β (Fig. S1B). The fluorescence intensity detected in the FRET channel (IFRET) (515–560 nm) of Epac1camps/AX4 cells excited with 435 nm can be expressed as IFRET = IFRET-corr + α × ICFP + β × IYFP-dir, where IFRET-corr is the expected true FRET signal, ICFP is the fluorescence intensities in the CFP channel, and IYFP-dir is the fluorescent intensities obtained by direct excitation at 500 nm. The acceptor intensity IYFP-dir was obtained per run basis, before time-lapse imaging. From the acquired images in the CFP and the FRET channel, we obtained the background-subtracted mean fluorescence intensities of the cell masks: ICFP and IFRET, respectively. Finally, we obtained the “FRET index” ICFP/IFRET-corr as a corrected indicator of the FRET efficiency.
Traveling-Wave Experiments.
The “lighthouse” device consists of a circular observation chamber whose ceiling has a port at the center for loading stimulus and three ports surrounding it to pump in “control stream,” which directs the stimulus flow laterally in a desired orientation (33). For stimulus solution, DB containing a high concentration of cAMP and 0.1 μg⋅mL–1 Alexa Fluor 594 (Invitrogen; A10438) was loaded at the rate of 0.375 μg·mL−1. DB containing a basal concentration of cAMP was used for the control stream. The flow direction was continuously changed while keeping the flow rates of the control stream at the chamber center constant by regulating four syringe pumps (pump 11 elite; Harvard). The entire sequence was automated by custom-made programs. The total flow rate of control stream was typically around 15 μL⋅min−1 depending on the direction and does not introduce shear-induced bias in cell migration (33). Suspension of starved cells at a density of 1 × 106 cells⋅mL–1 was backloaded from the outlet using a 1-mL syringe (Terumo). An inverted microscope (IX81; Olympus) equipped with an EMCCD camera (Evolve512; Photometrics) and 60× oil-immersion objective lens (PlanApoN, NA 1.42; Olympus) was used to obtain time lapse images. For Alexa 594, a 540-nm excitation filter (BP530-550; Olympus), a 575-nm long-pass filter (BA575nmIF; Olympus), and a 570-nm dichroic mirror (DM570, Olympus) were used. The average fluorescent intensities of Alexa 594 was flat-field corrected and used to estimate the cAMP concentration as described previously (18, 62).
Quantification of PHCRAC Translocation.
The dynamics of membrane translocation of PHCRAC-RFP (Fig. S3A) were observed by laser confocal live-cell imaging. To observe overall qualitative changes in the PHCRAC-RFP distribution (Fig. 4 A and B), low-magnification images were acquired using a 20× objective lens. The median of fluorescence intensities in each of the cell (cytosolic intensity) was analyzed. For quantitative analysis (Fig. 4 C–F and Fig. S3 B and C), high-magnification data taken with a 60× objective lens were analyzed essentially as described (63). In brief, the membrane region and fluorescent and nonfluorescent organellar regions were detected and eliminated from the region of interest (Fig. S3B). The membrane region was defined by the boundary between the cells and the background (Fig. S3B). Fluorescent and nonfluorescent objects within the cell membrane were detected by median filtering. The cell boundary region can be detected regardless of the degree of PHCRAC-RFP membrane translocation (Fig. S3B). The cytosolic intensity was then obtained by taking the median of the fluorescence intensity of the cytosolic region. The time series of the signal were normalized as follows (63):
where IC and IB are the median of the fluorescence intensity in the cytosol and the background regions, respectively. is the average of IC from five time points immediately before the application of extracellular cAMP. The data were corrected for photobleaching by subtracting the trend of decay from the time series data. The rate of photobleaching was estimated from an independent measurement of cells under no cAMP stimulation by fitting the time course of fluorescence intensities by a linear function (y = at + 1) (Fig. S3C, Left).
SI Equations
Proofs of Scale Invariance.
A system,
is said to describe fold-change detection (FCD) when any two proportional inputs z = z1(t) and z = z2(t), that is, for z1(t) > 0, z2(t) = pz1(t) for any constant p > 0, yields an identical output y(t) given that the system is initially at the steady state (5). The variable x(t) is an additional variable that is essential for adaptation of y(t) to constant input z (3) and for FCD as described below. According to Shoval et al. (5), mathematically, FCD holds if the system shows exact adaptation under constant input z and satisfies the following condition for any p > 0 with an appropriate function ϕ:
| [S1] |
In the present study, we extended the FCD framework to incorporate sensing and secretion of the same molecule so that z is no longer a parameter but a variable. Together with variables x and y, they constitute an autonomous closed-loop system:
| [S2] |
where y and z describe the concentration of the signaling molecules in the intracellular and extracellular space, respectively. The intracellular signaling molecule y is secreted at a constant rate kt per unit cell density ρ and diluted (or degraded) at a constant rate γ.
If the equations for x and y in Eq. S2 satisfy the condition (Eq. S1), given a transformation,
| [S3] |
it follows that
Therefore, Eq. S2 are invariant under the scale transformation (Eq. S3). Similarly, as long as the FCD condition (Eq. S1) is satisfied, a set of equation with a more generalized form,
is also invariant under the transformation (Eq. S3). Note that, even if the extracellular signaling molecule z is diffusive, that is, z is spatially extended and the dynamics are described by where D is the diffusion coefficient, the same holds true because is a linear operator.
Let us consider a more generalized system:
| [S4] |
where ξ (ρ) and h(y) are arbitrary functions of ρ and y, respectively. Here again, for f and g that obey the FCD condition (Eq. S1), if we consider a transformation,
where q is chosen such that ξ(pρ) = qξ(ρ) is satisfied, we see that
Thus, Eq. S4 are invariant under density change.
Last, let us consider a case where the rate of degradation is a function of cell density:
| [S5] |
Again, the equations for x and y satisfy the FCD condition (Eq. S1). The system (Eq. S5) in general is not invariant under scale transformation except in a case where the kinetics of extracellular signaling molecule is sufficiently fast. By assuming a quasi-steady state for z,
we see that Eq. S5 become the following:
Under the transformation
where q satisfies Θ(pρ) = qΘ(ρ),
Thus, the system (Eq. S5) is invariant under density change as long as the kinetics of z is sufficiently fast.
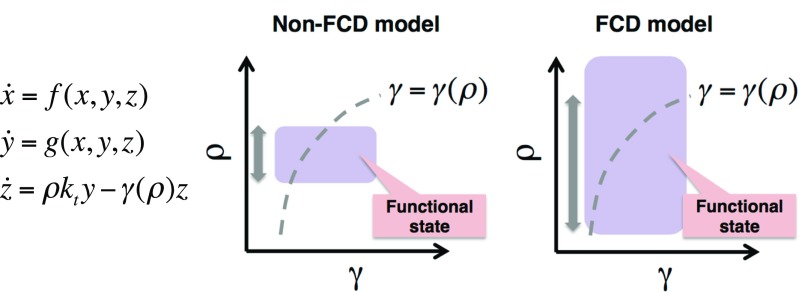
It should be noted that, even if the fast kinetics approximation does not hold, the FCD condition (Eq. S1) still enhances robustness of the system to variation in cell density ρ (Fig. S7). In contrast to the perfusion system (Eq. S2), the degradation rate γ in Eq. S5 is no longer a free parameter but depends on cell density ρ. Consequently, realizable states of the system in the phase diagram are restricted to the curve γ = γ(ρ). Because the FCD condition expands the area in the γ–ρ plane where the system assumes a qualitatively equivalent state (i.e., static or oscillatory) in the ρ direction, the length of the curve γ = γ(ρ) that overlaps with the state increases (gray arrows in Fig. S7). That is, the range of cell densities where the system is in a particular dynamical state increases; therefore, it improves the robustness to variations in cell density.
Fig. S7.
The robustness of oscillations also holds when the rate of degradation depends on cell density. Equations of a secrete-and-sense system with FCD (Left). The degradation rate of the extracellular signaling molecule γ depends on the cell density ρ. Realizable states of the system in the γ–ρ plane is restricted to a curve due to dependence of γ on ρ (Middle and Right; dashed lines). The shaded areas in the γ–ρ planes represent functional states (e.g., oscillatory states) of the system (Middle and Right; purple). The double-headed arrows indicate the density range in which the dotted lines and the purple areas overlap, that is, the functional (oscillatory) cell density range. Compared with non-FCD models (Left), the functional range expands in the ρ direction in FCD models (Right) due to the FCD property of the constituent cells (i.e., subsystem x and y).
Cell–Cell Variability.
The proof for the scale invariance described in the above section also holds when cell–cell variability is taken into account. Let us distinguish isolated cells by the suffix i (i = 1, 2, …, N) and describe the response of the ith cell to a common input z (i.e., extracellular cAMP) by , where xi is an internal variable required for adaptation and yi represents intracellular cAMP. For FCD at the single-cell level, we require that the functions fi and gi satisfy the following:
| [S6] |
for all i (i = 1, 2, …, N) with an appropriate transformation function ϕi and an arbitrary scaling factor p (>0). For the third equation that describes the dynamics of extracellular cAMP z in a perfusion chamber, we assume that extracellular medium is well-mixed and thus the secreted cAMP can be represented by the average . Thus, we arrive at the following:
| [S7] |
Following the same line of argument as in the above section, coupled differential equations of 2N + 1 variables (Eq. S7) are invariant under a transformation: .
Computational Search for Minimal FCD Circuits.
A computational search was performed to obtain minimal models with the FCD property. We limited our search to a class of networks with two nodes and three links of the following form:
where and denote the intermediate, the output, and the input variable, respectively. and are kinetic constants. The set of exact functions and used in the search are listed in Fig. S4A. The number of basic architectures in the computational search was 8 × 4 × 2 = 64. For each of the network topology examined, the kinetic constants were sampled from a logarithmic-scale grid search in the four-dimensional parameter space. The sampling range for the parameters was [0.1, 10], and the number of parameter set examined per model was . The input z(t) was given as two sequential step stimuli with the same fold increase; (Fig. S4B). The response dynamics under each step stimulus were evaluated essentially as described in earlier studies (3, 45). Each parameter set was evaluated by the criteria for the metrics described in Fig. S4C, and models that satisfied all criteria for more than 30% of the tested parameter sets were chosen. The metrics were calculated for both the initial and the second step stimuli.
From the computational search, we obtained the following set of models:
Model A
| [A] |
Model B
| [B] |
Model C
| [C] |
Model D
| [D] |
Model E
| [E] |
Model F
| [F] |
The validity of the computational search is supported from the fact that all of the selected models satisfy the FCD condition (Eq. S1); choose for model [A], model [C], and model [F], and for model [B], model [D], and model [E]. Models [A] and [B] are incoherent feedforward loops (Fig. S4D). Models [C] and [D] are negative-feedback loops (Fig. S4E). Earlier studies have found specific form of incoherent feedforward circuits (4) and negative-feedback circuits (5) that exhibit FCD. These correspond to models [A] and [C]. Concerning the dynamics of the output variable, models [E] and [F] are interchangeable with models [C] and [D] by transformation . Therefore, we adopted models [A]–[D] for further analysis. The four selected models were also found in a recent analytical search of a broader topological space (46). Models [A] and [C] are identical to those studied earlier as a representative model of FCD (4, 5).
Introduction of Cell–Cell Signaling to the Minimal FCD Models.
To describe the population-level dynamics in the perfusion chamber, we introduced to the selected FCD models an equation for the extracellular input variable z, that is, , which makes the system autonomous by feeding back the output to the input (Fig. 5C). Furthermore, to take into account the nonlinear input–output relation of the cAMP relay response (Fig. 2C), we replaced the term that describes the rate of increase in y with a Michaelis–Menten form. Note that the FCD property still holds by choosing the transformation function for models [A′] and [C′], and for models [B′] and [D′].
The four models are as follows:
Model A′
| [A′] |
Model B′
| [B′] |
Model C′
| [C′] |
Model D′
| [D′] |
Without loss of generality, the number of parameters in the equations for x and y was reduced by normalization as follows:
Model A′,
Model B′,
Model C′,
Model D′,
Note that the extracellular cAMP level z was not rescaled. Rewriting the transformed variables X, Y, and Z as new x, y, and z respectively, we obtain the following:
Model A″
| [A″] |
Model B″
| [B″] |
Model C″
| [C″] |
Model D″
| [D″] |
All of the above models exhibit spontaneous oscillations (Fig. S5) that are inherently robust to the variation in cell density ρ because of the symmetry of the equations to the scale transformation:
where for the models [A″] and [C″] and for models [B″] and [D″].
Furthermore, the models were modified to include the lower limit of detection for the extracellular input variable by replacing z on the right-hand side of the equation for x and y by z + δ, where δ is a positive constant. Fig. S5B shows phase diagrams of the modified models. As shown in the main text for model [A″] (Fig. 5E), all four models showed essentially the same dependence of oscillations on the dilution rate γ and cell density ρ (Fig. S5B). The results agree well with the perfusion chamber experiments (24). The obtained behaviors did not depend on how the lower-detection limit was implemented. For example, substituting x with x + δ in the Michaelis–Menten term introduces lower detection limit for the subsystem x, y, and similarly reproduced the triangular shape of the oscillatory domain in the phase diagram. Furthermore, the dependence of the oscillatory state on the elevated background level of the input variable z0 can be studied by replacing the equation for z with . Fig. S5C shows that the shape of the oscillatory domain in the phase diagram is conserved in all four models. Note that, in the present simulations, the oscillation takes a constant periodicity irrespective of cell density ρ and dilution rate γ. At the boundary between the oscillatory and the nonoscillatory state in the phase diagram, our previous study has shown a lengthening of the periodicity, which was suggested to be due to the stochasticity of the cAMP relay response (24). Such stochastic effects can be incorporated into our models by introducing additional noise terms without losing the essence of the scale invariant property.
Parameter Values.
In the present perfusion setup, a unit cell density of 1 ML (=6.6 × 103 cells per mm2) converts to the following:
where r is the radius of the perfusion chamber and R is the radius of cells. In addition, the dilution rate γ is determined by the ratio of flow rate to the total volume of the chamber. For experiments shown in Fig. 1,
The estimated value of the export rate is kt = 3.6 min−1 (24). Under the typical experimental parameters, the concentration of extracellular cAMP (z) can be approximated by the quasi–steady-state assumption, that is,
| [S8] |
In the experiment where exogenous cAMP was applied to populations of cells (Fig. 1 B and C), the ratio of change in extracellular cAMP is calculated by (zpeak + z0)/(zbasal+ z0), where zpeak and zbasal are the peak and basal extracellular concentrations of cAMP estimated from Eq. S8 in the absence of exogenous cAMP and substituting experimentally determined intracellular cAMP level, that is, 30-fold change from basal level of 0.4 μM cAMP (24). The estimated ratio changes in extracellular cAMP in the perfusion experiments are summarized in the Table S1.
M&G Model.
The M&G model (50) describes the kinetics of cAMP synthesis, secretion, and degradation according to the knowledge available at the time (64). Similar to our mathematical framework for the cAMP oscillations (Eq. 2), the M&G model assumes spatial uniformity and it is composed of two-variable equations describing cellular state (internal variable x and output variable, or intracellular cAMP, y) and one equation for the extracellular environment (input variable, or extracellular cAMP, z).
The equations are as follows:
where
The model successfully explains excitability and oscillations in cell suspension (50), perfused cells (28), as well as propagating waves in cells on a solid support (65–70). However, the model lacks the rescaling property in the subsystem x and y, and thus the oscillations are sensitive to variations in cell density (Fig. S6). The parameter values for M&G model are described in the legend to Fig. S6.
Discussion
The present study demonstrated that the cAMP relay response is adaptive and fold-change dependent at low extracellular cAMP concentrations (≤10 nM). Based on the observed input–output relation, we proposed a model that consists of elements that obey FCD that well describes the cell density and extracellular cAMP conditions that support the population-level oscillations. Recently, an alternative model based on the Fitzhugh–Nagumo equations was proposed (26). There, it is thought that population-level oscillations emerge as a result of a stochastic threshold-like response to fluctuating levels of extracellular cAMP. Such a view contrasts markedly with the model proposed here where a positive-feedback loop between intracellular and extracellular cAMP and adaptation of the response give rise to oscillations—a deterministic scheme that shares its core idea with other earlier models (50). The appearance of frequency selectivity and a refractory period (26) do not suffice as a criteria for model selection as these behaviors were also reproduced in the current adaptation-based model (Fig. S2 B and C and SI Discussion). Experimentally, the obtained dose–response (Fig. 2C) had no clear threshold but rather increased gradually—a feature not in support of an excitable noise-driven mechanism. Moreover, according to the Fitzhugh–Nagumo-type mechanism, inclusion of exogenous cAMP should give rise to more pulses of cAMP by increasing the chance to cross the response threshold. Our observations were quite the opposite. The oscillations were suppressed by exogenous cAMP (Fig. 1 B and C). Despite these caveats, we should note that the Fitzhugh–Nagumo-based model captures the sustained (i.e., nonadaptive) oscillatory response behavior (26) that occurs under prolonged stimulus in the non-FCD range (>10 nM cAMP) (24). These oscillations are driven intracellularly without the need for clearing of extracellular cAMP—a feature in favor of the Fitzhugh–Nagumo-type scheme. For the population-level oscillations, in contrast, a strict dependency on extracellular cAMP clearing has been demonstrated by a null-mutant of extracellular phosphodiesterase that cannot oscillate unless it is cleared of extracellular cAMP by perfusion (28). It may be that different cAMP receptor forms (52) or receptor types (53) with different binding constants transduce FCD and non-FCD signals.
The present analysis and the proposed theoretical framework suggest that, when an adaptive response governed by FCD is incorporated into a “secrete-and-sense” circuitry (12, 44), the resulting cell–cell communication is robust to cell density change due to the scale-invariant property of the system equations. In the present analysis, the extracellular signaling molecule z is described by a relatively simple equation owing to the first-order secretion kinetics (13) and the constant dilution rate realized by perfusion. In addition, density robustness can also be realized in more complex situations, for example, nonlinear secretion kinetics, a density-dependent degradation rate, and spatial inhomogeneity (SI Equations, Fig. S7, and SI Discussion). Although the FCD mechanism could explain the ability of Dictyostelium cells to execute aggregating behavior at a wide range of cell density (21, 22), the present findings do not rule out other mechanisms that may be at work in conjunction. cAMP-dependent regulation of a gene encoding extracellular PDE can provide robustness (28), in this case by keeping the level of extracellular cAMP within a desirable range. Cell–cell heterogeneity in the response sensitivity could also render oscillations robust to cell density change (Fig. 2F, Left). We should note, however, that FCD at the single cell–level (Fig. 2H) alleviates the requirement for averaging over many cells, which could be critical in nature where averaging is limited by diffusion. Given the ubiquity of adaptation and secrete-and-sense circuits (12), FCD-based robustness may have a wide connotation in other multicellular phenomena. A case in point is the collective oscillations of NADH in yeast cell suspension whose amplitude and frequency are conserved for three orders of magnitude in cell density (54). In higher organisms, morphogen fields are dynamic and their temporal changes appear to be read out to regulate cell fates (10, 55). Traveling waves are also prevalent in embryonic development (56, 57). It would be interesting to explore whether the same mathematical principle applies in these and other systems.
SI Discussion
Frequency Selectivity and the Effective Refractory Period.
Isolated cells were stimulated with periodic stimuli to mimic the oscillatory dynamics of extracellular cAMP concentrations. Fig. S2A shows the response by the cells to 30-fold change stimuli on top of 0.1 and 1 nM background cAMP. For both priming concentrations, the cells fully responded in phase with the stimuli given at 6-min intervals (Fig. S2A, Left). At 2-min period, the response became more erratic and attenuated (Fig. S2A, Right) suggesting the presence of refractoriness (15, 24, 26). Numerical simulations of the model demonstrated that such a frequency dependency is faithfully captured by the present model (Fig. S2B). Furthermore, the recovery curve of the response after prolonged stimulation (Fig. S2C) closely resembled the experimentally obtained kinetics of deadaptation (15, 16). The apparent refractoriness derives from the slow recovery of variable x after the stimulus release. Our simple adaptive model thus is able to capture one of the prominent feature of the cAMP relay—the attenuation of the response to repetitive stimulus at fast intervals.
Scale-Invariant Signaling in Various Conditions.
The symmetry of the system described in the main text assumed a simple governing equation for z in equations (Eq. 2) that essentially captures the dynamics of extracellular cAMP in a perfusion chamber. However, under more physiologically relevant conditions, accumulation of extracellular PDE would require more complex description of cAMP hydrolysis (28, 70). Moreover, depending on the conditions, secretion of cAMP may deviate from the first-order kinetics (13) used here. To further explore generality of the FCD-derived robustness, we investigated modifications to the equation for z in combination with x and y that obey the FCD property. We found that the scale-invariant property holds (SI Equations for proof) in at least two other conditions: (i) the term that describes secretion of signaling molecule consists of arbitrary functions of ρ and y [i.e., dz/dt = ξ(ρ)h(y) − γ z], (ii) z is coupled diffusively instead of globally as in the case of perfusion (i.e., dz/dt = ρkty − γ z + D∇2z). Therefore, spatial uniformity is not required for the scale invariance. In addition, provided that the kinetics of the extracellular molecule is sufficiently fast, (iii) the term that describes degradation (or dilution) of z may include an arbitrary function of ρ [i.e., dz/dt = ρkty − γ(ρ)z] as in the case where an enzyme is secreted by cells to degrade z. The results indicate that the causal relation between the rescaled response of each individual cells and a robust collective behavior could apply to more natural conditions for Dictyostelium development.
Materials and Methods
Strains and Cell Culture.
Dictyostelium discoideum AX4 cells expressing Epac1camps (Epac1camps/AX4) (24), PH domain of CRAC fused to monomeric red fluorescent protein (mRFP) (PHCRAC-RFP/AX4) (43), and both PHCRAC-RFP and Epac1camps (Epac1camps PHCRAC-RFP/AX4) were used. For coexpression, Epac1camps/AX4 cells were transformed with PHCRAC-RFP expression vector by electroporation. A clonal isolate showing normal development with relatively bright fluorescent for both probes was used for the analysis. Cells were grown at 22 °C in PS medium (58) with 10 μg/mL G418 and/or 60 μg/mL hygromycin B, where appropriate. Typically, 30-mL cell culture was shaken in an Erlenmeyer flask (250 mL; Bellco) at 155 rpm (Taitec; BR43-FL). Cells were propagated below ∼2 × 106 cells per mL. For live-cell imaging, cells were removed from growth medium by centrifugation for 3 min at 700 × g followed by resuspension in fresh developmental buffer (DB) (10 mM K/Na2 phosphate buffer, 1 mM CaCl2, 2 mM MgCl2; pH 6.5). The washing step was repeated twice. The cells were resuspended in ∼1-mL DB at ∼2 × 107 cells per mL and allowed to differentiate for 4–5 h in a centrifuge tube shaken at 155 rpm (Taitec; BR43-FL).
Perfusion and Live-Cell Microscopy.
Starved cells were plated on a glass-bottom dish at a cell density below 1 × 103 cells per cm2, and a perfusion chamber was constructed using an insert (RC-37F; Warner Instruments) as previously described (24), with the exception of results shown in Fig. 3, which used the lighthouse device (33) (SI Materials and Methods). After cells have attached to the bottom of the chamber, DB was perfused to remove effects from past stimuli at the rate of 4–8 mL/min, unless otherwise noted. For the cAMP relay study, the flow rate was kept at 8 mL/min for longer than 1 min before and after stepwise changes in the cAMP concentrations. At the given flow rate, one-half of the solution in the chamber was exchanged within 10 s as tested by monitoring fluorescein solution under a microscope. When there is no need to change the stimulus level, the flow rate was reduced to 4 mL/min. For observations of population-level cAMP oscillations, the flow rate was 1.5 mL/min.
Epifluorescent live-cell imaging of Epac1camps/AX4 cells was performed essentially as described in the previous work (24) using the same inverted microscopy system. In the present study, images were taken at 10- to 15-s intervals for total duration of ∼0.5–2 h. In addition, an image from the YFP channel was acquired to correct for cross-excitation immediately before time-lapse acquisition (SI Materials and Methods). To this end, cells were exposed for 30 ms with 495-nm light using an excitation filter (BP490-500HQ; Olympus), which was further attenuated by 6% using neutral density filters. The emitted light was separated from the excitation by a dichroic mirror (DM505; Olympus).
Confocal imaging of PHCRAC-RFP/AX4 and PHCRAC-RFP Epac1/AX4 was performed using an inverted microscope (IX-81; Olympus) equipped with an automated stage (BIOS-215T; Sigma Koki), a confocal scanning unit (CSU-X1; Yokogawa), and optical shutters (LS6ZM2; Uniblitz Electronics). An oil-immersion objective lens (60× PlanApo N, N.A. 1.42, or 20× UPlanSApo N, N.A. 0.85; Olympus) was used. The stage and the shutters were controlled by a stage controller (FC-101G; Sigma Koki) and a shutter driver (VMM-D3; Uniblitz Electronic), respectively. The device control and data acquisition were conducted using the Metamorph software (Molecular Devices). A 445-nm laser (40 mW; Vortran Laser Technology) and a 561-nm laser (25 mW; Melles Griot) were used as light sources. For imaging PHCRAC-RFP, cells were exposed to 561-nm laser for 30 ms. The laser was attenuated by 50% with a neutral density filter. The fluorescent light was passed through an emission filter (BA575IF; Olympus). For Epac1camps-expressing cells, 445-nm laser attenuated by 50% using neutral density filters was applied for 50 ms. A set of multiband dichroic mirror and filters (CFP/YFP/HcRed-3X3M-A; Semrock) was used except for the CFP excitation filter (BP425-445HQ; Olympus). Sixteen-bit 512 × 512 pixel images were captured at 3- to 10-s interval using an EMCCD camera (Evolve 512; Photometrics). All image acquisition was performed at 22 °C. Data were stored in tagged image file format (TIFF) files.
Supplementary Material
Acknowledgments
We thank all members of the S.S. Laboratory and the K. Kaneko Laboratory and T. S. Shimizu for stimulating discussions, P. R. ten Wolde for suggestions on an earlier version of the manuscript, and V. O. Nikolaev and M. J. Lohse for providing an Epac1camps plasmid. This work was supported by Japan Society for the Promotion of Science KAKENHI Grants JP25710022, JP15KT0076, JP16H01442, JP25103008 (to S.S.), and JP16K18537 (to A.N.); Fellows Grant 23-10097 (to K. Kamino); Japan Science and Technology Agency Precursory Research for Embryonic Science and Technology Grant JPMJPR11AD (to S.S.); and the Agency for Medical Research and Development, Platform for Dynamic Approaches to Living System.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1702181114/-/DCSupplemental.
References
- 1.Devreotes PN, Steck TL. Cyclic 3′,5′ AMP relay in Dictyostelium discoideum. II. Requirements for the initiation and termination of the response. J Cell Biol. 1979;80:300–309. doi: 10.1083/jcb.80.2.300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Koshland DE, Jr, Goldbeter A, Stock JB. Amplification and adaptation in regulatory and sensory systems. Science. 1982;217:220–225. doi: 10.1126/science.7089556. [DOI] [PubMed] [Google Scholar]
- 3.Ma W, Trusina A, El-Samad H, Lim WA, Tang C. Defining network topologies that can achieve biochemical adaptation. Cell. 2009;138:760–773. doi: 10.1016/j.cell.2009.06.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Goentoro L, Shoval O, Kirschner MW, Alon U. The incoherent feedforward loop can provide fold-change detection in gene regulation. Mol Cell. 2009;36:894–899. doi: 10.1016/j.molcel.2009.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shoval O, et al. Fold-change detection and scalar symmetry of sensory input fields. Proc Natl Acad Sci USA. 2010;107:15995–16000. doi: 10.1073/pnas.1002352107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lazova MD, Ahmed T, Bellomo D, Stocker R, Shimizu TS. Response rescaling in bacterial chemotaxis. Proc Natl Acad Sci USA. 2011;108:13870–13875. doi: 10.1073/pnas.1108608108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Adler M, Mayo A, Alon U. Logarithmic and power law input-output relations in sensory systems with fold-change detection. PLoS Comput Biol. 2014;10:e1003781. doi: 10.1371/journal.pcbi.1003781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kamino K, Kondo Y. Rescaling of spatio-temporal sensing in eukaryotic chemotaxis. PLoS One. 2016;11:e0164674. doi: 10.1371/journal.pone.0164674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Goentoro L, Kirschner MW. Evidence that fold-change, and not absolute level, of beta-catenin dictates Wnt signaling. Mol Cell. 2009;36:872–884. doi: 10.1016/j.molcel.2009.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wartlick O, et al. Dynamics of Dpp signaling and proliferation control. Science. 2011;331:1154–1159. doi: 10.1126/science.1200037. [DOI] [PubMed] [Google Scholar]
- 11.Lee REC, Walker SR, Savery K, Frank DA, Gaudet S. Fold change of nuclear NF-κB determines TNF-induced transcription in single cells. Mol Cell. 2014;53:867–879. doi: 10.1016/j.molcel.2014.01.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Youk H, Lim WA. Secreting and sensing the same molecule allows cells to achieve versatile social behaviors. Science. 2014;343:1242782. doi: 10.1126/science.1242782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dinauer MC, MacKay SA, Devreotes PN. Cyclic 3′,5′-AMP relay in Dictyostelium discoideum. III. The relationship of cAMP synthesis and secretion during the cAMP signaling response. J Cell Biol. 1980;86:537–544. doi: 10.1083/jcb.86.2.537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dinauer MC, Steck TL, Devreotes PN. Cyclic 3′,5′-AMP relay in Dictyostelium discoideum. V. Adaptation of the cAMP signaling response during cAMP stimulation. J Cell Biol. 1980;86:554–561. doi: 10.1083/jcb.86.2.554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dinauer MC, Steck TL, Devreotes PN. Cyclic 3′,5′-AMP relay in Dictyostelium discoideum. IV. Recovery of the cAMP signaling response after adaptation to cAMP. J Cell Biol. 1980;86:545–553. doi: 10.1083/jcb.86.2.545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fukujin F, Nakajima A, Shimada N, Sawai S. Self-organization of chemoattractant waves in Dictyostelium depends on F-actin and cell-substrate adhesion. J R Soc Interface. 2016;13:20160233. doi: 10.1098/rsif.2016.0233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Skoge M, et al. Cellular memory in eukaryotic chemotaxis. Proc Natl Acad Sci USA. 2014;111:14448–14453. doi: 10.1073/pnas.1412197111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nakajima A, Ishihara S, Imoto D, Sawai S. Rectified directional sensing in long-range cell migration. Nat Commun. 2014;5:5367. doi: 10.1038/ncomms6367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Alcantara F, Monk M. Signal propagation during aggregation in the slime mould Dictyostelium discoideum. J Gen Microbiol. 1974;85:321–334. doi: 10.1099/00221287-85-2-321. [DOI] [PubMed] [Google Scholar]
- 20.Lee KJ, Cox EC, Goldstein RE. Competing patterns of signaling activity in Dictyostelium discoideum. Phys Rev Lett. 1996;76:1174–1177. doi: 10.1103/PhysRevLett.76.1174. [DOI] [PubMed] [Google Scholar]
- 21.Hashimoto Y, Cohen MH, Robertson A. Cell density dependence of the aggregation characteristics of the cellular slime mould Dictyostelium discoideum. J Cell Sci. 1975;19:215–229. doi: 10.1242/jcs.19.1.215. [DOI] [PubMed] [Google Scholar]
- 22.Gingle AR. Critical density for relaying in Dictyostelium discoideum and its relation to phosphodiesterase secretion into the extracellular medium. J Cell Sci. 1976;20:1–20. doi: 10.1242/jcs.20.1.1. [DOI] [PubMed] [Google Scholar]
- 23.Wang B, Kuspa A. Dictyostelium development in the absence of cAMP. Science. 1997;277:251–254. doi: 10.1126/science.277.5323.251. [DOI] [PubMed] [Google Scholar]
- 24.Gregor T, Fujimoto K, Masaki N, Sawai S. The onset of collective behavior in social amoebae. Science. 2010;328:1021–1025. doi: 10.1126/science.1183415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kamino K, Fujimoto K, Sawai S. Collective oscillations in developing cells: Insights from simple systems. Dev Growth Differ. 2011;53:503–517. doi: 10.1111/j.1440-169X.2011.01266.x. [DOI] [PubMed] [Google Scholar]
- 26.Sgro AE, et al. From intracellular signaling to population oscillations: Bridging size- and time-scales in collective behavior. Mol Syst Biol. 2015;11:779. doi: 10.15252/msb.20145352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Börner S, et al. FRET measurements of intracellular cAMP concentrations and cAMP analog permeability in intact cells. Nat Protoc. 2011;6:427–438. doi: 10.1038/nprot.2010.198. [DOI] [PubMed] [Google Scholar]
- 28.Masaki N, Fujimoto K, Honda-Kitahara M, Hada E, Sawai S. Robustness of self-organizing chemoattractant field arising from precise pulse induction of its breakdown enzyme: A single-cell level analysis of PDE expression in Dictyostelium. Biophys J. 2013;104:1191–1202. doi: 10.1016/j.bpj.2013.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tomchik KJ, Devreotes PN. Adenosine 3′,5′-monophosphate waves in Dictyostelium discoideum: A demonstration by isotope dilution–fluorography. Science. 1981;212:443–446. doi: 10.1126/science.6259734. [DOI] [PubMed] [Google Scholar]
- 30.Devreotes PN, Potel MJ, MacKay SA. Quantitative analysis of cyclic AMP waves mediating aggregation in Dictyostelium discoideum. Dev Biol. 1983;96:405–415. doi: 10.1016/0012-1606(83)90178-1. [DOI] [PubMed] [Google Scholar]
- 31.Garcia GL, Parent CA. Signal relay during chemotaxis. J Microsc. 2008;231:529–534. doi: 10.1111/j.1365-2818.2008.02066.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kriebel PW, Barr VA, Rericha EC, Zhang G, Parent CA. Collective cell migration requires vesicular trafficking for chemoattractant delivery at the trailing edge. J Cell Biol. 2008;183:949–961. doi: 10.1083/jcb.200808105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nakajima A, Ishida M, Fujimori T, Wakamoto Y, Sawai S. The microfluidic lighthouse: An omnidirectional gradient generator. Lab Chip. 2016;16:4382–4394. doi: 10.1039/c6lc00898d. [DOI] [PubMed] [Google Scholar]
- 34.Postma M, Van Haastert PJM. Mathematics of experimentally generated chemoattractant gradients. Methods Mol Biol. 2016;1407:381–396. doi: 10.1007/978-1-4939-3480-5_26. [DOI] [PubMed] [Google Scholar]
- 35.McMains VC, Liao X-H, Kimmel AR. Oscillatory signaling and network responses during the development of Dictyostelium discoideum. Ageing Res Rev. 2008;7:234–248. doi: 10.1016/j.arr.2008.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sasaki AT, Chun C, Takeda K, Firtel RA. Localized Ras signaling at the leading edge regulates PI3K, cell polarity, and directional cell movement. J Cell Biol. 2004;167:505–518. doi: 10.1083/jcb.200406177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Comer FI, Lippincott CK, Masbad JJ, Parent CA. The PI3K-mediated activation of CRAC independently regulates adenylyl cyclase activation and chemotaxis. Curr Biol. 2005;15:134–139. doi: 10.1016/j.cub.2005.01.007. [DOI] [PubMed] [Google Scholar]
- 38.Comer FI, Parent CA. Phosphoinositide 3-kinase activity controls the chemoattractant-mediated activation and adaptation of adenylyl cyclase. Mol Biol Cell. 2006;17:357–366. doi: 10.1091/mbc.E05-08-0781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhang S, Charest PG, Firtel RA. Spatiotemporal regulation of Ras activity provides directional sensing. Curr Biol. 2008;18:1587–1593. doi: 10.1016/j.cub.2008.08.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Iijima M, Devreotes P. Tumor suppressor PTEN mediates sensing of chemoattractant gradients. Cell. 2002;109:599–610. doi: 10.1016/s0092-8674(02)00745-6. [DOI] [PubMed] [Google Scholar]
- 41.Brzostowski JA, et al. Phosphorylation of chemoattractant receptors regulates chemotaxis, actin reorganization and signal relay. J Cell Sci. 2013;126:4614–4626. doi: 10.1242/jcs.122952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Takeda K, et al. Incoherent feedforward control governs adaptation of activated ras in a eukaryotic chemotaxis pathway. Sci Signal. 2012;5:ra2. doi: 10.1126/scisignal.2002413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Taniguchi D, et al. Phase geometries of two-dimensional excitable waves govern self-organized morphodynamics of amoeboid cells. Proc Natl Acad Sci USA. 2013;110:5016–5021. doi: 10.1073/pnas.1218025110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Fujimoto K, Sawai S. A design principle of group-level decision making in cell populations. PLoS Comput Biol. 2013;9:e1003110. doi: 10.1371/journal.pcbi.1003110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Skataric M, Sontag ED. A characterization of scale invariant responses in enzymatic networks. PLoS Comput Biol. 2012;8:e1002748. doi: 10.1371/journal.pcbi.1002748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Adler M, Szekely P, Mayo A, Alon U. Optimal regulatory circuit topologies for fold-change detection. Cell Syst. 2017;4:171–181.e8. doi: 10.1016/j.cels.2016.12.009. [DOI] [PubMed] [Google Scholar]
- 47.Hamadeh A, Ingalls B, Sontag E. Transient dynamic phenotypes as criteria for model discrimination: Fold-change detection in Rhodobacter sphaeroides chemotaxis. J R Soc Interface. 2013;10:20120935. doi: 10.1098/rsif.2012.0935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Iglesias PA, Shi C. Comparison of adaptation motifs: Temporal, stochastic and spatial responses. IET Syst Biol. 2014;8:268–281. doi: 10.1049/iet-syb.2014.0026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Shankar P, Nishikawa M, Shibata T. Adaptive responses limited by intrinsic noise. PLoS One. 2015;10:e0136095. doi: 10.1371/journal.pone.0136095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Martiel JL, Goldbeter A. A model based on receptor desensitization for cyclic AMP signaling in Dictyostelium cells. Biophys J. 1987;52:807–828. doi: 10.1016/S0006-3495(87)83275-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Tang Y, Othmer HG. A G protein-based model of adaptation in Dictyostelium discoideum. Math Biosci. 1994;120:25–76. doi: 10.1016/0025-5564(94)90037-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zhang M, Goswami M, Sawai S, Cox EC, Hereld D. Regulation of G protein-coupled cAMP receptor activation by a hydrophobic residue in transmembrane helix 3. Mol Microbiol. 2007;65:508–520. doi: 10.1111/j.1365-2958.2007.05803.x. [DOI] [PubMed] [Google Scholar]
- 53.Insall RH, Soede RD, Schaap P, Devreotes PN. Two cAMP receptors activate common signaling pathways in Dictyostelium. Mol Biol Cell. 1994;5:703–711. doi: 10.1091/mbc.5.6.703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Aldridge J, Pye EK. Cell density dependence of oscillatory metabolism. Nature. 1976;259:670–671. doi: 10.1038/259670a0. [DOI] [PubMed] [Google Scholar]
- 55.Richards DM, Saunders TE. Spatiotemporal analysis of different mechanisms for interpreting morphogen gradients. Biophys J. 2015;108:2061–2073. doi: 10.1016/j.bpj.2015.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Ishimatsu K, Takamatsu A, Takeda H. Emergence of traveling waves in the zebrafish segmentation clock. Development. 2010;137:1595–1599. doi: 10.1242/dev.046888. [DOI] [PubMed] [Google Scholar]
- 57.Tsiairis CD, Aulehla A. Self-organization of embryonic genetic oscillators into spatiotemporal wave patterns. Cell. 2016;164:656–667. doi: 10.1016/j.cell.2016.01.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sawai S, Thomason PA, Cox EC. An autoregulatory circuit for long-range self-organization in Dictyostelium cell populations. Nature. 2005;433:323–326. doi: 10.1038/nature03228. [DOI] [PubMed] [Google Scholar]
- 59.Nikolaev VO, Bünemann M, Hein L, Hannawacker A, Lohse MJ. Novel single chain cAMP sensors for receptor-induced signal propagation. J Biol Chem. 2004;279:37215–37218. doi: 10.1074/jbc.C400302200. [DOI] [PubMed] [Google Scholar]
- 60.Gordon GW, Berry G, Liang XH, Levine B, Herman B. Quantitative fluorescence resonance energy transfer measurements using fluorescence microscopy. Biophys J. 1998;74:2702–2713. doi: 10.1016/S0006-3495(98)77976-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Xia Z, Liu Y. Reliable and global measurement of fluorescence resonance energy transfer using fluorescence microscopes. Biophys J. 2001;81:2395–2402. doi: 10.1016/S0006-3495(01)75886-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Nakajima A, Sawai S. Dissecting spatial and temporal sensing in Dictyostelium chemotaxis using a wave gradient generator. Methods Mol Biol. 2016;140:107–122. doi: 10.1007/978-1-4939-3480-5_8. [DOI] [PubMed] [Google Scholar]
- 63.Postma M, et al. Uniform cAMP stimulation of Dictyostelium cells induces localized patches of signal transduction and pseudopodia. Mol Biol Cell. 2003;14:5019–5027. doi: 10.1091/mbc.E03-08-0566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Goldbeter A. Biochemical Oscillations and Cellular Rhythms: The Molecular Bases of Periodic and Chaotic Behaviour. Cambridge Univ Press; Cambridge, UK: 1996. [Google Scholar]
- 65.Tyson JJ, Murray JD. Cyclic AMP waves during aggregation of Dictyostelium amoebae. Development. 1989;106:421–426. doi: 10.1242/dev.106.3.421. [DOI] [PubMed] [Google Scholar]
- 66.Tyson JJ, Alexander KA, Manoranjan VS, Murray JD. Spiral waves of cyclic AMP in a model of slime mold aggregation. Physica D. 1989;34:193–207. [Google Scholar]
- 67.Pálsson E, Cox EC. Origin and evolution of circular waves and spirals in Dictyostelium discoideum territories. Proc Natl Acad Sci USA. 1996;93:1151–1155. doi: 10.1073/pnas.93.3.1151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Lauzeral J, Halloy J, Goldbeter A. Desynchronization of cells on the developmental path triggers the formation of spiral waves of cAMP during Dictyostelium aggregation. Proc Natl Acad Sci USA. 1997;94:9153–9158. doi: 10.1073/pnas.94.17.9153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Geberth D, Hütt M-T. Predicting the distribution of spiral waves from cell properties in a developmental-path model of Dictyostelium pattern formation. PLoS Comput Biol. 2009;5:e1000422. doi: 10.1371/journal.pcbi.1000422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Pálsson E. A cAMP signaling model explains the benefit of maintaining two forms of phosphodiesterase in Dictyostelium. Biophys J. 2009;97:2388–2398. doi: 10.1016/j.bpj.2009.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.