Significance
Transport in the so-called “bad metallic” regime of strongly correlated electron systems with no well-defined electronic quasiparticles has been a long-standing challenge in theoretical physics. This challenge has motivated collection of an ample amount of data on bad metals. However, so far, emphasis has been given to the charge sector, with the host crystal lattice treated as a well-defined phonon background. In this paper, we show that, for cuprates in the bad metallic regime where resistivity exceeds the “Mott–Ioffe–Regel” limit, phonon excitations are also not well-defined. The data lead to a thermal transport scenario where entropy is carried by an overdamped diffusive fluid of electrons and phonons characterized by a unique velocity and a quantum-limited relaxation time .
Keywords: thermal diffusivity, bad metals, electron–phonon
Abstract
The thermal diffusivity in the plane of underdoped YBCO crystals is measured by means of a local optical technique in the temperature range of 25–300 K. The phase delay between a point heat source and a set of detection points around it allows for high-resolution measurement of the thermal diffusivity and its in-plane anisotropy. Although the magnitude of the diffusivity may suggest that it originates from phonons, its anisotropy is comparable with reported values of the electrical resistivity anisotropy. Furthermore, the anisotropy drops sharply below the charge order transition, again similar to the electrical resistivity anisotropy. Both of these observations suggest that the thermal diffusivity has pronounced electronic as well as phononic character. At the same time, the small electrical and thermal conductivities at high temperatures imply that neither well-defined electron nor phonon quasiparticles are present in this material. We interpret our results through a strongly interacting incoherent electron–phonon “soup” picture characterized by a diffusion constant , where is the soup velocity, and scattering of both electrons and phonons saturates a quantum thermal relaxation time .
The standard paradigm for transport in metals relies on the existence of quasiparticles. Electronic quasiparticles conduct electricity and heat. Phonon quasiparticles, the collective excitations of the elastic solid (here, we discuss acoustic phonons) also conduct heat. Transport coefficients, such as electrical and thermal conductivities, can then be calculated using, for example, Boltzmann equations (1). However, such an approach fails when the quasiparticle mean free paths become comparable with the quasiparticle wavelength. For electrons, it is the Fermi wavelength (2–4), whereas for phonons, it is the larger of the interatomic distance or minimum excited phonon wavelength (5, 6). Understanding transport in nonquasiparticle regimes requires a new framework and has become a subject of intense theoretical effort in recent years, triggering an urgent need for experimental results that can shed light on such regimes. In particular, in ref. 7, the diffusivity was singled out as a key observable for incoherent nonquasiparticle transport, possibly subject to fundamental quantum mechanical bounds.
In this work, we report high-resolution measurements of the thermal diffusivity of single-crystal underdoped YBCO6.60 (an ortho-II YBa2Cu3O6.60) and YBCO6.75 (an ortho-III YBa2Cu3O6.75). We are particularly interested in the anisotropy of the thermal diffusivity as measured along the principal axes and (which is the chain direction) in the temperature range 25–300 K. We use a noncontact optical microscope (see Fig. S1) to perform local thermal transport measurements on the scale of 10 m, hence avoiding inhomogeneities, particularly twinning and grain boundary effects. Our principal experimental results are as follows. (i) The measured thermal diffusivity is consistent with the previously measured thermal conductivity and specific heat, satisfying . The high-temperature specific heat is known to be dominated by phonons. However, (ii) the phonon mean free path implied by the magnitude of the measured diffusivity is of the order of or smaller than the phonon wavelength. In addition, (iii) the intrinsic thermal anisotropy is found to be almost identical to the electrical resistivity anisotropy, and (iv) the thermal anisotropy starts to decrease rather sharply below the charge order transition.
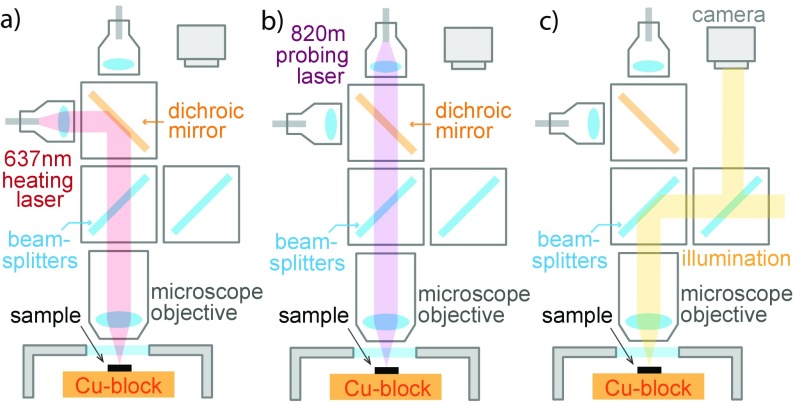
Fig. S1.
The schematic shows the optical paths of the setup. (A) Path of the heating laser. (B) Path of the probing laser. The reflected light traverses the same path before being gathered by a photodetector. (C) Path of camera vision. Cross-polarized picture is obtained by polarizing the incoming illumination and placing an analyzer in front of the camera.
A complete understanding of transport in the high-temperature regime of the YBCO (or similar) material system requires that we interpret our diffusivity results together with previously reported measurements of the charge sector on similar crystals at temperatures above the charge order transition, primarily photoemission spectroscopy (8, 9) and electrical resistivity (10–12). Those measurements suggest that the electronic mean free path is also comparable with or smaller than the electron wavelength and thus, at or beyond the MIR limit. [The MIR limit has been expressed in different ways in the literature (e.g., as or ; is the Fermi wavevector, is the lattice constant, and is the mean free path). These approaches typically produce the same order of magnitude estimate. In this paper, we use the criterion proposed in ref. 2 of , where .] The simultaneous destruction of phonon and electron quasiparticles together with comparable anisotropies in thermal and charge transport suggest that scattering is dominated by strong electron–phonon interaction. The lack of coherent response is, furthermore, incompatible with electron–phonon composite quasiparticles, such as polarons (13) or bipolarons (14). We are, therefore, led to conjecture a unique type of transport in the YBCO (or similar) system in the temperature regime where quasiparticles are not well-defined that is dominated by diffusion of an electron–phonon “soup.” Furthermore, all relaxation processes of electrons and phonons and hence, charge and heat are saturated at the thermal relaxation time . This “Plankian” timescale has previously been proposed to underpin transport across many families of unconventional metals (refs. 15–17references therein) and is widely observed in optical data on cuprates (18–21). A simple model based on the above ansatz shows excellent fit to the temperature dependence of the measured thermal diffusivity using measured material parameters. This approach generalizes the recently proposed incoherent metallic transport (7) to the case where the electronic system exhibits strong interactions with additional degrees of freedom—the phonons. An immediate additional generalization of our idea could apply to complex insulators at high fields, with magnetic or polarization excitations playing the role of the phonons.
Results and Discussion
Thermal Diffusivity Measurements.
For the high-resolution thermal diffusivity measurements, we use a photothermal microscope (SI Materials and Methods has a description of the photothermal microscope and its modes of operation), where a modulated power of a heating laser beam causes ripples in the temperature profile at the sample surface, which may be measured by a probing laser because of the change in reflectivity as a function of temperature. We obtain the diffusivity by fitting the phase delay between the source and the response signals as a function of the modulation frequency at fixed distance between the source and probe beam (Materials and Methods). In the case of an anisotropic sample, the extracted diffusivity depends on orientation as follows:
| [1] |
where and are the diffusivities of the two principle axes on the surface of the YBCO samples. Because , where the specific heat is a scalar quantity, the diffusivity inherits its spatial anisotropy from the thermal conductivity tensor . Several YBa2Cu3O6+x samples were measured; all showed consistent results with the two samples reported here: a detwinned single crystal of YBCO6.60 measuring ∼321 mm (Fig. S2A), and a detwinned single crystal of YBCO6.75 measuring ∼210.4 mm (Fig. S2B). In particular, Fig. S2B shows the surface of the YBCO6.75 with the focused laser spots under polarized light, where bright/dark stripes are the twin domains. The small scale of measurement enables us to measure local diffusivity in all directions of the Cu-O planes, while avoiding edges, twin boundaries, and other visible defects when possible. At room temperature (RT), both samples have reflectivity , and K−1 at 820 nm. The typical power of the probing laser is mW, and typical rms power of the heating laser is mW. Using thermal conductivities reported in existing literature (22), we estimate the increase in mean temperature caused by both lasers to be less than 1 K in the entire temperature range of interest. To check the alignment of the sample, we first measure diffusivity as a function of sample orientation relative to the axis of displacement of the laser spots shown in Fig. 1, Insets. Error bars are caused by the -m uncertainty in determining the distance between the two spots and thus, extracting from the data. The solid lines are a fit to Eq. 1, showing excellent agreement. The offset angle is left as a free parameter but agrees with the alignment to the sample edge to within . We find that the local orientations of the and axes swap between different twinning domains, verifying the single-domain nature of or measurements. Small variations (of order 10%) in diffusivity are measured at different areas on the sample surface, which we attribute to material inhomogeneity. After the principal axes are determined from the detailed anisotropy study, the temperature dependence of the diffusivity is measured along each of the principal axes in a continuous temperature sweep at a fixed frequency.
Fig. S2.
Cross-polarized images of the samples showing both laser spots: the left (smaller) spot is the 637-nm heating spot, and the right (larger) spot is the 830-nm probe laser spot. (A) A typical area of single-crystal detwinned YBCO6.60 and (B) a typical area of single-crystal detwinned YBCO6.75. Thin remnant strips of the opposite structural domain are visible as white lines but have been shown to have negligible effect on the anisotropy measurements. Insets show pictures of the crystals measured.
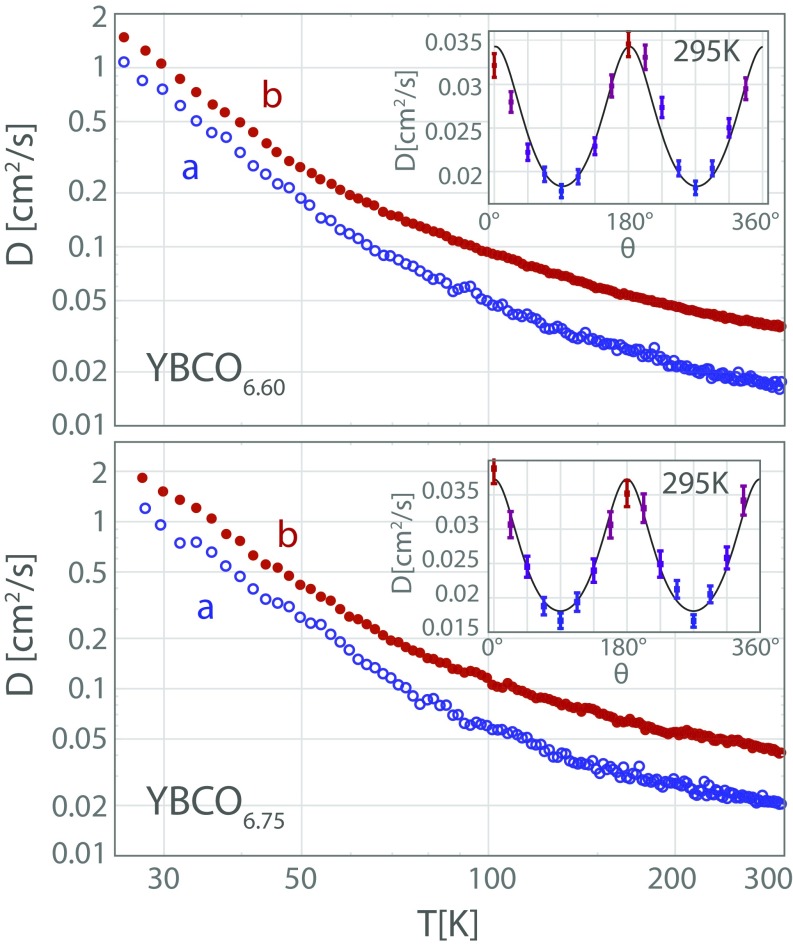
Fig. 1.
Thermal diffusivity of YBCO6.60 and YBCO6.75 single crystals extracted from phase measurements along a (blue) and b (chain direction, red) axes, and plotted on a log–log scale as a function of temperature in the range 25–300 K. Insets show diffusivity measured at RT as a function of orientation around the heating spot, with the solid lines representing fits to Eq. 1. Error bars are almost entirely caused by uncertainty in determining lasers spots separation.
Initial Observations.
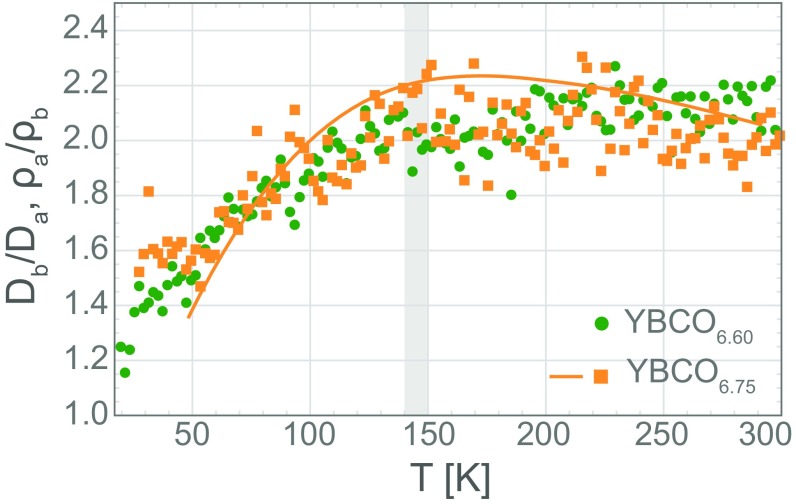
The temperature dependence of the diffusivities along both the and axes for two samples is shown in Fig. 1. We observe that the diffusivity increases at lower temperatures, increasing by almost two orders of magnitude in the temperature range studied here. Using existing measurements of specific heat on similar YBCO crystals (23), we obtain the respective thermal conductivities of the crystals; both show excellent agreement with previously measured thermal conductivities of YBCO crystals with similar doping [e.g., for YBCO6.60 was previously measured by Waske et al. (22) and Minami et al. (24)]. The temperature dependence of the thermal anisotropy, , for both samples is shown in Fig. 2. Three main features of the data are observed. First, the anisotropies of the two samples are similar. Second, the anisotropy is almost temperature-independent with at high temperatures but decreases sharply below the charge density wave (CDW) transition [ K (25)]. Third, the size and temperature dependence of the thermal anisotropy are very similar to those of the anisotropy of the electrical resistivity. In Fig. 2, we also plot the resistivity anisotropy of YBCO6.75 from ref. 12 measured on very similar crystals. Because the resistivity measures transport of the electronic system, we conclude here that the thermal diffusivity exhibits a strong electronic character. Furthermore, while at low doping levels, the charge order is strongly anisotropic (26) for the YBCO6.60 (27) and YBCO6.75 (28) reported here; an almost isotropic CDW transition would not strongly affect the diffusivity anisotropy of conventional phonons. Instead, in mirroring the behavior of the electrical resistivity, the decrease in anisotropy again indicates electronic contribution to the thermal diffusivity. The onset of CDW order can both change the scattering mechanism of the electrons and also lead to unique collective transport dynamics. The electronic excitations may ultimately regain their quasiparticle character, including possible polaronic behavior (13, 14). Furthermore, the CDW transition in this material is correlated with a strong electron–phonon interaction (29, 30). We further elaborate on these points below.
Fig. 2.
Anisotropy of the -plane thermal diffusivity as a function of temperature of YBCO6.60 (green circles) and YBCO6.75 (orange squares). Charge density order occurs at around K in both materials (25) and is marked by the gray region. Note that anisotropies decrease significantly below the transition, signifying the nontrivial role that the electronic system plays in the thermal transport. The solid line is the electrical anisotropy in the plane on similar crystals adopted from ref. 12.
Good Metals Vs. Bad Metals.
The conventional treatment of heat conduction in itinerant solids assumes the existence of well-defined quasiparticle excitations that transport entropy: electrons and phonons. The mean free paths, and , for the electrons and phonons, respectively, are assumed to be much larger than their respective wavelength. For electrons to be well-defined quasiparticles, we require that , where is the Fermi wavelength. The limiting case is called the MIR limit, beyond which the material is dubbed a “bad metal” (2). Analogously, for well-defined phonon excitations, we require that , where is the lattice constant, and ( is the sound velocity) is the highest acoustic phonon frequency excited at temperature (5, 6). If both conditions are met, the thermal conductivity of the solid will be the sum of the thermal conductivities of the electrons and phonons, which can also be written as products of the respective diffusivities and specific heat capacities:
| [2] |
The last equality states that the measured thermal diffusivity is a heat capacity-weighted average of the two diffusivities, and .
The consequences of Eq. 2 are well-shown in the case of both good and disordered metals, even at temperatures of the order of the Debye temperature. Table 1 gives examples of RT thermal transport parameters for good metals (copper, gold, silver, and tungsten), metals with large RT resistivity (mercury, constantan, and Inconel), and several cuprates, which are known to be bad metals at RT. In the case of good and disordered metals, ample data are available on identically prepared samples to confirm that, at RT, the thermal conductivity closely matches the measured diffusivity times the measured specific heat ( in Table 1). Furthermore, when the electronic thermal conductivity is calculated from the resistivity using the Wiedemann–Franz law () and the theoretical value of the Lorenz number W, the result is very close to the measured thermal conductivity, yielding a measured .
Table 1.
RT thermal transport parameters for selected good metals, disordered metals, and cuprates
| Metals | D, cm2/s | c, J/cm3⋅K | , W/cmK | , W/cmK | ,cm | , cm/s | , W/cmK | , W/cmK | , K | |
| Copper | 1.15 | 3.45 | 3.97 | 3.98 | 1.67 | 3.56 | 0.044 | 4.4 | 0.91 | 310 |
| Gold | 1.28 | 2.5 | 3.2 | 3.15 | 2.24 | 3.25 | 0.033 | 3.3 | 0.96 | 185 |
| Silver | 1.61 | 2.47 | 4.0 | 4.27 | 1.59 | 3.6 | 0.036 | 4.6 | 0.95 | 220 |
| Tungsten | 0.68 | 2.56 | 1.74 | 1.78 | 5.65 | 5.25 | 0.042 | 1.3 | 1.27 | 315 |
| Hg | 0.043 | 1.88 | 0.081 | 0.084 | 96 | 1.45 | 0.0085 | 0.074 | 1.11 | 110 |
| Constantan | 0.064 | 3.65 | 0.23 | 0.21 | 49.9 | 5.2 | 0.07 | 0.15 | 1.32 | 390 |
| Inconel 718 | 0.029 | 3.5 | 0.101 | 0.097 | 156 | 4.94 | 0.06 | 0.05 | 1.56 | 410 |
| YBCO6.6 (-dir) | 0.016–0.018 | 2.7 | 0.043–0.05 | 0.05–0.065 | 560–700 | 6.05 | 0.063 | 0.013 | 5.0–5.4 | 410 |
| YBCO6.75 (-dir) | 0.018–0.02 | 2.7 | 0.05–0.054 | 0.047–0.068 | 430–500 | 6.05 | 0.063 | 0.017 | 4.1–5.0 | 410 |
| LSCO (x = 0.13) | 0.021 | 2.67 | 0.056 | 0.057 | 700 | 5.9 | 0.06 | 0.01 | 4.5–5.5 | 400 |
| BSCCO:2,212 | 0.021 | 2.35 | 0.048 | 0.058 | 580–780 | 4.3 | 0.055 | 0.009 | 4.6–6.2 | 280 |
Comparison of RT thermal properties of good metals, disordered metals, and cuprates. LSCO data are for La1.87Sr0.13CuO4 (see Fig. S4). BSCCO data are for optimally doped Bi2Sr2CaCu2O8 as found in the literature. YBCO6.60(a-dir) and YBCO6.75(a-dir) a-direction data are on single crystals from similar doping, whereas diffusivity data are from this work. Discussions on , (with =a; a is the lattice constant), and = are in the text. (Table S2 provides the references from which the values in this table were obtained.)
Unfortunately, not much data are available for the cuprates where the diffusivity, specific heat, thermal conductivity, and resistivity have all been measured on the same sample or at least the same doping samples made with the same protocol. For example, -direction thermal conductivity on YBCO6+x was reported by Minami et al. (24), but for similar doping, their crystals show much larger resistivity than measurements done on crystals similar to our crystals (12). At the same time, Inyushkin et al. (40) measured twinned crystals with similar doping levels, which are expected to yield a larger value as the - and -directions average (50). We, therefore, base our estimates on a range of thermal parameters values as found in the literature.
Analyzing the available data for the cuprates, we first note that here , but now, . At the same time, we find it to be very close to and sometimes smaller than . This minimum phonon thermal conductivity is calculated as the product of the sound velocity, the lattice constant, and the specific heat and amounts to setting as discussed above. It is a lower bound to the total thermal conductivity of a system with well-defined quasiparticles regardless of electron participation (a complementary bound on using instead of is discussed below). For good metals, , and is as expected from electron-dominated thermal transport. Mercury at RT is a liquid with a relatively slow sound velocity. Nevertheless, it shows similar behavior to the best metallic elements with thermal transport dominated by electrons. However, with increasing resistivity caused by disorder, constantan and Inconel show a tendency to a decreased thermal conductivity and an increasing Lorentz number. The bad metal cuprates, however, show at RT , with anomalously large Lorentz number. These facts might raise doubts on whether high-temperature thermal transport in cuprates has any significant electronic contribution at all (cf. ref. 24) in apparent tension with the electronic character noted in the previous section.
Failure of the Quasiparticle Picture.
Although at lower temperatures, it is believed that quasiparticle excitations are well-defined (8, 51), the situation must change close to the MIR limit. Indeed, applying the conventional treatment to our diffusivity measurements in the temperature range 150 K raises several problems that challenge the self-consistency of the quasiparticle approach. Within a quasiparticle interpretation, , and therefore, we would conclude that the high-temperature thermal transport is dominated by phonons. Even without assuming quasiparticles, at high temperature, the phonon specific heat is overwhelmingly large compared with that of the electrons (23, 52). Thus, because the product of the specific heat and our measured diffusivity yields the commonly measured thermal conductivity, the naive conclusion is that phonons dominate the high-temperature thermal transport, and we should expect to measure . However, even in this phonon-dominated picture, we see that , and therefore, . Because RT is well below the Debye temperature for this material, it is appropriate to use a stricter bound on associated with (instead of ). Assuming that the highest-frequency phonon excited at RT is proportional to temperature, the corresponding minimum phonon wavelength is . The sound velocities of a similar YBCO6.60 crystal have been measured, yielding and (41). Shear sound velocity may be a factor smaller, which does not change the following arguments. Note that these velocities (along with the lattice constants) would yield a much more isotropic diffusivity than the measured . Assuming now 2D phonon transport, the “classical” phonon diffusivity satisfies , and thus, we estimate (for at RT), violating the condition for well-defined phonon excitations. A similar analysis was previously reported by Allen et al. (6) on Bi2Sr2CaCu2O8 single crystals, concluding that phonons are poorly defined in this system. However, their treatment of the electronic contribution relied on a standard application of the Wiedemann–Franz law, which was subsequently shown by Zhang et al. (53) to fail around RT. Finally, we note that (Table 1) the values of -direction for the YBCO6+x crystals are practically the same as the values for the more isotropic (in the Cu-O planes) cuprates. Similar observations can be found for the resistivity of the cuprates (e.g., -axes resistivities can be found in refs. 10 and 12). This fact must indicate that the chain direction has an excess electronic conduction rather than a phononic one.
The phonon quasiparticle approach is, therefore, not consistent. Likewise for the electrons, examination of the resistivity data for similar crystals at around RT yields (10, 12). Beyond the short mean free paths, the phonon dominance suggested by a quasiparticle interpretation is incompatible with the fact that our measured diffusivity anisotropy is similar to the electrical resistivity anisotropy and sensitive to the onset of charge order at 150 K. We are led to conclude that thermal transport has strong electronic in addition to phononic character, with no simple way to separate them, especially in view of the typically very strong electron–phonon interaction in the cuprates (9).
The Case for an Incoherent Electron–Phonon Soup.
We are, therefore, led to propose a nonstandard approach to transport in strongly interacting systems where neither elementary excitations are well-defined. Without quasiparticles, including the absence of emergent well-defined electronic excitations (e.g., collective modes related to a possible symmetry breaking or dressed coherent excitations, such as polarons and bipolarons), the mean free path has no meaning. However, microscopic relaxation timescales can still be defined. Following ref. 7, we conjecture that all microscopic dfs, electronic or phononic, saturate a (momentum nonconserving) relaxation bound, leading to overdamped diffusive transport with quantum thermal timescales . The resulting diffusion coefficient is connected to the thermal timescale through a (temperature-dependent) effective velocity, , such that
| [3] |
where the factor of 2 represents the quasi-2D diffusion in the Cu-O planes. This approach suggests that, in the strongly coupled, high-temperature limit, the electron–phonon system behaves as a composite, strongly correlated soup with an effective velocity . This velocity is expected to be between the faster Fermi velocity of the electrons and the much slower sound velocity of the phonons: .
To obtain an estimate of , we may attempt to extrapolate the expression for the thermal conductivity from the regime where quasiparticles are well-defined and Eq. 2 holds
| [4] |
to the new strongly coupled regime. Assuming a smooth interpolation between the two regimes, we bound the electron and phonon relaxation times in the above equation by
| [5] |
where and are numerical constants of order unity. The resulting expression for the diffusivity is
| [6] |
Eq. 6 now has the form Eq. 3 with , where
| [7] |
which clearly satisfies the condition . (We note that, in the expression for the thermal conductivity, only the heat capacity associated with the modes that propagate in the measured direction and carry entropy should be included. However, this difference may only change the expression by a factor of order unity.) More generally, one would like to identify with a universally defined nonquasiparticle velocity. It has been noted (54) that, in some nonquasiparticle systems, it is the “butterfly velocity” (55, 56) that appears in the diffusivity equation (Eq. 3).
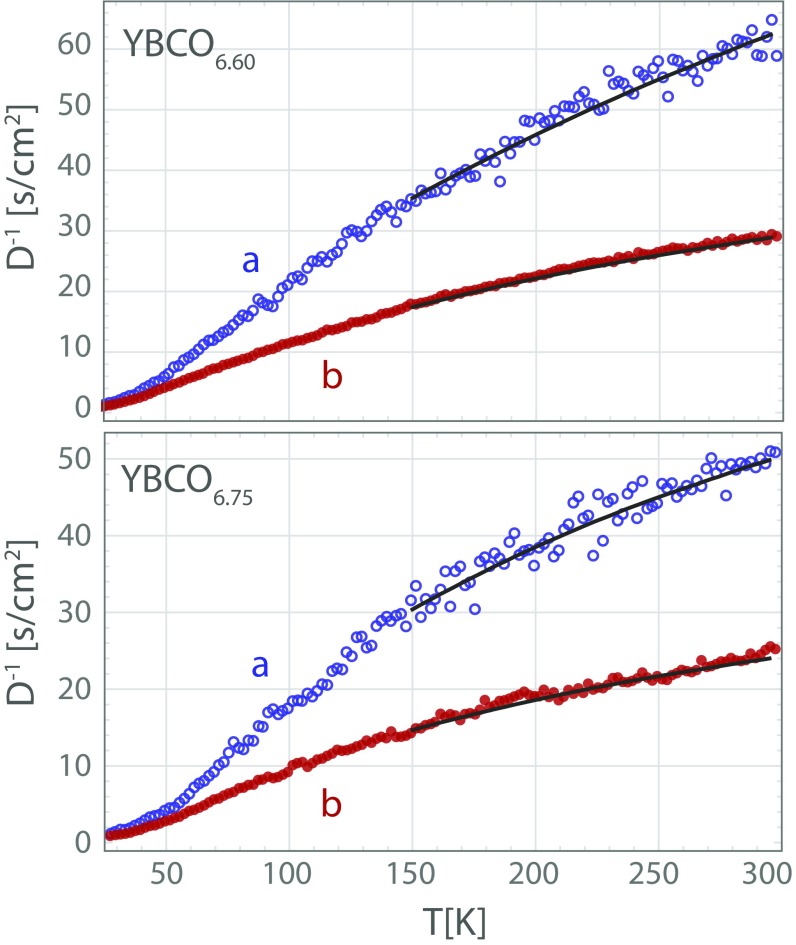
Fig. 3 shows the temperature dependence of with the fit to Eq. 6 above 150 K, where we are free of the interference with the onset of charge order (27, 28). Using the known temperature-dependent total heat capacity (23) and electronic specific heat (57) (at RT, , whereas ) and assuming in-plane Fermi velocity found, for example, in angle-resolved photoemission spectroscopy measurements cm/s (58), we find (e.g., for YBCO6.75) that, in the Cu-O planes, the prefactor and , whereas along the chains, and . Hence, the temperature-dependent microscopic velocity , defined in Eq. 7, exhibits significant character of both electrons and phonons, with similar coefficients of order unity and velocity . The small errors associated with the coefficients (SI Materials and Methods, Table S1 has a description of the photothermal microscope and its modes of operation) signal the robustness of the fit, whereas the independently measured temperature dependences of and are responsible for the curvature away from in Fig. 3. Furthermore, signatures of an electron–phonon soup are seen in the behavior of the electrical resistivity, which is not exactly linear over our temperature range. Comparing our diffusivity data with existing electrical resistivity measurements (10, 12) shows that, in the bad metal regime, , implying that the sound speed contributes to the electrical resistivity.
Fig. 3.
Inverse diffusivity along the (blue circles) and axes (red circles) for both materials. The solid lines are fits to Eq. 6.
Table S1.
Results for fitting constants in Eq. S9
| Sample/direction | ||
| YBCO6.60 | ||
| Plane | 0.14 ± 0.01 | 2.0 ± 0.1 |
| Chain | 0.413 ± 0.007 | 2.58 ± 0.06 |
| YBCO6.67 | ||
| Plane | 0.13 ± 0.02 | 2.1 ± 0.3 |
| Chain | 0.34 ± 0.06 | 2.6 ± 0.5 |
| YBCO6.75 | ||
| Plane | 0.25 ± 0.02 | 1.64 ± 0.09 |
| Chain | 0.53 ± 0.02 | 2.82 ± 0.2 |
The above analysis yields a nonstandard transport mechanism for strongly interacting systems that exceed the quasiparticle mean free path limit. Thermal transport proceeds by collective diffusion of a composite electron–phonon soup, which is distinct from any system exhibiting well-defined electron–phonon quasiparticles, such as polarons or bipolarons (13, 14). Entropy diffusion is characterized by thermal timescales and a unique velocity. Consequently, commonly used electronic transport characteristics, such as, for example, the Wiedemann–Franz law, are not well-defined in this regime. In the YBCO cuprates, this scenario seems to persist down to the charge order temperatures, below which electrons presumably start to regain their quasiparticle character and hence, decouple from the electron–phonon soup. Obviously, a main ingredient of this scenario is the strong electron–phonon interaction, which in turn, may have some impact on the high found in the cuprates.
Conclusions.
In conclusion, we have shown that the underdoped YBa2Cu3O6+x system above the charge order transition exhibits anomalous thermal transport. Neither the phonons nor the electrons are well-defined quasiparticles, whereas their strong mutual interactions cause both to saturate the relaxation timescale at . This state results in a unique type of heat transport carried by an incoherent composite fluid, which we dub the electron–phonon soup, characterized by an effective velocity . We suggest that such behavior is ubiquitous in strongly interacting complex systems at high temperatures and thus, propose that it may explain much of the anomalous transport in “bad metallic” systems [e.g., cataloged by Bruin et al. (17) and discussed in terms of spectral weight transfer in refs. 3, 4, and 59]. Additional diffusivity measurements on these systems may test this proposal.
Materials and Methods
Samples.
YBa2Cu3O6+y single crystals were grown in nonreactive BaZrO3 crucibles using a self-flux technique (60), with the Cu-O chains oxygen content accurately determined as described in ref. 61. The crystals used in our experiments were detwinned. No twinning domains can be observed on the surface of the YBCO6.60 sample, and sparse thin strips of remnant domains can be seen on the YBCO6.75, which was experimentally measured to have no effect on the measured diffusivity.
Diffusivity Measurements.
For the high-resolution thermal diffusivity measurements, we use a home-built photothermal microscope (62, 63) described in detail in SI Materials and Methods (SI Materials and Methods has a description of the photothermal microscope and its modes of operation). The output power of a heating laser is modulated sinusoidally at a frequency 1–50 kHz, much smaller than typical electronic equilibration time (64), whereas a second laser measures the differential reflectivity at a fixed distance () from it. The diffusivity is obtained by fitting the thermal phase delay between the source and the response signals as a function of frequency : (see, e.g., Fig. S3). Frequency sweeps at different distances yield consistent diffusivity values, verifying the heat propagation model that we used (SI Materials and Methods has details and a description of the photothermal microscope and its modes of operation).
Fig. S3.
Typical phase delay data (blue circles) obtained by sweeping modulation frequency. The red line is a fit using the form in Eq. S3.
Fits to Data.
We use Eq. 6 to fit the thermal diffusivity data. Literature values are used for the total specific heat (23), electronic specific heat (57), Fermi velocity (58), and sound velocities (41, 65).
SI Materials and Methods
Samples.
YBa2Cu3O6 + y single crystals were grown in nonreactive BaZrO3 crucibles using a self-flux technique (60), with the Cu-O chains oxygen content accurately determined as described in ref. 61. The CuO-chain oxygen content was set to 6.60, 6.67, and 6.75 by annealing in a flowing O2:N2 mixture and homogenized by further annealing in a sealed quartz ampoule together with ceramic at the same oxygen content. The absolute oxygen content () is accurate to 0.01 based on iodometric titration. The crystals used in our experiments were detwinned. No twinning domains can be observed on the surface of the YBCO6.60 sample, and sparse thin strips of remnant domains can be seen on the YBCO6.75, which was experimentally measured to have no effect on the measured diffusivity.
Principles of the Photothermal Apparatus.
For the high-resolution thermal diffusivity measurements, we use a home-built photothermal microscope (62, 63). The microscope views the sample through a sapphire optical window in a cryostat, with the sample mounted to a cold finger just under the window. A schematic is shown in Fig. S1. A heating laser at 637 nm and a probing laser at 820 nm are focused onto the sample surface by the microscope objective. The focused spots have Gaussian radii of approximately 1 and 2 m, respectively, because of the diffraction limit of the different wavelengths and can be moved independently over the sample surface. A camera allows us to align the spots and observe the sample surface nearby. Fig. S2 shows a camera view of the two beams on different surfaces that we examined.
The output power of the heating laser is modulated with a sinusoidal profile . The modulation frequency has a typical range of 1–50 kHz, much slower than the microscopic equilibration time, which is on the order of picoseconds (64). This low modulation frequency means that the parameters extracted are all within the dc limit of linear response and independent of the modulation frequency itself. The probing laser is aimed at a spot a small distance (typically m) away from the heating laser. The reflected light from the probing laser is diverted by an optical circulator and fed into a photodetector. The ac component of the photodetector signal is then fed to a lock-in amplifier referenced to the laser modulation, and the amplitude and phase are measured. The large differential reflectivity of the YBCO samples (about K−1) at the wavelength of the probe light allows us to study their thermal properties with minimal disturbance.
Measuring Thermal Diffusivity.
The diffusive transport of heat is governed by the diffusion equation
| [S1] |
where is the temperature disturbance above the ambient temperature , is the spherical radial coordinate given in terms of the Euclidean principal axes , is the absorbed power density, is the volumetric specific heat capacity, is the thermal diffusivity, and is the thermal conductivity. Note that and are themselves functions of , but in the limit of weak heating , we make the approximations and . As mentioned in the text, the temperature disturbance from both lasers is 1 K throughout the temperature range K, and therefore, this approximation is valid.
The modulated power of the heating laser causes ripples in the temperature profile at the sample surface, which may be measured by the probing laser. It is useful to write the response in frequency space , where
| [S2] |
We model the focused heat source as a point source, . This approximation is valid as long as the distance from the heating spot is much larger than the spot radius. In a semiinfinite isotropic system, the temperature profile is spherically symmetric and takes the form
| [S3] |
Our measurement gives us the response at the modulation frequency .
Although both the amplitude and the phase of the solution carry information about , in actual measurements, factors, such as mechanical vibrations, fluctuations in the laser power, and the temperature dependence of the differential reflectivity , affect the amplitude of the reflectivity oscillation. These factors do not affect the phase of the signal, which is, therefore, the more robust probe. We obtain by fitting the phase delay between the source and the response signals as a function of at fixed : . A typical fit is shown in Fig. S3. It is important to note that frequency sweeps at different distances yield consistent diffusivity values, verifying the assumptions that we used in obtaining the ideal solution.
Anisotropic Diffusion Equation.
A general system may be anisotropic but can be reduced to the isotropic case through a change of variables. To begin, we write down the heat diffusion equation for a generic system:
| [S4] |
It is interesting to note that the dimension of the diffusivity consists only of space and time: cm2/s. A coordinate isotropic solution can always be found through spatial rotation and scaling. Starting from the diagonal coordinates of the diffusivity tensor,
| [S5] |
where we choose to keep the first axis untouched and scale the rest accordingly: . In the new coordinates, diffusion is an isotropic process, and diffusivity is characterized by a single number. In this new set of coordinates , the absorbed power density transforms accordingly as
We now want to recover the anisotropic dependence on on the surface of the sample in the original coordinate. Let on the surface, and let be the original polar coordinate on the surface
| [S6] |
This expression leads to the exponent in Eq. S3 being rescaled as
| [S7] |
which leads to the extracted diffusivity
| [S8] |
Alignments and Data Collection.
To check the alignment and confirm the orientation of the sample, we first measure diffusivity as a function of frequency for different orientations around the heating spot. This anisotropy check is typically done at RT, and frequency sweeps are typically between 500 Hz and 20 kHz. For each orientation, we generate a set of data similar to that shown in Fig. S3, and from the fit, we extract the diffusivity . We then performed an overall fit of Eq. S8 to all sets of frequency sweeps at various sample orientations, where an additional offset angle is left as an additional free parameter. This offset is the difference between the arbitrary initial angle that we used and the actual principal directions of the crystal. All offset angles are later verified to align with the crystal edge within statistical uncertainties. Typical fits are shown in Fig. 1, Insets. We note that error bars are almost entirely caused by an uncertainty of m in determining laser spots separation because of their finite spread. Excellent fit to the functional form Eq. S5 is obtained on both samples (in the0 text), including in the region on the YBCO6.75 crystal with thin stripes of remnant domains (Fig. S2B), verifying that the anisotropic diffusivity measurements are effectively single domain in nature.
The temperature-dependent diffusivity on each axis is then taken by continuously varying the temperature at a fixed laser separation on each axis at a fixed modulation frequency (20 kHz) and the same region where the RT anisotropy has been measured.
Fits to the Electron–Phonon Soup Model.
We fit the thermal diffusivity measurement of three YBCO6 + x samples using the form
| [S9] |
where literature values are used for the total heat capacity (23), the electronic heat capacity (57), Fermi velocity (58), and sound velocities (41, 65). Table S1 lists the coefficients and in the plane () and chain () directions as extracted from the fits with their SEs.
Preliminary Measurements on LSCO.
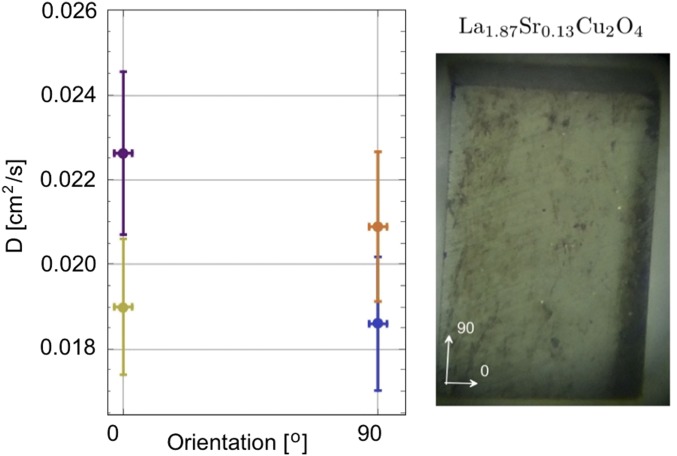
To complete the diffusivity data that we present in Table 1, we measured the thermal diffusivity on a -mm3 La2 −xSrxCu2O4 () single crystal. In Fig. S4, we show preliminary results of RT measurements together with a picture of the crystal. Although the surface of the crystal was scratched, high-quality data could be obtained in high-reflectivity regions. As expected, no obvious anisotropy was detected.
Fig. S4.
(Left) Typical data in two perpendicular orientations measured on an La1.87Sr0.13Cu2O4 single crystal. (Right) A picture of the surface of the crystal measured.
RT Thermal Transport Parameters Including References.
Table S2 provides the references for the thermal transport parameters of Table 1 in the main text.
Table S2.
RT thermal transport parameters for selected good metals, disordered metals, and cuprates
| Metals | D, cm2/s | c, J/cm3K | , W/cmK | , W/cmK | ,cm | , cm/s | , W/cmK | , W/cmK | , K | |
| Copper | 1.15d | 3.45a | 3.97 | 3.98a | 1.67a | 3.56a | 0.044 | 4.4 | 0.91 | 310b |
| Gold | 1.28e | 2.5a | 3.2 | 3.15a | 2.24a | 3.25a | 0.033 | 3.3 | 0.96 | 185b |
| Silver | 1.61d | 2.47a | 4.0 | 4.27a | 1.59a | 3.6a | 0.036 | 4.6 | 0.95 | 220b |
| Tungsten | 0.68f | 2.56a | 1.74 | 1.78a | 5.65a | 5.25a | 0.042 | 1.3 | 1.27 | 315b |
| Hg | 0.043g | 1.88a | 0.081 | 0.084a | 96b | 1.45a | 0.0085 | 0.074 | 1.11 | 110b |
| Constantan | 0.064h | 3.65b | 0.23 | 0.21a,b | 49.9a | 5.2a | 0.07 | 0.15 | 1.32 | 390c |
| Inconel 718 | 0.029w | 3.5b | 0.101 | 0.097b | 156b | 4.94b | 0.06 | 0.05 | 1.56 | 410c |
| YBCO6.6 (-dir) | 0.016–0.018x | 2.7i | 0.043–0.05 | 0.05–0.065l | 560–700m | 6.05r | 0.063 | 0.013 | 5.0–5.4 | 410k |
| YBCO6.75 (-dir) | 0.018–0.02x | 2.7i | 0.05–0.054 | 0.047–0.068l | 430–500m | 6.05r | 0.063 | 0.017 | 4.1–5.0 | 410k |
| LSCO (x = 0.13) | 0.021u | 2.67j | 0.056 | 0.057n | 700p | 5.9s | 0.06 | 0.01 | 4.5–5.5 | 400j |
| BSCCO:2,212 | 0.021v | 2.35k | 0.048 | 0.058o | 580–780q | 4.3t | 0.055 | 0.009 | 4.6–6.2 | 280k |
Comparison of RT thermal properties of good metals, disordered metals, and cuprates. LSCO data are for La1.87Sr0.13CuO4 (see Fig. S4). BSCCO data are for optimally doped Bi2Sr2CaCu2O8 as found in the literature. YBCO6.60(a-dir) and YBCO6.75(a-dir) a-direction data are on single crystals from similar doping, whereas diffusivity data are from this work. Discussions on , (with =a; a is the lattice constant), and = are in the text. Footnotes indicate the references for the quoted data.
Ref. 32.
Ref. 33.
Calculated from ref. 33.
Ref. 31.
Ref. 34.
Ref. 35.
Ref. 36.
Ref. 37.
Ref. 39.
Ref. 42.
Ref. 43.
Ref. 6.
Ref. 44.
Ref. 41.
Ref. 45.
Ref. 49.
See Fig. S4.
Ref. 46.
Ref. 38.
This work (spread caused by inhomogeneity).
Acknowledgments
We thank Subir Sachdev, Sam Lederer, and Steve Kivelson for many insightful discussions. This work was supported by the Gordon and Betty Moore Foundation through Emergent Phenomena in Quantum Systems (EPiQS) Initiative Grant GBMF4529 and a Department of Energy Early Career Award (to S.A.H.).
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1703416114/-/DCSupplemental.
References
- 1.Ziman JM. Electrons and Phonons: The Theory of Transport Phenomena in Solids. Oxford Univ Press; Oxford: 1960. [Google Scholar]
- 2.Emery VJ, Kivelson SA. Superconductivity in bad metals. Phys Rev Lett. 1995;74:3253–3256. doi: 10.1103/PhysRevLett.74.3253. [DOI] [PubMed] [Google Scholar]
- 3.Gunnarsson O, Calandra M, Han JE. Colloquium: Saturation of electrical resistivity. Rev Mod Phys. 2003;75:1085–1099. [Google Scholar]
- 4.Hussey NE, Takenaka K, Takagi H. Universality of the Mott-Ioffe-Regel limit in metals. Philos Mag. 2004;84:2847–2864. [Google Scholar]
- 5.Slack GA. The thermal conductivity of nonmetallic crystals. In: Ehrenreich H, Seitz F, Turnbull D, editors. Solid State Physics. Vol 34. Academic; London: 1979. pp. 1–71. [Google Scholar]
- 6.Allen PB, Du XQ, Mihaly L, Forro L. Thermal-conductivity of Insulating Bi2Sr2YCU2O8 and superconducting Bi2Sr2CaCu2O8 - failure of the phonon-gas picture. Phys Rev B. 1994;49:9073–9079. doi: 10.1103/physrevb.49.9073. [DOI] [PubMed] [Google Scholar]
- 7.Hartnoll SA. Theory of universal incoherent metallic transport. Nat Phys. 2015;11:54–61. [Google Scholar]
- 8.Norman MR, et al. Destruction of the fermi surface in underdoped high-Tc superconductors. Nature. 1998;392:157–160. [Google Scholar]
- 9.Lanzara A, et al. Evidence for ubiquitous strong electron-phonon coupling in high-temperature superconductors. Nature. 2001;412:510–514. doi: 10.1038/35087518. [DOI] [PubMed] [Google Scholar]
- 10.Segawa K, Ando Y. Transport anomalies and the role of pseudogap in the 60-K phase of YBa2Cu3O7−δ. Phys Rev Lett. 2001;86:4907–4910. doi: 10.1103/PhysRevLett.86.4907. [DOI] [PubMed] [Google Scholar]
- 11.Ando Y, Segawa K, Komiya S, Lavrov AN. Electrical resistivity anisotropy from self-organized one dimensionality in high-temperature superconductors. Phys Rev Lett. 2002;88:137005. doi: 10.1103/PhysRevLett.88.137005. [DOI] [PubMed] [Google Scholar]
- 12.Le Boeuf D. 2010. Reconstruction de la surface de Fermi dans l’etat normal d’un supraconducteur a haute Tc: Une etude du transport electrique en champ magnetique intense. PhD thesis (Université de Sherbrooke, Sherbrooke, QC, Canada)
- 13.Emin D. Large-bipolaron transport and cuprate superconductors. Phys Rev B. 1992;45:5525–5529. doi: 10.1103/physrevb.45.5525. [DOI] [PubMed] [Google Scholar]
- 14.Alexandrov AS, Mott NF. Bipolarons. Rep Prog Phys. 1994;57:1197–1288. [Google Scholar]
- 15.Sachdev S. Quantum Phase Transitions. 1st Ed Cambridge Univ Press; Cambridge, UK: 1999. [Google Scholar]
- 16.Zaanen J. Superconductivity: Why the temperature is high. Nature. 2004;430:512–513. doi: 10.1038/430512a. [DOI] [PubMed] [Google Scholar]
- 17.Bruin JAN, Sakai H, Perry RS, Mackenzie AP. Similarity of scattering rates in metals showing t-linear resistivity. Science. 2013;339:804–807. doi: 10.1126/science.1227612. [DOI] [PubMed] [Google Scholar]
- 18.Orenstein J, et al. Frequency- and temperature-dependent conductivity in YBa2Cu3O6+x crystals. Phys Rev B. 1990;42:6342–6362. doi: 10.1103/physrevb.42.6342. [DOI] [PubMed] [Google Scholar]
- 19.Schlesinger Z, et al. Infrared studies of the superconducting energy gap and normal-state dynamics of the high-Tc superconductor YBa2Cu3O7. Phys Rev B. 1990;41:11237–11259. doi: 10.1103/physrevb.41.11237. [DOI] [PubMed] [Google Scholar]
- 20.Liu HL, et al. Doping-induced change of optical properties in underdoped cuprate superconductors. J Phys Condens Matter. 1999;11:239–264. [Google Scholar]
- 21.van der Marel D, et al. Quantum critical behaviour in a high-T(c) superconductor. Nature. 2003;425:271–274. doi: 10.1038/nature01978. [DOI] [PubMed] [Google Scholar]
- 22.Waske A, Hess C, Buechner B, Hinkov V, Lin CT. Thermal conductivity of underdoped YBa2Cu3Oy. Physica C Supercond. 2007;460-462:746–747. [Google Scholar]
- 23.Loram J, Mirza K, Freeman P. The electronic specific heat of YBa2(Cu1−xZnx)3O7 from 1.6 K to 300 K. Physica C Supercond. 1990;171:243–256. [Google Scholar]
- 24.Minami H, et al. Influence of the pseudogap on the thermal conductivity and the Lorenz number of YBa2Cu3Ox above . Phys Rev B. 2003;68:220503. [Google Scholar]
- 25.Cyr-Choinière O, et al. Two types of nematicity in the phase diagram of the cuprate superconductor YBa2Cu3Oy. Phys Rev B. 2015;92:224502. [Google Scholar]
- 26.Blanco-Canosa S, et al. Resonant x-ray scattering study of charge-density wave correlations in YBa2Cu3O6+x. Phys Rev B. 2014;90:054513. [Google Scholar]
- 27.Ghiringhelli G, et al. Long-range incommensurate charge fluctuations in (Y,Nd)Ba2Cu3O6+x. Science. 2012;337:821–825. doi: 10.1126/science.1223532. [DOI] [PubMed] [Google Scholar]
- 28.Achkar AJ, et al. Distinct charge orders in the planes and chains of ortho-iii-ordered YBa2Cu3O6+δ superconductors identified by resonant elastic x-ray scattering. Phys Rev Lett. 2012;109:167001. doi: 10.1103/PhysRevLett.109.167001. [DOI] [PubMed] [Google Scholar]
- 29.Bonnoit C, et al. 2012. Probing electronic order via coupling to low energy phonons in superconducting Bi2Sr2−xLaxCuO6+δ. arXiv:1202.4994.
- 30.Le Tacon M, et al. Inelastic x-ray scattering in YBa23O6.6 reveals giant phonon anomalies and elastic central peak due to charge-density-wave formation. Nat Phys. 2014;10:52–58. [Google Scholar]
- 31.Parker W, Jenkins R, Abbott G, Butler C. Flash method of determining thermal diffusivity, heat capacity, and thermal conductivity. J Appl Phys. 1961;32:1679–1684. [Google Scholar]
- 32.Weast R, editor. CRC Handbook of Chemistry and Physics: A Ready-reference Book of Chemical and Physical Data. 66th Ed CRC; Boca Raton, FL: 1985. [Google Scholar]
- 33.Ekin J. Experimental Techniques for Low-temperature Measurements. Oxford Univ Press; London: 2006. [Google Scholar]
- 34.Yunus W, Fanny C, Moksin M, Phing T, Halim S. Cleo/Pacific Rim 2001: The 4th Pacific Rim Conference on Lasers and Electro-Optics. IEEE; New York: 2001. Thermal diffusivity measurement of gold alloys and superconducting ceramics using photoacoustic technique; pp. 226–227. [Google Scholar]
- 35.Hofmann F, et al. Non-contact measurement of thermal diffusivity in ion-implanted nuclear materials. Sci Rep. 2015;5:16042. doi: 10.1038/srep16042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ang C, Chan S, Tan H. Measurement of thermal diffusivity of mercury. J Appl Phys. 1974;45:179–181. [Google Scholar]
- 37.Sundqvist B. Thermal-diffusivity and thermal-conductivity of chromel, alumel, and constantan in the range 100-400-k. J Appl Phys. 1992;72:539–545. [Google Scholar]
- 38.Sweet J, Roth E, Moss M. Thermal-conductivity of Inconel-718 and 304 stainless-steel. Int J Thermophys. 1987;8:593–606. [Google Scholar]
- 39.Junod A, et al. Specific-heat of La2−xSrxCUO4 and YBa2Cu3O7 superconductors from 1-K to room-temperature. Jpn J Appl Phys. 1987;26:1119–1120. [Google Scholar]
- 40.Inyushkin A, Taldenkov A, Uvarova T. Thermal conductivity of oxygen-deficient YBa2Cu3O6+x. Phys Rev B. 1996;54:13261–13268. doi: 10.1103/physrevb.54.13261. [DOI] [PubMed] [Google Scholar]
- 41.Lei M, et al. Elastic constants of a monocrystal of superconducting YBa2Cu3O7−δ. Phys Rev B. 1993;47:6154–6156. doi: 10.1103/physrevb.47.6154. [DOI] [PubMed] [Google Scholar]
- 42.Junod A, et al. Specific heat up to 14 tesla and magnetization of a Bi2Sr2CaCu2O8 single-crystal thermodynamics of a 2d superconductor. Physica C Supercond. 1994;229:209–230. [Google Scholar]
- 43.Nakamura Y, et al. Inplane and out of plane thermal conductivity of La2−xSrxCuO4 single crystals. Physica C Supercond. 1991;185:1409–1410. [Google Scholar]
- 44.Ando Y, Boebinger GS, Passner A, Kimura T, Kishio K. Logarithmic divergence of both in-plane and out-of-plane normal-state resistivities of superconducting La2−xSrxCuO4 in the zero-temperature limit. Phys Rev Lett. 1995;75:4662–4665. doi: 10.1103/PhysRevLett.75.4662. [DOI] [PubMed] [Google Scholar]
- 45.Sarrao J, et al. Complete elestic-moduli of La2−xSrxCUO4 (=0.00 0.14) near the tetragonal-orthorhombic structural phase-transition. Phys Rev B. 1994;50:13125–13131. doi: 10.1103/physrevb.50.13125. [DOI] [PubMed] [Google Scholar]
- 46.Wu X, et al. Thermal-diffusivity of Bi2Sr2CaCu2O8 single-crystals. Physica C Supercond. 1993;218:417–423. [Google Scholar]
- 47.Fastampa R, Giura M, Sarti S, Marcon R, Silva E. In-plane and out of plane resistivities in BSCCO (2212) single crystals at different doping level. Int J Mod Phys B. 2003;17:867–872. [Google Scholar]
- 48.Triscone G, Junod A. Thermal and magnetic properties. In: Maeda H, Togano K, editors. Bismuth-Based High-Temperature Superconductors. CRC Press; Boca Raton, FL: 1996. p. 33. [Google Scholar]
- 49.Saunders G, et al. Anisotropy of the elastic and nonlinear acoustic properties of dense textured Bi2Sr2CaCu2O8+y. Phys Rev B. 1994;49:9862–9873. doi: 10.1103/physrevb.49.9862. [DOI] [PubMed] [Google Scholar]
- 50.Gold Z, Gagnon R, Ellman B, Taillefer L, Behnia K. Anisotropic thermal-conductivity of YBa2Cu3O7−δ. Physica C Supercond. 1994;235:1485–1486. [Google Scholar]
- 51.Deng X, et al. How bad metals turn good: Spectroscopic signatures of resilient quasiparticles. Phys Rev Lett. 2013;110:086401. doi: 10.1103/PhysRevLett.110.086401. [DOI] [PubMed] [Google Scholar]
- 52.Reeves ME, Ditmars DA, Wolf SA, Vanderah TA, Kresin VZ. Evidence for strong electron-phonon coupling from the specific heat of YBa2Cu3O7−δ. Phys Rev B. 1993;47:6065–6068. doi: 10.1103/physrevb.47.6065. [DOI] [PubMed] [Google Scholar]
- 53.Zhang Y, et al. Determining the Wiedemann-Franz ratio from the thermal hall conductivity: Application to cu and yba2cu3o6.95. Phys Rev Lett. 2000;84:2219–2222. doi: 10.1103/PhysRevLett.84.2219. [DOI] [PubMed] [Google Scholar]
- 54.Blake M. Universal charge diffusion and the Butterfly effect. Phys Rev Lett. 2016;117:091601. doi: 10.1103/PhysRevLett.117.091601. [DOI] [PubMed] [Google Scholar]
- 55.Shenker SH, Stanford D. Black holes and the butterfly effect. J High Energy Phys. 2014;03:067. [Google Scholar]
- 56.Roberts DA, Stanford D, Susskind L. Localized shocks. J High Energy Phys. 2015;03:051. [Google Scholar]
- 57.Moler KA, et al. Specific heat of YBa2Cu3O7−δ. Phys Rev B. 1997;55:3954–3965. [Google Scholar]
- 58.Fournier D, et al. Loss of nodal quasiparticle integrity in underdoped yba2cu3o6+x. Nat Phys. 2010;6:905–911. [Google Scholar]
- 59.Jaramillo R, Ha SD, Silevitch DM, Ramanathan S. Origins of bad-metal conductivity and the insulator-metal transition in the rare-earth nickelates. Nat Phys. 2014;10:304–307. [Google Scholar]
- 60.Liang R, Bonn D, Hardy W. Growth of high quality YBCO single crystals using BaZrO3 crucibles. Physica C Supercond. 1998;304:105–111. [Google Scholar]
- 61.Liang R, Bonn DA, Hardy WN. Evaluation of CuO2 plane hole doping in YBa2Cu3O6+x single crystals. Phys Rev B. 2006;73:180505. [Google Scholar]
- 62.Fanton JT. 1990. Analysis and applications of photothermal microscopy. PhD thesis (Stanford University, Stanford, CA)
- 63.Wu XD, Kino GS, Fanton JT, Kapitulnik A. Photothermal microscope for high-Tc superconductors and charge density waves. Rev Sci Instrum. 1993;64:3321–3327. [Google Scholar]
- 64.Li W, Zhang C, Wang X, Chakhalian J, Xiao M. Ultrafast spectroscopy of quasiparticle dynamics in cuprate superconductors. J Magn Magn Mater. 2015;376:29–39. [Google Scholar]
- 65.Shekhter A, et al. Bounding the pseudogap with a line of phase transitions in YBa2Cu3O6+δ. Nature. 2013;498:75–77. doi: 10.1038/nature12165. [DOI] [PubMed] [Google Scholar]