Significance
Methane, the second most important greenhouse gas, has varied markedly in its atmospheric growth rate. The cause of these fluctuations remains poorly understood. Recent efforts to determine the drivers of the pause in growth in 1999 and renewed growth from 2007 onward have focused primarily on changes in sources alone. Here, we show that changes in the major methane sink, the hydroxyl radical, have likely played a substantial role in the global methane growth rate. This work has significant implications for our understanding of the methane budget, which is important if we are to better predict future changes in this potent greenhouse gas and effectively mitigate enhanced radiative forcing caused by anthropogenic emissions.
Keywords: methane; hydroxyl; inversion; methyl chloroform; 1,1,1-trichloroethane
Abstract
The growth in global methane (CH4) concentration, which had been ongoing since the industrial revolution, stalled around the year 2000 before resuming globally in 2007. We evaluate the role of the hydroxyl radical (OH), the major CH4 sink, in the recent CH4 growth. We also examine the influence of systematic uncertainties in OH concentrations on CH4 emissions inferred from atmospheric observations. We use observations of 1,1,1-trichloroethane (CH3CCl3), which is lost primarily through reaction with OH, to estimate OH levels as well as CH3CC3 emissions, which have uncertainty that previously limited the accuracy of OH estimates. We find a 64–70% probability that a decline in OH has contributed to the post-2007 methane rise. Our median solution suggests that CH4 emissions increased relatively steadily during the late 1990s and early 2000s, after which growth was more modest. This solution obviates the need for a sudden statistically significant change in total CH4 emissions around the year 2007 to explain the atmospheric observations and can explain some of the decline in the atmospheric 13CH4/12CH4 ratio and the recent growth in C2H6. Our approach indicates that significant OH-related uncertainties in the CH4 budget remain, and we find that it is not possible to implicate, with a high degree of confidence, rapid global CH4 emissions changes as the primary driver of recent trends when our inferred OH trends and these uncertainties are considered.
Methane (CH4), the second most important partially anthropogenic greenhouse gas, is observed to vary markedly in its year to year growth rate (Fig. 1). The causes of these variations have been the subject of much controversy and uncertainty, primarily because there is a wide range of poorly quantified sources and because its sinks are ill-constrained (1). Of particular recent interest are the cause of the “pause” in CH4 growth between 1999 and 2007 and the renewed growth from 2007 onward (2–7). It is important that we understand these changes if we are to better project future CH4 changes and effectively mitigate enhanced radiative forcing caused by anthropogenic methane emissions.
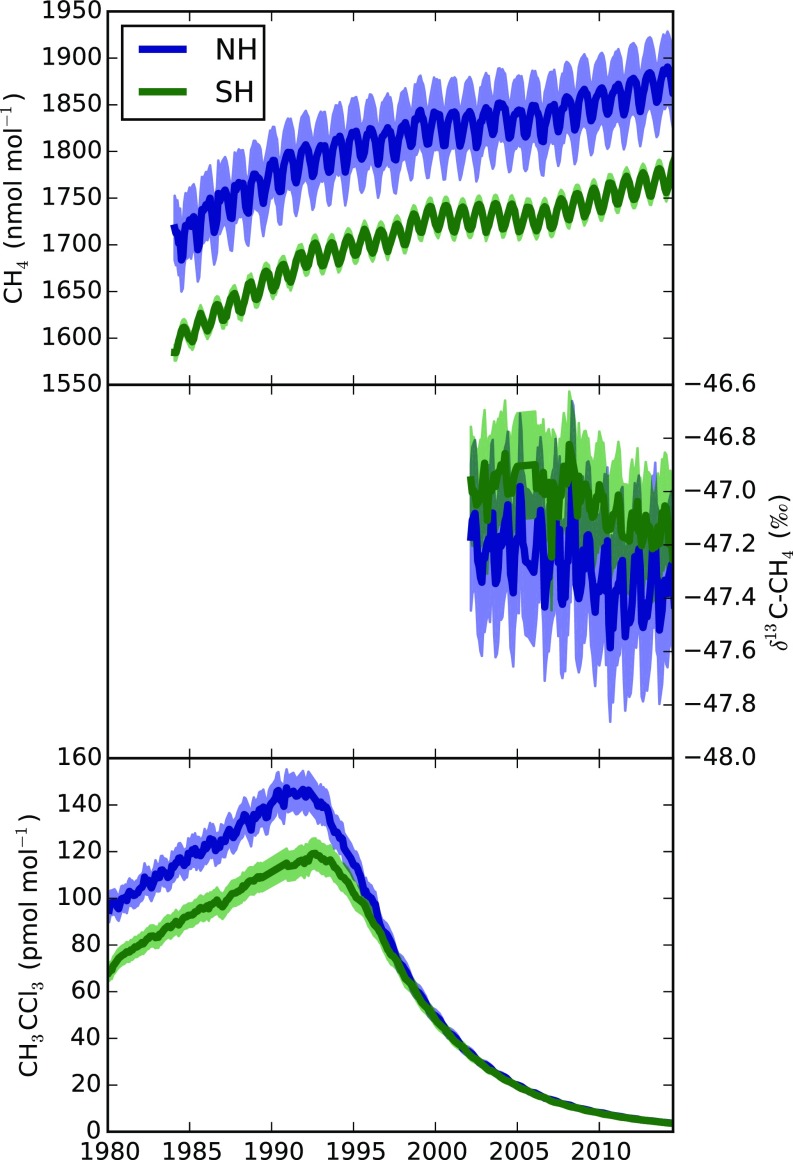
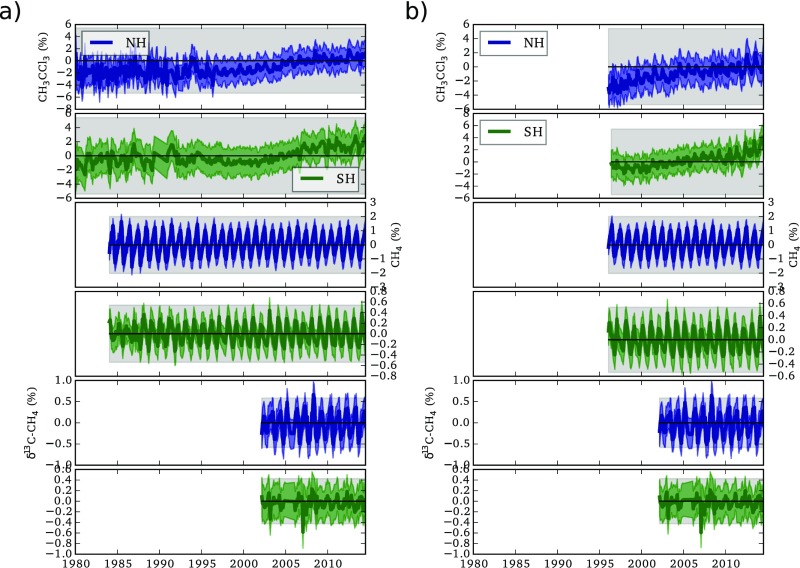
Fig. 1.
(Top) NOAA observations of CH4. (Middle) INSTAAR observations of δ13C-CH4. (Bottom) The AGAGE observations of CH3CCl3. Each plot shows the northern hemisphere (NH) and southern hemisphere (SH) means, and shading indicates the assumed 1-sigma model and measurement uncertainty as defined in SI Materials and Methods.
The major sources of CH4 include wetlands (natural and agricultural), fossil fuel extraction and distribution, enteric fermentation in ruminant animals, and solid and liquid waste. Our understanding of the sources of CH4 comes from two approaches: “bottom up,” in which inventories or process models are used to predict fluxes, or “top down,” in which fluxes are inferred from observations assimilated into atmospheric chemical transport models. Bottom-up methods suffer from uncertainties and potential biases in the available activity data or emissions factors or the extrapolation to large scales of a relatively small number of observations. Furthermore, there is no constraint on the global total emissions from bottom-up techniques. The top-down approach is limited by incomplete or imperfect observations and our understanding of atmospheric transport and chemical sinks. For CH4, these difficulties result in a significant mismatch between the two methods (1).
The primary CH4 sink is the hydroxyl radical (OH) in the troposphere, although smaller sinks also exist, such as methanotrophic bacteria in soils, oxidation by chlorine radicals in the marine boundary layer, and photochemical destruction in the stratosphere. Predictions of the magnitude and variability of OH in the current generation of atmospheric models have been shown to be diverse (8). Furthermore, because of its short lifetime, it is difficult to infer global OH concentrations using direct observations. Therefore, indirect observational methods are needed. The most commonly used approach has been to infer global OH concentrations from observed trends in 1,1,1-trichloroethane (CH3CCl3), whose primary sink is also reaction with OH in the troposphere (9–13). Recent work using this approach indicated that OH changes could have played a role in the pause in CH4 that occurred after 1998 (3, 14).
Previous studies have shown that OH trends inferred using CH3CCl3 could be highly sensitive to systematic errors in the assumed emissions trends, particularly in the 1980s and early 1990s when emissions were changing rapidly (15). Some authors have attempted to reduce this source of uncertainty by including CH3CCl3 emissions as part of the inversion (12). However, these studies assumed that emissions uncertainties were Gaussian and uncorrelated between years, potentially reducing the impact of systematic errors in the a priori emissions model. Furthermore, with a few exceptions (16), most work has derived OH separately to CH4 and its global 13C/12C source signature, limiting the propagation of uncertainty in OH through to the derived CH4 fluxes. The inability to quantify CH3CCl3 systematic emissions uncertainties may be particularly problematic in recent years when, as a result of its production and consumption ban under the Montreal Protocol, reported consumption has dropped to very low levels, but evidence of continued emissions can still be seen in atmospheric observations (Fig. S1) (17, 18). Therefore, the assumptions that were used in early estimates of CH3CCl3 emissions, which were based on industry surveys at a time when CH3CCl3 was widely used (19), are unlikely to hold in recent decades.
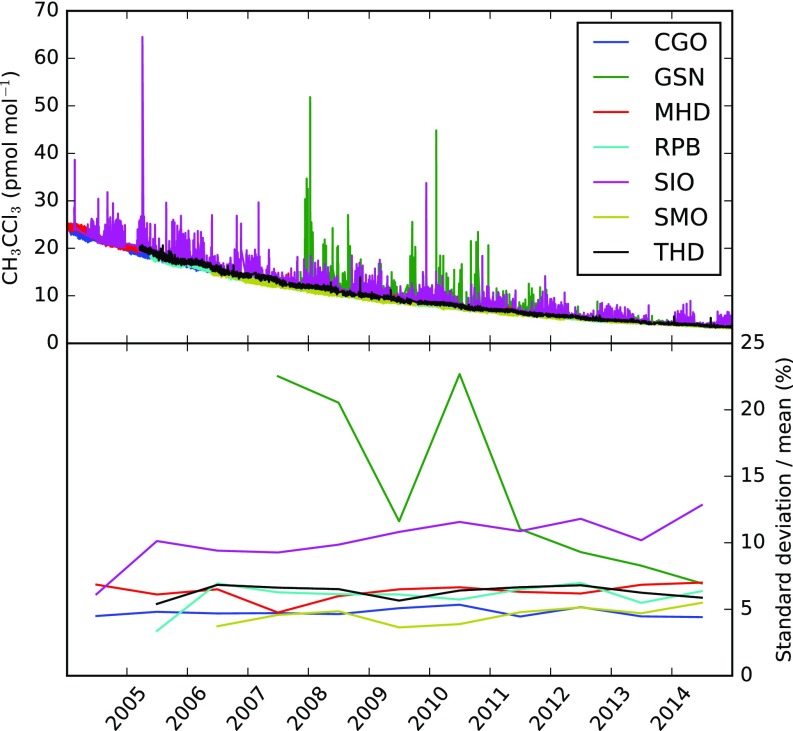
Fig. S1.
(Upper) High-frequency AGAGE Medusa observations at the baseline stations used in the global inversion in addition to; Scripps Institution of Oceanography, La Jolla, CA (SIO); and Gosan, South Korea (GSN). (Lower) Annual SDs relative to the annual mean mole fraction. CGO, Cape Grim, Tasmania; MHD, Mace Head, Ireland; RPB, Ragged Point, Barbados; SMO, Cape Matatula, Samoa; THD, Trinidad Head, CA.
In contrast to previous approaches, the method used in this paper explicitly includes a model of the CH3CCl3 emissions processes in the estimation scheme. Information regarding the global emissions of long-lived trace gases, such as CH3CCl3, can be derived simultaneously with their atmospheric sinks by jointly considering factors such as the long-term trend in concentration and the interhemispheric gradient (20). We extend this approach here by including the uncertain emissions and atmospheric model parameters jointly in a hierarchical Bayesian estimation framework that is informed by atmospheric data from multiple species. This method ensures that uncertainties in each component are propagated throughout the system. A full list of model parameters explored in the inversion is given in Table S1.
Table S1.
Parameters estimated in the inversions
| Parameter | Definition | PDF P1 | PDF P2 | Units | Frequency | Refs. | |
| Atmospheric model | |||||||
| OH | OH concentration | Gaussian | 1.1 | 0.1–0.2 | 106 radicals cm−3 | Annual | 55 |
| [OH]NH/SH | OH NH/SH imbalance | Uniform | −5 | 20 | % | Annual | 60 |
| fIHT | Interhemispheric exchange rate | Gaussian | 1.2−1 | 0.1 | y−1 | Annual | Methodology of ref. 47 |
| fSTE | Stratosphere–troposphere exchange rate | Uniform | 4−1 | 2−1 | y−1 | 49 | |
| fstrat | Stratospheric loss frequency | Uniform | (/2)−1 | (/20)−1 | y−1 | ||
| Socean | Scaling of ref. 53 flux | Gaussian | 1 | 0.1 | 53 | ||
| CH3CCl3 emissions model | |||||||
| Fprompt | Fraction released in year consumed | Uniform | 0 | 100 | % | Decadal | |
| Fbank | Bank fraction released | Uniform | 0 | 100 | % | Decadal | |
| Cscale | Scaling of consumption | Gaussian | 1 | 10 | % | Decadal | |
| Cunreported | Unreported consumption | Uniform | 0 | 10 | Gg y−1 | Decadal | |
| CH4 emissions model | |||||||
| QCH_4_global | Global CH4 emissions | Gaussian | 545 | 54.5–163.5 | Tg y−1 | Annual | 47, 52 |
| FCH_4_NH | Fraction of CH4 emissions in the NH | Uniform | 50 | 100 | % | Annual | |
| 13C-CH4 emissions model | |||||||
| QNH_source_ratio | Mean NH 13C-CH4 source -value | Gaussian | −56 | 10–30 | ‰ | Annual | 57 |
| QSH_source_ratio | Mean SH 13C-CH4 source -value | Gaussian | −56 | 10–30 | ‰ | Annual | 57 |
Each parameter is described by either a Gaussian or uniform prior PDF. The two PDF parameters, PDF P1 and PDF P2, denote either the mean and SD in the case of a Gaussian distribution or the lower and upper bounds in the case of a uniform distribution. The frequency column shows the time period over which parameters are estimated. No entry in this column shows that the parameter was assumed to be temporally invariant. Two values in the PDF P2 column denote the hyperparameter range explored in the inversion. NH, northern hemisphere; SH, southern hemisphere.
To focus on the uncertainties in the CH3CCl3 emissions model, we chose to use a computationally efficient “box model” of atmospheric transport and chemistry that included two tropospheric boxes and one stratospheric box. Previous authors have noted that the use of atmospheric box models with annually repeating transport can cause erroneous fluctuations in derived OH concentrations over periods of around 3 y or less, particularly during periods when emissions of CH3CCl3 were relatively large (15). However, recent studies have shown that, at least in recent years when atmospheric CH3CCl3 gradients are small, OH inversions based on box models agree very closely (to within 1%) with 3D model inversions using analyzed meteorology (13) or that OH variations derived using box models can be used to simulate realistic CH3CCl3 trends using 3D models (14). Therefore, in this paper, we primarily focus on longer-term OH trends, and we expect that our findings for recent decades would not be substantially different if a more complex model was used.
The atmospheric and emissions model parameters were constrained in a multispecies inversion using monthly mean observations of atmospheric CH3CCl3 from both the Advanced Global Atmospheric Gases Experiment (AGAGE) (21) and National Oceanic and Atmospheric Administration (NOAA) (4, 13) networks along with NOAA CH4 data and 13C-CH4 observations from the University of Colorado’s Institute of Arctic and Alpine Research (INSTAAR) (22, 23) (Fig. 1). Colocated AGAGE and NOAA observations were found to exhibit somewhat different long-term CH3CCl3 trends. Therefore, two sets of inversions were performed based on the CH3CCl3 observations from each network (Fig. S2). The AGAGE CH4 observations were not used in the main part of this study, because they were found to agree very closely with NOAA data but cover a shorter time period. Additional details about the observations are provided in SI Materials and Methods, and the site locations are shown in Table S2.
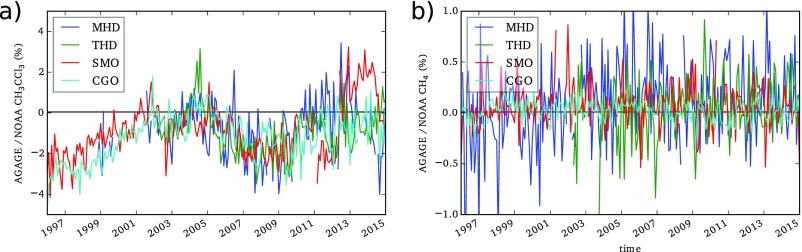
Fig. S2.
Percentage difference in the AGAGE and NOAA baseline monthly means at four colocated sites for (A) CH3CCl3 and (B) CH4. CGO, Cape Grim, Tasmania; MHD, Mace Head, Ireland; SMO, Cape Matatula, Samoa; THD, Trinidad Head, CA.
Table S2.
AGAGE, NOAA, and INSTAAR sampling locations used in this study
| Site code | Site name | Latitude (° N) | Longitude (° E) | Altitude (masl) | AGAGE ECD/Medusa changeover |
| AGAGE sites | |||||
| Sites used in global inversions | |||||
| ADR | Adrigole, Ireland (pre-1987) | 52 | −10 | 10 | |
| CGO | Cape Grim, Tasmania | −40 | 144 | 138 | 06/01/2010 |
| CMO | Cape Meares, Oregon (pre-1995) | 45 | −123 | 33 | |
| MHD | Mace Head, Ireland | 53 | −9 | 25 | 01/01/2011 |
| RPB | Ragged Point, Barbados | 13 | −59 | 19 | 11/01/2010 |
| SMO | Cape Matatula, Samoa | −14 | −170 | 52 | 01/01/2011 |
| THD | Trinidad Head, CA | 41 | −124 | 112 | 05/17/2012 |
| Sites used in regional inversions | |||||
| GSN | Gosan, Korea | 33 | 126 | 89 | |
| SIO | Scripps Institution of Oceanography, La | 33 | −117 | 20 | |
| Jolla, CA | |||||
| NOAA sites | |||||
| CH3CCl3 sites | |||||
| ALT | Alert, Canada | 83 | −62 | 210 | |
| BRW | Barrow, AK | 71 | −157 | 27 | |
| CGO | Cape Grim, Tasmania | −41 | 145 | 164 | |
| KUM | Cape Kumukahi, HI | 20 | −155 | 39 | |
| MHD | Mace Head, Ireland | 53 | −10 | 42 | |
| MLO | Mauna Loa, HI | 20 | −156 | 3433 | |
| NWR | Niwot Ridge, CO | 40 | −106 | 3482 | |
| PSA | Palmer Station, Antarctica | −65 | −64 | 15 | |
| SMO | Cape Matatula, American Samoa | −14 | −171 | 77 | |
| SPO | South Pole, Antarctica | −90 | −24 | 2837 | |
| SUM | Summit, Greenland | 73 | −38 | 3219 | |
| THD | Trinidad Head, CA | 41 | −124 | 120 | |
| CH4 sites | |||||
| ALT | Alert, Canada | 82 | −62 | 205 | |
| AMS | Amsterdam Island, France | −37 | 77 | 153 | |
| ASC | Ascension Island, United Kingdom | −7 | −14 | 89 | |
| ASK | Assekrem, Algeria | 23 | 5 | 2715 | |
| AZR | Terceira Island, Azores, Portugal | 38 | −27 | 23 | |
| BHD | Baring Head, New Zealand | −41 | 174 | 90 | |
| BMW | Tudor Hill, Bermuda | 32 | −64 | 59 | |
| BRW | Barrow, AK | 71 | −156 | 18 | |
| CBA | Cold Bay, AK | 55 | −162 | 30 | |
| CGO | Cape Grim, Tasmania | −40 | 144 | 138 | |
| CMO | Cape Mears, OR | 45 | −123 | 33 | |
| CRZ | Crozet Island, France | −46 | 51 | 202 | |
| EIC | Easter Island, Chile | −27 | −109 | 57 | |
| ICE | Storhofdi, Vestmannaeyjar, Iceland | 63 | −20 | 126 | |
| IZO | Izana, Tenerife | 28 | −16 | 2377 | |
| KEY | Key Biscane, FL | 25 | −80 | 5 | |
| KUM | Cape Kumukahi, HI | 19 | −154 | 8 | |
| MBC | Mould Bay, Canada | 76 | −119 | 33 | |
| MHD | Mace Head, Ireland | 53 | −9 | 25 | |
| MLO | Mauna Loa, HI | 19 | −155 | 3411 | |
| NWR | Niwot Ridge, CO | 40 | −105 | 3526 | |
| PSA | Palmer Station, Antarctica | −64 | −64 | 14 | |
| RPB | Ragged Point, Barbados | 13 | −59 | 19 | |
| SHM | Shemya Island, AK | 52 | 174 | 27 | |
| SMO | Cape Matatula, American Samoa | −14 | −170 | 52 | |
| SPO | South Pole, Antarctica | −89 | −24 | 2817 | |
| STM | Ocean Station M | 66 | 2 | 6 | |
| SUM | Summit, Greenland | 72 | −38 | 3214 | |
| SYO | Syowa Station, Antarctica | −69 | 39 | 12 | |
| THD | Trinidad Head, CA | 41 | −124 | 112 | |
| USH | Ushaia, Argentina | −54 | −68 | 30 | |
| UTA | Wendover, UT | 39 | −113 | 1332 | |
| UUM | Ulaan Uul, Mongolia | 44 | 111 | 1012 | |
| WLG | Mt. Waliguan, China | 36 | 100 | 3819 | |
| ZEP | Zeppelin, Ny Alesund, Norway | 78 | 11 | 479 | |
| INSTAAR | |||||
| δ13C-CH4 sites | |||||
| ALT | Alert, Canada | 82 | −62 | 205 | |
| ASC | Ascension Island, United Kingdom | −7 | −14 | 89 | |
| BHD | Baring Head, New Zealand | −41 | 174 | 90 | |
| CGO | Cape Grim, Tasmania | −40 | 144 | 138 | |
| KUM | Cape Kumukahi, HI | 19 | −154 | 8 | |
| MHD | Mace Head, Ireland | 53 | −9 | 25 | |
| MLO | Mauna Loa, HI | 19 | −155 | 3411 | |
| NWR | Niwot Ridge, CO | 40 | −105 | 3526 | |
| SMO | Cape Matatula, American Samoa | −14 | −170 | 52 | |
| SPO | South Pole, Antarctica | −89 | −24 | 2817 | |
| TAP | Tae-ahn Peninsula, Republic of Korea | 37 | 126 | 20 | |
| WLG | Mt. Waliguan, China | 36 | 100 | 3819 |
For AGAGE stations that switched from GC-ECD to Medusa measurements of CH3 CCl3, the date at which this occurred is given in the last column. masl,meters above sea level.
SI Materials and Methods
Atmospheric Observations.
Atmospheric measurements were taken from AGAGE (21) and its previous incarnations the Atmospheric Lifetime Experiment (ALE) and the Global Atmospheric Gases Experiment (GAGE). Measurements were also taken from NOAA (13, 40) and the University of Colorado’s INSTAAR (22). The sampling methodology is different in the AGAGE and NOAA/INSTAAR networks. The AGAGE measurements are made in situ at relatively high frequency (12 samples per day), whereas NOAA/INSTAAR measurements rely on flask samples collected at a wider number of locations but with lower temporal resolution than the AGAGE. AGAGE and NOAA maintain independent calibration scales for CH3CCl3 and CH4.
In this work, where we compare monthly mean atmospheric observations with a box model of atmospheric transport and chemistry that cannot resolve small-scale transport in the atmosphere, only “baseline” or “background” observations were used. These measurements are of air masses that are assumed to be representative of each hemisphere far from emissions sources. Flasks collected for NOAA/INSTAAR are typically collected under baseline conditions at many sites, and samples are flagged when nonbaseline conditions are suspected. For the global inversions in the text, the high-frequency AGAGE measurements were statistically filtered to remove nonbaseline data points (41).
CH3CCl3.
Atmospheric observations of CH3CCl3 were obtained from both AGAGE and NOAA. The AGAGE/ALE/GAGE measurements have been ongoing since 1978, and NOAA measurements by gas chromatography with mass spectrometric (GC-MS) detection began in 1992. We used AGAGE observations from the five longest running baseline stations (Mace Head, Ireland; Trinidad Head, CA; Ragged Point, Barbados; Cape Matatula, American Samoa; and Cape Grim, Tasmania, Australia) as shown in Table S2. These measurements were combined with earlier ALE/GAGE observations from Adrigole, Ireland and Cape Meares, OR, which preceded the Mace Head and Trinidad Head stations, respectively. Before 2010, the AGAGE measurements were made using gas chromatography with electron capture detector (GC-ECD). At various stages from 2010 onward, the precision on the GC-ECD degraded, and therefore, we used GC-MS observations from the “Medusa” system instead (42). The change occurred at different times depending on the station as detailed in Table S2. Hemispheric monthly averages of the baseline-filtered data were calculated only when all AGAGE stations within a particular hemisphere were operational.
Observations from the NOAA network from the sites in Table S2 were used. Certain sites from the full network were excluded from our analysis where evidence of above-baseline samples was found. The baseline data were averaged into monthly hemispheric means when at least three stations were available within each hemisphere.
AGAGE measurements of CH3CCl3 are reported on the Scripps Institution of Oceanography 2005 scale, and NOAA measurements are reported on the NOAA-03 scale.
The AGAGE and NOAA CH3CCl3 observations are colocated at four sites (Cape Grim, Tasmania; Mace Head, Ireland; Cape Matatula, Samoa; and Trinidad Head, CA.), allowing us to compare the observations of the two networks at these locations. Fig. S2A shows the difference between monthly means at these locations (note that a comparison where we find the closest AGAGE data point to each NOAA flask also shows the same features). Fig. S2 shows that, on average, the NOAA observations have been around 2% higher than the AGAGE observations between 1997 and 2015. However, this difference can be seen to drift markedly beginning at around 3% in the mid-1990s before closing to almost 0% in the early to mid-2000s and growing again in the late 2000s. From 2010 onward, any consistent difference between the networks becomes less clear, with different sites exhibiting different trends. The reasons for these variations in the AGAGE and NOAA networks are unclear, although the recent (post-2010) discrepancies likely relate to the much lower mole fractions present in the atmosphere later in the record. Given the differences between the two networks, we carried out inversions where the AGAGE or NOAA observations were used separately.
CH4.
Measurements of CH4 are available from AGAGE (43) and NOAA (40). The AGAGE measurements of CH4 are reported on the Tohoku University scale, and NOAA measurements are reported on the WMO X2004A scale. NOAA observations began in 1982, with the AGAGE/ALE/GAGE observations beginning in 1987. However, it was not until 1996 that all northern hemispheric AGAGE stations began measuring CH4.
A comparison of AGAGE and NOAA CH4 observations at four sites is shown in Fig. S2B. In contrast to CH3CCl3, the data indicate that agreement between the two networks has remained very close for the entire period.
Given the excellent agreement between the networks and the fact that NOAA observations are available farther back in time than the AGAGE observations, we have only used NOAA CH4 in the inversions shown in the text. Notwithstanding the agreement between the two networks at the colocated measurement sites, differences in the spatial extent of the two networks may be expected to lead to some discrepancy in the derived CH4 emissions in this work. However, such differences were found to be small compared with the derived uncertainties for this global study. Hemispheric monthly means were calculated using the methods described for CH3CCl3 above.
13C-CH4.
Observations of the 13C/12C isotopic ratio of atmospheric methane were taken from the University of Colorado’s INSTAAR (22), which analyzes samples collected at a subset of NOAA sites. We have chosen to use only long-running background INSTAAR sites as identified in ref. 26 and shown in Table S2. INSTAAR data are reported on the scale maintained by the University of California, Irvine based on the method described elsewhere (44–46).
Physical Model Description.
Our atmospheric box model consists of two tropospheric hemispheres that exchange air through turbulent diffusion at the equator at a rate fIHT. Previous estimates of the interhemispheric exchange rate were made using SF6 observations (47), where the gradient between two NOAA stations in the northern hemisphere and two in the southern hemisphere was used to infer an exchange rate of 1.4 y−1. We use the same methodology here but use the hemispheric mean from the entire NOAA SF6 network instead of four stations, which provides a more representative estimate of the air mixing rate between the two hemispheres of 1.2−1 0.1 y−1. We explore the range in this number in our inversion. We assume that the stratosphere can be represented by a single box, which contains 20% of the mass of the atmosphere. The transport between the troposphere and stratosphere is also assumed to be diffusive, with a rate , which we estimate to be between 2−1 and 4−1 y−1 (48, 49).
In our model troposphere, losses of CH3CCl3 and CH4 occur primarily through reaction with the hydroxyl radical (OH). These reactions are parameterized using temperature-dependent rate constants (50). A mean tropospheric temperature of 266 K was set in the model in the year 2000, which produces a tropospheric lifetime consistent with the information in ref. 51 when we used their estimated OH concentration (1.16 radicals cm−3). The influence of tropospheric temperature trends was included in our model by imposing temperature anomalies on this mean temperature from HadCRUT4 (52).
In addition to OH, CH4 is known to react with chlorine radicals in the troposphere and by oxidation in soils (1, 35). We imposed a simple first-order loss of CH4 in the tropospheric boxes, such that ∼25 Tg y−1 of CH4 was lost through reaction with Cl radicals and 28 Tg y−1 was lost to soils for a steady-state global mean atmospheric mole fraction of around 1,800 nmol mol−1 (1).
To simulate the loss of CH3CCl3 and CH4 in the stratosphere we assumed a simple first-order loss process. Our model stratosphere does not distinguish between different chemical processes, and the stratospheric loss rates for CH3CCl3 and CH4 were chosen such that the overall stratospheric lifetimes were consistent with recent photochemical model estimates (53). The inclusion of stratospheric lifetimes in the estimation framework is discussed in further detail below.
It has been shown that simulations that assumed a first-order loss of CH3CCl3 to the ocean (10, 24) may predict spurious OH concentrations, particularly around the time in the late 1990s when the atmospheric growth switched from being positive to negative (33). To address these issues, in this work, we subtract the time-varying net ocean flux calculated in ref. 33 from the CH3CCl3 flux that we estimate using the emissions model. CH4 is not thought to have a significant oceanic sink, and therefore, we assumed no oceanic losses in our model.
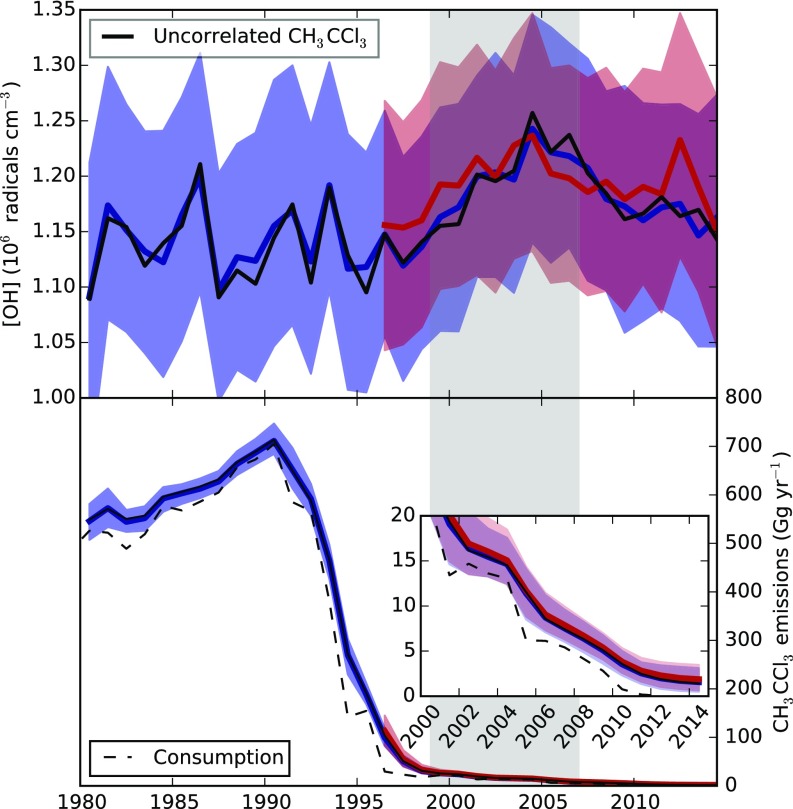
The atmospheric models used in the previous studies that are also shown in Fig. 2 are different from our model in some notable ways (13, 24), which explain part of the difference with our inversion (although it is important to note that the major differences are caused by the treatment of emissions). First, our model includes a stratospheric box, which the work in ref. 13 did not, but has fewer tropospheric and stratospheric boxes than in the work in ref. 24, which had a model that consisted of 12 rather than 3 boxes. Second, in contrast to both studies, our model accounts for the influence of global mean temperature changes on OH loss [the influence of this term is relatively small (14)]. Third and most important according to our sensitivity tests [and previous studies (33)], we include a time-varying estimate of the net ocean flux as opposed to the first-order loss used in these previous papers.
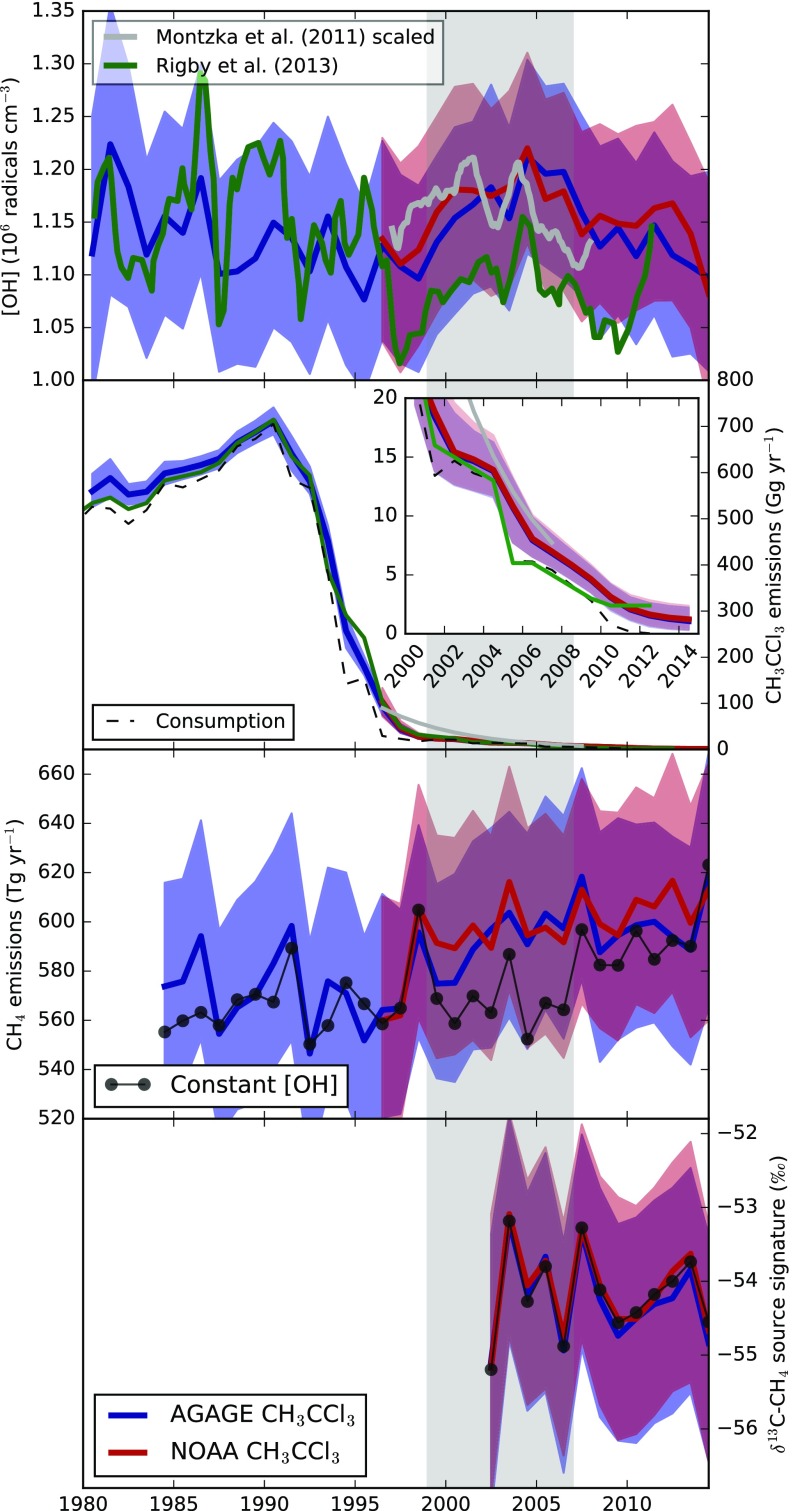
Fig. 2.
(Row 1) Inferred tropospheric annual mean OH concentration. (Row 2) Global CH3CCl3 emissions. (Row 3) Global CH4 emissions. (Row 4) Global 13C/12C source isotope ratio of CH4. The blue lines and shading show quantities inferred when AGAGE CH3CCl3 data were used, and the red lines and shading show those inferred using NOAA CH3CCl3 data. Lines indicate the medians, and the shading shows the 16th to 84th percentiles (∼1 sigma). The green and gray lines in rows 1 and 2 show estimates from previous studies that used the same observations but different methodologies and emissions (13, 24). Inset in row 2 zooms in on the CH3CCl3 emissions from 2000 to 2014. The black lines in rows 3 and 4 show the methane and isotopologue changes inferred when interannually repeating OH was used. The gray shading shows the approximate start and end of the methane pause. Numerical values of the quantities in this figure are available in Dataset S1.
Methane Isotopologue Simulations.
The isotopic composition of atmospheric methane was determined by separately simulating 13C-CH4 and 12C-CH4 in the model and then taking the ratio of the output mole fractions. Emissions of 13C-CH4 were calculated by applying a hemispheric source ratio to the 12C-CH4 emissions (where we have subtracted the 13C-CH4 emissions from the whole-CH4 emissions) and multiplying by the molar mass ratio (17.04/16.04). Where model -values have been compared with atmospheric observations, we have explicitly calculated the model mole fraction of 12C-CH4 by subtracting 13C-CH4 from “whole”-CH4 observations before taking the ratio of the minor and major isotopologues.
Tropospheric fractionation by OH was implemented by imposing a rate constant for 13C-CH4 that was a factor of 1.0039 smaller than for 12C-CH4 (36). We included fractionation caused by tropospheric Cl by tuning the tropospheric non-OH first-order loss in the model such that the model atmosphere was enriched in 13C-CH4 by 2.6‰ compared with a simulation with no tropospheric non-OH loss (35). Similarly, a fractionation factor of −20‰ was imposed for the CH4 soil sink (37). Overall fractionation of CH4 in the stratosphere caused by a range of chemical processes was parameterized by imposing a 13CH4 stratospheric loss rate that was 0.988 times smaller than for 12CH4 (34).
Given the long (i.e., decadal) timescales over which C-CH4 equilibrates in the atmosphere (29), our isotopologue model was found to be much more sensitive to initial conditions than simulations of CH3CCl3 and CH4, where errors in initial conditions were “forgotten” within 1 or 2 y. To minimize this effect on the outcome of our inversion, we included previously published hemispheric annual mean C-CH4 values in our inversion before INSTAAR data were available [before 2000 (26)]. We then discarded our derived source signatures for 2000 and 2001 in case they were influenced by the use of this coarse dataset.
CH3CCl3 Emissions Model Description.
To estimate emissions of CH3CCl3, we devised a simple model that takes estimates of the consumption or use of CH3CCl3 and transforms these into emissions based on certain assumptions about the rate at which release to the atmosphere occurs. Our model is somewhat similar to that used in previous work (19). However, in recent years, we propose that the assumptions in this earlier work may no longer be valid, primarily because use has become increasingly restricted under the Montreal Protocol (indeed, from 2013 onward, reported consumption dropped to zero). Therefore, rather than prescribing emissions model parameters, we specify a model framework and consumption estimates and then use the atmospheric data to explore the space of uncertain parameters.
The consumption that we base our model on is taken from reports to the United Nations Environment Program post-1992 and previously published estimates before 1992 (19). Our model assumes that some fraction () of CH3CCl3 consumption () is emitted in the year that it is reported. The fraction that was not emitted enters a bank (). Each year, some fraction the bank is released to the atmosphere (). We allow for potential inaccuracies in the consumption through two terms: a scaling factor, , and an “unreported” consumption term, , which parameterizes either unreported sales and use of CH3CCl3 or inadvertent production in some as yet unidentified application. Each of these uncertain parameters are estimated in the inversion. We assume that these terms can vary for each decade, . Therefore, for year ,
| [S1] |
| [S2] |
| [S3] |
where is the mass of CH3CCl3 released to the atmosphere in a particular year.
Estimation Framework.
In this work, we have a set of observations that we wish to use to inform us about the uncertain parameters within a physical model. This type of estimation problem can formulated within a hierarchical Bayesian framework (54), where the a posteriori probability density of a set of parameters, after incorporation of some dataset , is given by
| [S4] |
Here, is a vector of uncertain parameters for which we provide an estimate of the probability density function (PDF) that describes our prior beliefs . A set of “hyperparameters,” , can be specified to explore uncertainties in the factors that characterize the prior PDF itself (e.g., its mean and variance). The “likelihood” term, , describes a comparison of the data with the model subject to some uncertainties on the data and the model. In our framework, we assume a Gaussian likelihood function, such that
| [S5] |
where is the uncertainty covariance matrix associated with the model and the data. The list of model parameters explored in the inversion is shown in Table S1.
To explore the posterior PDF, we use an MCMC method (38), in which the posterior PDF can be explored by sequentially accepting or rejecting proposed model states as described in Algorithm S1. This method was used, because it is relatively simple to implement compared with more traditional methods for a system with a nonlinear model, hyperparameters on our prior PDFs, and some non-Gaussian prior PDFs. Our chains were found to converge after iterations, of which the first one-half were discarded as a “burn-in” so that little influence of the initial conditions remained in the posterior parameter set. For the accept or reject step, we proposed changes to each type of parameter individually (e.g., OH concentration, interhemispheric exchange rate, etc.). The probability of accepting a new state can be tuned by adjusting the proposal step sizes and (Algorithm S1). We found that the chains mixed most efficiently when the acceptance rate was between 25 and 50% (55).
Algorithm S1.
Metropolis Hastings algorithm applied to the parameter estimation problem described here. The algorithm is repeated for iterations, of which some initial subset is discarded as burn-in. At each iteration, a set of values for each parameter type (e.g., OH concentration, interhemispheric exchange rate, etc.) is proposed jointly (e.g., for all years). The scalars and are pseudorandom numbers chosen at each iteration from a uniform [] and Gaussian [] distribution, respectively
| Set |
| Forward model run to calculate |
| for do |
| for do |
| Propose new hyperparameter state for parameter PDF if |
| required: |
| Propose new parameter state for parameter : |
| Run model to determine |
| if , then |
| Accept proposed state |
| else |
| Reject proposed state |
Given the large number of iterations and the need to evaluate our forward model in each iteration, our approach relied on the forward model being computationally efficient. To achieve this efficiency, the model was written in Python and compiled using the Numba library (numba.pydata.org), which led to an execution time for a 30-y simulation of around 100 s on a standard desktop machine. With the estimation framework written in Python, the chains could be explored sufficiently within a few hours.
As with any Bayesian inversion, the values that describe the prior PDFs and the likelihood PDFs can have a significant impact on the outcome. In the following subsections, we describe how we have formulated these terms.
A priori constraints on model parameters.
Where available, we have attempted to justify the parameters that describe our a priori PDFs based on previous literature. Where we have limited knowledge relating to the uncertainty on a particular parameter that might have a significant impact on the outcome of our inversion (e.g., the prior OH concentration), we have included a hyperparameter that attempts to account for our limited knowledge. Therefore, the influence of any subjective choice of these parameters on the outcome of the inversion is somewhat diminished in this framework (54). The values chosen for each of our priors are summarized in Table S1.
We assumed a priori that annual OH concentrations did not vary in our model. Initial estimates of the annual OH concentration were taken from an ensemble of 3D atmospheric chemical transport model simulations (8). This study estimated global mass-weighted OH concentrations of 1.11 0.18 × 106 or 1.17 0.1 × 106 radicals cm−3 depending on which models were selected. Therefore, in our inversion, we assume a Gaussian distribution on the annual OH concentration with a mean of 1.11 × 106 radicals cm−3 and an uncertainty of between 0.1 and 0.2 × 106 radicals cm−3.
In a box model such as ours, it is difficult to choose an appropriate local stratospheric model lifetime that is based on previous empirical estimates, because our stratosphere is highly simplified. Furthermore, inverse estimates of the local lifetime that would be required to produce a realistic global stratospheric lifetime will be highly correlated with the model stratosphere–troposphere exchange rate. Therefore, we set a large range from which to choose an appropriate stratospheric local lifetime and provided the inversion with “observations” of the global stratospheric lifetime. For CH3CCl3, our global stratospheric lifetime was taken to be 40 (29–63) y (56). For CH4, we used the mean value (152 y) of a suite of atmospheric chemistry models in ref. 53 and assumed an uncertainty of around 16% based on the multimodel SD in the overall lifetime. In practice, it was difficult to incorporate the uncertainties in these values exactly into our system, because the a posteriori stratospheric lifetime uncertainty was found to be influenced by the derived parameter values throughout the estimation framework. Therefore, we “tuned” the uncertainties on the lifetimes provided to the inversion, such that the a posteriori mean and standard deviation (SD) were roughly consistent with the values above. Because these uncertainties are a minor component of the overall uncertainty in our quantities of interest (e.g., OH concentration), this tuning was found to have negligible influence on the outcome of our inversion.
The CH3CCl3 emissions model relies on several parameters that describe potential errors in the consumption reports and fractions of the consumption or the bank that are released to the atmosphere in any 1 y. To allow these factors to change with time, we solve for a new set of parameters each decade. For Fprompt and Fbank, we assumed a “worst case” scenario (that we had no prior information) and therefore, explored the full range (0–100%) with a uniform PDF. The uncertainty in the reported consumption Cscale was estimated to be 10%, with a Gaussian distribution. The unreported consumption was estimated to be in the range 0–10 Gg y−1. These ranges are necessarily somewhat arbitrary, because little information exists about these parameters. However, we find that our model is flexible enough that (i) parameter values can be chosen such that predicted emissions are consistent with previous studies (19) and (ii) the uncertainties in the a priori emissions predicted by our model are similar to or larger than those in ref. 19 depending on the time period.
We assumed a priori that CH4 emissions had no interannual variability. We estimated emissions on an annual basis based on prior estimates of 545 Tg y−1 (47). It is somewhat unclear what an appropriate value for the uncertainty on this term should be, and therefore, we allowed the uncertainty to be anywhere between 10 and 30% based roughly on the range in bottom-up inventories (1). As described above, by using a hyperparameter on this term, the influence of our somewhat subjective choice is reduced. We also assumed a priori that the hemispheric C-CH4 source signature did not vary interannually and had a prior value in each hemisphere of −54.3‰ (57). Based on the uncertainties in refs. 58 and 59, we allowed the uncertainty in this term to be between 10 and 30 ‰.
Model and data uncertainties.
The uncertainty covariance, , in our (assumed) Gaussian likelihood function contains estimates of the uncertainty caused by the measurements and the model. First, for the diagonal elements of this matrix, we used the annual mean variance of the mole fractions from each NOAA or INSTAAR sampling site in each hemisphere. In doing so, we assumed that the primary source of representation error in our 2D model was its inability to simulate subhemispheric spatial gradients (hence, the use of the variability in space of the NOAA sites) and subannual timescales (because we were only solving for annual emissions and hence, the use of the variability over 1 y). We used NOAA data for this calculation for CH3CCl3 and CH4 instead of the AGAGE data, because they have the widest spatial coverage. By this metric, the mean uncertainties on each monthly mean for CH3CCl3, CH4, and C-CH4 were 5, 5%; 2, 0.5%; and 0.5, 0.3%, respectively, where the pairs of numbers are given as northern hemisphere, southern hemisphere.
As shown in Fig. S2, we must also consider the possibility that one or both of the calibration scales for the AGAGE and NOAA may be drifting over the period of our study. To account for this potential drift, we assumed a structure to our uncertainty covariance given by, for monthly mean measurements and ,
| [S6] |
Here, is the timescale over which we assumed the scales could potentially drift, with an SD of . For CH3CCl3, based on Fig. S2A, we assumed that the scale drifted by 2% over 5 y. For CH4, based on Fig. S2B, we could not discern a significant drift over longer timescales, and therefore, we conservatively assumed a 0.2% drift only over 1-y timescales. Finally, for C-CH4, a previous intercomparison suggested an uncertainty in the scale of ∼0.1‰ (60). It also could not detect a drift in this scale over the 10-y period of overlap between different networks, and therefore, we assumed, again conservatively, a timescale of 10 y.
Description of Additional Inversion Outputs.
In addition to the outputs presented in the text, our inversion explores several model parameters that could have an impact on the inversion. Here, we briefly describe some of the more important additional outputs.
Interhemispheric transport.
As shown previously, the interhemispheric gradient of a long-lived trace gas can act as a constraint on global emissions (20). However, it is important to consider the impact of errors in the assumed model interhemispheric exchange timescale on the outcome of inversions that use this method. Previous studies carried out sensitivity tests to determine the level to which this term might impact their estimates. Here, we have included the interhemispheric exchange rate in the inversion, so that uncertainties can be propagated through the system. Our a posteriori estimates of the interhemispheric exchange timescale show that the posterior uncertainties are similar to those assumed a priori (Table S1). Therefore, we can conclude that there was little information available from the atmospheric observations to strongly constrain this term along with the other parameters. Compared with the prior value, there is a small (nonstatistically significant) decrease in this timescale from the 1980s to the 2010s of 1.25 0.1 to 1.18 0.1 y. This finding could indicate an acceleration in the rate of mixing between the two hemispheres over this time period. However, it is perhaps more likely that, in our simplified model, we are not able to fully account for the impact of changes in the intrahemisphere source distribution on the simulated atmospheric mole fractions. This limitation may be particularly true of CH3CCl3, which has emissions that have changed dramatically between the beginning and end of the simulation along with the accuracy in using measurements to assess the true hemispheric means.
Hemispheric emissions and OH distribution.
In addition to the interhemispheric exchange timescale, the assumed spatial distribution of emissions can have an impact on the derived emissions. Our a posteriori solution shows that the fraction of emissions in the northern hemisphere declined for CH3CCl3 from 99 1% in the 1980s to 96 3% in the 2010s. This finding is likely to be consistent with the reduction in use of this compound in industrialized countries throughout this time period. In contrast, we do not derive a significant trend in the CH4 northern hemisphere emissions fraction, which remains between 75 and 80% throughout.
The northern hemispheric excess OH was explored in the inversion. We find that there was little update of this parameter in the inversion from the prior distribution of −5 to 20%, although there is a slight preference toward similar OH concentrations in each hemisphere (similar to ref. 32). There are no significant trends in this parameter as a function of time in our inversion.
Comparison of isotopologue simulations with the work by Schaefer et al. (26).
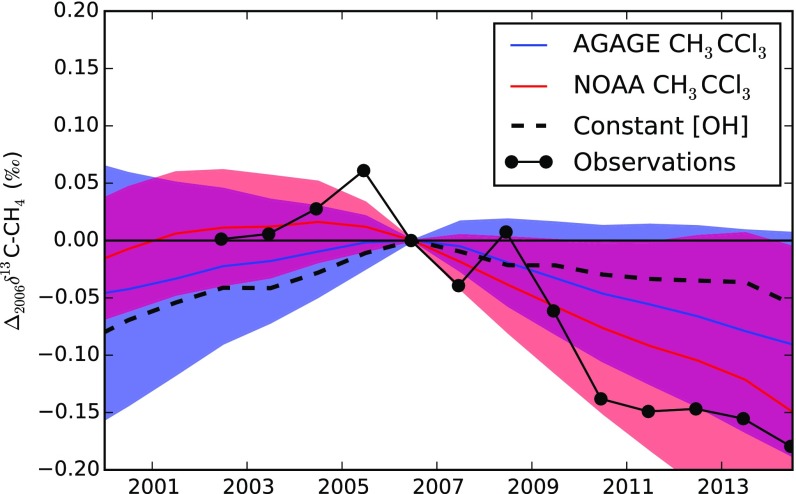
Previously, Schaefer et al. (26) examined the potential influence of a decrease in OH on the post-2006 atmospheric C-CH4 and ruled it out as a potential contributor to the decline. They propose that only a small decrease in OH could account for the methane rise from 2007 onward (0.15% y−1) but that this change could not account for the observed decline in C-CH4. In our model, it is not possible to reconcile the growth in methane with a change in OH on the order of 0.15% y−1 (rather, a change closer to 1% y−1 is needed). We believe that this discrepancy with ref. 26 is because they have used the OH change derived in ref. 13 up until 2006, after which they assume a 0.15% y−1 decline. Therefore, in total, they assumed a decline in OH of ∼12% from 2004 to 2014 (and therefore, an annualized trend of around 1.2% y−1), which is of a similar magnitude to our derived trend (Fig. 2). When we apply our derived trend to our isotopologue model, we have shown that we obtain some contribution to the decline in C-CH4 on the order of 0.1‰ (Fig. S6). This finding is in contrast to the work in ref. 26, which finds a much smaller contribution (around 0.01‰), despite the apparently similar OH trends in their test. It is unclear what the cause of this discrepancy is. Possibilities include (assuming no modeling errors) that (i) pre-2006 changes in the source ratio (which varied each year pre-2006 in the test in ref. 2626) could be masking the post-2006 OH-induced growth rate in ref. 26 or (ii) our post-2006 decline in C-CH4 is being influence by model spin up in some way that we have not accounted for in our ensemble of forward runs.
Fig. S6.
Simulation of the change in global C-CH4 relative to 2006 based on varying OH concentrations from the AGAGE and NOAA inversions (blue and red, respectively), with total CH4 emissions and its source 13C/12C ratio held fixed and varying CH4 emissions from the “constant OH” inversion with the source 13C/12C ratio held constant (dashed line). The black points indicate the observed global mean C-CH4. Each of these signals is a transient response in the model. Over timescales on the order of decades, C-CH4 returns to the values before any perturbations in either the OH concentration or the bulk emissions [similar behavior and response timescales were noted previously (29, 61)].
Results
Rows 1 and 2 in Fig. 2 show the simultaneously derived OH concentrations and CH3CCl3 emissions inferred from independent application of our approach using the AGAGE or NOAA observations. A comparison between the observations and the model is shown in Fig. S3. The median solution shows a relatively small OH trend in the 1980s and 1990s [with smaller interannual variability than previous CH3CCl3 inversions (11, 12, 24)] followed by an upward trend in OH concentration on the order of 10% from the late 1990s to 2004 (11 13 and 9 12% increases for AGAGE and NOAA, respectively, between 1998 and 2004). This trend is of a similar size to those highlighted in previous studies using CH3CCl3 (14, 24). Post-2004, our median estimate shows a decline in OH. This finding would suggest that at least some fraction of the post-2007 CH4 growth could be attributable to declining OH. By carrying out a set of linear regressions on the post-2007 OH estimates from our a posteriori ensemble of model states, we find a 70 or 64% probability that OH exhibited some level of negative trend during this period when AGAGE or NOAA data, respectively, were used (the mean differences between the 2004 and 2014 OH concentrations were −8 11% and −11 11%, respectively). In addition to this trend are several features of our OH inversion that are important to note. First, significant uncertainties remain in the global OH concentration, such that it is possible to draw a “constant OH” line that is consistent with the observation-derived OH within its uncertainties. Second, small differences in the CH3CCl3 trend and interhemispheric gradient measured by the two independent networks lead to variations in the derived OH concentration and CH3CCl3 emissions. However, these differences are small compared with the other uncertainties in the system.
Fig. S3.
Percentage difference between modeled and observed mole fractions (model/data) for CH3CCl3, NOAA CH4, and INSTAAR C-CH4 for (A) the AGAGE CH3CCl3 inversion and (B) the NOAA CH3CCl3 inversion. Gray shading indicates the diagonal elements of the model representation uncertainty covariance matrix (1 sigma). Blue lines show the median northern hemisphere (NH) mole fraction, and green lines show the southern hemisphere (SH) mole fraction. The blue and green shading shows the 1-sigma uncertainty in the a posteriori mole fractions. A seasonal cycle is apparent in the CH4 and C-CH4 residual. This finding is because we have assumed that CH4 emissions have no seasonal cycle, which is a clear oversimplification but one that we do not expect to have any impact on our results concerning quantities derived on timescales of at least 1 y. The figure also shows a (nonstatistically significant) trend in the CH3CCl3 residual, which is not inconsistent with the observations, because we have included off-diagonal terms in our representation uncertainty covariance that allow for multiyear trends of the order of a few percent. Therefore, the a posteriori uncertainties in OH and other quantities will be consistent with potential drifts in the atmospheric CH3CCl3 data, such as those shown in the figure. Fig. S4 shows the outcome of an inversion performed with this correlation-length scale set to zero and that it has little major impact on the median solution. In this solution, the “drift” between the observations and the posterior model is negligible.
Differences between our derived CH3CCl3 emissions and those assumed previously (Fig. 2, row 2) explain part of the discrepancy between our OH trends and those derived in previous studies (Fig. 2, row 1), although other factors, such as the treatment of the ocean sink, also contribute (SI Materials and Methods). Our global CH3CCl3 emissions estimates differ from the previous estimates shown in Fig. 2 in that they have been adjusted in the inversion to be consistent with atmospheric observations (and in particular, the interhemispheric CH3CCl3 mol fraction gradient) instead of being imposed based on bottom-up models or an assumed rate of decline (13, 24). The CH3CCl3 emissions derived in our inversion indicate that there was ongoing release of CH3CCl3 to the atmosphere, at least through 2014, despite national reports indicating that use of this substance ceased in 2013 (25). Analysis of high-frequency AGAGE data confirms that emissions persisted throughout this period upwind of some monitoring sites (Fig. S1).
In addition to our multispecies inversion, we carried out an inversion for OH concentrations and CH3CCl3 emissions using only CH3CCl3 observations (Fig. S4). We find that the OH concentrations and variability derived in this analysis lead to a similar result to the multispecies inversion, indicating that the constraint on OH is primarily from CH3CCl3 rather than CH4 and its 13C/12C ratio. Therefore, the timing of the rise and fall in inferred OH has not been significantly influenced by “knowledge” of the pause and renewed growth in CH4.
Fig. S4.
Outcome of inversion using CH3CCl3 data alone from either the AGAGE network (blue) or NOAA network (red). Upper shows the derived OH concentration, and Lower shows the derived CH3CCl3 emissions. Shading indicates the and percentile range, and the solid lines show the medians. The black lines show the AGAGE-only inversion with an assumed zero temporal correlation-length scale in the model mismatch uncertainty, which removes the long-term drift in the model data residual (Fig. S3). Inset shows CH3CCl3 emissions from 2000 to 2014.
Our multispecies inversion allows us to propagate information on the derived OH concentration and its uncertainty through to estimates of CH4 emissions. We find that, similar to OH concentration, it is possible to draw a “constant CH4 emissions” line within the derived uncertainties (Fig. 2, row 3). However, the median solution suggests a relatively steady upward trend from the mid-1990s to the mid-2000s followed by a period of smaller growth. We note that our result does not require a sudden, statistically significant increase in CH4 emissions in 2007, as suggested elsewhere, to explain the observations (5–7, 26, 27). Instead, it is implied that the rise in atmospheric mole fractions in 2007 is consistent with the decline in OH concentrations post-2004 overlaid on a gradual rise in CH4 emissions with some additional interannual variability on the order of 10 Tg y−1.
Row 3 in Fig. 2 also shows an inversion where OH is constrained to be interannually repeating. In this scenario, CH4 emissions remain at a relatively low level throughout the 2000s compared with the varying OH inversions until around 2007, when they sharply increase. Compared with the 5-y period before 2007, emissions from 2007 to 2011 (inclusive) were 22 9 Tg y−1 higher in this scenario [similar to other studies that had assumed constant OH (28)]. In contrast, for the inversions with the OH changes derived from AGAGE or NOAA CH3CCl3, this difference was found to be 4 23 or 9 22 Tg y−1, respectively.
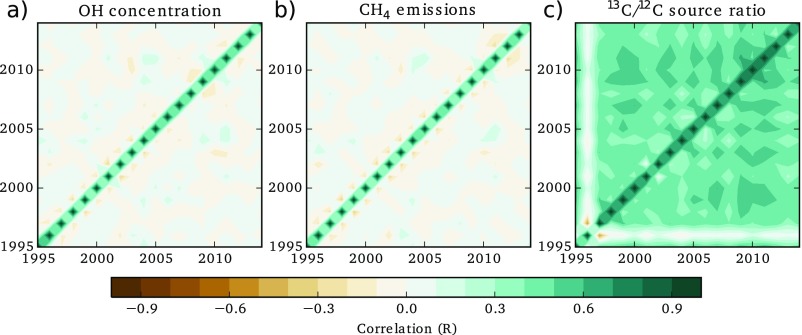
In our inversion, we determine the global 13CH4/12CH4 source signature that would be required to match the observed atmospheric C-CH4 (SI Materials and Methods) considering changes in OH and global CH4 emissions (Fig. 2, row 4). The observations and modeling framework provide relatively weak constraints on this term, such that the uncertainties on annual 13CH4/12CH4 source ratios are around an order of magnitude larger, at around 1‰, than the changes that would be required to match the observed trends, which are of the order of 0.1‰. Furthermore, we find that, because of the very long timescales over which methane isotopologues respond to source or sink perturbations (29), our derived source ratio values are significantly autocorrelated, meaning that, in our inversion, the derived annual values cannot be considered fully independent of one another (Fig. S5).
Fig. S5.
Correlation matrices for three annually derived quantities: (A) OH concentrations, (B) CH4 emissions, and (C) 13C/12C source ratios. The figure shows relatively small autocorrelation for OH and CH4 but significant off-diagonal elements for the source signature, indicating that estimates of the source signature in any 1 y are significantly correlated with surrounding years.
Discussion
We have presented an inversion that derives global OH concentrations simultaneously with CH3CCl3 and CH4 emissions and the 13CH4/12CH4 source ratio using atmospheric observations of CH3CCl3, CH4, and δ13C-CH4. Our median solution shows that OH increased from the late 1990s to 2004 before declining until 2014, albeit with an uncertainty that is of similar magnitude to the change. The median solution suggests that OH changes have contributed to the recent pause and growth in CH4 as reflected in the median CH4 emissions, which only change slowly after the late 1990s. In contrast, our constant OH inversion shows a relatively sudden emissions increase in 2007. It is interesting to note that these two sets of derived emissions agree relatively well during the 1990s (at levels of ∼560 Tg y−1) and after 2010 (∼600 Tg y−1), but the trajectory of the transition is different, with most of the increase occurring in the late 1990s if OH is allowed to change but primarily around 2007 if it is not. However, it is also important to note that the median solution of the constant OH inversion falls within the 1-sigma range of the “varying OH” inversions.
Notwithstanding the uncertainties, our findings are in contrast to recent work in which a 3D model of atmospheric transport and chemistry predicted only a gradual decrease in methane lifetime over the last three decades and therefore, that emissions changes were primarily responsible for the CH4 growth (7). We also provide an alternative perspective to another study that attributed much of the recent growth in CH4 and δ13C-CH4 to tropical wetland emissions based partly on the finding that there was no clear signal of an OH change in other reduced chemical tracers (CH3CCl3 had not been considered) (6). Other authors have investigated and ruled out OH changes as being the sole driver of recent trends in studies that used δ13C-CH4 and ethane (C2H6) to assign the growth in methane to livestock and oil and gas extraction, respectively (5, 26).
Forward model simulations with our derived OH and a constant 13C-CH4 source show a decline in atmospheric δ13C-CH4 post-2006, showing that OH trends likely contributed to the recent δ13C-CH4 trends in our inversion (Fig. S6). Although the precise contribution of OH to the observed trend is difficult to isolate from other influences, it is likely that our derived changes are not sufficient to explain the entire recent decline in δ13C-CH4 and that some change in the source signature has also occurred as has been suggested previously (26). However, as described above, the uncertainties on the source signature in our inversion are much larger than the required change in source signature, making the precise identification of a change in one or more source sectors difficult.
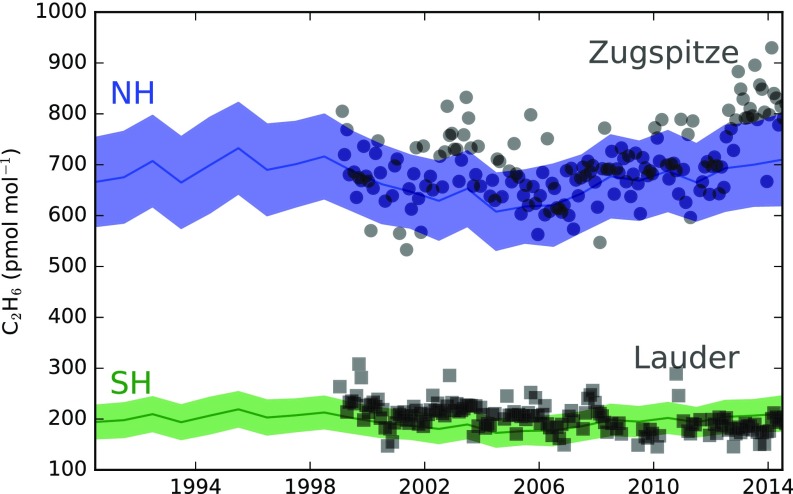
Some recent studies have pointed to an “upturn” in global concentrations of ethane (C2H6), coincident with the recent rise in CH4 (5, 30, 31), which may imply an increase in CH4 emissions caused by an increase in oil and gas extraction. Column-averaged measurements in the background atmosphere reveal trends in C2H6 between 2007 and 2014 of 23 (95% confidence interval = 18, 28) and −4 (95% confidence interval = −6, −1) pmol mol−1 y−1 in the northern and southern hemispheres, respectively (5). Because C2H6 is primarily removed from the atmosphere via reaction with OH, we also expect changes in OH to have an impact on C2H6 concentrations, even if emissions have not changed. By running our model forward with constant C2H6 emissions [which were tuned to match the mean northern and southern hemispheric observed mole fractions (5)] (Fig. S7) and our derived OH concentrations, we find that it is possible to explain a global background C2H6 growth rate of 9 (95% confidence interval = −11, 30) and 3 (95% confidence interval = −4, 11) pmol mol−1 y−1 in the northern and southern hemispheres, respectively, from 2007 to 2014. The timing of transition from declining to growing C2H6 mol fractions in the northern hemisphere coincides within 1 or 2 y with change from growing to declining OH in our inversion (Fig. S7). Therefore, it is possible that some of the recent upturn in northern hemispheric C2H6 is also caused by changes in OH concentration. Our constant emissions simulation does not match the continued downward trend in southern hemispheric C2H6, although the uncertainties in our estimates overlap with the observed trend.
Fig. S7.
Constant emission simulation of northern hemisphere (NH) and southern hemisphere (SH) ethane (blue and green, respectively) based on OH concentrations from the AGAGE CH3CCl3 simulation (blue). The gray data points are previously published deseasonalized column-averaged observations from Zugspitze (45° N, 11° E) and Lauder (45° S, 170° E) (5).
As we stress above, it is important to note the magnitude of the uncertainties in our inversions, which we believe are more comprehensive than previous work, because they incorporate several systematic factors, particularly relating to CH3CCl3 emissions. If OH changes and their uncertainty are not considered, a sudden and statistically significant increase in CH4 emissions after 2006 is required to fit the observations. Although we cannot rule out this scenario, in our inversions in which the recent CH3CCl3 budget is objectively considered, a trajectory in which CH4 emissions have changed more gradually during the late 2000s is also plausible. Our study highlights that without careful consideration of the CH4 sink and its uncertainty, it would be possible to draw misleading conclusions regarding the emissions trend when long-term records of background atmospheric observations are used. Our median estimate suggests an important role for OH in the recent CH4 pause and growth overlaid on a relatively gradual increase in CH4 emissions over the last two decades.
Materials and Methods
Atmospheric mole fractions were simulated using a box model atmosphere, which accounted for mixing between the two tropospheric hemispheres, and exchange with the stratosphere. Loss of CH3CCl3 and CH4 occurred primarily through reaction with OH in the model troposphere [with the potential for differences in the northern and southern OH concentrations (32)]. The model also included a first-order loss of each compound in the stratosphere (all stratospheric losses were considered to contribute to a single stratospheric loss rate), first-order sinks for CH4 in the troposphere because of reaction with chlorine and uptake by methanotrophs in soils (1), and an ocean uptake for CH3CCl3 according to previous ocean model estimates (33). Isotopic fractionation of CH4 was assumed to occur for each sink based on recent estimates (34–37). Emissions of CH3CCl3 were estimated using a model that took as an input consumption or use of CH3CCl3. Uncertain parameters in the atmospheric and emissions model were estimated in the inversion along with estimates of the annual hemispheric CH4 surface flux and 13CH4/12CH4 source signature and global annual OH concentration. By exploring some of the major unknown parameters in this multispecies framework, the influence of uncertainties in each parameter and the atmospheric data could be propagated through the system (Table S1 shows a list of model parameters). The AGAGE, NOAA, and INSTAAR data (Fig. 1) were used to constrain the model parameters using a hierarchical Bayesian framework, which was solved using a Markov Chain Monte Carlo (MCMC) algorithm (38). The MCMC approach iteratively explores model states, randomly accepting or rejecting proposed parameter values with a probability dependent on the ratio of posterior probability density of the “current” and proposed states. The outcome is a chain of parameter values that spans the posterior probability density functions. Atmospheric data from a subset of the three networks were used where predominantly “background” (unpolluted) air masses were sampled and time series of the order of a decade or more were available. The delta notation for observations of 13C/12C ratio in CH4 is defined as
| [1] |
where R is the 13C/12C ratio in CH4, and Rstd refers to a reference ratio (39); values are quoted in per mille (‰). Additional details are provided in SI Materials and Methods.
Supplementary Material
Acknowledgments
We thank E. Dlugokencky for his continuing efforts to produce the NOAA CH4 dataset and helpful comments on our manuscript. NOAA measurements of CH4 and CH3CCl3 are supported, in part, by the NOAA Climate Program Office’s AC4 Program and benefited from the technical assistance of C. Siso, B. Hall, G. Dutton, and J. Elkins. M.R. is supported by Natural Environment Research Council (NERC) Advanced Research Fellowship NE/I021365/1 and Natural Environment Research Council Grant NE/N016211/1. A.L.G. is supported by NERC Independent Research Fellowship NE/L010992/1. M.F.L. is supported by NERC Grants NE/I027282/1 and NE/M014851/1. The operations of the AGAGE instruments at Mace Head, Trinidad Head, Cape Matatula, Ragged Point, and Cape Grim are supported by NASA Grants NNX16AC98G [to Massachusetts Institute of Technology (MIT)], NNX07AE89G (to MIT), NNX11AF17G (to MIT), NNX07AE87G [to Scripps Institution of Oceanography (SIO)], NNX07AF09G (to SIO), NNX11AF15G (to SIO), and NNX11AF16G (to SIO); Department of Energy and Climate Change Contract GA01081 to the University of Bristol; the Commonwealth Scientific and Industrial Research Organization, Australia; and the Bureau of Meteorology, Australia. Measurements from Gosan, Korea are supported by the Basic Science Research Program through the National Research Foundation of Korea (Grant NRF-2013R1A1A2057880).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
See Commentary on page 5324.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1616426114/-/DCSupplemental.
References
- 1.Kirschke S, et al. Three decades of global methane sources and sinks. Nat Geosci. 2013;6:813–823. [Google Scholar]
- 2.Dlugokencky EJ, et al. Atmospheric methane levels off: Temporary pause or a new steady-state? Geophys Res Lett. 2003;30:3–6. [Google Scholar]
- 3.Rigby M, et al. Renewed growth of atmospheric methane. Geophys Res Lett. 2008;35:L22805. [Google Scholar]
- 4.Dlugokencky EJ, et al. Observational constraints on recent increases in the atmospheric CH4 burden. Geophys Res Lett. 2009;36:L18803. [Google Scholar]
- 5.Hausmann P, Sussmann R, Smale D. Contribution of oil and natural gas production to renewed increase in atmospheric methane (2007–2014): Top–down estimate from ethane and methane column observations. Atmos Chem Phys. 2016;16:3227–3244. [Google Scholar]
- 6.Nisbet EG, et al. Rising atmospheric methane: 2007-2014 growth and isotopic shift. Global Biogeochem Cycles. 2016;30:1356–1370. [Google Scholar]
- 7.Dalsøren SB, Isaksen ISA. CTM study of changes in tropospheric hydroxyl distribution 1990–2001 and its impact on methane. Geophys Res Lett. 2006;33:L23811. [Google Scholar]
- 8.Voulgarakis A, et al. Analysis of present day and future OH and methane lifetime in the ACCMIP simulations. Atmos Chem Phys. 2013;13:2563–2587. [Google Scholar]
- 9.Lovelock JE. Methyl chloroform in the troposphere as an indicator of OH radical abundance. Nature. 1977;267:32–32. [Google Scholar]
- 10.Prinn RG, et al. Evidence for substantial variations of atmospheric hydroxyl radicals in the past two decades. Science. 2001;292:1882–1888. doi: 10.1126/science.1058673. [DOI] [PubMed] [Google Scholar]
- 11.Prinn RG, et al. Evidence for variability of atmospheric hydroxyl radicals over the past quarter century. Geophys Res Lett. 2005;32:L07809. [Google Scholar]
- 12.Bousquet P, Hauglustaine DA, Peylin P, Carouge C, Ciais P. Two decades of OH variability as inferred by an inversion of atmospheric transport and chemistry of methyl chloroform. Atmos Chem Phys. 2005;5:2635–2656. [Google Scholar]
- 13.Montzka SA, et al. Small interannual variability of global atmospheric hydroxyl. Science. 2011;331:67–69. doi: 10.1126/science.1197640. [DOI] [PubMed] [Google Scholar]
- 14.McNorton J, et al. Role of OH variability in the stalling of the global atmospheric CH4 growth rate from 1999 to 2006. Atmos Chem Phys. 2016;16:7943–7956. [Google Scholar]
- 15.Krol M, Lelieveld J. Can the variability in tropospheric OH be deduced from measurements of 1,1,1-trichloroethane (methyl chloroform)? J Geophys Res. 2003;108:4125. [Google Scholar]
- 16.Pison I, Bousquet P, Chevallier F, Szopa S, Hauglustaine D. Multi-species inversion of CH4, CO and H2; emissions from surface measurements. Atmos Chem Phys. 2009;9:5281–5297. [Google Scholar]
- 17.Krol MC, et al. Continuing emissions of methyl chloroform from Europe. Nature. 2003;421:131–135. doi: 10.1038/nature01311. [DOI] [PubMed] [Google Scholar]
- 18.Reimann S, et al. Low European methyl chloroform emissions inferred from long-term atmospheric measurements. Nature. 2005;433:506–508. doi: 10.1038/nature03220. [DOI] [PubMed] [Google Scholar]
- 19.McCulloch A, Midgley PM. The history of methyl chloroform emissions: 1951-2000. Atmos Environ. 2001;35:5311–5319. [Google Scholar]
- 20.Liang Q, et al. Constraining the carbon tetrachloride (CCl4) budget using its global trend and inter-hemispheric gradient. Geophys Res Lett. 2014;41:5307–5315. [Google Scholar]
- 21.Prinn RG, et al. A history of chemically and radiatively important gases in air deduced from ALE/GAGE/AGAGE. J Geophys Res. 2000;105:17751–17792. [Google Scholar]
- 22.White J, Vaughn BH. 2015. University of Colorado, Institute of Arctic and Alpine Research (INSTAAR), Stable Isotopic Composition of Atmospheric Methane (13c) from the NOAA ESRL Carbon Cycle Cooperative Global Air Sampling Network, 1998-2014, Version: 2015-08-03. Available at ftp://aftp.cmdl.noaa.gov/data/trace_gases/ch4c13/flask/. Accessed April 1, 2016.
- 23.Miller JB, Mack KA, Dissly R, White JWC, Dlugockenky EJ, Tans PP. Development of analytical methods and measurements of 13C/12C in atmospheric CH4 from the NOAA Climate Monitoring and Diagnostics Laboratory Global Air Sampling Network. J Geophys Res. 2002;107:11-1–11-15. [Google Scholar]
- 24.Rigby M, et al. Re-evaluation of the lifetimes of the major CFCs and CH3CCl3 using atmospheric trends. Atmos Chem Phys. 2013;13:2691–2702. [Google Scholar]
- 25.UNEP 2016. UNEP Ozone Secretariat Data Centre. Available at ozone.unep.org/en/data-reporting/data-centre. Accessed February 21, 2015.
- 26.Schaefer H, et al. A 21st-century shift from fossil-fuel to biogenic methane emissions indicated by 13CH4. Science. 2016;352:80–84. doi: 10.1126/science.aad2705. [DOI] [PubMed] [Google Scholar]
- 27.Turner AJ, et al. A large increase in U.S. methane emissions over the past decade inferred from satellite data and surface observations. Geophys Res Lett. 2016;43:2218–2224. [Google Scholar]
- 28.Bergamaschi P, et al. Atmospheric CH4 in the first decade of the 21st century: Inverse modeling analysis using SCIAMACHY satellite retrievals and NOAA surface measurements. J Geophys Res Atmos. 2013;118:7350–7369. [Google Scholar]
- 29.Tans PP. A note on isotopic ratios and the global atmospheric methane budget. Global Biogeochem Cycles. 1997;11:77. [Google Scholar]
- 30.Helmig D, et al. Reversal of global atmospheric ethane and propane trends largely due to US oil and natural gas production. Nat Geosci. 2016;9:490–495. [Google Scholar]
- 31.Franco B, et al. Retrieval of ethane from ground-based FTIR solar spectra using improved spectroscopy: Recent burden increase above Jungfraujoch. J Quant Spectrosc Radiat Transf. 2015;160:36–49. [Google Scholar]
- 32.Patra PK, et al. Observational evidence for interhemispheric hydroxyl-radical parity. Nature. 2014;513:219–223. doi: 10.1038/nature13721. [DOI] [PubMed] [Google Scholar]
- 33.Wennberg PO, Peacock S, Randerson JT, Bleck R. Recent changes in the air-sea gas exchange of methyl choloroform. Geophys Res Lett. 2004;31 [Google Scholar]
- 34.Brenninkmeijer CAM, Lowe DC, Manning MR, Sparks RJ, van Velthoven PFJ. The 13c, 14c, and 18o isotopic composition of CO, CH4, and CO2 in the higher southern latitudes lower stratosphere. J Geophys Res. 1995;100:26163–26172. [Google Scholar]
- 35.Allan W, Struthers H, Lowe DC. Methane carbon isotope effects caused by atomic chlorine in the marine boundary layer: Global model results compared with Southern Hemisphere measurements. J Geophys Res. 2007;112 [Google Scholar]
- 36.Saueressig G. Carbon 13 and D kinetic isotope effects in the reactions of CH4 with O(1D) and OH: New Laboratory measurements and their implications for the isotopic composition of stratospheric methane. J Geophys Res. 2001;106:23127–23138. [Google Scholar]
- 37.Lassey KR, Etheridge DM, Lowe DC, Smith AM, Ferretti DF. Centennial evolution of the atmospheric methane budget: What do the carbon isotopes tell us? Atmos Chem Phys. 2007;7:2119–2139. [Google Scholar]
- 38.Hastings WK. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57:97–109. [Google Scholar]
- 39.Craig H. Isotopic standards for carbon and oxygen and correction factors for massspectrometric analysis of carbon dioxide. Geochim Cosmochim Acta. 1957;12:133–149. [Google Scholar]
- 40.Dlugokencky EJ, Steele LP, Lang PM, Masarie KA. The growth rate and distribution of atmospheric methane. J Geophys Res. 1994;99:17021–17043. [Google Scholar]
- 41.O’Doherty S, et al. In situ chloroform measurements at Advanced Global Atmospheric Gases Experiment atmospheric research stations from 1994 to 1998. J Geophys Res. 2001;106:20429–20444. [Google Scholar]
- 42.Miller BR, et al. Medusa: A sample preconcentration and GC/MS detector system for in situ measurements of atmospheric trace halocarbons, hydrocarbons, and sulfur compounds. Anal Chem. 2008;80:1536–1545. doi: 10.1021/ac702084k. [DOI] [PubMed] [Google Scholar]
- 43.Cunnold DM, et al. In situ measurements of atmospheric methane at GAGE/AGAGE sites during 1985–2000 and resulting source inferences. J Geophys Res. 2002;107:4225. [Google Scholar]
- 44.Stevens CM, Rust FE. The carbon isotopic composition of atmospheric methane. J Geophys Res. 1982;87:4879. [Google Scholar]
- 45.Tyler SC. Stable carbon isotope ratios in atmospheric methane and some of its sources. J Geophys Res. 1986;91:13232. [Google Scholar]
- 46.Lowe DC, Brenninkmeijer CAM, Tyler SC, Dlugkencky EJ. Determination of the isotopic composition of atmospheric methane and its application in the Antarctic. J Geophys Res. 1991;96:15455. [Google Scholar]
- 47.Patra PK, et al. TransCom model simulations of CH4 and related species: Linking transport, surface flux and chemical loss with CH4 variability in the troposphere and lower stratosphere. Atmos Chem Phys. 2011;11:12813–12837. [Google Scholar]
- 48.Cunnold DM, et al. The atmospheric lifetime experiment 3. Lifetime methodology and application to three years of CFCl3 data. J Geophys Res. 1983;88:8379–8400. [Google Scholar]
- 49.Cunnold DM, et al. Global trends and annual releases of CCI3F and CCI2F2 estimated from ALE/GAGE and other measurements from July 1978 to June 1991. J Geophys Res. 1994;99:1107–1126. [Google Scholar]
- 50.Sander SP, et al. 2011. Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies: Evaluation Number 17 (NASA Jet Propulsion Laboratory, Pasadena, CA), Tech Rep 17.
- 51.Spivakovsky CM, et al. Three-dimensional climatological distribution of tropospheric OH: Update andevaluation. J Geophys Res. 2000;105:8931–8980. [Google Scholar]
- 52.Morice CP, Kennedy JJ, Rayner NA, Jones PD. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 data set. J Geophys Res Atmos. 2012;117:D08101. [Google Scholar]
- 53.Chipperfield MP, et al. 2013. Model estimates of lifetimes. SPARC Report on the Lifetimes of Stratospheric Ozone-Depleting Substances, Their Replacements, and Related Species, eds Reimann S, Ko MKW, Newman PA, Strahan SE (WMO/ICSU/IOC World Climate Research Programme, Zurich), SPARC Rep No. 6, WCRP-15/2013, Chap 5. [Google Scholar]
- 54.Ganesan AL, et al. Characterization of uncertainties in atmospheric trace gas inversions using hierarchical Bayesian methods. Atmos Chem Phys. 2014;14:3855–3864. [Google Scholar]
- 55.Roberts GO, Gelman A, Gilks WR. Weak convergence and optimal scaling of random walk Metropolis algorithms. Ann Appl Probab. 1997;7:110–120. [Google Scholar]
- 56.Engel A, et al. 2013. Inferred lifetimes from observed trace-gas distributions. SPARC Report on the Lifetimes of Stratospheric Ozone-Depleting Substances, Their Replacements, and Related Species, eds Reimann S, Ko MKW, Newman PA, Strahan SE (WMO/ICSU/IOC World Climate Research Programme, Zurich), SPARC Rep No. 6, WCRP-15/2013, Chap 4. [Google Scholar]
- 57.Whiticar M, Schaefer H. Constraining past global tropospheric methane budgets with carbon and hydrogen isotope ratios in ice. Philos Trans R Soc Lond A. 2007;365:1793–1828. doi: 10.1098/rsta.2007.2048. [DOI] [PubMed] [Google Scholar]
- 58.Snover AK, Quay PD, Hao WM. The D/H content of methane emitted from biomass burning. Global Biogeochem Cycles. 2000;14:11–24. [Google Scholar]
- 59.Rigby M, Manning AJ, Prinn RG. The value of high-frequency, high-precision methane isotopologue measurements for source and sink estimation. J Geophys Res. 2012;117:1–14. [Google Scholar]
- 60.Levin I, et al. No inter-hemispheric δ13CH4 trend observed. Nature. 2012;486:E3–E4. doi: 10.1038/nature11175. [DOI] [PubMed] [Google Scholar]
- 61.Lassey KR, Lowe DC, Manning MR. The trend in atmospheric methane δ13C and implications for isotopic constraints on the global methane budget. Global Biogeochem Cycles. 2000;14:41–49. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.