Ambiguity in the causes for decadal trends in atmospheric methane and hydroxyl

Significance

Recent trends in atmospheric methane are not well understood as evidenced by multiple hypotheses proposed to explain the stabilization of methane concentrations in the early 2000s and the renewed growth since 2007. Here we use a multispecies inversion to determine the cause of these decadal trends. The most likely explanation for the renewed growth in atmospheric methane involves a decrease in hydroxyl (OH), the main sink for atmospheric methane, that is partially offset by a decrease in methane emissions. However, we also demonstrate that the problem of attributing methane trends from the current surface observation network, including isotopes, is underdetermined and does not allow unambiguous attribution of decadal trends.

Abstract

Methane is the second strongest anthropogenic greenhouse gas and its atmospheric burden has more than doubled since 1850. Methane concentrations stabilized in the early 2000s and began increasing again in 2007. Neither the stabilization nor the recent growth are well understood, as evidenced by multiple competing hypotheses in recent literature. Here we use a multispecies two-box model inversion to jointly constrain 36 y of methane sources and sinks, using ground-based measurements of methane, methyl chloroform, and the C¹³/C¹² ratio in atmospheric methane (δ¹³CH₄) from 1983 through 2015. We find that the problem, as currently formulated, is underdetermined and solutions obtained in previous work are strongly dependent on prior assumptions. Based on our analysis, the mathematically most likely explanation for the renewed growth in atmospheric methane, counterintuitively, involves a 25-Tg/y decrease in methane emissions from 2003 to 2016 that is offset by a 7% decrease in global mean hydroxyl (OH) concentrations, the primary sink for atmospheric methane, over the same period. However, we are still able to fit the observations if we assume that OH concentrations are time invariant (as much of the previous work has assumed) and we then find solutions that are largely consistent with other proposed hypotheses for the renewed growth of atmospheric methane since 2007. We conclude that the current surface observing system does not allow unambiguous attribution of the decadal trends in methane without robust constraints on OH variability, which currently rely purely on methyl chloroform data and its uncertain emissions estimates.

Atmospheric methane (${\mathrm{CH}}_4$) is the second strongest anthropogenic greenhouse gas (1) and concentrations have been increasing for much of the past century (2) due, primarily, to increasing anthropogenic emissions. Atmospheric concentrations stabilized in the early 2000s (3) (hereafter referred to as the “methane stabilization”) and began increasing again in 2007 (4, 5) (hereafter referred to as the “renewed growth”). There has been much speculation about the cause of these trends (3–24). Attribution has proved to be a difficult task in part because this period of renewed growth is characterized by a methane growth rate of $\sim$6 ppb/y, which represents a source–sink imbalance of only 3% [or an increase of 20 Tg/y compared with an estimated annual source of 550 Tg/y (13)].

Previous work investigating the trends in atmospheric methane has generally used observations of either atmospheric ethane or bulk carbon isotope ratios in atmospheric methane (${\delta }^{13}$CH₄), in conjunction with methane observations, to provide additional constraints on the sources of methane. This is because ethane is coemitted with methane from fossil-fuel sources, which represent $\sim$62% of the ethane budget (25), and has been used to infer changes in methane emissions from fossil-fuel sources. Similarly, ${\delta }^{13}$CH₄ has been used to determine the sources governing atmospheric methane concentrations because different methane sources and sinks have distinct isotopic signatures.

However, previous works using ethane and ${\delta }^{13}$CH₄ have come to differing conclusions about the causes of the stabilization in the early 2000s and the renewed growth since 2007. For example, Kai et al. (9) used isotope measurements and attributed the methane stabilization to a reduction in microbial sources whereas Aydin et al. (8) and Simpson et al. (12) used ethane observations and attributed it to a reduction in fossil-fuel sources. Levin et al. (11) found isotope measurements to be inconclusive. Similarly, Hausmann et al. (17), Franco et al. (18), and Helmig et al. (19) used ethane observations and attributed part of the renewed growth to fossil-fuel sources whereas Schaefer et al. (16), Rice et al. (22), Nisbet et al. (23), and Schwietzke et al. (24) reached differing conclusions using isotope measurements. Schaefer et al. (16) concluded that fossil fuels did not contribute to the renewed growth, Nisbet et al. (23) concluded that fossil fuels were not a dominant factor, Rice et al. (22) concluded that fugitive fossil-fuel sources have increased since 2000, and Schwietzke et al. (24) concluded that fossil-fuel sources have not increased. This prompts the question: Why do many, apparently, plausible explanations disagree with each other?

Quantitative attribution of methane emissions to fossil-fuel sources at global scales using ethane is hampered by the large variability in methane-to-ethane emission ratios and recent increases in ethane sources that emit little methane (26, 27). Similarly, there is a large overlap in the signatures from fossil-fuel and nonfossil methane sources. Part of this overlap is because fossil-fuel sources are not strictly thermogenic in origin with more than 20% of the world’s natural gas reserves coming from microbial activity (28–30). This overlap makes it difficult to draw quantitative conclusions about the methane sources, using atmospheric measurements of ${\delta }^{13}$CH₄ on global scales (SI Appendix, section 1).

In addition, changes in the hydroxyl radical (OH), the main sink for atmospheric methane, complicate the issue. Previous work has used observations of methyl chloroform (${\mathrm{CH}}_3{\mathrm{CCl}}_3$; abbreviated as “$\mathrm{MCF}$”) to provide constraints on global-to-hemispheric OH concentrations because the loss of methyl chloroform is controlled by OH (31–34). Recent work has shown how small increases in the OH sink can explain most of the methane stabilization (21).

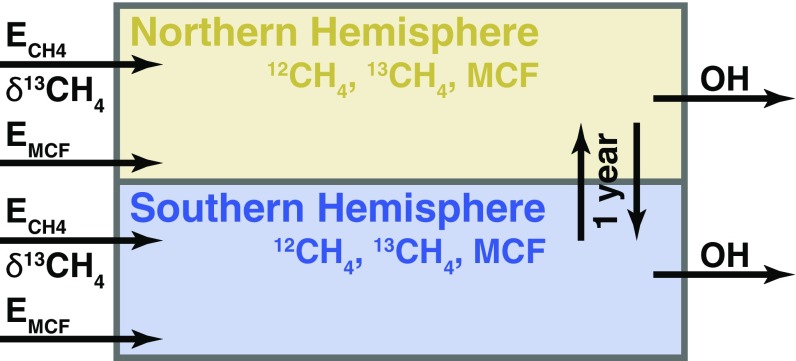
Here we present a simple two-box (Northern and Southern Hemisphere) model to investigate the cause of the methane stabilization and renewed growth. Fig. 1 shows a schematic of the two-box model. The model simulates annual hemispheric concentrations of ${}^{12}\mathrm{CH}_4$, ${}^{13}\mathrm{CH}_4$, methyl chloroform, and OH. We use atmospheric observations of methane, δ¹³CH₄, and methyl chloroform to constrain annual hemispheric emissions of methane, the isotopic composition of the emissions, methyl chloroform emissions, and the OH abundance in a nonlinear, stochastic, Bayesian inversion.

Fig. 1.

Schematic of the two-box model. Inputs are annual hemispheric OH anomalies, methyl chloroform emissions, methane emissions, and δ¹³CH₄ for the methane emissions. Outputs are annual hemispheric concentrations of methyl chloroform, methane, and the δ¹³CH₄ of atmospheric methane. Interhemispheric exchange time is 1 y.

Results

Most Likely Solution.

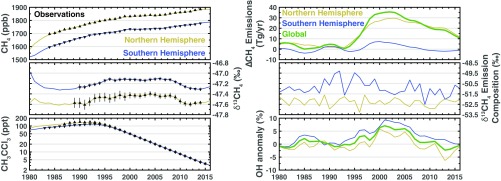
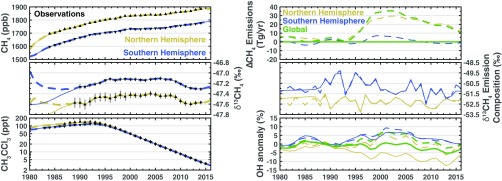
The most likely solution, defined as the largest posterior probability sampled, found here is that the renewed growth is due to a decline in the OH sink, partially offset by a decrease in methane emissions. Similarly, the stabilization is explained by an increase in the OH sink offsetting an increase in methane emissions. Fig. 2 shows the most likely solution from our nonlinear inversion for the drivers of decadal trends in atmospheric methane and OH as well as the modeled methane, δ¹³CH₄, and methyl chloroform concentrations. The posterior model accurately represents the observed concentrations of all three species. This shows how changes of a few percent in the methane sources and sinks can explain all of the observed hemispheric-scale variability in methane and methyl chloroform. The large uncertainty in isotopic signatures (SI Appendix, section 1) makes it difficult to draw quantitative conclusions from the isotopic composition of Northern and Southern Hemispheric methane sources.

Fig. 2.

Most likely solution. Left column shows observed (black triangles) and modeled (solid lines) concentrations of atmospheric CH₄ (Top), ${\delta }^{13}$CH₄ (Middle), and methyl chloroform (Bottom). The Northern Hemisphere is yellow and the Southern Hemisphere is blue. Right column shows the methane emissions (plotted as a deviation from the constant prior emissions; Top), the isotopic composition of the methane emissions (Middle), and the OH anomaly relative to a global mean concentration of $1\times {10}^6$ molecules (molec)/cm³ (Bottom).

In the most likely solution the renewed growth in methane is, counterintuitively, explained by a reduction in methane emissions. We find an $\sim$25-Tg/y decrease in global methane emissions from 2003 to 2016, during the period of renewed growth that started in 2007. This decrease in methane emissions is offset by an $\sim$7% decrease in global mean OH over the same period, which is constrained by methyl chloroform observations. The combination of this decrease in methane emissions and OH results in an increase in atmospheric methane concentrations, observed in both hemispheres.

In this solution, we find an $\sim$35-Tg/y increase in methane emissions from 1993 to 2003 and an $\sim$7% increase in global mean OH from 1991 to 2000, with the bulk of the methane emission increase occurring in the Northern Hemisphere. The rate of increase in the methane emissions slows after about 1998, resulting in relatively stable atmospheric methane concentrations. Northern Hemispheric isotope concentrations do not exhibit any systematic changes during this period.

The isotopic compositions of the Northern and Southern Hemispheric methane sources (Fig. 2, Middle Right) are, largely, decoupled from the changes seen in the methane emissions and OH. The Northern Hemispheric methane emissions undergo modest changes whereas the isotopic composition of those emissions fluctuate about −52.5‰. Conversely, the Southern Hemispheric methane emissions remain largely unchanged from 1980 to 2016 whereas the isotopic composition decreases by about 2‰  from 1990 (when publicly available isotope measurements began) to 2015.

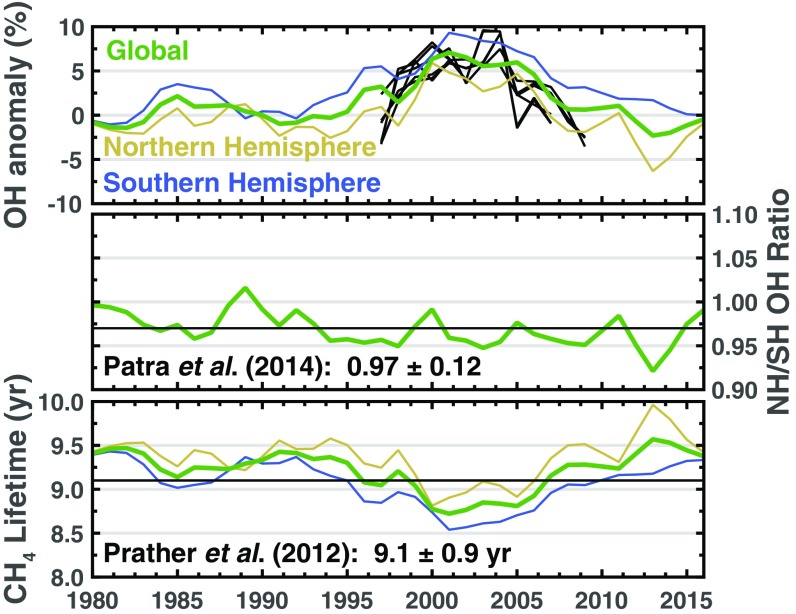
The OH anomalies derived here are consistent with previous work examining global mean OH (21, 31–34). In particular, Montzka et al. (31), Rigby et al. (33), and McNorton et al. (21) used methyl chloroform observations to derive anomalies in global mean OH. Fig. 3, Top shows that their OH anomalies exhibit a similarity to the OH anomalies found here. Patra et al. (34) found that the interhemispheric ratio of OH has been roughly constant from 2004 to 2011 ($0.97\pm 0.12$). Prather et al. (32) used observations of methyl chloroform to derive a methane lifetime of $9.1\pm 0.9$ y whereas our global mean methane lifetime from 1980 to 2016 is $9.2\pm 0.2$ y. The consistency between the results presented here and past findings is not particularly surprising because our work uses many of the same methyl chloroform datasets and prior emissions estimates as previous work.

Fig. 3.

Analysis of OH anomalies and the methane lifetime from the most likely solution. Top is the same as Fig. 2, Bottom Right but includes the OH anomalies from Montzka et al. (31), Rigby et al. (33), and McNorton et al. (21) (black lines). OH anomalies from Montzka et al. (31), Rigby et al. (33), and McNorton et al. (21) are offset such that their mean matches the mean 1997–2007 anomaly found here. Middle is the ratio of Northern to Southern Hemispheric OH and the black line is from Patra et al. (34). Bottom is the methane lifetime in our two-box model and the black line is the lifetime from Prather et al. (32). OH is the only sink included in our two-box model so the methane lifetime shown here is more representative of the actual methane lifetime, not a lifetime due to OH loss.

This most likely solution is found to be robust to small perturbations in the prior error variance parameters for methane emissions and OH anomalies (SI Appendix, section 4.1), interhemispheric exchange times (SI Appendix, section 4.4), and alternate observation operators (SI Appendix, section 4.2). However, we find the amplitude of the changes in methane emissions and OH anomalies is strongly sensitive to the methyl chloroform reaction constant with OH (SI Appendix, section 4.5). Whereas the exact magnitude of our most likely solution changes in the different sensitivity tests, the general spatiotemporal pattern of increasing methane emissions and OH anomalies in the mid-1990s and decreasing methane emissions and OH anomalies from 2000 to present is robust to small perturbations but not large perturbations (as we present in the following sections).

Assuming Fixed OH Concentrations.

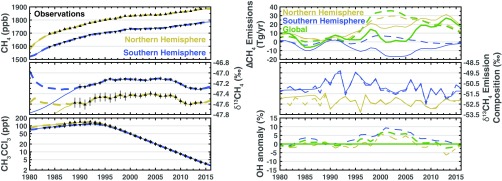
We performed a sensitivity test (Fig. 4) where the inversion assumed time-invariant OH concentrations (global mean OH concentration of $1\times {10}^6$ molec/cm³), thus linearizing the problem. The agreement with the observations is largely unchanged whereas methane emissions exhibit a fundamentally different temporal pattern. Here, we find that the renewed growth since 2007 is due to an $\sim$20-Tg/y increase in global methane emissions with each hemisphere contributing $\sim$10 Tg/y. The isotopic composition of the methane emissions is almost unchanged from the full nonlinear inversion, even though the methane emissions are radically different. MCF observations are reconciled through changes to the uncertain MCF emissions.

Fig. 4.

Sensitivity test with fixed OH concentrations. Details are the same as in Fig. 2. Dashed lines are from the most likely solution (Fig. 2).

The only discernible difference between the simulated concentrations in the full nonlinear case and this sensitivity test with fixed OH concentrations is in the first 5 y of the δ¹³CH₄ concentrations when there are no observations (Fig. 4, Left). The consistency of the isotopic compositions indicates that simulating the δ¹³CH₄ observations is largely unaffected by changes in the methane emissions or OH concentrations and that the δ¹³CH₄ observations are providing constraints only on the isotopic compositions of the sources; it does not indicate that this spatiotemporal pattern in the isotopic compositions is a robust feature. This difference in the first 5 y of δ¹³CH₄ concentrations is due to a slightly different treatment of the prior distribution for the initial conditions (Materials and Methods).

Assuming Fixed Methane Emissions.

As an extreme test, we performed an additional sensitivity study (Fig. 5) where the inversion assumed that methane emissions were time invariant (global methane emissions of 550 Tg/y), also linearizing the problem. Only modest changes to the OH concentrations are needed to explain the observed methane concentrations with fixed methane emissions and a small divergence in Northern and Southern Hemispheric OH can explain changes in the interhemispheric methane difference. The renewed growth is explained by an $\sim$3–5% decrease in global mean OH from 2005 to 2016. However, this sensitivity test does require larger changes to the methyl chloroform emissions (SI Appendix, Fig. S4), relative to the full nonlinear inversion. Again, the isotopic composition of the methane emissions is almost unchanged from the full nonlinear inversion and is identical to the isotopic composition of the methane emissions from the sensitivity test with fixed OH concentrations.

Fig. 5.

Sensitivity test with fixed methane emissions. Details are the same as in Fig. 2. Dashed lines are from the most likely solution (Fig. 2).

Assuming the methane emissions are fixed implicitly places a constraint on the magnitude of the interannual variability of the global mean OH concentration. This is because an increase (decrease) in the OH anomaly could be offset by an increase (decrease) in the methane emissions to satisfy the observational record. As such, assuming the methane emissions are a fixed parameter (as opposed to a parameter to be estimated) in an inversion solving for global mean OH limits the potential interannual variability of global mean OH.

There are no discernible differences between the simulated concentrations in the two sensitivity tests and, as with the fixed OH sensitivity test, the only difference between the simulated concentrations in the full nonlinear case and this sensitivity test is in the first 5 y of the δ¹³CH₄ concentrations (Figs. 4, Left and 5, Left).

Discussion and Conclusions

We performed a nonlinear Bayesian inversion to infer the most likely set of drivers of decadal trends in atmospheric methane and OH. Based on our assumptions (Table 1), we find that decreasing OH concentrations is the most likely explanation for the renewed growth since 2007, with methane emissions actually decreasing during that period. This result is robust to small perturbations in our prior assumptions but not to large perturbations. The isotopic composition of the Southern Hemispheric methane sources in our most likely solution decreased by $\sim$1‰  during this period whereas the emissions decreased by $\sim$10 Tg/y. This would indicate that the isotopically heavy sources in the Southern Hemisphere (such as biomass burning) may have decreased whereas the isotopically light sources remained constant. There is evidence from the satellite record of CO pointing to a decrease in Southern Hemispheric biomass burning since 2001 (35) but some of the decrease in CO could be due to anthropogenic sources (36). The isotopic composition of the Northern Hemispheric sources remains relatively stable during this period, indicating negligible changes in the proportion of emissions coming from isotopically light and heavy sources. Finally, the most likely solution found here suggests that the recent increase in atmospheric methane may be a transient feature driven by fluctuations in OH concentrations.

Table 1.

Prior distributions for components of the state vector

Model input	Distribution	$𝐚$	$𝐛$	$𝝁$	$𝝈$	$\tau$, y
Annual components (emissions, isotopic compositions, and anomalies)
NH ${\mathrm{CH}}_4$, Tg/y	${\mathcal{N}}_B$	300	500	412.5	20	5
SH ${\mathrm{CH}}_4$, Tg/y	${\mathcal{N}}_B$	100	250	137.5	20	5
NH ${\delta }^{13}{\mathrm{CH}}_4$, ‰	$\mathcal{U}$	−60.0	−45.0	—	—	—
SH ${\delta }^{13}{\mathrm{CH}}_4$, ‰	$\mathcal{U}$	−60.0	−45.0	—	—	—
NH MCF, Gg/y	${\mathcal{N}}_B$	−1.0	$\beta$	$\alpha$	$\gamma$	3
SH MCF, Gg/y	$\mathcal{U}$	−1.0	1.0	—	—	—
NH OH, %	${\mathcal{N}}_B$	−20	20	0	10	3
SH OH, %	${\mathcal{N}}_B$	−20	20	0	10	3
Initial conditions (IC)
NH ${\mathrm{CH}}_4$, ppb	$\mathcal{U}$	1,540	1,620	—	—	—
SH ${\mathrm{CH}}_4$, ppb	$\mathcal{U}$	1,480	1,580	—	—	—
NH ${\delta }^{13}{\mathrm{CH}}_4$, ‰	$\mathcal{U}$	−48.2	−46.6	—	—	—
SH ${\delta }^{13}{\mathrm{CH}}_4$, ‰	$\mathcal{U}$	−48.2	−46.6	—	—	—
NH MCF, ppt	$\mathcal{U}$	15	135	—	—	—
SH MCF, ppt	$\mathcal{U}$	15	135	—	—	—

α is the updated annual MCF emissions from Prinn et al. (39), β =max ([1:0 Gg=y, 2α]), and γ=max ([0:2α, 1:5 Gg=y]). ppb, parts per billion; ppt, parts per trillion.

It is important to be cautious with source attribution based on isotope measurements. The isotopic composition of the Northern and Southern Hemispheric methane emissions remained largely unchanged in our three inversions (compare Figs. 2, Middle Right, 4, Middle Right, and 5, Middle Right) even though the spatiotemporal patterns in the methane emissions were radically different. As such, the interpretation of the sources driving the changes in methane emissions would differ. There is also a large overlap in the isotopic composition of different sources, further complicating the interpretation of the isotope measurements.

As for the methane stabilization, we find an $\sim$30-Tg/y increase in Northern Hemispheric methane emissions from 1992 to 2003 combined with an increasing OH anomaly is the most likely explanation for the methane trends from the early 1990s through the early 2000s; this generally agrees with the recent findings from McNorton et al. (21) who find that changes in OH can explain most of the methane stabilization. Based on our analysis, this seems more likely than previous work that has argued for the collapse of the former Soviet Union as a cause of the methane stabilization in the early 2000s (3, 8, 12, 16). However, we stress that our study relates only to aggregated (hemispheric-scale) drivers of the methane growth rate and does not preclude large subhemispheric-scale changes.

We performed two sensitivity tests where different potential drivers of decadal trends were held constant in the inversion. These sensitivity tests yielded two important conclusions: (i) Multiple (fundamentally different) scenarios can explain the observations and (ii) previous work that did not jointly estimate methane and OH aliased errors from one species to another.

For the former conclusion, both sensitivity tests are able to simulate the observations to within the observational uncertainties and the main difference between their likelihoods is due to the specification of the prior and assumptions in the analysis. As for the latter, previous work has rarely jointly estimated all parameters (e.g., methane emissions and OH concentrations) and is predisposed to a subset of solutions. For example, Schaefer et al. (16) derive a step increase of 19.7 Tg/y in methane emissions starting in 2007 and then attempt to explain the cause with isotope measurements. Their result is similar to our sensitivity test with fixed OH concentrations (Fig. 4) where we find an $\sim$20-Tg/y increase in methane emissions starting in 2007. However, this solution is not the most likely one if we allow OH concentrations to vary. A similar argument can be made against using fixed methane emissions when estimating global mean OH concentrations.

The methane stabilization and renewed growth can be reconciled through small changes to the sources and sinks (on the order of a few percent, relative to their global budgets). As such, small changes in the sources and sinks can have important implications for the observed atmospheric concentrations and make quantitative determination of the causes a difficult task. We find here that global methane emissions and OH likely changed by $\pm$7% over 36 y but multiple scenarios can explain the observed changes in atmospheric methane, δ¹³CH₄, and methyl chloroform. As such, the apparent disagreement between past works on the causes of decadal trends in atmospheric methane (3–22) is, almost certainly, due to the problem being underdetermined.

Moving forward, stronger conclusions on the causes of decadal trends in atmospheric methane and OH could be drawn if we had other independent proxies for OH. Alternatively, a mechanistic explanation with supporting evidence for the potential changes in OH concentrations could allow us to draw stronger conclusions. For example, changes in $\mathrm{J}\left({\mathrm{O}}^1\mathrm{D}\right)$ due to stratospheric ozone could provide a large enough change in OH (37) but the changes in stratospheric ozone are only weakly correlated with the OH anomalies derived here (SI Appendix, section 5). Future work could also focus on obtaining higher spatially resolved constraints where the methane-to-ethane ratios and isotopic signatures of the sources are better constrained. This would also allow the use of more gradient information as could be discerned from satellite observations (15). More work is needed to discern the causes of decadal trends in atmospheric methane and OH.

Materials and Methods

The model and data used are available at https://github.com/alexjturner/BoxModel_PNAS_20161223.

Observational Records Used.

All datasets used are publicly available. Methane observations are from National Oceanic and Atmospheric Administration’s Earth System Research Laboratory (NOAA/ESRL). δ¹³CH₄ observations are from NOAA/ESRL; University of Washington, Seattle; University of Heidelberg, Heidelberg; and University of California, Irvine, CA. Methyl chloroform observations are from NOAA/ESRL and the Global Atmospheric Gases Experiment (GAGE)/Advanced GAGE (AGAGE) network. See SI Appendix, section 2 for more information on the observations.

Bootstrapping Hemispheric Averages and Uncertainties.

We construct a hemispheric average atmospheric methane, δ¹³CH₄, and methyl chloroform via bootstrapping from the different observational records. The observational records are deseasonalized with a site-specific stable seasonal filter and we require that each observational record has at least a 5 y of data. We then generate a hemispherically averaged observational record and uncertainty by randomly drawing $n$ observational records from the population of possible records, where $n$ is the total number of observational records for that hemisphere. These $n$ records are then combined using a block-averaging scheme with a 1-y window. This process is repeated 50 times. We then compute the mean and uncertainty from the 50 different time series. We also impose minimum uncertainty of 2 ppb and 0.03‰  for methane and δ¹³CH₄, respectively. Finally, we require that the uncertainty for older observations is greater than that for newer observations. See SI Appendix, section 2 for more information on the methodology.

Two-Box Model.

We use a two-box model with three species: ${}^{12}\mathrm{CH}_4$, ${}^{13}\mathrm{CH}_4$, and $\mathrm{MCF}$. The model simulates annual hemispheric concentrations for each species and considers loss, through reaction with $\mathrm{OH}$, and interhemispheric transport with a timescale of 1 y: ${\tau }_{\mathrm{NS}}=1$ y (shown schematically in Fig. 1).

This gives us a set of six coupled ordinary differential equations:

$$\begin{array}{c}\frac{\partial {[X]}_N(t)}{\partial t}=E_{X,N}(t)-k_{[X]}{[\mathrm{OH}]}_N(t){[X]}_N(t)+\frac{{[X]}_S(t)-{[X]}_N(t)}{{\tau }_{\mathrm{NS}}}\\ \frac{\partial {[X]}_S(t)}{\partial t}=E_{X,S}(t)-k_{[X]}{[\mathrm{OH}]}_S(t){[X]}_S(t)+\frac{{[X]}_N(t)-{[X]}_S(t)}{{\tau }_{\mathrm{NS}}},\end{array}$$

where $[X](t)$ and $E_X(t)$ are the hemispheric concentrations and emissions, respectively, for a given species. $N$ and $S$ subscripts denote Northern and Southern Hemispheres. We do not consider other minor loss terms for methane [e.g., methanotrophic bacteria in aerated soils, chlorine and atomic oxygen radicals in the stratosphere, or reactions with chlorine radicals from sea salt in the marine boundary layer (13)] or methyl chloroform [e.g., uptake by the ocean (38)]. Lifetimes and reaction rate constants ($k_{[X]}$) used here should be viewed as total atmospheric lifetimes, not the lifetime with respect to OH loss. OH is plotted as an anomaly relative to a global mean concentration of $1\times {\mathrm{\hspace{0.17em}10}}^6$ molec/cm³.

Nonlinear, Stochastic, Bayesian Inversion.

The two-box model ($𝐅$) can be used to relate a state vector ($𝐱$) to the observations ($𝐲$),

$$𝐲=𝐅(𝐱)+\mathit{ϵ},$$

but there will always be some error ($\mathit{ϵ}$) associated with the both the observations and the model. The state vector in our work is the annual hemispheric MCF emissions, OH anomalies, methane emissions, and their isotopic composition, as well as the initial conditions for methane, δ¹³CH₄, and MCF. We can estimate the terms in this state vector using Bayesian inference,

$$P(𝐱|𝐲)\propto P(𝐲|𝐱)\cdot P(𝐱),$$

where $P(𝐱|𝐲)$ is the posterior distribution, $P(𝐲|𝐱)$ is the likelihood distribution, and $P(𝐱)$ is the prior distribution. The two-box model is nonlinear due to the interaction between OH and methane: $k_{[{\mathrm{CH}}_4]}[\mathrm{OH}](t)[{\mathrm{CH}}_4](t)$. As such, we have adopted a stochastic method to infer the most likely solution.

We use the covariance matrix adaptation evolution strategy (CMA-ES) [Hansen (40) and references therein] to find the most likely solution. Typical sampling methods [such as Markov chain Monte Carlo (MCMC)] become prohibitively slow as the dimension of the state vector becomes large because they have trouble defining the proposal distribution. CMA-ES is an evolutionary algorithm that modifies the covariance matrix of the proposal distribution based on the fitness of multiple candidate solutions in a given generation. This allows CMA-ES to efficiently sample the posterior distribution. We restart CMA-ES with 10 different initializations and covariance matrices in an attempt to find a global minimum. In total, we draw 500,000,000 samples from the posterior distribution.

We assume the likelihood distribution is Gaussian with a diagonal covariance matrix populated by the uncertainties from the bootstrapping process. Because we are using a stochastic method, we can use non-Gaussian distributions that may be less restrictive and allow more flexible specification of the prior distribution. Our prior distribution is a convolution of uniform distributions: $\mathcal{U}(𝐚,𝐛)$ and bounded normal distributions (which can be written as the product of a normal distribution and a uniform distribution): ${\mathcal{N}}_B(𝐚\mathit{,}𝐛\mathit{,}𝝁\mathit{,}𝝈\mathit{,}\tau )=\mathcal{U}\left(𝐚\mathit{,}𝐛\right)\cdot \mathcal{N}\left(𝝁\mathit{,}𝚺(𝝈\mathit{,}\tau )\right)$, where $𝐚$ is the lower bound, $𝐛$ is the upper bound, $𝝁$ is the mean, $𝚺$ is the covariance matrix, $𝝈$ is the square root of the diagonal of $𝚺$, and $\tau$ is the temporal correlation length scale for $𝚺$. The prior distributions for each component of the state vector are shown in Table 1.

Linear, Gaussian, Bayesian Inversion for Sensitivity Tests.

The two-box model is nonlinear because of the interaction between OH and methane, as mentioned above. However, the model becomes linear if we assume that either methane or OH is fixed. As such, our sensitivity tests (presented in Figs. 4 and 5) have a linear response. For computational efficiency, we assume Gaussian errors in the sensitivity tests to obtain a closed-form solution for the posterior distribution [for example, Rodgers (41)],

$$\widehat{𝐱}={\left({{𝐒}_{𝐚}}^{-1}+{𝐊}^T{{𝐒}_{𝐨}}^{-1}𝐊\right)}^{-1}{𝐊}^T{{𝐒}_{𝐨}}^{-1}(𝐲-\mathrm{𝐊𝐱}),$$

where $\widehat{𝐱}$ is the maximum a posteriori solution, ${𝐒}_{𝐚}$ is the prior error covariance matrix, $𝐊$ is the Jacobian matrix of the two-box model, and ${𝐒}_{𝐨}$ is the observational error covariance matrix.