Competing magnetic orders in the superconducting state of heavy-fermion CeRhIn₅

Significance

Discovering new interdependences among magnetism, unconventional superconductivity and quantum criticality presents new insights into how electronic matter can organize itself into unexpected quantum states but also poses a fundamental challenge to current understanding. Here, we show that two qualitatively different types of magnetic order develop inside the pressure-induced superconducting state of Ce_0.95Nd_0.05RhIn₅. Field-induced magnetic order, derived from Cerium’s $4f$ electrons, competes with zero-field, spin-density order that forms by condensation of magnetic excitations in a spin resonance. The zero-field magnetism is tuned to quantum-critical points by pressure and magnetic field. These discoveries portend possibilities for new quantum states arising from magnetic orders and quantum criticality in other unconventional superconductors that host a spin resonance.

Abstract

Applied pressure drives the heavy-fermion antiferromagnet CeRhIn₅ toward a quantum critical point that becomes hidden by a dome of unconventional superconductivity. Magnetic fields suppress this superconducting dome, unveiling the quantum phase transition of local character. Here, we show that $5\%$ magnetic substitution at the Ce site in CeRhIn₅, either by Nd or Gd, induces a zero-field magnetic instability inside the superconducting state. This magnetic state not only should have a different ordering vector than the high-field local-moment magnetic state, but it also competes with the latter, suggesting that a spin-density-wave phase is stabilized in zero field by Nd and Gd impurities, similarly to the case of Ce_0.95Nd_0.05CoIn₅. Supported by model calculations, we attribute this spin-density wave instability to a magnetic-impurity-driven condensation of the spin excitons that form inside the unconventional superconducting state.

Unconventional superconductivity (SC) frequently is found as an antiferromagnetic (AFM) transition is tuned by chemical substitution or pressure toward a zero-temperature phase transition, a magnetic quantum-critical point. This observation has a qualitative explanation: The proliferation of quantum fluctuations of magnetic origin at low temperatures can trigger the formation of a new ordered state. Unconventional SC is a natural candidate state because it can be induced by an attractive Cooper-pair interaction provided by the fluctuating magnetism (1, 2). Typical examples include copper oxides, which, without chemical substitution, are AFM Mott insulators (3), metallic iron-based antiferromagnets that superconduct under pressure or with chemical substitutions (4), and rare-earth and actinide-based heavy-fermion compounds with large effective electronic masses (5).

A characteristic manifestation of the unconventional nature of the superconducting state is the momentum dependence of the SC gap $\mathrm{\Delta }$ that develops below the superconducting transition temperature ($T_c$). In contrast to conventional superconductors, $\mathrm{\Delta }$ is not uniform but instead has different signs in different regions of the Fermi surface. Despite the distinct chemical and electronic properties of these materials, the interplay between magnetism and SC is common among them, calling for a deep understanding of this relationship. In this regard, heavy-fermion materials offer an ideal platform to explore the relationship between these two phases.

An additional common feature among these different classes of superconductors is the emergence of a collective magnetic excitation below $T_c$ often attributed to the formation of a spin exciton (see a review in ref. 6). This collective mode, whose energy has been shown to scale with $\mathrm{\Delta }$ across different materials (7), is a direct consequence of the sign-changing nature of $\mathrm{\Delta }$. An example is the heavy-fermion superconductor CeCoIn₅, known to be very close to an AFM quantum-critical point without tuning (5). Indeed, its SC gap is sign-changing (8–10), and a spin resonance mode is observed below $T_c$ (11). The energy of this mode in CeCoIn₅ scales with its SC gap with the same proportionality found in copper oxide- and iron-based systems (7).

Recent inelastic neutron scattering experiments find that the resonance mode in CeCoIn₅ is incommensurate at the wavevector $𝐐=(0.45,0.45,0.5)$ (12). Due to Ce’s $4f$ crystal-field environment, this mode is a doublet and the corresponding fluctuations are polarized along the $c$ axis. When a magnetic field $H$ is applied in the tetragonal $ab$ plane, this mode splits into two well-defined branches (13, 14). The field dependence of the Zeeman-split lower-energy mode extrapolates to zero energy at $\sim 110$ kilo-oersted (kOe), which is remarkably close to the field where long-range AFM order develops inside the low-$T$, high-$H$ SC state (15–17). Spin-density wave (SDW) order in this so-called $Q$ phase has a small c-axis ordered moment of $0.15$ Bohr magneton (${\mu }_B$), which corresponds closely to the spectral weight of the low-energy resonance mode. Moreover, the SDW displays the same incommensurate wavevector $𝐐$ as the spin resonance mode (16). These observations suggest that the $Q$ phase is the result of a condensation of spin excitations (12, 14, 18).

In addition to the field-induced $Q$ phase, AFM order is found in Ce_0.95Nd_0.05CoIn₅ below $T_c$, in this case at zero field (19). The wavevector and moment size of the Nd-induced magnetism are the same as those observed in the $Q$ phase of CeCoIn₅ (20). Although the sign-changing $\mathrm{\Delta }$, with its nodes on the Fermi surface, plays a nontrivial role in enabling these orders, the obvious similarity between $H$- and Nd-induced magnetism strongly suggests that they have a common origin, namely condensation of the collective spin excitations that give rise to the resonance mode.

No evidence for the $Q$ phase has been found in other Ce$M$In₅ members ($M=$ Rh, Ir) or, for that matter, in any other superconductor. It is uncommon to find a magnetic transition below $T_c$ when both superconducting and magnetic states arise from the same electrons. Besides the example of CeCoIn₅, field-induced magnetism has been observed in La_1.9Sr_0.1CuO₄ (21, 22). This AFM order, however, is distinct from a $Q$-like phase and is closely related to the field-induced magnetism in the SC state of pressurized CeRhIn₅ (23). At zero pressure, CeRhIn₅ displays AFM order at $T_N=3.8$ K and ${𝐐}_{\mathrm{𝐀𝐅𝐌}}=(0.5,0.5,0.297)$ (24). Pressurizing CeRhIn₅ tunes its magnetic transition toward a quantum-critical point and induces SC that coexists with AFM order for pressures up to $P_{c1}=1.75$ GPa, where $T_c$ equals $T_N$. Above $P_{c1}$, evidence for $T_N$ is absent and only SC is observed (23, 25, 26). Application of a magnetic field, however, induces magnetism in the SC state between $P_{c1}$ and the quantum-critical point at $P_{c2}\approx 2.3$ GPa (23, 27). Unlike magnetic order in the $Q$ phase, which exists only inside the SC state, field-induced magnetism in CeRhIn₅ persists into the normal state above the Pauli-limited $H_{c2}$ and is a smooth continuation of the zero-field $T_N(P)$ boundary (23, 27). This magnetism may obscure or preempt the formation of a $Q$-like phase, but strong similarities of CeCoIn₅ to CeRhIn₅ at $P>P_{c1}$ (23, 28) suggest the possibility that AFM order might develop in the high-pressure SC state of Ce1−xNd_xRhIn₅ in zero field.

In this paper, we show that Nd induces a zero-field phase transition in the high-pressure SC phase of Ce_0.95Nd_0.05RhIn₅ and present evidence that the phase transition is due to magnetic order. This result generalizes the observation of magnetic order below $T_c$ in Ce_0.95Nd_0.05CoIn₅ because pressure suppresses the magnetic order at the same rate in both compounds. Our model calculations support our conclusion that the magnetism in Nd-doped CeRhIn₅ is due to the condensation of spin excitations promoted by magnetic impurity scattering, and is thus distinct from the local-moment magnetism in pure CeRhIn₅ promoted by the application of magnetic fields. In agreement with this proposal, we observe a competition between the field-induced magnetism, which displays the same behavior as in CeRhIn₅, and the Nd-induced magnetism in zero field. Hence, we expect a spin resonance with $c$-axis character below $T_c$ in CeRhIn₅ at pressures greater than $P_{c1}$. More generally, our work reveals a route to induce zero-field magnetic order via chemical substitution of magnetic impurities in other unconventional superconductors that host spin resonance modes.

Results

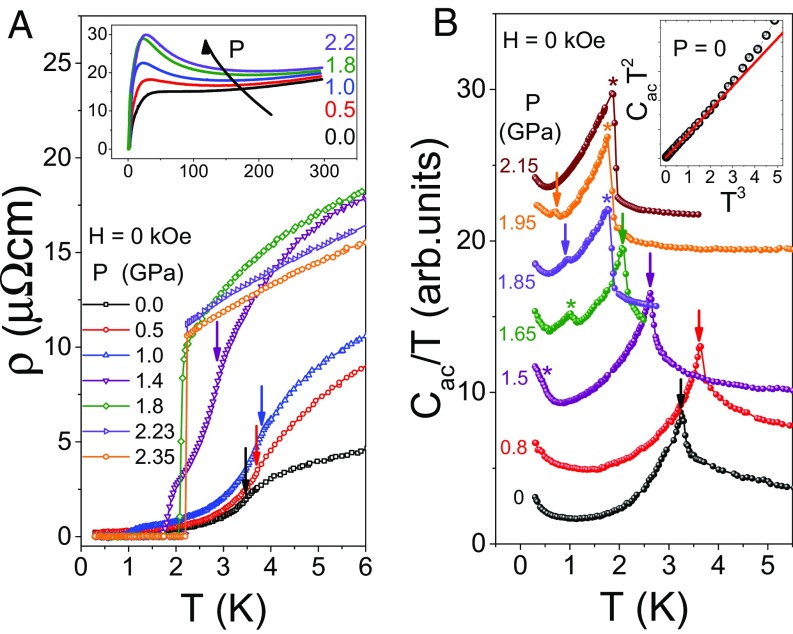
For comparison with Ce_0.95Nd_0.05CoIn₅, we grew crystals of Ce_0.95Nd_0.05RhIn₅ by an In-flux technique (29) and studied its pressure and field dependence by electrical resistivity and AC calorimetry measurements (see Materials and Methods for details). Fig. 1A shows the low-temperature electrical resistivity, $\rho (T)$, on sample s1 at representative pressures, and Fig. 1A, Inset displays $\rho (T)$ in the whole $T$ range. Although Nd substitution reduces $T_N(P=0)$ from 3.8 K to 3.4 K and slightly increases the residual resistivity ${\rho }_0$ to 0.2 $\mathrm{\mu }\mathrm{\Omega }\cdot \text{cm}$, the $P$ dependence reported in Fig. 1A is essentially identical to that of CeRhIn₅ below $P_{c1}^{\ast }=1.8$ GPa where $T_c$ equals $T_N$. We also note that, at zero pressure, the $H-T$ phase diagram of Ce_0.95Nd_0.05RhIn₅ closely resembles the one found in CeRhIn₅. These results indicate that $5\%$ Nd does not change drastically the local AFM character of $T_N$ below $P_{c1}^{\ast }$. Once $T_c$ exceeds $T_N$ at $P_{c1}^{\ast }$, there is no evidence for magnetism in $\rho (T)$, and the possibility of Nd-induced magnetism is obscured by the zero-resistance state below $T_c$. To investigate whether there is AFM order in the SC state, heat capacity measurements are necessary.

Fig. 1.

(A) Low-$T$ dependence of the in-plane electrical resistivity, $\rho (T)$, of Ce_0.95Nd_0.05RhIn₅ (s1) under pressure. Arrows mark $T_N$ determined by peaks in the first derivative. (Inset) The $\rho (T)$ over the entire $T$-range. (B) $C_{ac}/T$ vs $T$ for Ce_0.95Nd_0.05RhIn₅ (s2) under pressure. A vertical offset of 2.5 units is added for clarity. Arrows (asterisks) denote $T_N$ ($T_c$). (Inset) A linear fit in a $C_{ac}{T}^2$ vs $T^3$ plot.

Fig. 1B shows the $T$ dependence of heat capacity divided by temperature ($C_{\mathrm{ac}}/T$) for sample s2 at various pressures. At ambient pressure, $C_{\mathrm{ac}}/T$ peaks at $T_N$ as in CeRhIn₅. As $T$ is lowered further, however, $C_{ac}/T$ turns up below $\sim 1$ K, which was not observed in CeRhIn₅. We note that an upturn in $C/T$ also has been observed in a commercial quantum design physical property measurement system (PPMS) by means of quasiadiabatic thermal relaxation technique. This upturn is presumably associated with the nuclear moment of Nd ions, and it can be fit well by a sum of electronic ($\propto \gamma$) and nuclear ($\propto T^{-3}$) terms (30). Fig. 1B, Inset shows that $C_{ac}{T}^2$ is linear in $T^3$, consistent with the presence of a nuclear Schottky contribution. We note, however, that an upturn also is observed at $2.15$ GPa, where magnetic order is absent, suggesting that the hyperfine field may not be solely responsible for splitting the nuclear levels. Although Nd nuclei have large zero-field quadrupole moments, Kondo-hole physics cannot be ruled out as a possible source of the upturn (31, 32).

For pressures below $P_{c1}^{\ast }$, $T_N$ evolves with $P$ as it does in transport data. Evidence for bulk SC (marked by asterisks in Fig. 1B), however, is observed at lower temperatures relative to the zero-resistance state in $\rho (T)$. A difference between zero-resistance and bulk SC transitions also appears in CeRhIn₅ and has been attributed to filamentary SC due to the presence of long-range AFM order (33). Unlike CeRhIn₅ at pressures greater than $P_{c1}$, however, there is evidence for a phase transition in the SC state of Ce_0.95Nd_0.05RhIn₅ without an applied field. At $1.85$ GPa, an anomaly in $C_{ac}/T$ is observed at $1$ K (arrow in Fig. 1B), below the SC transition at $T_c$ = $1.77$ K. For reasons discussed below, this anomaly stems from a magnetic order, and it is fundamentally different from the AFM order displayed by the system for pressures smaller than $P_{c1}$. The shape and magnitude of the anomaly relative to that at $T_c$ are very similar to those at $T_N$ in Ce_0.95Nd_0.05CoIn₅ (see Supporting Information, Fig. S1), and the small entropy associated with it suggests that the magnetic order is most likely a small-moment density wave. As we will come to later, this evidence is most obvious in data shown in Fig. 3.

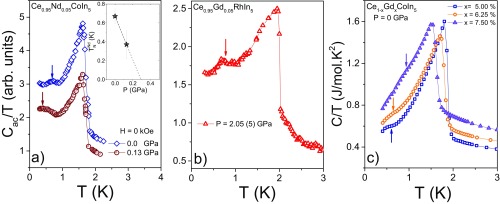
Fig. S1.

(A) $C_{ac}/T$ vs $T$ of Ce_0.95Nd_0.05CoIn₅ at two pressures. Arrows show $T_N$, and Inset shows its extrapolation to $T=0$. (B) $C_{ac}/T$ vs. $T$ of Ce_0.95Gd_0.05CoIn₅ at 2.05 GPa. (C) $C_{ac}/T$ vs. $T$ of Ce_1−xGd_xCoIn₅ ($x=0.05\text{,}0.0625\text{,}0.075$) at ambient pressure. The curves are shifted by $0.1$ J/mol$\cdot {\text{K}}^2$ for clarity. Arrows show $T_N$ determined as the minimum in the first derivative of the data.

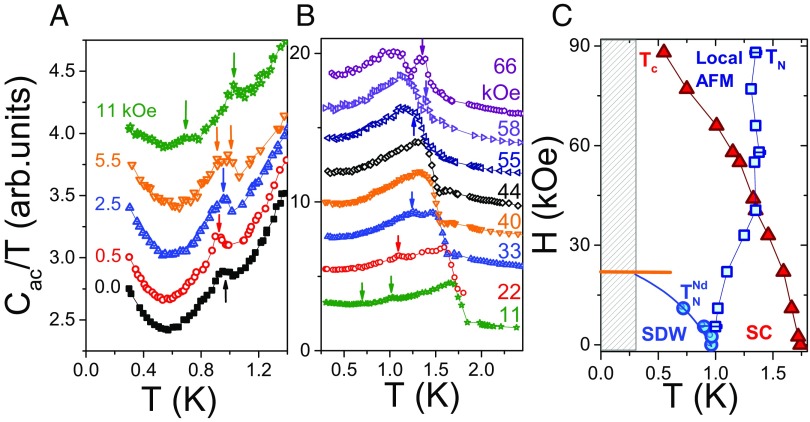
Fig. 3.

AC heat capacity, $C_{ac}$, of Ce_0.95Nd_0.05RhIn₅ (s2) at 1.85 GPa. (A) $T$ dependence of $C_{ac}/T$ at low fields. An offset of 0.2 has been added for clarity. (B) $T$ dependence of $C_{ac}/T$ at high fields. (C) $H\text{–}T$ phase diagram. The diagonal bars delimit the inaccessible temperature region in our experiments ($T<0.3$ K). The solid horizontal line at $H=22$ kOe indicates that no transition $T_N^{\mathrm{Nd}}$ is observed above $0.3$ K for this field. We note that only $T_N^{\mathrm{Nd}}$ is observed at zero field. The field-induced $T_N$ emerges at 11 kOe, as in pure CeRhIn₅.

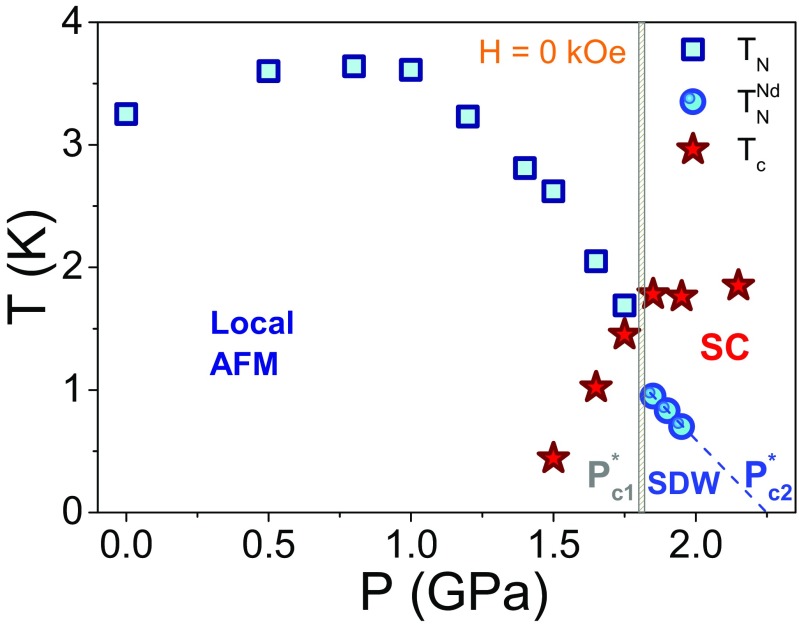
We summarize the zero-field results discussed above in the $T$–$P$ phase diagram shown in Fig. 2. Local-moment-like AFM order coexists with bulk SC in a narrow pressure range below $P_{c1}^{\ast }$. From just below to just above $P_{c1}^{\ast }$, $T_N(P)$ changes discontinuously, in contrast to field-induced magnetism in CeRhIn₅, which is a smooth continuation of $T_N(P)$ from below $P_{c1}$ (23). This result supports the interpretation that $H$- and Nd-induced magnetic orders have different origins. Therefore, the Nd-induced transition is labeled $T_N^{\mathrm{Nd}}$ to distinguish it from $T_N$ in pure CeRhIn₅. Above $P_{c1}^{\ast }$, $T_N^{\mathrm{Nd}}$ is suppressed at a rate of $-2.4$ K/GPa and extrapolates to zero temperature, i.e., a quantum-critical point, at $P_{c2}^{\ast }\sim 2.3$ GPa inside the superconducting phase. Whether the coincidence of $P_{c2}^{\ast }$ and $P_{c2}$ is accidental or not requires further investigation beyond the scope of our work. As shown in the Supporting Information (Fig. S1), the rate of suppression of this Nd-induced transition is the same rate found in Ce_0.95Nd_0.05CoIn₅ within experimental uncertainty, strongly indicating a common origin. Because entropy associated with the zero-field transition is rather small, as found in Ce_1−xNd_xCoIn₅, the typical signature of quantum criticality (i.e., divergence of $C/T$ at low $T$) is likely hidden by SC and by the upturn in $C/T$. We also note that the highest $T_c$ achieved in Ce_0.95Nd_0.05RhIn₅, $T_c^{\max }=1.85$ K, is $0.4$ K lower than $T_c^{\max }$ of CeRhIn₅. This same suppression of $T_c^{\max }$ is observed in Ce_0.95Nd_0.05CoIn₅ and indicates that Nd ions act similarly as magnetic pair-breaking impurities.

Fig. 2.

Zero-field $T\text{–}P$ phase diagram of Ce_0.95Nd_0.05RhIn₅ (s2) obtained from AC calorimetry measurements. Here, $P_{c1}^{\ast }\approx 1.8$ GPa and $P_{c2}^{\ast }\approx 2.3$ GPa.

To further investigate the nature of the Nd-induced magnetism, we turn to the field-dependent heat capacity data. Fig. 3A shows $C_{\mathrm{ac}}/T$ vs. $T$ at $1.85$ GPa ($>P_{c1}$) and low magnetic fields. The zero-field transition at $T_N^{Nd}=0.96$ K remains unchanged in a field of $2.5$ kOe. As the field is increased further, however, the specific heat anomaly splits, one anomaly moving to lower temperatures and the other moving to higher temperatures. At $11$ kOe, our data show features at $1$ K and $0.7$ K. Previous reports on CeRhIn₅ at similar pressures ($\sim 1.9$ GPa) show that the field-induced transition emerges at $T_N=1$ K when $H=11$ kOe (33). It is thus reasonable to associate the anomaly we observe at $1$ K and 11 kOe with the field-induced magnetism in CeRhIn₅. Further, Fig. 3B shows the high-$H$ evolution of $T_N$ with a field dependence very similar to that of CeRhIn₅: $T_N$ first increases with $H$ and then remains constant above the upper critical field $H_{c2}$. As shown in the $H\text{–}T$ phase diagram (Fig. 3C), this field-induced $T_N$ clearly competes with $T_N^{\mathrm{Nd}}$, as reflected in the rapid suppression of $T_N^{\mathrm{Nd}}$ as a function of $H$. In fact, no evidence for $T_N^{\mathrm{Nd}}$ is observed at fields $H\ge 22$ kOe, implying a field-induced quantum-critical point in addition to the pressure-induced, zero-field critical point of this order. Due to the reasons explained above, our results strongly point to two distinct types of magnetism emerging in Ce_0.95Nd_0.05RhIn₅. The first one is due to Nd ions, and it has the hallmarks of that in Ce_0.95Nd_0.05CoIn₅. The second is the $H$-induced magnetism that appears in pure CeRhIn₅ (23, 27).

Discussion

What is the role of Nd and why is it special? At a concentration of $5\%$, average spacing of $17$ Å and nonperiodic distribution on Ce sites, Nd is too dilute to induce magnetic order by dipole or indirect Ruderman–Kittel–Kasuya–Yosida interactions. Its role, then, must be more subtle. Using the bulk modulus of CeRhIn₅ and the unit cell volume variation in Ce_1−xNd_xRhIn₅, we estimate that Ce_0.95Nd_0.05RhIn₅ experiences an effective chemical pressure of $\mathrm{\Delta }P=0.25$ GPa relative to CeRhIn₅ (29). From the phase diagram of CeRhIn₅, this $\mathrm{\Delta }P$ would increase $T_N$ by $0.1$ K instead of producing the observed reduction. Hence, we conclude that chemical pressure per se is not the dominant tuning parameter.

The disruption of lattice periodicity by substituting Ce ions with magnetic Nd ions contributes to reducing $T_N$ at zero pressure (29). This conclusion is supported by the observation that nonmagnetic La substitution for Ce in CeRhIn₅ also depresses $T_N$ similarly (31, 34). The weak depression of $T_N$ and concomitant incremental increase in residual resistivity with Nd substitution by themselves cannot account for the observed zero-field magnetic order above $P_{c1}^{\ast }$. Neodymium, however, carries an additional magnetic moment that is unlikely to be quenched by Kondo screening. In the context of CeCoIn₅, Michal and Mineev (18) proposed that the $Q$ phase observed in the presence of an in-plane magnetic field is the consequence of the condensation of the spin-exciton collective mode found in the SC phase. Thus, it is natural to consider whether the Nd magnetic moments immersed in CeRhIn₅ at zero field could also promote a similar behavior.

As discussed in detail in Supporting Information (Figs. S2 and S3), condensation of spin excitons takes place when the spin-resonance-mode frequency ${\omega }_{\mathrm{res}}$ vanishes. Within a random-phase approximation (RPA) approach, ${\omega }_{\mathrm{res}}$ is given by the pole of the renormalized magnetic susceptibility, i.e., when ${\chi }_{\mathrm{AFM}}(𝐐,{\omega }_{\mathrm{res}})=1/U$, where $U$ is the effective electronic interaction projected in the SDW channel and ${\chi }_{\mathrm{AFM}}(𝐐,{\omega }_{\mathrm{res}})$ is the noninteracting magnetic susceptibility inside the SC state. When the ordering vector $𝐐$ connects points of the Fermi surface with different signs of the SC gap, ${\mathrm{\Delta }}_{𝐤}=-{\mathrm{\Delta }}_{𝐤+𝐐}$, ${\chi }_{\mathrm{AFM}}(𝐐,\omega )$ generically diverges when $\omega \to 2\mathrm{\Delta }$ and remains nonzero when $\omega \to 0$. Thus, even a very weak $U$ can, in principle, induce a resonance mode with frequency near $2\mathrm{\Delta }$. Once the interaction increases, ${\omega }_{\mathrm{res}}$ moves to lower frequencies. When the interaction overcomes a critical value, $U>U_c\equiv {\chi }_{\mathrm{AFM}}^{-1}(𝐐,0)$, the resonance mode vanishes and SDW order is established inside the SC dome.

Fig. S2.

The fermionic self-energy in the self-consistent approximation. The two diagrams on the right side show the contributions arising from impurities and from the pairing interaction, respectively.

Fig. S3.

The spin vertex dressed by the nonmagnetic impurity scattering.

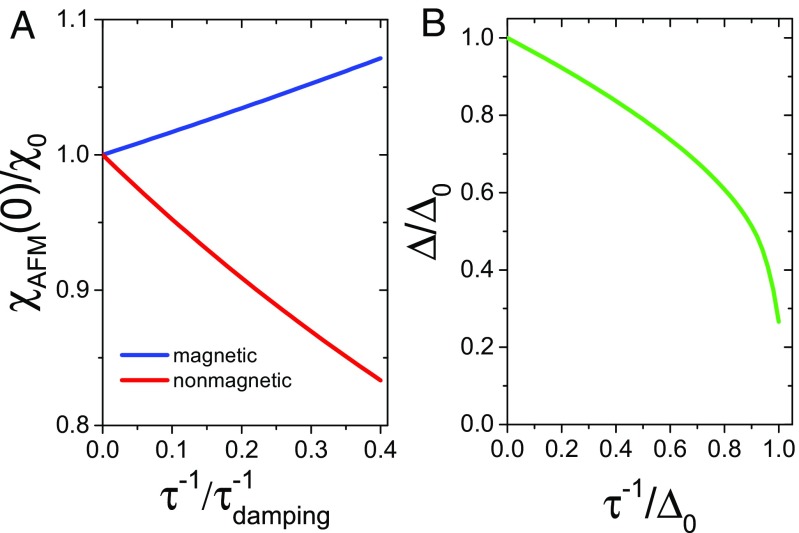
In our case, the interaction $U$ is presumably independent of pressure. Thus, in order for magnetic impurities to promote spin-exciton condensation, ${\chi }_{\mathrm{AFM}}(𝐐,0)$ must increase (i.e., the critical interaction value $U_c$ must decrease) as a function of the impurity potential. To investigate whether this is a sensible scenario, we considered a toy model consisting of two “hot spots” located at momenta $𝐤$ and $𝐤+𝐐$ at the Fermi surface such that ${\mathrm{\Delta }}_{𝐤}=-{\mathrm{\Delta }}_{𝐤+𝐐}$. Note that such a hot spots model has been previously used to study the effects of disorder on SC (35). To focus on the general properties of the model, we linearize the band dispersion around the hot spots and compute both ${\chi }_{\mathrm{AFM}}(𝐐,0)$ and the effective gap amplitude $\mathrm{\Delta }$ at $T=0$ as function of the total impurity scattering rate ${\tau }^{-1}$ within the self-consistent Born approximation (similarly to what was done in ref. 36 for $s^{+-}$ SC and perfectly nested bands). As shown in Fig. 4, whereas both magnetic and nonmagnetic impurity scattering suppress $\mathrm{\Delta }$ at the same rate (Fig. 4B), we find that ${\chi }_{\mathrm{AFM}}(𝐐,0)$ is suppressed for nonmagnetic impurity but enhanced by magnetic impurity scattering (Fig. 4A). Thus, in the case of nonmagnetic impurities, although the resonance-mode frequency may decrease compared with the clean case, it never collapses to zero. Because magnetic impurity scattering enhances ${\chi }_{\mathrm{AFM}}(𝐐,0)$ but does not necessarily destroy SC, the system may undergo an SDW transition inside the SC dome. Although the fate of the system will depend on microscopic details beyond those captured by the toy model considered here, our model nicely illustrates that it is plausible for magnetic impurity scattering to drive spin-exciton condensation in the SC phase. In this regard, we note that previous investigations of a microscopically motivated theoretical model also found that the $Q$ phase may be stabilized by magnetic impurities even at zero external field (37).

Fig. 4.

(A) Static spin susceptibility ${\chi }_{\mathrm{AFM}}(𝐐\text{,}\omega =0)$ as function of the total impurity scattering rate for the cases of nonmagnetic (red curve) and paramagnetic impurities (blue curve). (B) The suppression of the effective SC gap $\mathrm{\Delta }$ by both magnetic and nonmagnetic impurities. In these plots, we considered point-like impurities. Here, ${\mathrm{\Delta }}_0$ is the gap of the clean system whereas ${\tau }_{\mathrm{damping}}^{-1}$ is the Landau damping (see Supporting Information for details).

These results suggest that other magnetic impurities could induce the same type of SDW order in both CeCoIn₅ and pressurized CeRhIn₅. In fact, we show, in Supporting Information (Fig. S1), that easy-plane Gd³⁺ ions ($J=S=7/2$) also induce a transition in the heat capacity data of both Co and Rh members. This anomaly is similar to the one induced by easy-axis ($c$-axis) Nd³⁺ ions ($J=9/2$, $L=3$, $S=3/2$) discussed above. Hence, Nd is not “special” in inducing magnetic order in the superconducting states of Ce_0.95Nd_0.05CoIn₅ and Ce_0.95Nd_0.05RhIn₅, and other unconventional superconductors that host a spin resonance mode may also display zero-field magnetism via the same mechanism. Our results also imply that nonmagnetic impurities will not induce condensation of excitations, in agreement with experimental data on La-substituted CeRhIn₅ (34, 38, 39).

Finally, we note that the SDW ordering vector in Nd-doped CeCoIn₅ corresponds closely to the nodal structure (12) that is also found in the superconducting state of CeRhIn₅ (10). Hence, the magnetic wavevector of zero-field order above $P_{c1}^{\ast }$ in Ce_0.95Nd_0.05RhIn₅ should also be close to Q$\mathrm{=}\mathrm{(}\mathrm{0.45}\mathrm{,}\mathrm{0.45}\mathrm{,}\mathrm{0.5}\mathrm{)}$. As argued in ref. 12, field-induced magnetism in CeCoIn₅ ($Q$ phase) also appears to be a consequence of the condensation of the spin resonance mode. We, therefore, expect neutron scattering experiments to find a spin resonance of $c$-axis character below $T_c$ in CeRhIn₅ at $P>P_{c1}$.

Conclusion

In summary, we generalize the observation of Nd-induced magnetism in CeCoIn₅ to pressurized CeRhIn₅ and Gd-substituted members. This SDW order, which reflects the nodal gap symmetry, is argued to be a consequence of the condensation of spin excitations that arise inside the SC state. Given the several similarities between CeCoIn₅ and Ce₂PdIn₈ (40), Nd substitution might nucleate AFM order in its superconducting state. Appropriate substitutions in other unconventional superconductors that host a spin resonance also should induce zero-field magnetism by the same mechanism, and magnetism should be tunable to a quantum-critical point inside their SC phase.

Materials and Methods

The series Ce_1−xNd_xRhIn₅ was grown by the In-flux technique, and its properties are reported elsewhere (29). Crystals with x = 0.05 and free of unreacted In were mounted in a hybrid piston–cylinder pressure cell, filled with silicone fluid as the pressure medium, and a piece of Pb whose change in T_c served as a manometer. Gs-substituted crystals were grown using the same method. Electrical resistivity was measured by a four-probe method with current flow in the ab plane. Semiquantitative heat capacity was obtained by an AC calorimetry technique described elsewhere (41). Magnetic fields to 9 T were applied parallel to the ab plane. The results above have been reproduced in different crystals, and, for clarity, we show resistivity and calorimetry data for two representative samples labeled sample 1 (s1) and sample 2 (s2).

Supporting AC Calorimetry Measurements in CeCoIn₅ and CeRhIn₅

Single crystals of nominally Ce_0.95Nd_0.05CoIn₅ were grown from an excess In flux and characterized by pressure-dependent AC calorimetry, as described in the Materials and Methods section. These measurements were carried out in a pressure cell under conditions also discussed in the Materials and Methods section. Fig. S1 shows $C_{\mathrm{ac}}/T$ as a function of $T$ at two pressures. At atmospheric pressure (top curve), a pronounced peak in $C_{\mathrm{ac}}/T$ defines the superconducting transition temperature $T_c$ = 1.63 K that is followed at lower temperatures by an anomaly peaked near 0.7 K. These features in data at atmospheric pressure coincide well with those reported in ref. 15 (main text) and indicate that the nominal Nd content is very close to the actual content. Consequently, we associate the lower temperature anomaly with AFM order at $T_N^{\mathrm{Nd}}$. We note that the shapes of the two anomalies resemble those found in Ce_0.95Nd_0.05RhIn₅. As shown in Fig. S1A, an applied pressure of only 0.13 GPa reduces $T_N^{\mathrm{Nd}}$ to $\sim 0.4$ K. Assuming that $T_N^{\mathrm{Nd}}$ decreases linearly with $P$ (Fig. S1A, Inset) gives d$T_N^{\mathrm{Nd}}\text{/dP}\approx -2.3$ K/GPa. This rate of decrease is very close to that found in Fig. 2 where, for Ce_0.95Nd_0.05RhIn₅ above $P_{c1}$, d$T_N^{\mathrm{Nd}}/\text{dP}\approx -2.4$ K/GPa. The fact that Nd-induced zero-field AFM order in similarly doped CeCoIn₅ and CeRhIn₅ displays the same sensitivity to pressure strongly suggests that the zero-field magnetism has a common origin in both materials.

Single crystals of nominally Ce_0.95Gd_0.05RhIn₅ were grown from an excess In flux and characterized by pressure-dependent AC calorimetry, as described in the Materials and Methods section. Fig. S1B shows $C_{\mathrm{ac}}/T$ as a function of $T$ at 2.05 GPa. A pronounced peak in $C_{\mathrm{ac}}/T$ defines the superconducting transition temperature $T_c$ = 1.95 K that is followed at lower temperatures by an anomaly peaked near 0.7 K determined by the minimum in derivative of $C/T$.

Finally, single crystals of nominally Ce_1−xGd_xCoIn₅ ($x=0.05,0.0625,0.075$) were grown from an excess In flux and characterized by specific heat at ambient pressure in a commercial PPMS. Fig. S1C shows $C_{\mathrm{ac}}/T$ as a function of $T$ for all concentrations. A pronounced peak in $C/T$ defines the superconducting transition temperature $T_c$ = $1.8$ K, $1.7$ K, and $1.52$ K that is followed at lower temperatures by an anomaly peaked near $0.6$ K, $0.7$ K, and $0.97$ K.

Impact of Disorder on the Magnetic Susceptibility Inside the Superconducting State

To gain insight into the problem, and keep the calculation analytically tractable, we use the hot spots approximation. In particular, we consider two points on the Fermi surface, labeled $c$ and $d$, separated by the SDW vector Q, such that ${\mathrm{\Delta }}_{\text{𝒌}}=-{\mathrm{\Delta }}_{\text{𝒌}+\text{𝑸}}$. Next, we linearize the dispersions around the hot spots,

$${ϵ}_c(\text{𝒌})={\text{𝒗}}_c\cdot \text{𝒌},\hspace{1em}{ϵ}_d(\text{𝒌}+\text{𝑸})={\text{𝒗}}_d\cdot \text{𝒌},$$ [S1]

where the momentum k is measured with respect to ${\text{𝒌}}_F$ and ${\text{𝒗}}_{c/f}$ are the Fermi velocities. Here, we consider $v_c=v_d$ and let the relative angle between them be arbitrary but nonzero. The case ${\text{𝒗}}_c=-{\text{𝒗}}_d$ corresponds to perfect nesting, which was studied in ref. 36. Here, we focus on the case where nesting is not perfect. As long as the SDW instability is driven by the low-energy electronic states, the linearized approximation can be used to compute the leading contribution to the magnetic susceptibility.

There are two different types of impurity potentials: the nonmagnetic potential $u_{\text{𝒌}}$, which couples to the charge degrees of freedom, and the paramagnetic potential ${𝐮}_{\text{𝒌}}^p$, which couples to the spin degrees of freedom. Each impurity potential can be split into small-momentum scattering $u_0$ and ${𝐮}_0^p$ (which does not couple the fermions on the two hot spots) and large-momentum scattering $u_{\text{𝑸}}$ and ${𝐮}_{\text{𝑸}}^p$ (which couples the fermions on the two hot spots).

First, we study the impact of the various types of disorder on the pairing gap. Here, we assume the existence of an SC state, without discussing its origin. Thus, we consider a static pairing interaction $V$ corresponding to a repulsive interaction coupling fermions from different hot spots, such that ${\mathrm{\Delta }}_c=-{\mathrm{\Delta }}_d$. To proceed, it is convenient to define Nambu spinors ${\mathrm{\Psi }}_{i\text{𝒌}}^{†}=(f_{i,\text{𝒌}\uparrow }^{†},f_{i,-\text{𝒌}\downarrow })$. The Green’s function in Nambu space is then given by

$$\begin{array}{c}{G}_c^{-1}=Z_{\omega }^{-1}(i{\omega }_n{\sigma }_0-{\overline{\mathrm{\Delta }}}_{\omega }{\sigma }_1)-{ϵ}_c(\text{𝒌}){\sigma }_3,\hfill \\ G_d^{-1}=Z_{\omega }^{-1}(i{\omega }_n{\sigma }_0+{\overline{\mathrm{\Delta }}}_{\omega }{\sigma }_1)-{ϵ}_d(\text{𝒌}){\sigma }_3,\hfill \end{array}$$ [S2]

where $Z_{\omega }$ is the imaginary part of the normal component of the self-energy and ${\overline{\mathrm{\Delta }}}_{\omega }$ (the gap normalized by impurities) is the real part of the anomalous component of the self-energy. As shown in Fig. S2, the fermionic self-energy in the self-consistent approximation becomes, at $T=0$,

$${\mathrm{\Sigma }}_c(i{\omega }_n)=-\pi (u_0^2+u_{\text{𝑸}}^2+{(u_0^p)}^2+{(u_{\text{𝑸}}^p)}^2)N_f\frac{i{\omega }_n}{\sqrt{{\omega }_n^2+{\overline{\mathrm{\Delta }}}_{\omega }^2}}{\sigma }_0+\pi (u_0^2-u_{\text{𝑸}}^2-{(u_0^p)}^2+{(u_{\text{𝑸}}^p)}^2)N_f\frac{{\overline{\mathrm{\Delta }}}_{\omega }}{\sqrt{{\omega }_n^2+{\overline{\mathrm{\Delta }}}_{\omega }^2}}{\sigma }_1+V{N}_f{\int }_0^{\mathrm{\Lambda }}\frac{{\overline{\mathrm{\Delta }}}_{\omega }\text{d}\omega }{\sqrt{{\omega }^2+{\overline{\mathrm{\Delta }}}_{\omega }}}{\sigma }_1.$$ [S3]

To solve for $Z_{\omega }$ and ${\overline{\mathrm{\Delta }}}_{\omega }$, we average over impurities and introduce the scattering rates ${\tau }_{0/\text{𝑸}}^{-1}=2\pi N_f{u}_{0/\text{𝑸}}^2$ for nonmagnetic impurities and ${({\tau }_{0/\text{𝑸}}^p)}^{-1}=2\pi N_f{\sum }_i{({𝐮}_{0/\text{𝑸}}^p\cdot {\widehat{\text{𝒆}}}_i)}^2$ for paramagnetic impurities. In the hot spots model, the density of states is $N_f={\mathrm{\Lambda }}_{\parallel }/{(2\pi )}^2{v}_F$, with ${\mathrm{\Lambda }}_{\parallel }$ denoting the momentum cutoff parallel to the Fermi surface. We obtain

$$Z^{-1}(\omega )=1+\left(\frac{1}{2{\tau }_0}+\frac{1}{2{\tau }_{\text{𝑸}}}+\frac{1}{2{\tau }_0^p}+\frac{1}{2{\tau }_{\text{𝑸}}^p}\right)\frac{1}{\sqrt{{\overline{\mathrm{\Delta }}}_{\omega }^2+{\omega }^2}}$$ [S4]

$${\overline{\mathrm{\Delta }}}_{\omega }=-\frac{{\overline{\mathrm{\Delta }}}_{\omega }}{\sqrt{{\omega }^2+{\overline{\mathrm{\Delta }}}_{\omega }^2}}\left(\frac{1}{{\tau }_{\text{𝑸}}}+\frac{1}{{\tau }_0^p}\right)+V{N}_f{\int }_0^{\mathrm{\Lambda }}\frac{{\overline{\mathrm{\Delta }}}_{\omega }\text{d}\omega }{\sqrt{{\omega }^2+{\overline{\mathrm{\Delta }}}_{\omega }^2}}.$$ [S5]

From Eq. S5, it is clear that only the inter-hot-spot nonmagnetic impurity and the intra-hot-spot paramagnetic impurity suppress the SC gap. The last equation can be solved self-consistently to find ${\overline{\mathrm{\Delta }}}_{\omega }$; it is convenient then to define an effective SC order parameter given by

$$\mathrm{\Delta }=V{N}_f{\int }_0^{\mathrm{\Lambda }}\frac{{\overline{\mathrm{\Delta }}}_{\omega }\text{d}\omega }{\sqrt{{\omega }^2+{\overline{\mathrm{\Delta }}}_{\omega }^2}}.$$

This is the quantity plotted in Fig. 4B.

Next, we consider how the SDW vertex ${\mathrm{\Gamma }}_{\mathrm{SDW}}$ is dressed by impurity scattering. As shown in Fig. S3, the dressed SDW vertex can be conveniently written in Nambu space as

$${\mathrm{\Gamma }}_{\mathrm{SDW}}={\mathrm{\Gamma }}_{\mathrm{SDW}}^{\alpha }({\mathrm{\Psi }}_c^{†}{\sigma }_0{\mathrm{\Psi }}_d+h.c.)-i{\mathrm{\Gamma }}_{\mathrm{SDW}}^{\beta }({\mathrm{\Psi }}_c^{†}{\sigma }_1{\mathrm{\Psi }}_d-h.c.).$$

To calculate the dressed SDW vertex, we need to integrate over the two-dimensional momentum. To calculate these integrals, we apply the transformation

$$\int {\text{d}}^2\text{𝒌}⟹\int \frac{\text{d}{ϵ}_c\text{d}{ϵ}_d}{|{\text{𝒗}}_c\times {\text{𝒗}}_d|}.$$ [S6]

To simply the notation, we define the following quantities (see also ref. 36):

$$\begin{array}{c}{F}_{{\mathrm{\Delta }}^2}=\frac{\omega (\omega +\mathrm{\Omega })+{\overline{\mathrm{\Delta }}}_{\omega }{\overline{\mathrm{\Delta }}}_{\omega +\mathrm{\Omega }}}{\sqrt{{\omega }^2+{\overline{\mathrm{\Delta }}}_{\omega }^2}\sqrt{{(\omega +\mathrm{\Omega })}^2+{\overline{\mathrm{\Delta }}}_{\omega +\mathrm{\Omega }}^2}}\hfill \\ F_{\omega \mathrm{\Delta }}=\frac{\omega {\overline{\mathrm{\Delta }}}_{\omega +\mathrm{\Omega }}-(\omega +\mathrm{\Omega }){\overline{\mathrm{\Delta }}}_{\omega }}{\sqrt{{\omega }^2+{\overline{\mathrm{\Delta }}}_{\omega }^2}\sqrt{{(\omega +\mathrm{\Omega })}^2+{\overline{\mathrm{\Delta }}}_{\omega +\mathrm{\Omega }}^2}}\hfill \\ {\tau }_{\mathrm{damping}}^{-1}=N_{f}4|{\text{𝒗}}_c\times {\text{𝒗}}_d|=\frac{{\mathrm{\Lambda }}_{\parallel }{v}_f\sin \theta }{{\pi }^2}\hfill \end{array}.$$ [S7]

Direct evaluation of the vertex functions gives the coupled equations

$$\begin{array}{c}{\mathrm{\Gamma }}_{\mathrm{SDW}}^{\alpha }=1+{\tau }_{\mathrm{damping}}\left[\left(\frac{1}{2{\tau }_0}+\frac{1}{2{\tau }_{\text{𝑸}}}\right)-\frac{1}{3}\left(\frac{1}{2{\tau }_0^p}+\frac{1}{2{\tau }_{\text{𝑸}}^p}\right)\right]\left(-{\mathrm{\Gamma }}_{\mathrm{SDW}}^{\alpha }{F}_{{\mathrm{\Delta }}^2}+{\mathrm{\Gamma }}_{\mathrm{SDW}}^{\beta }{F}_{\omega \mathrm{\Delta }}\right)\hfill \\ {\mathrm{\Gamma }}_{\mathrm{SDW}}^{\beta }={\tau }_{\mathrm{damping}}\left[\left(\frac{1}{2{\tau }_0}-\frac{1}{2{\tau }_{\text{𝑸}}}\right)+\frac{1}{3}\left(\frac{1}{2{\tau }_0^p}-\frac{1}{2{\tau }_{\text{𝑸}}^p}\right)\right]\left({\mathrm{\Gamma }}_{\mathrm{SDW}}^{\alpha }{F}_{\omega \mathrm{\Delta }}+{\mathrm{\Gamma }}_{\mathrm{SDW}}^{\beta }{F}_{{\mathrm{\Delta }}^2}\right),\hfill \end{array}$$ [S8]

from which we can compute the magnetic susceptibility in Matsubara space,

$${\chi }_{\mathrm{SDW}}(\text{𝑸},i\mathrm{\Omega })=N_f{\tau }_{\mathrm{damping}}\int \frac{\text{d}\omega }{2\pi }({\mathrm{\Gamma }}_{\mathrm{SDW}}^{\alpha }{F}_{{\mathrm{\Delta }}^2}-{\mathrm{\Gamma }}_{\mathrm{SDW}}^{\beta }{F}_{\omega \mathrm{\Delta }}).$$ [S9]

Computing the static magnetic susceptibility ($\mathrm{\Omega }=0$) gives

$$F_{{\mathrm{\Delta }}^2}=1,F_{\omega \mathrm{\Delta }}=0⟹{\mathrm{\Gamma }}_{\mathrm{SDW}}^{\alpha }={\left[1+\frac{{\tau }_{\mathrm{damping}}}{2}\times \left(\frac{1}{\tau }-\frac{1}{3}\frac{1}{{\tau }^p}\right)\right]}^{-1},$$ [S10]

where we defined the total nonmagnetic scattering rate ${\tau }^{-1}={\tau }_0^{-1}+{\tau }_{\text{𝑸}}^{-1}$ and the total paramagnetic scattering rate ${({\tau }^p)}^{-1}={({\tau }_0^p)}^{-1}+{({\tau }_{\text{𝑸}}^p)}^{-1}$. Note that the dressed SDW vertex becomes a constant, independent of the frequency $\omega$. Clearly, although nonmagnetic scattering always reduces ${\chi }_{\mathrm{SDW}}(\text{𝑸},0)$, paramagnetic impurity scattering enhances it. In Fig. 4, we considered the case of point-like impurities, in which ${\tau }_0^{-1}={\tau }_{\text{𝑸}}^{-1}$ and ${({\tau }_0^p)}^{-1}={({\tau }_{\text{𝑸}}^p)}^{-1}$.