Specificity-Determining DNA Triplet Code for Positioning of Human Preinitiation Complex

Abstract

The notion that transcription factors bind DNA only through specific, consensus binding sites has been recently questioned. No specific consensus motif for the positioning of the human preinitiation complex (PIC) has been identified. Here, we reveal that nonconsensus, statistical, DNA triplet code provides specificity for the positioning of the human PIC. In particular, we reveal a highly nonrandom, statistical pattern of repetitive nucleotide triplets that correlates with the genomewide binding preferences of PIC measured by Chip-exo. We analyze the triplet enrichment and depletion near the transcription start site and identify triplets that have the strongest effect on PIC-DNA nonconsensus binding. Using statistical mechanics, a random-binder model without fitting parameters, with genomic DNA sequence being the only input, we further validate that the nonconsensus nucleotide triplet code constitutes a key signature providing PIC binding specificity in the human genome. Our results constitute a proof-of-concept for, to our knowledge, a new design principle for protein-DNA recognition in the human genome, which can lead to a better mechanistic understanding of transcriptional regulation.

Main Text

Transcription factors (TFs) are proteins that regulate gene expression. An established paradigm that TFs specifically recognize only relatively short (4–20 basepair (bp)) consensus DNA motifs (1, 2, 3, 4) has been recently challenged by different high-throughput methods both in vivo and in vitro (5, 6, 7, 8). Human preinitiation complex (PIC) represents one of the most striking examples where design principles of specific protein-DNA recognition remain unknown (5). In particular, in a recent study by Pugh and Venters (7) using the Chip-exo method, no specificity-determining consensus motifs for the positioning of PIC have been identified, thus challenging an established paradigm that the consensus TATA box motif provides the specificity (3, 4, 7).

Here, we reveal that the enrichment level of certain repetitive nucleotide triplets correlate with the genomewide binding preferences of TFIIB—a key component of PIC (7). The unprecedented, single-nucleotide resolution of the Chip-exo method (7) allows us to compare the computed model TF-DNA binding free energy with the measured TFIIB binding occupancy at each DNA basepair. Previously, we suggested a model for yeast PIC positioning based on a statistical, nonconsensus protein-DNA binding mechanism (6, 7, 8). The nonconsensus mechanism predicts that enrichment of certain repetitive DNA sequence elements can lead to an enhanced protein-DNA binding (6, 7, 8). Here, we show that this mechanism (albeit with entirely different DNA sequence symmetries) also describes the positioning of the human PIC, using a simple random-binder model based on a 64-letter triplet alphabet, with the human genomic DNA sequence constituting the only input into the model (see below).

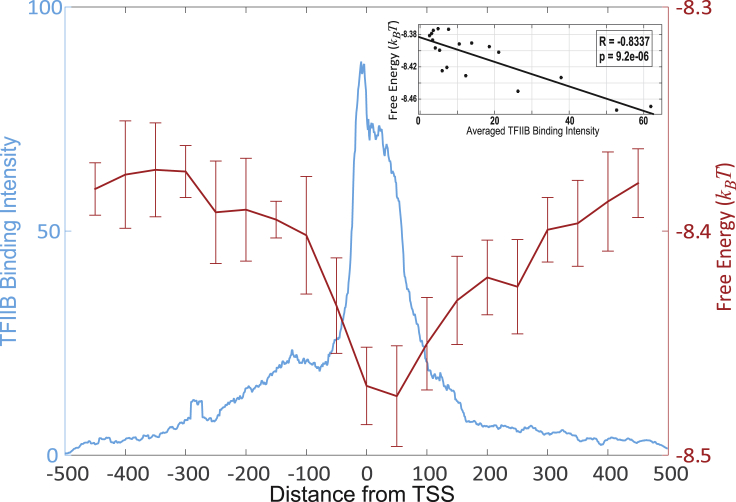
In particular, we analyzed the measured genomewide occupancy of TFIIB (Fig. 1), and revealed that the peak of this occupancy (positioned ∼50 bp downstream of the transcription start site (TSS); Fig. 1) is characterized by a highly nonrandom probability distribution of repetitive nucleotide triplets (Fig. 2). This finding has led us to develop a minimal random-binder model based on a 64-letter triplet code as follows. We consider a model TF forming M contacts with DNA, sliding along the DNA sliding window with the width L (Fig. S1). Such sliding window can be positioned at any genomic position. To assign the nonconsensus free energy to the middle of the sliding window, we define the partition function as follows:

$$Z=\sum _{i=1}^{L-M+1}\exp \left(-U\left(i\right)/k_{\text{B}}T\right),$$ (1)

where k_B is the Boltzmann constant and T is the temperature, with the interaction potential U, as follows:

$$U\left(i\right)=\sum _{j=i}^{i+M-1}\sum _{\alpha }{K}_{\alpha }{S}_{\alpha }\left(j\right),$$ (2)

where each sequence position i corresponds to a DNA triplet, and there are overall 64 possible nucleotide triplets, α (Fig. S1). Here, K_α is the vector containing 64 random energy parameters taken from the Gaussian distribution with the zero mean (for simplicity) and the standard deviation, σ = 2 k_BT (the magnitude of σ sets the energy scale in the problem corresponding to a typical energy of one bond between amino acid and nucleotide basepair (9, 10)); and S_α(j) is also a vector of length 64 with all but one zero elements. The only nonzero element (= 1) of S_α(j) corresponds to the nucleotide triplet of type α located at the sequence position j. After generating 250 random TFs, and averaging the resulting free energy, as follows:

$$F=-k_{\text{B}}T\ln \left(Z\right),$$ (3)

with respect to all TFs, we obtain the average nonconsensus free energy for a given genomic position. Moving the sliding window along the genome, and repeating the procedure described above, we obtain the genomewide average nonconsensus free energy landscape (Fig. 1). This landscape demonstrates a statistically significant, negative correlation with the measured TFIIB binding preferences (Fig. 1, inset). The lower the nonconsensus free energy, the higher the measured TFIIB binding intensity. We have verified that the obtained results are similar for all three possible reading frames (Fig. S2). We note that in the free energy calculation from Eqs. 1 and 2, once the reading frame is chosen, the energy needs to be computed with the step size of three nucleotides (Fig. S1). This is due to the fact that our effective energy model is defined at the triplet level and is not decomposable into, e.g., mononucleotide contributions.

Figure 1.

Free energy of nonconsensus triplets based TFIIB-DNA binding negatively correlates with the TFIIB binding intensity. Shown here is the computed average free energy of nonconsensus TFIIB-DNA binding and the profile of the average TFIIB binding intensity measured by Pugh and Venters (7) around the TSSs of 6097 genes. The average free energy was calculated every 50 bp, within the interval (−450, 450 bp). To compute the free energy, we used a sliding window of 100 bp. To compute error bars, we calculated the mean free energy for each chromosome and divided the results into five randomly chosen subgroups and computed the mean for each subgroup. The error bars are defined as 1 SD of the mean of free energy between the subgroups. (Inset) Given here is the correlation between the free energy and the TFIIB binding intensity with the Pearson correlation coefficient and the p value. To see this figure in color, go online.

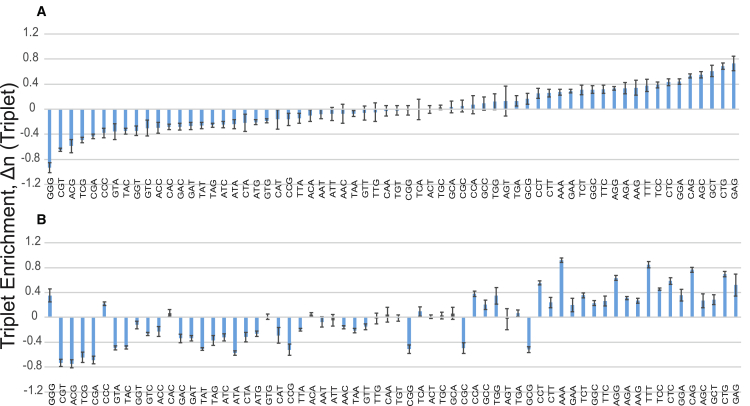
Figure 2.

Enrichment levels of 64 nucleotide triplets computed for the genomic regions characterized by high and low TFIIB binding intensity, respectively. (A) Shown here is triplet enrichment in the region of high TFIIB binding intensity (0, 100 bp). (B) Shown here is triplet enrichment in the region of low TFIIB binding intensity (−450, −350 bp). The enrichment is defined as Δn = n − 〈n〉_rand, where n and 〈n〉_rand represent the computed average number of nucleotide triplets in the set of actual and randomized DNA sequences, respectively. We used 10 randomized DNA replicas to compute 〈n〉_rand. Shaded bars represent triplets that did not exhibit a significant difference based on the two-sample Kolmogorov-Smirnov p value (Table S1). To compute error bars, we divided DNA sequences into four randomly chosen subgroups and computed the mean value of the enrichment for each subgroup. The error bars are defined as 2 SD of the mean between the subgroups. To see this figure in color, go online.

We stress the important fact that our random binder model does not involve any fitting parameters, and all the parameters, K_α, in the interaction potential, Eq. 2, are entirely random (see above). In other words, in the course of computing the free energy (Fig. 1), our computational procedure does not utilize training and validation datasets, respectively.

Highly nonrandom distribution of repetitive nucleotide triplets along the human genomic DNA provides the reason for the observed effect (Fig. 2). In particular, we analyzed the enrichment level for 64 possible nucleotide triplets in the region of the highest TFIIB binding intensity positioned in the interval (0, 100), and compared this enrichment with the one observed in the interval distant from the TSS (−450, −350) (Fig. 2). The computed triplet enrichment, Δn = n − 〈n〉_rand, is normalized by the GC content in each genomic region separately, and it thus represents a robust measure characterizing the enrichment of repetitive nucleotide triplet patterns. Here, n and 〈n〉_rand represent the computed average number of nucleotide triplets in the set of actual and randomized DNA sequences, respectively. We used 10 randomized DNA replicas to compute 〈n〉_rand.

To further validate statistical significance of our results, we computed the Kolmogorov-Smirnov p value for each nucleotide triplet (Table S1). This p value provides a statistical significance of the difference between the actual and randomized probability distributions, P(n) and P(n_rand), respectively (Table S1). For the genomic interval (0; 100), the majority (60 out of 64) of computed p values are highly significant (Fig. 2 A; Table S1). For example, the enrichment of GAG triplet and the depletion of GGG triplet, provide the strongest signature for the enhanced TFIIB binding intensity (Fig. 2 A). The pattern of nucleotide triplet enrichment is entirely different for the interval (−350, −450), with 54 out of 64 computed p values being significant (Fig. 2 B; Table S1).

We note that <30% of the analyzed genes possess translation start sites within the region (0, 100) (Fig. S3). We performed a control calculation, removing these sequences from our analysis of the triplet enrichment (Fig. S4). As a result, we obtained highly significant linear correlation between the original (Fig. 2 A) and control (Fig. S4) triplet enrichment with the linear correlation coefficient (R = 0.99). Therefore, the dominant effect to the observed triplet enrichment (depletion) (Fig. 2) does not originate from codon bias (Figs. S3 and S4).

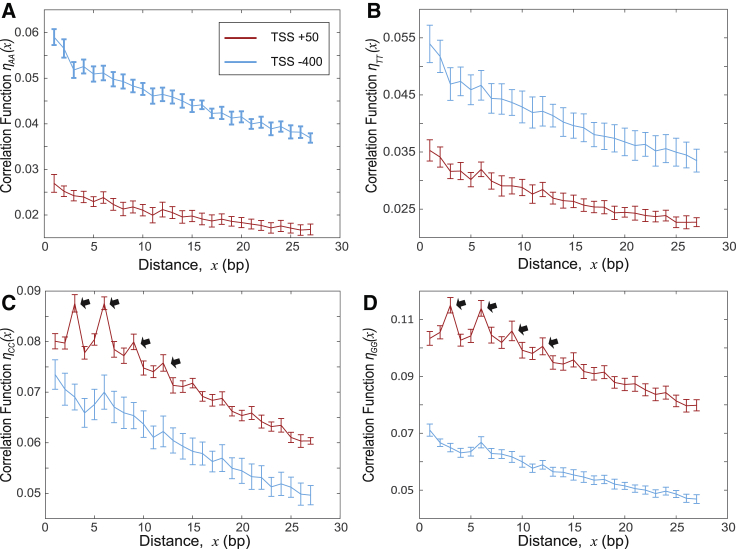
The obtained pattern of nucleotide triplet enrichment (Fig. 2) is validated by the computed pair correlation function, η_αα(x), representing the probability to find two nucleotides of type α separated by the relative distance, x (Fig. 3). Taken together, our results indicate that the nonconsensus mechanism provides the DNA binding specificity for TFIIB, meaning that the entire distribution of enrichment/depletion levels for the majority of nucleotide triplets (and not just one or two specific triplets) influences the TFIIB binding intensity.

Figure 3.

Normalized pair (binary) correlation functions for the nucleotide spatial distribution. (A–D) Shown here is the computed correlation function η_αα(x) = (N_αα(x) − < N_αα(x) > _rand)/L₀, where N_αα(x) represents the average number of nucleotide pairs of type α separated by the relative distance x bp, and L₀ is the width of the window. We used L₀ = 100 bp. We used DNA sequences of 6097 genes for two genomic regions: the region of high TFIIB binding intensity (0, 100 bp) (red lines); and the region of low TFIIB binding intensity (−450, −350 bp) (blue lines). To compute error bars, we calculated the mean for each chromosome and divided the results into five randomly chosen subgroups and computed the mean for each subgroup. The error bars are defined as 1 SD of the mean between the subgroups. The arrows in (C) and (D) emphasize the peaks of the correlation function. These peaks represent the enrichment of repeated DNA triplets. To see this figure in color, go online.

The peaks in the computed pair correlation functions (Fig. 3, C and D) demonstrate that certain repetitive DNA triplets represent statistically dominant repetitive sequence elements in the genomic regions characterized by high PIC occupancy (Fig. 2 A). To further validate this observation, we analyzed the enrichment (depletion) of doublets (16 possible nucleotide doublets) and quadruplets (256 possible nucleotide quadruplets) (Tables S2 and S3). We also computed the free energy landscape based on doublets (Fig. S5) and quadruplets (Fig. S6), using a variant of our simple random-binder model adopted for doublets and quadruplets, respectively (Figs. S5 and S6). Strikingly, although doublets and quadruplets do show statistically significant enrichment (depletion) (Tables S2 and S3), the computed free energy landscapes based on doublets and quadruplets, respectively, do not correlate with the measured binding preferences of PIC (Figs. S5 and S6). This is in striking contrast with the free energy landscape computed based on triplets (Fig. 1).

We emphasize that our simple approach does not take into account the effect of PIC competition (and its possible synergetic interactions) with other DNA binding proteins, or the effect of nucleosome binding preferences (4, 11, 12, 13). Our analysis focuses entirely on the nonconsensus effect, whereas the presence of yet unidentified specific, consensus motifs might significantly influence the resulting binding preferences. However, our main prediction that nonconsensus PIC-DNA binding dominated by entropy significantly influences PIC binding preferences in the human genome most likely represents the general rule rather than the exception.

In summary, using a statistical mechanics model without any fitting parameters with a genomic DNA sequence constituting the only input, we reveal that the nonconsensus nucleotide triplet code constitutes a key signature providing PIC binding specificity in the human genome. Our results need to be further validated in the future, using direct in vitro methods for measuring TFIIB-DNA binding preferences. Such measurements, using purified proteins and DNA, will clarify the question of how much indirect protein-DNA and nucleosome binding influence our model predictions.

Author Contributions

M.G. and D.B.L. designed research, performed research, and wrote the paper.

Editor: Wilma Olson.