COVARIATE-ADAPTIVE CLUSTERING OF EXPOSURES FOR AIR POLLUTION EPIDEMIOLOGY COHORTS

Abstract

Cohort studies in air pollution epidemiology aim to establish associations between health outcomes and air pollution exposures. Statistical analysis of such associations is complicated by the multivariate nature of the pollutant exposure data as well as the spatial misalignment that arises from the fact that exposure data are collected at regulatory monitoring network locations distinct from cohort locations. We present a novel clustering approach for addressing this challenge. Specifically, we present a method that uses geographic covariate information to cluster multi-pollutant observations and predict cluster membership at cohort locations. Our predictive k-means procedure identifies centers using a mixture model and is followed by multi-class spatial prediction. In simulations, we demonstrate that predictive k-means can reduce misclassification error by over 50% compared to ordinary k-means, with minimal loss in cluster representativeness. The improved prediction accuracy results in large gains of 30% or more in power for detecting effect modification by cluster in a simulated health analysis. In an analysis of the NIEHS Sister Study cohort using predictive k-means, we find that the association between systolic blood pressure (SBP) and long-term fine particulate matter (PM_2.5) exposure varies significantly between different clusters of PM_2.5 component profiles. Our cluster-based analysis shows that for subjects assigned to a cluster located in the Midwestern U.S., a 10 μg/m³ difference in exposure is associated with 4.37 mmHg (95% CI, 2.38, 6.35) higher SBP.

1. Introduction

Cohort studies provide a valuable platform for investigating health effects of long-term air pollution exposure by leveraging fine-scale spatial contrasts in exposure between subjects (Künzli et al., 2001; Dominici et al., 2003; Wilson et al., 2005). These studies facilitate a level of precision in exposure assignment that is not available in traditional analyses based upon aggregated data from administrative districts. However, cohort-specific exposure monitoring is rarely done at more than a small subset of subject locations for a short period of time, if at all (Cohen et al., 2009). Instead, pollutant concentrations measured at locations in regulatory monitoring networks, not at cohort locations, are used. This spatial misalignment between monitor and subject locations is often addressed through a two-stage modeling approach. First, an exposure prediction model is developed using the regulatory monitoring data, and predictions are made at cohort subject locations (e.g., Brauer et al., 2003; Keller et al., 2015). These predicted exposures are then used in regression analyses, where their association with health outcomes is estimated (e.g., Adar et al., 2010).

Fine particulate matter (particles with aerodynamic diameter less than 2.5 μm; PM_2.5) is a mixture of many components whose chemical composition varies widely due to sources, meteorology, and other factors (Bell et al., 2007). Variations in PM_2.5 composition can modify the association between total PM_2.5 mass and health effects (Brook et al., 2010; Franklin et al., 2008; Zanobetti et al., 2009), and analysis that distinguishes between different component profiles can improve our understanding of exposures’ health effects (Brauer, 2010).

Multi-pollutant exposures such as PM_2.5 component concentrations present challenges to the two-stage modeling approach for addressing spatial misalignment. Multi-dimensional prediction requires ignoring correlation between pollutants or making strong assumptions about correlation structure that may be difficult to verify with limited monitoring data. Interpreting coefficient estimates for simultaneous exposures to multiple pollutants presents challenges of generalizability. Reducing the dimension of a multi-pollutant exposure prior to prediction provides an attractive means to address these challenges in prediction and interpretation. Dimension reduction methods simplify the complex structure of multi-pollutant exposures by reducing them to a smaller set of low-dimensional observations that retain most of the characteristics of the original data but that can be predicted more reliably.

Clustering methods are a class of dimension reduction methods that partition multi-pollutant observations into a pre-specified number of clusters. For multi-dimensional observations of PM_2.5 components, this amounts to assigning each observation to a representative component profile. Oakes et al. (2014) highlight clustering as a promising approach for understanding multi-pollutant health effects. The ‘k-means’ algorithm is a popular clustering method that identifies clusters that minimize the distance between each observation and the center of its assigned cluster. Recent work has applied clustering methods (including k-means) to time series of PM_2.5 observations to find groups of days with similar component profiles in daily averages (Austin et al., 2012) and groups of locations with similar profiles in long-term averages (Austin et al., 2013). These clusters were used for analyzing exposures by city (Kioumourtzoglou et al., 2015), but have not been used for cohort subject locations. For cohort studies with spatially misaligned monitoring data, the lack of monitoring observations means we cannot directly cluster cohort locations using component profiles. One option is then to use k-means to cluster monitoring data and to subsequently predict cluster membership at subject locations. However, this can work poorly when membership in the clusters identified by k-means is not predictable using available geographic covariates. Modifying the k-means procedure to account for the covariates used in the subsequent prediction model provides a promising approach for efficient prediction of cluster membership at subject locations.

In this paper, we present a method for clustering multi-pollutant exposures in the context of cohort studies with spatially misaligned data and apply it to an analysis of PM_2.5 component exposure in a national cohort. Section 2 presents the motivating analysis of total PM_2.5 and systolic blood pressure in the Sister Study cohort. Section 3 describes an approach for clustering multi-pollutant data in a cohort study using a combination of existing methods. In Section 4, we introduce our new method for defining clusters that improves predictive accuracy at cohort locations. Section 5 details simulations illustrating this method, and in Section 6 we apply the method to the Sister Study cohort. We conclude in Section 7 with a discussion.

2. PM_2.5 and SBP in the Sister Study

The National Institute of Environmental Health Sciences (NIEHS) Sister Study cohort comprises 50,884 women with a sister with breast cancer from across the United States enrolled between 2003 and 2009. In a cross-sectional analysis of the Sister Study cohort, Chan et al. (2015) found that a difference of 10μg/m³ in annual average PM_2.5 was associated with 1.4 mmHg higher systolic blood pressure (SBP) [95% CI: 0.6, 2.3; p < 0.001]. Chan et al. (2015) used predictions of 2006 annual average ambient PM_2.5 exposures from a universal kriging (UK) model fit to monitoring data from the EPA Air Quality System (AQS) (Sampson et al., 2013). The UK model has two components: a regression on geographic covariates for the mean combined with spatial smoothing via a Gaussian Process. The geographic covariates included measures of land-cover, road network characteristics, vegetative index, population density, and distance to various geographic features, which Sampson et al. (2013) reduced in dimension using partial least squares. An exponential covariance structure was used for smoothing in the Gaussian Process.

During baseline home visits, blood pressure measurements were taken, along with anthropometric measurements and phlebotomy. Residential history of subjects is available for assigning long-term exposures based upon participant locations. In their health model, Chan et al. (2015) performed linear regression of SBP on PM_2.5, adjusting for age, race, SES status (household income, education, marital status, working more than 20 hours per week outside the home, perceived stress score, and SES Z-score), rural-urban continuum code, geographic location (via spatial regression splines), cardiovascular risk factors (BMI, waist-hip-ratio, smoking status, alcohol use, history of diabetes and hypercholesterolemia), and blood pressure medication use.

In order to better understand how the observed PM_2.5 effect varies by PM_2.5 composition, we will re-analyze the Sister Study cohort in Section 6 to investigate whether the association between PM_2.5 and SBP is modified by clustering subjects using component profiles of PM_2.5.

3. Clustering Spatially Misaligned Data

In this section we consider clustering PM_2.5 component observations into K component profiles, in the presence of spatial misalignment between the monitor and subject locations, by combining existing methods for unsupervised clustering and spatial prediction.

Ideally we would like to observe the matrix $\mathit{X}\in {ℝ}^{n\times p}$ of annual average mass fractions at n cohort locations for p components of PM_2.5, which we refer to as component species. However, we can only observe the matrix ${\mathit{X}}^{\ast }\in {ℝ}^{n^{\ast }\times p}$ of annual average mass fractions at n^* AQS monitoring locations. (Throughout this paper we use an asterisk to denote values at monitor locations, while values without an asterisk correspond to cohort locations). Geographic covariates such as distance to primary roadways and land use categorizations are available at both monitoring and cohort locations. Let ${\mathit{R}}^{\ast }\in {ℝ}^{n^{\ast }\times d}$ and $\mathit{R}\in {ℝ}^{n\times d}$ be matrices containing values of d geographic covariates (which may include spatial splines) at monitoring and cohort locations, respectively. Let ${\mathit{U}}^{\ast }\in {ℝ}^{n^{\ast }\times K}$ denote an assignment matrix for monitoring locations, with each row having a 1 in a single entry and zeros in all other entries. If $U_{ik}^{\ast }=1$, observation i is assigned to cluster k. Denote by 𝓤 the set of matrices of this form.

For a two-stage exposure-health analysis, we first cluster the mass fraction observations to reduce dimension and identify representative component profiles. Then only cluster labels (assignments) need to be predicted at cohort locations, not full exposure vectors. The procedure can be broken down into the following steps:

Step 1: Cluster monitoring data

1. Create cluster centers M = [μ₁ ⋯ μ_K] from the monitoring data X*.

2. Make cluster assignments U* at monitor locations s^∗ by assigning each location to the cluster with the closest center.

Step 2: Predict cluster membership

1. Train a classification model for predicting cluster assignments using covariates R* and cluster assignments U* at monitoring locations.

2. Predict cluster assignments $\widehat{\mathit{U}}$ at cohort locations using this classification model and covariates R.

Cluster assignments from Step 2(b) can be used as effect modifiers of the association between health outcomes and total PM_2.5 mass, which we assume has already been predicted at subject locations. By separating the procedure into two steps (clustering and prediction), we allow for flexibility in the choice of a prediction model, recognizing that different methods may perform better in certain scenarios.

In the following subsections we describe the procedure in more detail. In Section 4 we present an alternative to k-means clustering for Step 1(a), which leads to improved performance in Step 2 and increased power to detect effect modification in a health analysis.

3.1. Step 1: Clustering Monitoring Data

The widely-used k-means algorithm provides a straightforward way to simultaneously define cluster centers for the mass fraction data (Step 1(a)) and make cluster assignments at monitor locations (Step 1(b)). The k-means solution is a reduction, indexed by the assignment matrix U^∗, of multivariate data (X^∗) into K clusters, each identified by its center (or representative vector) μ_k, that minimizes the within-cluster Sum-of-Squares (wSS^∗):

$$wS{S}^{\ast }=\frac{1}{n^{\ast }}{\Vert {\mathit{X}}^{\ast }-{\mathit{U}}^{\ast }{\mathit{M}}^{\mathbf{\top }}\Vert }_F^2,$$ (1)

where M = [μ₁ ⋯ μ_K]. The center for the kth cluster is the mean of the vectors assigned to that cluster: ${\mathit{\mu }}_k=\frac{1}{N_k^{\ast }}{\sum }_{i:U_{ik}^{\ast }=1}{\mathit{x}}_i^{\ast }$, where $N_k^{\ast }={\displaystyle {\sum }_{i=1}^{n^{\ast }}{U}_{ik}^{\ast }}$ is the number of observations in the kth cluster. Implementations of the k-means algorithm, often that of Hartigan and Wong (1979), exist in many statistical packages, which makes this approach easy to implement using existing software.

3.2. Step 2: Predicting Cluster Membership

The classification model chosen for Step 2 can be any multi-class prediction method. Here we focus on multinomial logistic regression although we also consider other methods such as support vector machines (SVMs) in the simulations and particulate matter analysis.

For multinomial logistic regression, let Z_i ∈ {1, …, K} denote the assignment of observation i to one of K classes (here, clusters from Step 1). The multinomial logistic regression model postulates that

$$\begin{array}{l}\log \frac{P\left(Z_i=k\right)}{P\left(Z_i=K\right)}={\mathit{r}}_i^{\mathbf{\top }}{\mathit{\gamma }}_k\text{for}k=1,\dots K-1,\\ P\left(Z_i=K\right)=1-{\displaystyle \sum _{i=1}^{K-1}P\left(Z_i=k\right)},\end{array}$$ (2)

where Γ = (γ₁, …, γ_K−1) is a matrix of regression coefficients and ${\mathit{r}}_i^{\mathbf{\top }}$ is a row of R. The system (2) defines a generalized linear model, and maximum likelihood estimates of Γ can be computed using a standard iteratively-reweighted least squares algorithm. Rewriting (2) as the softmax function

$$P\left(Z_i=k;\mathbf{\Gamma },{\mathit{r}}_i\right)=\frac{\exp \left({\mathit{r}}_i^{\mathbf{\top }}{\mathit{\gamma }}_k\right)}{1+{\displaystyle {\sum }_{k\prime =1}^{K-1}\exp \left({\mathit{r}}_i^{\mathbf{\top }}{\mathit{\gamma }}_{k\prime }\right)}}$$ (3)

and plugging in the maximum likelihood estimates $\widehat{\mathbf{\Gamma }}=\left({\widehat{\mathit{\gamma }}}_1,\dots ,{\widehat{\mathit{\gamma }}}_{K-1}\right)$ yields classification probabilities for each observation. The matrix $\widehat{\mathit{U}}$ of predicted cluster membership is created by assigning each observation to the cluster with the largest classification probability:

$${\widehat{u}}_{ik}=\{\begin{array}{l}1\text{if}P(Z_i=k;\widehat{\mathbf{\Gamma }},{\mathit{r}}_i)>P(Z_i=k\prime ;\widehat{\mathbf{\Gamma }},{\mathit{r}}_i)\text{for}k\prime \ne k,\hfill \\ 0\text{otherwise}.\hfill \end{array}$$ (4)

3.3. Evaluating Predictive Error

The performance of the clustering procedure can be evaluated by the mean-squared prediction error (MSPE) across cohort locations, $\mathit{MSPE}=\frac{1}{n}{\Vert \mathit{X}-\widehat{\mathit{U}}{\mathit{M}}^{\mathbf{\top }}\Vert }_F^2$, which gives the sum of squared distances between observations X and the centers of the clusters to which each observation is predicted to belong $(\widehat{\mathit{U}}{\mathit{M}}^{\mathbf{\top }})$. MSPE can be broken down into two components: representativeness of the cluster centers and accuracy of predicted cluster membership.

Similar to representativeness at monitor locations, which is quantified by wSS^∗ as defined in (1), cluster representativeness at cohort locations is computed as $\mathit{wSS}=\frac{1}{n}{\Vert \mathit{X}-\mathit{U}{\mathit{M}}^{\mathbf{\top }}\Vert }_F^2$. The matrix $\mathit{U}=\arg {\min }_{\stackrel{\sim }{\mathit{U}}\in 𝓤}{\Vert \mathit{X}-\stackrel{\sim }{\mathit{U}}\mathit{M}\Vert }_F^2$ contains assignment to the nearest cluster (which may not be the cluster to which a location was predicted to belong).

The accuracy of predicted cluster membership is quantified using two metrics, classification accuracy (Acc) and mean-squared misclassification error (MSME). Classification accuracy is the proportion of locations correctly classified: $\mathit{Acc}=\frac{1}{n}{\displaystyle {\sum }_{k=1}^K{\displaystyle {\sum }_{i:{\mathit{U}}_{ik}=1}1}({\widehat{\mathit{U}}}_{ik}=1)}$. The straightforward interpretation of Acc makes it an attractive metric. However, Acc does not account for the magnitude of misclassification. MSME provides this information, by averaging the squared distances between the closest cluster centers UM^⊤ and the predicted cluster centers $\widehat{\mathit{U}}{\mathit{M}}^{\mathbf{\top }}$. That is, $\mathit{MSME}=\frac{1}{n}{\Vert \mathit{U}{\mathit{M}}^{\mathbf{\top }}-\widehat{\mathit{U}}{\mathit{M}}^{\mathbf{\top }}\Vert }_F^2$.

All of these measures require knowing the (typically unavailable) cohort observations X, but in applications can be estimated via cross-validation. Because wSS and MSME are on the same scale, we can directly compare them to assess the tradeoff between representativeness and prediction accuracy, analogous to trading off between bias and variance to achieve lower mean squared error in parameter estimation.

4. Covariate-adaptive Clustering of Spatially Misaligned Data

The k-means algorithm clusters multi-pollutant observations at monitored locations, but does not account for the need to predict cluster membership at cohort locations (Step 2), which is required for spatially misaligned data. There is no reason to expect that membership in clusters identified by k-means using pollutant observations at monitoring locations will be accurately predicted at subject locations using geographic covariates. If cluster membership cannot be predicted well at subject locations, then the identified clusters are of little use for epidemiological analysis.

To address this problem, we propose incorporating the geographic covariates that will be used for predicting cluster membership into the procedure for defining cluster centers. We first use a soft-assignment procedure, described in Section 4.1, that yields cluster centers. We then make hard assignments to clusters by minimizing the distance between observations and their assigned cluster center, in the same manner as k-means. We refer to this clustering procedure as predictive k-means.

4.1. Defining Cluster Centers for Predictive k-means

Let $Z_i^{\ast }$ be a latent random variable that takes on values k = 1,…, K and represents cluster membership. We relate this variable to the covariates ${\mathit{r}}_i^{\ast }$ via a multinomial logistic regression model. Let $q_k\left({\mathit{r}}_i^{\ast },\mathbf{\Gamma }\right)$ denote $P\left(Z_i^{\ast }=k;\mathbf{\Gamma },{\mathit{r}}_i^{\ast }\right)$, with the latter defined as the softmax function in (3). Conditional on the value of $Z_i^{\ast }$, assume that the observation ${\mathit{x}}_i^{\ast }$ is normally distributed as $\left({\mathit{x}}_i^{\ast }|Z_i^{\ast }=k\right)~{\mathcal{N}}_p({\mathit{\mu }}_k,{\sigma }^2\mathit{I})$. This model implies the following log-likelihood function:

$$\ell (\mathbf{\Gamma },\mathit{M},{\sigma }^2|{\mathit{X}}^{\ast };{\mathit{R}}^{\ast })={\displaystyle \sum _{i=1}^n\log }\left({\displaystyle \sum _{k=1}^K{q}_k\left({\mathit{r}}_i^{\ast },\mathbf{\Gamma }\right){(2\pi {\sigma }^2)}^{-p/2}}\times \exp \left(-\frac{1}{2{\sigma }^2}{\Vert {\mathit{x}}_i^{\ast }-{\mathit{\mu }}_k\Vert }^2\right)\right).$$ (5)

The log-likelihood in (5) corresponds to a one-level mixture of experts problem (Jordan and Jacobs, 1994). Mixture of experts models use a set classification models (the ‘experts’) that are combined via a ‘gating’ network that uses soft assignment to select between experts. By incorporating hierarchical levels of gating networks, mixture of experts models can be quite flexible. Following the approach of Jordan and Jacobs (1994), we solve (5) using the EM algorithm with iterative updates to ${\widehat{\mathit{\mu }}}_k$, ${\widehat{\sigma }}^2$, and $\widehat{\mathbf{\Gamma }}$. Details of the algorithm are provided in the Supplemental Material (Keller et al., 2017).

Using this approach, the cluster centers μ_k (columns of M) depend upon the covariates R^∗ via a multinomial logistic regression model for cluster assignment. The incorporation of prediction covariates into the cluster centers improves the accuracy of predicting cluster membership at cohort locations.

The parameter estimates $\widehat{\mathbf{\Gamma }}$ provide ‘working’ cluster assignments for monitor locations. This suggests an alternative approach for prediction in which the cluster membership at cohort locations is predicted using $q_k({\mathit{r}}_i,\widehat{\mathbf{\Gamma }})$ instead of building a separate classification model (Step 2). Such an approach, however, does not use optimal assignments (conditional on identified cluster centers) at monitor locations. In the simulations and PM_2.5 analysis, we compare this approach to multinomial logistic regression and classification using an SVM.

4.2. The Role of the Variance

The parameter σ² implicitly controls the tradeoff between representativeness and predictive accuracy. As σ² → 0, the optimization problem of maximizing the log-likelihood (5) reduces to the k-means optimization problem, assuming all q_k are non-zero (Bishop, 2006, Chap. 9). For predictive k-means, we restrict σ² to be positive, but small values of σ² allow for increased representativeness (smaller wSS) while larger values of σ² allow for improved predictive accuracy (smaller MSPE and MSME) at the cost of decreasing representativeness.

Here we estimate σ² using maximum likelihood, as described in Section 4.1. An alternative approach is to select σ² using cross-validation (CV). The predictive k-means procedure (selection of cluster centers, assignment of monitors to clusters, fitting of classification model, and prediction of cluster membership) could be repeated on CV data sets for various fixed values of σ², and then the value of σ² that yielded the smallest cross-validated value of MSPE selected for use in the primary analysis. However, this can be computationally impractical in situations where CV is already being used for model selection. For that reason, we do not select σ² by CV in the analysis of PM_2.5 components in Section 6, but we provide an example of this approach in the simulations.

5. Simulations

We conducted two sets of simulations to demonstrate the clustering approaches presented here. The first set illustrates the differences between the clusters from predictive k-means and standard k-means procedures in a two-dimensional setting that allows for easy visualization of the centers. The second set demonstrates the methods in a higher-dimensional setting and includes a simulated health analysis to elucidate benefits in power achieved by using clusters from predictive k-means.

5.1. Two-dimensional Exposures

For the first simulation set, we consider two-dimensional exposures (X₁, X₂) and three independent covariates (R₁, R₂, and W). Only R₁ ~ N(0, 1) and R₂ ~ N(0, 1) are observed, while W ~ Bernoulli(0.5) is unobserved. The covariates determine membership in one of four underlying clusters (denoted by Z ∈ {1, 2, 3, 4}), constructed so that two clusters cannot be distinguished using the observed covariates:

$$Z=\{\begin{array}{cc}1& \text{if}{R}_1<0\text{and}W=1,\text{for}\text{all}{R}_2,\\ 2& \text{if}{R}_1<0\text{and}W=0,\text{for}\text{all}{R}_2,\\ 3& \text{if}{R}_1>0\text{and}{R}_2>0,\text{for}\text{all}W,\\ 4& \text{if}{R}_1>0\text{and}{R}_2<0,\text{for}\text{all}W.\end{array}$$

Conditional on cluster membership, the exposures X₁ and X₂ are normally distributed: (X₁|Z = k) ~ N(μ_k1, 1) and (X₂|Z = k) ~N(μ_k2, 1), where μ₁ = (−4, 1), μ₂ = (−4, −1), μ₃ = (4, 1), and μ₄ = (4, −1). By design, observations from clusters 1 and 2 cannot be distinguished using the observed covariates available for prediction.

For a set of 1000 replications, each with a sample size of n = 1000, cluster centers were identified using the k-means and predictive k-means procedures described in Sections 3 and 4. The iterative optimization algorithms for both methods are not guaranteed to find global optima (Jordan and Jacobs, 1994), so 50 different starting values were used for optimization. For each replication, a second sample of 1000 observations was drawn from the same data generating mechanism and underlying cluster membership at these test locations predicted using multinomial logistic regression with covariates R₁ and R₂. This simulation was done twice, once identifying K = 3 clusters and once identifying K = 4 clusters.

When K = 3, we are selecting a number of clusters fewer than the number in the data generating model. This scenario is plausible in applications when the underlying data generating mechanism is not fully known. We see in Figure 1a that k-means correctly identified two cluster centers (either μ₁ and μ₂ or μ₃ and μ₄) and would estimate the center of the third cluster as approximately (4, 0) or (−4, 0), respectively. Because k-means does not incorporate R₁ or R₂ into the cluster centers, the estimated centers are evenly split between these two possibilities. On the other hand, Figure 1b shows that the predictive k-means procedure estimated centers in approximately the same location for all replications: (4, 1), (4, −1), and (−4, 0). The first two clusters correspond to μ₃ and μ₄, while the third center estimated by predictive k-means is directly between μ₁ and μ₂, which are indistinguishable by the prediction covariates R₁ and R₂.

Fig 1.

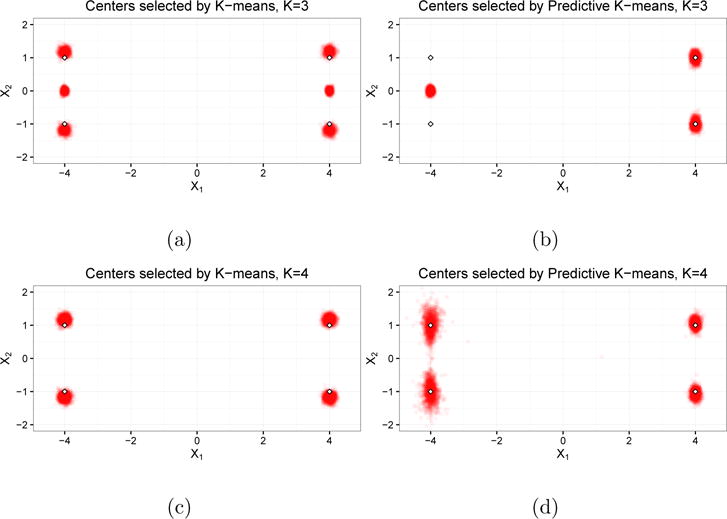
Cluster centers from Simulation 1. Figures (a) and (c) are the centers identified by regular k-means when K = 3 and K = 4, respectively. Figures (b) and (d) are the centers identified by predictive k-means when K = 3 and K = 4, respectively. Each point in the clouds is a cluster center from a single replication; the outlined diamonds denote the latent cluster centers.

Measures of representativeness and predictive accuracy are reported in Table B.1 of the Supplemental Material (Keller et al., 2017). The classification accuracy of k-means is 0.83, and predictive k-means improves upon this by eight percentage points (0.91). While wSS is less than 1% higher for predictive k-means than for regular k-means, misclassification error (MSME) drops by more than 50% (0.54 for predictive k-means compared to 1.13 for regular k-means).

When K = 4, we are selecting the same number of clusters as in the data generating mechanism. In this scenario, predictive k-means also provides measurable improvement in predictive accuracy, as MSME drops by almost 25% (from 2.02 to 1.53) with little loss in representativeness (wSS increases by 2%). Predictive k-means achieves this tradeoff by selecting centers corresponding to clusters 1 and 2 (Figure 1d) that are closer to one another than the centers identified by k-means (Figure 1c). This reduces prediction error when cluster membership is incorrectly predicted.

These simulations demonstrate how when informative covariates (R₁, R₂) are allowed to influence cluster centers, we can get substantial improvements in predictive accuracy with little loss in representativeness. This simulation was repeated using uninformative covariates (i.i.d. N(0, 1) random variables independent of all other covariates and the outcome) in the predictive k-means procedure and to predict cluster membership in the test set. The results from this simulation, also presented in Table B.1 of the Supplemental Material (Keller et al., 2017), show that predictive k-means performs essentially the same as k-means when the covariates do not provide useful information.

5.2. Multi-pollutant Spatial Exposures

For the second set of simulations, we simulated long-term average observations for p = 15 pollutants at 7,333 AQS monitor locations throughout the contiguous United States.

We first assigned each location to belong to one of three latent spatial clusters and one of three latent non-spatial clusters, with membership denoted by A_i ∊ {1, 2, 3} and B_i ∊ {1, 2, 3}, respectively. To assign A_i, a correlated spatial surface was simulated according to the model $\mathit{z}~N({\stackrel{\sim }{\mathit{x}}}^L+{\stackrel{\sim }{\mathit{y}}}^L,0.25\mathit{V})$, where ${\stackrel{\sim }{x}}_i^L$ and ${\stackrel{\sim }{y}}_i^L$ are normalized versions of the Lambert coordinates $x_i^L$ and $y_i^L$. The matrix V has exponential covariance structure: $V_{ij}=\exp \left(-\left|\right|\left(x_i^L,y_i^L\right)-\left(x_j^L,y_j^L\right)|{|}_2/400\right)$. This surface was partitioned into tertiles to give the values A_i. Membership in the non-spatial clusters (B_i) was assigned using i.i.d. draws from a uniform distribution.

Conditional on latent cluster membership, the pollutant observations x_i at each location were simulated from a log-normal distribution:

$$(x_{ij}|A_i=k,B_i=k\prime )~LN(\log (4+a_{jk}+b_{jk\prime })-0.125,0.25)$$

for j = 1, …, p. The component means E[x_ij|A_i = k, B_i = k′] = 4+a_jk+b_jk are combinations of coefficients determined from spatial and non-spatial cluster memberships. Each a_jk (for j = 1, …, p and k = 1, …, K) is an independent observation from the normal distribution $N(0,{\sigma }_A^2)$. Similarly, $b_{jk}~N(0,{\sigma }_B^2)$. We considered two settings for $\left({\sigma }_A^2,{\sigma }_B^2\right)$: (1, 2), which induces greater separation between clusters in the non-spatial partition than between clusters in the spatial partition, and (2.5, 0.5), which results in greater separation between clusters in the spatial partition. In the latter scenario we expect both k-means and predictive k-means to find similar cluster centers, since the greatest between-cluster separation is among clusters that depend upon spatial covariates. The component concentrations were converted to mass fractions by dividing by total particulate matter, i.e. ${\stackrel{\sim }{x}}_{ij}=x_{ij}/P{M}_i$, where $P{M}_i={\displaystyle {\sum }_{j=1}^p{x}_{\mathit{ij}}}$.

For each of 500 replications, 200 locations were randomly selected as ‘monitors’ and the remaining locations served as ‘cohort’ locations. Cluster centers were estimated from the mass fractions ${\stackrel{\sim }{x}}_{ij}$ ‘monitor’ locations via regular k-means and predictive k-means, using a matrix of thinplate regression splines (TPRS) with 15 degrees of freedom (df) as R*. We present results for estimating the mixture model variance parameter σ² via maximum-likelihood and via CV. Cluster membership at ‘cohort’ locations was predicted using multinomial logistic regression (MLR), an SVM, and the working coefficients from the mixture of experts model.

Predicted cluster assignments were then used as interaction variables in a linear regression analysis of the association between SBP and PM. Blood pressure measurements for each ‘cohort’ location were simulated as $y_i=115+{\displaystyle {\sum }_{j=1}^p}{x}_{ij}{\beta }_j+{\epsilon }_i$, where ${\epsilon }_i~N\left(0,{\sigma }_{\mathrm{SBP}}^2\right)$. The values of β_j were chosen so that the variability in the SBP–PM association was the same among the latent spatial and non-spatial clusters. For each set of predicted cluster assignments $\stackrel{⌢}{\mathit{U}}$, we fit the linear model $\mathrm{E}[y_i|P{M}_i,{\stackrel{⌢}{U}}_i]={\beta }_0+{\beta }_{02}{I}_{{\stackrel{⌢}{U}}_{i=2}}+{\beta }_{03}{I}_{{\stackrel{⌢}{U}}_{i=3}}+{\beta }_{1}P{M}_i+{\beta }_{12}P{M}_i{I}_{{\stackrel{⌢}{U}}_{i=2}}+{\beta }_{13}P{M}_i{I}_{{\stackrel{⌢}{U}}_{i=3}}$. A Wald test of the null hypothesis H₀: β₁₂ = β₁₃ = 0 was performed to determine whether there were between-cluster differences in the association between SBP and PM.

When $\left({\sigma }_A^2,{\sigma }_B^2\right)=\left(1,2\right)$, overall prediction error was lowest for predictive k-means with σ² selected by CV and MLR used as the classifier (MSPE = 15.03). Misclassification error (MSME) was more than 50% smaller for predictive k-means compared to regular k-means (1.72 compared to 4.18) and classification accuracy was 15 percentage points higher (see Table 1). The clusters identified by predictive k-means were only slightly less representative (wSS of 13.57 and 13.69) than those identified by k-means (13.38).

Table 1.

Measures of representativeness (wSS) and predictive accuracy (MSPE, MSME, Acc) for Simulation 2. Clusters centers were identified by k-means and predictive k-means, using either maximum likelihood (EM) or cross-validation (CV) for selecting σ². Predictions were made using multinomial logistic regression (MLR), support vector machines (SVM), and the working coefficients from the Mixture of Experts algorithm (ME-Working).

$\left({\sigma }_A^2,{\sigma }_B^2\right)$	Clustering Method	Prediction Method	MSPE	wSS	MSME	Acc
(1, 2)	k-means	MLR	16.80	13.38	4.18	0.45
		SVM	17.09	13.38	4.43	0.42
	Predictive k-means with ${\widehat{\sigma }}^2$ selected by EM	MLR	15.43	13.57	2.45	0.58
		SVM	15.75	13.57	2.47	0.54
		ME-Working	15.68	13.57	2.63	0.55
	Predictive k-means with ${\widehat{\sigma }}^2$ selected by CV	MLR	15.03	13.69	1.72	0.60
		SVM	15.27	13.69	1.86	0.57
		ME-Working	15.17	13.69	1.81	0.58
(2.5, 0.5)	k-means	MLR	14.12	12.97	1.92	0.75
		SVM	14.31	12.97	2.07	0.72
	Predictive k-means with ${\widehat{\sigma }}^2$ selected by EM	MLR	13.79	12.90	1.46	0.79
		SVM	13.89	12.90	1.54	0.78
		ME-Working	14.01	12.90	1.65	0.76
	Predictive k-means with ${\widehat{\sigma }}^2$ selected by CV	MLR	13.75	12.90	1.37	0.80
		SVM	13.88	12.90	1.48	0.78
		ME-Working	13.85	12.90	1.44	0.78

The power for detecting a between-cluster difference (at the α = 0.05 level) in health effect is plotted in Figure 2 for varying values of σ_SBP. In the setting $\left({\sigma }_A^2,{\sigma }_B^2\right)=\left(1,2\right)$, all three prediction methods gave similar results for predictive k-means with σ² selected by maximum likelihood, while MLR performed best for clusters from regular k-means and predictive k-means with σ² chosen by CV. The highest power was obtained by predictive k-means with σ² selected by CV (0.76 at σ_SBP = 4), followed by predictive k-means with σ² chosen by maximum likelihood (0.60) and regular k-means (0.42). When true (oracle) cluster assignments were used, the power from regular k-means clusters (0.90) exceeded that from predictive k-means clusters with σ² chosen by maximum likelihood (0.78). This demonstrates that the benefits in power for predictive k-means are due to the improved predictive accuracy, despite the slight loss in representativeness.

Fig 2.

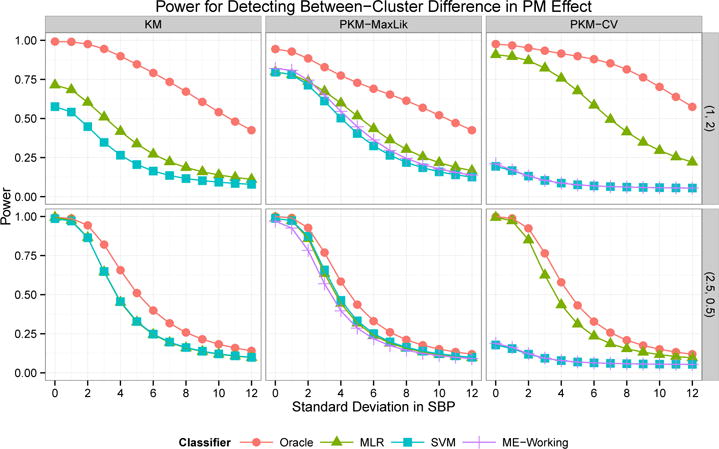
Power for detecting a between-cluster difference in SBP-PM association from Simulation 2. Clusters identified by k-means (KM) and predictive k-means with σ² chosen by maximum likelihood (PKM-MaxLik) or cross-validation (PKM-CV). Cluster membership was predicted using multinomial logistic regression (MLR), SVM, working coefficients from the mixture of experts model (ME-Working), or oracle assignment using true exposure values. The rows correspond to $\left({\sigma }_A^2,{\sigma }_B^2\right)=\left(1,2\right)$ and $\left({\sigma }_A^2,{\sigma }_B^2\right)=\left(2.5,0.5\right)$.

When $\left({\sigma }_A^2,{\sigma }_B^2\right)=\left(2.5,0.5\right)$, representativeness was essentially the same for both methods (12.97 for k-means, 12.90 for predictive k-means). Although overall prediction error was only slightly smaller for predictive k-means, prediction accuracy was 4 percentage points higher and misclassification error approximately 25% lower for predictive k-means (1.46 and 1.37 versus 1.92). The power for detecting effect modification was essentially the same for all clustering and classification methods, with the exception of low power when the SVM approach and the mixture of experts working coefficients were used for predictive k-means with σ² chosen by CV (see Figure 2). These results show that predictive k-means and k-means have comparable performance in settings where they are identifying similar cluster centers.

6. PM_2.5 Components and NIEHS Sister Study

To expand upon the analysis of Chan et al. (2015), we investigated the relationship between SBP and long-term exposure to PM_2.5, grouping subjects by predicted membership in clusters with different component profiles. Our analysis included 47,206 cohort subjects with complete covariate information.

We obtained data for 130 AQS monitoring locations that in 2010 measured mass concentration for twenty-two PM_2.5 component species (elemental carbon [EC], organic carbon [OC], ${\text{NO}}_3^{-}$, ${\text{SO}}_4^{2-}$, Al, As, Br, Cd, Ca, Co, Cr, Cu, Fe, K, Mn, Na, S, Si, Se, Ni, V, and Zn) in addition to measurements of PM_2.5 mass made in accordance with Federal Reference Methods. Annual averages were computed by averaging all available daily observations from each monitoring location having at least 41 measurements in the calendar year with a maximum gap of 45 days between observations. We converted mass concentrations to mass fractions by dividing the annual average of each species at a monitoring location by the annual average PM_2.5 concentration at that location. To make the distribution of mass fractions within each component more symmetric, we log-transformed the mass fractions.

We applied the predictive k-means method to this monitoring data, selecting the number of clusters and the covariates by 10-fold cross-validation. Because of the limited number of observations (n* = 130), we only investigated K ≤ 10. Using a matrix of more than 200 geographic covariates at monitor locations, we computed the first three scores from a principal component analysis (PCA). We considered models with either 2 or 3 PCA scores and TPRS with either 5 or 10 df, with the same covariates used for determining cluster centers and in the classification model. The smallest cross-validation MSPE was for the model with K = 8 clusters and a combination of 2 PCA scores and 10 df TPRS as the covariates. Table 2 provides CV performance metrics for different prediction methods and Table C.1 in the Supplemental Material (Keller et al., 2017) provides metrics for other choices of K. A support vector machine (SVM) was used as the classification model, because it resulted in better cross-validated predictive accuracy (MSPE = 18.33) than multinomial logistic regression (21.28) or using the working coefficients from the mixture-of-experts model (24.33). For comparison, we applied regular k-means to the component data using the same prediction covariates. Cross-validated MSME was slightly worse for regular k-means (18.95), and MSME was notably higher (7.06) compared to predictive k-means (5.97).

Table 2.

Measures of clustering performance from 10-fold cross-validation of the PM_2.5 component data when K = 8 and the covariates are 2 PCA components and TPRS with 10 df.

Clustering Method	Prediction Method	MSPE	wSS	MSME	Acc
k-means	Multinom Logit	20.10	14.46	8.96	0.67
	SVM	18.95	14.46	7.06	0.68
Predictive k-means with ${\widehat{\sigma }}^2$ selected by EM	Multinom Logit	21.28	14.88	9.90	0.62
	SVM	18.33	14.88	5.97	0.70
	ME-Working	24.33	14.88	13.00	0.61

The cluster centers identified by predictive k-means are plotted in Figure 3. Many of the monitor locations in the Midwest and Mid-Atlantic regions were assigned to Cluster 1 (n* = 32), which has above-average mass fractions of ${\text{SO}}_4^{2-}$ and ${\text{NO}}_3^{-}$, suggestive of high ambient ammonia levels from agricultural emissions favoring particulate over gaseous ${\text{NO}}_3^{-}$ (U.S. EPA, 2003). Cluster 2 (n* = 26) included monitors from New England, the south-eastern coast, and parts of the upper Midwest, and had higher fractions of Cd, V and Ni, which are associated with ship emissions (Thurston et al., 2013) and residual oil burning in New York City (Peltier et al., 2009). Monitors in the Southeast were mostly assigned to Cluster 3 (n* = 27) and had a component profile notable for its relatively low fraction of particulate nitrate ( ${\text{NO}}_3^{-}$) relative to sulfate ( ${\text{SO}}_4^{2-}$), a pattern that has previously been attributed to high amounts of acidic sulfate and low levels of ammonia in the region (Blanchard and Hidy, 2003). The California monitors were grouped into Cluster 4 (n^∗ = 8), which also had low sulfur fractions and large fractions of sodium and nitrate particles, likely from marine aerosols and agricultural emissions, respectively. Cluster 5 (n^∗ = 8) included monitors from the Pacific Northwest and Southwest, with high fractions of almost all pollutants except sulfate. Cluster 6 (n^∗ = 20) had high fractions of Fe, Zn, and Mn, which are indicative of emissions from steel furnaces and other metal processing (Thurston et al., 2013), and the monitors assigned to this cluster were all near industrial plants of some kind. Cluster 7 (n^∗ = 8) had high fractions of the crustal elements Si, Ca, K and Al, indicative of the surface soil composition in the Western U.S. (Shacklette and Boerngen, 1984). The eigth cluster was a single site outside of Pittsburgh, PA, which has been previously noted for non-attainment of air quality standards due to nearby industrial sources (U.S. EPA, 2006).

Fig 3.

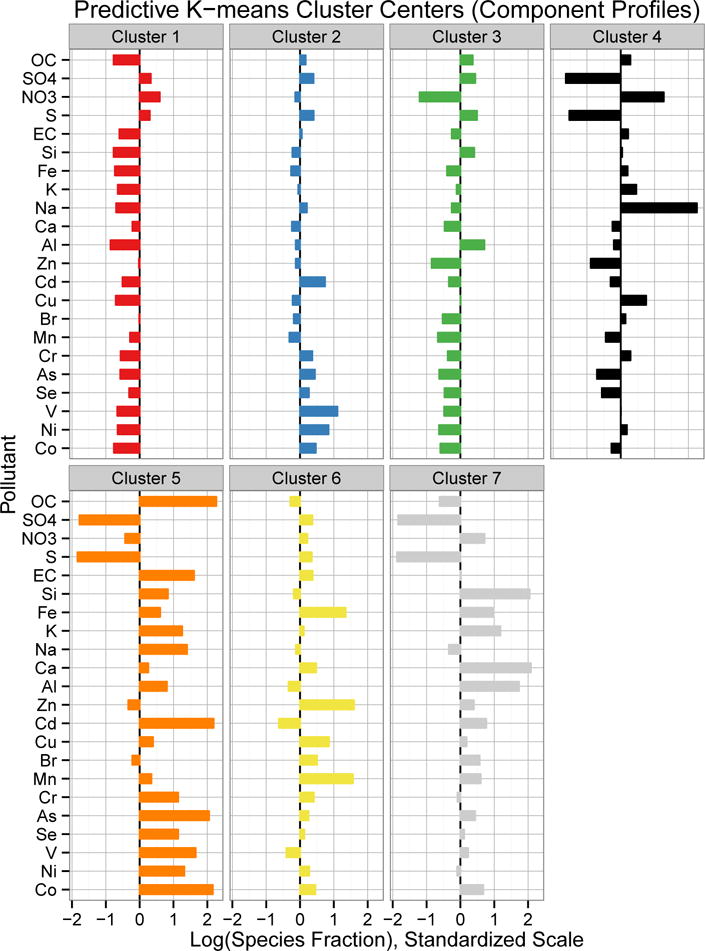
Cluster centers identified by predictive k-means in the 2010 annual average PM_2.5 component data. Species mass fractions were log transformed and then standardized, so values shown represent relative composition. Components are ordered by decreasing mass concentration.

Predicted assignments to the predictive k-means clusters at Sister Study cohort locations are mapped in Figure 4b. Predicted membership at cohort locations tended to follow the same general spatial patterns as monitor assignments, with some differences in the Mountain West and Mid-Atlantic regions. A majority of subjects were predicted to belong to Clusters 1 (n = 12, 828), Cluster 2 (n = 13, 926), or Cluster 3 (n = 9, 915).

Fig 4.

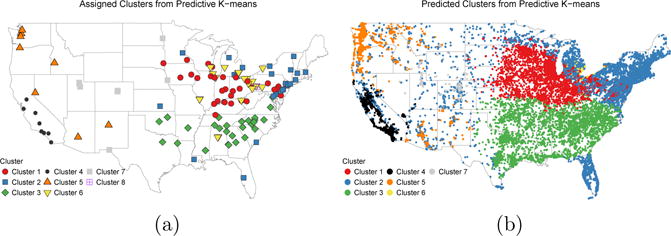
(a) Assigned predictive k-means cluster membership at AQS monitor locations. (b) Predicted cluster membership at Sister Study cohort locations (jittered to protect confidentiality).

Using a linear model for SBP with the same confounders as Chan et al. (2015) (see Section 2), we estimated the association between SBP and long-term PM_2.5 exposure, stratifying exposure by cluster. We used predictions of 2010 annual average PM_2.5 concentrations from a universal kriging model following the same approach as Sampson et al. (2013). The association coefficient estimates are provided in Table 3. The estimated difference in SBP associated with a 10 μg/m³ difference in PM_2.5 overall (without clustering) was 1.81 mmHg, which is higher than, but still contained within the confidence interval for, the estimate obtained by Chan et al. (2015) for 2006 annual average exposure. When estimating cluster-specific associations, Cluster 1 had a much stronger association (4.37 mmHg higher SBP for each 10 μg/m³ difference in PM_2.5, 95% Confidence Interval [CI]: 2.38, 6.35) than the estimate that pools all subjects together. The point estimates for Clusters 3 and 4 were also higher (2.91 and 3.51, respectively) than the unclustered estimate. Although the point estimates for Clusters 5 and 6 were quite large (3.07 and 5.60, respectively), their confidence interval were quite large and include 0. In Clusters 2 and 7, there was no evidence of an association between PM_2.5 and SBP. A Wald test for effect modification showed that the differences between clusters were statistically significant (p = 0.020). As a sensitivity analysis, we explored adjusting for finer scale spatial variation and allowing the coefficients for the covariates in the health model to vary by PM_2.5 cluster assignment, however this did not substantively change the results (data not shown).

Table 3.

Estimated difference in SBP (in mmHg) associated with a 10 μg/m³ difference in annual ambient PM_2.5 exposure. Cohort is partitioned by membership in clusters from predictive k-means.

Exposure	n	Est.	95% CI	p-value
Overall PM2.5	47,206	1.81	(0.74, 2.88)	<0.001
PM2.5 by Cluster				0.015a
Cluster 1	12,828	4.37	(2.38, 6.35)	0.000016
Cluster 2	13,926	0.77	(−1.19, 2.74)	0.44
Cluster 3	9,915	2.91	(0.19, 5.62)	0.036
Cluster 4	4,033	3.51	(0.68, 6.34)	0.015
Cluster 5	4,057	3.07	(−1.07, 7.21)	0.15
Cluster 6	1,029	5.60	(−0.71, 11.9)	0.08
Cluster 7	1,418	−2.11	(−6.55, 2.33)	0.35

^ap-value for a Wald test for a difference between cluster coefficient estimates.

For comparison, we used regular k-means to cluster the PM_2.5 component data and predicted cluster membership at cohort locations using the same prediction covariates. The clustering results and a table of association estimates are provided in Supplemental Material Section D (Keller et al., 2017). The cluster centers (Figure E.1) are quite similar to those from predictive k-means, and the map of k-means cluster assignments at subject locations (Figure E.2) looks visually similar to that from predictive k-means. However, there are some notable differences in the estimated health effects. The estimate for k-means Cluster 1 is attenuated by more than 30% compared to the predictive k-means analysis. Only 267 subjects were predicted to belong to k-means Cluster 6 (compared to 1,209 assigned to predictive k-means Cluster 6), resulting in a highly variable estimate. For Cluster 3, the k-means analysis estimates an attenuated effect, while the predictive k-means cluster yields a similar, but larger and statistically significant association.

As a further sensitivity analysis, Section C of the Supplemental Material (Keller et al., 2017) presents results for analysis for different numbers of clusters. In general, we see that under other choices of K, the strongest significant health effects are still estimated in subjects residing in the Midwest, South, and California.

7. Discussion

We have presented a novel approach for clustering multivariate environmental exposures and predicting cluster assignments in cohort studies of health outcomes. The motivating application is air pollution epidemiology, where multi-pollutant exposure data are available from regulatory monitoring networks, but these monitors do not measure exposure at cohort locations. We first demonstrated how dimension reduction could be performed through the existing method of k-means clustering followed by spatial prediction. However, the clusters identified by k-means may not be predictable at subject locations, which makes them of limited use for epidemiological analysis. To address this, we introduced the predictive k-means method, which incorporates prediction covariates into the estimation of cluster centers.

Through simulations, we demonstrate that clusters from predictive k-means provide substantial gains in prediction accuracy compared to the k-means approach. The simulations did not provide strong evidence to favor one of the three classification approaches compared (multinomial logistic regression, working coefficients from the mixture of experts model, and an SVM), however the SVM clearly outperformed the alternatives in the analysis of the PM_2.5 component data. In addition to improved predictive accuracy, the simulations demonstrated that predictive k-means clusters yield higher power for detecting effect modification by cluster membership.

The mixture model (4.1) that is the foundation of the predictive k-means method includes several assumptions about the data that are not required to hold for the method to show benefit. In particular, the model assumes multivariate normality, independence between pollutants, and constant variance across clusters. However, we emphasize that we employ this mixture model as a tool for constructing cluster centers for analysis, and do not assume that this parametric mixture model can fully represent the complicated processes that generate the particular matter components under study. Furthermore, we violated each of these assumptions in the design of Simulation 2 and still demonstrated benefit from predictive k-means. A potential extension of predictive k-means for future work is to allow the cluster variance parameter (σ²) to vary between clusters rather than assuming a constant value for the entire dataset.

As with any cluster analysis, the choice of the number of clusters is important. In our analysis of the PM_2.5 component data, we chose K = 8 based upon a cross-validation analysis. We restricted the candidate choices to K ≤ 10 due to the need to have enough monitors assigned to each cluster so that a prediction model could be developed. The results of Simulation 1 suggest that the benefits of predictive k-means remain even when the chosen number of clusters does not match the underlying data generation mechanism.

A challenge for the predictive k-means approach is adequately accounting for uncertainty in cluster assignments in the health model. The health estimates presented here condition on cluster assignment and do not incorporate further uncertainty. When multinomial logistic regression is used as the prediction method, cluster assignment probabilities are available for propagation, conditional on cluster centers. This could be approached as a categorical extension of the multi-pollutant measurement error approaches of Bergen and Szpiro (2015). But when an SVM is used for classification, as in the data analysis here, no probabilistic uncertainties for the assignment are available. Accounting for uncertainty in predicted cluster assignment at the same time as determining the cluster centers is more difficult. Even for fixed K, choosing different covariates for the predictive k-means model can result in different clusters, which makes interpretation of the clusters across models unclear. A direction for addressing this problem is the post-selection inference approaches of Berk et al. (2010) and Lee et al. (2016).

We found a significant association in the NIEHS Sister Study between SBP and 2010 long-term ambient PM_2.5 exposure that was higher than previous estimates based upon 2006 exposure when ignoring PM_2.5 composition (Chan et al., 2015). Although all baseline measurements on Sister Study participants were complete prior to 2010, we used 2010 measurements due to changes in the collection of PM_2.5 speciation data during prior years. Using clusters identified by predictive k-means, we found that this association varied significantly by PM_2.5 composition and was strongest among subjects predicted to belong to Clusters 1 and 3, which included most subjects living in the Midwest and Southeast. These results are consistent with the findings of Thurston et al. (2013), who found that PM_2.5 exposure dominated by secondary aerosols were significantly associated with mortality. The strength of the estimated effects in clusters with component profiles notable for secondary aerosols may be due in part to the available speciation data, since the relatively small number of monitors means that the component data, and the clusters derived from them, capture regional variation better than small scale (within-city and near-source) variability.

By incorporating covariate information into cluster centers, the predictive k-means procedure performs dimension reduction appropriate for spatially-misaligned data. This method provides a useful tool for understanding how differences in exposure composition are associated with health effects.