IC-Finder: inferring robustly the hierarchical organization of chromatin folding

Abstract

The spatial organization of the genome plays a crucial role in the regulation of gene expression. Recent experimental techniques like Hi-C have emphasized the segmentation of genomes into interaction compartments that constitute conserved functional domains participating in the maintenance of a proper cell identity. Here, we propose a novel method, IC-Finder, to identify interaction compartments (IC) from experimental Hi-C maps. IC-Finder is based on a hierarchical clustering approach that we adapted to account for the polymeric nature of chromatin. Based on a benchmark of realistic in silico Hi-C maps, we show that IC-Finder is one of the best methods in terms of reliability and is the most efficient numerically. IC-Finder proposes two original options: a probabilistic description of the inferred compartments and the possibility to explore the various hierarchies of chromatin organization. Applying the method to experimental data in fly and human, we show how the predicted segmentation may depend on the normalization scheme and how 3D compartmentalization is tightly associated with epigenomic information. IC-Finder provides a robust and generic ‘all-in-one’ tool to uncover the general principles of 3D chromatin folding and their influence on gene regulation. The software is available at http://membres-timc.imag.fr/Daniel.Jost/DJ-TIMC/Software.html.

INTRODUCTION

The organization of eukaryotic DNA into a heterogeneous chromatin fiber contributes to gene regulation by controlling the accessibility of promoter and regulatory sequences to the transcriptional machinery (1). Until recently, this organization has been essentially studied locally by considering the genome as a unidimensional object whose local structure is modulated by epigenomic information like histone marks, DNA methylation or chromatin-binding proteins (1). However, recent progresses of genome-wide chromatin conformation capture techniques (Hi-C) have suggested that, at higher scales, chromosomes are linearly folded into subnuclear 3D domains, the so-called topologically-associating domains (TADs) (2), characterized by high contact frequencies within the domains and partial insulation between adjacent consecutive domains. Theses domains extend over few kilobases up to megabases (3) and even larger in inactivated mammalian X chromosomes (4). TADs have been shown to be mainly conserved across tissues and across neighbor species (2,3,5,6), and small observed discrepancies are associated with development and cell differentiation (5). TADs themselves organize into higher hierarchies of interaction compartments up to chromosome territories that depend on the differentiation states (7–9). Understanding the functional roles of such—hierarchical—compartmentalization is challenging and remains under active investigation. However, enrichment of architectural or insulator proteins like cohesin or CTCF at TAD boundaries or the relative uniformity of the epigenomic information within a domain (3,10,11), suggest an important role in regulating gene expression like promoting the promoter–enhancer interactions (12).

Different approaches have been developed to infer the elementary segmentation of chromatin into TADs and its higher order organization. An important family of methods relies on transforming the 2D information given by Hi-C maps into a 1D signal and on identifying local extrema or strong local variations that can be subsequently associated with TAD boundaries (2,3,10,13,14). For example, Dixon et al. derive a directionality index (DI) that estimates the difference between upstream and downstream interactions for a locus and that has maximal variation around boundaries (2). Recently, Shin et al. base their approach (TopDom) on finding the local minima of the average contact frequency in the neighborhood of a locus (14). Other approaches use dynamic programming to optimally segment chromosomes into TADs (3,9,15,16). For example, HiCSeg applies 2D segmentation techniques originally used in image processing to segment Hi-C map into diagonal units, the TADs (16). In addition to TAD calling, some methods allow also to capture different levels of organization (7–9,15). For example, based on an approximation of a linear model of contact enrichment, TADtree infers the best TAD hierarchy and allows the detection of nested TADs (9).

The aforementioned approaches have allowed to get new biological insights from Hi-C experiments, from the enrichment of CTCF sites at TAD boundaries in mammals (2) to the characterization of inter-TAD regions in drosophila (6) or to the structural rearrangements of meta-TAD hierarchical organization during murine neuronal differentiation (8). However, they all suffer from one or several of the following drawbacks: (i) the program is not publicly available; (ii) obtaining a good segmentation needs fine-tuning of—sometime numerous—parameters that could be challenging for non-expert user; (iii) the method is computationally time demanding; (iv) prediction robustness is not estimated; (v) the method infers TAD positions but not the higher-order organization or vice-versa.

Here, we introduce IC-Finder, a robust computationally-efficient algorithm to segment Hi-C maps into interaction compartments (IC) like TADs. The method is based on a hierarchical clustering-like approach that depends on only two intuitive parameters which do not need to be tuned and whose default values have been learned in order to give optimal results on a large variety of experimental Hi-C data. Based on statistical resampling of the investigated map, IC-Finder allows to quantify the reliability of the predicted compartmentalization of genome. Moreover, the program offers the option to infer higher-order levels of chromatin organization. The source code is open-access, user-friendly and is available at http://membres-timc.imag.fr/Daniel.Jost/DJ-TIMC/Software.html. In order to validate our approach and to compare IC-Finder with other existing methods, we build a controlled benchmark of Hi-C maps whose segmentation is known. We show that IC-Finder is top-ranked with high sensitivity and specificity. As illustrations of the method, we use IC-Finder to investigate the effect of normalization schemes on the predicted segmentation, and to quantify the correlation between epigenomic information and spatial chromatin compartmentalization at different organizational levels in human and fly.

MATERIALS AND METHODS

IC-Finder algorithm

IC-Finder takes as an input a Hi-C matrix C(i, j) (size N × N) whose entries correspond to the contact frequencies between loci i and j.

Constrained hierarchical clustering

We aim to cluster loci that are consecutive along the genome and that share the same pattern of interactions (Figure 1A). In statistical learning, a very useful and standard method of cluster analysis is the unsupervised hierarchical clustering approach (HCA). HCA is an iterative method to group objects into a hierarchy of clusters. At the beginning of the algorithm, each column of the Hi-C map represents a cluster. Then, the closest pair of clusters are merged together. This process is reiterated until just one cluster is remaining. In standard HCA, merging is authorized between any pairs of clusters. Here, to maintain the linear connectivity of the chromosome, we consider only pairs of nearest-neighbor clusters along the genome. Closeness between clusters is defined by a distance metric D and a linkage method S. D represents the metric used to compute distances between columns of the Hi-C map and S is the strategy chosen to compute distances between current clusters. After testing several combinations of metric and linkage, we find that the correlation distance D_c coupled to a weighted-mean linkage S_wm give a good balance between specificity and sensitivity for the predicted partitions (Supplementary Figure S2):

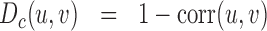(1)

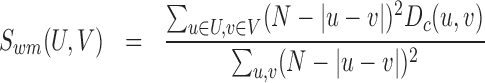(2)

with corr(u, v) the Pearson correlation between columns u and v and U, V two neighboring clusters. Hi-C maps contain often many zeros. These empty bins may represent a lack of information (due, for example, to unmappable reads) or an actual absence of contacts. Being unable to distinguish between the two, we choose to ignore the rows and columns containing >75% missing values among the 20 coefficients surrounding the diagonal. These rows and columns are removed before starting the segmentation process. Moreover, if the number of non-zero rows is <10, we do not consider such distance in the computation of linkage.

Figure 1.

(A) Pipeline of the IC-Finder algorithm: a Hi-C map (left bottom) is transformed into a distance map (left top). Construction of the hierarchical organization (right) is performed using agglomerative hierarchical clustering on the distance map. At a given stage of the clustering, a choice to stop merging consecutive clusters is made regarding the heterogeneity σ_norm inside the candidate merged cluster. (B) Prediction robustness estimated using Poisson resampling of the original map (left): probability p_d that two loci are predicted to ‘colocalize’, i.e. to belong to the same interaction domain (right top) and the probability p_b that a locus is predicted as a domain boundary (right bottom). (C) Different types of outputs given by IC-Finder: TAD boundaries determined by the program in default mode, and p_d, p_b and TAD boundary for different hierarchy of folding when the corresponding options are activated. Examples are given for the region 12–14.5 Mb of fly chromosome 3R (10).

An important issue in HCA is to find a systematic criterion to select the relevant segmentation among all the hierarchical possibilities inferred by the method. Here, we base our criterion on the observation that contacts inside a compartment should be homogeneous in a polymer sense, meaning that contact frequencies between pairs of monomers should only depend on the genomic distance between the monomers. Practically, at each step of the HCA, we define a stopping rule to evaluate if the two selected clusters have to be merged together: having a putative merged cluster c(i, j), i.e. a submatrix of C(i, j) corresponding to the two neighbor clusters, we compute the normalized matrix

(3)

Then, we estimate the variance σ of c_n. In order to correct for experimental noise in the data, we normalize σ by the median local variation of c_n in the region close to the diagonal (for genomic distance between 3 and 40 bins). If σ_norm < σ₋ (weak heterogeneity), the two clusters are merged together, if σ_norm > σ₊ (strong heterogeneity), the boundary between the two clusters is fixed. To improve the predictions and avoid numerous false positives (Supplementary Figure S1B), instead of having only one threshold separating the low and high variance region, we introduce a buffer zone (σ₋ < σ_norm < σ₊) where additional tests are performed (Supplementary Figure S1A). In this zone, a local directionality index (2) is computed around the putative boundary

(4)

with A (resp. B) the number of reads that map from a given bin to the upstream (resp. downstream) part of the tested region (Supplementary Figure S1A). The boundary will remain fix (i) if at least 2/3 of the DIs before (resp. after) it are negative (resp. positive), (ii) if the variation of DI is positive when crossing the boundary and (iii) if for at least 2/3 of the bins, the relative variation 2(A − B)/(A + B) is superior to 0.1. Condition (iii) was included to increase algorithm robustness regarding data noise. We optimize the value of σ₋ and σ₊ on manually annotated segmentations of small pieces of experimental Hi-C maps (chromosome 3R of drosophila late embryos at 10kbp-resolution (10); chromosome 12 of human IMR90 cell line at 40 kb-resolution (2) and 50 Mb of chromosome 3 of human GM12878 cell line at 10kbp-resolution (3)) (Supplementary Figure S3 and Supplementary data), to achieve the best correspondence between IC-Finder predictions and the annotated ICs. Hi-C data used for parameter inference and for testing IC-Finder were downloaded from the Gene Expression Omnibus website (17) with the accession numbers GSE34453 for (10), GSE35156 for (2) and GSE63525 for (3). Note that the inferred default values for σ₋ and σ₊ can be tuned by the user to eventually improve the segmentation on specific genomic regions.

IC-Finder options

Prediction robustness

Numbers of observed contacts in Hi-C experiments are often small (ranging from 0 to few thousands for a 10-kb binning) and therefore they are strongly subject to statistical errors. To estimate how this uncertainty on the measurements propagates on the predicted segmentation, IC-Finder performs many resampling of the original Hi-C map and run the clustering algorithm on these new maps (Figure 1B). Combining these results for many resampled maps (100 by default), we compute the probability p_d(i, j) for two loci to belong to the same interaction compartment and the probability p_b(i) for a locus to be at a boundary between two domains.

To resample an experimental map, we first multiply the original input Hi-C matrix C(i, j) map by a constant factor f = N_c/∑_iC(i, i + 1) with N_c the total number of counts on the first diagonal in the raw data for the same genomic region (i.e. before any normalization process that might have reshaped the Hi-C data). If unknown, by default, we assume N_c = 904 that represents the typical number obtained in recent Hi-C experiments at a 10-kb binning (3,10). This step is crucial to renormalize the data in terms of real counts. Then, we model the contact frequencies of this modified matrix as independent Poisson processes and for each pair (i, j) of loci, we randomly generate a new contact frequency from a Poisson distribution of average f C(i, j).

Hierarchical organization

Investigation of the hierarchical organization is performed by imposing σ₋ = σ₊ ≡ σ_o and by running the constrained hierarchical algorithm described above for incremental σ_o-values (by default σ_o = 5) (Figure 1C).

Generation of the benchmark of simulated Hi-C maps

To optimize and test the algorithm, we designed a set of simulated Hi-C-like maps whose optimal—irreducible—segmentation is known. Recently, we developed a polymer model that is able to semi-quantitatively describe the formation and dynamics of TADs observed in Hi-C maps based solely on the epigenomic information (18–20). Using a version of this model, we compute the average contact probability between any pairs of genomic loci for 100 randomly generated epigenomic landscapes. We take care to choose interacting parameters to reproduce the typical behavior observed in experimental Hi-C maps (formation of TADs, long-range interactions between TADs, average contact probability scaling as s⁻¹ with s the genomic distance between two loci). Our simulated maps were also resampled using a Poisson-distribution to simulate local intensity variations also observed in real maps (see Supplementary Figure S4). The benchmark data are available in Supplementary Data.

Statistical comparison between two partitions

Given two partitions P_p and P_t of the same ensemble, the domain true positive rate TPR_d, or sensitivity, of P_p against P_t is defined as the probability that two loci belong to the same domain in P_p, knowing they are clustered in P_t:

(5)

where δ_{i, j} = 1 (0) if i, j belong (or not) to the same cluster in P_p, and the same for η_{i, j} but regarding P_t. If known from the resampling option, δ and η could be replaced by probabilities of being in the same compartments. The domain false discovery rate FDR_d of P_p against P_t is defined as the probability that two loci do not belong to the same domain in P_t, knowing they are clustered in P_p

(6)

Identically, we define the boundary true positive rate TPR_b as the probability that a locus is a boundary in P_p (±1 bin) knowing it is a boundary in P_t (idem for the boundary false discovery rate FDR_b).

Epigenomic colocalization score

For a given locus i, we define 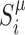the proportion of epigenomic state μ at the corresponding locus (). For a pair of epigenomic state (μ, ν), the epigenomic colocalization score C_{μ, ν} is defined as

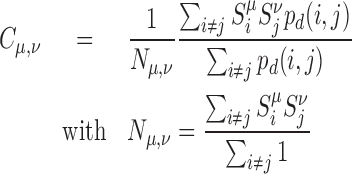(7)

with p_d(i, j) the probability that i and j are predicted to belong to the same IC. Eq. 7 represents the average value of 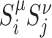for colocalized loci normalized by the corresponding value along the genome (N_{μ, ν}). C_{μ, ν} ≥ 1 (resp. ≤1) indicates that association of loci having the μ and the ν epigenomic states are enriched (resp. depleted) in IC.

RESULTS

A robust algorithm to partition Hi-C maps

Description of the method

IC-Finder is a program that allows to segment Hi-C maps into interaction compartments (IC) (Figure 1A, see Material and Methods for details on the algorithm). Given a matrix of interaction frequencies extracted from a Hi-C experiment, IC-Finder infers the boundaries between consecutive IC along the genome. The algorithm is based on three statements: (i) the 3D chromatin organization is hierarchical; (ii) genomic loci belonging to the same IC should have similar patterns of interactions with the rest of the genome; and (iii) due to the intrinsic polymeric nature of chromatin, intra-IC interactions should be homogeneous in a polymer sense, meaning the contact frequency between two intra-IC loci should depend only on the genomic distance between them. Following statements (i) and (ii), we base IC-Finder on a constrained agglomerative hierarchical clustering-like algorithm: starting with each locus in its own cluster, the algorithm iteratively merges together pairs of clusters that, at the current step, have the most correlated patterns of interaction. To avoid the formation of non-consecutive domains, we constrain the next candidates to be nearest-neighbor along the linear genome. Statement (iii) suggests that the heterogeneity of interactions inside a cluster (σ_norm) should be a good variable to guide our choice of an optimal partition of the constructed hierarchical tree. Practically, this choice is performed ‘on the fly’ during the algorithm by computing, at each step, σ_norm inside the putative cluster formed by the two candidates: for weak σ_norm, the two clusters are indeed merged together; for strong σ_norm, the clusters are not merged together and the boundary between them is maintained along the rest of the algorithm; for intermediate σ_norm values, additional tests based on the directionality index are performed to avoid false positive decisions and to insure a good compartmentalization (Supplementary Figure S1). Threshold values that define this buffer zone have been learned from various manually-annotated experimental Hi-C maps (Supplementary Figure S3) to optimally improve the predictions of IC-Finder. While with the default threshold values IC-Finder gives excellent results for all sort of Hi-C maps (see below), IC-Finder offers the option to manually tune these parameters to eventually optimize the segmentation based on a user-defined criterion.

A Matlab/GNU Octave routine for IC-Finder is available at http://membres-timc.imag.fr/Daniel.Jost/DJ-TIMC/Software.html and in the Supplemental Data.

Test of reliability and comparison with other methods

We test the reliability of IC-Finder on a controlled benchmark of 100 simulated Hi-C maps that we designed to have the same properties of real Hi-C maps and for which we know the target segmentations (Supplementary Figure S4, see Materials and Methods). Note that this benchmark was not used to calibrate the default parameters of the algorithm. For each map, we compute the domain and boundary true positive rate (TPR) and false discovery rate (FDR) of our prediction compared to the target segmentation. A perfect match between the two would lead to TPR = 1 and FDR = 0. In Figure 2A and B, we plot contour lines that encompass 98% of the 100 (TPR,FDR)-points, showing that our algorithm with default parameters performs extremely well with high sensitivity and low false discovery rate. Moreover, IC-Finder almost perfectly predicts the distribution of domain size (Figure 2C).

Figure 2.

(A) Probability that two loci are correctly predicted to belong to the same domain (TPR_d) as a function of the probability that two loci are wrongly predicted to belong to the same domain (FDR_d) estimated on the benchmark for seven programs (see color legend). For each program, we plot the contour line encompassing 98% of the 100 tested maps. (B) Same as in (A) but for boundary predictions (TPR_b versus FDR_b). (C) Distribution of domain size predicted by the different methods. The black line is the distribution of the target segmentations. (D) CPU time needed to segment a Hi-C map of size N × N on a standard laptop for the seven programs. (E) Examples of target and predicted segmentation by each investigated program.

Next, we compare the performance of IC-Finder with other existing programs that also segment Hi-C data into TADs (Armatus (15), Directionality Index (DI) (2), HICSeg (16), Insulation method (13), TADtree (9) and TopDom (14)) over our designed benchmark. For each method (except IC-Finder and Armatus), we manually tune the—sometime various—parameters to optimize the segmentation (see Supplementary Figure S5). We observe that IC-Finder and TopDom give similar results and outperform the other methods in term of reliability (Figure 2A, B, C and E). In terms of numerical efficiency, IC-Finder is faster that any other methods for large maps (Figure 2D) with often orders-of-magnitude differences. For example, on a 3GHz computer, it takes 4 min to segment the whole human genome (at a 40 kb resolution) with IC-Finder, while it takes 6 min with TopDom and >3 h with DI.

As a second comparative test, we run IC-Finder on the same—experimental Hi-C—examples used by the other methods to illustrate their predictive power in their respective publication (Mouse ES cells and human IMR90 cell line from (2)). Locally, all the methods show significant inconsistency between them (Figure 3A and Supplementary Figure S7). IC-Finder is closer to TopDom with a better correspondence at the domain scale than at the boundary scale. This is a consequence of the important noise present in the studied maps (see below) that leads to a fuzzier definition of boundaries (on less noisy data like the benchmark dataset, both methods have a very good correspondence). At the global scale, IC-Finder and TopDom give also similar results with comparable domain size distributions (Supplementary Figure S6B and D), while Armatus has the tendency to find lots of small domains and the Directionality Index to segment maps into bigger domains (see examples on Supplementary Figure S6A and C).

Figure 3.

(A) Domain (left) and boundary (right) TPR and FDR between the segmentations given by IC-Finder (taken as the reference) and the segmentations obtained by three other methods for Hi-C data from Mouse ES cells and Human IMR90 cell line (data from (2)). (B) For each method, domain (left) and boundary (right) TPR and FDR between the predicted segmentations of two biological replicates. Each symbol of the same color represents the TPR/FDR obtained in a given drosophila cell line (S2, KC, BG3 or OSC, data from (6)).

As a final test, we evaluate the consistency of the predicted TADs on biological Hi-C replicates. We use data from Ulianov et al. (6) where two replicates have been produced for each of four different drosophila cell lines (S2, KC, BG3 and OSC). For a given method (IC-Finder, TopDom, Armatus or DI), in each cell line, we compare the predictions obtained for the two replicates by computing the TPR/FDR between the two segmentations (Figure 3B). We find that IC-Finder, TopDom and Armatus give strongly consistent predictions with high TPR and low FDR in all the cell lines (see examples on Supplementary Figure S8A). The directionality index leads to more replicate-dependent partitions, suggesting that DI is more sensitive to noise than the other methods. Predicted domain sizes distributions are also very similar between the two replicates for all investigated methods except for DI (see examples on Supplementary Figure S8B). Interestingly, the comparison between cell lines shows that TAD positions are very conserved among different cell types in drosophila (Supplementary Figure S9) (6), confirming observations in mammals that TADs are elementary functional units of organization that may played key roles in regulating gene expression (2,3,5,12).

IC-Finder option 1: improving the prediction reliability

Hi-C experiments may integrate many sources of errors that may affect the resulting Hi-C maps. Among them, sampling errors due to the finite number of cells used in the experiments combined to the weak efficacy of the whole Hi-C protocol are likely to represent an important source of noise in the map, especially for bins with low number of contacts. This rises the question of the robustness of the predicted segmentation regarding such uncertainties. IC-Finder offers the option to quantify the reliability of its prediction by performing a statistical resampling of the input Hi-C map (see Materials and Methods). In particular, it estimates the probability that two loci are predicted to belong to the same topological domain and the probability for a locus to be predicted as a boundary between two domains (Figure 1B). While computationally more time-demanding, this option gives a much more clear and reliable picture of the compartmentalization of a map and allows to quantify how precise are the predictions given by IC-Finder. For example, while the interaction compartment (a) in Figure 1C is well defined, the position of its left boundary is fuzzy. This is of course crucial when comparing chromatin folding observables like the position of the IC boundaries or the colocalization of loci in the same IC with other epigenomic or genomic information that are position-dependent.

IC-Finder option 2: inferring the hierarchical organization of chromatin

In addition to the elementary partition of chromosome into topologically-associating domains (2,3), Hi-C experiments have clearly revealed the existence of higher-order organization levels highlighting the hierarchical 3D folding of chromatin: consecutive TADs may be organized into larger interaction compartments that themselves may form larger clusters (7–9). By varying the threshold separating the regions of lowly and highly heterogeneous clusters used to define boundaries between adjacent ICs during the clustering algorithm (see above), IC-Finder offers the option to access such higher layers of organization. Figure 1C illustrates the hierarchical segmentation inferred by IC-Finder for the region 12–14.5 Mb of fly chromosome 3R in late embryos (10). Of course, options 1 and 2 could be coupled in order to get a full reliable picture of the hierarchy of chromatin folding (Supplementary Figure S10).

Applications of IC-Finder

Impact of Hi-C map normalization scheme

In addition to sampling errors, Hi-C protocols may give rise to many systematic biases, including the distance between restriction enzyme cut sites or the GC content of reads, that may strongly affect the measured contact frequency (21). Along the years, several strategies have emerged to remove these systematic biases and normalize the data (21–26). Among them, we can distinguish two families: (i) parametric approaches that explicitly model these biases (21,22); and (ii) renormalization approaches that assume that every fragment should be observed the same number of times (23–26). Applications of these schemes to raw Hi-C data may lead to quantitative differences in the contact maps (Figure 4C).

Figure 4.

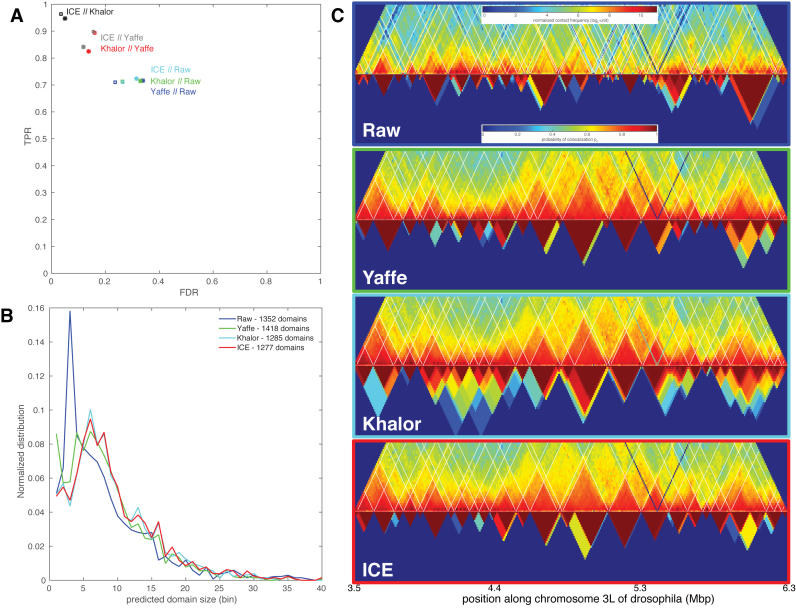
(A) Domain (squares) or boundary (stars) true positive rate as a function of the false discovery rate between segmentations obtained from two different Hi-C normalization scheme. (B) Distribution of domain size predicted by IC-Finder for the different schemes. The total number of domains is given in the legend. (C) Examples of predicted segmentations for a genomic region of chromosome 3L of drosophila (10). Top: Hi-C map and boundaries predicted by default. Bottom: probability p_d for two loci to be predicted as belonging to the same topological domain (IC-Finder option 1).

In this section, we ask how the normalization process affects the detection of TADs or ICs and if the different schemes lead to consistent results. We test three normalizations that we applied to drosophila Hi-C experiments (10) (Yaffe from (21), Khalor from (23) and ICE from (25)) and compare them to segmentations obtained for raw data. Statistical analysis of the obtained segmentations shows that ∼70% of the boundaries found in the raw data are conserved after normalization and conversely about 30% of the predicted frontiers from normalized maps are not present in the raw data (Figure 4A). Systematic biases observed in raw Hi-C maps lead to more irregular interaction patterns along the diagonal (Figure 4C) which propagate into the compartment detection that predicts lots of small domains (Figure 4B). Normalization schemes regularize the maps leading to larger domains. Within a normalization family, segmentation results are highly consistent (see ICE || Khalor in Figure 4A) with similar numbers and sizes of domains (Figure 4B). Between families, results are also generally consistent, even if we observe small discrepancies (Figure 4A), due mainly to the prediction of more small domains with the Yaffe method (Figure 4B).

Correlation with epigenomic information

In this section, we study how epigenomic information might be associated to 3D compartmentalization. In particular, we ask if interaction domains are homogeneous in terms of epigenomic content and if domain boundaries are enriched in specific epigenomic states. We address these questions for drosophila late embryos and human GM12878 cell line. For these strains, we take Hi-C maps for every chromosome respectively from Sexton et al. (10) and Rao et al. (3). We then run IC-Finder on these contact maps with the resampling option using the default parameters, i.e. inferring the elementary segmentation into TADs, and using option 2 (σ_o = 5), i.e. accessing a higher degree of hierarchy (Supplementary Figure S10). Recently, from Chip-Seq data of various histone marks obtained in human, drosophila and worm, Ho et al. showed that the local epigenomic information could be characterized by 16 different epigenomic states and their local repartition along the genome could be inferred using HMM methods (11). These states correspond to enhancers, active genes, polycomb-repressed regions, constitutive heterochromatin or null—low signal—chromatin (see legend in Figure 5A and D). We collect these epigenomic patterns for our two species of interest (at https://www.encodeproject.org/comparative/chromatin/) and statistically compare them to the 3D segmentation. Note that centromeric and pericentromeric regions, mainly composed by constitutive and null heterochromatin, were not considered in our analysis.

Figure 5.

(A, D) Epigenomic colocalization score C_{μ, ν} of the 16 epigenomic states for fly (A) and human (D). (B, E) Epigenomic colocalization score computed for the 6 or 4 epigenomic families at the TAD level (left, default parameter in IC-Finder) or at a higher hierarchy (right, σ_o = 5). (C, F) Cumulative distribution functions of the relative distance to the nearest TAD boundary for every family. Color code as in panels B and E. The black curves represent the average behavior.

To investigate if 3D compartments present a uniform epigenomic content, we ask if two different genomic regions in the same compartment have the same—or different—epigenomic states. Practically, for every pair of epigenomic states (μ, ν), we estimate C_{μ, ν}, the so-called epigenomic colocalization score, that quantify if a locus of epigenomic state μ (chosen among the 16 possible states) tends to be significantly more (C_{μ, ν} > 1) or less (C_{μ, ν} < 1) colocalized with other loci of state ν than expected (see Materials and Methods for the mathematical definition of C_{μ, ν}). Figure 5A and D shows the C_{μ, ν} matrices obtained for the 16 epigenomic states with the default parameters, i.e. at the TAD level. We observe that the diagonal elements of the matrices (C_{μ, μ}) are all higher than 1 implying that neighbor genomic regions with the same epigenomic state tend to share the same TAD. Standard agglomerative hierarchical clustering (correlation distance, mean linkage) of the C_{μ, ν} matrices shows that groups of states are strongly colocalized and interactions between these groups are depleted in TADs (Figure 5B and E, left). This strongly suggests that the internal epigenomic composition of TAD is relatively homogeneous in such groups. In flies, we find six families: an active cluster grouping promoter and transcription states, an enhancer cluster, an active intron-rich cluster (Transcription 5’ 2 and Gene, H4K20me1 states), a Polycomb-repressed cluster, a null—low-signal—cluster and a heterochromatin cluster. In human, only four families are emerging: an active cluster, an enhancer cluster, a Polycomb-repressed cluster and a heterochromatin/low signal cluster. These families are highly similar between the two species, while some exceptions are present highlighting specificities in the epigenomic regulation in each species. For example, the presence of H4K20me1 in introns of long active genes in drosophila while it is associated with polycomb-repressed genes in human (11). Interestingly, we observe that the epigenomic colocalization score between active and repressed families is lower in fly than in human, suggesting that insulation of active and repressed families is stronger in fly and that the fly 3D organization is slightly more correlated to epigenomic information.

To investigate if domain boundaries are enriched in specific epigenomic states, for each genomic locus of a given epigenomic family found previously, we compute the relative distance to the nearest TAD boundary: a distance of 0 (resp. 0.5) means that the locus is at the boundary (resp. in the middle) of an IC. Figure 5C and F (left) shows the cumulative distribution functions (CDF) of these distances for every family. If the CDF of a given epigenomic family is below (resp. above) the black dashed curve closed to the boundary (distance 0), it means that this family is less (resp. more) found at domain boundaries than expected (Supplementary Figure S11). In general, we observe that active families are enriched at the boundaries of domains while inactive families are more enriched in the core of the TADs. With the notable exception that in flies the heterochromatin family is enriched at the boundaries illustrating the scattering of constitutive heterochromatin into small domains (Supplementary Figure S12) in this organism (except at the centromeres and for pericentromeric regions that were not considered in our study) (10). As previously, the correlation between epigenomics and TAD localization (enrichment or depletion at the boundaries) is more pronounced in drosophila.

To investigate if higher degrees of organization are also correlated to epigenomics, we compute the epigenomic colocalization score and the distribution of relative distance for the six or four families found at the TAD level but at a higher hierarchy (Figure 5B and E, right and Supplementary Figure S10B and D). In fly, we observe a strong loss of colocalization for active families while facultative (polycomb-repressed) and constitutive heterochromatin are still self-enriched in IC. Strikingly, except the Heterochromatin family that remains isolated in small ICs, other families are now poorly insulated from each other by interaction compartments (C_{μ, ν} ≈ 1), suggesting that at this degree of organization, small active TADs have merged with larger inactive TADs into big compartments that are less epigenomically defined (Supplementary Figure S10B). Boundaries of such ICs are still enriched in active genes but less than at the TAD level, suggesting a weak loss of association between active genes and boundaries at this upper level of hierarchy. In human, at this level of hierarchy, families remain partly self-colocalized and insulated, while boundaries are only weakly enriched in active families. Interestingly, while the epigenomic colocalization score slightly decreases for inactive families, it weakly increases for active families. This suggests that at this hierarchy, IC compartments are better associated with active chromatin (Supplementary Figure S10D).

DISCUSSION AND CONCLUSION

In this article, we have presented a new method, IC-Finder, that allows to extract from Hi-C contact maps, a 3D segmentation of the genome into interaction compartments. Numerous recent experimental evidences have enlightened the functional role of these ICs that may constitute insulated neighborhoods and may help maintaining a proper gene expression pattern, by either promoting or repressing long-range contacts between enhancers or silencers and promoters (27,28). A prerequisite to better understand the mechanisms behind the formation and control of ICs is therefore to properly identify them. Consequently, several methods have already been developed in the past years (3,9,14–16).

A main originality—and strength—of IC-Finder is that it has been designed under the assumption that Hi-C maps reflect the underlying polymeric nature of chromatin (29). This was motivated by our recent work on chromatin folding where we showed that experimental data in fly are compatible with a block copolymer model when mapping blocks with the epigenomic information (18–20). This led us to propose a hierarchical clustering approach whose stopping criterion accounts for such polymeric properties. The method depends on only two contrast parameters whose default values have been assigned by a learning approach on a restricted experimental set. Importantly, we were able to test the reliability and the performance of IC-Finder on a benchmark of in silico Hi-C maps that we built by simulating contact frequency of block copolymers with different epigenomic segmentations. As compared to other works, this confers the advantage of testing and comparing methods on realistic maps with known segmentations. Particularly, we showed that IC-finder (with the default—untuned—parameters) not only outperforms all the other published methods (except TopDom (14)) in identifying the ICs but is numerically more efficient especially for large maps and offers unique integrated options to investigate the hierarchical chromatin folding and to accounts for experimental uncertainties.

Indeed, since experimental maps are inherently noisy, in particular due to finite sampling errors, inferred ICs and their boundaries should be preferentially defined in a statistical sense. We addressed this issue by proposing a resampling method that improves the reliability of our inference scheme. IC-finder is the first segmentation method that allows to estimate the robustness of its prediction regarding the experimental errors. We believe this option should be generalized to other works on IC segmentation to provide a more robust and fair - probabilistic rather than deterministic - description of ICs and their boundaries.

It is already clear from a visual inspection of Hi-C maps that there is not a uniquely-defined segmentation but rather a full hierarchy of organization into ICs: several consecutive small ICs may be clustered to form larger ICs. Interestingly, such hierarchy is a hallmark of the folding properties of a block copolymer as illustrated by the in silico contact maps (Supplementary Figure S4): due to the specific attractions that promote internal folding, epigenomic blocks constitute the first—irreducible- layer of organization; however, the existence of specific long-range interaction between ICs may induce the formation of complex—higher order—patterns. A consequence of this hierarchy is that there exist many possible—ordered—choices of segmentations for the same map. By default, IC-Finder identifies one level of the hierarchy that, we expect, corresponds to the finest-grained segmentation given the experimental noise. However, it offers the option to investigate the higher degrees of organization by tuning the contrast parameters that control the merging of consecutive putative ICs into the algorithm. In this way, it is similar to TADtree (9) or Armatus (15) which also allow to uncover the hierarchical properties of chromatin folding.

As an application of IC-Finder, we compared the segmentations of Hi-C maps obtained before and after different normalization procedures (21,23,25). We found that almost 30% of ICs are not conserved between raw data and any normalization scheme and we revealed a slight but significant discrepancy between the different normalization approaches. This confirms that normalization is a key issue when analyzing Hi-C maps and that any segmentation should be conditioned to the used normalization.

We finally asked whether the segmentation obtained in fly and human cells is related or not to the segmentation into chromatin states obtained recently by a HMM approach (11). Despite some species specificity, our results clearly demonstrate that ICs in fly and in human are preferentially associated with specific groups of epigenomic states among which the enhancer, the active, the PcG and the heterochromatin epigenomic family. This further confirms the view that the hierarchical folding of the genome results partly from the specific ‘like-like’ clustering of chromatin states and can thus be well described by a block copolymer framework (18,19,30). However, recent studies in human (3) have revealed that IC might also result from the active process of loop extrusion that produces different patterns of interactions as the one expected by a copolymer model (28,31). Improvement of the IC-Finder approach would thus require to also account for this active folding mechanism. More generally, it is likely that the progresses in experimental Hi-C techniques would reveal higher-complexities at smaller scales in the organization of the—putatively assumed—irreducible ICs. This will prompt us to renew our parameter learning process and as mentioned just before probably complement our strategy of segmentation based on a refined theoretical chromatin folding prior.

In conclusion, IC-Finder, based on mechanistic—polymeric—folding principles, is the first IC calling method to allow within the same, user-friendly, publicly-available and numerically-efficient software, to infer robustly the elementary segmentation of a Hi-C map without the need of parameter tuning, to investigate the different degrees of chromatin organization, and to estimate the prediction robustness regarding experimental errors. It represents a valuable ‘all-in-one’ tool to investigate the relation between the spatial organization of the genome and its link to epigenome and gene regulation. In particular, it might be used to build predictive models relating epigenomic information and 3D features like IC boundaries or long-range contacts (32–34).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Agence Nationale de la Recherche [ANR-15-CE12-0006 EpiDevoMath]; Fondation pour le Recherche Médicale [DEI20151234396]; Institut Rhône-Alpin des Systèmes Complexes and program AGIR of University Grenoble Alpes. Funding for open access charge: FRM.

Conflict of interest statement. None declared.