Comparative analyses of the thermodynamic RNA binding signatures of different types of RNA recognition motifs

Abstract

RNA recognition motifs (RRMs) are structurally versatile domains important in regulation of alternative splicing. Structural mechanisms of sequence-specific recognition of single-stranded RNAs (ssRNAs) by RRMs are well understood. The thermodynamic strategies are however unclear. Therefore, we utilized microcalorimetry and semi-empirical analyses to comparatively analyze the cognate ssRNA binding thermodynamics of four different RRM domains, each with a different RNA binding mode. The different binding modes are: canonical binding to the β-sheet surface; canonical binding with involvement of N- and C-termini; binding to conserved loops; and binding to an α-helix. Our results identify enthalpy as the sole and general force driving association at physiological temperatures. Also, networks of weak interactions are a general feature regulating stability of the different RRM–ssRNA complexes. In agreement, non-polyelectrolyte effects contributed between ∼75 and 90% of the overall free energy of binding in the considered complexes. The various RNA binding modes also displayed enormous heat capacity differences, that upon dissection revealed large differential changes in hydration, conformations and dynamics upon binding RNA. Altogether, different modes employed by RRMs to bind cognate ssRNAs utilize various thermodynamics strategies during the association process.

INTRODUCTION

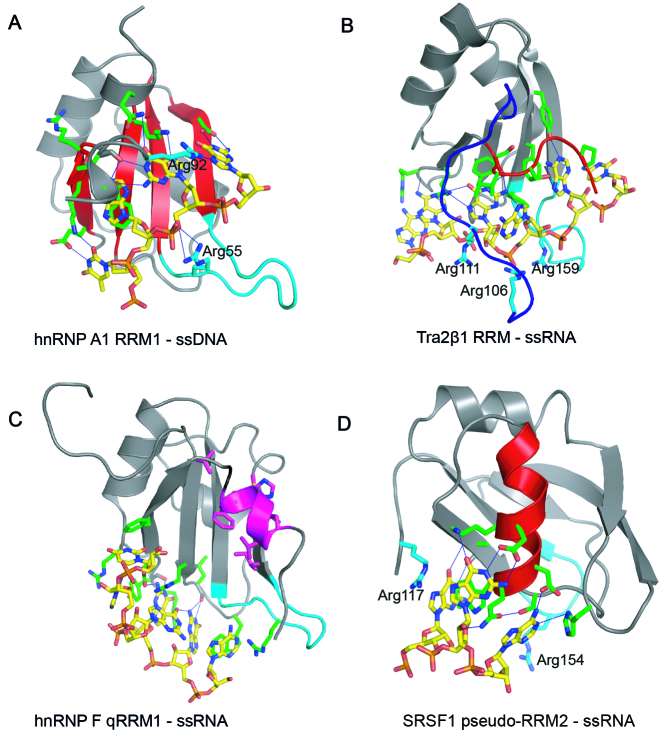
The RNA recognition motif (RRM) is the most abundant domain regulating alternative splicing, albeit by unclear thermodynamic strategies. It is present in all life kingdoms, and is conserved from yeasts to humans (1–3). RRMs are characterized by two conserved consensus sequences consisting of mostly aromatic and aliphatic residues, termed RNP1 ([RK]-G-[FY]-GA-[FY]-[ILV]-X-[FY]) and RNP2 ([ILV]-[FY]-[ILV]-X-N-L), where X can be any amino acid residue (4). The core RRM structure consists of two α-helices packed against four β-strands. RNP1 and RNP2 are located on β3 and β1 strands, respectively. In the canonical RNA binding mode, the conserved aromatic residues in RNP1 and RNP2 provide general binding affinity, with specificity mediated by additional side-chains (4). The canonical RNA binding mode is represented by hnRNP A1 RRM1 (Figure 1A and Table 1). Residues positioned on the β-sheet surface specifically recognize cognate 5΄ TAGG 3΄ deoxyribonucleotides (5). 5΄ UAGG 3΄ ribonucleotides are similarly recognized. Tra2β1 RRM specifically binds 5΄ GAA 3΄ nucleotides by residues positioned on both the β-sheet surface, as well as the N- and C-terminal segments (Figure 1B and Table 1) (6). Tra2β1 RRM–ssRNA complex formation thus proceeds with significant reduction in flexibility of the protein extremities. RRMs are however much more structurally versatile, and can bind ssRNA using completely different types of surfaces when the RNP1 and RNP2 sequences are poorly conserved. This is exemplified by hnRNP F qRRM1 and SRSF1 pseudo-RRM2 (Figure 1C and D, (7,8)). hnRNP F qRRM1 is a quasi-RRM, characterized by highly conserved R-G-L-P-(W/F/Y) and (R/K)-(X5)-R-Y-(V/I/L)-E-(V/I/L)-F consensus sequences in loop 1 and loop 5 respectively, as well as an additional positively charged residue in loop 3 (7). Consequently, hnRNP F qRRM1 utilizes residues located on the surface-exposed loops to specifically bind a tract of three consecutive guanines (5΄ GGG 3΄; Figure 1C) (9). SRSF1 pseudo-RRM2 belongs to pseudo-RRMs and is characterized by the S₁₃₃WQDLKD₁₃₉ conserved motif located on α-helix 1 (α1). SRSF1 pseudo-RRM2 specifically recognizes 5΄ GGA 3΄ nucleotides using the conserved residues on α1 (Figure 1D and Table 1) (8). Remarkably, the sequence-specificity of the different RNA binding modes mentioned is quite similar as it involves 3 to 4 nt containing at least three purine bases (Table 1). In contrast to the detailed information on the structural mechanisms of different ssRNA binding modes of RRMs, the accompanying thermodynamics are however poorly understood.

Figure 1.

RRM–ssRNA/ssDNA complexes showing different binding modes. Cartoon representations illustrating the binding of: (A) 5΄–TAGG–3΄ ssDNA to the β-sheet surface (colored red) of hnRNP A1 RRM1 (PDB ID: 2UP1); recognition of –UAGG—RNA sequence is the same. (B) 5΄–AAGAAC–3΄ RNA to the β-sheet surface of Tra2β1 RRM with the involvement of the N- (blue) and C-terminal segments (red) (PDB ID: 2KXN). (C) 5΄–AGGGAU–3΄ RNA to the loop region of hnRNP F qRRM1 (PDB ID: 2KFY); the AGG*G*AU RNA sequence modified by 7-deazaguanine is recognized in the same manner. Residues participating in the hydrophobic core are highlighted in magenta (D) 5΄–AAGGAC–3΄ RNA to α-helix-1 (colored red) of SRSF1 RRM2 (PDB ID: 2M8D). All pictures were created in PYMOL. The proteins and the ssRNA/ssDNA oligonucleotides are colored in gray and yellow respectively. Amino acid side chain contacting the RNA are shown as sticks and colored green. Hydrogen bonds are shown as blue discontinuous lines. Arginine residues involved in ionic bonds are shown as sticks and labeled. The β2/β3 loop region is colored in cyan.

Table 1. Summary of structural features and binding thermodynamics.

	hnRNP A1 RRM1	SRSF1 pseudo-RRM2	hnRNP F qRRM1	Tra2β1 RRM	ΔNTra2β1
5΄ RNA 3΄ §	UUAGGU	AAGGAC	AGG*G*AU	AAGAAC	AAGAAC
Binding mode	Canonical (β-sheet)	Pseudo-RRM (α-helix 1)	quasi-RRM (Loops)	Canonical + N and C-termini	Canonical + C-terminus
Intermolecular hydrogen bonds	5	5	5	6	5
Hydrophobic interactions	3	2	3	3	3
Mean ΔGobs (kcal mol−1)	−8.0 ± 0.5	−9.9 ± 0.3	−8.7 ± 0.2	−8.8 ± 0.3	−8.4 ± 0.2
ΔGPE/(%)	28	26	10	23	ND
ΔGnPE/(%)	72	74	90	77	ND
ΔCp,obs/cal K−1 mol−1	−130 ± 27	−338 ± 17	−40 ± 30	−300 ± 23	−166 ± 40
ΔCpf,ASA/cal K−1 mol−1	−96	−90	−164	−348	−263
ΔCpb,ASA/cal K−1 mol−1	−84	−10	−29	−131	−115

^§RNA sequence used in study. Nucleotides specifically recognized by the RRMs are highlighted in bold. *7-deazaguanine. ND: not determined. ΔG_obs was determined by ITC in 20 mM CH₃COOH, 50 mM L-arginine, 50 mM L-glutamate, 0.05% β-mercaptoethanol–NaOH pH 5.5 at different temperatures (see also Table 2). The mean ΔG_obs was obtained by averaging ΔG_obs across the considered temperature range. ΔG_PE and ΔG_nPE are the percentage contributions of the polyelectrolyte effect (ion-release) and non-polyelectrolyte effect to the overall free energy of binding at 1M Na⁺ concentration, respectively. To determine ΔG_PE and ΔG_nPE, ITC titrations were performed at 283.15 K temperature in 20 mM CH₃COOH, 50 mM L-arginine, 50 mM L-glutamate, 0.05% β-mercaptoethanol–NaOH pH 5.5 and different concentrations of NaCl salt (see Figure 5A). ΔC_p,obs is the observed experimental heat capacity. ΔC_p^b_,ASA and ΔC_p^f_,ASA are the expected heat capacities semi-empirically calculated using the bound or free conformations of the binding components, respectively.

In spite of the vastly different RNA binding modes, each of the complexes of hnRNP A1 RRM1, Tra2β1 RRM, hnRNP F qRRM1 or SRSF1 pseudo-RRM2 bound to cognate ssRNAs contain 5 to 6 intermolecular hydrogen bonds (Table 1 and Figure 1). Intermolecular hydrogen bonds and stacking interactions are key regulators of the stability of protein–RNA complexes (4,9–11). All complexes except SRSF1 pseudo-RRM2–ssRNA have three main hydrophobic interactions involving: Trp 20, Tyr 82 and Phe 84 in hnRNP F qRRM1 (9), Phe 123, Phe 161 and Phe 163 in Tra2β1 RRM (6) and Phe 17, Phe 57 and Phe 59 in hnRNP A1 RRM1 (5). In SRSF1 pseudo-RRM2–ssRNA complex, Trp 134 and His 183 contact RNA bases (8). The rather similar set of non-covalent forces stabilizing the different interfaces raise important thermodynamic questions regarding: the relative binding strengths to cognate RNAs under the same conditions; the effect of temperature on the thermodynamic binding parameters characterizing the binding modes; the thermodynamic contributions of hydration, conformational changes and dynamics; and considering that several RRMs such as Tra2β1 RRM possess positively charged patches thought to contribute significantly in RNA binding (10), it is also important to understand how different binding modes employ electrostatic force from release of ions condensed on the RNA backbone to enhance complex stability. To address these questions, we performed microcalorimetric and semi-empirical analyses on the association of hnRNP A1 RRM1, Tra2β1 RRM, SRSF1 pseudo-RRM2 and hnRNP F qRRM1 with cognate ssRNAs. Our results reveal the various thermodynamics strategies employed by the different binding modes to bind to their cognate RNA.

MATERIALS AND METHODS

Buffer

All the experiments were carried out in 20 mM CH₃COOH, 50 mM L-arginine, 50 mM L-glutamate–NaOH pH 5.5 buffer containing 0.05% β-mercaptoethanol. The inclusion of arginine and glutamate was necessary to increase the stability and solubility of the free proteins. They, however, do not interfere with the association process (12).

Protein constructs, expression and purification

qRRM1 of hnRNP F (aa 1–102), hnRNP A1 RRM1 (aa 2–97), RRM of hTra2β1 (aa 106–201) and RRM2 of SRSF1 (aa 107–203) containing N-terminal hexa-histidine tags (and an additional GB1 solubility tag in SRSF1 RRM2) were expressed in Escherichia coli BL21 (DE3) codon plus strains at 37°C in Luria-Bertani media as previously described (6,9,13). The proteins were purified by Nickel affinity chromatography.

Oligonucleotides

5΄-AAGGAC-3΄, 5΄-AAGAAC-3΄ and 5΄-UUAGGU-3΄ PAGE-purified RNAs were purchased from Dharmacon (USA) in lyophilized form. The oligomers were deprotected and lyophilized according to manufacturer's instructions. Modified 5΄-AGG*G*AU-3΄ RNA, where G* is 7-deazaguanine, was purchased from Metabion (Germany). The RNA was purified by reverse phase HPLC, and the mass was verified by MALDI mass spectrometry. 7-deazaguanine prevents G-quadruplex formation without affecting protein/RNA complex formation (14). RNA concentrations were determined by UV-absorption spectroscopy on heat-denatured RNAs. To prepare the RNA for isothermal titration calorimetry (ITC) measurements, lyophilized RNAs were resuspended in the dialysis buffer of protein, incubated at ∼85°C temperature for ∼2 min and cooled at room temperature for at least 30 min.

Isothermal titration calorimetry (ITC)

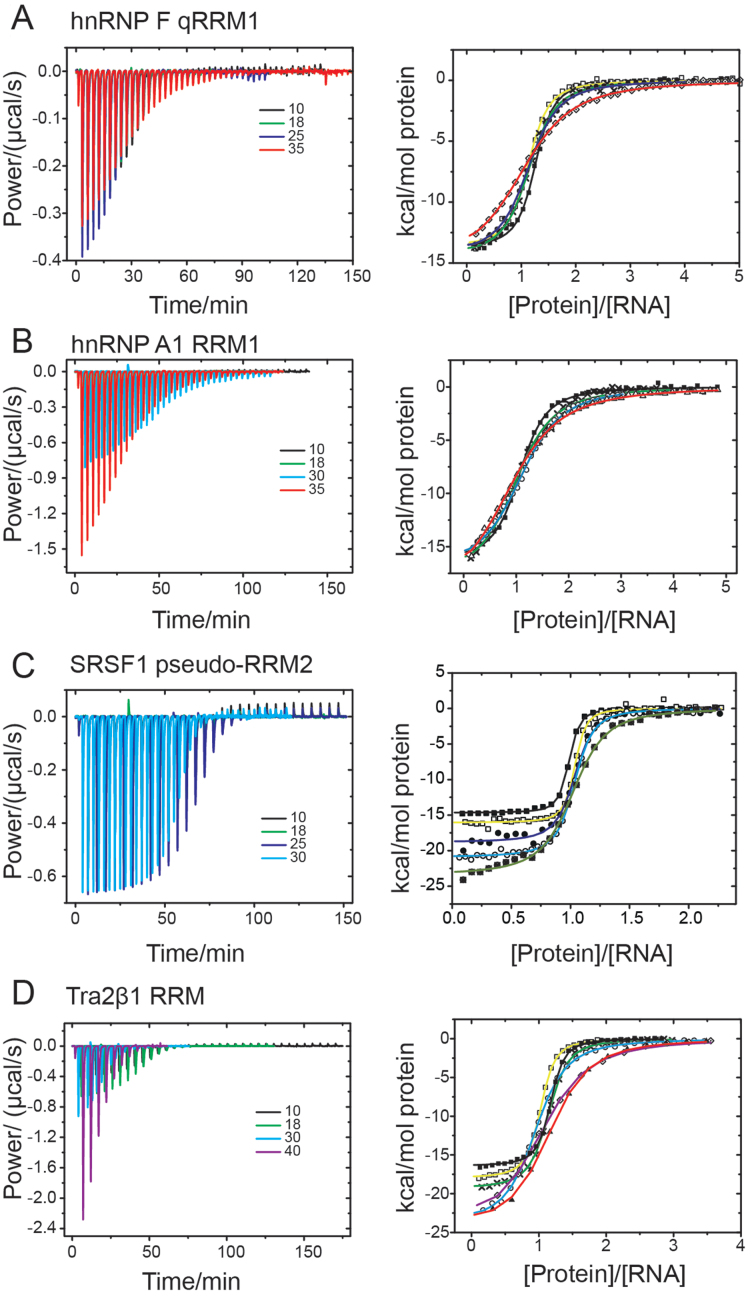
ITC experiments were carried out with a VP-ITC calorimeter (GE Healthcare). Protein samples were thoroughly dialyzed against the experimental buffer. The sample cell was filled with 5–15 μM RNA. The protein concentration in the injection syringe was 50–450 μM. The injection volume was ∼8 μL and the stirrer speed 300 rpm. Non-specific heat effects were small (Figure 2), and were therefore determined by subtracting the integrated heats detected after complete saturation from the recorded isotherm. The ITC data were described by a 1:1 binding model to extract the association constant K_obs, the molar binding enthalpy ΔH and the stoichiometry n by non-linear regression analysis using MicrocalOrigin7 (Equation 1);

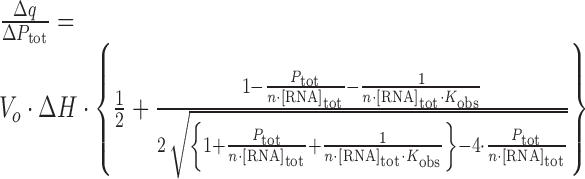(1)

Figure 2.

Representative isothermal titration calorimetry (ITC) data. ITC titration data upon titration of (A) hnRNP F qRRM1 (aa 1–102), (B) hnRNP A1 RRM1 (aa 2–97), (C) SRSF1 pseudo-RRM2 (aa 107–203) and (D) Tra2β1 (aa 106–201) into 5΄-AGG*G*AU-3΄, 5΄-UUAGGU-3΄, 5΄-AAGGAC-3΄ and 5΄-AAGAAC-3΄ cognate RNAs, respectively (where G* is 7-deazaguanine). The experiments were conducted at different temperatures: 10 (full squares), 14 (open squares), 18 (cross), 25 (full circles), 30 (open circles), 35 (full triangle), 38 (crossed squares) and/or 40°C (open diamond with dot). Left panels show variation of differential power as function of time. Several curves overlay in the left panels. Right panels show the integrated heats as function of the molar concentration of protein to RNA. The continuous line is the fit according to Equation (2). The heats of dilution were negligible. Solution conditions contained 20 mM CH₃COOH, 50 mM L-arginine, 50 mM L-glutamate, 0.05% β-mercaptoethanol–NaOH pH 5.5.

Where Δq is the apparent heat change due to complex formation at injection k, Δ[P]_tot is the total concentration of protein titrated into the cell at injection k, P_tot is the total concentration of protein in the cell, V_o is the effective volume of the cell, [RNA]_tot is the total concentration of RNA in the sample cell. Minor effects of concentration determination reflect in a small deviation of the stoichiometry n from 1.0 (±0.1). The effect on the molar enthalpy was corrected as; ΔH_obs = ΔH × n (15). The molar free energy change ΔG_obs was determined as, ΔG_obs = −RT·ln(K_obs). The molar entropy change −TΔS_obs was calculated according to: −TΔS_obs = ΔG_obs − ΔH_obs. ITC experiments were conducted at different temperatures (10–40°C) in 20 mM CH₃COOH, 50 mM L-arginine, 50 mM L-glutamate–NaOH pH 5.5 containing 0.05% β-mercaptoethanol. The effective concentration of Na⁺ ions was 20 mM, and 50 mM Glu·Arg salt. The solution conditions are similar to those used in the structural studies of SRSF1 pseudo-RRM2 or Tra2β1 RRM in complex with RNA (8,10). There was no evidence of formation of non-specific complexes in the nuclear magnetic resonance (NMR) data obtained under these conditions. Experiments were also conducted in the presence of different concentrations of sodium chloride.

Water-accessible surface area (ASA) and semi-empirical heat capacity

The accessible surface area (ASA) was determined using the method of Lee and Richards (16) as implemented by Hubbard and Thornton in the program NACCESS (17) (http://www.bioinf.manchester.ac.uk/naccess/). The probe radius and slice-width were set to 1.4 and 0.05 Å, respectively. The heat capacity effects upon binding (ΔC_p^b_,ASA and ΔC_p^f_,ASA) were determined according to the Makhatadze and Privalov model ((18); Equation 2).

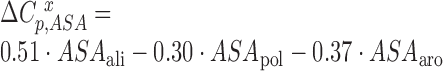(2)

Where 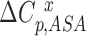is the expected heat capacity; , and 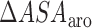are the changes in the aliphatic, polar or aromatic ASAs, respectively. In this model, the aliphatic, polar and aromatic atoms have distinct heat capacity contributions. All non-oxygens and non-nitrogens were regarded as non-polar; except for all carbon atoms within the cyclic rings of RNA bases, or Trp and Tyr side chains, that were classified as aromatic. All oxygens, phosphates and nitrogens were classified as polar.

Estimation of numbers of hydrogen bonds

Hydrogen bonds within the protein–RNA complexes: SRSF1 pseudo-RRM2-AAGGAC (PDB ID: 2M8D), hnRNP A1 RRM1-TAGG (PDB ID: 2UP1), Tra2β1 RRM-AAGAAC (PDB ID: 2KXN) and hnRNP F qRRM1-AGGGAU (PDB ID: 2KFY), were determined using the program HBPlus using default distances and angles (19). A hydrogen bond was considered valid if present in at least 50% of the NMR conformers, with the exception of the crystal structure of hnRNP A1 RRM1-TAGG (substructure of UP1 in complex with DNA; PDB ID: 2UP1). Bifurcated hydrogen bonds were considered as one.

Ionic contacts

The numbers of ionic bonds present at the protein-nucleic acid interfaces were calculated using the relevant PDB structures (2M8D, 2UP1, 2KXN and 2KFY). The ionic bonds were identified by the WHATIF server (http://swift.cmbi.ru.nl/servers/html/index.html) and own Awk scripts. The maximum separation between nucleic acid phosphates (OP1 or OP2) and the nitrogen atoms of either Lys, Arg or His (NH1, NH2, NE, NE2 or NZ) was set to 7 Å. Additionally, a contact was considered valid if present in more than half of the NMR conformers.

Molecular dynamics simulations

To obtain conformations of free unbound RNA, we performed molecular dynamics (MD) simulations starting from the bound RNA conformations (extracted from the PDB structures of the complexes). The RNAs were neutralized with Na⁺ counterions and solvated with TIP3P water in a periodic octahedron box (20). The simulations were run using sander.MPI as implemented in Amber9 package (21,22) using the ff03 force-field (23). The production runs were maintained at 303.15 K temperature by a Langevin thermostat (24). Pressure was maintained at 1.0 bar by isotropic scaling of velocity. The cut off distance for long range non-bonded interactions was 10 Å. Long-range electrostatic interactions were treated using particle-mesh Ewald settings (25). Bond lengths were controlled by SHAKE, with all bonds containing hydrogen atoms constrained (26). The equations of motion were integrated with a time-step of 2 fs for a total duration of at least ∼1 ns. A series of minimizations and short equilibration MD runs were carried out prior to the production run.

RESULTS

Favorable enthalpy drives the association of different RNA binding modes with cognate RNAs

To determine the thermodynamic signatures characteristic of ssRNA binding by the different binding modes, we performed titrations by ITC. The sequences of cognate RNAs for hnRNP A1 RRM1, SRSF1 pseudo-RRM2, Tra2β1 RRM and hnRNP F qRRM1 were 5΄-UUAGGU-3΄, 5΄-AAGGAC-3΄, 5΄-AAGAAC-3΄ and 5΄-AGG*G*AU-3΄, respectively; with G* representing 7-deazaguanine (Table 1). Substitution of guanine with 7-deazaguanine does not affect RNA binding by qRRM1 but prevents quadruplex formation of the free RNA (14). Each RRM was titrated into the cognate RNA within 275.15–315.15 K temperature. The experiments were conducted in 20 mM CH₃COOH, 50 mM L-arginine, 50 mM L-glutamate–NaOH pH 5.5 containing 0.05% β-mercaptoethanol, in accordance with NMR structural studies on SRSF1 seudo-RRM2 and Tra2β1 RRM (8,10). Non-specific complexes were not detected at the same ionic strength in our previous structural studies (8–10). Representative ITC isotherms for the formation of the different RRM–ssRNA are shown in Figure 2A–D. The integrated heats were described by a 1:1 binding model in Origin 7 (Equation 1) to extract the molar enthalpy of association (ΔH_obs) and association constant (K_obs). From these quantities, the molar entropy of association (−TΔS_obs) and free energy of association (ΔG_obs) were also determined (‘Materials and Methods’ section). All binding isotherms were monophasic and exhibited molar equivalence points in the range 1.0–1.1 protein–ssRNA in agreement with structural data (5,8–10,27). Interestingly, independent of binding mode, sequence-specific binding of ssRNA by the RRM was driven by favorable enthalpy changes and opposed by likewise unfavorable entropy changes (Table 2 and Figure 3A). Our results are in agreement with the reported thermodynamics of non-specific canonical binding of poly(U) and poly(A) RNAs by several classical RRMs (28). The determined thermodynamic parameters do not contain contributions from changes in protonation state upon complex formation, as evidenced by ITC titrations at pH 5.5 in different buffer systems, which is also in agreement with previous studies on various RRM–ssRNA complexes (28). In addition, the acetate buffer has very low ionization enthalpy, ΔH_ion ∼−0.098 kcal mol⁻¹ (29,30), which therefore strongly minimizes protonation effects; and the very low ionization enthalpy is negligible relative to the magnitudes of our measured enthalpies.

Table 2. Thermodynamic parameters of RRM–ssRNA association.

	Temperature K	ΔHobs kcal mol−1	ΔGobs kcal mol−1	-TΔSobs kcal mol−1
Tra2β1 RRM	283.16	−17.5 ± 3.4	−9.1 ± 0.1	8.4 ± 3.5
	287.16	−18.9 ± 0.9	−9.1 ± 0.1	9.9 ± 0.9
	291.17	−21.1 ± 0.3	−9.0 ± 0.1	12.1 ± 0.2
	298.17	−23.8 ± 2.0	−8.9 ± 0.1	14.9 ± 2.0
	303.17	−24.2 ± 4.4	−8.8 ± 0.1	15.4 ± 4.4
	308.16	−26.4 ± 0.9	−8.5 ± 0.1	17.9 ± 0.8
	313.18	−26.0 ±1.7	−8.3 ±0.2	17.7 ± 1.9
SRSF1 pseudo-RRM2	283.16	−14.3 ± 0.4	−9.6 ± 0.5	4.7 ± 0.0
	287.16	−16.3 ± 0.8	−10.1 ± 1.0	6.2 ± 0.2
	291.16	−16.2 ± 1.3	−10.1 ± 1.5	6.1 ± 0.2
	298.16	−19.0 ± 0.1	−10.2 ± 0.4	8.8 ± 0.3
	303.17	−20.7 ± 0.8	−9.6 ± 0.8	11.1 ± 0.1
	311.16	−24.2 ± 0.8	−9.5 ± 2.0	14.7 ± 1.1
hnRNP F qRRM1	287.15	−15.4 ± 0.4	−8.9 ± 0.0	6.5 ± 0.4
	291.15	−16.6 ± 0.2	−8.7 ± 0.0	7.9 ± 0.2
	298.16	−17.1 ± 3.7	−8.7 ± 0.1	8.4 ± 3.8
	308.15	−16.9 ± 1.2	−8.4 ± 0.0	8.5 ± 1.2
hnRNP A1 RRM1	283.15	−17.2 ± 0.6	−8.5 ± 0.0	8.8 ± 0.7
	291.15	−19.4 ± 0.0	−8.3 ± 0.1	11.1 ± 0.1
	303.15	−20.0 ± 1.0	−7.8 ± 0.0	12.1 ± 0.9
	308.15	−21.1 ± 0.2	−7.4 ± 0.0	13.7 ± 0.2

Thermodynamic binding parameters for the formation of Tra2β1 RRM-AAGAAC, SRSF1 pseudo-RRM2-AAGGAC, hnRNP F qRRM1-AGG*G*AU and hnRNP A1 RRM1-UUAGGU complexes. The ITC experiments were conducted at various temperatures in 20 mM CH₃COOH, 50 mM L-arginine, 50 mM L-glutamate, 0.05% β-mercaptoethanol–NaOH pH 5.5. ΔH_obs, ΔG_obs, -TΔS_obs and ΔC_p,obs is the molar enthalpy change, molar free energy change, molar entropy change and the heat capacity change of association, respectively.

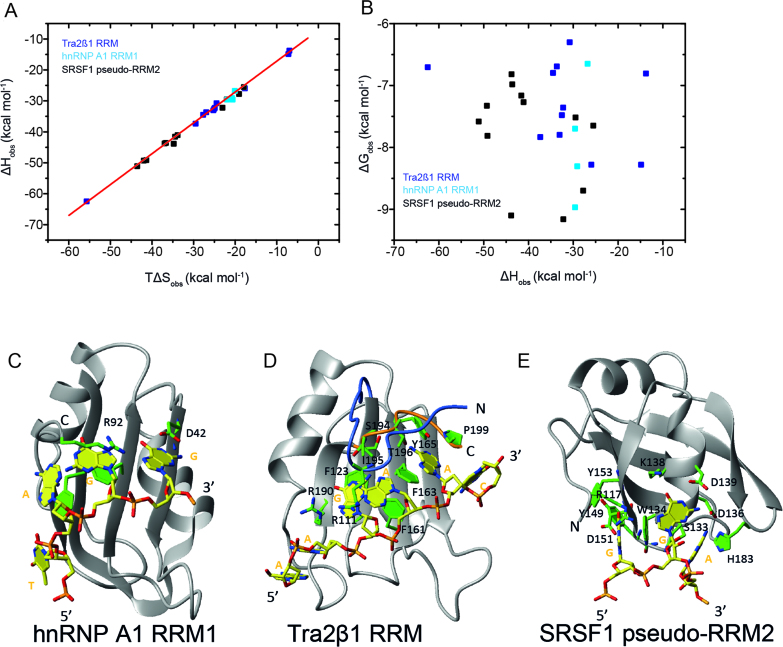
Figure 3.

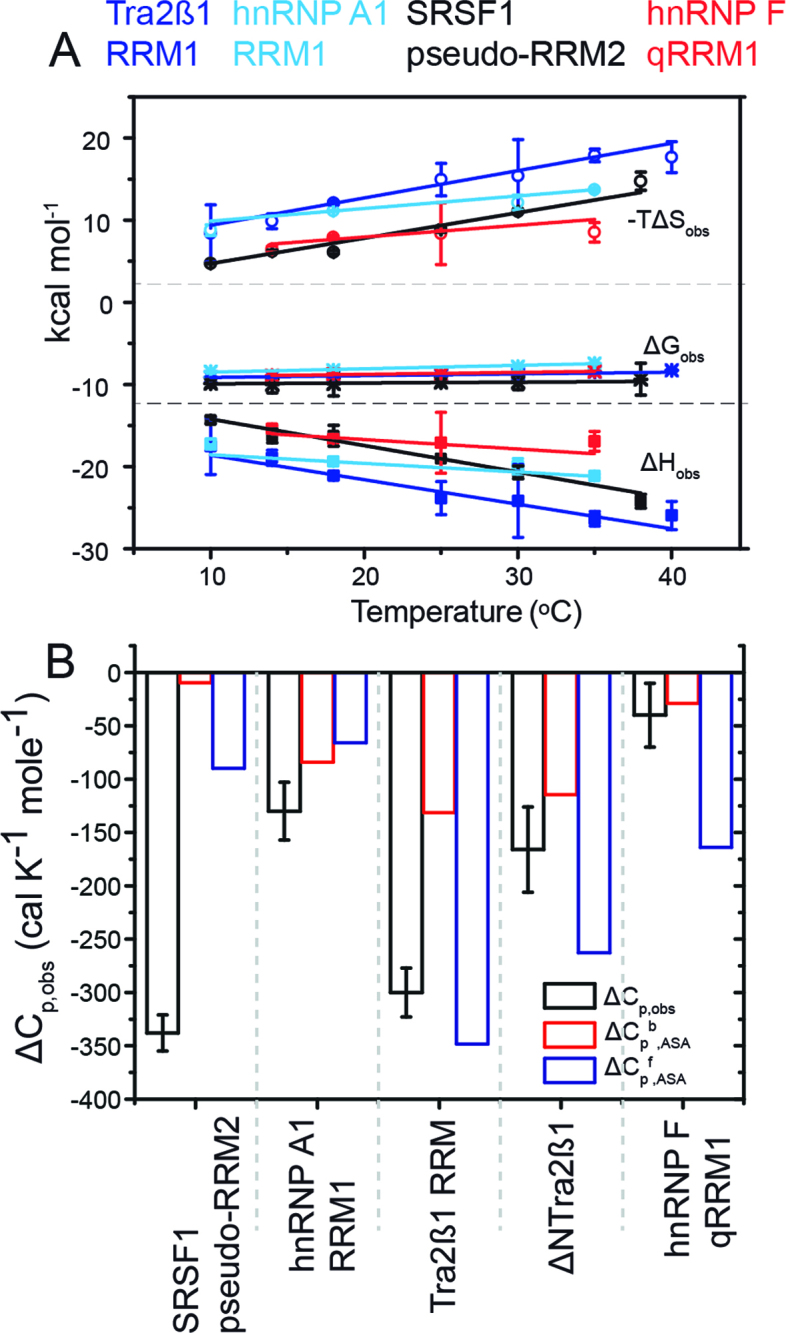
Enthalpy is the general force driving RRM–ssRNA association. Dissection of temperature-dependence of enthalpy change (heat capacity) reveals differential hydration effects, conformational transitions and dynamics upon binding RNA. (A) Plots of the observed molar enthalpy (ΔH_obs), molar free energy (ΔG_obs) and molar entropy of association (-TΔS_obs) determined directly by ITC upon injecting 100–250 μM of RRMs into 5–15 μM cognate RNAs at various temperatures. The thermodynamic parameters were extracted upon fitting Equation (2) to the data shown in Figure 2B. (B) Dissection of heat capacity effects. The experimental observed ΔC_p,obs ( = ΔΔH_obs/ΔT) is shown in black. The errors are standard deviations of the mean determined by Jackknife analyses of the temperature-dependence of the molar enethalpy. Expected ΔC_p was calculated by NACCESS (probe radius and slice-width of 1.4 and 0.05 Å, respectively) based on the bound conformations of the binding partners (ΔC_p^b_,ASA; red) and structures of the free components (ΔC_p^f_,ASA; blue). The structures used in semi-empirical calculations are: hnRNP F qRRM1 (PDB ID: 2HGL, 2KFY), Tra2β1 RRM (PDB ID: 2RRB, 2KXN), hnRNP A1 RRM1 (PDB ID: 1L3K, 2UP1) and SRSF1 pseudo-RRM2 (PDB ID: 2O3D, 2M8D). Models of flexible free RNA oligomers and N- and C-terminal protein segments were modeled using the ff03 force-field in Amber9.

Different RNA binding modes bind to cognate ssRNAs with similar affinity

The differences in ΔG_obs among the RRM–ssRNA complexes were suprisingly small, in light of the different binding modes (Figure 3A and Table 1). Still, the largest ΔG_obs (-RTlnK_obs) was detected in SRSF1 pseudo-RRM2–ssRNA complex by 10–20%. The mean free energy ΔG_obs,mean of the ssRNA complex of SRSF1 pseudo-RRM2, averaged across the considered temperature range, was −9.9 ± 0.3 kcal mol⁻¹. ΔG_obs,mean for ssRNA complexes of Tra2β1 RRM and hnRNP F qRRM1 were almost the same, totaling −8.8 ± 0.3 and −8.7 ± 0.2 kcal mol⁻¹, respectively (Figure 3A and Table 1). The least ΔG_obs,mean observed in hnRNP A1 RRM1–ssRNA complex was −8.0 ± 0.5 kcal mol⁻¹. Since the complexes contained similar types and numbers of non-covalent contacts but variations in ΔG_obs, we speculated the existence of strong isothermal enthalpy-entropy compensation. In this way, favorable energetic contributions of intermolecular contacts during complex formation are compensated variably by entropic forces.

Different RNA binding modes similarly employ isothermal enthalpy-entropy compensation in ssRNA binding

To better understand the role of enthalpy-entropy compensation during complex formation, we evaluated the thermodynamic consequences of various amino acid substitutions (Figure 4A–E and Supplementary Table S1). The relevant enthalpic and entropic information were determined by ITC and combined with previous data (Supplementary Table S1; (6,8)). Published enthalpy-entropy data on hnRNP F qRRM1 was excluded because the AGGGAU RNA used in the experiments partially populates G-quadruplexes (9,14). About 90% of the tested variants represent alanine substitutions (Supplementary Table S1). All substituted residues in hnRNP A1 RRM1 (R55, D42 and R92) contact the nucleic acid ((5), Figure 4C). In Tra2β1 RRM, the amino acid replacements (Table 1 and Figure 4D) can be categorized as substitutions of aromatic amino acids (F123, F161 and Y165A), N-terminal residues (R111A and ΔNTra2β1 (residues 106–116 removed)), C-terminal residues (S194A, I195A, T196A, P199A) and others (R190A, Y165F/T196A). Amino acid replacements did not alter the global fold of the protein (6). In SRSF1 pseudo-RRM2, the conserved residues of α1 that are involved in the sequence-specific binding were substituted (8), as well as four additional residues (H183, R117, Y149 and Y153) (Supplementary Table S1 and Figure 4E).

Figure 4.

Networks of weak interactions regulate complex stability in all complexes independent of the mode employed to bind RNA. Plots show the thermodynamic parameters describing the formation Tra2β1 RRM1/5΄-UGAAGAAC-3΄, SRSF1 pseudo-RRM2/5΄-AAGGAC-3΄ or hnRNP A1 RRM1/5΄-UUAGGUC-3΄ protein/RNA complexes determined by ITC titrations after substitution of various amino acids. (A) ΔH_obs plotted against TΔS_obs (B) ΔG_obs plotted against ΔH_obs. The experimental temperatures were 313 K (Tra2β1 RRM and SRSF1 pseudo-RRM2) and 303 K (hnRNP A1 RRM1). Protein/RNA titrations of SRSF1 pseudo-RRM2 and Tra2β1 RRM were conducted under the same solution conditions as in Figure 2. Data on hnRNP A1 RRM1 were collected in the presence of 10 mM NaH₂PO₄, 2 mM β-mercaptoethanol at pH 6.5. Overview of the solution structures of hnRNP A1 bound to the TAGG sequence (C), Tra2β1 RRM bound to the AAGAAC RNA (D), and SRSF1 pseudo-RRM2 bound to the GGA sequence (E). Structure of the complex is shown in ribbon (protein backbone) and stick (RNA) representation. The protein backbone is shown in gray and heavy atoms are shown in orange (P atoms), yellow (C atoms for RNA), green (C atoms for protein), red (O atoms) and blue (N atoms).

Figure 4A shows that all the complexes show strong isothermal enthalpy-entropy compensation upon amino acid substitution. The combined compensation plot of SRSF1 pseudo-RRM2, Tra2β1 RRM and hnRNP A1 RRM1 showed a near-perfect linear dependence of ΔH_obs as function of TΔS_obs (slope = 0.99; R² = 0.99). Thus, the extent of isothermal enthalpy-entropy compensation was the same in all the considered complexes, and could therefore not account for the differences in ΔG_obs (Tables 1 and 2). In all three cases, the corresponding ΔG_obs shows non-systematic variation with ΔH_obs (Figure 4B), suggesting the observed compensation is physicochemical and not a consequence of correlated errors.

Strong networks of weak interactions are a general feature of RRM–ssRNA binding interfaces

By dissecting the isothermal enthalpy-entropy compensation (Figure 4), we however identified evidence for the existence of networks of weak interactions that provide significant adaptability of the binding sites, and could explain the non-additive effect of intermolecular contacts on ΔG_obs (Table 1). First, the existence of strong compensation indicates that upon removal of a specific contact, new linkages are formed to maintain the same complex stability. The entropy remains unfavorable for complex formation. Second, residues that do not have direct contacts with RNA at a structural level, such as Y149A (but not Y153A) in SRSF1 pseudo-RRM2, significantly reduce complex stability by at least 1 kcal mol⁻¹ (Supplementary Table S1 and Figure 4D). The V137A substitution in Tra2β1 RRM also reduces complex stability. These results point to linkage between binding site residues and distant ones through secondary contacts. Third, the lack of a clear trend with respect to the energetic contribution of hydrogen bonds, aromatic stacking and non-polar interactions emphasize the networked nature of contacts. For instance, the removal of the hydrogen bonds formed to the RNA by the residues K138 and S133 in SRSF1 pseudo-RRM2 resulted in a much more favorable binding enthalpy relative to the wild-type protein instead of a less favorable one (Figure 4E and Supplementary Table S1). Hydrogen bond breakage is an endothermic process; thus new contacts are mostly likely formed that account for the exothermic effect. In agreement with our data, interaction networks were previously observed in the RNA complexes of U1A RRM1 ((31–33), see ‘Discussion’ section).

Furthermore, we identify discernible ‘hot-spots’ at the binding interface of Tra2β1 RRM. ‘Hot spots’ are contacts the removal of which abolishes binding (F123 and F161 (Supplementary Table S1)). Similarly, the removal of conserved aromatics drastically weakens binding in hnRNP A1 (34). Although, the quality of enthalpy/entropy data on hnRNP F is compromised by G-quadruplex formation (7,14), the removal of aromatics at the binding interface of hnRNP F qRRM1 also precludes complex formation (7). In summary, we identify evidence of strong networking of non-covalent interactions in all the different RNA binding modes, and hot spots that have large effects on complex stability.

Different RNA binding modes exhibit large differences in heat capacities

Figure 3A (and Table 2) shows that in all RRM–ssRNA complexes ΔH_obs and –TΔS_obs vary with temperature, hence indicating a negative experimental heat capacity change upon binding (ΔC_p,obs = (ΔΔH_obs/T)_p; Figure 3B). The different binding modes exhibit widely varying experimental heat capacity changes. ΔC_p,obs for SRSF1 RRM2–ssRNA was the largest, equaling −338 ± 17 cal K⁻¹ mol⁻¹ (Figure 3B). ΔC_p,obs for Tra2β1 RRM–ssRNA was slightly lower, amounting to −300 ± 23 cal K⁻¹ mol⁻¹. ΔC_p,obs for the hnRNP A1 RRM1–ssRNA complex was ∼2.5-fold less than the value for either Tra2β1–ssRNA or SRSF1–ssRNA, equaling −130 ± 27 cal K⁻¹ mol⁻¹. The errors represent standard deviations of the mean, and were determined by Jackknife analyses on the temperature-dependence of ΔH_obs. Interestingly, ΔC_p,obs of hnRNP F qRRM1–ssRNA was the smallest and almost close to zero, totaling merely −40 ± 30 cal K⁻¹ mol⁻¹. The small magnitude of ΔC_p,obs in hnRNP F qRRM1–ssRNA contrasts with what has been measured in protein–DNA complexes where formation of sequence-specific complexes is characterized by large negative changes in ΔC_p,obs (35–38), and possibly would signal for a tendency of the protein to slide on the 5΄ GGG 3΄ trinucleotide.

Differences in heat capacities reflect differential changes in hydration and conformational changes upon complex formation

The major contribution to ΔC_p,obs is change in hydration (38–41). ΔC_p,obs can thus be estimated from semi-empirical computations that are based on changes in type and magnitude of water-ASA upon complex formation (18,42–43). We computed ASA by NACCESS according to the method of Lee and Richards (16) as implemented by Hubbard, using a slice width of 0.05 Å. The expected heat capacity changes ΔC_p,ASA were determined from ASA in accordance with the Makhatadze and Privalov model ((18), Equation 2). The model has distinct polar, non-polar and aromatic components, thereby enables accurate quantification of the expected heat capacities of aromatic carbon atoms located within the cyclic rings of purine and pyrimidine RNA bases or Trp and Tyr side chains. However, other semi-empirical heat capacity parameterization schemes yielded similar results (40,42–43). The expected heat capacity ΔC_p^b_,ASA was calculated by extracting the hypothetical structures of the free proteins and oligonucleotides from the known structures of the respective complexes (Figure 3B and Table 1).

In hnRNP F qRRM1–ssRNA and hnRNP A1 RRM1–ssRNA complexes, ΔC_p^b_,ASA and ΔC_p,obs were equivalent within experimental error. In Tra2β1 RRM–sRNA and SRSF1–sRNA complexes, the calculated ΔC_p^b_,ASA were significantly smaller (less negative) than the experimental ΔC_p,obs. This led us to suspect that binding was associated with conformational changes of the proteins and/or oligonucleotides (35,39,44–45). Therefore the expected heat capacity change ΔC_p^f_,ASA describing the association of free unbound RRM conformations with those of free ssRNA was computed (Figure 3B). The structures of the free proteins are available (27,46–48). The structures of the free ssRNAs were modeled by MD simulations in explicit solvent starting from the bound conformations, using the ff03 force-field (23) implemented in the Amber9 package (21,22). The ssRNAs do not adopt any specific structure on the basis of thermograms determined by differential scanning calorimetry. In hnRNP A1 RRM1–ssRNA, ΔC_p,obs ≈ ΔC_p^b_,ASA ≈ ΔC_p^f_,ASA, suggesting binding via rigid-body interactions. In SRSF1 pseudo-RRM2–ssRNA and Tra2β1 RRM–ssRNA, the calculated ΔC_p^f_,ASA were in much better agreement with the experimental ΔC_p,obs than ΔC_p^b_,ASA, demonstrating the presence of large conformational transitions that have significant heat capacity effects. Indeed, structural studies indicate that the N-terminus of SRSF1 pseudo-RRM2 is flexible in the free state, and becomes structured upon RNA binding ((8), Supplementary Figure S1). In the SRSF1 pseudo-RRM2–ssRNA complex, the N-terminus lies above the β-sheet surface, stabilized by contacts between R117 and the RNA. R118 also interacts with Tyr149 located in the β2-strand, as supported by the clear presence of an intramolecular nuclear overhauser effect (8). In Tra2β1 RRM, the C- and N-termini are freely flexible in unbound form, but are structured upon RNA binding (Figure 1,(10)).

To confirm the rigid body binding character of hnRNP A1 RRM1, a truncated variant of Tra2β1 RRM lacking the flexible N-terminal segment (residues 106–115; ΔNTra2β1) was produced (6). ΔNTra2β1 binds RNA using the β-sheet surface, with the involvement of only the C-terminal segment. Heat capacity data obtained upon binding of the ΔNTra2β1 tail variant to AAGAAC RNA showed a much improved agreement between ΔC_p^b_,ASA and ΔC_p,obs than in Tra2β1 RRM (Figure 3B), thereby confirming that RNA binding to the β-sheet surface most likely proceeds by rigid-body interactions. Mutation of the C-terminal segment of Tra2β1 RRM was not possible because it leads to a drastic loss in binding affinity for RNA (6). Altogether, our data reveals that different RNA binding modes of RRMs employ hydration and conformational changes variably in binding to cognate RNAs.

hnRNP F qRRM1 and SRSF1 pseudo-RRM2 undergo significant changes in dynamics upon RNA binding

Contrary to the good agreement between ΔC_p,obs and ΔC_p^f_,ASA observed in hnRNP A1–ssRNA and Tra2β1 RRM1–ssRNA, large residual heat capacities (ΔΔC_p) were observed in hnRNP F qRRM1–ssRNA and SRSF1 pseudo-RRM2–ssRNA (Figure 3B).The residual heat capacity ΔΔC_p = ΔC_p,obs - ΔC_p^f_,ASA amounts to +124 and −248 cal K⁻¹ mol⁻¹ in hnRNP F qRRM1–ssRNA and SRSF1 pseudo-RRM2–ssRNA complexes, respectively (Figure 3B). Besides hydration and conformational changes, other known contributions to ΔC_p,obs are proton-linkage (49), incomplete hydration of the binding interfaces (50–52) and changes in dynamics upon binding (36,51,53). Proton-linkage effects do not play a role because the acetate buffer has negligible ionization enthalpy, and the ionization enthalpy of acetate has negligible temperature-dependence (30). In addition, there were no protonation effects on the basis of ITC titrations performed in buffers with different ionization enthalpies. Incomplete hydration of the binding interfaces (burial of water molecules) contributes −8 to −15 cal K⁻¹ mol⁻¹ to heat capacity, depending on whether the water molecule is positioned in a non-polar environment or participates in a hydrogen bonding network (54–56). Thus, correction for heat capacity due to buried water molecules (ΔC_p,waters) results in less negative corrected experimental heat capacity ΔC_p^w_,obs; ΔC_p^w_,obs = ΔC_p,obs - ΔC_p,waters. For this reason, incomplete dehydration could partially account for residual heat capacity in SRSF1 pseudo-RRM2–ssRNA. The effect is however expected to be small since all the considered complexes bind similar sequences, with the same types of non-covalent forces, using similarly small surface areas. It is therefore most likely that SRSF1 pseudo-RRM2–ssRNA binding to ssRNA proceeds with a decrease in dynamics (thermal fluctuations) of the binding partners. Structural data supports this conclusion because the N-terminus of the protein that is not oriented in the free state, becomes structured in the complex ((8), Supplementary Figure S1). In hnRNP F qRRM1–ssRNA complex, consideration of heat capacities of any buried waters would actually increase the discrepancy between the experimental and expected heat capacities. Nonetheless, water molecules located at the binding interface of hnRNP F qRRM1–ssRNA are in dynamic exchange with bulk solvent, and only a single water molecule is buried (57). Thus, the corresponding heat capacity contribution from incomplete dehydration is almost negligible totaling between −8 to −15 cal K⁻¹ mol⁻¹. ΔΔC_p in hnRNP F qRRM1–ssRNA was +124 cal K⁻¹ mol⁻¹. It is therefore most likely that hnRNP F qRRM1–ssRNA complex formation proceeds with increase in dynamics of the binding components. Altogether, our data indicate that differential dynamics regulate the binding of different RRMs to cognate ssRNAs.

Polyelectrolyte effects

To investigate the partitioning of the stability of RRM–ssRNA complexes into electrostatic and non-electrostatic effects, we employed the ‘oligolysine model’ by Record et al. (58–60). This model is a molecular thermodynamic analyses of ion effects; precisely, a semi-empirical extension of the original counterion-condensation theory of Manning (58,60–62). The model shows good agreement between thermodynamic and structural data, as shown by the review on several different protein–DNA complexes (63), model oligolysines (64) and other systems (65). The equilibrium constant, K_obs, describing association between proteins and nucleic acids is predicted to decrease with increasing salt concentration because of the reduced gain of entropy of mixing experienced by cations bound to backbone phosphate groups upon release into the bulk at elevated salt concentrations. The dependence can be formally expressed as:

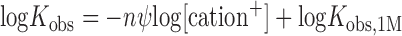(3)

where [cation⁺] is the concentration of monovalent ions, n is the number of ionic bonds made between fully positively charged amino acid side chains and the phosphate oxygen atoms of the nucleic acid, and ψ defines the thermodynamic fraction of a monovalent ions bound by a phosphate group (58,64). Ψ is determined empirically. The slope of logK_obs versus log[cation⁺], SK_obs = nψ, quantitates the number of ions released from the protein–nucleic acid interface into the bulk upon complex formation.

To determine the gross energetic balance of contributions to the free energy of binding (ΔG_obs), we determined K_obs at 10°C by ITC at different concentrations of NaCl (0.1–0.8 M) (Figure 5A). Measurements at 40°C, the temperature at which the NMR structures have been determined, were hindered by the low binding affinity at higher salt concentrations at that high temperature. Titrations at 1.0 M NaCl were similarly not possible. The salt-independent free energy contribution to binding, which excludes the polyelectrolyte effect, was then determined as ΔG_nPE = −2.303RTlogK_obs at 1.0 M Na⁺ concentration. The electrostatic contribution due to ion-release or the polyelectrolyte effect (ΔG_PE) was then calculated at our standard buffer conditions as follows:

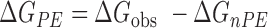(4)

ΔG_PE and ΔG_nPE have been previously named electrostatic and non-electrostatic components in previous literature (63); but we avoid that terminology so as to properly classify hydrogen bonds as electrostatic contacts. The results of our analyses are shown in Figure 5B (see also Table 1 and Supplementary Table S2). The percentage contribution of ΔG_PE to ΔG_obs for Tra2β1 RRM–ssRNA, SRSF1 RRM2–ssRNA and hnRNP A1 RRM1–ssRNA is between 25 and 30% (23, 23 and 28%, respectively). Interestingly, the magnitude of the electrostatic component during formation of several protein–hairpin RNA complexes is the same (66–69). In hnRNP F qRRM1–ssRNA however, ΔG_PE is at least 2.5-fold smaller (∼10%). Altogether, the results indicate non-polyelectrolyte effects are the general force driving association between different RNA binding modes of RRMs with cognate RNAs. This is in agreement with the domination of the binding affinity by an extensive network of hydrogen bonds and van der Waals interactions.

Figure 5.

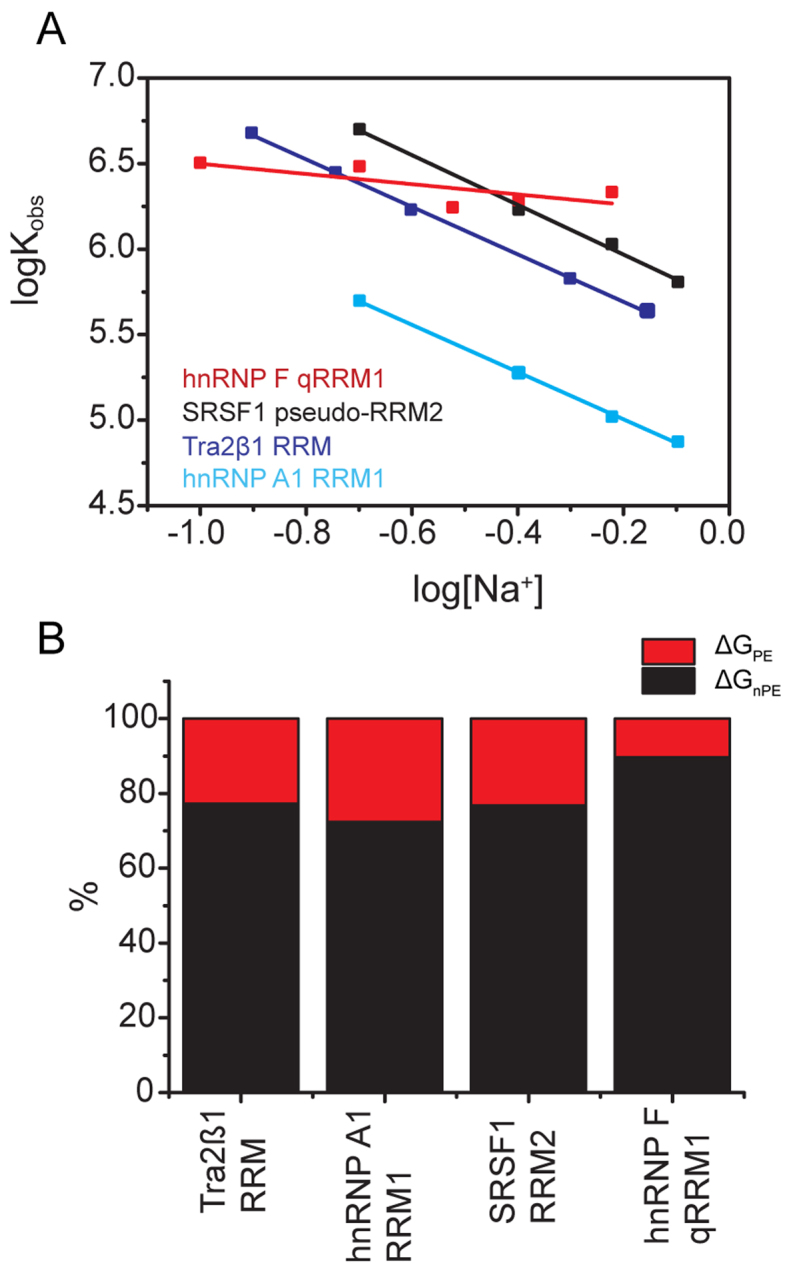
Non-polyelectrolyte (‘non-electrostatic’) effects are the general force driving cognate RNA recognition by different RNA binding modes. (A) Variation of the logarithm of the association constant K_obs as function of concentration of Na⁺ ions (log[Na⁺]) upon formation of RRM–ssRNA complexes. The data were collected by ITC by injecting 100–500 μM free RRMs into 5–25 μM cognate RNAs at 10°C temperature, in 20 mM CH₃COOH, 50 mM L-arginine, 50 mM L-glutamate, 0.05% β-mercaptoethanol–NaOH pH 5.5, at various concentrations of NaCl. (B) Partitioning of the overall free energy. The graph shows the percentage electrostatic contribution due to ion-release (ΔG_PE), as well as the contribution from non-polyelectrolyte effects (ΔG_nPE). The components were calculated from data shown in (A).

β2/β3 loop and N- or C-terminus mediate ionic bond formation

In an attempt to explain why the magnitude of the electrostatic component is the same in all complexes except hnRNPF qRRM1–ssRNA, we analyzed ionic bond formation in the structures of the complexes. The number of ionic bonds present in each complex were extracted from the magnitude of the slope of logK_obs versus log[cation⁺] (SK_obs; Figure 5A). Experiments with Tra2β1 RRM–ssRNA, hnRNP A1 RRM1–ssRNA and SRSF1 pseudo-RRM2–ssRNA yielded SK_obs∼ −1.41 ± 0.04. Since SK_obs = nψ, and taking ψ to be similar for both ssDNA and ssRNA (ψ = 0.71; (65)), we determined that Tra2β1 RRM–ssRNA, hnRNP A1 RRM1–ssRNA and SRSF1 pseudo-RRM2–ssRNA each make two ionic bonds with the cognate RNAs. In contrast, qRRM1–ssRNA apparently makes no such ionic bonds (SK_obs = −0.30). The data are summarized in Supplementary Table S2. To identify the protein residues participating in the contacts, we analyzed the available NMR structures of the complexes, focusing on the contacts formed between phosphate oxygens and fully charged atoms of arginine and lysine side chains. As a valid contact was considered the one that occurred in at least 50% of the conformers. In accordance with previous studies which show that energetically important ionic contacts formed between amino acids and phosphate oxygens occur within 3–7 Å distance (70–74), we analyzed the available structures of RRM–ssRNA complexes for ionic bonds within that distance and found the following contacts: R117 and R154 for SRSF1 pseudo-RRM2, R106, R111 and R159 for Tra2β1 RRM, R55 and R92 for hnRNP A1 RRM1 and none for hnRNP F qRRM1. Thus, we observe an almost perfect agreement between thermodynamic and structural data. In support of the ionic contacts, replacement of R55 or R92 of hnRNP A1 RRM1 with alanine led to 36- and 5-fold reduction in affinity for RNA, respectively (Supplementary Table S1). NMR and crosslinking data confirm that R117 and R154 of SRSF1 are involved in complex formation (27). Mapping these contacts in the complexes (Figure 1, cyan) shows that the β2/β3 loop and one of the terminal segments (N or C) participate in the formation of ionic bonds. In the case of hnRNP F qRRM1–ssRNA, there are no charged residues in the N-terminal segment. Moreover, the C-terminal segment forms an α−helix structure that packs against the β-sheet to form a hydrophobic core that shifts the β2/β3 loop away from contacting the RNA (Figure 1C, magenta).

DISCUSSION

Favorable enthalpy is a general feature of RRM–ssRNA complex formation

HnRNP A1 RRM1, SRSF1 pseudo-RRM2, Tra2β1 RRM and hnRNP F qRRM1 sequence-specifically recognize sequences that are quite similar and composed of purine triplets (Table 1). Remarkably, in spite of this sequence-similarity, completely different surfaces are employed in RNA recognition ((7,8,10,27,47,75), summarized in Table 1). However, despite the detailed knowledge from structural work on RNA recognition by the different RRM binding modes, the thermodynamic strategies of these different RRMs are still not comprehensively understood. In this study we show that the association of different RNA binding modes with cognate RNAs is characterized by favorable enthalpies and opposed by unfavorable entropy in the physiological temperature range (Figures 2 and 3). This observation is in agreement with previous reports on the non-specific canonical binding of poly(U) and poly(A) RNAs by classical RRMs (28). The favorable enthalpy change emphasizes the role of hydrogen bonds and van der Waals intermolecular contacts to the binding affinity. The unfavorable entropy change most likely reflects the loss of degrees of freedom in the binary complex, the loss of which is likely dominated by a rigidification of the flexible backbone of the unstructured free oligonucleotide at the binding site. The dominance of the flexibility of the RNA is supported by the fact the RRM–ssRNA association process remains enthalpically-driven, and entropy-opposed, independent of even drastic amino acid substitutions (Figure 4 and Supplementary Table S1). We therefore conclude that enthalpy is the general force driving RRM–ssRNA association at physiological temperatures independent of the mode of RNA binding employed.

Complex stability is predominantly regulated by strong networks of non-covalent forces

Comparative analyses performed on the stabilities of the various RRM–ssRNA complexes indicated SRSF1 pseudo-RRM2 bound tightest to cognate RNA, followed by Tra2β1 RRM and hnRNP F qRRM1, with the least ΔG_obs detected in hnRNP A1 RRM1 (Table 1 and Figure 3A). The same relative complex stabilities were observed at high concentrations of 1.0 M Na⁺ (ΔG_obs = ΔG_PE + ΔG_nPE; Supplementary Table S2), thereby confirming the absence of non-specific effects at lower Na⁺ concentrations. Interestingly, the differences in ΔG_obs could however not be explained on the basis of the numbers and types of non-covalent bonds in the complexes (Figure 1). Instead, it was accounted for by the presence of strong networks of the non-covalent interactions. Evidence for such networks of contacts was extracted from analyses of isothermal enthalpy-entropy compensation behavior upon mutation of various amino acid residues (Figure 4). Several reasons including the observation of strong reduction in complex stability upon mutating residues that are located distant from the binding sites and not involved in RNA binding justified the conclusion. In agreement with our data, networks of contacts and non-additivity of individual interactions have been similarly reported in U1A RRM1 (31–33). By using energetic pairwise coupling, Hall et al. identified strong cooperative interactions among binding site residues, and with distant ones. For instance, mutation of conserved aromatics located at the β-sheet surface (Y13 or F56) of U1A RRM1 affected the binding strength less than glycine residues that did not contact the RNA (33). The effect was explained in terms of possible dynamic changes, mediated by incremental changes in hydrogen bonding patterns, torsion angles and stability. The complexes considered in this study could operate under similar mechanisms. For instance, Y149 in SRSF1 pseudo-RRM2 is not involved in direct RNA binding but is in contact with Arg118 from the N-terminus, and is therefore most likely important for the stabilization of Arg117, which is in direct contact with the RNA. Our results also identified hot spots at the binding interfaces of the different RNA binding modes except in the case of SRSF1 pseudo-RRM2. The hot spots are composed mainly of aromatic residues that are required to form stable complexes. The aromatic residues could act as focal points of energetic coupling of the networked interactions in a manner analogous to Tyr 13 in U1A RRM1 (31). Further studies are still however required to understand the intricate dynamics and linkages of the networks. In conclusion, our data supports the existence of networks of weak interactions at the binding sites of different RNA binding modes, and possible focal points for such networks.

RRMs differentially employ hydration, conformational changes and dynamics to bind to cognate ssRNAs

The dissection of the experimental heat capacity by semi-empirical relations revealed important insights on the four RNA binding modes. In hnRNP A1 RRM1–ssRNA, ΔC_p,obs ≈ ΔC_p^b_,ASA ≈ ΔC_p^f_,ASA, thereby signaling rigid-body binding character. Preliminary NMR studies however indicate that the C-terminus of hnRNP A1 RRM1 becomes slightly ordered in the complex (our unpublished data). Thus this event most likely has minor heat capacity consequences. In the case of Tra2β1 RRM–ssRNA, SRSF1 pseudo-RRM2–ssRNA and hnRNP F qRRM1–ssRNA, ΔC_p^b_,ASA ≠ ΔC_p^f_,ASA, indicating that conformational rearrangements upon binding have significant energetic consequences. In agreement, the N- and C-termini restructure upon RNA binding in Tra2β1 RRM (Figure 1), and the N-terminus of SRSF1 pseudo-RRM2 becomes ordered in the complex (Supplementary Figure S1). In hnRNP F qRRM1–ssRNA, structural data detects no significant large conformational transitions upon RNA binding (7,76) and the room mean square deviation of the core RRM atoms is only ≈1.05 Å. The conformational transitions experienced in hnRNP F qRRM1 are therefore most likely due to changes in side-chain conformations of several amino acid residues. Although ΔC_p,obs ≈ ΔC_p^f_,ASA in hnRNP A1 RRM1–ssRNA and Tra2β1 RRM–ssRNA complexes, there were large residual heat capacities (ΔΔC_p) in hnRNP F qRRM1–ssRNA and SRSF1 pseudo-RRM2–ssRNA complexes (Figure 3B). The residual heat capacity in hnRNP F qRRM1–ssRNA is most likely explained by significant increase in dynamics of the binding components upon complex formation. The exact details on these dynamics however require further investigation. In contrast, SRSF1 pseudo-RRM2 binding to cognate ssRNA most likely proceeds with rigidification of the binding partners. In agreement, structural studies on SRSF1 pseudo-RRM2 indicate that the flexible N-terminus rigidifies upon complex formation ((8), Supplementary Figure S1). Altogether, this study concludes that various modes of RNA binding utilized by RRMs differentially employ hydration, conformational changes and dynamics to bind to cognate ssRNAs.

With the exception of hnRNP F qRRM1, different RNA binding modes display the same magnitude of the electrostatic component to the overall free energy of binding

The formal application of Equation (4) ascribes the total binding energy determined at 1.0 M salt to non-polyelectrolyte effects. Therefore, the binding free energy at high salt can be attributed to the salt-independent effects: van der Waals interactions, hydrogen bonding and dehydration effects. The dominance of non-polyelectrolyte effects (ΔG_nPE ∼70–75% of ΔG_obs) points to the specific character of the association process and is in line with the presence of approximately five hydrogen bonds (counting bifurcated bonds once; Table 1 and Figure 1), stacking interactions and relatively large non-polar interaction areas (2360–3830Ų; Supplementary Table S3). Similar magnitudes of the component due to the polyelectrolyte effect (ΔG_PE ∼25–30% of ΔG_obs; referred to as the electrostatic component) were reported in U1A RRM1–U1hpII stem-loop ((77,78); although eight ions are released), FOX-1 RRM–ssRNA (69) and several other protein–hairpin RNA complexes (66–68), leading us to conclude that the small electrostatic contribution from ion-release is possibly accounted for by the structural flexibility of the nucleic acid. Only in the case of hnRNP F qRRM1–ssRNA, we detected a very small ΔG_PE of ∼10% of ΔG_obs (Figure 4 and Table 1). In contrast, formation of several specific and non-specific protein–dsDNA complexes is driven to at least 60–70% of ΔG_obs by electrostatic contributions due to release of ions condensed on the DNA (63). The principal structural difference between dsDNA and ssRNA could be evoked as an explanation. In dsDNA the backbone phosphates are structurally constrained by the rigid double helix structure. They could serve as a convenient scaffold to gain unspecific binding energy because the entropic cost for making ionic pairs with charged side chains is kept low. In the flexible ssRNA, however, formation of ionic pairs with backbone phosphates is expected to pose a significant entropic penalty. Flexible regions of the RRMs such as loops contacting the ssRNA may also contribute. In summary, non-polyeletrolyte effects are the predominant force stabilizing RRM–ssRNA complexes, independent of the mode of RNA binding. The magnitude of the electrostatic contribution due to ion-release is the same in three of the four complexes. The flexibility of the single-stranded nucleic acid most likely dominates the energetic contributions due to the polyelectrolyte effect.

Flexible β₂/β₃ loop and N- or C-terminal segments strongly mediate ionic interactions

Residues identified to participate in ionic bond formation in SRSF1 pseudo-RRM2–ssRNA, Tra2β1 RRM–ssRNA and hnRNP A1 RRM1–ssRNA complexes are located in two specific regions; the β2/β3 loop, and one of the terminal segments (N- or C-; Figure 1). This conclusion is further supported by the observation that the hnRNP F qRRM1–ssRNA complex, which cannot form ionic bonds, lacks positively charged residues at the N-terminal extremity and the C-terminal segment participates in a hydrophobic core that hinders ionic bond formation (Figure 1). In agreement with this conclusion, residues R194 and K156 that form important ionic contacts with the RNA in Fox-1 are located at the C-terminal end and the β2/β3 loop respectively (69). The other two residues forming ionic bonds (R127 and R184) are located at the β₁/α₁ and α₂/β₄ loops in accordance with the unusual binding mode of Fox-1 in which these two loops and the β-sheet surface are involved in binding. In further support to our conclusion, K50 that is located in the β2/β3 loop of the U1A RRM1 (that binds RNA canonically) was shown to be important for the electrostatic attraction of the RNA into the binding site on the basis of a combination of mutagenesis and surface plasmon resonance studies (78,79). We therefore conclude that the β2/β3 loop region of the different RRMs could be a conserved source of electrostatic stabilization due to ion-release, which could predominantly account for the fact that rates of RRM-RNA association are enhanced by about three orders of magnitude compared to the rates expected for macromolecules of the same size (11). The structural conservation of ionic contacts to the β2/β3 loop reinforces the conclusion that the different RNA binding modes predominantly share the same electrostatic signature.

CONCLUSION

Our comparative study on RNA recognition by different modes of RRM–RNA recognition established that different RNA binding modes employ diverse thermodynamic strategies to sequence-specifically bind to cognate RNAs, despite the fact that they adopt the same protein fold, recognize similar sequence motifs and bind with similar binding affinity.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Swiss National Science Foundation National Center of Competence in Research (SNF-NCCR) in Structural Biology (51NF40-117229 to F.A.) and SNF (31-115982 to I.J.). Funding for open access charge: The open access publication charge for this paper has been waived by Oxford University Press - NAR Editorial Board members are entitled to one free paper per year in recognition of their work on behalf of the journal.

Conflict of interest statement. None declared.