Predicting the kinetics of RNA oligonucleotides using Markov state models

Abstract

Nowadays different experimental techniques, such as single molecule or relaxation experiments, can provide dynamic properties of biomolecular systems, but the amount of detail obtainable with these methods is often limited in terms of time or spatial resolution. Here we use state-of-the-art computational techniques, namely atomistic molecular dynamics and Markov state models, to provide insight into the rapid dynamics of short RNA oligonucleotides, in order to elucidate the kinetics of stacking interactions. Analysis of multiple microsecond-long simulations indicates that the main relaxation modes of such molecules can consist of transitions between alternative folded states, rather than between random coils and native structures. After properly removing structures that are artificially stabilized by known inaccuracies of the current RNA AMBER force field, the kinetic properties predicted are consistent with the timescales of previously reported relaxation experiments.

Introduction

The importance of ribonucleic acid (RNA) in molecular biology is constantly growing, as researchers discover new roles played by non-coding RNAs in the cell.¹ In many cases RNA function relies on complex multi-step conformational transitions that occur in response to cellular signals,² calling for an effort in determining not only RNA structure but also RNA dynamics. RNA stability depends on a large variety of interactions, including stacking, hydrogen bonding, and interactions with water and ions.³ In vacuum, stacking interactions arise from complex interactions between aromatic rings.⁴ However, in biological environment these interactions are heavily mediated by water. Dinucleotides and short oligonucleotides are perfect models to study stacking in RNA. While the equilibrium properties have been extensively characterized by NMR measurements^5–13 their kinetics have been only studied in a limited number of temperature-jump (T-jump) experiments.^14–16 Molecular dynamics (MD) provides a tool that can be used to characterize in detail the time evolution of these systems at picosecond and Angstrom resolution, and can supply insightful fine-detailed information that can complement experimental measurements.¹⁷ Several MD studies on RNA oligonucleotides have been published to date (see, e.g., refs.^{10,11,13,18–23}). MD was also used to characterize the stacking free energy associated with base fraying²⁴ and the stacking thermodynamics in DNA.²⁵ However, all these works were focused on the equilibrium properties rather than on the relaxation times. Kinetics of RNA tetraloops have been investigated,²⁶ but the complexity of the system led to unconverged results.

In this work we present a systematic analysis of the kinetic processes for RNA oligonucleotides, as predicted by MD simulations. We used Markov state models (MSMs) and hidden Markov models (HMMs), to provide a complete description of the transitions characterized by the slowest relaxation times. We studied a number of dinucleoside monophosphates, a trinucleotide (AAA), and a tetranucleotide (AAAA) so as to characterize the dependence of kinetics on length and sequence. Results are compared with available experiments. Whereas some of the reported transitions correspond to known artifacts of the current force field, our results can explain the overall trends. Importantly, we suggest that measured autocorrelation times may not be directly associated to transitions between helix and coil structures but to transitions between kinetic traps characterized by different stacking patterns.

Methods

Molecular dynamics simulations

MD simulations were run with different salt concentrations, ionic strength, sequence, and oligonucleotide length. The dinucleotides and trinucleotide simulations were performed using GROMACS 4.6.7.²⁷ The tetranucleotide simulation was run using AMBER 11.²⁸ We used AMBER force-field parameters²⁹ with parmbsc0³⁰ and χOL3³¹ corrections. Trajectories of di- and tri-nucleotides were generated in the isothermal-isobaric ensemble using stochastic velocity rescaling³² and the Parrinello-Rahman barostat.³³ Thermostat and barostat used in AAAA simulations are described in.¹³ RNA molecules were solvated in explicit water (TIP3P parameters³⁴), adding Na⁺ counterions to neutralize the RNA charge, plus additional NaCl to reach the nominal concentration. Details of all simulations are reported in Tab. 1. For each of the studied systems we ran several MD simulations, starting from different initial configurations, and stored on the disk frames with the time stride indicated in Tab 1.

Table 1.

Details of the MD simulations and of the MSM construction.

Sequence	T(K)	Na + (M)	N. traj.	Total length (μs)	Stride (ps)	TICA lagtime (ns)	TICA dimensions	Total N. of microstates	MSM lagtime (ns)	N. of active microstates
CC	277	1.0	4	9.6	10	1.0	10	400	0.5	367
AC	277	1.0	4	9.7	10	1.0	10	400	0.5	374
CA	277	1.0	4	9.1	10	1.0	10	400	0.5	381
AA	277	1.0	4	8.9	10	1.0	10	400	0.5	397
CC	300	1.0	8	7.0	10	1.0	10	400	0.5	377
AC	300	1.0	8	7.0	10	1.0	10	400	0.5	375
CA	300	1.0	8	6.6	10	1.0	10	400	0.5	383
AA	300	1.0	16	7.0	10	1.0	10	400	0.5	398
AAA	300	0.1	17	57.0	100	5.0	19	100	5.0	100
AAAA	275	0.13	4	35	100	5.0	44	400	20.0	399

Markov state model

MSMs are powerful tools that enable extraction of relevant kinetic information from multiple MD simulations. See^35–37 for a brief introduction to this topic, or^38,39 for a more detailed discussion. Here we summarize the basic concepts which are relevant for the present work.

The idea behind a MSM is to reduce the complexity of an MD simulation by dividing the phase space into discrete microstates (e.g. clustering the frames of the trajectory). It is then possible to compute the transition matrix, whose elements, T_{i j}, represent the probability that the system, starting from microstate i, will transition to microstate j after a time, τ.

If these microstates are obtained by a sufficiently fine discretization of the slow collective coordinates of the system, powers of this transition matrix can model the long-time evolution of the dynamics, i.e. the kinetics and stationary behavior of the system, with excellent accuracy.³⁸

By performing a spectral analysis of matrix T we can decompose the dynamics of the system into independent processes, each represented by the ith eigenvector of T.³⁸ The timescales of such processes can be computed from the eigenvalues, λ_i, of T as

$$t_i=-\frac{\tau }{ln\left|{\lambda }_i\right|}$$ (1)

In order to analyze the trajectories produced from the MD we considered the following set of coordinates:

1. G-vectors (4D vectors connecting the nucleobases ring centers, as described in⁴⁰)

2. Backbone dihedrals

3. Sugar ring torsional angles

4. Glycosidic torsional angles

The dimensionality of the input data was then reduced using time-lagged independent components analysis (TICA).^41–43 Data were projected on the slowest time-lagged independent components (TICs) using a kinetic-map projection⁴⁴ and then discretized in microstates using a k-means clustering algorithm.⁴⁵ A lag-time τ was used to construct MSMs that approximate the dynamics of the discretized systems. Detailed balance was imposed by constructing reversible MSMs using the procedure described in Ref.³⁸ Statistical uncertainties were estimated by means of the Markov chain Monte Carlo sampling of transition matrices from the posterior distribution, with a reversible prior, as described in.⁴⁶ All details and parameters used in the MSMs construction are reported in Tab. 1. Preliminary tests on selected systems showed that the results of our models do not vary significantly when changing the values of such parameters (data not shown). The MSM construction and analysis was performed using the software PyEMMA 2.2.⁴⁷

Combined discretization of dinucleotides trajectories

Since the dinucleotide systems share the same number of residues and the same backbone, the number of coordinates is the same for all of them. This can be exploited to perform TICA on a virtual trajectory obtained merging all the individual trajectories of the dinucleotides. We discretized the merged trajectories using k-mean clustering. For each dinucleotide system, we then built a separate MSM. Since not all microstates are visited by all the eight systems, each of the resulting MSMs will be defined on a subset of the total number of microstates, that we call “active set”. From Tab. 1 we notice that the fraction of active states is always close to 1, indicating that the systems share several common features.

Analysis of the kinetics

From the eigenvectors and the eigenvalues of the transition matrix of an MSM we can obtain detailed information about the slow processes occurring during the simulations, as well as a precise estimation of their predicted timescales.

The eigenvectors of the different dinucleotides’ MSMs were then compared using an appropriate measure of similarity. Since the active sets of different MSMs is different we first mapped all the eigenvectors, ψ, to a common 400-dimensional space, defining

$${\stackrel{\sim }{\psi }}_i=\{\begin{array}{l}\sqrt{{(p_{eq})}_i}{\psi }_i\text{if}i\in A\hfill \\ 0\text{otherwise}\hfill \end{array}$$ (2)

Here, i is the index of the microstate, A is the set of active microstates, and p_eq is the stationary distribution of the MSM considered. The eigenvectors are normalized so that ${\mathrm{\sum }}_i{\stackrel{\sim }{\psi }}_i^2=1$. We then compute the similarity between two eigenvectors, ψ̃^α, ψ̃^β, from different MSMs as the square of their scalar product, (ψ̃^α · ψ̃^β)². We also used kernel principal components analysis (KPCA)⁴⁸ to project the first three eigenvectors of the eight dinucleotides’ MSMs on a 2-D surface, in order to visually group similar processes from different MSMs. As kernel definition we used Φ(ψ̃) = ψ̃ ⊗ ψ̃, where ⊗ denotes the outer product. This is invariant for changes in sign of ψ̃. This analysis was possible since the MSMs share a common set of microstates, given that the clustering was performed on the joint set of MD data of all dinucleotide systems.

As a further analysis of the dinucleotides’ slow processes, we computed the correlations of these eigenvectors with all the dihedral angles of the dinucleotides. The variables with the highest correlation coefficient with a given eigenvector should be the best suited to describe the correspondent transition (as explained in⁴²). To avoid ambiguities due to the periodicity of dihedrals we compute the correlation between eigenvector ψ and torsion θ as max_η[corr_t (ψ_t, cos(θ_t + η))], where ψ_t is the value of the eigenvector ψ on the microstate visited by the system at time t, θ is the value of the torsion at time t, corr_t indicates the Pearson product-moment correlation coefficient computed considering all the frames in the MD trajectories.

The major non-bonded interaction in short oligonucleotides is the stacking interaction between consecutive nucleobases. In order to study this we used the stacking definition proposed in,¹³ that takes into account 1) the distance between the centers of mass of the two nucleobases, 2) the angle defined by the distance vector between the two centers of mass and the vector normal to the first base plane, 3) the angle between the two vectors normal to the two bases’ planes. These quantities are combined in a score, s, that goes from −2 to +2. Nucleotides are considered stacked if s > 1, unstacked otherwise.

The definition used for stacking contains terms that affect UV absorption.⁴⁹ For comparing the time dependence of conformational changes predicted with MD simulations with those measured experimentally, however, it is not necessary to quantify the change in absorption. It is only necessary to assume that different states will have different absorbances.

To further simplify the tri- and tetranucleotide models and analyze their features we used the kinetic information from the MSMs to lump the microstates into a few metastable macrostates. This was done using a HMM, as described in.⁵⁰ The idea of this method is to model the system as a Markov chain between a small number of hidden macrostates, each of which has a different probability distribution to generate one of the output microstates, which are the ones observed in the simulation. The parameters that define a HMM are the transition probabilities between hidden states and the probabilities of observing each microstate given the current hidden macrostate of the system. The optimal values of these parameters can be found via a likelihood-maximization procedure, that we carried out using the dedicated algorithm included in PyEMMA 2.2.⁴⁷ The resulting metastable macrostates were then analyzed by looking at the distributions of selected observables (dihedrals, distances between key atoms, G-vectors,⁴⁰ and stacking score¹³ between bases).

Comparison with relaxation experiments

MSM predictions can be compared with relaxation experiments that probe the kinetics of biomolecules. An exhaustive explanation of the theory behind this comparison is given in Refs.^51,52 Here we will briefly summarize the key concepts.

Consider a system described by a MSM with n microstates and transition matrix T. In a typical relaxation experiment a perturbation of the thermodynamic state of the system (e.g. a change in temperature) results in the starting distribution, p₀, becoming out of equilibrium. The system then relaxes to its new equilibrium distribution. The relaxation process is monitored by measuring the evolution of an observable, A, which is a suitable function of the state of the system. The time-evolution of A during the relaxation process is given by

$$A(t)=A_{eq}+\sum _{i=2}^{n}exp\left(-\frac{t}{t_i}\right){\gamma }_i$$ (3)

Where A_eq is the value of A at the final equilibrium, and γ_i is the amplitude of the ith decay process, which in general depends both on the shape of p₀ and on the nature of the observable A. The decay constant of the ith process, t_i, is given by the ith implied timescale of the transition matrix governing the system’s dynamics.

Calculation of the amplitudes, γ_i, requires accurate knowledge of the initial state of the system. When this information is not available, the relaxation time can be approximated by the autocorrelation time of A(t), which is given by

$${\tau }_{\mathit{corr}}(A)=\sum _{i=2}^n{t}_i{c}_i$$ (4)

where the amplitudes, c_i, are closely related with the factors γ_i. See⁵¹ for a more detailed derivation.

Results

Dinucleotides CC, AC, CA, AA

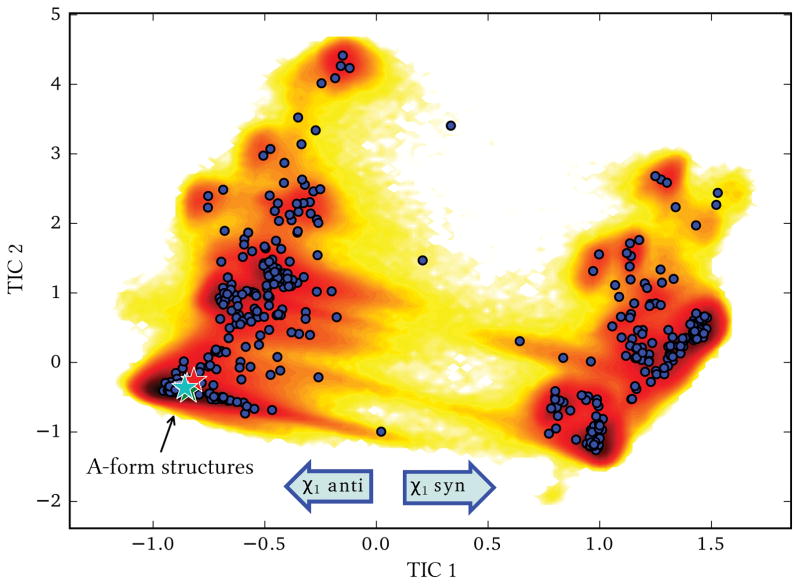
We here report the kinetic analysis performed on all the dinucleotides. Trajectories for all the investigated dinucleotides were merged together and analyzed with a single TICA. TICA provides a low dimensional projection for a complex data set, similarly to principal component analysis, but defined so as to maximize the autocorrelation times of its components. The complex phase space of the different dinucleotides can then be conveniently projected on the 2-D surface defined by the first two TICs (see Fig. 1).

Figure 1.

2-D histogram of the joint MD data of the 4 dinucleotides, projected on the first 2 TICs; blue circles represent the centers of the microstates obtained from the k-means clustering. The native A-form structures are indicated with stars.

An initial analysis of the TICA components and the trajectories shows that the 1st TIC classifies the structures based on the value of the torsional angle χ₁ relative to the rotation of the glycosidic bond of the 5′ nucleobase (anti=negative values, syn=positive values). This suggests that this isomerization is the slowest kinetic process in dinucleotides.

We then constructed a separate MSM for each of the investigated systems. The convergence of the MSMs was validated by monitoring the convergence of the implied timescales as a function of the lagtime (see Fig. SI 1). In Tab. SI 1 we report the slowest timescales of the nine resulting MSMs at the chosen lag-time of 0.5 ns.

The four dinucleotides exhibit different timescales. In particular, at temperature T = 277 K the largest timescales for CC and CA are in the order of 200–300 ns, whereas for AA and AC it is around 40 ns. The situation is analogous at T = 300 K, but the timescales are shorter, in agreement with expectations for higher temperatures.

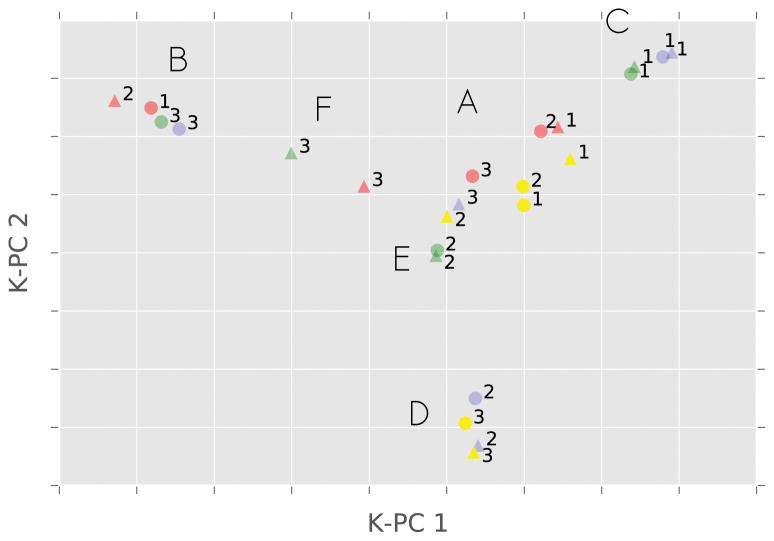
Fig. SI 2 shows the first three eigenvectors for each of the dinucleotides’ MSM, projected on the first two TICs. Since there are a large number of eigenvectors, it is convenient to exploit the fact that some of them share common features and define groups of similar processes occurring in different dinucleotides. In order to do this we evaluate the similarity of two eigenvectors using the square of their scalar product. A table summarizing the similarity between the eigenvectors relative to all systems is reported in Fig. SI 3. The KPCA algorithm was then used to project them on a 2-D plane where we can easily identify clusters of similar processes (Fig. 2).

Figure 2.

First three eigenvectors of each of the eight dinucleotides’ MSMs, projected on the plane defined by the first two directions identified by KPCA. Numbers indicate eigenvectors’ indexes. Colors indicate the sequence: CC (blue); AC (yellow); CA (green); AA (red). Shapes indicate the simulation conditions: T = 277 K (circle), T = 300 K (triangle).

Using the information from the 2-D projection shown in Fig. 2 and looking at the correlations between each eigenvector and the dihedrals angles (See fig. SI 4), it is possible to identify five groups of eigenvectors that share similar features between them and are separate from the main group (labeled as A) by the KPCA.

1. Group A This group collects together all the eigenvectors that are not classified in other groups by the KPCA.

2. Group B These eigenvectors represent the flipping of the χ₁ torsion. This process is extremely slow (200–300 ns at T = 277) when this nucleobase is a cytosine (CC and CA), while it is much faster (< 20 ns) when the base is an adenine (AA and AC). This effect is likely caused by the stabilization of the syn conformation due to a hydrogen bond between the carbonyl group of the cytosine at the 5′ end and the 5′OH in the corresponding ribose ring.

3. Group C These processes are related to the rotation of the dihedral χ₂. Cytosines at the 3′ end show a much faster dynamics (~30–40 ns at T = 277) than those at the 5′ end.

4. Groups D, E, F These processes are instead linked to the formation of specific structures. The conformation of the backbone in these structures is the same found in RNA Z-helices. They are in general characterized by γ₂ in trans conformation (γ₂ > 150° or γ₂ < −150°), and a low distance (< 0.4 nm) between the O4′ atom on the sugar ring of the 5′-end nucleotide and the center of mass of the 3′ base.⁵³ These three groups represent the formation of Z-motifs, that differ in the orientation of the χ₁, χ₂ glycosidic torsion or in the pathway of the process.

We notice that the identification of individual eigenvectors is arbitrary when the corresponding timescales are comparable within their respective statistical errors. For a more detailed discussion of this issue see the caption of Fig. SI 3.

As a further check of the robustness of our results, we tested the dependence on the ionic concentration of the MSMs of the dinucleotides, without finding any significative difference (data not shown).

Trinucleotide AAA

We here report the MSM obtained for the AAA trinucleotide. The MSM was validated with the implied timescales test (see Fig. SI 5). The MSM of the trinucleotide AAA identified a very slow process (t = 213 ± 9 ns). The fastest processes are dominated by two timescales around 40 ns (see Tab. S2). In order to gain further insight on the nature of the first three slow processes identified by the MSM, we coarse-grained the microstates space into 4 metastable sets, using an HMM. A schematic representation of the HMM is shown in Fig. 3 and Fig. SI 6.

Figure 3.

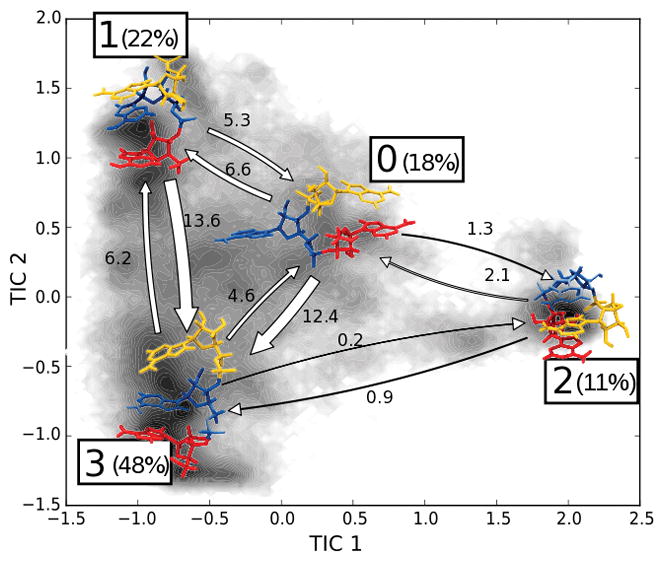
Schematic representation of the 4-state HMM of AAA. A1 (red), A2 (blue), A3 (yellow). Percentages indicate the equilibrium population of each state; the width of the arrows is proportional to the transition rate between the states which are also indicated in μs⁻¹ units. Shading indicates the distribution of the simulation data on the TICA plane.

A first observation about the HMM is that state #2 corresponds to a particularly stable state. The transition in and out of this state has a very large timescale (200 to 300 ns). The equilibrium populations of the four states is reported in Fig. 3.

In order to understand the nature of these four states we analyzed the distribution of key observables (angles, distances, G-vectors, and stacking score) in the different HMM states, see Fig. SI 7, SI 8, SI 9.

From this analysis we discovered that state #2 corresponds to an intercalated structure, in which base A3 stacks between bases A1 and A2. State #3 corresponds to the native state, with a single A-form helix conformation, having all χ torsions in anti conformation. State #0 acts as an intermediate state, often visited by the system before transitioning to state #2. In state #1 the sequence of stacking interaction is analogous to state #3, while the main difference lies in the orientation of base A2, that in state #1 corresponds to a syn conformation of the torsion χ₂.

We also noticed that a significant fraction of the structures corresponding to state #0 present an A1–A3 stacking. This state is nevertheless well separated kinetically from #2. In fact, while in state #2 the stacking of A2–A3 occurs simultaneously with the stacking of A1–A3, in the intermediate state #0 the two stacking interactions are never formed together.

We also observed a recurrent hydrogen bond forming between the non-bridging oxygen of the phosphate group of base 2 and the 5′ hydrogen of base 1, in the intercalated structures. Fig. SI 8 shows the distribution of the distance between these two atoms in the four metastable states, along with other pairs of atoms that may form hydrogen bonds. The formation of this hydrogen bond is clearly a fundamental step in the formation of the intercalated structures.

The distribution of the dihedral angles, particularly the couple α_i+1,ζ_i, is also informative, as shown in Fig. SI 9:

1. states #1 and #3 are characterized by α₂ and ζ₁ < 0

2. state #2 is characterized by α₂ and ζ₁ > 0

3. state #0 has α₂, ζ₁, α₃, and ζ₂ > 0

State #0 and #2 are also distinguished by the value of the angle χ₁ (syn in #0, high-anti in #2). The distributions of the three γ dihedrals do not vary significantly between the four metastable states, and we can exclude the presence of kinetically stable Z-motifs, in contrast with what was observed for the AA dinucleotide. We also checked that the occupation of any Na⁺ binding site is lower than 5% in all the metastable states.

Tetranucleotide AAAA

The analysis of the MSM of the AAAA tetranucleotide follows a scheme similar to that described for the trinucleotide. The complexity and the number of available conformations grow exponentially with the number of bases in an oligonucleotide. For this reason it is particularly challenging to sample all the relevant conformational space for a tetranucleotide using only plain MD.^19,20 In fact, even if our simulations have lengths of several microseconds, many transitions are observed only once. This reflects on the quality of the MSM, as it can be seen from the implied timescales plot (see Fig. SI 10), and leads to extremely large statistical uncertainties. From Tab. 1 we can also observe that one of the 400 microstates was not included in the MSM, since it was visited only once at the beginning of one MD trajectory, so that no entering event was measurable at the selected lagtime.

Nevertheless it is possible to qualitatively compare the predictions of the MSM for AAAA with those described above for shorter oligonucleotides.

The first two implied timescales exhibited by the system (see Tab. SI 3) are in the microseconds range (3.1 ± 1.1 and 1.3 ± 0.6 μs), and are associated with the formation of two different intercalated structures, analogous to the ones described for the trinucleotide. For AAAA, 2D NMR spectra show that intercalation is present in less than 5% of the population (see Fig. SI 11).

Again, to simplify the model we built an HMM, coarse-graining the MSM into 4 metastable macrostates (see Fig. SI 12). Fig. 4 shows a schematic representation of the HMM projected on the first two TICs. Also in this case the TICA identifies the formation of the intercalated structures (State #3) as the slowest process.

Figure 4.

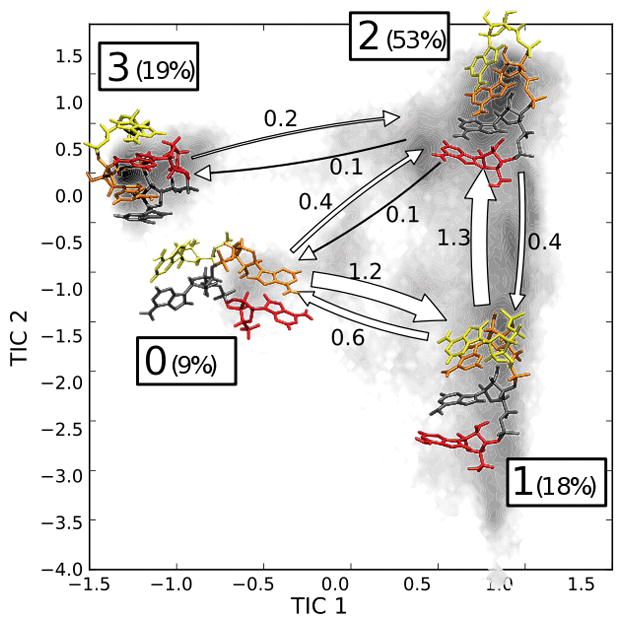
Schematic representation of the 4-state HMM of AAAA. A1 (red), A2 (blue), A3 (orange), A4 (yellow). Percentages indicates the equilibrium population of each state; the width of the arrows is proportional to the transition rate between the states which are also indicated in μs⁻¹ units. Shading indicates the distribution of the simulation data on the TICA plane.

Two of the resulting states (#1 and #2) display a canonical stacking pattern whereas the other two states (#3 and #0) are characterized by the stacking of non-consecutive bases (see Fig. SI 13). Specifically, state #2 contains the canonical A-form helix, whereas in state #1 base A3 is flipped to syn conformation. States #3 and #0 instead are distinguished by their stacking pattern, and they share the same features reported for trinucleotides, that is, α and ζ in g+ conformation and the presence of stabilizing hydrogen bonds with non-bridging oxygens (Fig. SI 14, SI 15). State #3 contains intercalated structures analogous to the one reported in previous works,^{11,13,19,22,54} while state #0 presents A2 and A4 flipped out and stacked on each other. It is reasonable to expect other combinations of base orientation and stackings to arise when increasing the sampling.

Unfortunately the large statistical errors in the HMM timescales make it difficult to discriminate quantitatively the different processes, and to clearly assign an implied timescale to each of them.

Comparison with Temperature-jump experiments

The timescales predicted by our MSMs can be compared with relaxation times measured using T-jump experiments in.¹⁵ A proper comparison should follow the procedure explained in,⁵¹ where the relaxation of an experimental observable can be decomposed in exponential contributions coming from each MSM eigenvector. This requires knowledge of the experimental observable. In¹⁵ the relaxation is measured with UV absorption. We modeled this using the stacking score proposed in.¹³ To estimate the relaxation rate without the need of further assumptions on the equilibrium distribution of the systems prior to T-jump, we computed the autocorrelation time of the stacking score.

The results of this calculation are reported in Tab. 2, along with the experimental relaxation times measured in.¹⁵ For AAA and AAAA we report the autocorrelation time (Eq. 4) relative to the slowest stacking interaction (A1–A2 for AAA, A1–A3 for AAAA). We excluded from the calculations the contributions of the formation of intercalated/non-canonical structures, since the increased stability of such structures is a known limitation of the current force field.^{11,13,19,22,54} This was done by using Eq. 4 and setting to zero the amplitudes, γ_i, of the relative processes. As a cross check for this procedure we also constructed a new MSM where we remove from the active set the intercalated microstates, identified from the analysis of the sign of the relevant eigenvectors of the original MSM. The resulting timescales and autocorrelation times are within the statistical error of the ones derived with the original MSM (data not shown).

Table 2.

Autocorrelation times of the stacking score predicted by the different MSMs, compared with the experimental relaxation times (1 M Na⁺).

Molecule	τ (ns)	Exp. (ns)15
T = 277 K
CC	24 ± 2	30 ± 6
AC	9 ± 1	42 ± 8
CA	25 ± 1	30 ± 6
AA	9.1 ± 0.2	50 ± 10
AAAA	171a,b ± 26	-
T = 300 K
CC	7.2 ± 0.4	-
AC	3.44 ± 0.03	-
CA	4.8 ± 0.1	-
AA	3.36 ± 0.04	29c ± 6
AAA	25.8 ± 0.4	45c ± 9
AAAA	-	270c,d ± 27 (20%)
	-	47c,d ± 5 (80%)

^aSimulations performed at 275 K.

^bValue for A1–A3 a stack not observed by NMR;¹³ values for A1–A2, A2–A3, and A3–A4 are 78 ± 16, 81 ± 16, and 92 ± 26 ns, respectively.

^cExperiments performed at 297 K.

^dRef.¹⁵ reports two relaxation times, with the relative amplitudes shown in brackets.

We notice that the contributions of the slow modes of CC and CA to the stacking score kinetics are extremely small, since the autocorrelation time is almost ten times shorter than the associated timescale (Tab. SI 1). The values of τ_corr predicted for CC, CA, AAA and AAAA are in good agreement with the experimental relaxation times. On the other hand, the values obtained for AA and AC are significantly shorter than the experimental values.

The T-jump relaxations at 297 K reported in¹⁵ also included a long relaxation time of 600–900 ns for A₂, A₃, A₄, A₅, and A₁₄ in 1 M Na⁺ when the transition was probed with > 280 nm light. In the same study, relaxation times of 200 ± 20 ns and 700 ± 140 ns were reported for poly(A) in 0.2 M Na⁺. These experiments were conducted with a cable discharge temperature jump apparatus where up to 200 kV/cm is transiently applied to the sample.¹⁴ An independent study using a laser induced temperature jump of poly(A) in 0.2 M Na⁺, T = 298 K, however, reported only a 270 ± 70 ns relaxation at 285 nm.¹⁶ None of the MD simulations of A₂ and A₃ generated a timescale longer than 300 ns. It is therefore possible that the high electric field in the cable discharge experiments somehow affected the RNA, leading to the appearance of an artifactual relaxation process.

Discussion

What can we learn from this analysis about the kinetic properties of oligonucleotides?

The slow implied timescales observed for CC and CA are one order of magnitude longer than the experimental relaxation times (Tab. SI 1). These timescales are related to the transition from anti to syn of the cytosine at the 5′ end and are likely caused by the formation of a hydrogen bond between the carbonyl group of the cytosine at the 5′ end and the 5′OH in the corresponding ribose ring. An explanation for this inconsistency may be found in the inaccuracy of the force field, which is a known limitation in the field of MD simulations of RNA. Syn cytosines are rare in non-catalytic RNAs⁵⁵ and may be over represented in simulations. However, we notice that it was not necessary to remove these timescales to obtain a reasonable agreement between the autocorrelation time of the stacking score and the experimental relaxation times. This is essentially due to the fact that these slow syn/anti flips are poorly correlated with the stacking score.

The slowest timescales observed in AAA and AAAA are related to the formation of kinetically stable intercalated structures. For AAAA the presence of a significant population of intercalated structures in solution has been ruled out by careful interpretation of the NOE data.^11,13 In these experiments, all the observed signals have similar linewidths and only non-exchangeable protons are analyzed allowing the contacts predicted from the intercalated structures and not observed in the experimental spectrum to be used in the characterization of the structural ensemble.⁵⁶ A portion of the 2D NOESY spectrum of AAAA is reported in Fig. SI 11. This inconsistency suggests that this metastable structure is an artifact of the simulation, likely caused by an imperfect parametrization of the force field. Analysis of the intercalated states revealed some structural details that seem to play a crucial role in stabilizing these structures. In particular these are 1) the formation of a hydrogen bond between the non-bridging oxygen of the phosphate group of one nucleotide and a hydroxyl from another nucleotide¹³, 2) the transition from negative to positive of the torsional angles α_i+1, ζ_i (see Fig. SI 9, SI 15). We propose that this information must be kept in mind when trying to modify the parameters to improve force-field accuracy. In particular it has been shown that tuning the parametrization of the dihedrals α and ζ significantly improves agreement with NOE data for several tetranucleotides and tetraloops.^22,23,57 We observe that the overstabilization of intercalated structures might also be related to an overestimation of stacking interactions in the AMBER force field that has been suggested in ref.⁵⁸ In the present work, to obtain reasonable kinetic properties without performing new simulations with a corrected force field we found it necessary to remove these structures from the ensemble.

Once the unphysical structures and transitions have been removed from the MSM, it is possible to use the remaining eigenvalues and eigenvectors to estimate the experimental relaxation times. It is important to recall that for an appropriate comparison with experimental data it is necessary to define an observable that is proportional to the measured intensity. We here used the stacking score defined in ref.¹³ The autocorrelation time of this score is reported in Tab. 2 and can be directly compared with experiments, with which it is in good agreement. It must be mentioned that the self-diffusion coefficient of the TIP3P water model is approximately 2.5 times larger than the experimental one.^59,60 This might induce an artificial acceleration of processes depending on water rearrangement. Considering experimental error, the largest difference between autocorrelation times and experimental relaxation rates may be as small as 7-fold, corresponding to a difference of 1 kcal/mol in activation free energy at 300 K.

The virtual removal of structures that we considered to be artificially stabilized by inaccuracies in the force field was instrumental in achieving an agreement with experimental timescales. This removal has been justified by comparison with NMR experiments. We suggest that force field refinements should be mainly driven by comparison with equilibrium experiments in solution, as it has been done in a very recent work.²³ Hypothetically, a correction to the force field that fixes these problems might also affect the transition rates. However, corrections designed to penalize specific rotamers as those used in refs^22,23,57 are not expected to affect the transition rates between non-penalized metastable states. Moreover, once the force field has been refined so as to provide equilibrium populations in agreement with solution data, possible mismatches between the predicted time scales and the relaxation times observed in experiments might be used to identify errors in the parametrization of energetic barriers and suggest further refinements.

For the dinucleotides and trinucleotide we additionally assessed the influence of Na⁺ ions. Our results confirm that monovalent ions do not play any significant role in the kinetic of RNA oligonucleotides, as was also reported in Ref.¹⁵ We notice that in a previous work we did not find a significant dependence of RNA dynamics on monovalent ion concentration.⁶¹

In general, the predicted relaxation time in all the considered systems is not determined by the rate of the helix ↔ coil transition. It is instead related to the rate of transitions between different structures, stabilized by stacking or other kinds of interactions. Examples of this are the Z-motifs in dinucleotides, or helices with flipped nucleotides in longer sequences. This suggests that the timescales obtained from relaxation experiments of oligonucleotides may be due to transitions between different “folded states”, rather than between stacked, native structure and random coil. That is, these relaxation rates are dominated by the presence of various “kinetic traps”, i.e. kinetically stable structures where the system may get stuck for a relatively long time before being able to reach its minimum free-energy conformation.

This paper demonstrates how MD simulations and MSMs can be used to provide deeper interpretation of experimental measurements of the kinetics of RNA folding. While most experimental methods report weighted averages for an ensemble of structures, MD follows transitions of a single molecule at atomistic resolution. If the simulations are statistically converged, then the results from MSM analysis can be compared to experimental measurements. Although current RNA force fields do not accurately predict structural ensembles,^13,19 the results presented here suggest that the latest AMBER force field can reproduce the order of magnitude of T-jump relaxation times^15,16 measured for short oligonucleotides. Most current tests of force fields use structural data from NMR and x-ray diffraction as benchmarks. The results presented above indicate that comparison to experimental kinetic data can provide new benchmarks in the future. Moreover, when MD simulations accurately predict structures, they can generate more detailed interpretations of experiments and suggest new experiments to test hypotheses.

Other Information Available

Trajectories and analysis scripts used in this paper are available at http://github.com/srnas/oligonucleotides-kinetics.