Modeling Molecular Interactions in Water: From Pairwise to Many-Body Potential Energy Functions

Abstract

Almost 50 years have passed from the first computer simulations of water, and a large number of molecular models have been proposed since then to elucidate the unique behavior of water across different phases. In this article, we review the recent progress in the development of analytical potential energy functions that aim at correctly representing many-body effects. Starting from the many-body expansion of the interaction energy, specific focus is on different classes of potential energy functions built upon a hierarchy of approximations and on their ability to accurately reproduce reference data obtained from state-of-the-art electronic structure calculations and experimental measurements. We show that most recent potential energy functions, which include explicit short-range representations of two-body and three-body effects along with a physically correct description of many-body effects at all distances, predict the properties of water from the gas to the condensed phase with unprecedented accuracy, thus opening the door to the long-sought “universal model” capable of describing the behavior of water under different conditions and in different environments.

1. Introduction

Computer simulations have become an indispensable tool for characterizing the properties of water at the molecular level, often providing fundamental insights that are otherwise difficult to obtain by other means. However, both the realism and the predicting power of a computer simulation directly depend on the accuracy with which the molecular interactions and the overall system dynamics are described. Rigorously, realistic computer simulations of water should include an accurate representation of the underlying Born–Oppenheimer potential energy surface (PES) in combination with a proper treatment of the nuclear motion at a quantum-mechanical level.¹⁻³ Along these lines, different theoretical and computational approaches have been proposed, which can be conveniently separated in two main groups depending on how the water PES is described. The first group includes simulation approaches that use a set of predefined analytical functions to represent the underlying PES of the water system of interest as a function of the corresponding molecular coordinates. These analytical potential energy functions are historically referred to as “force fields”.⁴⁻⁸ The second group includes the so-called “ab initio” approaches in which the water PES is obtained “on the fly” by performing quantum-chemical calculations to solve the electronic time-independent Schrödinger equation for a given molecular configuration.⁹⁻¹⁴ Ab initio approaches can be further distinguished in methods based on wave function theory (WFT) and density functional theory (DFT). Independent of how the water PES is represented, the nuclear dynamics can then be described at the classical level using Newton’s equations of motion or at the quantum-mechanical level by solving the corresponding nuclear time-dependent Schrödinger equation using grid methods, wave packets, semiclassical approaches, and methods built upon Feynman’s path-integral formalism.¹⁵⁻²¹

As part of this thematic issue “Water - The Most Anomalous Liquid”, this article reviews recent progress in the development and application of analytical potential energy functions (PEFs) that aim at correctly representing many-body effects in water from the gas to the liquid phase. Specific focus is on different classes of PEFs built upon a hierarchy of approximate representations of many-body effects and on their ability to accurately reproduce reference data obtained from state-of-the-art (i.e., correlated) electronic structure calculations. With this objective in mind, we introduce and describe the many-body expansion (MBE) of the interaction energy in section 2. Purely pairwise PEFs are only briefly mentioned in section 3, while different classes of many-body PEFs are described in section 4. Within each class, the accuracy of the individual PEFs is assessed systematically through the analysis of the energetics of water clusters for which correlated electronic structure calculations are possible. To determine how the accuracy of each PEF in representing the fundamental interactions between water molecules translates into the ability of the same PEF to reproduce measurable quantities, comparisons with experimental data for representative structural, thermodynamic, and dynamical properties of liquid water are also discussed. Although the ability to correctly reproduce the experimental data is the ultimate goal of a computer simulation, “getting the right results for the right reasons” is even more important for the correct interpretation of the underlying molecular mechanisms. We will show that the apparent perfect agreement with the results of experimental measurements that are mainly sensitive to the average molecular behavior is often the result of error cancellation between different many-body contributions to the total interaction energy. These deviations from the actual Born–Oppenheimer PES effectively preclude a rigorous and quantitative interpretation of the experimental measurements, which has led, in the past, to the proliferation of water models. As discussed in section 4, the advent of explicit many-body PEFs holds great promise for a physically correct, molecular-level description of the properties of water across different phases. Building upon recent achievements and, in several cases, unprecedented accuracy of many-body PEFs, future development and applications to aqueous systems are presented in section 5.

2. Many-Body Expansion of the Interaction Energy

The global PES of a system containing N interacting water molecules can be formally expressed in terms of the many-body expansion of the interaction energy as a sum over n-body terms with 1 ≤ n ≤ N,²²

1

where r_i collectively denotes the coordinates of all atoms of the ith water molecule. In eq 1, V_1B is the one-body (1B) potential that describes the energy required to deform an individual molecule from its equilibrium geometry. All higher n-body (nB) interactions, V_nB, are defined recursively through

2

The PEFs developed for computer simulations of water can be conveniently classified according to the level of approximation used to represent the different terms of eq 1. Starting with the 1B term, most common, and least realistic, force fields assume rigid geometries for the water molecules, with intramolecular flexibility being explicitly taken into account only in more sophisticated energy expressions. The different treatment of the V_1B term thus leads to a separation of the existing PEFs in two main groups, the “rigid-monomer” and the “flexible-monomer” PEFs. Within each group, analytical PEFs for water can be further distinguished based on how all V_nB terms of eq 1, with n > 1, are described.

Most common force fields only include up to the two-body (2B) term and assume that the sum of pairwise additive contributions provide a sufficiently accurate representation of the actual multidimensional Born–Oppenheimer PES. In the so-called “effective” pair potential energy functions, all three-body (3B) and higher-body contributions are merged into an effective 2B term. Analytical PEFs that are obtained by fitting to experimental data, commonly referred to as “empirical” force fields, are most often of this type. Experimental data may also be combined with results from quantum chemical calculations to fit empirical force fields. Alternatively, analytical PEFs can be systematically derived by fitting to electronic structure data for water dimers, trimers, etc. In this case, the application of eq 1 leads to ab initio representations of the multidimensional Born–Oppenheimer PES. If the fit is carried out only on dimer energies, the many-body expansion of the total interaction energy is truncated at the 2B level, resulting in a strictly pairwise additive representation of the PES. In most analytical PEFs that go beyond the pairwise approximation, higher-order terms are collectively represented through classical many-body polarization.

More recently, ab initio PEFs including explicit 3B terms have also been developed. For water in the condensed phase, many-body interactions are responsible for nontrivial effects, which may either lower (cooperative effects) or increase (anticooperative effects) the total interaction energy relative to the sum of all pairwise contributions. Several systematic studies of the interaction energy for small clusters carried out using electronic structure methods shows that eq 1 converges rapidly for water. However, nonadditive effects are generally nonnegligible,²²⁻³¹ with 3B contributions being as large as ∼15–20% of the total interaction energy for cyclic structures. Four-body (4B) effects are responsible, on average, for ∼1% of the total interaction energy.^23,29−31 Taking advantage of the rapid convergence of eq 1, a novel computational scheme, called “stratified approximation many-body approach” or SAMBA, has recently been shown to provide highly accurate interaction energies for water clusters through the application of progressively lower-level electronic structure methods to subsequent terms of the MBE.³¹

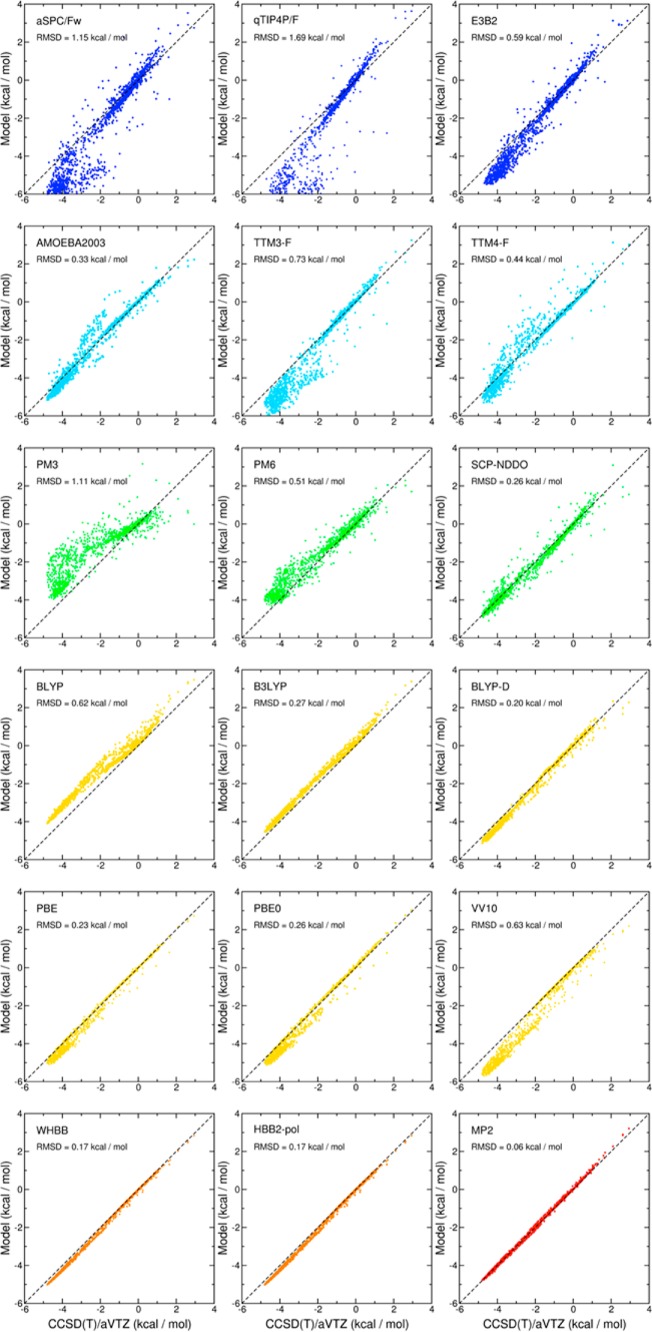
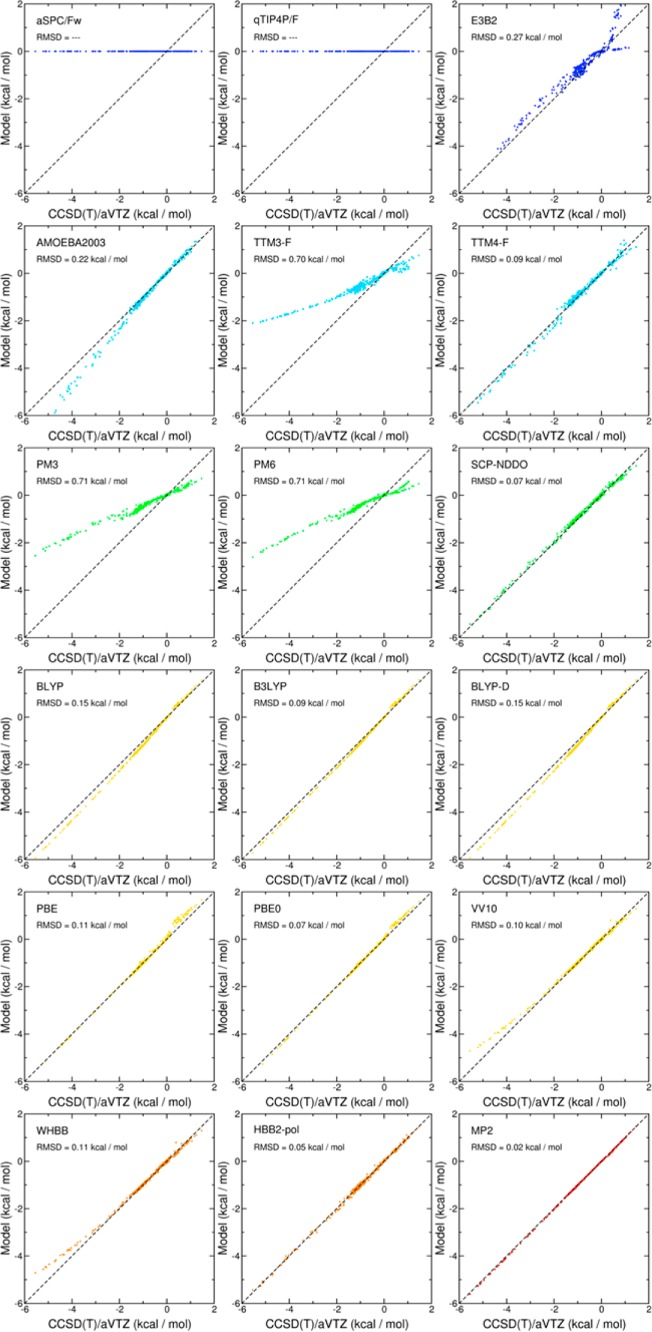
Besides representing a rigorous approach to the development of analytical PEFs for molecular systems ranging from the gas-phase dimer to small clusters and the liquid phase, the MBE in eq 1 also provides a quantitative way to assess the ability of existing models in describing the water interactions. In this context, Figures 1 and 2, which are derived from the analysis originally reported in ref (32), show correlation plots between 2B and 3B reference interaction energies with the corresponding values calculated using several empirical nonpolarizable (blue) and polarizable (light blue) force fields, semiempirical methods (green), DFT models (yellow), explicit many-body PEFs (orange), and second-order Møller–Plesset (MP2) theory (red). The reference energies were calculated at the coupled cluster level including single, double, and perturbative triple excitations [i.e., CCSD(T)] with the aug-cc-pVTZ basis set^33,34 and corrected for the basis set superposition error (BSSE) using the counterpoise method.³⁵

Figure 1.

Correlation plots for 2B interaction energies. Plotted on the x axes are the BSSE-corrected CCSD(T) reference energies calculated with the aug-cc-pVTZ (aVTZ) basis set for ∼1400 water dimers. On the y axes are the corresponding energies calculated with the different water PEFs. Color scheme: empirical models = blue, polarizable models = light blue, semiempirical models = green, DFT models = yellow, explicit many-body models = orange, and MP2 = red. All data were taken from ref (32).

Figure 2.

Correlation plots for 3B interaction energies. Plotted on the x axes are the BSSE-corrected CCSD(T) reference energies calculated with the aug-cc-pVTZ (aVTZ) basis set for ∼500 water trimers. On the y axes are the corresponding energies calculated with the different water PEFs. Color scheme: empirical models = blue, polarizable models = light blue, semiempirical models = green, DFT models = yellow, explicit many-body models = orange, and MP2 = red. All data were taken from ref (32).

Since, by construction, the 2B term of the empirical pairwise additive PEFs (i.e., aSPC/Fw³⁶ and q-TIP4/F³⁷) tries to effectively compensate for the neglect of higher-order contributions, large deviations from the reference CCSD(T)/aug-cc-pVTZ values are found over the entire range of interaction energies considered in Figure 1. The explicit inclusion of 3B contributions (e.g., E3B2³⁸) and polarization effects (e.g., AMOEBA2003,³⁹ TTM3-F,⁴⁰ and TTM4-F⁴¹) clearly improves the agreement with the reference data at the 2B level and provides a more physically realistic description of higher-body effects. The comparison with the CCSD(T)/aug-cc-pVTZ data also indicates that the overall accuracy of the different polarizable models considered in this analysis is particularly sensitive to the specific functional form used to represent induction effects (see section 4.2).

Semiempirical models (e.g., PM3,⁴² PM6,⁴³ and SCP-NDDO^44,45) display similar accuracy as polarizable force fields, with the SCP-NDDO model, which includes an additional term describing induction interactions, providing the closest agreement with the reference data. In general, DFT models, including GGA without (e.g., BLYP^46,47 and PBE⁴⁸) and with (e.g., BLYP-D⁴⁹) dispersion corrections, hybrid (e.g., B3LYP⁵⁰ and PBE0⁵¹), and nonlocal functionals (e.g., VV10⁵²), predict 2B and 3B interaction energies in reasonably good agreement with the CCSD(T)/aug-cc-pVTZ values. Appreciable differences, however, can be found at the 2B level, which vary significantly depending on how exchange, correlation, and dispersion contributions are treated within each functional. The current status of DFT models for water has recently been reviewed in ref (259). Figures 1 and 2 also show that high accuracy, often superior than that associated with DFT models and comparable to that obtained at the MP2 level of theory, can be achieved by analytical many-body PEFs (e.g., WHBB⁵⁴ and HBB2-pol⁵⁵) that explicitly include 2B and 3B contributions derived from multidimensional fits to correlated electronic structure data and describe higher-order effects through (classical) many-body induction.

In the following sections, all different classes of many-body PEFs for water, which are built upon different levels of approximations to eq 1, are reviewed systematically in terms of their ability to accurately reproduce reference data obtained from both state-of-the-art electronic structure calculations and experimental measurements. The objective of this review article is to provide the reader with a comprehensive overview of modern PEFs that aim at modeling the molecular properties of water through a physically correct representation of many-body effects. Due to space constraints and considering that many of the PEFs described in this review are still under development, only a limited number of direct comparisons between different PEFs is presented. These comparisons, along with tables summarizing the “performance” of different PEFs in reproducing experimental data, are used to assess both merits and shortcomings of different theoretical and computational approaches to model many-body effects in water. The reader is referred to other articles of this thematic issue for specific applications of computer simulations to the study of structural, thermodynamic, and dynamical properties of water under different conditions and in different environments.

3. Pairwise Additive Analytical Potential Energy Functions

To date, pairwise additive PEFs, like the aSPC/Fw³⁶ and q-TIP4P/F³⁷ models of Figures 1 and 2, are the most common representations of the interactions between water molecules used in conventional computer simulations. By construction, these PEFs do not include an explicit treatment of many-body effects but approximate the total interaction energy through an effective 2B term that is empirically parametrized to reproduce experimental data. In addition, the vast majority of these PEFs, including the popular TIPnP⁵⁶⁻⁵⁸ and SPC*^59,60 families among many others, assume the water molecules to be rigid. Since this class of PEFs has recently been reviewed, it will not be further discussed here, and we direct the interested reader to refs (61) and (62) for specific details.

Building upon rigid-monomer parametrizations, intramolecular flexibility has also been added empirically to some of the most popular pairwise additive PEFs, which have then been employed in both classical and quantum molecular simulations.^{36,37,63−70} Although the overall performance of flexible force fields (e.g., the aSPC/Fw³⁶ and q-TIP4P/F³⁷ models) is comparable to that of the original rigid models, the inclusion of intramolecular flexibility enables a more direct assessment of nuclear quantum effects in determining both thermodynamic and dynamical properties.^37,66,69 The interested reader is directed to the review article in this thematic issue devoted specifically to the analysis of nuclear quantum effects in water.⁷¹

A different class of pairwise potentials can be derived from eq 1 relying only on ab initio data for the water dimers but still assuming rigid monomers. The first such potential, MCY, was developed by Matsuoka et al.⁷² The MCY potential was parametrized by fitting two analytical functions to reproduce the energetics of 66 water dimer structures calculated at the configuration interaction level including single excitations (CIS). The original MCY potential was subsequently used as a starting point for further improvements which led to the development of a new version of the potential with flexible monomers,⁷³ a refinement of the parameters based on the analysis of the vibrational frequencies,⁷⁴⁻⁷⁶ and other more general reparameterizations.⁷⁷ Several strictly pairwise PEFs, derived entirely from ab initio data, were proposed in the 1990s,^78,79 which served as a starting point for subsequent developments of rigorous many-body representations of the interaction energies (see section 4.3).

The MCY functional form was employed by Mas et al. to parametrize an analytical PEF for water using symmetry adapted perturbation theory (SAPT) calculations performed on over 1000 water dimers with rigid monomers.^80,81 Within the SAPT formalism, individual contributions to noncovalent interactions between two molecules can be directly determined through perturbation theory, avoiding separate calculations of monomer and dimer energies.⁸² Although SAPT provides a systematic decomposition of the total interaction energy into physically based components (e.g., electrostatics, exchange, induction, and dispersion), the water model developed by Mas et al. was directly obtained from a linear least-squares fit of the total energy to the MCY functional form.^80,81 The agreement between the calculated and measured second virial coefficient demonstrated the overall accuracy of the SAPT-derived PEF, which effectively represents the first attempt at using large sets of high-level ab initio data to construct an accurate representation of the 2B term of the MBE for water shown in eq 1.

When employed in computer simulations, both empirical and ab initio pairwise PEFs have been successful at reproducing at least some of the water properties, providing fundamental insights at the molecular level. However, by construction, pairwise representations of the total interaction energy suffer from intrinsic shortcomings that limit their transferability to more complex aqueous solutions and heterogeneous environments. These shortcomings are primarily associated with the specific functional form adopted by pairwise PEFs which, including only up to 2B contributions, neglect all many-body effects (see Figure 2).⁸³ Therefore, the logical next step toward accurate representations of the interactions between water molecules requires the development of analytical PEFs that include either implicitly or explicitly nonadditive effects arising from many-body interactions.

4. Many-Body Analytical Potential Energy Functions

4.1. Implicit Many-Body Potential Energy: Empirical Models

Several theoretical analyses based on electronic structure data have demonstrated that many-body interactions contribute, on average, ∼ 20% to the total interaction energy of water clusters, with 3B contributions representing up to ∼18%.^{22−30,84−86} As discussed in section 3, in pairwise PEFs such as those employed in the popular TIPnP⁵⁶⁻⁵⁸ and SPC*^59,60 force fields, many-body contributions are only represented in an effective way in a mean-field fashion.⁸⁷ This appears to be a reasonable approximation for a qualitative modeling of homogeneous aqueous systems like bulk water as shown by the success of some pairwise force fields in reproducing several structural, thermodynamic, and dynamical properties of liquid water.^61,62 Although it was shown that many-body effects can be decomposed, at least to some extent, into effective pairwise contributions using force-matching,⁸⁸ more recent studies have demonstrated that the explicit account of 3B effects is essential for a physically correct description of heterogeneous environments such as the air/water interface.^89,90

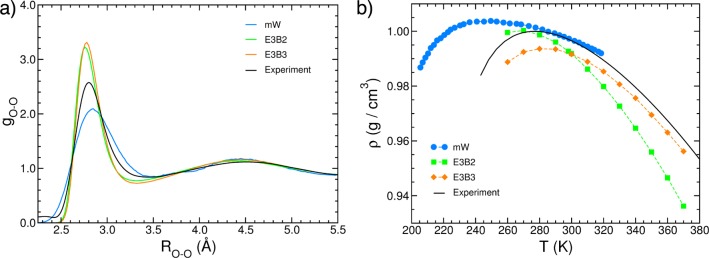
3B interactions have also been shown to play an important role in coarse-grained (CG) representations of the actual multidimensional Born–Oppenheimer PESs.⁹¹⁻¹⁰¹ By construction, many-body effects in CG models can hardly be accounted for by using only pairwise potential energy functions. For example, Johnson et al. derived coarse-grained effective pair potentials from simulations with the TIP4P-Ew rigid and nonpolarizable model⁵⁸ and demonstrated that pairwise CG models can reproduce some water-like anomalies but are unable to simultaneously reproduce structural and thermodynamic properties.¹⁰² A more quantitative representation of many-body effects in CG models of water can be achieved by adding an empirical 3B term to the pairwise expression of the interaction energy.^100,103 An example of CG representations including 3B effects is the mW model,¹⁰⁰ which adopts the same 2B and 3B energy expressions as the Stillinger-Weber model for silicon,¹⁰⁴ and was parametrized to reproduce the experimental melting temperature, enthalpy of vaporization, and density of liquid water at ambient conditions. The mW model qualitatively reproduces the structure (Figure 3a) and the temperature dependence of several thermodynamic properties of liquid water, including the density maximum at ambient pressure although the actual location is shifted to a slightly lower temperature relative to the experimental value (Figure 3b). It was also shown that mW is more accurate than some atomistic models (e.g., SPC/E, TIP3P, and TIP4P) in representing several thermodynamic properties, including the melting temperature of ice I_h, the liquid density at the melting point, the enthalpy of melting, and the surface tension.^100,105

Figure 3.

(a) Comparison between oxygen–oxygen radial distribution functions of liquid water at ambient conditions derived from X-ray diffraction measurements (black)¹⁰⁸ and calculated from molecular dynamics simulations performed with the coarse-grained mW model (blue)¹⁰⁰ and the empirical E3B models (green and orange).^38,107 (b) Comparison between the experimental and calculated temperature dependence of the density of liquid water at ambient pressure. The experimental values (black) are from ref (304).

Explicit 3B terms have also been introduced in atomistic force fields. For example, the E3B models utilize the TIP4P and TIP4P/2005 force fields as baseline PEFs to which an explicit three-body term is added to recover cooperative and anticooperative effects associated with different hydrogen-bonding arrangements.^38,106,107 Additional 2B terms are also added to the original pairwise expressions to remove spurious 3B contributions. The E3B2 model was parametrized to reproduce six experimental properties (diffusion constant, rotational correlation time, liquid density, surface tension, melting point, and ice I_h density).³⁸ The addition of an explicit 3B term was shown to improve the accuracy with which the properties of water in heterogeneous environments, including water clusters and the air/water interface, could be calculated.^38,89,106 The E3B2 model correctly reproduces several properties of the liquid phase, although the calculated oxygen–oxygen radial distribution function shown in Figure 3a appears to be too structured compared to the most recent results derived from neutron-diffraction measurements.¹⁰⁸ The static dielectric constant and low-frequency infrared spectra calculated with the E3B2 model for both liquid water and ice I_h are also in good agreement with the corresponding experimental data over wide temperature ranges, although one distinct fitting parameter is required for each phase.¹⁰⁹ A new parametrization of the E3B model (E3B3) has recently been introduced.¹⁰⁷ E3B3 is built upon the TIP4P/2005 force field and shows higher accuracy than the original E3B2 model, especially in reproducing the temperature dependence of structural and thermodynamic properties (e.g., the liquid density shown in Figure 3b). Although the E3B models represent an improvement over common pairwise additive force fields, a recent analysis of the heterodyne-detected vibrational sum-frequency generation (HD-vSFG) spectrum of the air/water interface in terms of many-body contributions suggests that, due to the empirical parametrization, 3B effects are possibly overemphasized in the E3B models.⁹⁰

4.2. Implicit Many-Body Potential Energy: Polarizable Models

Alternatively to empirical parametrizations, it is possible to develop PEFs that take into account many-body contributions derived from a systematic decomposition of the intermolecular interactions based on quantum-chemical calculations. Several energy decomposition analysis (EDA) methods have been developed over the years. These methods can be classified as variational such as the Kitaura-Morokuma and similar schemes^110−120 or perturbational.^121−126 In most cases, these methods decompose the intermolecular interaction energies into several terms including Coulomb, exchange-repulsion, dispersion, polarization, charge-transfer, and possibly higher-order terms. The last four terms effectively encompass many-body contributions to the interaction energy.

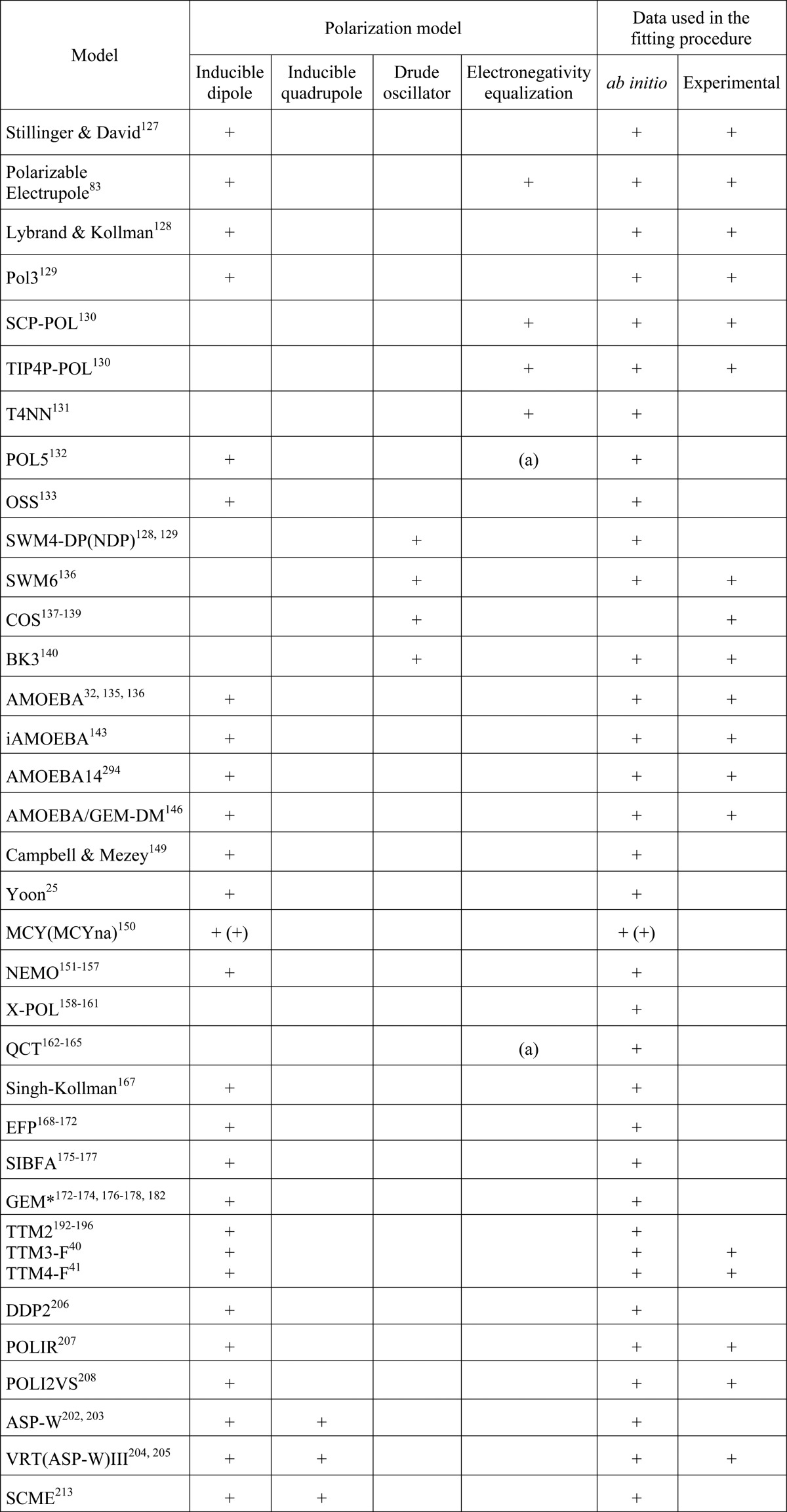
The most common approach to including many-body effects in analytical PEFs is through the addition of a polarization (i.e., induction) term to the energy expression. As for the pairwise PEFs described in section 3, polarizable force fields can be classified as empirical or ab initio, depending on how the parametrization is performed. A list of popular polarizable models, including specific details about the induction scheme adopted in the energy expression and type of data used in the parametrization, is reported in Table 1.

Table 1. List of Polarization Models and Fitting Methodology for Various Implicit Polarizable Water Models^a.

^aThe polarization model relies on machine learning.

One of the earliest attempts to account explicitly for polarization effects in the interactions between water molecules is represented by the model constructed by Stillinger and David which was applied to small clusters and ion monohydrates.¹²⁷ Besides including isotropic dipole polarizability on the oxygen atom of each water molecule, the model was based on charged ions and a dissociable form of the intramolecular potential energy. Another early simulation study of polarization effects in liquid water was performed by Barnes et al. using the polarizable electrupole (PE) model.⁸³ The PE model describes each water molecule as a single site carrying both the experimental static dipole and quadrupole moments along with an isotropic dipole polarizability. This specific functional form was derived from the results of electronic structure calculations indicating the presence of 20–30% stronger hydrogen bonds in trimers and tetramers than in the dimer as well as a strong increase of the molecular dipole moment in going from the gas phase to bulk ice I_h. Although the PE model did not display high accuracy, it inspired subsequent developments of polarizable force fields. Indeed, representing many-body effects through polarizable dipoles has become standard practice.

On the basis of the early studies by Stillinger and David¹²⁷ and Barnes et al.,⁸³ several empirical polarizable force fields have been developed, including the model by Lybrand and Kollman,¹²⁸ the POL3 model,¹²⁹ the SCP-pol and TIP4P-pol models,¹³⁰ the TIP4P-based polarizable model parametrized with neural networks,¹³¹ the five-site model by Stern et al.,¹³² as well as ab initio polarizable force fields such as OSS.¹³³ As discussed by Guillot,⁶¹ the history of force field developments has shown that simply adding dipole polarizability to existing point-charge models does not lead to the general improvement in accuracy and/or transferability that might be expected. A likely reason for this is that the electric field generated by point-charge water models is too inaccurate for realistic dipole induction calculations.

Alternatively to point dipoles, polarization contributions have also been included in water force fields through the charge-on-spring (also known as Drude oscillator) scheme. In the most common implementations, an additional partial charge is connected by a harmonic spring to one of the sites (usually the oxygen atom or the site carrying the negative charge) that are used to define the electrostatic properties (e.g., dipole and quadrupole moments) of an isolated water molecule. Examples of charge-on-spring water models are the SWM4-DP,¹³⁴ SWM4-NDP,¹³⁵ SWM6,¹³⁶ COS,^137−139 and BK3¹⁴⁰ models. A quantum-mechanical treatment of the Drude oscillator, which allows for a rigorous description of both many-body polarization and dispersion, has recently been proposed and shown to enable accurate simulations of water across different phases.^ref141 Since these polarizable force fields assume rigid-monomer geometries and thus neglect 1B contributions to the interaction energy, they will not be discussed further here. The interested reader is directed to the original studies for specific details.

An example of an analytical PEF that was derived using both experimental and ab initio data is the AMOEBA model.^39,141,142 New versions of AMOEBA, termed inexpensive AMOEBA (iAMOEBA) and AMOEBA14, have recently been proposed.¹⁴³ iAMOEBA only includes contributions to the polarization term from the permanent fields and the remaining parameters have been optimized to reproduce both ab initio and selected experimental data. Although the iAMOEBA model improves the description of water clusters and liquid water compared to the original AMOEBA model, non-negligible deviations from highly correlated electronic structure reference data were found at the 3B level.¹⁴⁴ Torabifard et al. have recently reported an AMOEBA water model based on a different set of distributed multipoles obtained from GEM.¹⁴⁵ Several properties have been calculated across a range of temperatures and compared to the experimental counterparts. This new AMOEBA model shows very good agreement for density, heat of vaporization, and diffusion coefficients over the tested temperature range.¹⁴⁶ Other polarizable water models that rely on the use of diffuse functions (e.g., single spherical Gaussians) instead of point charges or multipoles have also been proposed.^147,148

One of the first ab initio water PEFs taking explicitly induced multipolar polarizabilities into account was developed by Campbell and Mezei.¹⁴⁹ This PEF was fitted to the energies of 229 water dimers calculated at the HF level. Several other potential energy functions have been proposed, which make only use of ab initio data in the fitting process. These PESs include the models by Yoon et al.²⁵ and Li et al.,¹⁵⁰ the NEMO model by Karlstrom and co-workers,^151−157 the X-pol model by Gao and co-workers,^158−161 the multipolar model of Popelier and co-workers based on quantum chemical topology,^162−165 and the model by Torheyden and Jansen.¹⁶⁶

Other PESs derived from ab initio data include additional many-body terms to improve the description of the intermolecular interactions between water molecules. One of the first examples that attempted to reproduce every component of the Kitaura-Morokuma decomposition is the Singh-Kollman model.¹⁶⁷ The effective fragment potential (EFP) also includes terms such as charge transfer to account for many-body effects.^168−172 Similar analytical PEFs have recently been proposed.¹⁷³ SIBFA is an example of a force field based on the individual reproduction of each term of the ab initio energy decomposition analysis.^174−177 The SIBFA functional form uses damped distributed point multipoles for the calculation of the intermolecular Coulomb interactions as well as the electrostatic potential and electric field necessary for the calculation of the second order (polarization and charge-transfer) terms.

The Gaussian electrostatic model (GEM) follows the same philosophy as SIBFA in systematically reproducing each EDA term.^178−185 However, GEM uses explicit molecular electronic density for each fragment instead of a discrete distribution. The use of explicit densities results in a more accurate description of the intermolecular interaction, especially at medium to short range, since the penetration errors are virtually eliminated.¹⁴⁵ Recently, a new water PEF based on GEM and AMOEBA, called GEM*, has been developed. GEM* combines the Coulomb and exchange-repulsion terms from GEM with the polarization, bonded and (modified) dispersion terms from AMOEBA. GEM* was fitted exclusively to ab initio data from water dimers and trimers and reproduces both binding energies of water clusters^186−188 and bulk properties such as the heat of vaporization.¹⁸⁹ In the first implementation of GEM*, all quantum data was obtained at the MP2/aug-cc-pVTZ level (including the reference molecular density) for comparison with the reference AMOEBA03 potential. In general, the calculation of the exchange contribution in some of the above-mentioned force fields, such as GEM and SIBFA, is performed in a pairwise manner. However, many-body effects from exchange interactions also arise from higher-order terms (e.g., polarization, charge transfer, and dispersion). These effects can be included explicitly through, for example, the use of the Axilrod–Teller triple dipole function employed by Li et al.¹⁵⁰ and the triple overlap function as included in SIBFA.¹⁹⁰ Recent efforts have focused on ways to improve the efficiency for the evaluation of the integrals required by GEM* (and GEM) as well as on more accurate fits performed using reference data from both higher-level electronic structure calculations and MB-pol dimer and trimer potential energy surfaces.^144,191

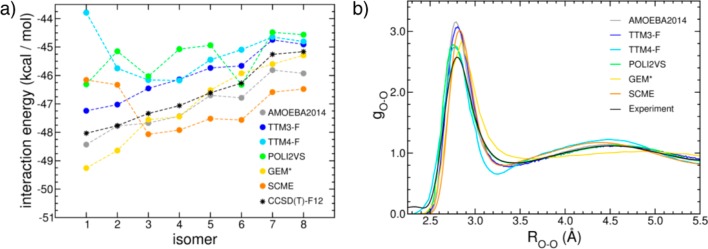
In the 2000s, Xantheas and co-workers introduced the TTM (Thole-type model) potential energy functions^192−196 that, for the first time, made use of a highly accurate 1B term derived from high-level ab initio calculations by Partridge and Schwenke.¹⁹⁷ The latest versions of the TTM models (TTM3-F⁴⁰ and TTM4-F⁴¹) employ point dipoles with Thole-type damping¹⁹⁸ between the charges and the induced dipoles and between the induced dipoles themselves. As shown in Figures 1 and 2, while both TTM3-F and TTM4-F PEFs deviate significantly from the CCSD(T) reference data at the 2B level, TTM4-F effectively reproduces 3B effects with the same accuracy as MP2, reinforcing the notion that high-order interactions in water can be effectively represented through classical many-body polarization. The TTM PEFs were shown to reproduce the properties of water clusters, liquid water, and ice reasonably well.^199−202 Since the 1B term of the TTM PEFs correctly describes intramolecular charge transfer, both TTM3-F and TTM4-F reproduce the observed increase of the HOH angle going from the gas to the condensed phase and the correct IR spectrum of the HOH bend. However, some inaccuracies were identified in modeling the OH stretching vibrations, with both TTM3-F and TTM4-F predicting an absorption line shape that is red-shifted compared to experiment.^203−205 In addition, as shown in Figure 4, the apparent agreement with reference data achieved by the TTM3-F model is often the result of fortuitous error cancellation between different terms of the MBE. Closely related to the TTM family are the DDP2,²⁰⁶ POLIR,²⁰⁷ and POLI2VS²⁰⁸ polarizable force fields, with the last two models being specifically developed to simulate the infrared spectrum of liquid water. Direct comparisons between AMOEBA14, TTM3-F, TTM4-F, POLI2VS, and GEM* are shown in Figure 4.

Figure 4.

(a) Interaction energies of the water hexamer isomers calculated with six polarizable force fields using the MP2 optimized geometries of ref (218) shown in Figure 5. Also shown as a reference are the corresponding values obtained at the CCSD(T)-F12 level in the complete basis set limit.²¹⁷ (b) Comparison between the oxygen–oxygen radial distribution functions of liquid water at ambient conditions derived from X-ray diffraction measurements (black)¹⁰⁸ and calculated from molecular dynamics simulations performed with six polarizable force fields. The AMOEBA2014 and POLI2VS results are from refs (268) and (208), respectively.

Following a different approach based on intermolecular perturbation theory, an important early attempt to reach higher accuracy in modeling water clusters, at the expense of computational efficiency, was made by Stone and co-workers through the development of the anisotropic site potential (ASP-W).²⁰⁹ The ASP-W model, as the subsequent improved versions ASP-W2 and ASP-W4,²¹⁰ is based on a distributed multipole expansion of the electric field around the water molecule, with the expansion going from point charges (monopoles) up to the quadrupole on the oxygen atom and dipole on the hydrogen atoms. Induction effects are treated by dipole as well as quadrupole polarizabilities, and the dispersion and short-range exchange-repulsion energy components are treated by detailed anisotropic functions fitted to ab initio data. Despite their elaborate construction, the ASP-W models were shown to contain inaccuracies in the description of water clusters, while simulations of liquid water have not yet been attempted. Building on the studies by Stone and co-workers, Goldman et al. took advantage of accurate experimental measurements of vibration–rotation tunneling (VRT) spectra of the water dimer and performed several reparametrization of the original ASP-W model to match the experimental tunneling splittings.²¹¹ The latest version, called VRT(ASP-W)III, describes the dimer potential energy surface with spectroscopic accuracy, albeit with fixed intramolecular geometry. When applied to Monte Carlo simulations of liquid water, VRT(ASP-W)III predicted a too weakly structured liquid compared to experimental diffraction data, even without the inclusion of nuclear quantum effects.²¹²

The recently proposed single-center multipole expansion (SCME) model²¹³ follows a similar philosophy as the ASP models but includes an important simplification which renders it more computationally efficient as well as physically transparent. From the analysis of electric fields in ice and around water clusters, Batista et al.^214,215 observed that an electric induction model based on a multipole expansion around a single site (the molecular center of mass) agree well with DFT and MP2 calculations when the expansion is carried out up to and including the hexadecupole moment, with induction effects treated by dipole and quadrupole polarizabilities. The importance of including the hexadecupole moment in the electrostatics of ice was also highlighted in the work of Tribello and Slater,²¹⁶ who showed that effective force fields consistently fail to describe the energetics of different proton ordering in ice due to their inadequate description of higher-order multipoles. Reducing the number of multipole sites from three to one requires significantly less computational effort in the iterative solution of the polarization equations. At the same time, it makes the model conceptually simpler since atomic multipole moments of molecules are poorly defined and not experimentally measurable, while the gas-phase molecular multipoles can be obtained from experiments or from ab initio calculations. In the SCME model, the electrostatic multipole expansion, which is switched off at short range using damping functions, is combined with a dispersion energy expression including C₆, C₈, and C₁₀ coefficients derived from ab initio calculations and an empirical density-dependent isotropic short-range repulsion energy, both centered on the oxygen atom. Promising results were obtained in the description of water clusters, ice, and liquid water,²¹³ although some shortcomings of the SCME model are apparent in the comparisons shown in Figure 4.

To provide the reader with a general overview of the accuracy with which different implicit polarizable models describe the properties of liquid water, a compendium of structural, energetic, and thermodynamic quantities extracted from the original references is reported in Table 2. In general, all models correctly describe both density and enthalpy of vaporization at room temperature, albeit noticeable variations in their performance are observed for various other properties, with percentage deviations from the reference data being, in some cases, larger than 10%. In particular, the heat capacity and dielectric constant appear to be the properties more difficult to reproduce.

Table 2. Compendium of Structural, Energetic, and Thermodynamic Properties^a.

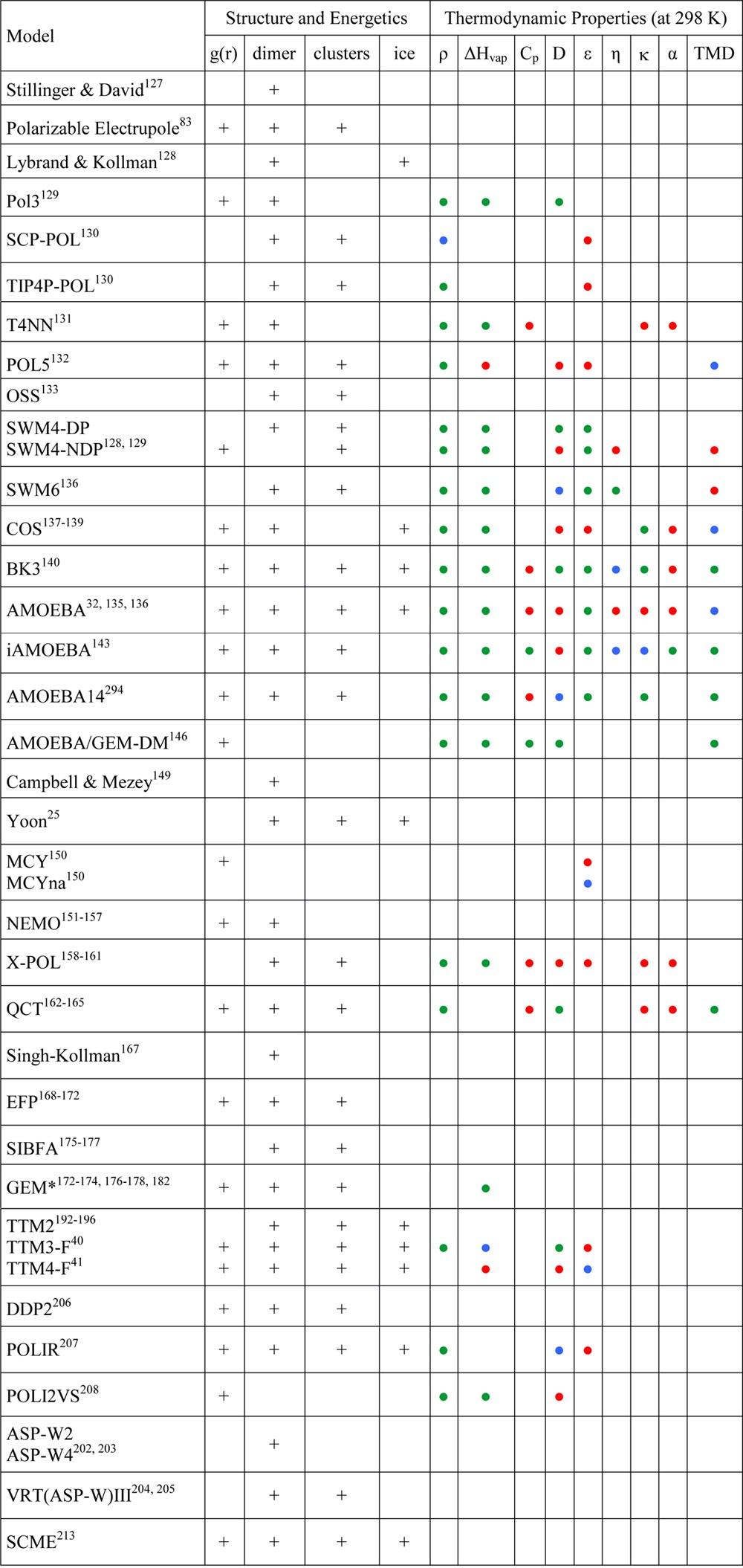
^aCalculated using different implicit polarizable water models as reported in the respective original studies. + indicates that the corresponding quantity is reported in the original references. All thermodynamic properties are given as percentage deviations of the calculated values with respect to the corresponding experimental data. Green circles: <5%; blue circles: 5%–10%; red circles: >10%. In cases where a range of temperatures was analyzed in the original studies, the average deviation is reported. g(r) = radial distribution functions, ρ = liquid density, ΔH_vap = enthalpy of vaporization, C_p = heat capacity, D = diffusion coefficient, ε = dielectric constant, η = viscosity, κ = isothermal compressibility, α = thermal expansion coefficient, and TMD = temperature of maximum density.

More direct comparisons are made in Figure 4, where predictions for interaction energies of the low-lying hexamer isomers and the oxygen–oxygen radial distribution function of the liquid at ambient conditions are analyzed for the most recent polarizable models with flexible monomers. The hexamer cluster is specifically chosen for this comparison because it is the smallest water cluster for which the lowest energy isomers assume fully three-dimensional structures (Figure 5), which resemble the hydrogen-bonding arrangements found in the liquid and ice. Among the six polarizable PEFs, AMOEBA2014 provides the closest agreement with the interaction energies calculated at the CCSD(T)-F12 level in ref (217) using the MP2-optimized geometries of ref (218). Both the TTM3-F and GEM* PEFs correctly predict the energy order for the different isomers, with the largest absolute deviation from the CCSD(T)-F12 values being slightly more than ∼1 kcal/mol. It was shown, however, that TTM3-F achieves high accuracy in the relative energies of the different isomers through some fortuitous cancellation of errors between 2B and 3B contributions.²¹⁷ Besides providing larger deviations from the reference data, the remaining three polarizable PEFs (TTM4-F, POLI2VS, and SCME) considered in this analysis also predict a different energy order compared to the CCSD(T)-F12 results.

Figure 5.

Low-energy isomers of the water hexamer.

The comparison between the oxygen–oxygen radial distribution functions calculated from classical molecular dynamics simulations and the corresponding experimental results derived from X-ray scattering measurements of liquid water at ambient conditions¹⁰⁸ indicates that all six polarizable force fields overestimate the height of the first peak. It should be noted, however, that the shape of this peak, associated with molecules located in the first hydration shell, is sensitive to nuclear quantum effects which are neglected in classical molecular dynamics simulations.²¹⁹ While all six polarizable force fields correctly reproduce outer hydration shells at larger water–water separations, the current version of GEM* and the TTM4-F model predict a too weakly and too strongly structured liquid, respectively.

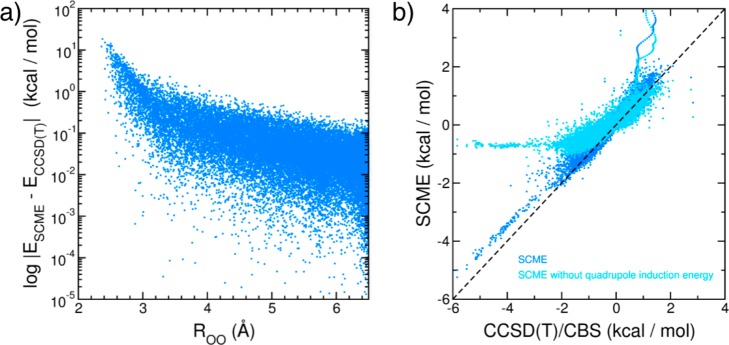
A quantitative assessment of the strengths and weaknesses of the current version of the SCME PEF can be derived from the analysis of the lower-order terms contributing to the overall interaction energy. Figure 6a shows the absolute difference between the SCME and CCSD(T) 2B energies, E_SCME – E_CCSD(T), calculated as a function of the oxygen–oxygen distance for a set of 27029 dimers extracted from path-integral molecular dynamics simulations performed with the many-body HBB2-pol potential energy function.¹⁹¹ While SCME predicts accurate energetics for monomer separations larger than ∼3.5 Å, large deviations from the CCSD(T) reference data are found at short range. This short-range error is associated with the breakdown of the multipole expansion as the electron clouds of neighboring monomers start to overlap and reveals deficiencies in the multipolar damping functions together with the isotropic exchange-repulsion energy model adopted by SCME. While a systematic improvement of the damping functions is possible,²²⁰ a potentially more efficient route to describe quantum mechanical effects (e.g., exchange-repulsion and charge transfer) at short range is to replace the current empirical repulsion energy with an explicit many-body potential obtained from the application of machine-learning techniques (see section 4.3). Figure 6b shows the correlation between 3B energies obtained from SCME and CCSD(T) calculations for a set of 12347 trimer geometries.¹⁴⁴ Since the short-range repulsion is partially canceled from the 3B energies, the SCME results are in relatively good agreement with the reference data. For illustrative purposes, a comparison between SCME three-body energies calculated by neglecting the induced quadrupole moments and the corresponding CCSD(T) reference data is also shown in Figure 6b. This comparison suggests that inducing the quadrupole moments may be important to enhance the binding energy for a large range of strongly hydrogen-bonded trimer geometries. However, since both AMOEBA and TTM4-F achieves high accuracy in the representation of 3B interactions by only employing inducible dipole moments (Figure 2), the role played by inducible quadrupole moments appears to be related to the specific electrostatic scheme adopted by individual PEFs (such as SCME) and merits more systematic comparative analysis.

Figure 6.

(a) Logarithmic-scale errors in SCME²¹³ two-body absolute energies relative to CCSD(T)/CBS reference data reported in ref (191). (b) Correlation plot between SCME (y axis) and CCSD(T)/CBS (x axis) three-body energies calculated for the set of trimer geometries reported in ref (144). Results obtained with the full SCME three-body energies are shown in blue, while the results obtained when the SCME quadrupole induction energy is neglected are shown in light blue.

4.3. Explicit Many-Body Potential Energy

Since the MBE converges rapidly for water,^{30,31,84,85,221,222}eq 1 suggests that it is possible to effectively express the energy of systems containing N water molecules in terms of low-order interactions, which, in turn, can be calculated with high accuracy using correlated electronic structure [e.g., CCSD(T)] methods. On the basis of this observation and building upon the MCY pairwise potential energy function described in section 4.1, the first many-body PEF for water with rigid monomers was developed by Niesar et al.^223,224 This PEF contains explicit 2B and 3B terms derived respectively from fourth-order Möller-Plesset (MP4) and HF calculations, along with a classical description of higher-body polarization interactions.

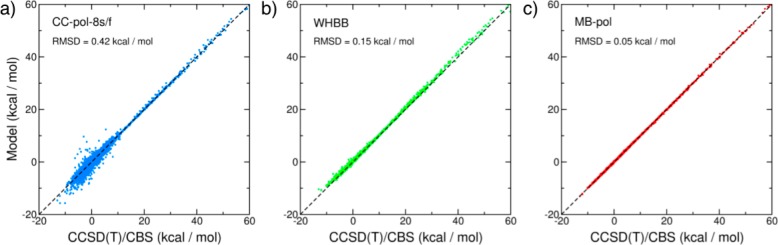
Subsequent improvements in the SAPT methodology enabled the development of a new global PEF (SAPT-5s+3B) for water with rigid monomers, including explicit 2B and 3B terms.^225−227 The new analytical 3B term was obtained from a fit to 7533 trimer energies calculated at the Hartree–Fock level using the SAPT formalism. SAPT-5s+3B was shown to accurately reproduce the vibration–rotation tunneling (VRT) spectrum of both (H₂O)₂ and (D₂O)₂ dimers as well as the second virial coefficient and the far-infrared spectrum of the water trimer. These studies eventually led to the development of the rigid-monomer CC-pol family of water PESs,^228−233 whose latest version, CC-pol-8s, is a 25-site model with explicit 2B and 3B terms fitted to CCSD(T)-corrected MP2 dimer energies and SAPT trimer energies, respectively. All higher-order interactions in CC-pol are represented through classical polarization. CC-pol accurately reproduces the VRT spectrum of the water dimer and predicts the structure of liquid water in reasonable agreement with the experimental data. Within the CC-pol scheme, a refined 2B term with explicit dependence on the monomer flexibility, CC-pol-8s/f, has recently been reported.²³⁴ As shown in Figure 7a, CC-pol-8s/f reproduces the interaction energies of more than 40000 water dimers calculated at the CCSD(T)/CBS level of theory with a root-mean-square deviation (RMSD) of 0.42 kcal/mol per dimer and the experimental VRT spectrum with high accuracy (Table 3).

Figure 7.

Correlation plots for 2B interaction energies calculated with the CC-pol-8s/f (panel a), WHBB (panel b), and MB-pol (panel c) many-body potential energy functions. Plotted on the x axes are the CCSD(T)/CBS reference energies calculated for 42394 water dimers in ref (191). On the y axes are the corresponding energies calculated with the different water PEFs.

Table 3. Measured and Calculated VRT Levels and Tunneling Splittings for the (H₂O)₂ Dimer^a.

		experiment	HBB2	CCpol-8s/f	MB-pol
Ka = 0
OO	(2)	153.62(1.88)	148.57(1.14)	149.63(1.23)	154.31(2.41)
	(1)		145.00(3.48)	143.20(3.27)	149.44(1.97)
AT	(1)		128.91(0.74)	132.10(1.48)	129.44(0.24)
	(2)	120.19(0.74)	121.01(8.41)	117.50(8.67)	119.07(10.15)
AW	(2)	108.89(0.02)	105.78(0.03)	107.82(0.10)	108.87(0.13)
	(1)	107.93(2.95)	105.35(1.99)	109.23(3.29)	108.38(3.24)
DT	(1)		116.54(4.84)	113.35(5.91)	113.83(5.61)
	(2)	64.52(2.54)	67.18(2.03)	61.33(2.48)	61.31(2.54)
GS	(2)	11.18(0.65)	10.16(0.60)	12.75(0.61)	12.05(0.69)
	(1)	0.00(0.75)	0.00(0.68)	0.00(0.72)	0.00(0.81)
Ka = 1
OO	(2)		152.50(1.12)	152.07(1.48)	156.60(2.71)
	(1)		150.52(1.04)	153.54(2.54)	152.69(4.13)
AT	(1)		142.25(4.33)	142.42(4.04)	143.68(4.87)
	(2)		136.24(5.31)	136.52(4.66)	137.04(5.95)
AW	(2)	123.56(3.41)	122.25(2.48)	123.12(3.16)	123.65(3.83)
	(1)	109.98(5.24)	108.95(4.55)	108.28(4.76)	109.65(5.89)
DT	(1)		94.25(2.66)	92.18(3.34)	91.22(3.47)
	(2)	87.75(1.11)	89.55(0.54)	86.37(1.32)	85.63(1.00)
GS	(2)	14.39(0.70)	14.00(0.64)	15.45(0.67)	15.04(0.77)
	(1)	11.66(0.54)	11.50(0.49)	12.36(0.51)	12.18(0.48)

^aThe energy levels are labeled as ground state (GS), donor torsion (DT), acceptor wag (AW), acceptor twist (AT), and intermolecular stretch (OO). The energies (in cm^–1) correspond to the origins o₁(K) and o₂(K) of the levels (1) and (2) with quantum numbers K = 0 and K = 1, respectively. The values in parentheses are the interchange tunneling splittings i₁(K) and i₂(K). The values for HBB2, which corresponds to the 2B term of WHBB are taken from ref (295), those for CCpol-8sf from ref (296), and those for MB-pol from ref (191). The experimental values are taken from refs (297−301).

The first global full-dimensional water PEF (WHBB) was reported by Wang et al.^54,235−238 As in the TTM PEFs, the 1B term of WHBB is described by the spectroscopically accurate monomer PEF developed by Partridge and Schwenke,¹⁹⁷ while the 2B and 3B terms were fitted to CCSD(T) and MP2 data, respectively, using permutationally invariant polynomials.²³⁹ All long-range many-body effects in WHBB are represented by the same Thole-type polarizable model used in the TTM3-F model.⁴⁰ In combination with the many-body PEF, a two-body dipole moment surface for water was also reported as part of the WHBB suite.^54,235,236 To date, WHBB has been applied to dynamical calculations of several properties of water clusters, including energies^240,241 and free energies,²⁴² as well as in static calculations of the vibrational frequencies of clusters,^243,244 liquid water,^245,246 and ice.²⁴⁷ WHBB reproduces the CCSD(T)/CBS interaction energies of the dimer data set of ref (191) with an RMSD of 0.15 kcal/mol per dimer (Figure 7b) and predicts vibrational transitions in excellent agreement with the experimental VRT spectrum (Table 3). Although WHBB is highly accurate for very small water clusters, its accuracy appears to deteriorate as the system size increases as demonstrated by the poor agreement obtained with CCSD(T) and quantum Monte Carlo (QMC) reference data for the hexamer isomers and liquid configurations.²¹⁷ As discussed in ref (217), this lack of transferability of WHBB from small clusters to condensed-phase systems is possibly related to inaccuracies in the specific functional form adopted to merge explicit short-range and effective long-range many-body interactions.

Building upon the results obtained with CC-pol and WHBB, the full-dimensional HBB2-pol many-body PEF was introduced by Babin et al. in ref (55). As in the TTM and WHBB PESs, the 1B term of HBB2-pol is described by monomer PEF developed by Partridge and Schwenke.¹⁹⁷ The 2B interaction at short range is represented by the HBB2 potential,²³⁵ which smoothly transitions at long-range into the sum of two separate terms describing electrostatic and dispersion energy interactions. The induction contributions to nonpairwise additive interactions in HBB2-pol are taken into account through Thole-type point polarizable dipoles on all atomic sites using the TTM4-F scheme.⁴¹ In addition, an explicit 3B component is used to account for short-range interactions, such as exchange-repulsion and charge transfer. The inclusion of induction interactions at all monomer separations in the 3B term of HBB2-pol enables the use of lower degree permutationally invariant polynomials than previously reported for WHBB, resulting in a sizable decrease in the computational cost associated with both energy and force calculations. HBB2-pol is the first full-dimensional analytical PES that accurately predicts the properties of water from the gas to the condensed phase, reproducing the second and third virial coefficients, the relative energies of small water clusters, and both structural and dynamical properties of liquid water.⁵⁵ From the analysis of the HBB2-pol oxygen–oxygen radial distribution function, it was found that the inclusion of explicit 3B short-range effects is critical to correctly reproduce the structure of liquid water at ambient conditions. Moreover, HBB2-pol simulations performed using path-integral molecular dynamics combined with the replica exchange method were shown to predict the correct relative stability of (H₂O)₆ and (D₂O)₆ clusters over a wide range of temperatures.²⁴⁸

A new full-dimensional many-body PEF, MB-pol, has recently been introduced Babin et al. and shown to achieve unprecedented accuracy in predicting the properties of water across different phases.^144,191,249 The MB-pol functional form includes the 1B term by Partridge and Schwenke¹⁹⁷ as well as explicit 2B and 3B terms derived from large data sets of dimer and trimer interaction energies calculated at the CCSD(T) level of theory in the complete basis set limit.^144,191,249 All higher-body terms in MB-pol are represented by many-body polarization using a slightly modified version of the induction scheme adopted by the TTM4-F PEF.⁴¹ MB-pol can thus be viewed as a flexible polarizable model supplemented by short-range 2B and 3B terms that take effectively into account quantum-mechanical interactions arising from the overlap of the monomer electron densities. Specifically, MB-pol thus contains many-body effects at all monomer separations as well as at all orders, in an explicit way up to the third order and in a mean-field fashion at higher orders. As shown in Figure 7c, MB-pol reproduces the CCSD(T)/CBS interaction energies of more than 40000 water dimer with an RMSD of 0.05 kcal/mol per dimer, which reduces to 0.03 kcal/mol for dimers with energies below 25 kcal/mol. Similarly to CC-pol-8s/f and WHBB, MB-pol reproduces the experimental VRT spectrum of the water dimer with high accuracy (Table 3). MB-pol correctly reproduces the second virial coefficient,¹⁹¹ the relative energies of small water clusters,¹⁴⁴ and the structural, thermodynamic, and dynamical properties of liquid water at ambient conditions.²⁴⁹ A recent analysis²¹⁷ of the water properties from the gas to the liquid phase shows that MB-pol predicts interaction energies and vibrational frequencies for small water clusters in close agreement with the reference values obtained from highly correlated electronic structure calculations²⁵⁰ as well as the energetics of liquid configurations in agreement with quantum Monte Carlo reference data.²⁵¹ Importantly, the analysis reported in ref (217) also demonstrates that MB-pol achieves higher accuracy in the description of liquid configurations than existing DFT models that are commonly used in ab initio molecular dynamics simulations of water (see Figures 8,9, and 10).

Figure 8.

(a) Interaction energies of the water hexamer isomers calculated with the SCME/GAP, WHBB, and MP-pol many-body potential energy functions using the MP2 optimized geometries of ref (218). Also shown as a reference are the corresponding values obtained at the CCSD(T)-F12/VTZ-F12 level of theory in the complete basis set limit.²¹⁷ (b) Same comparison as in (a) using seven popular DFT models. (c) Same comparison as in (a) using the same seven DFT models as in (b) with the D3 pairwise additive dispersion correction of ref (257).

Figure 9.

Errors, ΔE = E_nB^model – E_nB, relative to the CCSD(T)-F12/VTZ-F12 reference values of ref (217) for the individual terms (nB) of the many-body expansion of the interaction energy calculated using many-body PEFs and DFT models for the (a–c) prism, (d–f) cage, and (g–i) cyclic chair hexamer isomers. The first column (a, d, and g) reports the results obtained with the SCME/GAP, WHBB, and MB-pol many-body potentials. The second (b, e, and h) and third (c, f, and i) columns report the results obtained with the same seven DFT models of Figure 8 without and with the D3 dispersion correction, respectively.

Figure 10.

(a) Mean absolute deviations in the total energy relative to quantum Monte Carlo reference data calculated using the WHBB and MB-pol many-body PEFs, the TTM3-F and TTM4-F polarizable force fields, and several DFT models for configurations (in periodic boundary conditions) extracted from path-integral molecular dynamics simulations of water performed with the vdW-DF and vdW-DF2 functionals in ref (251). All data from ref (217). (b) Comparison between the oxygen–oxygen radial distribution functions calculated for liquid water in refs (249) and (292) from classical molecular dynamics simulations using the MB-pol many-body PEF and the BLYP, BLYP-D3, B3LYP-D3 functionals, respectively. (c) Comparison between the oxygen–oxygen radial distribution functions calculated for liquid water in refs (249) and (293) from classical molecular dynamics simulations using the MB-pol many-body PEF and the PBE, PBE+TS(vdW), PBE0, and PBE0+TS(vdW) functionals, respectively.

An alternative approach to the permutationally invariant polynomials that are used to describe 2B and 3B interactions in the WHBB,^54,235−238 HBB2-pol,⁵⁵ and MB-pol^144,191,249 PEFs is represented by the Gaussian process regression, also known as krieging or kernel ridge regression.^252,253 In this method, a (typically high-dimensional) function is expressed as a linear combination of nonlinear basis functions (often Gaussians) that are centered on the actual data points. The Gaussian Approximation Potential (GAP)^254,255 framework uses this method to generate PEFs, utilizing both ab initio energies and gradients in a consistent and essentially parameter-free manner. In the case of small molecules, the GAP basis functions are rotationally invariant because the molecule geometry is described by internuclear distances and are made permutationally invariant by averaging them over the permutational symmetry group.

GAP was used to generate a 12-dimensional potential energy surface for the water dimer based on 9000 configurations with an RMSD of <0.01 kcal/mol per dimer. When combined with a description of the beyond-2B terms based on BLYP calculations and the Partridge-Schwenke model for the 1B term, the GAP PEF achieved a relative RMSD of <0.1 kcal/mol for the hexamer isomers.¹⁹⁴ However, the absolute binding energy errors were found to be significantly larger (0.3 kcal/mol for hexamers and 0.6 kcal/mol pentadecamers), due to the cooperative effects discussed in section 4.2, which are poorly described at the DFT/BLYP level (see Figure 9).¹⁹⁵ Similarly, relative binding energies of ice phases calculated with GAP were found to be accurate (<0.1 kcal/mol) although this PEF systematically overestimates the binding energies by ∼1.5 kcal/mol due to the overpolarisation associated with the BLYP functional. Changing the description of the many-body terms to the PBE exchange-correlation functional was found to have a somewhat remarkable effect: while PBE gives an intrinsically better description of the 2B terms, its description of the beyond-2B terms is significantly worse than BLYP, leading to relative errors on the order of 3 kcal/mol for ice phases and clusters derived from ice-like configurations.¹⁹⁶ These observations provide some possible explanations for the persistent failure of commonly used DFT models in accurately describing the properties of water.

Following the same strategy adopted to derive the HBB2-pol^32,55 and MB-pol^144,191,249 PEFs, the GAP approach has recently been used to correct the shortcomings of the polarizable SCME model (see section 4.2) in the representation of short-range 2B and 3B interactions. The resulting SCME/GAP PEF contains 2B and 3B GAP corrections derived from fits to the CCSD(T) 2B energies of ref (256) and to the same CCSD(T)/CBS 3B energies used to optimize the 3B permutationally invariant polynomials of the MB-pol PEF, respectively.¹⁴⁴ Although the SCME/GAP model is still under development, preliminary results shown in Figures 8 and 9 indicate that the addition of the short-range GAP corrections significantly improves the ability of the original SCME model to predict both the energetics and the individual many-body contributions to the interaction energies of the hexamer isomers.

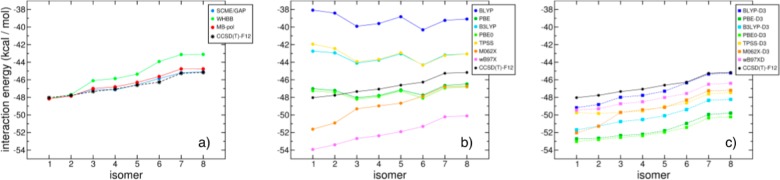
Similar to section 4.2, the interaction energies of the hexamer isomers calculated with several many-body PEFs are analyzed in Figure 8. To provide the reader with a quantitative assessment of the accuracy of existing many-body PEFs, direct comparisons with the corresponding quantities obtained from ab initio calculations are also reported. In Figure 8a, the interaction energies of low-lying hexamer isomers calculated with the SCME/GAP, WHBB, and MB-pol PEFs are compared with the corresponding CCSD(T)-F12/VTZ-F12 reference values of ref (217). All three many-body PEFs predict the correct energy order, with SCME/GAP and MB-pol providing the closest agreement with the CCSD(T)-F12/VTZ-F12 values for all isomers.

To put the results obtained with many-body PEFs in perspective, comparisons between the CCSD(T)-F12/VTZ-F12 interaction energies and the corresponding values calculated using seven popular DFT models (without and with the D3 dispersion correction²⁵⁷) commonly used in computer simulations of water are shown in Figure 8 (panels b and c). All DFT calculations were carried out with Gaussian 09²⁵⁸ using the aug-cc-pVQZ basis set. The analysis of Figure 8b clearly shows that among the seven functionals without the D3 dispersion correction, only M062X and ωB97X predict the correct energy order of the hexamer isomers. However, the deviations from the CCSD(T)-F12/VTZ-F12 reference data can be as large as 6 kcal/mol, which is significantly larger than the differences obtained with all three many-body PEFs. Although the addition of the D3 dispersion correction²⁵⁷ improves the agreement with the CCSD(T)-F12/VTZ-F12 values, none of the DFT models considered in this analysis achieves the same accuracy as SCME/GAP and MB-pol.

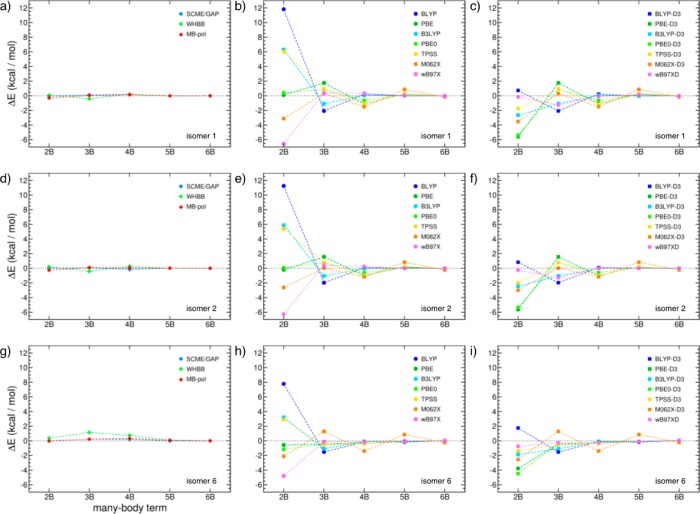
A more quantitative assessment of the accuracy of both many-body PEFs and DFT models, the many-body decomposition of the interaction energy for the prism (isomer 1), cage (isomer 2), and cyclic chair (isomer 6) hexamers is reported in Figure 9. Specifically, the errors (ΔE = ΔE_nB^model – ΔE_nB) relative to the CCSD(T)-F12/VTZ-F12 reference values reported in ref (217) were calculated for each term (from 2B to 6B) of eq 1. The results shown in the first column of Figure 9 (panels a, d, and g) indicate that all many-body PEFs closely reproduce the reference values for each term of the MBE. However, non-negligible deviations in the 3B and 4B terms, which become more apparent for the cyclic chair isomer, result in WHBB being overall less accurate than the SCME/GAP and MB-pol at reproducing the hexamer interaction energies as shown in Figure 8. On the other hand, large deviations from the reference data are found, especially at the 2B level, when the calculations are carried out with DFT models without the dispersion correction (panels b, e, and h of Figure 9). In this case, the PBE and PBE0 functionals provide the closest agreement with the CCSDT(T)-F12/VTZ-F12 values, although the associated errors are appreciably larger than those obtained with explicit many-body PEFs. Overall, the inclusion of the D3 dispersion correction improves the description of the 2B contributions (panels c, f, and i of Figure 9). However, while the dispersion correction improves significantly the accuracy of the BLYP functional, both PBE-D3 and PBE0-D3 2B terms become less accurate than those obtained with the original functionals. Since the D3 dispersion correction is strictly pairwise additive, it does not improve the description of higher-order interaction terms, which are found to deviate from the CCSD(T)-F12 reference values by as much as 2 kcal/mol. Interestingly, both M062X and M062X-D3 appear to benefit from fortuitous error cancellation between even- and odd-order interaction terms. Among all functionals considered in this analysis, ωB97XD provides the most accurate description of each term of the MBE, independently of the isomer. However, the deviations from the CCSD(T)-F12 reference values associated with ωB97XD are still noticeably larger than those found with the WHBB, SCME/GAP, and MB-pol many-body PEFs.

Particularly remarkable is the close similarity between the results obtained with the SCME/GAP and MB-pol PEFs which effectively demonstrates both the accuracy and efficiency of the many-body-plus-polarization scheme originally introduced with the HBB2-pol PEF. Within this scheme, individual many-body contributions are explicitly added to a baseline energy expression that implicitly represents many-body effects through classical polarization. These individual terms (e.g., 2B and 3B permutationally invariant polynomials for MB-pol and GAP functions for SCME/GAP) effectively correct the deficiencies of a classical representation of the interaction energies, recovering quantum-mechanical effects such as exchange-repulsion and charge transfer. Since MB-pol and SCME/GAP use different induction schemes and short-range corrections, the close agreement between the MB-pol and SCME/GAP results thus demonstrates that the many-body-plus-polarization scheme is robust with respect to the specific functional form adopted by the individual PEFs. Interestingly, SCME/GAP uses the same trimer training set as MB-pol to effectively achieve the same accuracy in the representation of 3B interaction energies, which emphasizes the importance of shared databases of high-quality electronic structure data for developing accurate analytical PEFs. It should also be noted that, although current implementations of many-body-plus-polarization scheme such as HBB2-pol, MB-pol, and SCME/GAP include explicit corrections up to the 3B level, this choice only represents the optimal compromise between accuracy and computational efficiency. By construction, the many-body-plus-polarization scheme is not limited by the number of explicit terms of the many-body expansion that can be included in the energy expression nor by the order of permutationally invariant polynomials (for HBB2-pol and MB-pol) and number of Gaussian functions (for SCME/GAP).

While, as of today, SCME/GAP has not been applied to any water system in periodic boundary conditions, the accuracy of WHBB and MB-pol was further assessed in ref (217) through a direct comparison with quantum Monte Carlo interaction energies calculated for liquid water configurations extracted from path-integral molecular dynamics simulations carried out with the vdW-DF and vdW-DF2 functionals.²⁵¹Figure 10a shows the results obtained in refs (251) and (217) for several DFT models and the TTM3-F and TTM4-F polarizable force fields, respectively. QMC has been shown to be a reliable benchmark in the study of small water clusters, predicting relative energies with an accuracy comparable to that of CCSD(T). As a measure of accuracy, the mean absolute deviation (MAD) between the energies E_i^(PEF) obtained with each PEF and the reference QMC energies E_i was calculated in ref (217) as

6

In eq 6, N_c is the total number of water configurations used in the analysis and 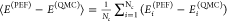is the average energy difference for all N_c configurations, which is used to effectively align the zero of energy with the reference QMC data. As discussed in detail in ref (217), the comparison with the QMC results demonstrates that MB-pol provides a highly accurate description of the energetics of liquid water, outperforming both current DFT and existing analytical PEFs. Figure 10a also shows that the accuracy of WHBB deteriorates for liquid configurations, leading to an MAD value relative to the QMC reference data which is ∼15 times larger than MB-pol and ∼4 times larger than the corresponding values obtained with the TTM3-F and TTM4-F polarizable force fields. It should be noted, however, that, as shown by the analyses presented in Figure 8 and in ref (217), fortuitous cancellation of errors between different terms of the many-body expansion of the interaction energy may also affect the energetics of the liquid configurations calculated using both DFT models and polarizable force fields.

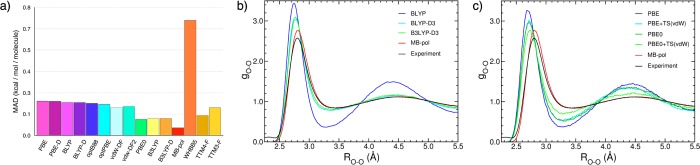
Since molecular dynamics simulations of liquid water with WHBB are currently unfeasible due to the associated computational cost,²¹⁷Figure 10 (panels b and c) shows the oxygen–oxygen radial distribution functions calculated from classical molecular dynamics simulations of liquid water at ambient conditions using both MB-pol and several DFT models with and without dispersion corrections. These comparisons further demonstrate the accuracy of MB-pol, which predicts the structure of water in excellent agreement with that derived from X-ray scattering measurements. The small differences between the experimental and MB-pol results seen in the first peak of the oxygen–oxygen radial distribution function are associated with nuclear quantum effects, which are quantitatively recovered in path-integral molecular dynamics simulations with MB-pol as shown in ref (249). It is now well-established that GGA functionals (e.g., BLYP and PBE) predict a too-structured liquid. The agreement between the DFT results and the experimental data improves when dispersion corrections and/or Hartree–Fock exchange is added to the functional. However, as Figure 10 (panels b and c) shows, independently of the specific details of the functional, noticeable differences still exist between the DFT and experimental results, with the former consistently predicting a too short oxygen–oxygen distance between molecules in the first solvation shell.

To characterize the accuracy of MB-pol in a more quantitative way, we use a new scoring scheme that has recently been introduced to compare the performance of DFT models in reproducing different water properties.²⁵⁹ This scheme was used to assign a percentage score to several DFT models according to their performance in reproducing the properties of the water monomer, dimer, and hexamer, as well as of ice structures. Specifically, the properties considered in the analysis of ref (259) are the harmonic frequency of the monomer symmetric stretch (f_ss^mono), the dimer binding energy (E_b), the binding energy per monomer of the cyclic-chair isomer (isomer 6 of Figure 5) of the hexamer cluster (E_b^ring), the sublimation energy of ice I_h (E_sub), the difference per monomer between the binding energies of the prism (isomer 1 of Figure 5) and cyclic-chair (isomer 6 of Figure 5) isomers of the hexamer cluster (ΔE_b^prism–ring), the difference of the sublimation energies of ice I_h and ice VIII (ΔE_sub), the equilibrium oxygen–oxygen distance of the dimer (R_OO^dim), and the equilibrium volumes per water molecule of ice I_h (V_eq) and ice VIII (V_eq^VIII). The scores are assigned by considering the deviations from the corresponding reference data obtained from high-level electronic structure calculations or experimental measurements. A score of 100% is assigned if the magnitude of the deviation is less than a predefined tolerance δx_tol, and a deduction of 10% is applied for each successive increment δx_tol in |x – x_ref|. A zero score is given if |x – x_ref| > 11 δx_tol. The interested reader is referred to ref (259) for a detailed discussion of the specific values of δx_tol for the different water properties. As shown in Table 4, MB-pol scores 90% or higher for all properties except for the equilibrium volume per water molecule of ice VIII, outperforming all DFT models considered in ref (259). The average score for MB-pol is 93% using the reference values reported in the original analysis of ref (259), which becomes 96% if more accurate reference values for the harmonic frequency of the monomer symmetric stretch and oxygen–oxygen distance in the water dimer are considered.³⁰² In addition, as shown in Table 5, molecular dynamics simulations of liquid water at ambient conditions carried out with MB-pol at both classical and quantum mechanical levels predict thermodynamic and dynamical properties in excellent agreement with the corresponding experimental values.^90,249

Table 4. Comparison between the Percentage Scores of MB-pol and Several DFT Models Computed Using the Scoring Scheme Introduced in ref (259)^a.

model	fssmono (cm–1)	Ebdim (meV)	Ebring (meV)	EsubIh (meV)	ΔEbprism-ring (meV)	ΔEbIh-VIII (meV)	ROOdim (Å)	VeqIh (Å3)	VeqVIII (Å3)	total
reference	3812 3835b	217.6	319	610	13	33	2.909 2.9127b	32	19.1
MB-pol	3833	215.2	309.5	614	22.5	15	2.92	31.61	18.64
	90, 100	100	100	100	100	90	90, 100	90	80	93, 96
LDA	60	0	–	0	–	10	0	–	–	14
PBE	50	100	80	80	0	0	100	70	20	56
BLYP	20	70	80	50	0	0	60	100	0	42
PBE0	80	100	90	90	0	0	90	70	40	62
revPBE-DRSLL	30	70	60	50	100	100	0	30	0	49
optPBE-DRSLL	40	100	100	50	100	100	60	90	30	74
optB88-DRSLL	60	100	90	20	100	100	50	50	100	74
rPW86-DF2	20	100	100	100	100	100	40	50	0	68
PBE-TS	50	80	60	0	100	40	90	30	50	56
PBE0-TS	80	90	80	40	100	60	90	40	70	72
BLYP-D3	20	100	90	30	100	40	70	50	90	66

^aIf not indicated otherwise, all reference values and DFT scores are taken from Table X of ref (259). Also listed as reference values (second entries) are the harmonic frequency of the monomer symmetric stretch and oxygen–oxygen distance in the water dimer calculated in ref (302). For MB-pol, the first entry corresponds to the value calculated for each property, while the second and, when available, third entries are the percentage scores relative to the corresponding reference values. The reader is referred to ref (259) for specific details about the scoring scheme and a complete discussion of the DFT results.

^bFrom ref (302).

Table 5. Thermodynamic and Dynamical Properties of Liquid Water at 298 K as Predicted by Classical and Quantum Simulations with the MB-pol Potential^90,249a.

	density (g cm–3)	enthalpy of vaporization (kcal mol–1)	diffusion (Å2 ps–1)	orientational relaxation time (ps)	surface tension (mN m–1)
experiment	0.997	10.52	0.23	2.5(2)b	71.73
classical	1.004(1)	10.9(2)	0.12(1)	5.3(2)	68(2)
quantum	1.001(2)	10.1(4)	0.22(3)	2.3(3)	–

^aBoth density (ρ) and enthalpy of vaporization (H_vap) were calculated in the constant temperature–constant pressure (NPT) ensemble, while the orientational relaxation time (τ₂) and diffusion coefficient (D) were calculated in the constant energy–constant volume (NVE) ensemble. If not indicated otherwise, all experimental data are taken from Table 2 of ref (62). The numbers in parentheses are the uncertainties in the last figure.

^bFrom ref (303).

On the basis of a systematic analysis of the convergence of the electrostatic properties of water,²⁶⁰ full-dimensional many-body representations for the dipole moment (MB-μ) and polarizability (MB-α) have also been developed and used in combination with the MB-pol PEF to perform many-body molecular dynamics (MB-MD) simulations of the vibrational (infrared and Raman) spectra of liquid water as well as of sum-frequency generation (SFG) spectra of the air/water interface.^90,261,262 In both cases, good agreement with the experimental results is found across the entire frequency range (Figure 11). Direct comparisons with the experimental spectra demonstrate that, while an accurate description of many-body interactions is required to correctly model the (vibrational) structure of liquid water, the explicit treatment of nuclear quantum effects in the simulations is necessary to correctly capture zero-point energy effects. Importantly, as shown in Figure 11 and discussed in detail in refs (261) and (90), while MB-MD simulations using the MB-pol PEF combined with the MB-μ and MB-α many-body representations of the water dipole moment and polarizability correctly reproduce both the shifts and the shapes of the main spectroscopic features, a more rigorous treatment of quantum dynamical effects, such as Fermi resonances and high-frequency anharmonic vibrations, is needed for bringing the stimulated spectra in quantitative agreement with the experimental measurements.

Figure 11.

Comparisons between experimental (top) and simulated (bottom) infrared spectra of liquid water (left) and heterodyne detected vibrational sum-frequency spectra of the air/water interface (right). All simulations were performed using many-body molecular dynamics (MB-MD) carried out at both classical (blue traces) and quantum (red traces) levels using the MB-pol PEF combined with many-body representations of the water dipole moment (MB) and polarizability. On the left panels, χ_SSP is the resonant sum-frequency susceptibility, and S, S, and P are the components related to the polarization conditions of the sum-frequency, visible, and IR beams, respectively. S and P denote beam polarizations parallel and perpendicular to the surface, respectively. See refs (261) and (90) for specific details.

While employing an accurate PEF is the obvious requirement for a physically correct molecular-level description of the water properties, the optimal balance between accuracy and efficiency often is the ultimate criterion that dictates which PEF to use in actual simulations, since the computational cost associated with each PES directly determines the ability to calculate statistically converged quantities. To provide the reader with general estimates of the computational cost associated with the different classes of PEFs analyzed in this review, Table 6 shows the results of a performance analysis, originally reported in ref (217), carried out on a single Intel Xeon E5-2640 processor for a system consisting of 256 water molecules in periodic boundary conditions. This comparison shows that MB-pol achieves high accuracy at a cost of ∼50× that of an empirical pairwise additive PEF such as q-TIP4P/F and ∼6× that of an implicit many-body (i.e., polarizable) PEF such as TTM3-F.

Table 6. Cost Associated with Different PEFs (with Flexible Monomers) for a Molecular Dynamics Step in a System Containing 256 Water Molecules in Periodic Boundary Conditions^a.

PEF	class	cost per MD step relative to q-TIP4P/F
q-TIP4P/F37	pairwise additive PEF	1×
TTM3-F40	implicit many-body PEF	7×
MB-pol144,191,249	explicit many-body PEF	47×

^aAll timings are relative to q-TIP4P/F,³⁷ an empirical point-charge pairwise additive PEF, and were obtained using a modified version of DL_POLY2 using a single core of a typical Intel Xeon E5-2640 based workstation.

The analysis of explicit many-body PEFs clearly demonstrates that the MBE shown in eq 1 can effectively be used to construct highly accurate representations of the water interactions rigorously derived from correlated electronic structure data. MB-pol is the first, and currently only, successful example, of such PEFs which, correctly representing many-body effects at both short and long ranges, consistently predicts the properties of water with high accuracy from the gas to the condensed phase.

5. Conclusions and Future Directions

We have reviewed the current status of analytical potential energy functions for molecular-level computer simulations of water across different phases. Starting from simple pairwise additive functions, specific emphasis has been put on recent developments focusing on a correct description of many-body effects. Thanks to the improved understanding of hydrogen bonding and weak interactions, which has been accompanied in the past decade by progress in algorithms for molecular simulations and increased computing power, inclusion of many-body effects either implicitly, through the addition of induction terms, or explicitly, through the addition of separate terms to the energy expressions, has become routine.

While the parametrization of many-body PEFs based on experimental data is still common and effectively appears to be the most promising approach for the development of coarse-grained models (e.g., the mW model¹⁰⁰), the use of large sets of ab initio data in the fitting procedure is gaining appeal. In particular, fits to highly correlated electronic structure data, which can now be obtained at the “gold standard” CCSD(T) level for small water clusters,^{218,250,263−266} represent a viable route to the development of transferable and accurate many-body PEFs. Different schemes are currently used to cast the information encoded in the ab initio data into mathematical expressions that can be both easily implemented and efficiently computed. Following earlier work on polarization effects (e.g., see ref (267) for a recent review), several water models have been developed which represent many-body effects through induction interactions described by various schemes, including inducible point dipoles (e.g., AMOEBA,^{39,141−143,268} TTM,^{40,41,192−196} DDP2,²⁰⁶ POLIR,²⁰⁷ and POLI2VS²⁰⁸), charge-on-spring models (e.g., SWM,^134−136 COS,^137−139 and BK3¹⁴⁰), and multipolar expansions (e.g., ASP-W and SCME). While these models exhibit higher transferability than effective pairwise force fields (e.g, TIPnP⁵⁶⁻⁵⁸ and SPC*^59,60), they are still limited in the ability of consistently reproducing the properties of water from the gas to the condensed phase.

The limitations of polarizable PEFs can be traced to the difficulty of correctly representing both short-range interactions associated with quantum-mechanical effects (e.g., exchange-repulsion and charge transfer which arise from the overlap of the monomer electron densities) and long-range interactions that depend on the monomer properties (e.g., dipole moment and polarizability) through classical expressions describing electrostatic, repulsion, and dispersion contributions. A more physically correct description of the interaction energy can be obtained by employing schemes based on the decomposition of the ab initio energy into individual contributions. Following this approach, the SIBFA,^174−177 GEM,¹⁴⁵ and GEM*^186−189 models are constructed from a systematic reproduction of each energy term, which generally leads to a more accurate description of the intermolecular interaction especially at medium to short range.

Due to its rapid convergence for water, the many-body expansion of the interaction energy can be directly used to develop many-body analytical PEFs that express the energy of systems containing N water molecules as an explicit sum over individual interaction terms derived from highly correlated electronic structure calculations. CC-pol,^228−234 WHBB,^54,235−238 HBB2-pol,⁵⁵ SCME/GAP, and MB-pol^{144,191,249,261} are recent examples of explicit many-body PEFs which, containing explicit 1B, 2B, and 3B terms supplemented by many-body induction, exhibit a high degree of transferability from small clusters in the gas phase to the liquid phase. Different mathematical functions, including permutationally invariant polynomials²³⁹ and Gaussian approximation potentials,²⁵⁴ have been used to reproduce the multidimensional complexity of 2B and 3B interactions.

As shown in Figures 8–10 and Tables 4 and 5, the MB-pol PEF consistently reproduces with high accuracy the vibration–rotation tunneling spectrum of the water dimer, the energetics of small clusters, and the structural, thermodynamic, dynamical, and spectroscopic properties of liquid water, explicitly including nuclear quantum effects. Comparisons with quantum Monte Carlo reference data also indicates that MB-pol predicts the energetics of liquid configurations and ice phases with higher accuracy than DFT models commonly used in water simulations.²¹⁷ A systematic analysis of many-body effects performed with the MB-pol PEF as a function of the system size shows that both the explicit inclusion of short-range representations of 2B and 3B effects into the potential energy function and a physically correct incorporation of short- and long-range contributions are necessary for an accurate representation of the water interactions from the gas to the condensed phase.²¹⁷

As stated in ref (269), “If the ultimate goal of simulations is to predict reliably, not reproduce, experimental results, then simulations must be built on physically justifiable models”. In this context, the development of many-body potential energy functions certainly represents a major step toward the long-sought-after “universal model” capable of describing the behavior of water under different conditions and in different environments. However, significant challenges, both theoretical and computational, remain which should be addressed in the future before many-body approaches can become common practice in molecular simulations of aqueous systems. First, the nonstandard expressions used to explicitly describe individual terms of the many-body expansion of the interaction energy (e.g., 2B and 3B contributions) require the development of specialized software. Although progress in this direction has been made with the implementation of the MB-pol PEF as an independent plugin for the reference platform of the OpenMM toolkit,²⁷⁰ the availability of functionalities for the explicit treatment of many-body terms in common software for molecular simulations is extremely limited. Considering the algorithmic complexity of some of the mathematical functions used to describe many-body interactions, future collaborations between theoretical/computational chemists/physicists and computer scientists are desirable for the development of efficient software that can take full advantage of modern hardware. Importantly, as demonstrated by the similar accuracy achieved by SCME/GAP and MB-pol, building shared databases of high-quality electronic structure data will be critical to the development of accurate many-body PEFs for generic aqueous systems. Efforts along these lines are already ongoing.

Second, by construction, a many-body PEF is designed to represent the underlying Born–Oppenheimer potential energy surface, which implies that nuclear quantum effects should be explicitly included in the actual molecular simulation. Efficient algorithms to effectively take into account nuclear quantum effects through the application of colored-noise thermostats^271,272 and ring-polymer contraction schemes²⁷³ have recently been proposed and should be investigated within the many-body formalism (see the review article in this thematic issue devoted specifically to nuclear quantum effects in water⁷¹).

Third, exploration of the transferability of many-body approaches to complex (heterogeneous) aqueous systems has only recently begun.^274−281 Although initial results for ion–water clusters are promising, the generalization to aqueous solutions of arbitrary complexity requires further theoretical and computational developments.

Finally, with the exception of a few early attempts,^127,133 all analytical PEFs described in this review enforce the water molecules to maintain their distinct molecular nature, neglecting autoionization events. While this is a good approximation for the description of pure water systems, the ability of correctly modeling the behavior of hydronium and hydroxide ions becomes increasingly important for molecular simulations of heterogeneous aqueous solutions. Ongoing work in this area is focusing on the extension of the many-body formalism to reactive representations²⁸² as well as on the integration of current (nonreactive) many-body potential energy functions in adaptive quantum mechanical/molecular mechanical (adQM/MM) schemes.^283−291

Biographies

G. Andrés Cisneros received a B.Sc. in Chemistry from the National Autonomous University of Mexico (UNAM) and a Ph.D. in Chemistry from Duke University. Afterward, he worked as an intramural postdoctoral fellow in the National Institute of Environmental Health Sciences/NIH. He is currently an Associate Professor in the Department of Chemistry at Wayne State University. His research interests include development and application of accurate methods for chemical/biochemical simulations with emphasis on force field and QM/MM development, and the study of DNA replication/repair systems and ionic liquids.

Kjartan Thor Wikfeldt obtained his Ph.D. degree from the group of Prof. Lars G.M. Pettersson at Stockholm University, Sweden, in 2011, and subsequently held postdoctoral research positions in Prof. Angelos Michaelides’ group at University College London, UK, and in Prof. Hannes Jónsson’s group at the University of Iceland. Currently, he has joint research associate positions at the University of Iceland and Stockholm University where he focuses on computational research related to liquid water, crystalline and amorphous ice, and chemical reactions on ice surfaces in interstellar molecular clouds.

Lars Ojamäe received his Ph.D. in inorganic chemistry from Uppsala University in 1993, worked as a postdoc at the Ohio State University and the University of Turin, as assistant professor at Stockholm University and associate professor and then full professor at Linköping University, where he currently heads the physical chemistry subdivision. His research activities focus on computational-chemistry modeling of hydrogen-bonded systems such as ice and clathrates, as well as chemical reactions at surfaces of relevance for catalysis, solar cells, and nanoparticles.

Jibao Lu received his Ph.D in condensed matter physics in Prof. Ying Dai’s group at Shandong University (China) in 2012. Since then, he has worked as a postdoc at the University of Utah. His research interests involve the development of coarse-grained models, computational study of water-like tetrahedral liquids, anion-exchange membranes for alkaline fuel cells, and photocatalytic and magnetic semiconductors.

Yao Xu earned his B.Sc. in Applied Chemistry from Beijing University of Chemical Technology (China) in 2006 and his Ph.D. in Chemical Physics from the University of Nevada, Reno under the supervision of Prof. David M. Leitner in 2013. He currently is a postdoctoral researcher in the group of Prof. Martina Havenith at Ruhr University Bochum, Germany. He is interested in connecting solvation dynamics with biomolecular functions by molecular simulation and laser spectroscopy.

Hedieh Torabifard received her B.Sc. in Chemistry from Shahid Beheshti University (Iran) in 2008 and her M.Sc. in Physical Organic Chemistry in 2011 from Sharif University of Technology (Iran). She is currently a Ph.D. student in the group of Prof. G. Andrés Cisneros at Wayne State University. Her research interests involve the development of multipolar–polarizable force fields for condensed systems and QM/MM studies of biochemical systems.

Albert P. Bartók received his Ph.D. in 2010 after studying in Cambridge under the supervision of Prof. Mike Payne and Prof. Gábor Csányi. He held a Junior Research Fellowship in Magdalene College until 2013 and has been a Leverhulme Early Career Fellow since then. His main research interest is fitting accurate potentials using probabilistic machine learning techniques.

Gábor Csányi obtained a B.A. in Mathematics from the University of Cambridge in 1994 and a Ph.D. in Physics at the Massachusetts Institute of Technology in 2001. He is on the faculty of the Engineering Laboratory at the University of Cambridge, and his research focuses on developing new methods and algorithms for molecular simulation.

Valeria Molinero received her Ph.D. in Physical Chemistry from the University of Buenos Aires in 1999, worked as associate scientist at Caltech and Arizona State University, and joined the faculty at the University of Utah in 2006, where she is Professor of Chemistry and Director of the Henry Eyring Center for Theoretical Chemistry. She is interested in the interplay between microscopic structure, dynamics, and phase transformations in materials. The modeling of water, its anomalies and phase transitions has been a focus in her research in the last years.

Francesco Paesani received his Ph.D. in Theoretical Physical Chemistry from the University of Rome “‘La Sapienza”’ (Italy) in 2000. He was a postdoctoral fellow at the University of California, Berkeley, working with Professor Birgitta Whaley on the spectroscopy and superfluid behavior of helium droplets at low temperature. Subsequently, he was a postdoctoral researcher in the group of Professor Gregory Voth at the University of Utah working on the development of new methodologies to model quantum dynamics in the condensed phase. In 2009, he joined the faculty of the University of California, San Diego, where he is currently an Associate Professor in the Department of Chemistry and Biochemistry. In 2016, he was awarded the ACS Early Career Award in Theoretical Chemistry. Research in his group focuses on the development, implementation, and application of new theoretical and computational methodologies at the intersection between chemistry, physics, and computer science for molecular-level simulations of fundamental processes from the gas to the condensed phase.

The authors declare no competing financial interest.