Skip to main content
PMC home page
Development (Cambridge, England) logoLink to Development (Cambridge, England)
. 2017 May 15;144(10):1876–1886. doi: 10.1242/dev.146761

Actomyosin-based tissue folding requires a multicellular myosin gradient

Natalie C Heer 1, Pearson W Miller 2,3, Soline Chanet 1, Norbert Stoop 3, Jörn Dunkel 3, Adam C Martin 1,*
PMCID: PMC5450837  PMID: 28432215

Abstract

Tissue folding promotes three-dimensional (3D) form during development. In many cases, folding is associated with myosin accumulation at the apical surface of epithelial cells, as seen in the vertebrate neural tube and the Drosophila ventral furrow. This type of folding is characterized by constriction of apical cell surfaces, and the resulting cell shape change is thought to cause tissue folding. Here, we use quantitative microscopy to measure the pattern of transcription, signaling, myosin activation and cell shape in the Drosophila mesoderm. We found that cells within the ventral domain accumulate different amounts of active apical non-muscle myosin 2 depending on the distance from the ventral midline. This gradient in active myosin depends on a newly quantified gradient in upstream signaling proteins. A 3D continuum model of the embryo with induced contractility demonstrates that contractility gradients, but not contractility per se, promote changes to surface curvature and folding. As predicted by the model, experimental broadening of the myosin domain in vivo disrupts tissue curvature where myosin is uniform. Our data argue that apical contractility gradients are important for tissue folding.

KEY WORDS: Epithelia, Fold, Gradient, Myosin, Twist

Summary: A combination of experimental work and theory reveals how gradients in transcription, signaling and resulting contractility shape tissue folding.

INTRODUCTION

Actomyosin-associated folding of epithelial sheets is a common mode of morphogenesis during the development of complex organs and organisms. Defects in these folding events can lead to congenital birth defects, including spina bifida, which can be caused by failure of the neural plate to fold and fuse (Copp and Greene, 2010; Wallingford et al., 2013). Actomyosin-based epithelial folding is often associated with apical constriction, a process in which apical actomyosin contractility causes columnar epithelial cells to adopt a wedge shape by reducing their apical cell surface area (Martin and Goldstein, 2014). One unanswered question is how apical contractility must be spatially patterned in a tissue to generate three-dimensional (3D) form.

Drosophila gastrulation is a classic example of tissue folding in response to apical constriction. Cells on the ventral side of the embryo fold into the embryo as one of the first tissue rearrangements during development. The domain of invaginating cells is specified by two embryonic transcription factors, Twist and Snail (Leptin and Grunewald, 1990; Thisse et al., 1987). At the time of gastrulation, snail expression extends nine cells from the ventral midline (VM) (to form an 18-cell-wide domain) (Ip et al., 1992). twist expression extends a few cells further than snail (Leptin, 1991). Both genes are initially expressed in a narrower domain of cells that expands over time (Leptin, 1991). Expression of both twist and snail requires the maternal transcription factor Dorsal. twist is necessary for persistent apical constriction and non-muscle myosin 2 (myosin) accumulation (Mason et al., 2016; Xie and Martin, 2015). Two transcriptional targets of Twist appear to act in parallel to regulate actomyosin contractility in the ventral furrow: folded gastrulation (fog) and T48. Fog is a secreted protein that activates a maternally provided Gα12/13, concertina, through a G protein-coupled receptor (GPCR) pathway (Costa et al., 1994; Kerridge et al., 2016; Manning et al., 2013; Parks and Wieschaus, 1991; Xie et al., 2016). T48 is a transmembrane protein that contains a PDZ-binding consensus motif (Kolsch et al., 2007). T48 and Gα12/13 activation at the apical surface appear to recruit and activate RhoGEF2, a Rho guanine nucleotide exchange factor with a PDZ domain and a regulator of G protein signaling (RGS) domain (Barrett et al., 1997; Hacker and Perrimon, 1998). There, active RhoGEF2 can activate RhoA (Rho1 in flies), which, in turn, promotes apical actomyosin contractility (Kolsch et al., 2007; Mason et al., 2016). The effector of RhoA, Rho kinase (ROCK; Rok), is required for apical myosin accumulation in the ventral furrow (Dawes-Hoang et al., 2005).

As the tissue folds, there is significant variation in the extent and timing of apical constriction along the ventral-lateral axis of the furrow (Leptin and Grunewald, 1990; Oda et al., 1998; Sweeton et al., 1991) (Fig. 1A). Specifically, cells closer to the VM constrict earlier and to a greater extent than cells farther from the VM, despite the fact that all cells express twist prior to constriction (Leptin, 1991). The Twist target fog is transcribed in a subset of ventral cells that extends six cells from the VM (Costa et al., 1994); this region corresponds to the region of earliest constriction (Sweeton et al., 1991). Recently, it was shown that expression of the Twist transcriptional targets fog and T48 occurs in a graded manner along the ventral-lateral axis (Lim et al., 2017). The intensity profile of myosin during gastrulation has been illustrated at the tissue level, with highest myosin concentrations at the VM (Lim et al., 2017; Spahn and Reuter, 2013). However, whether there are cell-to-cell differences in transcription and active myosin levels and how patterns of transcription and contractility relate to each other is unknown. Most importantly, it is not known whether the variation in apical constriction/contractility is relevant to tissue folding.

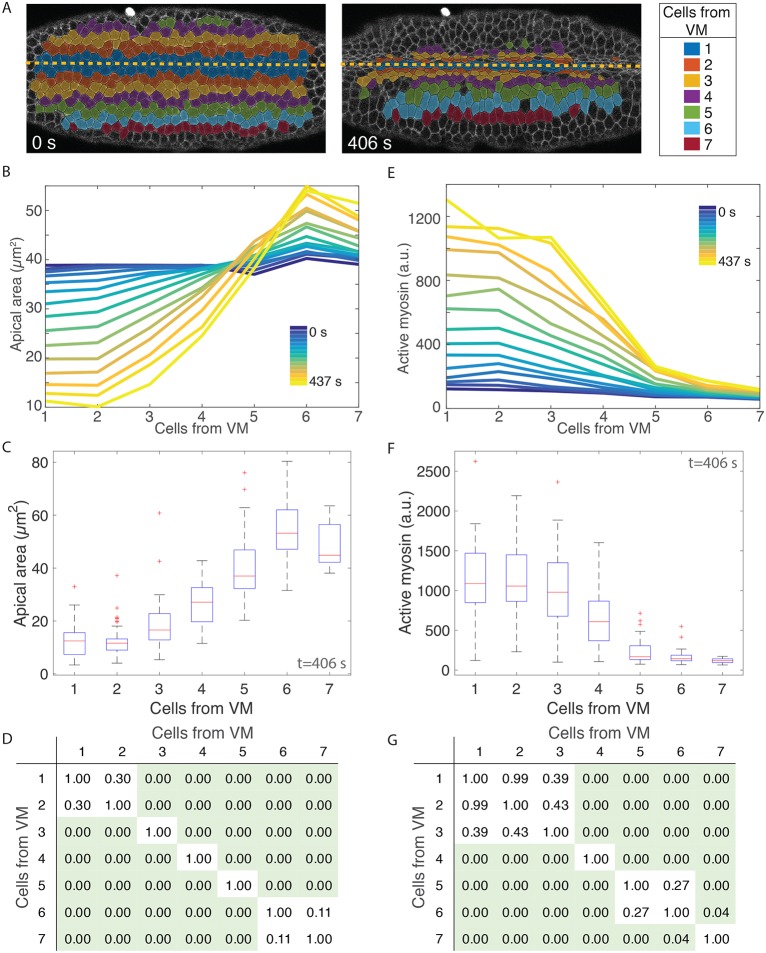
Fig. 1.

Fig. 1.

Open in a new tab

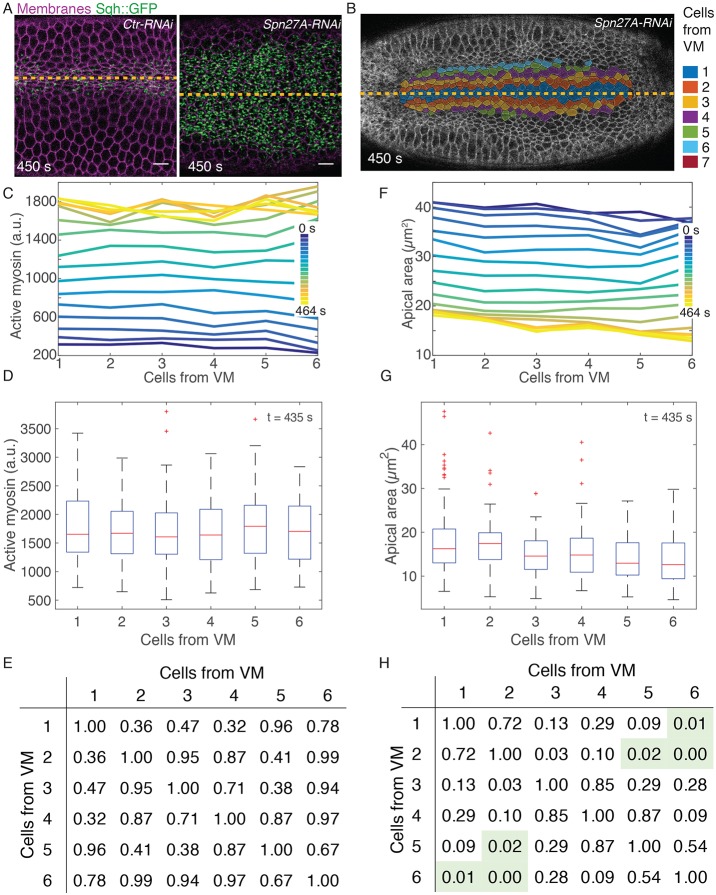
Apical area and active myosin intensity are present in a ventral-lateral gradient. (A) Cell position bins relative to the ventral midline (VM, yellow dashed line). (B,E) Apical area (B, y-axis) or total active myosin intensity (E, y-axis) plotted for each ventral-lateral cell position bin (x-axis) for each time frame (color bar) as the embryo furrows. (C,F) Distribution of cell areas (C) or total active myosin intensity (F) for cells in different position bins at time point t=406 s. Red lines indicate median values, box indicates inner quartiles, dashed lines indicate outer quartiles. (D,G) Pairwise statistical comparisons between different cell bins. Tables show P-values from a two-sample Kolmogorov–Smirnov (K–S) test comparing the distribution of apical area (D) and active myosin (G) in each cell bin with every other cell bin. Green shading indicates statistical significance (P<0.05). All data in A-G are from a single embryo. (B,E) n varies for each cell bin and time point. n=17 cells/bin (minimum) and 47 cells/bin (average). (C,D,F,G) n values are 58, 48, 50, 40, 32, 30 and 17 cells (for bins 1-7, respectively).

Here, we demonstrate that there is a gradient in myosin contractility across the ventral furrow. This gradient starts two to three cells from the VM and extends to approximately six cells from the VM. In this region, two to six cells from the VM, each subsequent cell has lower levels of active myosin. This contractility gradient originates from the dorsal morphogen gradient, and perturbation of the dorsal morphogen gradient changes the spatial patterning of contractility. Our 3D model of the gastrulating embryo predicts the importance of contractility gradients in generating a tissue fold. Our experimental data validated a prediction of the model: tissue bending was associated with contractile gradients, but not absolute levels of contractility.

RESULTS

Ventral furrow formation is associated with a multicellular contractility gradient, originating two to three cells from the VM

To determine how tissue-scale contractility is organized in the ventral furrow, we imaged embryos with labeled myosin (Sqh::GFP) and membrane (Gap43::mCherry) (Martin et al., 2010; Royou et al., 2002). We segmented all images from time-lapse movies of the folding process and partitioned cells into bins based on the initial distance of the cell centroid from the VM (see example in Fig. 1A). As previously observed (Jodoin and Martin, 2016), cells do not intercalate during furrow formation, and cell positions for bins at later time points show the same relative positions as at the initial reference time point (Fig. 1A). Thus, we were able to measure cell apical cross-sectional area over time as a function of relative position from the VM.

In agreement with a previous live-imaging study, which quantified groups of cells (Oda et al., 1998), we found that apical area reduction was not uniform along the ventral-lateral axis. Prior to the onset of constriction, all cells along the ventral-lateral axis had an apical area of ∼40 µm2 (Fig. 1B, blue curves; Fig. S1A,B, blue curves). Over time, cells within four cells of the VM reduced their apical area and cells farther than five cells from the VM expanded their apical area (Fig. 1B, blue to yellow curves; Fig. S1A,B, blue to yellow curves). At late time points, the apical area distributions for the two cells adjacent to the VM were not statistically different, but each subsequent cell from the VM had significantly larger apical area until six cells from the VM (Fig. 1C,D; Fig. S1C,D). We refer to this pattern in the resulting apical area as a gradient in apical constriction. Differences in cell area were not seen when cells were binned based on their position along the orthogonal anterior-posterior axis of the embryo, demonstrating that the apical constriction gradient occurs mainly along the ventral-lateral axis (Fig. S2).

To measure the levels of ‘active’ myosin in the cell apex, we have used an image-processing method to capture activated, cortical myosin molecules and exclude cytoplasmic, ‘inactive’ myosin (see Materials and Methods). Several arguments support the fact that we have measured active myosin: (1) Drosophila myosin 2 can exist either as a single molecule in an inactive, folded conformation or as an active bipolar filament consisting of 12 molecules, depending on phosphorylation of its regulatory light chain (Vasquez et al., 2016), (2) inhibition of ROCK, a kinase that phosphorylates and activates myosin filament formation and motor activity, results in the immediate dissolution (within 10-15 s) of the intense cortical myosin structures that we measure (Coravos and Martin, 2016), and (3) the amount of myosin that we measured using this method correlates well with apical constriction in single cells (Martin et al., 2009; Xie and Martin, 2015). For all of these reasons, we conclude that the intensity of the cortical myosin structures measured in this study represents active myosin.

We found that there was a multicellular gradient in active myosin that accompanied ventral furrow formation. Specifically, active myosin intensity distributions were highest on average in the two cells adjacent to the VM (Fig. 1E-G; Fig. S1E-H). The average amount of active myosin in the third cell from the VM was often lower, but this was not always statistically significant (Fig. 1E-G; Fig. S1G-J). Beginning three cells from the VM, every subsequent cell position consistently exhibited a significantly lower active myosin distribution than the one before (Fig. 1F,G; Fig. S1G-J). Thus, there is a multicellular gradient in myosin activity that starts two to three cells from the VM and extends to six cells from the VM. We refer to this as a ventral-lateral contractility gradient.

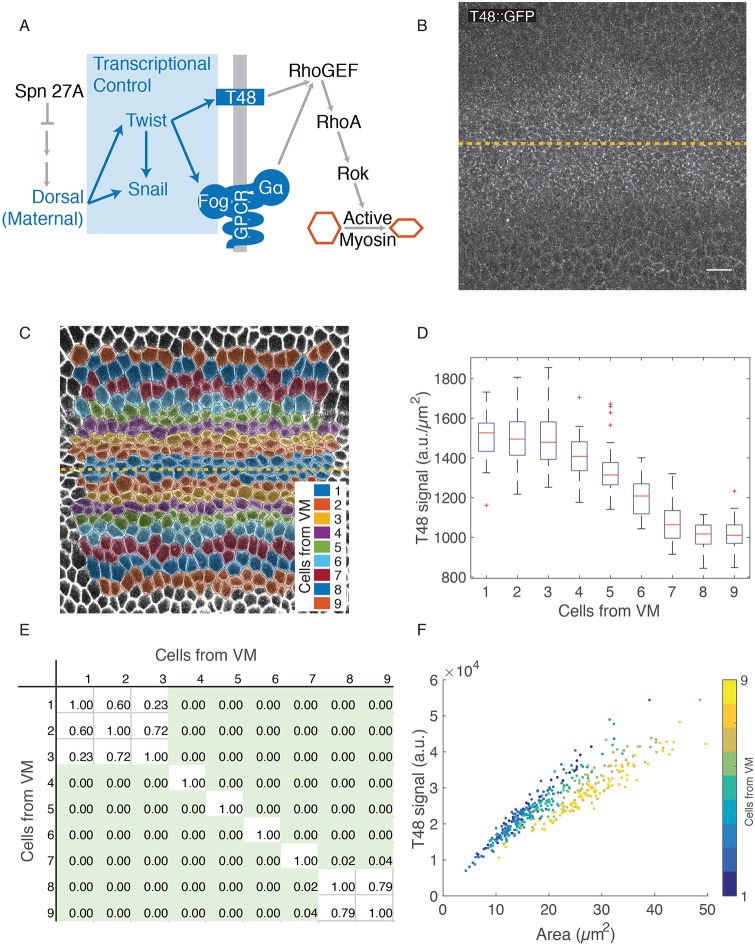
An upstream regulator of contractility, T48, exists in a gradient

To determine the source of the active myosin gradient, we examined an upstream component of the signaling pathway that regulates ventral furrow formation, the integral membrane protein T48 (Fig. 2A). We engineered a T48 allele with an internal GFP tag. The GFP::T48 fusion allele was expressed from the endogenous T48 promoter using bacterial artificial chromosome-mediated recombineering (Venken et al., 2006). GFP::T48 was visualized in fixed embryos stained with a GFP antibody (Fig. 2B). We segmented the image based on phalloidin staining and binned cells with respect to their position from the VM (Fig. 2C; Fig. S3A). We found that average signal density of GFP::T48 is highest in cells closest to the VM (Fig. 2D; Fig. S3B). Similar to the distribution of active myosin, a difference in T48 levels first appears between cells 3 and 4 from the VM. The gradient in T48 seems to extend slightly further than the gradient in myosin (encompassing seven to eight cells on either side of the midline) (Fig. 2D,E; Fig. S3B,C). The fact that there is a T48 gradient is consistent with the myosin gradient resulting from upstream signals.

Fig. 2.

Fig. 2.

Open in a new tab

T48::GFP signal density is graded three to eight cells from the VM. (A) Schematic of the signaling pathway that promotes apical constriction. Gray line represents apical membrane. GPCR, G protein-coupled receptor. (B) Image of GFP::T48 (anti-GFP) embryo with VM centered (dashed yellow line). (C) Cell bins (colored) manually determined in a fixed embryo. Image is of a phalloidin-stained embryo. (D) GFP::T48 density (fluorescence intensity µm−2) (y-axis) as a function of position from the VM (x-axis, see C). (E) Pairwise statistical comparisons between different cell bins. Table shows P-values from a two-sample K-S test comparing the distribution of T48 (a.u. μm−2) in each cell bin with every other cell bin. Green shading indicates statistical significance (P<0.05). (F) Total GFP::T48 signal per cell (y-axis) as a function of apical cell area (x-axis). Cell bin is denoted (color bar). (B-F) n is one embryo and 45, 43, 44, 44, 44, 47, 50, 51 and 50 cells (for bins 1-9, respectively). Scale bar: 10 µm.

The measured gradient in T48::GFP signal density (a.u. per µm2) could reflect the gradient in apical constriction, rather than a gradient in T48 gene expression. As cells apically constrict, T48::GFP on apical membranes could be concentrated. To test this, we measured the total amount of T48 at the apical surface of a cell. We found that total signal is strongly correlated with cell area, possibly due to a low signal-to-noise ratio (Figs 2F and S3D). However, for cells of a given area, cells closest to the VM have a higher level of total T48::GFP signal, suggesting that differential expression of T48 accounts for at least some of the difference in signal density (Figs 2F and S3D, blue versus yellow points). This is supported by recent work measuring T48 expression in the ventral domain that found that T48 and fog, another Twist target, are expressed earlier in cells closest to the VM (Lim et al., 2017). Our data demonstrates that between three and seven cells from the VM there are differences in both T48 density and overall levels, in a pattern that mirrors active myosin.

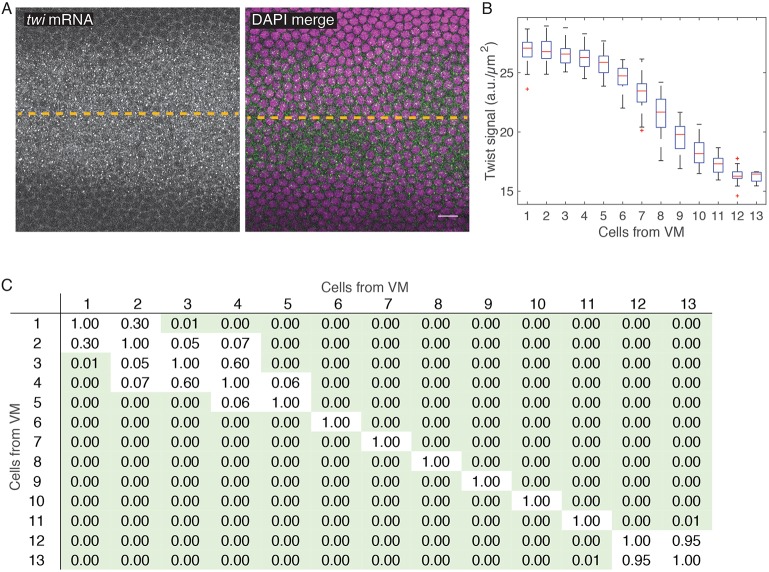
twist mRNA is present in a gradient at the onset of cycle 14

It has been previously shown that Dorsal, a maternal morphogen that is required for twist transcription, is active in a gradient along the ventral-lateral axis with highest nuclear levels in the most ventral cells (Kanodia et al., 2009; Reeves et al., 2012). twist expression levels have previously been described as being uniform across the central region of the ventral furrow with a gradient of twist at the edge of the furrow, where cells stretch (Leptin, 1991). We measured twist mRNA levels at the beginning of nuclear cycle 14, about an hour before gastrulation, using quantitative fluorescence in situ hybridization (FISH). We found that twist mRNA was detected as small puncta in the cytoplasm of ventral cells (Fig. 3A). We measured twist mRNA levels by quantifying the mean intensity of the twist FISH signal in the cytoplasm adjacent to each nucleus (McHale et al., 2011). At early nuclear cycle 14, twist is expressed in a gradient around the VM. The gradient begins two to three cells from the VM and extends to about 12 cells from the VM (Fig. 3B,C). Early differences in twist levels are consistent with, and could explain, the later differences in transcription and downstream signaling measured in this paper and previously (Costa et al., 1994). Time delays due to transcription of target genes and the translation of Twist and target genes could explain the delay between the measurement of twist mRNA and the downstream gradients. Thus, there is an early, transient gradient in twist mRNA levels that could explain the subsequent gradient in apical T48 levels, myosin activity, and contractility.

Fig. 3.

Fig. 3.

Open in a new tab

twist mRNA expression is graded 3-12 cells from VM at early nuclear cycle 14. (A) Images show twist mRNA (left) or twist mRNA and DAPI (green and magenta, respectively) in single z-slices, en face, just apical to cortical nuclei. Dashed line indicates VM. (B) Cytoplasmic twist signal (y-axis, fluorescence intensity/µm2) plotted as a function of position from the VM (x-axis, determined by average cell diameter). (C) Pairwise statistical comparisons between different cell bins. Table shows P-values from a two-sample K-S test comparing the distribution of twist (a.u. μm−2) in each cell bin with every other cell bin. Green shading indicates statistical significance (P<0.05). n is one embryo with 45, 43, 44, 44, 44, 47, 50, 51, 50, 50, 56, 30 and 5 cells (for bins 1-13, respectively). Scale bar: 10 µm.

Mechanical model demonstrates that contractile gradients promote curvature

To understand the mechanisms underlying furrow formation by contractility gradients, we studied a 3D continuum model of the Drosophila embryo during gastrulation. At this developmental stage, the embryo consists of a thin, single-layer epithelial sheet of approximately ellipsoidal shape. Its mechanics can be described mathematically by an elastic shell (Koiter shell model; Ciarlet, 2000), represented by its middle surface (Fig. 4A); for further explanation see Materials and Methods. Passive mechanical stresses appear whenever the middle-surface geometry deviates from its original shape by local stretching or bending deformations. Active stresses from apical constriction were incorporated into this model by modifying the local preferred curvature of the middle surface (mimicking constriction at the apical surface); these cause active bending moments that drive furrow formation (Fig. 4B). This is analogous to the bending of bimetallic strips, which assume a curved state when one of the two adjacent layers expands less strongly than the other in the presence of a thermal stimulus (Timoshenko, 1925). Similarly, apical contraction is expected to create a preferred tissue curvature. To relate the local myosin activity to active stress generation, we analyzed how apical constriction affects preferred curvature in a vertex-based cell model (Fig. 4B). This allowed us to relate active stresses to a dimensionless parameter M. M measures the relative strength of active and passive stresses and fully determines the induced shape deformation. The parameter M can thus be understood as a dimensionless contractility coefficient that is proportional to the local myosin activity. This theoretical framework allowed us to efficiently study spatial patterns of contractility and compare the predicted 3D shell shapes against our experimental data for wild-type and mutant embryos.

Fig. 4.

Fig. 4.

Open in a new tab

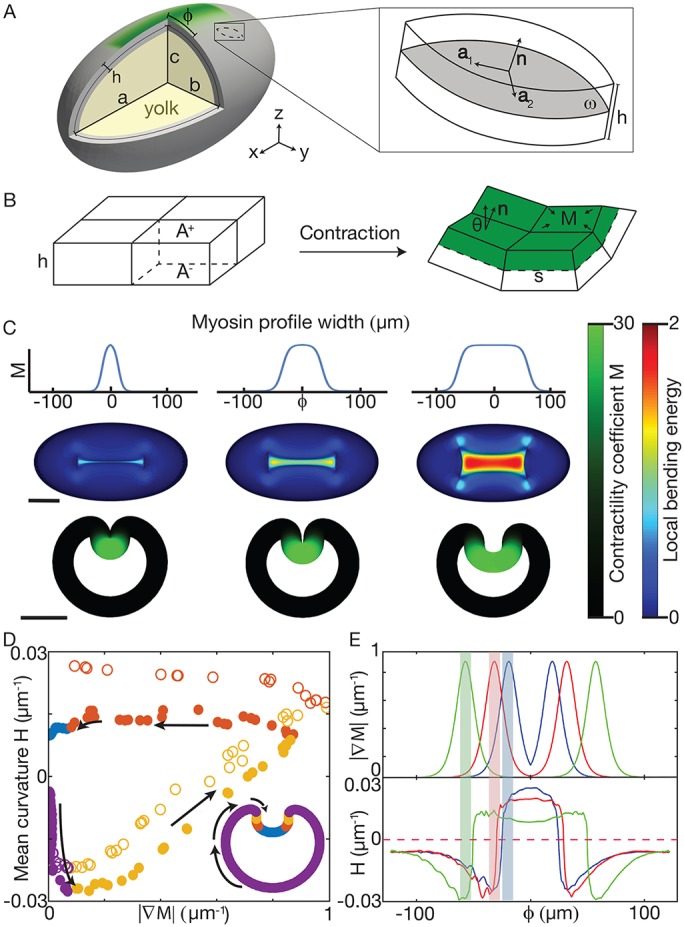
Continuum mechanical model associates curvature with contractility gradients. (A) Ellipsoid model schematic with surface tangents (a1 and a2) and normal (n). φ is distance from VM. (B) Schematic showing how contractility (M) on surface A+ changes the preferred curvature. (C) Profiles of M (top) used for simulation, with w=19 μm (left), w=31 μm (middle) and w=56 μm (right), and the resulting shape (bottom). In each case, steepness parameter k=0.19 μm−1 and M0=30. Bending energy (color bar) is a proxy for the difference between local preferred and actual curvature (Materials and Methods). Scale bars: 100 µm. (D) Mean curvature of the middle plane as a function of the gradient in contractility (M) for small w (open circles) and large w (closed circles). Although the VM has the highest concentration of myosin, there is no contractility gradient and no further increase in curvature (blue). (E) Myosin gradient (top) aligned with maximum curvature (bottom) as a function of φ. The location of peak contractility M is highlighted with shaded bars. Blue line corresponds to leftmost simulation in C, red to the middle simulation and green to the rightmost.

Guided by our myosin activity measurements in wild-type embryos, we approximated the contractility profile as 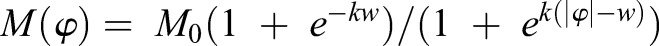Inline graphic. Here, φ is the distance from the VM, M0 denotes the maximum value of M (assumed at φ=0), k is a steepness coefficient characterizing the profile decay, and w is the width of the profile (Fig. 4C). We adjusted k, M0 and w to fit the distribution of myosin and apical constriction that we observed in wild-type embryos.

To test whether the gradient in contractility was important for folding, we compared furrow formation in the model for increasing values of w (Fig. 4C). For low values of w, we observed furrows that were morphologically similar to those of wild-type embryos (Fig. 4C, left and middle). Increasing w increased the width of the region of contractility and resulted in a region around φ=0 where the contractility profile is flat (Fig. 4C, right). Simulated equilibrium shapes showed that, as the distance between regions of graded contractility increased, the furrow width also increased, leaving a relatively flat surface in the region of uniform contractility (Fig. 4C). Importantly, changes in shell curvature were associated with the position of the gradient in M (Fig. 4D). This was the case regardless of the width of the myosin profile. Changes in shell curvature always occurred near the boundary where there was a gradient in M. In contrast, where there was an extended region of uniform M, curvature was low (Fig. 4D,E).

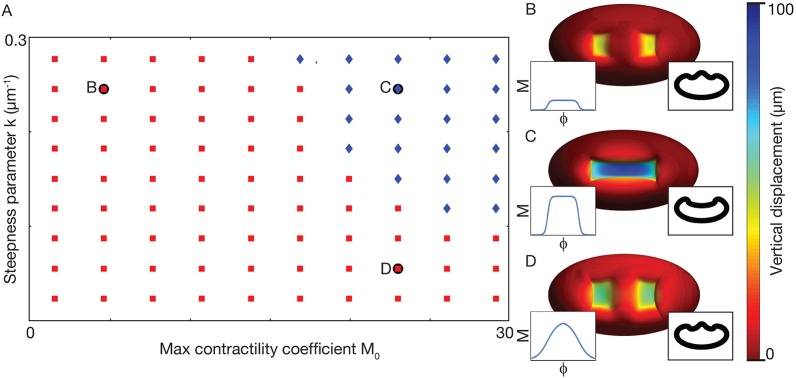
We next explored how our model responded to changes in M0 and k, i.e. the level of contractility and steepness of the contractility gradient, respectively. We found that with low contractility M0, but normal steepness k, our model does not form a furrow (Fig. 5A,B). Additionally, in our model, having high contractility M0, but a low steepness k for the gradient, also fails to form a furrow and instead results in an hour-glass shaped flattened depression (Fig. 5A,D). Only when both M0 and k are above a certain threshold will the model form a furrow (Fig. 5A,C). Thus, our model predicts that furrow formation in embryos will fail if either the total activity of active myosin or the steepness of the gradient is too small.

Fig. 5.

Fig. 5.

Open in a new tab

Parameter scan shows folding requires increased contractility and a contractility gradient. (A) Phase diagram showing parameters for which a furrow forms (blue) and for which a furrow fails to form (red). Letters indicate parameters that correspond to the examples in B-D. (B) Low contractility parameter, M0=6, does not furrow. (C) High contractility and presence of gradient (M0=24 and k=0.256 μm−1, respectively) results in furrow. (D) Low steepness parameter, k=0.064 μm−1, does not furrow. Insets indicate M as a function of φ and cross-section views along the long axis of the ellipsoid. In each case, width w=43 μm.

Experimental flattening of the active myosin gradient in vivo disrupts tissue curvature

Our 3D model simulations predicted that tissue folding occurs where there is a gradient in contractility. To show that uniform levels of active myosin were insufficient to cause tissue bending, we attempted to flatten the active myosin gradient in vivo using a genetic perturbation. Spn27A is a negative regulator of ventral cell fate in the Drosophila embryo (Fig. 2A). Hypomorphic alleles of Spn27A and depletion of Spn27A using RNA interference (RNAi) have been shown to increase the width of the ventral domain (Ligoxygakis et al., 2003; Chanet et al., 2017). We hypothesized that increasing Dorsal activity could lead to an extended region of uniform Dorsal activity around the VM. We first tested the effect of Spn27A depletion on the upstream gradient in twist mRNA and found that, as expected, twist expression levels were uniform in an expanded region around the VM in Spn27A-RNAi embryos (Fig. S4). We next examined the effect of Spn27A depletion on the contractility gradient, and found that the region of uniform active myosin was broadened (Fig. 6A). Embryos depleted of a control gene (Rh3) exhibited a gradient in active myosin similar to that of wild-type embryos (Fig. S5A-F). In contrast, Spn27A depleted embryos did not exhibit a normal gradient; instead they exhibited uniform active myosin within six cells of the VM (Fig. 6C-E; Fig. S6A-F). Furthermore, the uniform levels of active myosin were associated with uniform apical constriction compared with the normal apical area gradient seen in the control RNAi embryos (compare both Fig. 6F-H and Fig. S6G-J with Fig. S5G-J). Because Spn27A attenuates Dorsal activity, our data suggest that the gradient in twist, active myosin, and apical constriction is the result of the gradient in Dorsal transcriptional activity.

Fig. 6.

Fig. 6.

Open in a new tab

Active myosin gradient is dependent on dorsal patterning. (A) Apical surface projection (see Materials and Methods) showing myosin (Sqh::GFP) and membrane (Gap43::mCherry) in Rh3-RNAi (Ctr-RNAi) or Spn27A-RNAi embryos. (B) Cell outlines (Gap43::mCherry) and cell position bins, relative to VM (yellow line). (C,F) Plots of average active myosin intensity (C) or apical area (F) as a function of position from VM. Different color lines are different time points. (D,G) Distributions of active myosin (D) and apical area (G) for cell position bins at 435 s time point. Red lines indicate median value, boxes indicate inner quartiles, dashed lines indicate outer quartiles. (E,H) Tables of P-values generated from a two-sample K–S test comparing the distribution of active myosin (E) or apical area (H) in each cell bin with every other cell bin. Green shading indicates statistical significance (P<0.05). Data shown in A-H are from the same Spn27A-RNAi embryo. Ctr-RNAi image is from the embryo quantified in Fig. S5A,C,E,G,I. n=17 cells/bin (minimum) and 50 cells/bin (average). Scale bars: 10 µm.

In accordance with the prediction of our 3D continuum mechanical model (Fig. 4C, right), Spn27A-depleted embryos exhibited reduced cross-sectional curvature in the region surrounding the VM, whereas the tissue does curve where there is a gradient of apical myosin activity at the edge of the broadened ventral domain (Figs 7A and S7A,B). This failure to form a sharp furrow was associated with defective/reduced apical constriction, specifically along the ventral-lateral axis (Fig. S7C). This phenotype is consistent with the prediction of our model that increasing the width (w) of the region of contractility results in an expanded furrow, which is flattened at the VM where there is no myosin gradient.

Fig. 7.

Fig. 7.

Open in a new tab

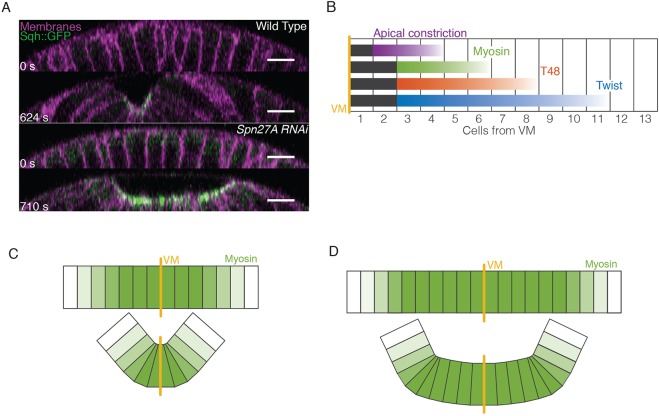
Model of ventral furrow formation. (A) Orthogonal projections in the z-plane of the ventral cross-section of wild-type (from Fig. 1) and Spn27A-RNAi (from Fig. 6) embryos. (B) Summary of gradients observed for twist mRNA (early nuclear cycle 14), T48::GFP, active myosin, and apical constriction in wild-type embryos. Uniform signal levels are in black, gradients are in color. (C) Gradient of myosin activation promotes cell wedging around the VM due to force imbalance, which folds the tissue. (D) Expansion of the ventral domain (i.e. Spn27A-RNAi) leads to an extended region of uniform myosin, in which forces are more balanced and bending is inhibited near the VM. Scale bars: 10 µm.

DISCUSSION

In many cases, epithelial folding is thought to result from myosin accumulating at the site of the fold (Lecuit et al., 2011; Leptin, 2005; Martin and Goldstein, 2014). Here, we show that active myosin accumulation fails to effectively change tissue curvature, except in regions in which neighboring cells or tissue regions are accumulating different amounts of apical, active myosin. This conclusion is based on several pieces of evidence: (1) there is a gradient in mean levels of active myosin, which originates two to three cells from the VM and extends to six cells from the VM (Fig. 7B), (2) there are graded levels of both twist and its transcriptional target GFP::T48 that originate three cells from the VM and extend slightly farther than mean levels of active myosin (Fig. 7B), (3) mechanical modeling of a 3D elastic shell requires a contractility gradient to form a fold that resembles a ventral furrow, and (4) experimentally expanding and flattening the myosin gradient in vivo results in an abnormal tissue shape that is predicted by the mechanical model. Thus, changes in tissue curvature and folding occur at sites of active myosin gradients. In the case of the Drosophila ventral furrow, the gradient in active myosin is the result of a gradient in the activity or levels of upstream transcription factors.

Gradients in the level of contractility, in our case apical contractile myosin, promote curvature by promoting a contractile force imbalance between neighboring regions of cells (Fig. 7C). In the case of the wild-type ventral furrow, this imbalance occurs along the ventral-lateral axis. Cells within two to three rows from the VM, accumulate similar levels of active myosin and constrict the same amount. Despite uniform active myosin in these central four to six cells, it appears that these cells are able to pull the surrounding tissue and effectively constrict. Beyond two to three cells from the VM, each cell exhibits progressively lower apical, active myosin, T48 and twist levels and constricts later and to a lesser extent (Fig. 7B,C).

Furrow formation requires asymmetric constriction (i.e. a wedge shape), such that the cells' apical surface remains stretched along the anterior-posterior axis and constricted along the orthogonal (ventral-lateral) axis (Martin et al., 2010). When mechanically isolated, ventral furrow cells constrict symmetrically, suggesting that the elongated shape of the cell apical surface is the result of differences in forces generated by the surrounding tissue (Martin et al., 2010). We propose that the contractility gradient we measured in this paper allows cells to constrict more along the ventral-lateral axis because of less resistance from the surrounding tissue. This results in wedge-shaped cells and promotes curvature/folding specifically along the ventral-lateral axis (Fig. 7C).

In contrast to wild-type embryos, uniform contractility levels (i.e. in Spn27A-RNAi) increase the resistance to apical constriction from neighboring cells; thus, cells do not constrict enough to generate high curvature (Fig. 7A,D). Consistent with this interpretation, Spn27A-RNAi exhibited a defect in constriction along the ventral-lateral axis (Fig. S7C). Spn27A-RNAi embryos could occasionally fold and internalize the mesoderm, but these folds consistently exhibited a flattened depression and the invagination was often uneven and not temporally smooth.

A 3D elastic shell model supports the importance of contractile gradients in tissue folding

The in vivo experimental outcomes described above are consistent with our mechanical model. We found that having a contractile gradient around the circumference of an ellipsoid resulted in a sharp, narrow furrow. In contrast, increasing the width of the contractile zone between opposing contractile gradients resulted in a flattening of the tissue at the VM, similar to observations in Spn27A-RNAi embryos. In a systematic parameter scan of our model, the ventral furrow fails to develop if either contractility or the steepness of the gradient is too small. Thus, it is not simply absolute apical myosin activity that is required for shape, but active myosin differentials between neighboring regions or cells.

Our mechanical model differs from previous models of Drosophila gastrulation. It represents the first 3D continuum model of ventral furrow formation in which apical constriction is the only active force input into the system (Conte et al., 2009; Conte et al., 2008; Odell et al., 1981; Polyakov et al., 2014; Spahn and Reuter, 2013). In particular, our theoretical analysis implies the role of active myosin gradients in tissue bending. Spahn and Reuter explored the role of a gradient in contractility on the pattern of cellular constriction, but their planar model did not reveal the importance of the gradient to folding (Spahn and Reuter, 2013). Conte and colleagues presented a 3D model of Drosophila gastrulation, but needed to introduce ectodermal pushing to generate folding (Conte et al., 2008). Our results suggest that the embryo does not require ectodermal pushing if there is a contractility gradient.

We note that contractility conditions for successful furrow formation are intrinsic 3D effects not captured by 2D cross-section models. In particular, 2D models assume spatial invariance along the anterior-posterior axis and thus can be thought of as a model of furrow formation on an infinite cylinder. A cylinder has vanishing Gaussian curvature and axially invariant deformations introduce bending, but no stretching deformations. By contrast, furrow formation on an ellipsoid requires stretching of the membrane due to positive Gaussian curvature. The high energetic cost of stretching thus presents an effective energy barrier against such deformations, an important mechanical effect neglected in 2D models. Therefore, 2D models might significantly underestimate the conditions required for the furrow to form. The present 3D analysis underscores the mechanical importance of contractility gradients for the robust formation of the ventral furrow.

There are some limitations to our particular modeling approach. The most important is that the height of the elastic shell in our model is constant. This is not the case in vivo, where apical constriction initially results in cells lengthening along their apical-basal axis, followed by shortening along same axis (Sweeton et al., 1991). This final shortening step is associated with the generation of the highest curvature (Polyakov et al., 2014). Given that our model successfully predicts several experimental observations, the concept that a given magnitude of apical contractility generates a local preferred curvature of the surface of a shell provides a useful framework with which to understand tissue folding. The final tissue curvature will also be governed by the extent to which epithelial cells lengthen (which minimizes curvature) versus expanding their basal domain (which promotes curvature). A future experimental challenge will be to understand the cell biological and physical mechanisms that control epithelial cell height during this process. Regardless of the specific mechanisms that control cell height, the spatial pattern of contractility will play a central role in governing final tissue shape.

Evidence for the presence and function of a contractile gradient in the ventral furrow

Because of our ability to resolve cell shape and active myosin at cellular resolution, we have been able to show that there is a gradient in apical myosin that starts three cells from the VM and extends six cells distal to the VM. Thus, a four-cell wide domain exhibits a contractility gradient, with differences in contractility existing between individual rows of cells with given ventral-lateral positions (Fig. 7B). Interestingly, the domain with uniform active myosin levels is about the width of a hinge point associated with mouse neural tube closure (Smith et al., 1994). The gradient we measured depends on a gradient in twist and probably also T48. This was the basis for our mechanical model of folding. Importantly, we show that flattening of this gradient leads to defects in tissue shape (i.e. reduced tissue curvature at the VM).

Other work also supports the importance of an active myosin gradient. Mutation of a possible attenuator of Fog signaling, Gprk2, results in a broader activation of myosin (Fuse et al., 2013). Interestingly, the Gprk2 mutant exhibited delayed folding at the VM and instead only displayed changes in curvature at the edges of the myosin domain (Fuse et al., 2013). The Gprk2 mutant phenotype resembles that of Spn27A-RNAi. Thus, multiple mutant phenotypes are consistent with the requirement of an active myosin gradient to promote tissue curvature, which reinforces our conclusions.

MATERIALS AND METHODS

Fly stocks and genetics

Fly lines and crosses are listed in Table S1. Embryos were collected from cages at 25°C except where noted.

Cloning

GFP was inserted in the T48 coding sequence at amino acid residue 85, with a standard linker (amino acids GGSG) added before and after the GFP. The T48::GFP construct was inserted in the bacterial artificial chromosome (BAC) (CH321-58L17) using standard recombineering techniques (Venken et al., 2006; Warming et al., 2005). We injected nanos-integrase; attp40; vk33 embryos with the purified BAC and selected for transgenic flies using white expression as a marker. Primers for T48 transgenic were as follows: 5′ upstream homology arm: 5′-ATGCGGTCGGTGGAAGTGGC-3′; 3′ upstream homology arm: 5′-GCTCACGCCCGAGCCGCCCATGCCGGGCAGCACCAC-3′; 5′ GFP with linker: 5′-GGCGGCTCGGGCGTGAGCAAGGGCGAGGAGCTGTTCACCGG-3′; 3′ GFP with linker: 5′-GCCCGAGCCGCCCTTGTACAGCTCGTCCATGCCGAGAGTG-3′; 5′ downstream homology arm: 5′-GTACAAGGGCGGCTCGGGCCTGCAAAATTCAGGTGGG-3′; 3′ downstream homology arm: 5′-CACACGCTTTATTTGGGGCTC-3′.

Live and fixed imaging

Embryos were prepared for live imaging as previously described (Martin et al., 2009). Images were acquired on a Zeiss 710 microscope with an Apochromat 40×/1.2 numerical aperture W Korr M27 objective. Pinhole size: 2.2 or 2.4 airy units. A 488/561 beam splitter was used. Channels were excited (argon 488 laser, 2.6% or 4.5%; DPSS 561-10, 2% or 2.8%) and acquired (detected range: 493-561 nm and 599-696 nm) concurrently.

Immuno- and phalloidin staining was performed using standard methods (Martin et al., 2009). GFP antibody (rabbit, 1:500; Abcam, ab290) and AlexaFluor 647 phalloidin (Invitrogen) were used. All imaging was carried out on a Zeiss 710 confocal microscope with a Plan-Apochromat 63×/1.4 numerical aperture Oil DIC M27 objective. Pinhole size: 1 airy unit. Channel 1: DPSS 651-10 laser (1%), detector range: 574-712 nm. Channel 2: argon 488 laser (2%), detector range: 493-574 nm.

For quantitative FISH, embryos were fixed (8% paraformaldehyde, 45 mins) and stained as described by Little et al. (2011). Probes complementary to the twist open reading frame were conjugated to AlexaFluor 594 (Life Technologies). DAPI was used to detect nuclei. Embryos were mounted in Aqua Poly/Mount (Polyscience). All imaging was carried out on a Zeiss 710 confocal microscope with a Plan-Apochromat 63×/1.4 numerical aperture Oil DIC M27 objective. Channels were acquired on separate tracks. Pinhole size: 1 airy unit. Track 1: Diode 405-30 (0.5%) detector range: 410-582 nm. Track 2: HeNe594 (15%) detector range 602-734 nm. Each line was scanned four times and the sum recorded.

Image processing

All image analysis was performed in Fiji (http://fiji.sc) (Schindelin et al., 2012) and MATLAB (MathWorks). Custom software for image processing is available upon request.

Analysis of active myosin

First, cytoplasmic background signal (defined as the mean cytoplasmic signal plus 2.5 standard deviations) was subtracted from the myosin channel (Martin et al., 2009; Vasquez et al., 2014). This subtraction left only the concentrated apical signal that evidence suggests is active myosin. The maximum myosin signal intensity in the z-plane was used to generate a rough map of the embryo surface. A Fourier transform was used to generate a smooth continuous surface. Myosin signal was averaged over the 4 µm above the surface and membrane signal was the sum of the signal from 1-2 µm below the surface. (Membrane signal was only used for segmentation, not quantification.)

Immunostained images

T48 signal was quantified in a single apical slice from a 3D image. Fixed embryos were flattened during mounting so the surface projections used in live embryos were not necessary. The T48 signal was not background subtracted.

All live and immunostained images were then segmented using an existing MATLAB package, Embryo Development Geometry Explorer (EDGE) (Gelbart et al., 2012). Membrane signal (Gap43::mCherry) or cortical actin (phalloidin) were used to detect cell boundaries and track cells in time for live images. Errors in segmentation were corrected manually. Our segmentation algorithm was used to determine centroid position, cell diameter, cell area and total myosin or T48 signal intensity within a cell.

Quantification of twist mRNA in OreR and Spn27A-RNAi embryos

FISH signal was performed using a previously published software package, which partitions the cytoplasm into ‘cells’ based on nuclear position and subtracts the nuclear volume from measurements of average cytoplasmic signal per ‘cell’ (McHale et al., 2011). This package was used to determine cell centroid position for each cell, average cytoplasmic signal per pixel for each cell, and average cell diameter for the image.

Image analysis

For all image quantifications, data was aggregated into ‘cell bins’. Cells were assigned to bins based on the ventral-lateral position of the cell centroid. We first identified the approximate position of the VM in all images. In live images, the VM was defined as the position at which the furrow closes over (Figs 1 and 6; Figs S1, S5 and S6). In fixed images, the signal was first confirmed to be symmetric, and the position of the VM was determined by symmetry of the signal (Figs 2 and 3; Figs S3 and S4). We were unable to determine the precise VM position in Spn27A-RNAi embryos stained for twist mRNA because the boundaries of the domain expressing twist mRNA extended beyond the field of view. In this case (Fig. S3), we did not assume symmetry of the signal, and simply determined the distribution of twist mRNA in a ventral region. When assigning cells to bins based on centroid position, live images were binned based on initial position of the cell centroid before tissue contraction and folding and the boundaries of the bins were set by the average cell diameter along the ventral-lateral axis (Figs 1 and 6; Figs S1, S5 and S6). For example, cell bin 1 includes all cells with a cell centroid that fell within one average cell diameter of the VM. For fixed images in which cells had already begun to constrict, the width of each bin was set manually to approximate the width of cells at that ventral-lateral position (Fig. 2; Fig. S3). For fixed images in which cells had yet to constrict, the boundaries of each bin were determined by an average cell diameter estimate (Fig. 3; Fig. S4). We used MATLAB to generate box-and-whiskers plots depicting the distribution of data.

In some time series, image acquisition began slightly after myosin accumulation, in which case t=0 s is the first acquired image in the time series. In other time series, the image acquisition began long before furrow formation, in which case we truncated the time series so that the initial time point is ∼1 min before cells begin to constrict.

Apical cell length measurement

Cell length was measured as the projected length along either the ventral-lateral or anterior-posterior axes. Embryos were aligned in time based on the onset of apical constriction. Measurements were made for cells within approximately two cell diameters of the VM.

Statistical analysis

Testing for statistical significance was carried out using the MATLAB statistical toolbox. We used the non-parametric two sample Kolmogorov–Smirnov to generate all reported P-values.

Theoretical model

At gastrulation, the epithelial sheet consists of ∼6000 cells and its shape closely resembles that of an ellipsoid with major axis a of ∼250 μm and minor axes b=c of ∼125 μm (Fig. 4A). As both the length and diameter of the embryo are much larger than the average cell diameter of ∼7-8 μm and thickness h of ∼35 μm, the mechanics of the epithelial cell sheet can approximately be described by the Koiter shell model (Ciarlet, 2000). This continuum theory accounts for mechanical strain and stresses in terms of the deviation of the shell's middle-surface ω from a reference shape 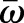Inline graphic. Explicitly, the elastic energy 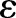Inline graphic of the shell is given by:

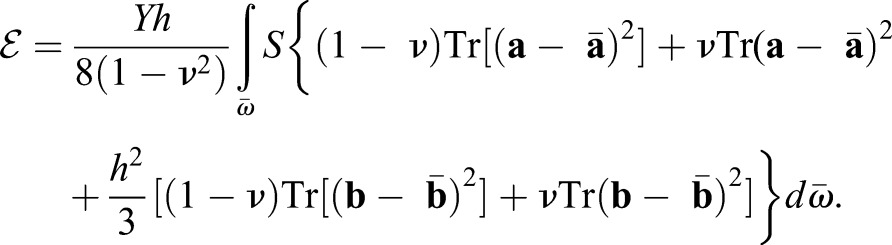graphic file with name develop-144-146761-e1.jpg (1)

Here, Y is the Young's modulus, ν the Poisson Ratio (we set 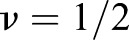Inline graphic corresponding to an incompressible material), and the integral extends over the surface 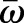Inline graphic. The parameter S accounts for the spatially dependent stiffness variations and is typically set to S=1 for passive equilibrium materials. However, when including apical constriction stresses, S becomes myosin dependent, as outlined below. The first term in the integral corresponds to a stretching energy, and the second term captures the energetic cost of bending the surface. Tr denotes a generalized trace, similar to the usual matrix trace (see supplementary Materials and Methods for details). 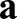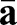Inline graphic and Inline graphic are the 2×2 metric tensors of the deformed surface ω and reference surface 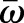Inline graphic. They describe the local geometry of the surface by measuring the lengths of and angles between tangent vectors 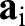Inline graphic at any point of the surface (Fig. 4A). Specifically, the components of 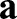Inline graphic are given by 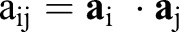Inline graphic with · the usual (vector) dot product. The first term in Eqn 1 thus measures the deviations of lengths and angles between the reference and deformed configurations, thereby capturing the energetic cost of stretching and shearing the surface. 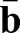Similarly, the curvature tensors Inline graphic and Inline graphic measure the local curvature of the deformed and the reference surface, respectively; see supplementary Materials and Methods for their precise definitions. 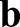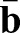Thus, the integrand in the second line assigns an energetic cost whenever there is a mismatch between the local and preferred curvatures Inline graphic and Inline graphic, respectively.

The Koiter shell energy in Eqn 1 describes the mechanics of a passive shell. To include the internal stresses due to active myosin, we consider a patch of neighboring rectangular ‘model’ cells (Fig. 4B). The inner and outer faces represent the apical and basal surfaces of the epithelial cells, respectively. We assume that the most relevant forces are caused by compression/stretching of the upper and lower cell faces. If the cell patch is initially in a stress-free flat state, active myosin stresses are introduced by adding an additional surface tension term to the apical face of the cells. The energy E of each cell then reads

graphic file with name develop-144-146761-e2.jpg (2)

where A+ and A− denote the areas of the outer (contracting) and inner cell faces, A0 is the stress-free reference area of each face, and K their stiffness in the absence of myosin. ρM is the myosin concentration and CM a proportionality constant. We note that the dimensionless ratio 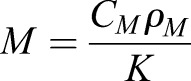Inline graphic alone determines the myosin-induced shape deformation. M can thus be understood as a dimensionless contractility coefficient that is proportional to the local active myosin concentration. 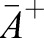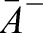Assuming a constant cell volume and constant thickness h, we can determine the equilibrium shape of the patch for given value of M in terms of the equilibrium areas Inline graphic and Inline graphic that minimize Eqn 2. 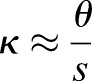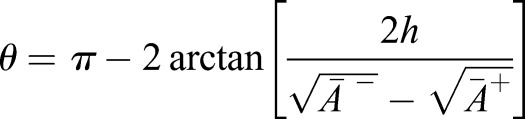Reducing the geometry to its middle surface, we find that the initially flat patch effectively obtains a new, myosin-induced target curvature κ given by Inline graphic with Inline graphic the angle between the middle-surface normal of neighboring cells and 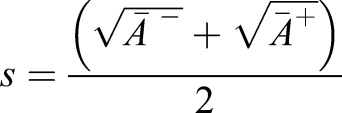Inline graphic the distance between cell centers on the middle-surface (Fig. 4B). The exact dependence of κ on M is given in the supplementary Materials and Methods. Taking the continuum limit (see supplementary Materials and Methods), we obtain the myosin-induced target curvature tensor 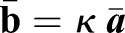Inline graphic and the material stiffening parameter S=1+M. The mismatch of local shell curvature 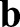Inline graphic and myosin-induced spontaneous curvature 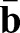Inline graphic drives furrow formation in our model. In our simulations, we add to Eqn 1 two additional energy terms representing the incompressibility of the embryo yolk and the stiffness of the vitelline membrane. The resulting continuum model was simulated using the algorithm previously described (Vetter et al., 2013).

Acknowledgements

We thank N. Perrimon, L. Perkins and the Transgenic RNAi Project at Harvard Medical School (National Institutes of Health/National Institutes of General Medical Sciences R01-GM084947) for providing transgenic RNAi stocks. We also thank A. McHale for the software used to analyze of FISH images. We thank S. Little for his FISH protocol and C. Engbert for help implementing the protocol. We thank R. Horvitz, R. Gupta, and current and former Martin lab members for helpful discussions and feedback.

Footnotes

Competing interests

The authors declare no competing or financial interests.

Author contributions

Conceptualization: N.C.H., P.W.M., N.S., J.D., A.C.M.; Methodology: N.C.H., P.W.M., S.C., N.S., J.D., A.C.M.; Software: N.C.H., P.W.M.; Investigation: N.C.H., S.C.; Resources: N.C.H., S.C.; Writing - original draft: N.C.H., A.C.M.; Writing - review & editing: N.C.H., P.W.M., S.C., N.S., A.C.M.; Visualization: N.C.H., P.W.M., N.S.; Supervision: N.S., J.D., A.C.M.; Project administration: J.D., A.C.M.; Funding acquisition: J.D., A.C.M.

Funding

This work was funded by the National Institutes of Health (R01GM105984 to A.C.M.) and the American Cancer Society (125792-RSG-14-039-01-CSM to A.C.M.). This work was supported in part by the NIH Pre-Doctoral Training Grant T32GM007287. P.W.M. acknowledges financial support from Department of Defense (DoD) through the National Defense Science and Engineering Graduate Fellowship (NDSEG) Program. This work was supported by an Alfred P. Sloan Research Fellowship (to J.D.) and by a James S. McDonnell Foundation Complex Systems Scholar Award (to J.D.). Deposited in PMC for release after 12 months.

Supplementary information

Supplementary information available online at http://dev.biologists.org/lookup/doi/10.1242/dev.146761.supplemental

References

  1. Barrett K., Leptin M. and Settleman J. (1997). The Rho GTPase and a putative RhoGEF mediate a signaling pathway for the cell shape changes in Drosophila gastrulation. Cell 91, 905-915. 10.1016/S0092-8674(00)80482-1 [DOI] [PubMed] [Google Scholar]
  2. Chanet S., Miller C. J., Vaishnav E. D., Ermentrout B., Davidson L. A. and Martin A. C. (2017). Actomyosin meshwork mechanosensing enables tissue shape to orient cell force. Nat. Commun. (in press) doi:10.1038/ncomms15014 10.1038/ncomms15014 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Ciarlet P. G. (2000). Mathematical Elasticity: Theory of Shells. Vol. 3. Amsterdam, The Netherlands: North Holland. [Google Scholar]
  4. Conte V., Munoz J. J. and Miodownik M. (2008). A 3D finite element model of ventral furrow invagination in the Drosophila melanogaster embryo. J. Mech. Behav. Biomed. Mater. 1, 188-198. 10.1016/j.jmbbm.2007.10.002 [DOI] [PubMed] [Google Scholar]
  5. Conte V., Muñoz J. J., Baum B. and Miodownik M. (2009). Robust mechanisms of ventral furrow invagination require the combination of cellular shape changes. Phys. Biol. 6, 016010 10.1088/1478-3975/6/1/016010 [DOI] [PubMed] [Google Scholar]
  6. Copp A. J. and Greene N. D. (2010). Genetics and development of neural tube defects. J. Pathol. 220, 217-230. 10.1002/path.2643 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Coravos J. S. and Martin A. C. (2016). Apical sarcomere-like actomyosin contracts nonmuscle drosophila epithelial cells. Dev. Cell 39, 346-358. 10.1016/j.devcel.2016.09.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Costa M., Wilson E. T. and Wieschaus E. (1994). A putative cell signal encoded by the folded gastrulation gene coordinates cell shape changes during Drosophila gastrulation. Cell 76, 1075-1089. 10.1016/0092-8674(94)90384-0 [DOI] [PubMed] [Google Scholar]
  9. Dawes-Hoang R. E., Parmar K. M., Christiansen A. E., Phelps C. B., Brand A. H. and Wieschaus E. F. (2005). Folded gastrulation, cell shape change and the control of myosin localization. Development 132, 4165-4178. 10.1242/dev.01938 [DOI] [PubMed] [Google Scholar]
  10. Fuse N., Yu F. and Hirose S. (2013). Gprk2 adjusts Fog signaling to organize cell movements in Drosophila gastrulation. Development 140, 4246-4255. 10.1242/dev.093625 [DOI] [PubMed] [Google Scholar]
  11. Gelbart M. A., He B., Martin A. C., Thiberge S. Y., Wieschaus E. F. and Kaschube M. (2012). Volume conservation principle involved in cell lengthening and nucleus movement during tissue morphogenesis. Proc. Natl. Acad. Sci. USA 109, 19298-19303. 10.1073/pnas.1205258109 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hacker U. and Perrimon N. (1998). DRhoGEF2 encodes a member of the Dbl family of oncogenes and controls cell shape changes during gastrulation in Drosophila. Genes Dev. 12, 274-284. 10.1101/gad.12.2.274 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ip Y. T., Park R. E., Kosman D., Yazdanbakhsh K. and Levine M. (1992). Dorsal-twist interactions establish snail expression in the presumptive mesoderm of the Drosophila embryo. Genes Dev. 6, 1518-1530. 10.1101/gad.6.8.1518 [DOI] [PubMed] [Google Scholar]
  14. Jodoin J. N. and Martin A. C. (2016). Abl suppresses cell extrusion and intercalation during epithelium folding. Mol. Biol. Cell 27, 2822-2832. 10.1091/mbc.E16-05-0336 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Jodoin J. N., Coravos J. S., Chanet S., Vasquez C. G., Tworoger M., Kingston E. R., Perkins L. A., Perrimon N. and Martin A. C. (2015). Stable force balance between epithelial cells arises from F-actin turnover. Dev. Cell 35, 685-697. 10.1016/j.devcel.2015.11.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Kanodia J. S., Rikhy R., Kim Y., Lund V. K., DeLotto R., Lippincott-Schwartz J. and Shvartsman S. Y. (2009). Dynamics of the Dorsal morphogen gradient. Proc. Natl. Acad. Sci. USA 106, 21707-21712. 10.1073/pnas.0912395106 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kerridge S., Munjal A., Philippe J.-M., Jha A., de las Bayonas A. G., Saurin A. J. and Lecuit T., (2016). Modular activation of Rho1 by GPCR signalling imparts polarized myosin II activation during morphogenesis. Nat. Cell Biol. 18, 261-270. 10.1038/ncb3302 [DOI] [PubMed] [Google Scholar]
  18. Kolsch V., Seher T., Fernandez-Ballester G. J., Serrano L. and Leptin M. (2007). Control of Drosophila gastrulation by apical localization of adherens junctions and RhoGEF2. Science 315, 384-386. 10.1126/science.1134833 [DOI] [PubMed] [Google Scholar]
  19. Lecuit T., Lenne P.-F. and Munro E. (2011). Force generation, transmission, and integration during cell and tissue morphogenesis. Annu. Rev. Cell Dev. Biol. 27, 157-184. 10.1146/annurev-cellbio-100109-104027 [DOI] [PubMed] [Google Scholar]
  20. Leptin M. (1991). Twist and snail as positive and negative regulators during Drosophila mesoderm development. Genes Dev. 5, 1568-1576. 10.1101/gad.5.9.1568 [DOI] [PubMed] [Google Scholar]
  21. Leptin M. (2005). Gastrulation movements: the logic and the nuts and bolts. Dev. Cell 8, 305-320. 10.1016/j.devcel.2005.02.007 [DOI] [PubMed] [Google Scholar]
  22. Leptin M. and Grunewald B. (1990). Cell shape changes during gastrulation in Drosophila. Development 110, 73-84. [DOI] [PubMed] [Google Scholar]
  23. Ligoxygakis P., Roth S. and Reichhart J.-M. (2003). A serpin regulates dorsal-ventral axis formation in the Drosophila embryo. Curr. Biol. 13, 2097-2102. 10.1016/j.cub.2003.10.062 [DOI] [PubMed] [Google Scholar]
  24. Lim B., Levine M. and Yamakazi Y. (2017). Transcriptional pre-patterning of Drosophila gastrulation. Curr. Biol. 27, 286-290. 10.1016/j.cub.2016.11.047 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Little S. C., Tkačik G., Kneeland T. B., Wieschaus E. F. and Gregor T. (2011). The formation of the Bicoid morphogen gradient requires protein movement from anteriorly localized mRNA. PLoS Biol. 9, e1000596 10.1371/journal.pbio.1000596 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Manning A. J., Peters K. A., Peifer M. and Rogers S. L. (2013). Regulation of epithelial morphogenesis by the G protein-coupled receptor mist and its ligand fog. Sci. Signal. 6, ra98 10.1126/scisignal.2004427 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Martin A. C. and Goldstein B. (2014). Apical constriction: themes and variations on a cellular mechanism driving morphogenesis. Development 141, 1987-1998. 10.1242/dev.102228 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Martin A. C., Kaschube M. and Wieschaus E. F. (2009). Pulsed contractions of an actin-myosin network drive apical constriction. Nature 457, 495-499. 10.1038/nature07522 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Martin A. C., Gelbart M., Fernandez-Gonzalez R., Kaschube M. and Wieschaus E. F. (2010). Integration of contractile forces during tissue invagination. J. Cell Biol. 188, 735-749. 10.1083/jcb.200910099 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Mason F. M., Xie S., Vasquez C. G., Tworoger M. and Martin A. C. (2016). RhoA GTPase inhibition organizes contraction during epithelial morphogenesis. J. Cell Biol. 214, 603-617. 10.1083/jcb.201603077 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. McHale P., Mizutani C. M., Kosman D., MacKay D. L., Belu M., Hermann A., McGinnis W., Bier E. and Hwa T. (2011). Gene length may contribute to graded transcriptional responses in the Drosophila embryo. Dev. Biol. 360, 230-240. 10.1016/j.ydbio.2011.08.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Oda H., Tsukita S. and Takeichi M. (1998). Dynamic behavior of the cadherin-based cell-cell adhesion system during Drosophila gastrulation. Dev. Biol. 203, 435-450. 10.1006/dbio.1998.9047 [DOI] [PubMed] [Google Scholar]
  33. Odell G. M., Oster G., Alberch P. and Burnside B. (1981). The mechanical basis of morphogenesis. I. Epithelial folding and invagination. Dev. Biol. 85, 446-462. 10.1016/0012-1606(81)90276-1 [DOI] [PubMed] [Google Scholar]
  34. Parks S. and Wieschaus E. (1991). The Drosophila gastrulation gene concertina encodes a G alpha-like protein. Cell 64, 447-458. 10.1016/0092-8674(91)90652-F [DOI] [PubMed] [Google Scholar]
  35. Polyakov O., He B., Swan M., Shaevitz J. W., Kaschube M. and Wieschaus E. (2014). Passive mechanical forces control cell-shape change during Drosophila ventral furrow formation. Biophys. J. 107, 998-1010. 10.1016/j.bpj.2014.07.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Reeves G. T., Trisnadi N., Truong T. V., Nahmad M., Katz S. and Stathopoulos A. (2012). Dorsal-ventral gene expression in the Drosophila embryo reflects the dynamics and precision of the dorsal nuclear gradient. Dev. Cell 22, 544-557. 10.1016/j.devcel.2011.12.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Royou A., Sullivan W. and Karess R. (2002). Cortical recruitment of nonmuscle myosin II in early syncytial Drosophila embryos: its role in nuclear axial expansion and its regulation by Cdc2 activity. J. Cell Biol. 158, 127-137. 10.1083/jcb.200203148 [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Schindelin J., Arganda-Carreras I., Frise E., Kaynig V., Longair M., Pietzsch T., Preibisch S., Rueden C., Saalfeld S., Schmid B. et al. (2012). Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676-682. 10.1038/nmeth.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Smith J. L., Schoenwolf G. C. and Quan J. (1994). Quantitative analyses of neuroepithelial cell shapes during bending of the mouse neural plate. J. Comp. Neurol. 342, 144-151. 10.1002/cne.903420113 [DOI] [PubMed] [Google Scholar]
  40. Spahn P. and Reuter R. (2013). A vertex model of Drosophila ventral furrow formation. PLoS One 8, e75051 10.1371/journal.pone.0075051 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Sweeton D., Parks S., Costa M. and Wieschaus E. (1991). Gastrulation in Drosophila: the formation of the ventral furrow and posterior midgut invaginations. Development 112, 775-789. [DOI] [PubMed] [Google Scholar]
  42. Thisse B., Stoetzel C., El Messal M. and Perrin-Schmitt F., (1987). Genes of the Drosophila maternal dorsal group control the specific expression of the zygotic gene twist in presumptive mesodermal cells. Genes Dev. 1, 709-715. 10.1101/gad.1.7.709 [DOI] [Google Scholar]
  43. Timoshenko S. (1925). Analysis of bi-metal thermostats. J. Opt. Soc. Am. Rev. Sci. 11, 233-255. 10.1364/JOSA.11.000233 [DOI] [Google Scholar]
  44. Vasquez C. G., Tworoger M. and Martin A. C. (2014). Dynamic myosin phosphorylation regulates contractile pulses and tissue integrity during epithelial morphogenesis. J. Cell Biol. 206, 435-450. 10.1083/jcb.201402004 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Vasquez C. G., Heissler S. M., Billington N., Sellers J. R. and Martin A. C. (2016). Drosophila non-muscle myosin II motor activity determines the rate of tissue folding. eLife 5, e20828 10.7554/elife.20828 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Venken K. J., He Y., Hoskins R. A. and Bellen H. J. (2006). P[acman]: a BAC transgenic platform for targeted insertion of large DNA fragments in D. melanogaster. Science 314, 1747-1751. 10.1126/science.1134426 [DOI] [PubMed] [Google Scholar]
  47. Vetter R., Stoop N., Jenni T., Wittel F. K. and Herrmann H. J. (2013). Subdivision shell elements with anisotropic growth. Int. J. Numer. Method. Eng. 95, 791-810. 10.1002/nme.4536 [DOI] [Google Scholar]
  48. Wallingford J. B., Niswander L. A., Shaw G. M. and Finnell R. H. (2013). The continuing challenge of understanding, preventing, and treating neural tube defects. Science 339, 1222002 10.1126/science.1222002 [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Warming S., Costantino N., Court D. L., Jenkins N. A. and Copeland N. G. (2005). Simple and highly efficient BAC recombineering using galK selection. Nucleic Acids Res. 33, e36 10.1093/nar/gni035 [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Xie S. and Martin A. C. (2015). Intracellular signalling and intercellular coupling coordinate heterogeneous contractile events to facilitate tissue folding. Nat. Commun. 6, 7161 10.1038/ncomms8161 [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Xie S., Mason F. M. and Martin A. C. (2016). Loss of Galpha12/13 exacerbates apical area-dependence of actomyosin contractility. Mol. Biol. Cell 27, 3526-3536. 10.1091/mbc.E16-05-0305 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Development (Cambridge, England) are provided here courtesy of Company of Biologists

RESOURCES