SEGGA: a toolset for rapid automated analysis of epithelial cell polarity and dynamics

Abstract

Epithelial remodeling determines the structure of many organs in the body through changes in cell shape, polarity and behavior and is a major area of study in developmental biology. Accurate and high-throughput methods are necessary to systematically analyze epithelial organization and dynamics at single-cell resolution. We developed SEGGA, an easy-to-use software for automated image segmentation, cell tracking and quantitative analysis of cell shape, polarity and behavior in epithelial tissues. SEGGA is free, open source, and provides a full suite of tools that allow users with no prior computational expertise to independently perform all steps of automated image segmentation, semi-automated user-guided error correction, and data analysis. Here we use SEGGA to analyze changes in cell shape, cell interactions and planar polarity during convergent extension in the Drosophila embryo. These studies demonstrate that planar polarity is rapidly established in a spatiotemporally regulated pattern that is dynamically remodeled in response to changes in cell orientation. These findings reveal an unexpected plasticity that maintains coordinated planar polarity in actively moving populations through the continual realignment of cell polarity with the tissue axes.

Highlighted article: SEGGA is an easy to use software that allows for the quantitative analysis of changes in cell shape, movement and polarity at single-cell resolution during epithelial remodeling in various species.

INTRODUCTION

Changes in epithelial organization are essential for tissue development, regeneration and repair. Advances in microscopy have made it possible to visualize dynamic interactions between cells in their normal physiological environment, embedded within populations of hundreds of cells or more, at unprecedented spatial and temporal resolution. These advances provide an opportunity to understand how tissue structure at the multicellular scale is achieved through changes in the shape, polarity and behavior of individual cells. Although a tremendous amount of information about single-cell and collective cell behaviors can be obtained from live imaging studies, the availability of accurate and high-throughput methods for cell tracking and analysis is currently a rate-limiting step in making use of this information. Image analysis tools that detect cell nuclei can reliably track nuclear movements in C. elegans (Bao et al., 2006; Santella et al., 2010; Giurumescu et al., 2012), zebrafish (Keller et al., 2008), Drosophila (McMahon et al., 2008; Schindelin et al., 2012; Stegmaier et al., 2016) and mice (Lou et al., 2014). However, it is not possible to accurately determine cell shape and interactions from the positions of cell nuclei, as mathematical approaches that predict the outer contours of cells based on the locations of the cell centers often fail for cells that are elongated or irregular in shape, which are typical of developing epithelia (Zallen and Zallen, 2004; Blankenship et al., 2006; Williams et al., 2014). Although computationally challenging, image analysis tools that directly detect cell boundaries are necessary to rigorously analyze cell shape, interactions and polarity in order to determine how changes in these properties contribute to tissue structure.

Time-lapse movies of cell behaviors in vivo are essential to elucidating mechanisms of epithelial morphogenesis at single-cell resolution. However, long-term tracking studies of cells in tissues are currently limited by the accuracy and throughput of available image analysis methods. Fully automated methods for image segmentation and analysis, which are optimized for speed, increase the throughput of data analysis by tolerating a non-negligible frequency of errors that would otherwise require substantial effort to correct. These methods are well suited for large tissues in which error correction is impractical, short-term behaviors during which time errors are less likely to accumulate, and tissues that do not undergo substantial rearrangement (Blanchard et al., 2009; Aigouy et al., 2010; Fernandez et al., 2010; Bosveld et al., 2012; Mosaliganti et al., 2012; Khan et al., 2014; Guirao et al., 2015; Heller et al., 2016; Stegmaier et al., 2016). However, segmentation errors that lead to 1% untracked cells in each frame of a movie are predicted to interrupt more than half of all cell trajectories after 70 time points, making fully automated methods of limited use for long-term tracking. As an alternative strategy, several methods enable the user to inspect and manually correct the segmentation output (McMahon et al., 2008; Fernandez-Gonzalez and Zallen, 2011; Gelbart et al., 2012; Giurumescu et al., 2012; Mashburn et al., 2012; Barbier de Reuille et al., 2015; Cilla et al., 2015; Morales-Navarrete et al., 2015; Rozbicki et al., 2015). These methods have the potential to achieve high accuracy but require substantial effort to manually correct the segmentation at each time point, decreasing the throughput of these approaches. In addition, the practical applications of non-commercial image analysis tools are often limited by other considerations, such as the computational expertise required to install and troubleshoot published algorithms, the cost of commercial software packages required to run them, incomplete documentation of software dependencies and installation protocols, and the absence of integrated tools for data analysis. The development of software that is easy to use, produces rapid and accurate segmentation, and performs a wide range of measurements and analyses will be important to take advantage of live imaging technologies and make quantitative image analysis methods accessible to the scientific community.

Here we describe SEGGA, an image analysis software for automated image ʻSEGmentation, Graphical visualization and Analysis' that can be used to systematically track changes in cell shape, behavior and polarity in epithelial tissues. SEGGA provides a suite of tools for fully automated image processing, image segmentation, cell tracking, data analysis and data visualization, as well as semi-automated error correction tools that expedite the process of obtaining accurate segmentation. SEGGA is available as a pre-compiled module that runs free of charge on Mac, Windows and Linux operating systems, and contains a graphical user interface that allows users with no prior computational expertise to perform all steps of image segmentation, correction and analysis. SEGGA is also available as open-source code that can be extended or modified in MATLAB (MathWorks).

SEGGA is designed for the study of epithelial tissues, which determine the structure of many organs in the body and have several advantages in terms of computational studies of multicellular organization. First, many epithelial tissues can be approximated as monolayers, for which two-dimensional analyses are sufficient to capture many salient characteristics of cell shape, topology (neighbor relationships) and rearrangement. Second, epithelial tissues are often well-represented by polygonal lattices, greatly simplifying the analysis. Third, many epithelial tissues display polarity in the plane of the tissue, referred to as planar polarity, which is a powerful model for studying coordination between cells (Hale and Strutt, 2015; Yang and Mlodzik, 2015). Here we use SEGGA to study epithelial dynamics during convergent extension in the Drosophila embryo. These findings address the contributions of distinct cell behaviors to convergent extension and reveal that planar polarity is rapidly established and dynamically remodeled in response to changes in cell orientation. These studies highlight the use of SEGGA as a general tool for studying cellular and molecular mechanisms of epithelial remodeling.

RESULTS

SEGGA: a method for automated image segmentation and cell tracking

We developed SEGGA to analyze cell behavior and polarity in epithelia at single-cell resolution. To illustrate the applications of SEGGA, we analyzed cellular dynamics during convergent extension, a conserved morphogenetic process that produces the elongated body axis of frogs, fish, flies, chicks and mice (Keller et al., 2000; Wallingford, 2012; Takeichi, 2014; Walck-Shannon and Hardin, 2014). In Drosophila, convergent extension in the embryonic germband epithelium occurs primarily through polarized cell rearrangements in the absence of cell division, insertion or delamination (Irvine and Wieschaus, 1994). We analyzed time-lapse movies of convergent extension in Drosophila embryos that express fluorescent markers that label the cell membrane, using tools in SEGGA for image segmentation, error correction, cell tracking, data analysis and data visualization (Fig. 1A-D).

Fig. 1.

Overview of image analysis tools in SEGGA. (A) Automated image segmentation tools in SEGGA represent epithelial tissues as two-dimensional polygonal lattices in which each cell is assigned a unique identity. (B) Semi-automated error correction tools improve the accuracy of segmentation. Left, before correction; right, after correction. (C) Automated tracking tools follow cell trajectories and changes in cell shape, neighbor relationships and polarity over time. (D) Multiple forms of data analysis and display are available in SEGGA. White, Resille:GFP. Anterior left, ventral down.

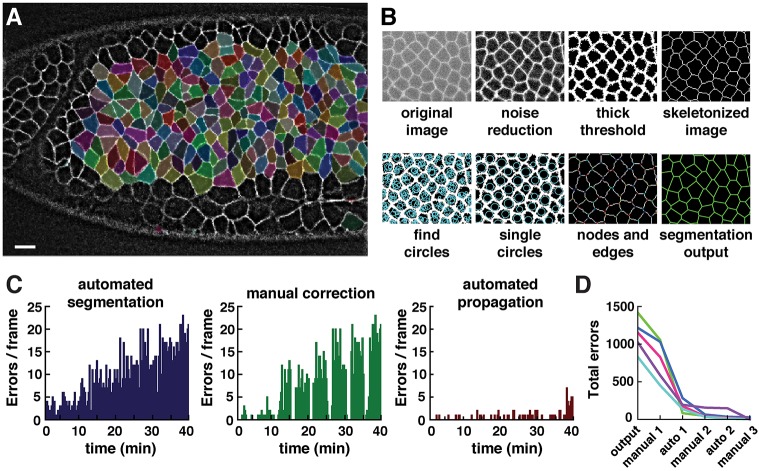
In the first step of segmentation, image processing and thresholding functions were used to produce a skeletonized representation of the cell boundaries (Fig. 2A,B). To correct for undersegmentation (the failure to detect cells that are present in the image), we implemented an independent method for cell detection that progressively expands circles starting from all non-boundary pixels until the circles contact high-intensity regions likely to represent cell boundaries. For each overlapping set of circles, the single largest circle was retained and defined as a single cell. Discrepancies in which individual cells contained more than one circle were resolved by expanding boundary pixels until a new interface separated the two circles, or by drawing the closest approximation to a line dividing the cell. To correct for oversegmentation (the assignment of more cells than are present in the image), cells below a certain size were automatically removed using a threshold set by the user. Images were then reskeletonized to determine the placement of nodes and edges in the final segmentation. The result is a polygonal lattice of cells, each composed of a unique set of nodes and edges, that can be used as the basis for cell tracking and analysis (Fig. 2A,B).

Fig. 2.

Automated and semi-automated tools in SEGGA enable rapid and accurate cell segmentation. (A) Segmented cells in a wild-type Drosophila embryo during axis elongation (white, Resille:GFP). Cell shapes are well represented by a polygonal lattice (cells highlighted in random colors). Anterior left, ventral down. Scale bar: 10 µm. (B) Overview of image segmentation steps in SEGGA. (C) Errors in the initial segmentation output (left) were manually corrected in every twentieth frame (middle) and corrections were automatically propagated to other time points (right). Images were acquired every 15 s; n=average of 390 cells/image. (D) In general, three rounds of manual correction and two rounds of automated propagation produced 100% accurate tracking for movies of Drosophila axis elongation. n=5 movies; each line represents one movie.

Cells were tracked over time in time-lapse movies using a simple nearest-neighbor search. For two consecutive images, A and B, cell a in A was tracked to cell b in B if the centroid of b was closest to the centroid of a, and the centroid of a was closest to the centroid of b (isomorphic mapping). The trajectories of successfully tracked cells were then used to improve the assignment of untracked cells. Any remaining cells that could not be isomorphically mapped between two time points were flagged as errors in the user interface. Cells that move, divide, delaminate from or insert into the epithelium can all be tracked in SEGGA (see Materials and Methods). Cell division, delamination and insertion do not occur during convergent extension in Drosophila and were not included in the present analysis, but an example showing tracking of these cell behaviors in SEGGA is provided for a time-lapse movie of the mouse neural plate (Movie 1).

Semi-automated error correction tools enable rapid and accurate image segmentation

The goal of automated image analysis is to obtain quantitative information about large populations of cells at many points in time. However, in the initial SEGGA output, 3-5% of cells could not be associated with a corresponding cell at the previous or following time points, an error rate comparable to the reported accuracy of other methods (Mosaliganti et al., 2012; Stegmaier et al., 2016). This frequency of errors is not compatible with long-term tracking, as many cell trajectories are interrupted by segmentation errors during the course of a typical movie. To address this problem, we implemented a semi-automated method to expedite the user-guided correction of tracking errors. Cells that could not be tracked at the previous or following time points were highlighted as errors in a graphical user interface that provides a range of correction capabilities, including adding edges, removing edges, and moving, expanding or merging nodes (Fig. 1B). Corrections were made by the user at a subset of time points and these corrections were automatically propagated to other time points through a frame-by-frame comparison method starting from the corrected time points (Fig. 2C). This process can be repeated as needed to achieve 100% accurate tracking (Fig. 2D). The time required to obtain fully accurate cell tracking using semi-automated propagation of manual corrections was several times faster than the time required to correct every image in the movie by hand. Therefore, these semi-automated user-guided correction tools in SEGGA can be used to obtain fully accurate cell tracking on a timescale that is practical for quantitative studies of cell dynamics.

Analysis of cell dynamics during convergent extension

As a demonstration of the functionality of SEGGA, we used this software to analyze cell behavior during convergent extension in the Drosophila embryo. During convergent extension, neighboring cells along the anterior-posterior (AP) axis of the germband epithelium become separated by intercalating dorsal and ventral cells, causing the embryo to elongate along the head-to-tail axis and narrow along the dorsal-ventral axis (Fig. 3A) (Irvine and Wieschaus, 1994). Convergent extension in Drosophila has been shown to occur through a combination of cell shape changes and polarized cell rearrangements, also known as cell intercalation (Irvine and Wieschaus, 1994; Bertet et al., 2004; Blankenship et al., 2006; Butler et al., 2009; Lye et al., 2015). The relative contributions of these cell behaviors to tissue elongation across many genetic backgrounds are not well understood. In addition, intercalating cells display a planar polarized localization of proteins involved in contraction and adhesion that are required for axis elongation and intercalary behavior (Walck-Shannon and Hardin, 2014). However, the dynamic processes by which planar polarity is established and maintained as cells move and rearrange within the sheet are not known. We performed a quantitative analysis of convergent extension in SEGGA to address these questions.

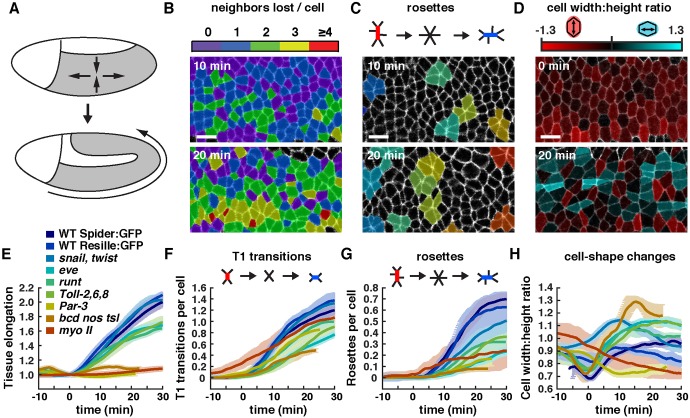
Fig. 3.

Contributions of cell shape changes, T1 transitions and rosette rearrangements to Drosophila axis elongation. (A) Schematic of Drosophila axis elongation. The germband (gray) narrows along the dorsal-ventral axis and elongates along the AP axis. Anterior left, ventral down. (B-D) Color maps showing (B) the number of neighbors lost per cell, (C) rosettes of five or more cells (random colors) and (D) the cell width-to-height ratio (log₂ scale) in wild-type (WT) Spider:GFP embryos. (E) Tissue length along the AP axis normalized to the value at t=0. (F,G) Number of T1 transitions (F) and rosettes (G) per cell (cumulative). (H) Cell width-to-height ratio (not log₂ scale). Plotted values were smoothed over a seven-frame window. A single mean value was obtained for each embryo and the mean±s.e.m. between embryos is shown. n=7 WT Spider:GFP, n=3 WT Resille:GFP, n=5 snail^IIG05 twist^DfS60, n=5 Toll-2^Δ76 Toll-8⁵⁹ Toll-6^5A, n=3 runt^LB5, n=5 eve^R13, n=5 Par-3 (baz^GD21), n=2 myo II (sqh¹) and n=3 bcd^E1 nos^L7 tsl¹⁴⁶ embryos analyzed. An average of 224 cells were tracked for at least 50 time points in each movie, with images acquired every 15 s. Tissue elongation was significantly reduced in Toll-2,6,8, runt, eve, Par-3, bcd nos tsl and myo II (P≤0.02, t-test). T1 transitions and rosettes were reduced in Toll-2,6,8, eve, Par-3 and bcd nos tsl (P≤0.05). Rosettes (but not T1 transitions) were reduced in runt and myo II (P≤0.006). The cell width-to-height ratio was increased in bcd nos tsl, eve and Toll-2,6,8 and decreased in Par-3 and myo II (P≤0.01). All statistical comparisons were performed using the t=30 min value as the test statistic. Most mutants expressed Spider:GFP and were compared with WT Spider:GFP for statistical analysis, except bcd nos tsl, which expressed Resille:GFP and was compared with WT Resille:GFP. Scale bars: 10 µm.

We used SEGGA to track and analyze cell behavior in the anterior and central regions of the developing germband in order to identify the essential behaviors that contribute to tissue elongation in these regions of the embryo. The SEGGA output includes measurements of several aspects of cell shape and topology (neighbor relationships), as well as customizable color-coded spatial maps that display quantitative measurements superimposed on the image data (Fig. 3B-D, Movies 2-4, Materials and Methods). Together, these features enable the user to measure multiple properties of cells, analyze how they change over time, and directly visualize the spatial and temporal organization of cell properties within the tissue.

We first analyzed cell intercalation, which is proposed to provide the driving force for convergent extension of the Drosophila body axis (Irvine and Wieschaus, 1994; Bertet et al., 2004; Blankenship et al., 2006). Two types of cell rearrangement contribute to tissue elongation in this system: local cell rearrangements involving neighbor exchange among four cells (Bertet et al., 2004), also known as T1 transitions (Weaire and Rivier, 1984), and collective rearrangements leading to the formation of multicellular rosettes containing five or more cells (Blankenship et al., 2006) (Fig. 3F,G). Analysis of wild-type movies in SEGGA revealed that these behaviors occur in an approximately 2:1 ratio, resulting in the separation of a majority of cells from two or more of their original neighbors (Fig. S1A-C, Movies 2 and 3). We analyzed these cell rearrangements in wild-type embryos and in the presence of mutations that disrupt cell intercalation, cell shape changes, and tissue elongation to different extents (Fig. 3E-H). In particular, we analyzed mutants that do not fully elongate due to defects in AP patterning (eve, runt and bcd nos tsl) (Irvine and Wieschaus, 1994; Zallen and Wieschaus, 2004; Blankenship et al., 2006; Butler et al., 2009), cell contraction or adhesion {myosin II [also known as spaghetti squash (sqh) – FlyBase] and Par-3 [bazooka (baz)]} (Bertet et al., 2004; Zallen and Wieschaus, 2004; Blankenship et al., 2006; Simões et al., 2010; Kasza et al., 2014) or Toll receptor signaling [Toll-2 (18 wheeler), Toll-6 and Toll-8 (Tollo)] (Paré et al., 2014). The frequency of T1 transitions and rosette behaviors strongly correlated with the extent of elongation when compared across 25 different genetic backgrounds (Fig. 4A-C), consistent with an important role for cell rearrangements in tissue elongation.

Fig. 4.

Relationship between cell behavior and tissue elongation across genotypes. (A-C) Tissue elongation versus the number of (A) total cell rearrangements, (B) T1 transitions per cell and (C) rosettes per cell. (D) Tissue elongation versus the cell width-to-height ratio at the end of axis elongation (t=30 min). A single mean value was obtained for each embryo and the mean±s.e.m. between embryos is shown. n=3-8 embryos/genotype, except myosin II where n=2. Pearson's correlation coefficient (r) is shown.

Cell shape changes have been proposed to account for approximately one-third of the total tissue elongation in Drosophila (Butler et al., 2009; Lye et al., 2015). In particular, cell shape changes throughout the germband are induced by internalization of the ventral furrow (Butler et al., 2009; Lye et al., 2015), and cell shape changes in the posterior germband occur in response to posterior midgut invagination (Collinet et al., 2015; Lye et al., 2015). We focused on the anterior and central regions of the germband in this study. Consistent with previous findings (Butler et al., 2009), our analysis in SEGGA confirmed that wild-type cells transiently elongate toward the ventral midline at the onset of elongation (t=0 min), coinciding with the time of ventral furrow formation (Fig. 3H). Color maps of the cell width-to-height ratio show that most cells are vertically elongated at the start of elongation, and that these transform into a mixture of vertically elongated, horizontally elongated, and isotropic cells as elongation proceeds (Fig. 3D, Movie 4).

To investigate whether the ventral furrow is required for cell behaviors during tissue elongation, we analyzed cell behavior in snail twist double mutants, which fail to form mesoderm and completely abolish all steps of ventral furrow formation (Leptin and Grunewald, 1990; Costa et al., 1993). In snail twist embryos, cells were no longer transiently elongated toward the ventral midline at t=0, and had an average cell width-to-height ratio close to 1 at the start and end of elongation (Fig. 3H), consistent with previous results in twist single mutants (Butler et al., 2009; Lye et al., 2015). Despite the absence of a contribution from cell elongation, tissue elongation occurred normally in snail twist mutants (Fig. 3E). This tissue elongation is due to cell rearrangements, which were largely unaffected in snail twist mutants, which had only a slight reduction in rosette formation (P=0.08; Fig. 3F,G). In addition, increased apical cell area made a minor contribution to tissue elongation in snail twist embryos (Fig. S2A). These results demonstrate that the ventral furrow is dispensable for cell intercalation and tissue elongation.

Supporting the finding that cell elongation does not contribute significantly to tissue elongation in the anterior and central regions of the germband, changes in cell shape and area were not correlated with the extent of tissue elongation when compared across 25 genetic backgrounds (Fig. 4D, Fig. S2A). Notably, the largest increase in the cell width-to-height ratio was observed in bcd nos tsl mutants, which lack AP patterning and completely fail to elongate, indicating that these changes can occur in the absence of tissue elongation. Together, these results indicate that although cell shape changes contribute positively to tissue elongation in some backgrounds, these changes are not essential for tissue elongation in the anterior and central regions of the germband.

Analysis of spatiotemporal patterns of planar polarity in SEGGA

Computational tools in SEGGA can be used to analyze dynamic changes in the cortical polarity of individual cells. Convergent extension in Drosophila is driven by the planar polarized localization of proteins to different regions of the cell cortex. Proteins involved in actomyosin contractility localize to interfaces between anterior and posterior cells (referred to here as vertical edges), including non-muscle myosin II (Bertet et al., 2004; Zallen and Wieschaus, 2004), filamentous actin (F-actin) (Blankenship et al., 2006) and the myosin activators Rho kinase (Rok), Shroom and the active form of the Rho GTPase (Simões et al., 2010, 2014; Munjal et al., 2015). Conversely, proteins involved in cell adhesion, such as E-cadherin, β-catenin, α-catenin and Par-3, are enriched at the reciprocal transverse domains (Zallen and Wieschaus, 2004; Blankenship et al., 2006; Simões et al., 2010; Levayer et al., 2011; Sawyer et al., 2011; Tamada et al., 2012; Levayer and Lecuit, 2013; Warrington et al., 2013). Myosin II planar polarity emerges just prior to the onset of tissue elongation (Kasza et al., 2014; Tetley et al., 2016). However, how myosin planar polarity relates to the dynamics of other proteins involved in convergent extension, and how these polarities are maintained as cells move and rearrange, have not been examined.

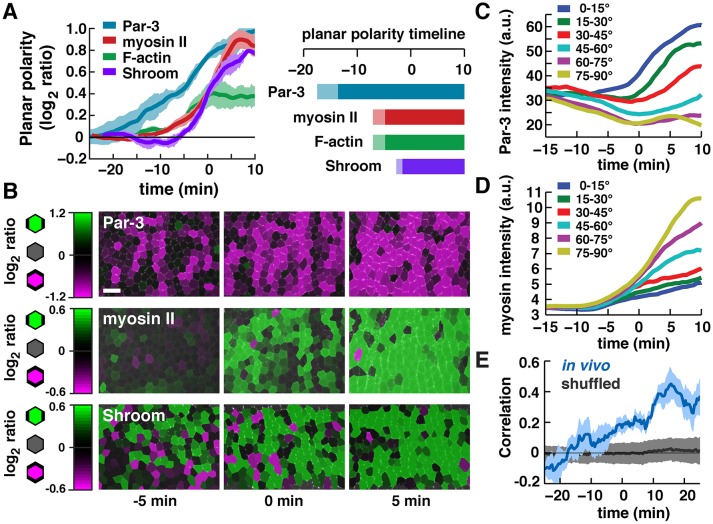
Accurate segmentation is necessary to analyze asymmetries in cortical protein localization, as even slightly misplaced boundaries in the segmentation can fail to overlap with narrow regions of cortical signal. To analyze planar polarity, we implemented tools in SEGGA to maximize edge overlap with the high-intensity cortical pixels in the image in order to improve the accuracy of segmentation (Fig. S3A-C, see Materials and Methods). Optimized edge positions were used to measure planar polarity on a cell-by-cell basis and analyze how this polarity changes over time in embryos expressing fluorescently tagged proteins. This analysis revealed that the Par-3 adherens junction regulator displayed detectable planar polarity 15 min before the start of elongation (Fig. 5A-C). By contrast, myosin II and F-actin did not display detectable planar polarity until ∼10 min before the start of elongation, and Shroom planar polarity was not detected until ∼5 min before the start of elongation (Fig. 5A,B,D). Similar results were obtained for Par-3 and myosin II when the fluorophores were reversed (Fig. S4A-F). These results demonstrate that planar polarity is rapidly established in a 15-20 min time window prior to the onset of elongation, and suggest that Par-3 is planar polarized significantly earlier than proteins involved in actomyosin contractility.

Fig. 5.

Emergence of planar polarity in the Drosophila embryo. (A) Timing of planar polarized protein localization. Plot shows the log₂ ratio of Par-3 intensity at transverse edges (0-30°) to vertical edges (60-90°) or the log₂ ratio of myosin II, F-actin and Shroom intensity at vertical to transverse edges (0° is parallel to the AP axis). Planar polarity was calculated separately for each cell and normalized to the local background intensity. Plotted values were smoothed over a seven-frame window. A single mean value was obtained for each embryo at each time point and the mean±s.e.m. between embryos is shown. Right: light bars, log₂ ratios >0.1 and <0.2; dark bars, log₂ ratios >0.2. Markers used were Par-3:GFP, myosin:GFP, Venus:Shroom[ΔRokBD] (an inactive variant of Shroom lacking its Rho-kinase-binding domain) and GFP fusions to the actin-binding domains of Moesin and Utrophin to visualize F-actin. n=3-4 movies/condition; an average of 272 cells/time point were analyzed for each movie. (B) Color maps of Par-3, myosin II and Shroom planar polarity at the indicated time points. Each row shows images from a single movie. Scale bar: 10 µm. (C,D) Average edge intensities binned by angle in a single Par-3:GFP; myosin:mCherry movie. Average of 1095 edges/time point. (E) Correlation between the extent of Par-3 and myosin II planar polarity within cells. n=4 movies of embryos expressing Par-3:GFP and myosin:mCherry. Blue curve, mean±s.d. for correlation measurements; black curve, correlations recalculated after edge intensity values were randomly shuffled within 5° bins.

This timeline of planar polarity is consistent with two models. In one model, protein localization to vertical and transverse edges could occur in response to different upstream signals. Alternatively, a single polarity mechanism could simultaneously direct protein localization to different domains at the cell cortex. To distinguish between these possibilities, we analyzed the correlation between Par-3 and myosin II planar polarity on a cell-by-cell basis. For individual cells, the extent of Par-3 and myosin II polarity was positively correlated (Fig. 5E). This correlation was abolished when protein intensities were randomly distributed to other edges within the same 5° angular range (Fig. 5E), indicating that this correlation is not the result of overall patterns of planar polarity within the tissue. Similar results were obtained when the fluorophores were reversed (Fig. S5A,B). These results indicate that Par-3 and myosin II polarities are not independently established during convergent extension. Instead, cells that are more strongly polarized for one protein are also more strongly polarized for the other, suggesting that a common mechanism coordinates the localization of both proteins to distinct cortical domains.

Protein localization is dynamically remodeled during intercalation

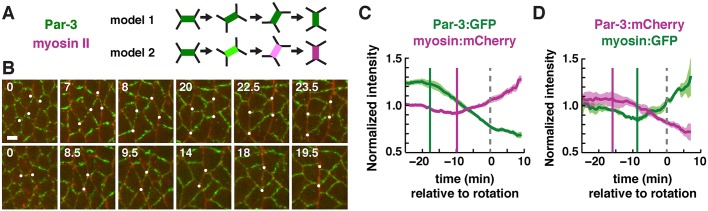
Planar polarity during convergent extension in Drosophila is established through local, contact-dependent signals provided by the AP patterning system and its targets, including transmembrane receptors in the Toll receptor family that are expressed in a striped pattern (Irvine and Wieschaus, 1994; Zallen and Wieschaus, 2004; Paré et al., 2014). During convergent extension, cell rearrangement and cell shape changes are predicted to cause cells to deviate from their initial orientation with respect to the tissue axes. This raises the question of how planar polarity is affected as cells rearrange during elongation. If planar polarity is established only once in response to the initial striped pattern, then a cell boundary that rotates is predicted to retain proteins that are consistent with its initial orientation, but do not reflect the current orientation of that edge with respect to the tissue axes (Fig. 6A, model 1). Alternatively, if cells can dynamically remodel their polarity in response to changes in orientation, then protein localization is predicted to change to match the new orientation of edges as they rotate (Fig. 6A, model 2).

Fig. 6.

Planar polarity is actively remodeled in moving cell populations. (A) Transverse edges that rotate into a vertical orientation as a result of cell rearrangements could retain Par-3 (model 1) or lose Par-3 and recruit myosin (model 2). (B) Stills of three Par-3-positive transverse edges (green) that rotate into a vertical orientation and accumulate myosin II (red). Time (min) relative to the start of edge rotation. Scale bar: 5 μm. (C) Par-3:GFP and myosin:mCherry intensity at edges that rotate from <45° to >70° (0° is parallel to the AP axis). Edge intensities were normalized to the mean intensity of all edges at that time point. A single mean value was obtained for each embryo and the mean±s.e.m. between embryos is shown. Time relative to the edge passing 70° (t=0, gray dashed line). Par-3 levels decreased (green bar) before myosin II levels increased (magenta bar). n=4 Par-3:GFP; myosin:mCherry movies; 89-240 rotating edges/movie. Vertical bars are guides to the eye. (D) Similar results were obtained with the fluorophores reversed. n=4 Par-3:mCherry; myosin:GFP movies; 19-54 rotating edges/movie.

To distinguish between these possibilities, we used edge tracking tools in SEGGA to analyze the localization of Par-3 and myosin II at rotating edges in embryos that express these proteins tagged with GFP or mCherry (Fig. 6B). These measurements identified a subset of edges (5-10% of edges tracked/movie) that rotate from a transverse orientation to a vertical orientation during convergent extension. These edges did not retain Par-3 as predicted by model 1, but instead showed a progressive loss of Par-3 and an increase in myosin II levels consistent with their new orientation, as predicted by model 2 (Fig. 6C). Following these edges over time revealed that the decrease in Par-3 intensity started before the increase in myosin intensity (Fig. 6C), similar to the order in which these proteins become localized prior to elongation (Fig. 5A). The same order of events was observed when the fluorophores were reversed (Fig. 6D). Edges that rotated from a vertical to a transverse orientation were much rarer, which is likely to be because vertical edges rapidly contracted and disappeared before they could rotate. These results show that cells can respond to changes in cell orientation, and that the planar polarized localization of myosin II and Par-3 are dynamically remodeled as cells rearrange during convergent extension.

SEGGA is a generally applicable method for analysis of cell shape and topology in epithelia

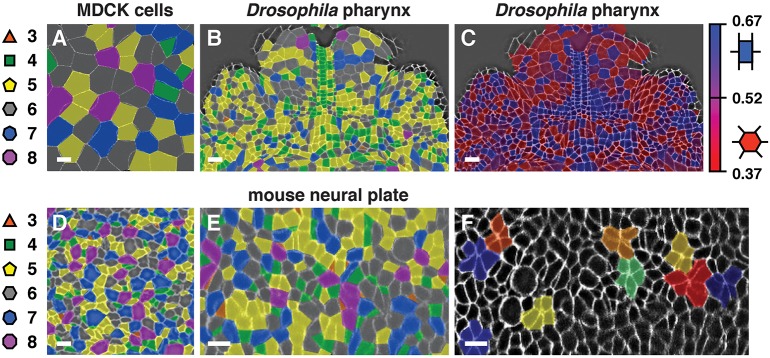
The methods that we developed in SEGGA are in principle applicable to studies of epithelial organization in any system, but image analysis algorithms that are optimized for one system are not always readily transferable to others. To evaluate if SEGGA works on other tissues, we used it to analyze images of epithelial cells from fixed embryos, live embryos and cultured cells from other organisms. We found that SEGGA performed well on images of mammalian MDCK cells (Fig. 7A), the presumptive pharynx of the Drosophila embryo (Fig. 7B,C) and the mouse embryonic neural plate (Fig. 7D-F). These images include examples from multiple organisms and from both fixed and live cells. Color maps highlight unique features of each tissue, such as cell topology, rectangularity and rosette formation (Fig. 7A-F). These results demonstrate that SEGGA works on epithelial tissues in flies, mice and cultured cells and highlight the general utility of this method for analyzing diverse processes of epithelial organization.

Fig. 7.

Segmentation of different epithelial tissues in SEGGA. Segmentation results in SEGGA for Madin-Darby canine kidney (MDCK) cells stained for p120 (A), the presumptive pharynx of a stage 13 Drosophila embryo stained for β-catenin (B,C) (ventral view, anterior up), the E8.5 mouse cephalic neural plate stained for ZO1 (Tjp1) (D) and stills from a time-lapse movie of the E8.0 mouse spinal neural plate labeled with membrane-localized GFP (E,F). Color maps highlight cell topology (A,B,D,E), rectangularity (C) and rosettes (F). Background images are shown with (F) or without (A-E) image processing. The images shown are color-coded annotations of images provided by H. Yu and A. Reynolds (A), M. Tamada (B,C) (Tamada and Zallen, 2015), J. Grego-Bessa and K. Anderson (D) (Grego-Bessa et al., 2015) and E. Brooks and A. Sutherland (E,F). Scale bars: 10 µm.

DISCUSSION

This study describes the application of SEGGA, a computational method for the analysis of epithelial cell polarity and behavior in large cell populations. SEGGA provides a suite of tools for automated cell segmentation and tracking, semi-automated error correction, and quantitative analysis of cell shape, organization and planar polarity. Here we used this method to perform a broad survey of cell behavior during convergent extension in the Drosophila embryo. These studies show that although extrinsic forces from the ventral furrow influence cell shape in the germband, these forces are dispensable for tissue elongation. Instead, cell rearrangement correlates more strongly with elongation across many genotypes. These results are consistent with a model in which cell intercalation is the primary mechanism driving convergent extension in Drosophila, whereas cell shape changes reflect the passive deformation of cells in response to extrinsic forces (Butler et al., 2009; Collinet et al., 2015; Lye et al., 2015). Finally, we show that planar polarity in the Drosophila embryo is rapidly established prior to the onset of elongation through a reproducible succession of ordered cell polarization events. Single-cell tracking studies reveal that these planar asymmetries, once established, can be dynamically remodeled in response to changes in cell orientation. These results describe a systematic, quantitative and generally applicable approach that can be used to elucidate the single-cell and collective cell behaviors that influence tissue structure.

The applications described here highlight several advantages of the SEGGA software. First, SEGGA provides a wide range of functions, including tools for image segmentation, correction, data graphing and analysis, which allow the user to go from raw data to a quantitative analysis of multiple aspects of cell and tissue dynamics. Second, SEGGA contains a novel semi-automated method for propagating user-guided corrections to other time points that substantially accelerates the process of correcting errors to achieve highly accurate image segmentation. Third, SEGGA generates customizable color maps that can be used to identify spatial and temporal patterns of cell behavior, allow the user to directly inspect the results of the computational analysis, and facilitate the display of time-lapse data for teaching and presentation purposes. Fourth, SEGGA is available as open-source code in MATLAB and as a compiled version that can be run free of charge, which will facilitate the use and extension of this software on a wide range of platforms. This study highlights the applications of SEGGA and provides an example of how it can be used as a quantitative method to study the cellular and molecular mechanisms that establish tissue structure in a wide range of tissues and organisms.

The establishment and maintenance of planar polarity in the Drosophila embryo are spectacular in terms of their speed and resilience. Our results demonstrate that this process is remarkably fast: cells transition from unpolarized to nearly fully polarized in ∼20 min. This is distinct from other epithelia such as the Drosophila wing, in which planar polarity is established over the course of several hours (Hale and Strutt, 2015; Yang and Mlodzik, 2015). Our cell-based analysis reveals a correlation between the extent of Par-3 and myosin II planar polarity: cells with a strong planar polarized localization of one protein were more likely to have a strong planar polarized localization of the other. This correlation points to a shared mechanism that regulates Par-3 and myosin II asymmetry within cells. An upstream regulator that could coordinate the distributions of these two proteins is Rho kinase, which can directly phosphorylate both proteins and is itself asymmetrically localized (Simões et al., 2010). Alternatively, Par-3 has been shown to exclude myosin II from the cortex, suggesting an alternative mechanism that could coordinate these two polarities (Simões et al., 2010). We found that Par-3 planar polarity is established before the detectable planar polarized localization of F-actin, myosin II and Shroom. This order of events is slightly different from results obtained in fixed embryos, in which the planar polarized localization of Par-3 occurs at the same time as that of myosin II (Blankenship et al., 2006). These differences are likely to be due to the increased sensitivity of the Par-3:GFP marker used for live imaging analysis, and the ability of time-lapse movies to distinguish events that occur in rapid succession and cannot be resolved in fixed embryos. However, it is important to consider that some markers may be less sensitive in a live imaging context. In particular, we previously detected F-actin planar polarity at earlier stages in fixed embryos using phalloidin staining (Blankenship et al., 2006). The later onset of F-actin planar polarity in movies might be due to the low signal-to-noise ratio of the GFP markers used to visualize F-actin in living embryos. Alternatively, distinct F-actin structures might be differentially detected by the actin-binding domains of Utrophin and Moesin compared with the F-actin structures detected by phalloidin, as these markers have been shown to associate with distinct populations of F-actin in cultured cells (Belin et al., 2014).

Global patterns of planar polarity in the Drosophila wing shift from a radial to a proximodistal orientation during wing development as a consequence of cell division and local cell rearrangements (Classen et al., 2005; Aigouy et al., 2010). By contrast, it is less clear how stable patterns of tissue-level planar polarity are maintained despite the dynamic reorganization of cells in actively moving cell populations. Surprisingly, we discovered that cells in the Drosophila embryo reorient their planar polarity as they rearrange through a mechanism of dynamic cell repolarization. This unexpected plasticity raises questions about the spatial cues that orient cell polarity and behavior during axis elongation. Planar polarity in the Drosophila embryo is induced by contact-dependent signals that are provided by local differences in Toll receptor and pair-rule gene expression between neighboring cells (Irvine and Wieschaus, 1994; Zallen and Wieschaus, 2004; Paré et al., 2014). As these neighbor relationships are maintained as edges rotate, the remodeling of planar polarity at rotating edges must rely on distinct cues. In one model, myosin could be recruited to rotating edges by mechanical tension, which is anisotropically distributed in the tissue and is highest at vertical edges (Rauzi et al., 2008; Fernandez-Gonzalez et al., 2009). Edges that rotate into a vertical orientation are predicted to be exposed to increased tension, which is sufficient to stabilize cortical myosin levels (Fernandez-Gonzalez et al., 2009; Pouille et al., 2009). The tension-dependent remodeling of planar polarity could help to maintain a consistent spatial pattern of protein localization that allows cells to dynamically repolarize in order to undergo multiple rounds of cell rearrangement during axis elongation. The simultaneous loss of Par-3 at rotating edges raises the possibility that Par-3 or its upstream regulators are also responsive to mechanical changes at the cell cortex. An understanding of how cells repolarize in response to changes in cell orientation can help to elucidate how multicellular tissues establish stable polarized structures in the presence of the dynamic cell behaviors that occur during development, and how they maintain these structures despite cell death, damage and turnover in the adult.

MATERIALS AND METHODS

SEGGA software

The SEGGA code was implemented in MATLAB (MathWorks), and a home window in the graphical user interface links to modules for image processing and segmentation, error correction, single image analysis, single movie analysis, multiple movie analysis, and polarity analysis. Further information about this software is provided in the supplementary Materials and Methods.

Fly stocks and genetics

In this study we expanded on our previous analysis in SEGGA and developed new measurements to analyze published movies that were generated as described (Blankenship et al., 2006; Simões et al., 2010, 2014; Tamada et al., 2012; Paré et al., 2014; Vichas et al., 2015). In addition, new embryos imaged in this study were grown at 21-25°C and imaged at room temperature. These include snail^IIG05 twist^DfS60 zygotic mutants (Leptin and Grunewald, 1990) expressing Spider:GFP, arm^043A06 (β-catenin) maternal mutants (Tolwinski and Wieschaus, 2001) expressing Spider:GFP, sqh-sqh:GFP (myosin II regulatory light chain) (Royou et al., 2004), UAS-Baz:mCherry (Par-3) (McGill et al., 2009), sqh-GFP:moesin (moesin F-actin-binding domain) (Kiehart et al., 2000), sqh-utrophin:GFP (utrophin F-actin-binding domain) (Rauzi et al., 2010) and UASp-Venus:Shroom[ΔRokBD] (Δaa 1324-1576, which removes the Rho-kinase-binding domain) (Simões et al., 2014). GFP:moesin and utrophin:GFP were combined for F-actin analysis.

Par-3, myosin II and Shroom were analyzed in the F2 progeny of the following crosses (matαtub-Gal4:VP16 67;15, a gift of D. St Johnston, Gurdon Institute, University of Cambridge, UK): (1) UAS-Baz:GFP; sqh-sqh:mCherry×matαtub-Gal4:VP16 67;15; (2) UAS-Baz:mCherry; sqh-sqh:GFP×matαtub-Gal4:VP16 67;15; and (3) UAS-Venus:Shroom[ΔRokBD]×matαtub-Gal4:VP16 67;15.

Further details of fly stocks and genetics are provided in the supplementary Materials and Methods.

Time-lapse imaging

Time-lapse movies were generated on PerkinElmer RS5 or Ultraview VOX spinning disk confocal microscopes using Zeiss Plan-Neo 40×/1.3 NA or Plan-Apo 40×/1.3 NA oil-immersion objectives. z-stacks were acquired at 1 µm z-steps and 15 s intervals (single-color movies) or 30 s intervals (two-color movies). Processed projections at the level of the adherens junctions were used to analyze cell behavior. Maximum intensity projections of up to 10 µm were used to analyze planar polarity.

Statistics

Cell shape, rearrangement and polarity were analyzed for each cell and a single mean value was obtained for each embryo at each time point. The mean±s.e.m. between embryos is shown unless otherwise indicated. P-values were calculated using the f test, followed by the appropriate t-test (t-test or U-test). The t=30 min value was the test statistic.

Note added in proof

A recent publication describes a different method for cell tracking using watershed segmentation and optic flow that will also be useful for automated image analysis (Wang et al., 2017).