Dynamics of Blood Flow and Thrombus Formation in a Multi-Bypass Microfluidic Ladder Network

Abstract

The reaction dynamics of a complex mixture of cells and proteins, such as blood, in branched circulatory networks within the human microvasculature or extravascular therapeutic devices such as extracorporeal oxygenation machine (ECMO) remains ill-defined. In this report we utilize a multi-bypass microfluidics ladder network design with dimensions mimicking venules to study patterns of blood platelet aggregation and fibrin formation under complex shear. Complex blood fluid dynamics within multi-bypass networks under flow were modeled using COMSOL. Red blood cells and platelets were assumed to be non-interacting spherical particles transported by the bulk fluid flow, and convection of the activated coagulation factor II, thrombin, was assumed to be governed by mass transfer. This model served as the basis for predicting formation of local shear rate gradients, stagnation points and recirculation zones as dictated by the bypass geometry. Based on the insights from these models, we were able to predict the patterns of blood clot formation at specific locations in the device. Our experimental data was then used to adjust the model to account for the dynamical presence of thrombus formation in the biorheology of blood flow. The model predictions were then compared to results from experiments using recalcified whole human blood. Microfluidic devices were coated with the extracellular matrix protein, fibrillar collagen, and the initiator of the extrinsic pathway of coagulation, tissue factor. Blood was perfused through the devices at a flow rate of 2 µL/min, translating to physiologically relevant initial shear rates of 300 and 700 s⁻¹ for main channels and bypasses, respectively. Using fluorescent and light microscopy, we observed distinct flow and thrombus formation patterns near channel intersections at bypass points, within recirculation zones and at stagnation points. Findings from this proof-of-principle ladder network model suggest a specific correlation between microvascular geometry and thrombus formation dynamics under shear. This model holds potential for use as an integrative approach to identify regions susceptible to intravascular thrombus formation within the microvasculature as well as extravascular devices such as ECMO.

Electronic supplementary material

The online version of this article (doi:10.1007/s12195-016-0470-7) contains supplementary material, which is available to authorized users.

Introduction

Microfluidic flow chambers are powerful research tools as they require small amounts of blood samples to allow for investigation of blood cell–cell and cell–matrix interactions and thrombus formation under the dynamics of physiologically relevant levels of shear. Currently, the majority of microfluidic platforms used to assess thrombus formation rely on the coating of a single channel with extracellular matrix proteins, such as collagen, tissue factor (TF), or von Willebrand factor (VWF), to mimic a site of vascular injury.12,49 These platforms have proven to be useful for the study of the biophysical and molecular mechanisms of thrombus growth at a fixed shear rate. Further, their utility has been demonstrated in studying complex shear-dependent interactions between platelets and vascular wall and diagnosing clotting disorders, such as VWF disease.19,64 However, a single channel system fails to capture the complexities of branched vessel networks prevalent throughout the human circulatory system, or that exist in extravascular therapeutic device designs. In this report, we use a computational model to predict thrombus formation patterns within a multi-bypass network of channels. Our predictions were then tested experimentally following perfusion of recalcified human blood through the microfluidic device.

Within multi-bypass microfluidic geometries, whole blood is subject to complex flow dynamics. The presence of junctions and bifurcations in vascular networks can result in skewed velocity profiles, flow separation and secondary flows, attributed to sudden directional and dimensional changes within the channel network.35,48 Subsequently, low flow regions develop, which allow for the accumulation of blood cells and accumulation of procoagulant proteases.38 Moreover, blood leukocytes have been shown to preferentially adhere to surfaces downstream of channel bifurcations in vitro and in vivo.53 Other flow disturbances imparted by complex geometries include stagnation points and fluid acceleration and deceleration, both of which have been associated with increased thrombus formation.43,60

The kinetics of thrombus formation within a multi-bypass channel geometry evolves over time as the blood flow is diverted due to the formation of an occlusive clot within the channel. Microvascular stenosis leads to a temporal increase in local shear rates, whereas occlusive thrombus formation leads to dramatic decreases in shear and local areas of blood stasis. Platelet adhesion and thrombin generation have been shown to increase within low shear zones at the downstream face of a forming thrombi.4,43 Moreover, endothelial cells change their morphology and switch from an anticoagulant to a procoagulant phenotype within poststenotic zones, providing further evidence that the biorheology of blood flow is intimately related to the maintenance of blood vessel patency.54,60

Thrombus formation within a vessel network architecture can alter the distribution of blood cells within the bloodstream. In laminar blood flow, blood cells are distributed radially with platelets marginated to the outer vessel wall and red blood cells (RBCs) preferentially comprising the inner core.15,20,55,56 Shear rate has been shown to have a direct effect on blood viscosity due to an increase in RBC–RBC interactions, mediated by fibrinogen, occurring at shear rates below 100 s⁻¹.50 In select regions of the branching vasculature, multiple and altered layers of RBCs and platelets have been observed to transiently divide the blood into relatively hemoconcentrated and hemodiluted streams, a phenomena known as plasma skimming.46 For instance, organs containing microvessel channel networks, such as the spleen, placenta or the bone marrow exhibit high levels of plasma skimming,28 which has been implicated to play a role in venous thrombosis in these vascular beds.7,45

This report describes a finite element simulation model of the biorheology of thrombus formation patterns within a multi-bypass microfluidic ladder network, which is subsequently validated with primary experiments using whole human blood. Our model predicts thrombus nucleation points at select regions of bifurcations, stagnation and recirculation based on velocity, shear rate and cell distribution profiles. Our model takes into account the effect of thrombus growth and thrombin generation on blood flow within the ladder network. Overall, we demonstrate an integrated computational and experimental approach aimed to predict areas of thrombus formation within a branched microvascular geometry.

Methods and Materials

Materials

Dade^® Innovin^® was purchased from Siemens. All other materials were purchased from Sigma-Aldrich or previously cited sources.65 Hepes-Tyrode buffer (129 mM NaCl, 20 mM HEPES, 12 mM NaHCO₃, 2.9 mM KCl, 1 mM MgCl₂, 0.34 mM Na₂HPO₄·12H₂O; pH7.3) was modified with 0.045 g of glucose per 50 mL of buffer on the day of experiment and kept in the 30 °C bath until use.

Fabrication of Mask and Microfluidic Device

The microfluidic ladder network was designed in AutoCAD to emulate the physiological parameters of postcapillary venules. The network was designed to consist of two sets of inlets and outlets entering two main channels (100 µm wide by 100 µm high) interconnected with ten equally spaced bypass channels (50 µm wide by 100 µm high); the first four bypasses are shown in Fig. 1a. Paired contralateral inlets and outlets were stoppered and reopened at select iterations to achieve directional blood flow, originating from channel 1 and exiting from channel 2, while buffer was perfused from channel 2 to channel 1. The mask was fabricated using standard photolithography and soft lithography techniques.39,41 Our design was molded using a 10:1 ratio (w/w) of Sylgard^® 184 polydimethylsiloxane (PDMS) polymer to curing agent. A BD-20AC Corona Treater (Electro-Technic products, Inc) was used to plasma bond PDMS molds onto microscopy slides. The final devices were assembled into the flow system as shown in Fig. 1b.

Figure 1.

Modeling human blood flow and thrombus formation dynamics within a multi-bypass ladder network. Parameters of a multi-bypass microfluidic ladder network device design (a) and an experimental prototype as visualized by differential interference contrast (DIC) microscopy (b). Network features two main channels and ten bypasses (bp 1–10); micrograph shows the first four bypasses. Black bars indicate a stoppered inlet and outlet; red arrows depict the direction of blood flow. Stoppered inlets and outlets were re-opened during the washing step.

Coating of Microfluidic Devices with Collagen and Tissue Factor

Microfluidic devices were coated as previously described.66 In short, devices were incubated with fibrillar collagen (150 µg/mL in 10 mM acetic acid) for 1 h with rotation at room temperature. Next, devices were rinsed with phosphate buffered saline (PBS) and incubated with a solution of Dade^® Innovin^® (0.1 nM tissue factor, TF, in ddH₂O). Surfaces were then blocked with 5 mg/mL denatured bovine serum albumin (BSA) for 1 h at room temperature. In parallel, control devices were incubated with appropriate dilution buffers, as described above, and blocked with BSA.

Blood Collection and Preparation

Whole blood was drawn by venipuncture from healthy adult volunteers into sodium citrate (0.38% w/v) in accordance with the Oregon Health & Science University Institutional Review Board. Blood was used within 2 h of the blood draw. To allow detection of platelet-rich clot formation, blood was incubated with the mitochondrial dye 3,3′-Dihexyloxacarbocyanine Iodide (DiOC₆; 2 µM final). To initiate coagulation, blood was recalcified to a final concentration of 7.5 mM CaCl₂ and 3.5 mM MgCl₂ immediately prior to perfusion through the microfluidic device.

Ex vivo Blood Flow Assays

Coated microfluidic devices were assembled into a pump-driven flow system. Modified Hepes-Tyrodes buffer was perfused through the device with a Harvard 2000 syringe pump in order to wet the channels and remove any air bubbles. We stoppered a contralateral channel inlet and outlet prior to perfusion of blood in order to reserve them for washing (inlet leading to channel 2 and outlet leaving channel 1; Fig. 3a). DiOC₆-stained sodium citrate (0.38% w/v) anticoagulated whole blood was recalcified and perfused through the coated microfluidic device at a flow rate of 2 µL/min. Real-time platelet aggregation was recorded using Zeiss Axio Imager 2 microscope (Carl Zeiss MicroImaging GmbH, Germany). After 30 min of blood perfusion, inlet and outlet channels were opened and networks were perfused with modified Hepes-Tyrodes buffer for an additional 20 min, followed by imaging with differential interference contrast (DIC) and fluorescent light microscopy as previously described.2 The surface areas of thrombi formed within each bypass and adjacent areas, as marked in Supplemental Fig. 1, were quantified using ImageJ and normalized per experiment to bypass 1. Average surface area fold changes and standard error means, SEM, were reported for 5 independent experiments (Fig. 3d).

Figure 3.

Temporal thrombus growth within ladder network. DiOC₆-labeled whole human blood was perfused at a 2 µL/min flow rate through a PDMS-ladder network coated with collagen and tissue factor; real-time images of thrombus formation were recorded using differential interference contrast, DIC (a) and fluorescence microscopy (b). Networks were subsequently washed with modified Hepes-Tyrodes buffer for 20 min prior to DIC imaging (c). Representative images shown, n = 5. Total surface areas of thrombi per bypass were quantified and normalized to bp1 (d).

Modeling

Fluid Dynamics

The local hemodynamic environment was modeled using a commercial finite element software (COMSOL). The model included blood being perfused at a constant flow rate of 2 µL/min through an inlet as shown in Fig. 1. The exit pressure of the outlet was maintained at atmospheric pressure. At these low flow rates, the Reynolds number (Re) is less than 1. Re <1 implies that the flow is viscous dominated, resulting in a creeping flow. The Navier–Stokes modeling equations for incompressible creeping flow are given as follows5:

$$\mathit{\rho }\frac{\mathit{\partial }u\left(x,y\right)}{\mathit{\partial }t}=-\mathrm{\nabla }P+\mathrm{\nabla }·\left(\mathit{\mu }\left(\mathrm{\nabla }u+{\left(\mathrm{\nabla }u\right)}^{\text{T}}\right)\right)$$

where ρ is the density of blood cells, which was set at 1060 Kg/m³, P is pressure, t is time, μ is the viscosity of blood, and u is the velocity profile. Blood viscosity was estimated using a Power law which is given as follows22,27:

$$\mathit{\mu }=\mathit{\lambda }{\left|\dot{\mathit{\gamma }}\right|}^{n-1}$$

$$\mathit{\lambda }\left(\dot{\mathit{\gamma }}\right)={\mathit{\mu }}_{\infty }+\mathrm{\Delta }\mathit{\mu }exp\left[-\left(1+\frac{\left|\dot{\mathit{\gamma }}\right|}{a}\right)exp\left(-\frac{b}{\left|\dot{\mathit{\gamma }}\right|}\right)\right]$$

$$n\left(\dot{\mathit{\gamma }}\right)=n_{\infty }-\mathrm{\Delta }nexp\left[-\left(1+\frac{\left|\dot{\mathit{\gamma }}\right|}{c}\right)exp\left(-\frac{d}{\left|\dot{\mathit{\gamma }}\right|}\right)\right]$$

where ${\mathit{\mu }}_{\infty }=0.035,n_{\infty }=1.0,\mathrm{\Delta }\mathit{\mu }=0.25,\mathrm{\Delta }n=0.45,a=50,b=3,c=50\text{and}d=4$.

The shear rate profile of the microfluidic network was modeled as follows:

$$\dot{\mathit{\gamma }}=\frac{1}{2}\left[\mathrm{\nabla }u+{\left(\mathrm{\nabla }u\right)}^{\text{T}}\right]$$

where $\dot{\mathit{\gamma }}$ is the shear rate, and $\mathrm{\nabla }u$ is the gradient of the velocity. Using the above modeling equations, a velocity profile, shear rate and velocity streamlines were generated for the microfluidic network.

Prediction of Blood Cell Distribution

A particle-tracing module within COMSOL was used to predict the distribution of platelets and RBCs within the channels. In the circulation, platelets marginate to preferentially populate a 2-5 μm layer near the wall, whereas RBCs form a core in the center of the channel. We modeled particle distribution changes within the complex geometry over time. Platelets and RBCs were modeled as spheres of 1.8 µm and 8 µm diameters, respectively, with a density of 1060 kg/m³. Particles with two different radii were released from the inlet at a predefined distribution: platelets were released with a normal distribution centered along the walls, whereas RBCs were released with a normal distribution at the center of the channel with a variance of 50 µm. The particle count ratio was set as 10 RBCs to 1 platelet and the RBC-core was set to occupy approximately 50% of the channel at the entrance, assuming a hematocrit of 0.5.

The initial velocity of the particles at the inlet was set to be zero. Particles were transported by the viscous drag force on them due to the bulk flow.5 As the particles moved through the channels, they were subject to a drag force, given as:

$F=\frac{18\mathit{\mu }}{{\mathit{\rho }}_{\text{p}}{d}_{\text{p}}^2}{m}_{\text{p}}{V}_{\text{rel}}$,

where $F$ is the drag force, $\mathit{\mu }$ is the viscosity, ${\mathit{\rho }}_{\text{p}}$ is the particle density, $d_{\text{p}}$ is the particle diameter, $V_{\text{rel}}$ is the relative velocity, $m_{\text{p}}$ is the particle mass.46 Particle trajectories were coupled to the continuous phase in a unidirectional manner.

Prediction of Thrombus Nucleation Points

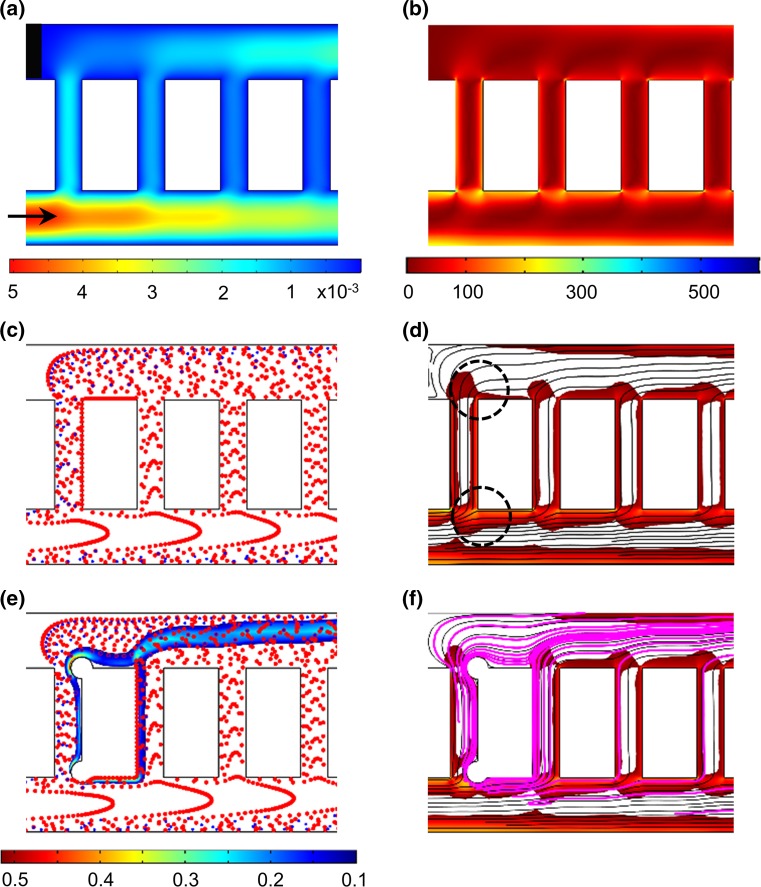
Initial thrombus nucleation points were predicted by integrating the blood flow velocity, shear rate, and blood cell distribution profiles as described above. The probability of a thrombus nucleating at a point within the network geometry was expected to increase with increased cell residence times, abrupt changes in shear and higher platelet counts.15,16,20,51,55,56 Velocity streamline profiles initiated at the channel inlet predicted platelet residence times within the ladder network. Based on the assumption of a no-slip condition at the wall, the residence time was expected to be relatively higher near the walls of the channels as compared to the center of the channels, and reach infinity at the stagnation points created by the splitting of the bloodstream where the main channel and bypass intersection formed a right angle. Based on the geometry, abrupt changes in the shear rate were expected immediately distal to the main channel intersection with bypasses.21,52 The plasma skimming effect was assumed to control the average number of platelets and RBCs present at each segment of the channel. Thrombus formation, modeled as solid spheres with a constant surface concentration of thrombin, was incorporated at these nucleation points (Figs. 2e, 2f).

Figure 2.

Prediction of thrombus formation within the ladder network: nucleation and evolution. Computer simulation of blood flow velocity profile (a; µL/min), shear rate profile (b; s⁻¹) and the initial blood cell distribution profile (c). A combination of velocity streamlines and shear rate gradient predicted a higher probability for the nucleation site for thrombus formation on the channel walls immediately downstream of intersections between main channels and bypasses (highlighted with black circles) (d). Computer simulations repeated in the presence of an obstruction to predict adjusted blood cell distribution profile during clot growth and thrombin convection mol/m³ (e) and combination of thrombin convection profile (purple) over bulk flow velocity streamlines and shear rate profile (f). Shear rates below 30 s⁻¹ were subtracted from the shear rate heat maps on the overlays (d and f) for visibility of velocity streamlines.

Thrombin Mass Transfer

The mass transfer of thrombin within the microfluidic network was modeled to predict sites associated with increased thrombin levels. All clots were assumed to have thrombin surface concentrations of 0.5 mol/m³.10

The equations used to obtain the concentration profiles is given below:

$$\mathrm{\nabla }·\left(-D_i\mathrm{\nabla }{C}_i\right)+u·\mathrm{\nabla }{c}_i=0$$

where $D_i$ is the diffusivity of thrombin and was set at 10 µm²/s, while $u$ is the velocity profile in the network.34 This equation along with the Navier–Stokes equation and continuity were solved simultaneously to obtain concentration and velocity profiles. The Peclet number $\left(\text{LU/D}\right)$ of this flow was ≫1, implying that the mass transfer of thrombin within the bloodstream is expected to be largely dominated by convection as compared to diffusion. Therefore the mass transfer of the most of the thrombin within bloodstream was expected to follow the streamlines as depicted in Fig. 2f.

Prediction of the Effect of Thrombi Formation Propagation Within Ladder Network

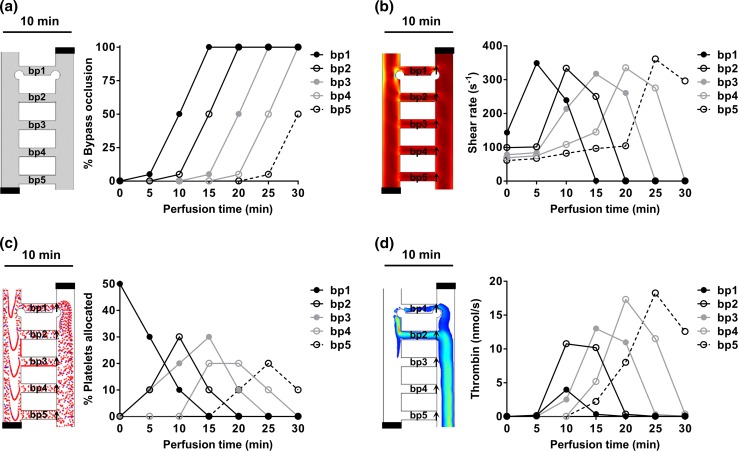
Based on experimental observations of the thrombogenicity of collagen and TF-coated surfaces,61,66 a simplified bypass-to-bypass thrombus propagation profile was developed and used to run simulations to study the dynamical effect of thrombus formation on the shear rate, platelet distribution and thrombin molar rate per bypass within the network. Simulations were performed for six scenarios corresponding to 0–30 min of perfusion time in 5 min steps. The thrombus formation within bypass 1 was expected to progress to 5, 50 and 100% occlusion by 5, 10 and 15 min respectively. Geometric occlusion events were modeled as a pair of circular thrombi originating from the intersecting edges of each bypass with main channels 1 and 2. The bypass-to-bypass thrombus propagation relationship was set such as when the thrombus formation within the bypass ‘n’ reached 50% occlusion then the thrombus in bypass 'n + 1' would reach 5% occlusion (Fig. 4a).

Figure 4.

Prediction of the effect of thrombus formation within a ladder network. Computer simulations of the effects of thrombus formation on the dynamics of blood flow dynamics were performed at discrete time and bypass-to-bypass locations (a). The changes in shear profile (b; s⁻¹), platelet distribution profile (c) and concentration profile of thrombin (d; nmol/s) at each bypass were calculated as a function of time. Arrows indicate regions of measurement integration.

Simulations for each metric per scenario were conducted at steady state. To estimate changes in the shear rate profile per bypass, a cut line method was used to monitor the changes in average shear rate as a function of occlusion percentage at each region marked by arrows (Fig. 4b). The effect of sequential occlusion on the platelet trajectory was modeled by creating a particle counter at the exit of each bypass. The number of platelets travelled through each bypass were counted as a function of occlusion at the location indicated by arrows (Fig. 4c). The sequential evolution of thrombus formation within the ladder network was expected to lead to dynamic changes in the thrombin flux in these bypasses and along the main channels. To estimate the amount of thrombin within the ladder network as a function of occlusion, a cut line method was used to calculate the average thrombin molar flow rate at regions indicated by arrows (Fig. 4d). A derivation of the equations used in our model is included in Supplemental Materials.

Results

Modeling Human Blood Flow and Thrombus Formation Dynamics Within a Multi-bypass Ladder Network

At sites of vascular injury, blood cells and proteins are subject to an evolving hemodynamic environment that determines the rate and morphology of thrombus formation. The goal of this project was to develop a computational model to predict the spatial and temporal dynamics of thrombus formation within a ladder network geometry. The predictions of the location and patterns of thrombus formation were then validated with primary experiments using whole human blood. We aimed to understand the contribution of complex branching and asymmetric geometries on thrombus initiation and propagation. Branching, stagnation points, and expansions were among the features of the microfluidic ladder channel. By having a multi-bypass model, we were able to study re-direction of flow from one bypass to the next as a result of the formation of an occlusive thrombus within the bypass channels. The microfluidic network ladder design in this report was designed to fall within the Stokes flow regime (Re ≪ 1) and therefore did not contain inertial driven features associated with larger diameter geometries (Fig. 1).

Prediction of Thrombi Formation Within a Ladder Network: Nucleation and Evolution

Four key parameters were simulated to predict the spatial and temporal dynamics of thrombus formation. These factors were: (i) blood flow velocity, (ii) shear rate gradient, (iii) blood cell distribution and (iv) thrombin convection profiles.

• I. Blood Flow Velocity Our COMSOL model predicted a series of stagnation points in which the blood velocity is close to zero and thus assumed to promote thrombus formation immediately downstream.4 Formation of the stagnation points were predicted to occur at corners where the main channels intersect with bypass channels (Fig. 2a).
• II. Shear Rate Rradient Our model predicted a relative increase in local shear rates along the channel 1 wall and at corners at intersections between channel 1 and bypasses leading to channel 2 (Fig. 2b). Thrombus formation was predicted to be favored near stagnation sites where the shear rate was predicted to undergo a rapid change in magnitude.24 A combination of shear rate gradient and velocity profiles predicted a higher probability for thrombus nucleation on the channel walls immediately downstream of intersections between main channels and bypasses (Fig. 2d; black circles).
• III. Blood Cell Distribution Our model predicted that upwards of 50% of platelets were initially expected to separate into the first bypass (bp 1), due to the effect of plasma skimming (Fig. 2c). Thus, the increased concentration of platelets in the first bypass was predicted to preferentially increase the rate of thrombus formation within the first bypass. Our model then predicted relatively decreased concentrations of platelets per unit volume in each subsequent bypass. However, as the flow rate decreased through the first bypass due to the formation of an occlusive thrombus within bp 1, the relative flow rate and subsequent concentration of platelets was predicted to increase in the second bypass (bp 2), leading to an increased probability of thrombus formation in bp 2 as a function of time (Fig. 2e).
• IV. Thrombin Convection Nucleation of the initial site of thrombus formation, as predicted by blood velocity, shear gradient and cell distribution profile, was expected to serve as a local source of a thrombin generation. Thrombin is a potent serine protease with a diverse set of biological functions including the activation of platelets, activation of coagulation factors V, VIII and FXI, and cleavage of fibrinogen to form polymerized fibrin, all of which contribute to thrombus formation under flow.23 Our model predicted that thrombin mass transfer in the bloodstream occurs via convection along the blood bulk flow (Fig. 2f).

To summarize, our model predicted a higher probability of thrombus nucleation immediately downstream to locations in which the blood flow velocity is close to zero, and both shear gradients and platelet concentrations are higher as compared to the parameters found in the bulk bloodstream.

Temporal Thrombus Growth Within a Ladder Network

We next studied the role of microfluidic channel geometry on platelet deposition and fibrin formation within a multi-bypass ladder network in an ex vivo blood flow assay. Platelet adhesion and aggregation were observed after the perfusion of recalcified whole human blood through the ladder network which was coated with collagen and TF (Fig. 3a, Supplemental Video 1 and 2). DiOC₆-labeled (green) platelet aggregate formation was monitored in real-time using fluorescent light microscopy and revealed a pattern of increased platelet aggregate formation at the stagnation regions formed at intersection points between main channels and bypasses, starting at bypass 1 (Fig. 3b). Moreover, after washing away non-adherent cells, an increase in the spatial distribution of fibrin was observed at the nucleation points and in regions where our model predicted transitions from high to low shear (Fig. 3c). These experimental results validated the prediction of the thrombus nucleation at intersection points between the bypasses and main channels (Fig. 2d). Quantitative analysis of the surface area of thrombi formed as a function of location demonstrated that thrombus formation occurred sequentially from bypass 1 to bypass 2 and onwards to bypass 10, with preceding bypasses promoting larger thrombi formation, by surface area, in the subsequent bypass (Fig. 3d).

Prediction of the Effect of Thrombi Formation Propagation Within a Ladder Network

To predict the dynamical effect of thrombus formation on blood biorheology within the microfluidic network, iterative simulations were performed and the effects of thrombus formation on shear, platelet distribution and thrombin molar rate were simulated at each bypass. Six separate scenarios with a set ratio of thrombus formation within bypasses were simulated. The scenario before blood entered a bypass, and thus prior to thrombus formation, was defined as a null scenario. Next, scenarios reflected thrombus growth within bypass 1 (bp1) in discrete time intervals of 5 min corresponding to 5, 50 and 100% occlusion by 5, 10 and 15 min, respectively. For each scenario, a correlation between thrombus growth in a preceding and subsequent bypasses was set so that when a thrombus in bypass ‘n’ reached 50% occlusion, thrombus growth would commence in bypass ‘n + 1’ and reach 5% occlusion (Fig. 4a; Left panel shows simulation set up for a scenario at 10 min).

Our simulations showed that shear rate increases at bypass 1 (arrow) with 5% occlusion and start to fall at 50% occlusion as blood flow starts to redirect to and result in an increase in shear in the subsequent bypass (Fig. 4b). Shear rate was expected to drop to zero once the bypass reached full occlusion. Our model predicted that platelet trajectories in the ladder network were sensitive to changes in the geometry due to thrombus formation. The sequential growth of thrombi was predicted to lead to increasing resistance in each bypass resulting in redirection of flow and platelets to subsequent bypasses. Our model predicts that approximately half of the platelets will travel through bypass 1 prior to thrombus formation and that platelet concentrations within bypass 1 will decrease as the bypass starts to occlude, resulting in shunting of blood flow to downstream bypasses (Fig. 4c). Our model predicted that the thrombin convection profile at each subsequent bypass would be higher than at the previous bypass (Fig. 4d). The presence of thrombi in an upstream bypass was predicted to serve as a surface for thrombin generation and convection into the blood flow. At complete occlusion of bypass 1, the overall molar flow rate of thrombin was expected to reach zero due to zero velocity.

Prediction of the Effect of the Flow Recirculation on Platelet Aggregation and Fibrin Formation

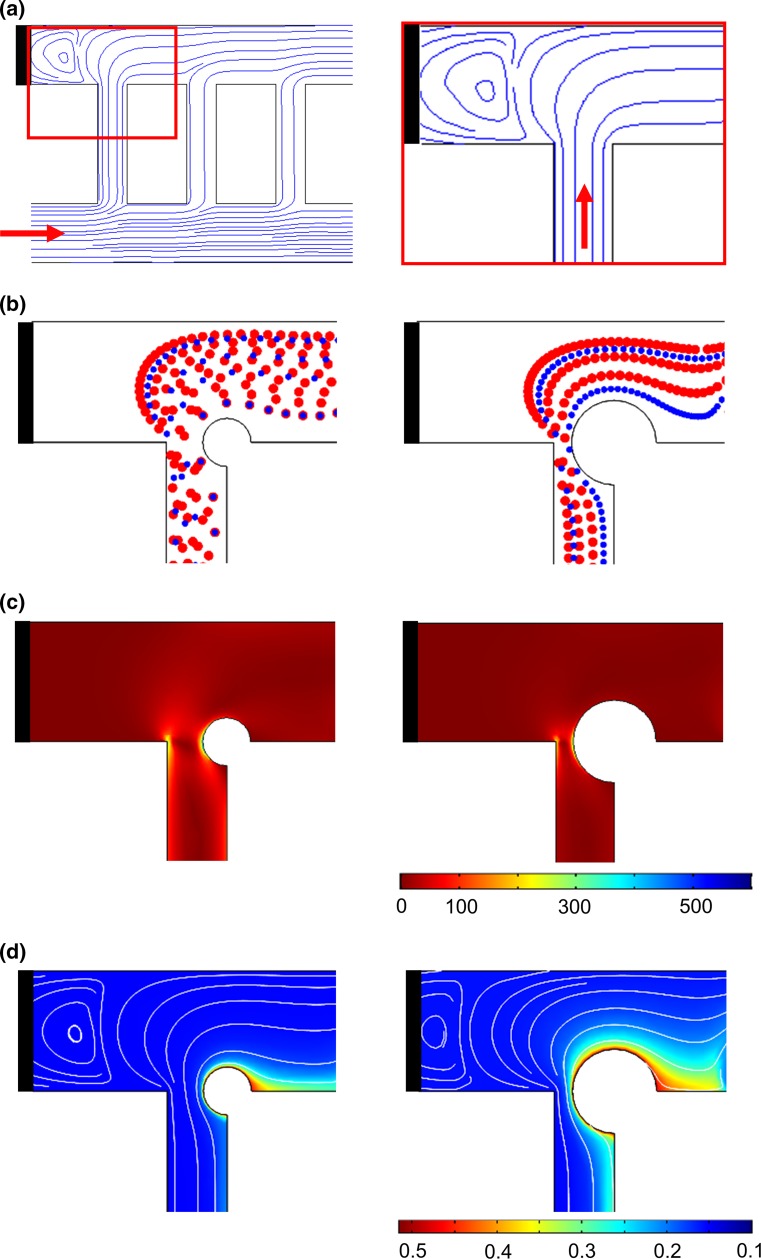
In addition to predicting stagnation points and rapidly changing shear gradients within our ladder network, our model also predicted formation of a recirculation zone at the stoppered inlet of channel 2 due to the flow obstruction at the entrance of blood into the channel 2 from channel 1 via the first bypass, bp 1 (Fig. 5a). As the blood circulates through the first bypass, the boundary between the plasma layer and the no-flow zone moves along the direction of the plasma layer, thus creating a recirculation zone in the no-flow region. Our model predicted that platelets entering the recirculation zone would be exposed to lower levels of shear, and therefore would be less likely to aggregate as compared to the corners of the t-branch between bp 1 and channel 2, where platelets were predicted to experience the greatest acceleration in the change in shear (Fig. 5b and 5c). A decrease in flow rate was predicted to occur as the channel was occluded with a growing thrombus, resulting in partial flow redistribution to the other channels. The shear rate in the obstructed section of bp 1 was predicted to significantly increase due to the decrease in cross-sectional area. Our model predicted an increase in convection of thrombin into the recirculation zone as a function of obstructive thrombus formation as a combined result of the increased rate of thrombin generation at the site of thrombus formation, an increase in plasma recirculation and reduced elimination by convection (Fig. 5d).

Figure 5.

Prediction of the effect of the flow recirculation on platelet aggregation and fibrin formation. Computer simulation of the streamlines of the bulk blood flow through the network ladder predicts flow distortions at the intersection of the first bypass (bp 1; resulting in a zone of recirculation), at the stoppered channel (black bar), and at channel 2 (a). Simulation of blood cell transport during thrombus formation: <50% of bypass obstruction, left, and >50% bypass obstruction, right (b); shear rate profile (c) and thrombin convection profile mol/m³ (d) within these regions.

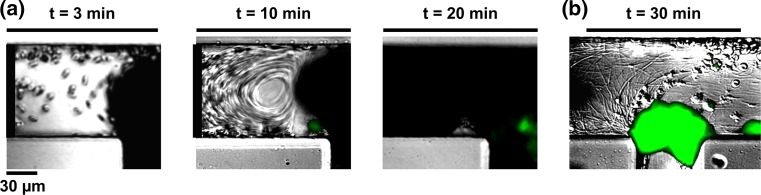
Effect of Flow Recirculation on Platelet Aggregation and Fibrin Formation

To examine the role of blood flow recirculation on platelet aggregation and fibrin formation, a second set of contralateral inlet and outlet channels was stoppered (inlet leading to channel 2 and outlet leaving channel 1), after equilibration of the microfluidic network with buffer and before addition of recalcified whole human blood; this introduced a blood flow recirculation zone immediately next to the first bypass (bp 1). Upon blood entry into the first bypass from channel 1, blood flow was diverted into channel 2 by the pull of a syringe pump connected to the outlet (Fig. 6a). Within minutes, we observed the transfer of blood cells from the blood bulk flow into the recirculation zone. A robust degree of fibrin formation was observed within the recirculation zone, while interestingly, we observed little platelet deposition or aggregation within the recirculation zone (Fig. 6b). Fibrin strands were formed in the direction of the predicted stream lines of blood flow within the recirculation zone

Figure 6.

Effect of flow recirculation on platelet aggregation and fibrin formation. Dynamics of whole human blood flow at the intersection where the first bypass meets a stoppered channel, creating a recirculation zone (black bar); platelet aggregation was recorded using differential interference contrast, DIC and fluorescence microscopy in real time (a) while fibrin was imaged following a washing step (b). Representative images shown, n = 3.

Discussion

Microfluidic devices have provided benefit in acting as a platform for understanding the mechanisms underlying the processes of occlusive thrombus formation within the vasculature and have potential for development as point-of-care therapeutic devices.3,19,47,64,67 Notably, development of microfluidic oxygenator units to promote gas exchange has been of significant interest in the field.17,31,42,57,62 Microfluidic networks may have utility in extracorporeal devices to trap bubbles and emboli as well as measure levels of reagents and toxins.25,26,29,36 However, the role of the microfluidic network geometry in the thrombogenicity of devices such as extracorporeal oxygenation machine (ECMO), left ventricular assist devices, and nanomembrane hemodialysis cassettes is not well defined.6,8,67 An integrated approach of studying blood flow and thrombus formation within microfluidic networks in the presence of coagulation may be useful in understanding how the physical biology of a microfluidic device promotes thrombus formation, which may help in the development of safer therapeutic device designs. Moreover, this approach may further help predict the risk of thrombus formation within physiological microvascular network geometries found in human organs, such as the spleen, placenta, kidney and brain.1,28,32

In this report, we have described a proof-of-principle integrated approach of studying blood flow and thrombus formation patterns in a multi-bypass microfluidic ladder network as summarized in Fig. 7. Incorporating computer simulation and experimental design, we were able to characterize the spatial and temporal distribution of platelet aggregation and fibrin formation as a function of the biorheological parameters of blood flow velocity and shear gradients and platelet and RBC distribution. We were able to determine how the initial conditions evolved as a function of sequential occlusive thrombus formation in bypasses within our ladder network. Our integrated approach utilized fundamental fluid dynamics principles to solve the effect of an evolving channel geometry due to the formation of an occlusive thrombus within the bypass geometry. Our approach can be used to develop generalizable predictions of sites of thrombus formation within microfluidic network geometries. Our findings suggest that the rate of thrombus formation is enhanced in zones of prolonged platelet residence times and rapid shear gradients, blood compositions favoring platelet enrichment, and sites with elevated thrombin concentrations.

Figure 7.

An integrated approach to study thrombus formation within a microfluidic network. Integrated approach of creating simulations of blood flow velocity, shear and blood cell distribution profiles to predict the site of thrombus formation. Modeling was repeated to account for the dynamical response of blood rheology and thrombin generation as a function of temporal thrombus formation.

Our microfluidic ladder network was comprised of T-junctions connecting two parallel main channels and bypasses with 90 degree angles. Sharp angle bends were previously shown to cause skewed velocity flow profiles, decreases in velocity at fixed pressure drops as well as flow separation and recirculation zones, particularly in high Reynolds number flow.18,33,63 Finite element simulations of a Newtonian fluid flow at different angle bifurcations have shown that for a fixed pressure drop, the variation of the bifurcation angle from 60 to 120 degrees resulted in an average velocity reduction of 1–4% compared to a channel with no bend., with laminar flow being maintained at a low Reynolds number.63 Moreover, flow simulations of non-Newtonian power-law fluids encountering a 90° bifurcation have shown that recirculation zones and flow separations should not form when the Reynolds number is below 5.30 In our setup we perfused whole blood, simulated as a power law fluid with index n ≤ 1, through a microfluidic network with Reynolds numbers below 1, and observed no turbulence in the flow field imparted by the sharp angle (Supplemental Video 1). However, we did note asymmetry in the velocity profile that could potentially influence thrombi formation. Our future work will look to incorporate quantitative methods to record blood cell flow in real time in order to validate the predicted flow profiles through the network geometry.

This report focused on thrombus formation patterns within the Stokes flow regime (Reynolds number; Re ≪ 1) and simplification of classifying blood cells as particles with constant diameters. Future work will focus on improving our model to predict the dynamics of thrombus formation in larger channels, with larger Reynolds numbers, which would need to take into account contributions from inertial flows and recirculation zones at sharp angles.30 Furthermore, in certain vessel geometries, inherent blood cell shape and deformability would be expected to play an important role.13,14,59 Another limitation of our model was the assumption that thrombin remained active in the bloodstream and that mass transfer via convection from upstream thrombi within the network contributed to the downstream flux of thrombin within subsequent bypasses. Thrombin is known to be rapidly inactivated by plasma inhibitors such as antithrombin III and heparin cofactor II9,37,58; on the other hand, thrombin catalyzes its own feedback generation through activation of the coagulation factor XI. Our future work will focus on incorporating the kinetic parameters of thrombin generation and inactivation into our model of thrombin formation and downstream propagation within a ladder network. Our goal is to integrate this approach to predict the prothrombotic phenotype of specific vascular beds, such as encountered in the brain and lung, as well as extending our models to study the flow patterns within extravascular devices, such as ECMO.

Geometric factors of a bypass significantly influence thrombus formation, notably in complex configurations found in artificial flow networks. Extravascular therapeutic devices such as ECMO are used to pump and oxygenate a patient’s blood during heart or lung surgery/failure. In veno-arterial ECMO, blood is oxygenated while it travels from a femoral vein into an artificial membrane lung consisting of a branched network of thousands of small tubes before returning to the circulation via a femoral artery.40 The blood flow within network is affected by changes in dimension, disturbances in the tubing such as stagnation points and stenoses, branching channels, and curved geometries. Our model and experimental data identify stagnation points and large shear gradients as regions of increased thrombogenicity. Along these lines, large expansions or contractions associated with rapid flow acceleration and deceleration have been shown to influence platelet aggregation both in vitro and in vivo.43,60 Moreover, curved channels have been shown to cause velocity profile shifts resulting in secondary flow and exhibit increased potential as sites of thrombus formation.11,44 Current ECMO designs require a systemic anticoagulant such as heparin to maintain patency, putting the patient at risk for serious bleeding complications. A better understanding of the thrombogenic profile of devices that contain ladder networks may help in optimizing geometric designs to decrease thrombin generation, thus lowering the risk of device failure due to occlusive thrombus formation.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Abbreviations

PDMS

Polydimethylsiloxane

RBCs

Red blood cells

TF

Tissue factor

VWF

Von Willebrand factor

DiOC₆

3,3′-Dihexyloxacarbocyanine iodide