An analytical study of photoacoustic and thermoacoustic generation efficiency towards contrast agent and film design optimization

Abstract

Photoacoustic (PA) and thermoacoustic (TA) effects have been explored in many applications, such as bio-imaging, laser-induced ultrasound generator, and sensitive electromagnetic (EM) wave film sensor. In this paper, we propose a compact analytical PA/TA generation model to incorporate EM, thermal and mechanical parameters, etc. From the derived analytical model, both intuitive predictions and quantitative simulations are performed. It shows that beyond the EM absorption improvement, there are many other physical parameters that deserve careful consideration when designing contrast agents or film composites, followed by simulation study. Lastly, several sets of experimental results are presented to prove the feasibility of the proposed analytical model. Overall, the proposed compact model could work as a clear guidance and predication for improved PA/TA contrast agents and film generator/sensor designs in the domain area.

1. Introduction

Laser-induced photoacoustic (PA) effect, or more generally thermoacoustic (TA) effect induced by other spectra of electromagnetic (EM) wave, refers to the acoustic generation by EM absorption, heating and thermoelastic expansion [1]. In recent years, PA/TA effect has been intensively studied in various biomedical imaging embodies, such as microscopy, tomography, and endoscopy [2], [3], [4], [5], [6], [7], [8]. Although the intrinsic contrast of biological tissues is quite rich within the EM absorption spectrum, the PA/TA signal strength coming from the EM absorption is usually quite weak, which is due to the constrained EM exposure limit (e.g. ANSI standard for light), and extremely low energy conversion efficiency of thermoelastic effect (e.g. 10⁻⁸) [1]. To further improve the detection sensitivity and imaging depth, many contrast agents have been designed to achieve improved EM absorption, including various kinds of dyes, nanoparticles and carbon nanotubes (CNT) [9], [10], [11], [12], [13], [14], [15], [16], [17]. Almost all of the exogenous contrast agents were engineered to increase the EM absorption rate at specific wavelengths, so that the induced PA/TA signal is strengthened effectively. However, as we know, although EM absorption rate is a key parameter related with PA/TA generation, it is not the only important parameter, because PA/TA generation involves multiple physical processes including absorption, heating, thermoelastic expansion and mechanical vibration. A few recent pieces of work showed that by coating the highly absorbing nanoparticles with a dedicated shell or aggregating the nanoparticles for better thermal confinement, PA signals could be amplified effectively with improved light-sound conversion efficiency [18], [19], [20]. On the other hand, some recent demonstrations of PA/TA thin films have been reported for strong acoustic generation and sensitive EM detection by combining both strong EM absorption and thermoelastic expansion [21], [22], [23], [24]. Although a lot of previous work on PA/TA physics and modelling has been reported in the literature achieving both high accuracy in complex scenarios [25], [26], [27], [28], [29], [30], there is few study about how to utilize the PA/TA physics to guide practical engineering applications, such as the contrast agent and film design mentioned above.

Regarding the EM excitation mode, existing analytical analysis of PA/TA effect is usually based on the assumption that short pulse illumination could be treated as an impulse input, so that satisfying thermal and stress confinements, PA/TA signal is linearly proportional to several coefficients like absorption rate and Gruneisen coefficient [6]. However, in many cases such as microsecond-pulse or continuous-wave (CW) modulated PA/TA effect [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], the EM illumination cannot be simply treated as impulse input due to the unsatisfied thermal and stress confinements. Lastly, treating the contrast agents or film as a damped mechanical oscillator [35], [36], [41], the selectivity and signal strength will be further improved by matching its mechanical resonance frequency with EM modulation frequency. It provides PA/TA resonance spectroscopy going beyond its EM absorption spectroscopy.

In this paper, a 1D compact model by incorporating above mentioned issues, including various thermal and mechanical parameters, modulation frequency, and resonance effect. The proposed model could be used as a guideline for designing optimized contrast agents for PA/TA imaging beyond the pure EM absorption improvement in existing literatures, as well as further improvement of PA/TA generator/sensor film design. The model is verified through simulation and comparison with reported experimental results. Some predictive discussions are also included to trigger improved design in the future work.

2. Analytical analysis

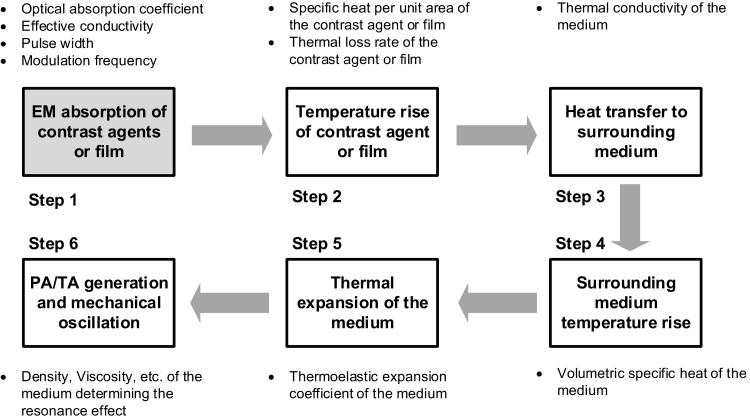
Before starting the derivation of the analytical model, an intuitive illustration is necessary to better understand the whole process of PA/TA generation. As shown in Fig. 1, the PA/TA generation from the contrast agent or film generally involves six steps.

• •EM absorption of the contrast agent or film (related with optical absorption coefficient for light; effective conductivity for microwave; pulse width for pulse source; modulation frequency for CW source).
• •Temperature rise of the contrast agent or film (related with specific heat per unit area of the contrast agent or film; thermal loss rate of the contrast agent or film).
• •Heat transfer to the surrounding medium (related with the thermal conductivity of the medium), where the medium is normally biological tissue, water, or PDMS.
• •Surrounding medium temperature rise (related with volumetric specific heat of the medium).
• •Thermal expansion of the medium (related with thermoelastic expansion coefficient of the medium).
• •PA/TA generation and mechanical oscillation (related with the density, acoustic velocity, viscosity of the medium, etc.)

Fig. 1.

The intuitive illustration of the PA/TA generation process of contrast agent or film through EM absorption.

As mentioned in the introduction session, the EM absorption (optical absorption coefficient, effective conductivity) of the contrast agent or film in the highlighted box is the major parameter in the conventional design. However, the design consideration of the pulse width, modulation frequency, and other parameters in another five steps has not been systematically studied up to now. The detailed derivation of the analytical model is provided below. Simulation and measurement results based on this model will be presented in the following sections.

2.1. Step 1 EM absorption

The analytical modelling of optical and microwave absorption has been well documented in the literature [6]. To complete the overall analysis, we revisit the optical and microwave absorption equations here:

$$H\left(t\right)=\{\begin{array}{c}\hfill {\mu }_a\Phi \left(t\right)\hfill \\ \hfill \sigma \langle E^2\left(t\right)\rangle \hfill \end{array},$$ (1)

where $H\left(t\right)$ is the heating function caused by EM absorption. The two terms on the right side of Eq. (1) represent the optical absorption and microwave absorption respectively, where μ_a and $\Phi \left(t\right)$ are the optical absorption coefficient and optical fluence rate, σ and E are the effective conductivity and electrical field strength. $\langle \mathrm{...}\rangle$ represents short-time averaging.

2.2. Steps 2–5: thermoelastic conversion

EM illumination from the light ($\Phi \left(t\right)$) or microwave source ($E\left(t\right)$) could be in pulse or intensity modulated mode. Although different EM modulation pattern is achievable, here we assume that the single-tone sinusoidal modulation is used for the heating source $H\left(t\right)$. Based on Fourier series theory, any modulation pattern could be treated as summation of single-tone sinusoidal modulations with different frequencies. For example, the conventional pulse mode light or microwave illumination could be treated as overlapping of multiple sinusoidal modulations, where the pulse width in pulsed mode is related with dominant frequency of multiple sinusoidal modulations (e.g. shorter pulse width is related with higher dominant frequency). Therefore, utilizing single-tone sinusoidal modulation is a good simplification for all the arbitrary EM modulation patterns without losing generality.

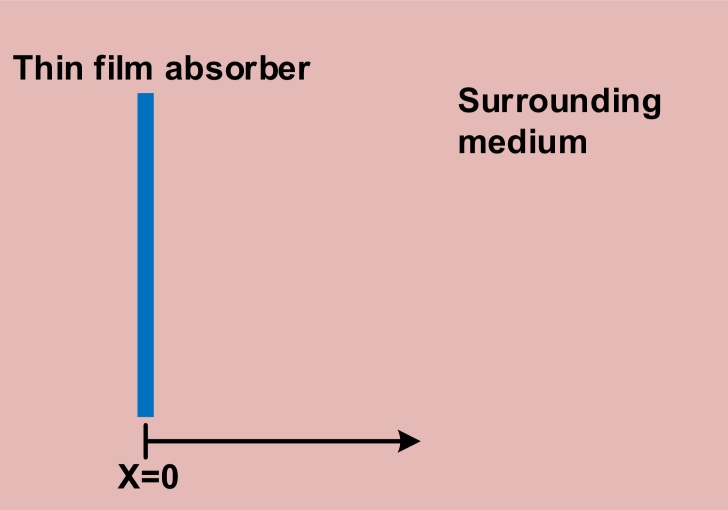
There is no doubt that a thin film model is suitable for the PA/TA generator/sensor film design [42]. For contrast agent, due to the size and shape difference of various kinds of dyes, nanoparticles, carbon nanotubes, etc., it is also good to simplify the contrast agent as a film on a sufficiently small scale, which is based on the fact that the temperature rising, heating transfer to surrounding medium, and thermoelastic vibration happen around the interface between contrast agents and the medium, as shown in Fig. 2.

Fig. 2.

The simplified model for the PA/TA generation from contrast agents and thin film.

The fundamental energy conservation equation of thin film heated by the heating function $H\left(t\right)={\displaystyle \hat{H}}\cos \left(\omega t+\phi \right)$ from EM absorption is [42]:

$$H\left(t\right)=a{\beta }_0{T}_f+a{Q}_0+a{c}_s\frac{d{T}_f}{dt},$$ (2)

where the first term refers to the heat loss of the film (a is the area of the film; β₀ is the heat loss rate of the thin film related with conduction, convection and radiation; T_f is the temperature of the film), the second term refers to the heat transferred from the film to the surrounding medium Q₀, and the last term refers to the heat consumed for temperature rise of the film (c_s is the heat capacity per unit area of the film). The related parameters are all listed in Table 1.

Table 1.

Physical parameters and their description.

Symbol	Unit	Description
$$H\left(t\right)$$	W/m2	Input heating function from the absorption of EM energy
$${\displaystyle \hat{H}}$$	W	Power absorption magnitude
$$a$$	m2	Area of the thin film
$${\beta }_0$$	W/(m2 K)	Rate of heat loss per unit area of the film due to conduction, convection, and radiation
$$T_f$$	K	Temperature of the thin film above its surrounding medium
$${{\displaystyle \hat{T}}}_f$$	K	Temperature wave magnitude
$$Q_0$$	W/m2	Heat flow per unit area to the surrounding medium
$$c_s$$	J/(m2 K)	Heat capacity per unit area of thin film
$$T$$	K	Temperature of surrounding medium
$$\alpha$$	m2/s	Thermal diffusivity of the medium
$$\kappa$$	W/(m K)	Thermal conductivity of the medium
$$\beta$$	K−1	Thermal expansion coefficient
$$v$$	m/s	Particle velocity of the medium
$$\psi$$	m2/s	Velocity potential
$$x$$	m	Distance between the source and detector
$${\rho }_0$$	kg/m3	Density of the medium
$$c_p$$	J/(m3 K)	Volumetric heat capacity of the medium
$$v_s$$	m/s	Acoustic velocity of the medium
$$\eta ,\xi$$	cP	Viscosity of the medium
$$d_t$$	m	Thickness of the film

The fundamental equation of the heat conduction from film to the surrounding medium is [42]:

$$\frac{\partial T}{\partial t}-\alpha \frac{{\partial }^{2}T}{\partial x^2}=0,$$ (3)

where T is the temperature of the surrounding film, α is the thermal diffusivity of the medium. Due to the single-tone modulation of the EM illumination, the thin film temperature wave solution of Eq. (2) has the form of:

$$T_f\left(t\right)={{\displaystyle \hat{T}}}_f\cos (\omega t+\phi )\mathrm{.}$$ (4)

Then the medium temperature wave solution of Eq. (3) has the form of:

$$T\left(x,t\right)={{\displaystyle \hat{T}}}_f{e}^{-kx}\cos (\omega t-kx+\phi ),$$ (5)

where $k=\sqrt{\omega /\alpha }$.

The heat flow per unit area from the film to the surrounding medium could be expressed as:

$$Q_0=-\kappa {\frac{\partial T\left(x,t\right)}{\partial x}|}_{x=0}=-\kappa k{{\displaystyle \hat{T}}}_f\left[\sin \left(\omega t+\phi \right)-\cos \left(\omega t+\phi \right)\right],$$ (6)

where κ is the thermal conductivity of the surrounding medium. Substitute Eq. (4) and Eq. (6) to Eq. (2), we have:

$$\begin{array}{l}H\left(t\right)=a{\beta }_0{{\displaystyle \hat{T}}}_f\cos (\omega t+\phi )-a\kappa k{{\displaystyle \hat{T}}}_f\left[\sin \left(\omega t+\phi \right)-\cos \left(\omega t+\phi \right)\right]\\ -a{c}_s\omega {{\displaystyle \hat{T}}}_f\sin (\omega t+\phi )\\ =a{{\displaystyle \hat{T}}}_f\left[\left({\beta }_0+\kappa k\right)\cos (\omega t+\phi )-\left(c_s\omega +\kappa k\right)\sin \left(\omega t+\phi \right)\right].\end{array}$$ (7)

From Eq. (7), we have

$${\displaystyle \hat{H}}=a{{\displaystyle \hat{T}}}_f\sqrt{{\left({\beta }_0+\kappa k\right)}^2+{\left(c_s\omega +\kappa k\right)}^2}\mathrm{.}$$ (8)

Then we can have the temperature wave magnitude:

$${{\displaystyle \hat{T}}}_f=\frac{{\displaystyle \hat{H}}}{a\sqrt{{\left({\beta }_0+\kappa k\right)}^2+{\left(c_s\omega +\kappa k\right)}^2}}\mathrm{.}$$ (9)

The temperature variation and volume expansion within one wavelength region of the temperature wave (${\lambda }_T=2\pi /k=2\pi \sqrt{\alpha }/\sqrt{\omega }$) have the follow relation:

$$\beta \frac{T_f\left(t\right)}{{\displaystyle \overline{T}}}=\frac{\Delta V}{V}=\frac{\Delta {\lambda }_T}{{\lambda }_T},$$ (10)

where β is the thermal expansion coefficient of the medium. Substitute Eq. (4) into Eq. (10), then we have:

$$\Delta {\lambda }_T={\lambda }_T\beta \frac{T_f\left(t\right)}{{\displaystyle \overline{T}}}=\frac{2\pi \sqrt{\alpha }\beta }{T_c\sqrt{\omega }}{{\displaystyle \hat{T}}}_f\cos \left(\omega t+\phi \right)\text{.}$$ (11)

Then we have the particle velocity:

$$v=\frac{\Delta \lambda }{\Delta t}=-{\lambda }_T\beta \frac{T_f\left(t\right)}{{\displaystyle \overline{T}}}=-\frac{2\pi \sqrt{\alpha }\omega \beta }{T_c\sqrt{\omega }}{{\displaystyle \hat{T}}}_f\sin \left(\omega t+\phi \right)\text{.}$$ (12)

Then the velocity potential is:

$$\psi =-\frac{2a}{4\pi r}\left|v_{\max }\right|\sin \left(\omega t-\frac{2\pi x}{\lambda }\right)\text{.}$$ (13)

where x is the 1D position along its propagation direction X shown in Fig. 2.

Based on Eq. (9) and Eq. (13), then the pressure wave is:

$$\begin{array}{l}p=-{\rho }_0\frac{\partial \psi }{\partial t}=\frac{{\rho }_{0}a\omega }{2\pi x}\left|v_{\max }\right|\cos \left(\omega t-\frac{2\pi x}{\lambda }\right)\\ =\frac{{\rho }_{0}a\omega }{2\pi x}\frac{2\pi \sqrt{\alpha }\omega \beta }{T_c\sqrt{\omega }}{{\displaystyle \hat{T}}}_f\cos \left(\omega t-\frac{2\pi x}{\lambda }\right)\\ =\frac{{\rho }_{0}a\omega }{2\pi x}\frac{2\pi \sqrt{\alpha }\omega \beta }{T_c\sqrt{\omega }}\frac{{\displaystyle \hat{H}}}{a\sqrt{{\left({\beta }_0+\kappa k\right)}^2+{\left(c_s\omega +\kappa k\right)}^2}}\cos \left(\omega t-\frac{2\pi x}{\lambda }\right).\end{array}$$ (14)

As the thermal diffusivity α and $k=\sqrt{\omega /\alpha }$ are intermediate parameters, we have the below relationships:

$$\alpha =\frac{\kappa }{c_p},\kappa k=\kappa \sqrt{\frac{\omega }{\alpha }}=\sqrt{\omega c_p\kappa }\text{.}$$ (15)

Substitute Eq. (15) into Eq. (14), and with some mathematical derivation, we can have the initial pressure amplitude:

$$p_0=\left|p\right|=\frac{1}{x}{\displaystyle \hat{H}}\frac{{\rho }_0\beta \sqrt{\omega }}{{\displaystyle \overline{T}}}\frac{\omega }{\sqrt{c_p\left[2\omega c_p+\left(2{\beta }_0+2\omega c_s\right)\sqrt{\frac{\omega c_p}{\kappa }}+\frac{{\beta }_0^2+{\omega }^2{c}_s^2}{\kappa }\right]}}\text{.}$$ (16)

Up to now, the initial PA/TA pressure has been modelled with ‘thermal confinement term’:

$$thermalconfinementterm=\frac{\omega }{\sqrt{c_p\left[2\omega c_p+\left(2{\beta }_0+2\omega c_s\right)\sqrt{\frac{\omega c_p}{\kappa }}+\frac{{\beta }_0^2+{\omega }^2{c}_s^2}{\kappa }\right]}}\text{.}$$ (17)

The thermal confinement term increases with frequency and converges to $\frac{1}{c_s}\sqrt{\frac{\kappa }{c_p}}$ at sufficiently high frequency (equivalent to ultrashort delta pulse illumination).

In the literature, the PA/TA pressure under finite-duration excitation pulse is derived as the convolution between impulse response by delta pulse excitation and time-domain profile of excitation pulses [29], which however cannot give an intuitive insight of the stress confinement. To complete the simple and compact analytical model, we hypothesize that the influence of stress confinement could be simply modelled in forms of a high-pass filter, covering delta-function excitation (ω → ∞) to long-pulse function excitation (ω → 0) with reasonable accuracy:

$$stressconfinementterm=\frac{\sqrt{\omega }}{\sqrt{\omega +\frac{v_s}{d_t}}}\text{.}$$ (18)

where v_s is the acoustic velocity of the surrounding medium, d_t is the thickness of the film. By incorporating Eq. (18) into Eq. (16), we have the complete initial PA/TA pressure expression:

$$p_0=\left|p\right|=\frac{1}{x}{\displaystyle \hat{H}}\frac{{\rho }_0\beta }{{\displaystyle \overline{T}}}\frac{\omega }{\sqrt{c_p\left[2\omega c_p+\left(2{\beta }_0+2\omega c_s\right)\sqrt{\frac{\omega c_p}{\kappa }}+\frac{{\beta }_0^2+{\omega }^2{c}_s^2}{\kappa }\right]}}\frac{\sqrt{\omega }}{\sqrt{\omega +\frac{v_s}{d_t}}}\text{.}$$ (19)

When both thermal and stress confinements are satisfied at sufficiently high frequency (e.g. ultrashort pulse illumination), the initial PA/TA pressure could be simplified as:

$$p_{0i}=\left|p\right|=\frac{1}{x}{\displaystyle \hat{H}}\frac{{\rho }_0\beta }{{\displaystyle \overline{T}}}\frac{1}{c_s}\sqrt{\frac{\kappa }{c_p}}\text{.}$$ (20)

2.3. Step 6: damped mechanical resonance

Although Eq. (19) has given an analytical expression about the relationship between PA/TA initial amplitude with various EM, thermal, mechanical parameters and modulation frequency, it is still not sufficient enough to explain its frequency domain response. When assuming impulse EM illumination (infinitely short pulse), we cannot observe the theoretically infinitely short PA/TA signal. On the contrary, we normally observe a PA/TA pulse with certain central frequency at MHz range and finite bandwidth, even after calibrating the bandwidth limitation of ultrasound transducer and acoustic attenuation. It shows that the theoretically infinitely short PA/TA signal undergoes a bandpass filtering when vibrating the medium, which could be well explained by the combined effect of PA/TA elastic resonance effect [35] and bandpass shaping of the PA/TA signal. Although this damped oscillation may induce some error in calculating sound attenuation in liquids, it is a straightforward and intuitive way to model this effect, and more helpful in the guidance of the engineered design of contrast agents and film.

2.3.1. Frequency domain analysis

With initial PA/TA pressure as the single-tone sinusoidal driving source, the medium vibration $p_v\left(t\right)$ will follow a second-order differential pressure equation driven by the PA/TA initial pressure [35]:

$$\frac{{\partial }^2}{\partial t^2}{p}_v\left(t\right)+k_0^2\frac{\xi +\frac{4}{3}\eta }{{\rho }_0}\frac{\partial }{\partial t}{p}_v\left(t\right)+k_0^2{v}_s^2=p_0\cos \left(\omega t-\frac{2\pi x}{\lambda }\right)\text{,}$$ (21)

where $k_0=2\pi /d_t$ is the propagation constant of the absorber, η and ξ are the shear viscosity and bulk viscosity of the vibrating medium. This second-order differential equation could be modelled as a harmonic oscillator, with central frequency ω_c:

$${\omega }_c=\sqrt{\frac{4{\pi }^2}{d_t^2}{v}_s^2-\frac{1}{2}{\left(\frac{4{\pi }^2}{d_t^2}\frac{\xi +\frac{4}{3}\eta }{{\rho }_0}\right)}^2}\text{.}$$ (22)

The quality factor Q_c is:

$$Q_c=\sqrt{\frac{{\rho }_0^2{v}_s^2}{\frac{4{\pi }^2}{d_t^2}{\left(\xi +\frac{4}{3}\eta \right)}^2}-\frac{1}{2}}\text{.}$$ (23)

Moreover, by incorporating the PA/TA initial pressure Eq. (19) with the bandpass filtering effect, the final PA/TA vibrating pressure could be expressed as:

$$\begin{array}{l}{p}_{0s}=p_0\times \frac{1}{\sqrt{{\left(k_0^2{v}_s^2-{\omega }^2\right)}^2+{\left(k_0^2\frac{\xi +\frac{4}{3}\eta }{{\rho }_0}\omega \right)}^2}}\\ =\frac{1}{x}{\displaystyle \hat{H}}\frac{{\rho }_0\beta }{{\displaystyle \overline{T}}}\frac{\omega }{\sqrt{c_p\left[2\omega c_p+\left(2{\beta }_0+2\omega c_s\right)\sqrt{\frac{\omega c_p}{\kappa }}+\frac{{\beta }_0^2+{\omega }^2{c}_s^2}{\kappa }\right]}}\frac{\sqrt{\omega }}{\sqrt{\omega +\frac{v_s}{d_t}}}\\ \times \frac{1}{\sqrt{{\left(\frac{4{\pi }^2}{d_t^2}{v}_s^2-{\omega }^2\right)}^2+{\left(\frac{4{\pi }^2}{d_t^2}\frac{\xi +\frac{4}{3}\eta }{{\rho }_0}\omega \right)}^2}}.\end{array}$$ (24)

2.3.2. Time domain analysis

By treating the initial PA/TA pressure as the response from an impulse driven source, the time-domain expression derived from Eq. (20) and Eq. (21) is [41]:

$$p_v\left(t\right)=\left(\frac{1}{x}{\displaystyle \hat{H}}\frac{{\rho }_0\beta }{{\displaystyle \overline{T}}}\frac{1}{c_s}\sqrt{\frac{\kappa }{c_p}}\right)e^{-\frac{2{\pi }^2}{d_t^2}\frac{\left(\xi +\frac{4}{3}\eta \right)}{{\rho }_0}t}\cos \left(\sqrt{\frac{4{\pi }^2}{d_t^2}{v}_s^2-\frac{1}{2}{\left(\frac{4{\pi }^2}{d_t^2}\frac{\xi +\frac{4}{3}\eta }{{\rho }_0}\right)}^2}t-\frac{\pi }{2}\right)\otimes H_T\left(t\right)\text{,}$$ (25)

where $H_T\left(t\right)$ is the time-domain impulse response of the ultrasound transducer. It is seen that the PA/TA vibration could be treated as a sinusoidal signal with its amplitude attenuated exponentially over time, which matched well with the measured PA/TA signal profile in the literatures.

3. Simulation results

3.1. Intuitive analysis

Before performing simulation study, it is important to draw some intuitive conclusions from the analytical expressions from Eq. (24) of single-tone modulation source and Eq. (25) of impulse illumination source. To generate strong PA/TA signals from the contrast agent or film generator/sensor, here are some key parameters that should be carefully considered:

• •EM absorption of the contrast agents or film: This is the most straightforward approach to improve the initial PA/TA pressure by increasing the absorption rate, e.g. optical absorption coefficient for light source, or effective conductivity for microwave, even imaginary permeability for magnetic illumination. Majority of the previous work in contrast agents and thin film design are focused on EM absorption improvement [43], [44].
• •Thermal expansion coefficient of the surrounding medium: The thermal expansion coefficient determines how much displacement could be generated from specific temperature rise. Therefore, it is closely related with the PA/TA generation efficiency from EM absorption to thermoelastic vibration. Some recent work on film design has optimized the thermal expansion coefficient using polydimethylsilane (PDMS) [23], [24].
• •Thermal conductivity of the surrounding medium: From Fig. 1, we could observe that the heat from the EM absorption in the film is transferred to the surrounding medium followed by thermoelastic expansion (Steps 2–3). Therefore, the large thermal conductivity of the surrounding medium is crucial to the effective heat transfer from the film to the surrounding medium.
• •Rate of heat loss per unit area of the film: As we prefer more heat energy is transferred from the film to the surrounding medium, the other heat loss of the film is better to be avoided. So that the heating loss of the film due to conduction, convection, and radiation, is preferred to be as small as possible.
• •Heat capacity per unit area of the thin film: From thermodynamics, we know that the heat transfer rate from film to the surrounding medium is positively related with the temperature difference between them. So that under same EM energy absorption, a smaller heat capacity could lead to a larger the temperature rise of the film to increase the temperature difference and heat transfer efficiency. To achieve this, CNT has been selected in the previous literature for enhanced PA/TA generation [24].
• •Volumetric heat capacity of the surrounding medium: Similar with the above parameter, a smaller volumetric heat capacity of the surrounding medium could give a higher temperature rise with same heat energy transferred to the medium. Therefore, the larger temperature rise in the medium will lead to stronger PA/TA pressure generation.
• •Viscosity of the medium: From Eq. (25), the viscosity of the medium determines the exponential decay term, where higher viscosity will render weaker PA/TA generation. Therefore, a smaller viscosity is usually preferred for efficient PA/TA generation. In addition, from Eq. (23), a higher viscosity will result in smaller quality factor of the vibration medium, which could limit its resonance amplitude with single-tone modulation source [35].
• •Modulation frequency for single-tone modulation Source: From Eq. (24), there should be an optimum modulation frequency to maximize PA/TA signal. The underlying reason is that although higher modulation frequency will achieve larger initial PA/TA pressure due to better thermal and stress confinement, it will finally converge to a constant. On the other hand, the bandpass filtering effect will hinder the high-frequency component of the PA/TA pressure. Therefore, an optimum frequency exists compromising the thermal/stress confinement and the bandpass limitation.

• •Pulse width for pulse modulation Source: From Eqs. (19)-(20), for pulse mode illumination, the PA/TA signal will increase and converge to a constant with shorter pulse width due to the thermal and stress confinements. Unlike single-tone modulation, the ultrashort pulse could be treated as an impulse illumination, which can excite the impulse response of the vibrating medium. Some published data has proved the prediction experimentally [23], [45].

A summary of the design guideline is listed in Table 2, where ‘+’ indicates that the larger value is preferred. On the contrary, ‘−’ indicates that the smaller value is preferred for stronger PA/TA signal generation.

Table 2.

Optimization design guideline (‘+’: larger preferred; ‘−’: smaller preferred).

Symbol	Description	Optimization design
$${\displaystyle \hat{H}}$$	Power absorption magnitude	+
$$\beta$$	Thermal expansion coefficient	+
$$\kappa$$	Thermal conductivity of the medium	+
$${\beta }_0$$	Rate of heat loss per unit area of the film	–
$$c_s$$	Heat capacity per unit area of thin film	–
$$c_p$$	Volumetric heat capacity of the medium	–
$$\eta ,\xi$$	Viscosity of the medium	–
$${\tau }_p$$	Laser pulse width	–
$$\omega$$	Modulation frequency	depends

3.2. Quantitative analysis

For quantitative analysis, real value for the various parameters in Eqs. (24) and (25) are needed. Because CNT is one of the most popular materials for contrast agent and thin film, and water is the dominant component of biological tissue, here we utilize the physical parameters of CNT and water as the default value for the quantitative simulation.

• •EM absorption rate and thermal expansion coefficient: From Eq. (19)–(20), it is clearly shown that both EM energy absorption ${\displaystyle \hat{H}}$ and thermal expansion coefficient β are linearly proportional to the PA/TA signal amplitude. So there is no need to simulate this case as it is obviously predicted.
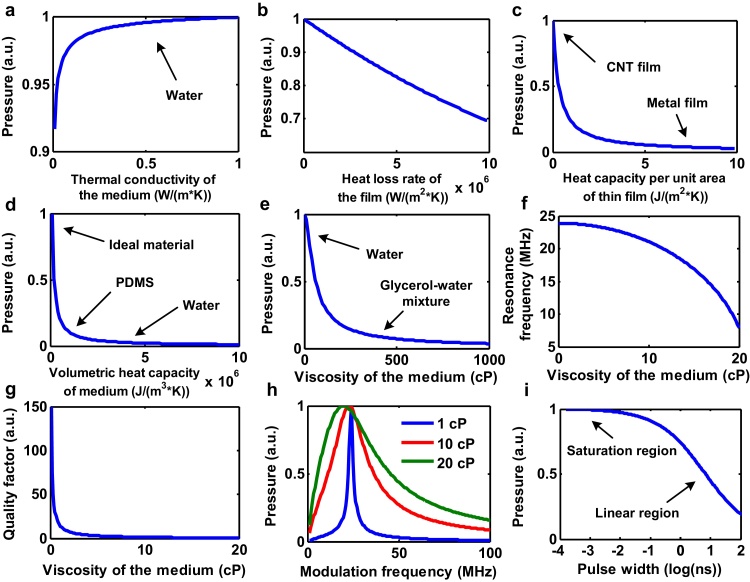
• •Thermal conductivity of the medium: As predicted in the above intuitive analysis, larger thermal conductivity is usually preferred for maximized PA/TA generation. In the simulation, the conductivity of the medium is swept from 0.01 to 1 W/(m K) by keeping other parameters constant in Table 3. The result is shown in Fig. 3a, where the normalized PA/TA pressure is increasing and converging to a constant with increasing thermal conductivity. Water with thermal conductivity of 0.6 W/(m K) is quite close to the maximum pressure, which indicates that water has a good enough thermal conductivity for efficient PA/TA generation.
• •Rate of heat loss per unit area of the thin film: From the prediction above, a smaller heat loss of the thin film (better thermal confinement) is preferred for maximized PA/TA generation, which is clearly demonstrated in Fig. 3b.
• •Heat capacity per unit area of the thin film: From the previous prediction, a smaller heat capacity per unit area of the thin film is preferred to maximize generated PA/TA pressure due to enhanced temperature rise and heat transfer. The simulation result shown in Fig. 3c proves the prediction, where the PA/TA generation efficiency is nonlinearly increasing with decreasing heat capacity. In addition, the data of CNT film and metal film is also annotated in the figure, showing that even though they have similar conductivity and microwave absorption, CNT film is able to generate stronger TA pressure than metal film. This has been experimentally demonstrated in [42], where an efficient TA loudspeaker is constructed.
• •Volumetric heat capacity of the surrounding medium: Similar with the above parameter, the volumetric heat capacity of the surrounding medium is also key important for efficient PA/TA generation. As shown in Fig. 3d, a smaller heat capacity could render a larger PA/TA pressure. PDMS exhibits a higher PA/TA generation efficiency partially due to its smaller heat capacity of 1.409e⁶ J/(m³ K) than water of 4.179e⁶ J/(m³ K), which is demonstrated in previous literatures [23], [24]. Furthermore, ideal material with even smaller volumetric heat capacity is highly expected to maximize the efficiency, which is annotated in Fig. 3d.
• •Viscosity of the medium: From Eq. (24), the higher viscosity will induce more severe acoustic absorption, rendering a reduced PA signal pressure. The simulation result in Fig. 3e shows the PA/TA generation efficiency versus the viscosity ranging from 0 to 20 cP. Here, water is an ideal medium due to its ultralow viscosity, while the glycerol-water mixture increases the viscosity and degrades the efficiency. Some published results have proved this phenomenon [46]. Furthermore, from Eqs. (22) and (23), the resonance frequency and quality factor of the vibrators are also related with viscosity, and the simulation results are shown in Fig. 3f and g. As expected, higher viscosity induces stronger acoustic attenuation, especially for high frequency components, which results in smaller resonance frequency and quality factor. Some preliminary results in [35], [41] have shown its feasibility for tissue characterization.
• •Modulation frequency for single-tone modulation source: As predicted, under single-tone modulation source, the PA/TA pressure will exhibit a resonance spectrum due to the bandpass filtering effect, which is clearly shown in the simulation results in Fig. 3h. With three different medium viscosity values, these spectrums demonstrate shifted central frequency and reduced quality factor, which are predicted in previous discussion. Interestingly, the spectrum is asymmetric with elevated band at higher frequency. This is caused by the thermal and stress confinement term in Eq. (24), which is better satisfied when the modulation frequency is higher. This simulation results have a good match with the published results in literature [35].
• •Pulse width for pulse modulation source: Increase of frequency is equivalent to decrease of pulse width. According to Eq. (19) for pulse-mode modulation source, PA/TA pressure will increase with increasing frequency (reducing pulse width) when the single pulse energy is kept the same, and finally converge to a constant when thermal and stress confinements are fully met. From the simulation result in Fig. 3i, basically there are two regions (linear region and saturation region) under different pulse width. Shortening the pulse width in the linear region could significantly enhance the PA/TA generation efficiency, which has been demonstrated in [39]. On the other hand, when the pulse width is short enough to satisfy the thermal and stress confinements, the PA/TA pressure remains constant under the ideal impulse illumination, which is experimentally demonstrated in the Supplementary material of ref [23].

Table 3.

The physical parameters of CNT film and water medium.

Symbol	Unit	CNT/Water	Symbol	Unit	CNT/Water
$$\beta$$	K−1	210e−6	$$c_p$$	J/(m3 K)	4.179e6
$$\kappa$$	W/(m K)	0.6	$$\eta ,\xi$$	cP	0.89
$${\beta }_0$$	W/(m2 K)	28.9	$${\tau }_p$$	ns	100
$${\rho }_0$$	kg/m3	1000	$$\omega$$	MHz	10
$$c_s$$	J/(m2 K)	5e−3	$$d_t$$	μm	50

Fig. 3.

Simulation results of (a) pressure versus thermal conductivity of medium, (b) pressure versus heat loss rate of the film, (c) pressure versus heat capacity per unit area of the thin film, (d) pressure versus volumetric heat capacity of the medium, (e) pressure versus viscosity of the medium, (f,g) resonance frequency and quality factor versus viscosity of the medium, (h) pressure versus modulation frequency under different medium viscosity, (i) pressure versus laser pulse width.

3.3. Frequency-dependent analysis

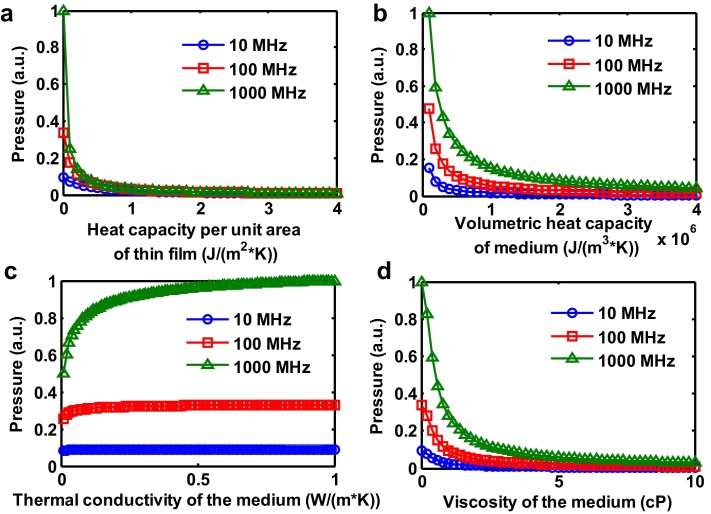
Previous simulations are conducted by assuming a fixed modulation frequency (10 MHz) or pulse width. In this part, frequency-dependent simulations are performed under three different modulation frequencies: 10 MHz, 100 MHz, and 1000 MHz (Fig. 4). There is no surprise that no matter what modulation frequency is chosen, the trend of PA/TA pressure is same versus the four physical parameters (heat capacity of thin film and medium, thermal conductivity of the medium, and viscosity of the medium). However, at higher modulation frequency (or shorter pulse width), the significance of these physical parameters is obviously enhanced (green line with triangle symbol) than that at lower frequency (blue line with circle symbol). This phenomenon gives us an indication that at higher frequency or shorter pulse width, a better design of the physical parameters for contrast agent and PA/TA sensor will impact the PA/TA generation efficiency more significantly, and deserves a more detailed research. Although the simulation results by varying each variable may not give very accurate quantitative prediction like numerical simulation, the designer could quickly identify the key parameters that determine the PA/TA generation efficiency and analyse trade-off between various parameters.

Fig. 4.

Frequency-dependent PA/TA pressure versus different physical parameters: (a) heat capacity per unit area of thin film, (b) volumetric heat capacity of medium, (c) thermal conductivity of the medium, and (d) viscosity of the medium.

3.4. Case study of CNT/PDMS vs CNT/water

Due to the larger thermal expansion coefficient and smaller specific heat, PDMS has been selected as a better vibrator than water to build the PA/TA film generator or sensor [23], [24]. Therefore we would like to make a quantitative comparison between CNT/PDMS and CNT/water composites. The main parameters that differ between them are listed in Table 4. By substituting the parameters into Eq. (24) in two cases (low frequency without satisfying thermal/stress confinements, and high frequency with fully satisfying thermal/stress confinements), the PA/TA pressure comparison results are calculated as 1:12.9, and 1:7.7. It shows the indication that with longer pulse width (especially for microwave-induced thermoacoustic effect), the PDMS could provide more PA/TA pressure improvement than that of shorter pulse width (e.g. photoacoustic effect).

Table 4.

Comparison table of CNT/water and CNT/PDMS.

Symbol	Unit	Description	Water[47]	PDMS[23]
$$\kappa$$	W/(m K)	Thermal conductivity of the medium	0.6	0.15
$$\beta$$	K−1	Thermal expansion coefficient	210e−6	920e−6
$${\rho }_0$$	kg/m3	Density of the medium	1000	965
$$c_p$$	J/(m3 K)	Volumetric heat capacity of the medium	4.179e6	1.409e6
$$v_s$$	m/s	Acoustic velocity	1480	1000
PA/TA pressure comparison (Modulation frequency: 10 MHz, pulse width: 100 ns)			1: 12.9
PA/TA pressure comparison (Modulation frequency: 10 GHz, pulse width: 100 ps)			1:7.7

4. Experimental results

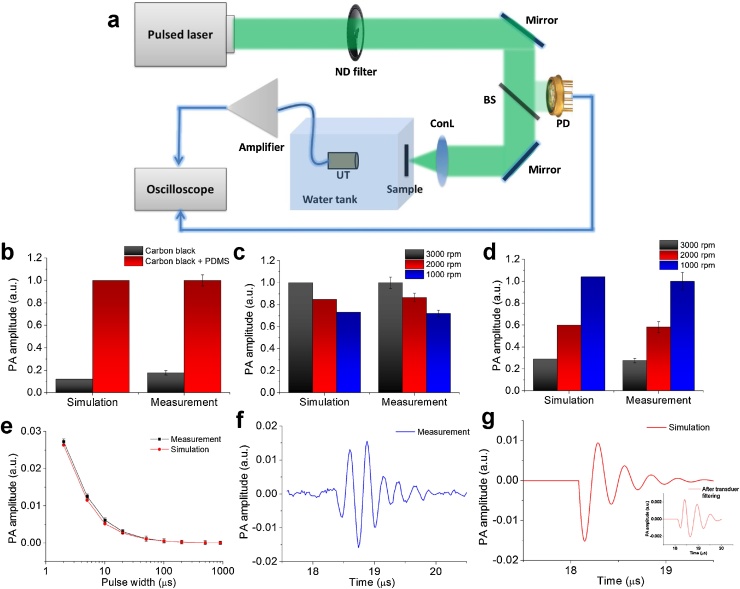
Although reported experimental results in literature have proved some of the predictions in this paper, such as the viscosity versus PA generation efficiency [35], [46], [48], here we present several sets of controlled experiments to demonstrate feasibility of the proposed analytical model based on carbon black + PDMS composite film samples. The photoacoustic measurement setup in Fig. 5a consists a pulsed laser source (DPSS-532, Crylas Inc. GmbH) with 532 nm wavelength, 1.8 ns pulse width, 1 mJ pulse energy, and 20 Hz repetition rate. The laser beam was attenuated by a variable neutral density filter (NDC-50S–1 M, Thorlabs), and guided onto the sample by a pair of mirrors and a condenser lens to form a focal spot with ∼0.5 mm diameter. A beam sampler (BSF10-A, Thorlabs) was used to sense some of the light to be detected by a photo detector (DET36A, Thorlabs) to monitor the laser pulse energy fluctuation. To guarantee the approximate 1D case, the thin film sample was attached to the inner wall of the transparent water tank for an optimized optical and acoustic coupling, which is perpendicular to the light path. An unfocused ultrasound transducer (V382, Olympus) with 3.5 MHz central frequency and 60% fractional bandwidth was place inside the water facing to the incoming light pass to maximize the detection sensitivity. It receives the PA signal, which was then amplified by a low-noise preamplifier (5662, Olympus). An oscilloscope (WaveRunner 640Zi, LeCroy) was utilized to record both the PA signal and PD signal at sampling rate of 100 MSPS. The data was process off-line using MATLAB (2010b, MathWorks). For all of the composite films, we used glass as the substrate to deposit carbon black thin film and PDMS. Indian ink provides a nearly uniform absorption spectrum over a wide spectral range and also maintains stable absorption properties over a long time period [49]. Glass slide substrates (25 mm x 25 mm) were cleaned prior to coating with acetone, isopropyl alcohol (IPA) and DI water. Further, black ink solution was spin-coated on the glass substrate at rates of 1000, 2000 and 3000 rpm for 30 s to form films of varying thickness c.a 50 μm, 25 μm and 10 μm respectively [50]. After the spin-coating process, the samples were thermally cured for 15 min at 100 °C in an oven. Further, the PDMS base and curing agent (Sylgard 184) were mixed at a ratio of 10:1. The mixture was then poured onto the carbon black film coated glass slides, followed by spin coating at 1000, 2000 and 3000 rpm for 30 s to form PDMS thickness of c.a 75 μm, 50 μm and 25 μm respectively [51]. The composite layered sample was further thermally cured by placing in an oven maintained at 100 °C for 30 min.

Fig. 5.

(a) The experimental setup. ND filter: neutral density filter; PD: photodiode; BS: beam sampler; ConL: condenser lens; UT: ultrasound transducer. The simulation and measurement PA signals of (b) two samples between pure carbon black film and carbon black + PDMS composite film, (c) three carbon black + PDMS composite film samples with different thicknesses of carbon black layer, and (d) another three carbon black + PDMS composite film samples with different thicknesses of PDMS layer by controlling the rotating speed of spin-coating, (e) tuning the laser pulse width from 2 to 1000 μs. (f–g) Measured and simulated PA signals in time domain. Inset: simulated PA signal after transducer’s filtering effect.

The first experiment was designed to compare two different films, one of them is pure carbon black layer, another one is the carbon black + PDMS composite layer. Under nanoscale short pulse laser illumination (1.8 ns), the simulation result shows a PA signal enhancement factor of ∼8.3, and the measurement result also shows a significant enhancement of ∼5.6 (Fig. 5b). It proved the expectation that both simulation and measurement results shows PA improvement by adding the PDMS layer. The measurement result gives a lower value of enhancement than simulation, which may be caused by the acoustic attenuation and reflection of the PDMS layer, and the limited bandwidth of the ultrasound transducer that degrades the PA signal’s amplitude in the measurement. The second set of experiment was designed to evaluate the heat capacity per unit area of the absorbing layer. By controlling the rotating speed (1000, 2000 and 3000 rpm) of spin-coating during the fabrication, samples with different thicknesses of carbon black have been fabricated (Methods). It is expected that by keeping other parameters constant (e.g. optical absorption, etc.), a thinner absorbing layer will give a higher temperature rise and heat transfer efficiency to generate stronger PA signal (Table 2). Both the simulation and measurement results show the similar trend, where smaller spin-coating speed (larger thickness) gives weaker PA amplitude (Fig. 5c). The third experiment was designed to evaluate the bandpass filtering effect of the film and transducer (Eq. (24)). By increasing the thickness of the PDMS layer, the central frequency of the PA signal generated by the film is expected to decrease predicted from the model (Eq. (22)). Considering the nanoscale short laser pulse width (1.8 ns), the input light could be treated as the impulse response, so the PA frequency response is mainly determined by the thickness of the PDMS layer. As expected, with smaller spin-coating speed (larger thickness), the PA amplitude is increasing due to the PA signal’s central frequency is moving closer to the central frequency of ultrasound transducer (Fig. 5d).

Except the comparison of different samples using short pulse laser in the above session, the next experiment was designed to explore the pulse-dependent PA signal amplitude, which is physically related with the thermal and stress confinement. As predicted from the model, by decreasing the laser pulse width, the PA amplitude will increase and then reach saturation (thermal and stress confinements satisfied). In this experiment, due to the inability of pulse width tuning of the pulsed laser, it was replaced by a custom-designed laser diode, whose pulse width could be tuned by a function generator [32]. The laser pulse width was tuned from 2–1000 μs within the operation bandwidth of the laser driver module. After normalizing the pulse energy, the result shows that by increasing the laser pulse width, the PA amplitude decreases accordingly (Fig. 5e). With same laser pulse energy, it well proves that due the unsatisfactory thermal and stress confinements with longer laser pulse, the PA intensity decreases according to Eq. (19). This agrees well with the prediction from dedicated model in the literature [29]. Lastly, the time-domain PA signals were compared between simulation (Eq. (25), Fig. 5g) and measurements (Fig. 5f). The damping effect caused by the bandpass filtering effect shows a good agreement between the simulation and measurement results. However, in previous literature, the analytical model only gave a dipolar N shape PA signal [4]. The discrepancy of this two time-domain PA signals is at the rising part of the PA signal, which may be caused by the inhomogeneous light absorption and reflection within the sample during the experiment and not considered in this analytical model. Moreover, the frequency response of the ultrasound transducer also acts a bandpass filter to the impulse-response PA signal, further distorting the measured PA waveform. After bandpass filtering by the transducer, the simulated PA signal’s waveform (Fig. 5g: inset) shows a higher similarity with the measured signal.

5. Discussion and conclusion

Regarding the applicability of this model, we would like to clarify that the model and simulation are based on 1D case, and it may behave differently for 2D and 3D cases when thickness >10 μm. For such more complex cases, a simple analytical model may not give a very accurate estimation of the PA generation. However, it can be expected that the model in this study is also potential to give some guidelines for more complex film/nanoparticle designs, which needs further validation by dedicated 3D numerical simulations and experiments. Regarding the samples used in simulations and experiments, although CNT and carbon black have some difference in terms of the conductivity, heat loss and inner structure of the materials, at macroscopic scale, both carbon black and CNT are good optical absorbers and can work well to generate strong PA signals.

Although there are many studies on contrast agents and film design to improve the PA/TA generation efficiency, the underlying physics is the thermoelastic expansion mechanism, which is intrinsically very low efficient. Utilizing the proposed analytical model as guideline could optimize the generation efficiency, however, it is ultimately limited by the low-efficiency thermal expansion phenomenon. To overcome this limitation, some recent studies demonstrate that contrast agent could be designed to trigger nonlinear PA generation by forming micro/nano bubbles and induce significantly enhanced PA amplitude with bubble explosion [52], [53], [54], [55]. But, the random bubble explosion and much higher required laser intensity may hinder its wide applications in bio-imaging, which deserve further exploration in the future work.

In conclusion, a compact and comprehensive analytical model describing PA/TA generation is proposed for contrast agent and film sensor design. Through theoretical analysis, simulation, and experimental comparison, the proposed model is well proved with both existing published results and several controlled experiments in different scenarios of film thickness, modulation frequency, pulse width, thermal/stress confinement, etc. More importantly, this model provides a straightforward guideline for high efficient PA/TA generation from nanoparticles and thin film ultrasound generator, which could trigger deeper research and broaden the scope in this area.

Conflict of interest

The authors declare that there are no conflicts of interest.

Biographies

Fei Gao received his B.S. degree in electrical engineering from Xi'an Jiaotong University, Xi'an, China in 2009. He received the PhD degree in electrical and electronic engineering at Nanyang Technological University, in 2015. He was a postdoctoral visiting scholar at Stanford University in 2015. After that, he joined NTU working as a research fellow and electromagnetic-ultrasound group leader. He joined ShanghaiTech University as an assistant professor in Jan. 2017. His research interests include fundamental study and system development of thermoacoustic and photoacoustic imaging modalities, circuit and system for biomedical applications. He has authored and co-authored over 40 journal and conference papers, one book chapter, and one patent filed.

Xiaohua Feng obtained his B.S. degree in electrical engineering from Xidian University, Xi'an, China in 2011. He obtained his PhD degree in School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore in 2016. He will join California Institute of Technology as a postdoctoral researcher under the supervision of Prof. Lihong V. Wang in early 2017. His research interest includes microwave induced thermoacoustic imaging, photoacoustic imaging, pulsed radio frequency pain relief therapy, and biomedical circuits and system design.

Yuanjin Zheng (M’02) received the B.Eng. and M.Eng. degrees from Xi’an Jiaotong University, Xi'an, China, in 1993 and 1996, respectively, and the Ph.D. degree from the Nanyang Technological University, Singapore, in 2001. From July 1996 to April 1998, he was with the National Key Laboratory of Optical Communication Technology, University of Electronic Science and Technology of China. In 2001, he joined the Institute of Microelectronics (IME), Agency for Science, Technology and Research (A*STAR), and had been a principle Investigator and group leader. With the IME, he has led and developed various projects on CMOS RF transceivers, ultra-wideband (UWB), and low-power biomedical ICs etc. In July 2009, he joined the Nanyang Technological University, as an assistant professor and program director for Bio-imaging program. His research interests are biomedical sensors and imaging, thermoacoustic and photoacoustic imaging, and SAW/BAW/MEMS sensors. He has authored or coauthored over 250 international journal and conference papers, 22 patents filed, and several book chapters.