A pressure-induced topological phase with large Berry curvature in Pb_1−xSn_xTe

Under pressure, the semiconductor PbSnTe transitions from an insulator to a Weyl metal that displays a large Berry curvature.

Abstract

The picture of how a gap closes in a semiconductor has been radically transformed by topological concepts. Instead of the gap closing and immediately reopening, topological arguments predict that, in the absence of inversion symmetry, a metallic phase protected by Weyl nodes persists over a finite interval of the tuning parameter (for example, pressure P). The gap reappears when the Weyl nodes mutually annihilate. We report evidence that Pb_1−xSn_xTe exhibits this topological metallic phase. Using pressure to tune the gap, we have tracked the nucleation of a Fermi surface droplet that rapidly grows in volume with P. In the metallic state, we observe a large Berry curvature, which dominates the Hall effect. Moreover, a giant negative magnetoresistance is observed in the insulating side of phase boundaries, in accord with ab initio calculations. The results confirm the existence of a topological metallic phase over a finite pressure interval.

INTRODUCTION

Topological concepts have greatly clarified the role of symmetry in protecting electronic states in a host of materials. In bulk semiconductors, topological insights have revised the picture of how the energy gap closes (say, under pressure P). In the old picture, the gap Δ closes at an “accidental” value of P before reopening at higher P. The new view (1–4) predicts instead that, when inversion symmetry is broken, a gapless metallic state featuring pairs of Weyl nodes persists over a field interval (P₁→P₂). They act as sources and sinks of Berry curvature (an effective magnetic field in k space). The metallic phase is protected because the nodes come in pairs with opposite chiralities (χ = ±1). Hence, they cannot be removed except by mutual annihilation (which eventually occurs at the higher pressure P₂). To date, these predictions have not been tested.

Here, we show that Pb_1−xSn_xTe exhibits a pressure-induced metallic phase described by the Weyl scenario. The Pb-based rock salts (5–7) have been identified as topological crystalline insulators with surface states protected by mirror symmetry (8–12). We focus on their Dirac-like bulk states (13, 14), which occur at the L points of the Brillouin zone (BZ) surface. Pb_1−xSn_xTe exhibits an insulator-to-metal (IM) transition at P ~ 10 kbar (7). However, the IM transition is little explored. We report that the metallic state appears by nucleating 12 small Fermi surface (FS) nodes. The breaking of time-reversal symmetry (TRS) in applied B leads to a large Berry curvature Ω. Finally, we also observe an anomalously large negative magnetoresistance (MR), which is anticipated in the Weyl scenario.

RESULTS

Phase diagram under pressure

Crystals of Pb_1−xSn_xTe were grown by the vertical Bridgman technique (see Materials and Methods). Transport measurements at temperatures T down to 2 K were carried out in a Be-Cu pressure cell (with a maximum pressure of P_max ~ 28 kbar) on four samples with Sn contents x = 0.5 (samples A1 and A2), 0.32 (Q1), and 0.25 (E1) (Table 1). In A1 and A2, indium (6%) was added to tune the chemical potential (see Materials and Methods).

Table 1. Parameters of samples of Pb_1−xSn_xTe investigated.

Columns 2, 3, 4, and 5 report the Sn content x, the mobility μ, the Hall carrier density n_H, and the conductivity σ (at B = 0), respectively. The minus sign in n_H (sample Q1) indicates n-type carriers. All quantities in the table were measured at 5 K at the pressure P given in the last column. Samples A1 and A2 are slightly doped with In to tune the chemical potential [composition (Pb_0.5Sn_0.5)_1−yIn_yTe, with the In content y = 0.06].

Sample	x	μ (cm2/Vs)	nH (cm−3)	σ (mΩ cm)−1	P (kbar)
A1	0.5	18,000	1.59 × 1017	0.41	25
A2	0.5	29,000	1.56 × 1017	0.68	25.4
E1	0.25	500,000	9.35 × 1015	0.70	21.7
Q1	0.32	4.2 × 106	−1.05 × 1016	7.02	21

Figure 1 provides an overview of the IM transitions in samples A2 and E1. As P increases from 0 kbar (ambient pressure) to 25.4 kbar, the resistivity profile ρ versus T changes from insulating to metallic behavior in A2 (Fig. 1A). Close examination reveals a kink in ρ, indicating a sharp transition at T_c = 62 to 70 K (arrows in inset). Figure 1B shows the rapid increase in the zero-B conductivity σ ≡ 1/ρ at 5 K as P exceeds the critical value P₁ ~ 15 kbar at the IM transition. The resistivity curves in sample E1 (x = 0.25) are broadly similar except that ρ at ambient P attains much higher values at 5 K (3 × 10⁴ Ω cm). As P increases from ambient to P₁ (12 kbar), an IM transition occurs to a metallic state (with ρ decreasing by over seven decades at 5 K). In samples E1 and Q1 (which have smaller Sn content than A1 and A2), the second critical pressure P₂ = 25 kbar is accessible in our experiment. The profile of σ versus P at 5 K (Fig. 1D) shows the metallic phase sandwiched between the two insulating phases.

Fig. 1. The phase diagram of Pb1−_xSn_xTe inferred from the resistivity ρ versus temperature T and pressure P.

(A) Curves of ρ versus T in sample A2 (x = 0.5) in zero B measured at selected P. At 5 K, ρ decreases by four orders of magnitude as P→25.4 kbar (the IM transition). The inset shows the kinks (arrows) in ρ (between 62 and 70 K), which signal a transition to a state with broken inversion symmetry. (B) Steep increase of the conductivity σ = 1/ρ at 5 K in the metallic phase (shaded in blue; P > P₁). (C) ρ versus T at selected P in sample E1 (x = 0.25). The insulating state is recovered at P₂ ~ 25 kbar. The inset plots the dielectric response ε₁ measured versus applied electric field E at 2 K and ambient P (a spontaneous value ε₁ ~ 5 × 10⁴ is measured as E→0). (D) σ versus P at 5 K to display the metallic state in E1 (shaded in blue) sandwiched between P₁ and P₂. (E and F) Calculated Weyl node trajectories (Supplementary Materials), magnified 10× relative to the BZ scale (with B = 0). In (E), the vector d || [111] (arrow) is the assumed FE displacement. (F) Top view (sighting || d). Under pressure, the 12 Weyl nodes at L₁, L₂, and L₃ trace out elliptical orbits until they annihilate at the black points. The Weyl nodes at L₀ trace an orbit that undulates about a circular path [over a restricted pressure interval (Supplementary Materials)].

The end member SnTe is known to be ferroelectric (FE) (15), but the existence of FE distortion is less obvious for finite Pb content. To establish inversion symmetry breaking, we performed dielectric measurements (see Materials and Methods) on sample E1, which has a very large ρ below 10 K (>10³ Ω cm). By varying the E-field (12→100 V/cm), we show that a large spontaneous dielectric response ε₁ ~ 5 × 10⁴ exists in the limit E→0 (Fig. 1C, inset). The spontaneous polarization P_s provides direct evidence that the insulating state below P₁ in E1 is FE. Although dielectric measurements cannot be performed in A2 (carrier screening is too strong), the kink in ρ (arrow) implies that P_s appears at 62 to 70 K.

In parallel, we performed ab initio calculations (see details in the Supplementary Materials), in which the lattice parameter a is varied to simulate pressure. To break inversion symmetry, we assumed a weak FE displacement d || [111]. The calculations reveal that, above P₁, two pairs of Weyl nodes appear near each of the points L₁, L₂, and L₃ (these are equivalent in zero B; see Fig. 1, E and F). As P increases, the 12 nodes trace out elliptical orbits (shown expanded by a factor of 10 relative to the BZ caliper) and eventually annihilate pairwise (indicated by black dots), consistent with the scenario described by Murakami (2) and Murakami and Kuga (3). The red and blue arcs refer to nodes with χ = 1 and −1, respectively. The splitting of the node at L₀ occurs in a much narrower pressure interval.

Quantum oscillations

The samples’ high mobilities μ (20,000 to 4 × 10⁶ cm²/Vs; see Table 1) allow us to “count” the number of FS pockets by monitoring the Shubnikov–de Haas (SdH) oscillations. As shown in Fig. 1 (B and D), σ increases steeply with the reduced pressure ΔP = P − P₁. Figure 2A shows the resistivity ρ_xx measured in sample A2 in a transverse magnetic field B (|| $\widehat{\mathbf{z}}$) at selected values of P. From the linear variation of 1/B_n versus the integers n (where B_n is the peak field in ρ_xx; see Fig. 2B), we find that the FS caliper area S_F increases from 1.6 to 2.7 T between 19 and 25.4 kbar. The most prominent peak in Fig. 2A corresponds to the n = 1 Landau level (LL). The SdH-derived Fermi wave vector k_F corresponds to a hole density ${\mathit{p}}_{\text{SdH}}=\frac{4}{3}\mathrm{\pi }{{\mathit{k}}_{\mathrm{F}}}^3/{(2\mathrm{\pi })}^3$ per spin (assuming a spherical FS).

Fig. 2. The nucleation of small FS pockets above P₁ observed by SdH oscillations.

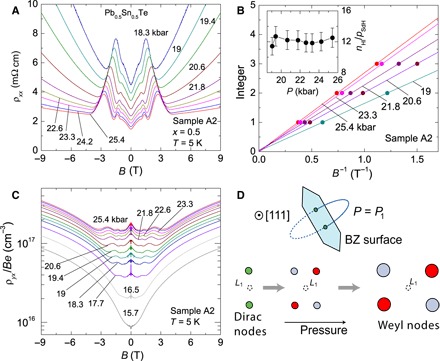
(A) Resistivity ρ_xx versus a transverse B measured at 5 K and with P fixed at values 18.3 to 25.4 kbar (sample A2). At each P, the oscillations below 3 T correspond to SdH oscillations (the largest peak corresponds to the n = 1 LL). (B) Inverse peak fields 1/B_n of ρ_xx versus the integers n. The slopes yield small extremal FS cross sections S_F (1.6 to 2.7 T), which increase with ΔP = P − P₁. The inset shows that the ratio n_H/p_SdH equals 12 ± 1, independent of P (see text). (C) Hall resistivity (divided by Be) ρ_yx/Be versus B. At low B (where SdH oscillations occur), the flat profile allows ρ_yx/Be to be identified with the total hole density n_H. The strong increase in ρ_yx/Be above 3 T reflects the Berry curvature term (Fig. 3). (D) Top-down view (along [¯1¯1¯1]) of the L₁ hexagon face in zero B. At P₁, two Dirac nodes nucleate around L₁ because of inversion-symmetry breaking. With increasing P, the four Weyl FS near L₁ move apart and expand in volume [chirality χ = 1 (red) and −1 (gray)].

The sharp increase in hole density is also evident in the Hall resistivity ρ_yx (which is B-linear in weak B). To highlight its behavior, we plot the ratio ρ_yx/Be versus B (Fig. 2C). In weak B (for example, |B| < 3.5 T in the top curve), the ratio is B-independent, which allows the ratio to be identified with the Hall density n_H (the abrupt increase above 3 T arises from the interesting anomalous Hall term discussed below). From n_H, we derive μ ~ 1.8 × 10⁴ and 2.86 × 10⁴ cm²/Vs in A1 and A2, respectively, at 25 kbar.

Crucially, we find that n_H always exceeds p_SdH by an order of magnitude. This implies a large number N_F of identical pockets. The ratio n_H/p_SdH = N_F equals 12 ± 1 over the whole pressure interval (Fig. 2B, inset). Because a smaller N_F (for example, 4, 6, or 8) can be excluded, the results strongly support the choice d || [111], which leads to three equivalent L points.

Anomalous Hall effect

We next describe the evidence for a topological metallic phase. The Hall resistivity ρ_yx displays a highly unusual field profile. As B increases, the initial B-linear behavior abruptly changes, bending over to a nominally flat profile (Fig. 3A). At first glance, this recalls the anomalous Hall effect (AHE) in a ferromagnet (16) where the intrinsic AHE arises from a large Berry curvature rendered finite by the spontaneous breaking of TRS, but there is a subtle difference. In PbSnTe, TRS remains unbroken under P, so the AHE should be absent in the Weyl phase if B = 0 (Ω cancels pairwise between Weyl nodes with χ = ±1). However, when TRS is broken in field B, the cancellation is spoiled by the Zeeman energy (see below). The field Ω leads to a large AHE signal. We remark that, in weak B (with Ω negligible), the initial slope of ρ_yx is dominated by the ordinary Hall effect, as evidenced by the linearity of n_H versus p_SdH in Fig. 2B [by contrast, in a ferromagnet, the AHE term is dominant even in weak B, so the weak-B ρ_yx and n_H are unrelated (16)].

Fig. 3. The Berry curvature term in the Hall response.

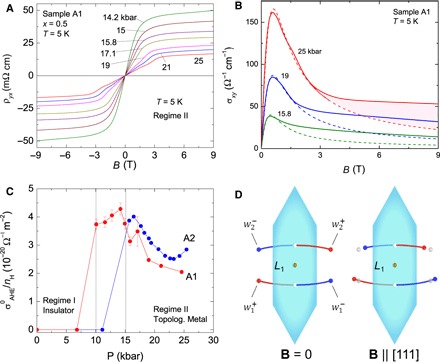
(A) Observed curves of ρ_yx versus B at 5 K with P fixed at values above P₁. Instead of the conventional B-linear profile, ρ_yx bends over at low B (2 to 3 T), implying an extraordinary contribution to σ_xy at large B. (B) σ_xy versus B (derived from the measured ρ_ij) at three values of P. The Drude expression fits well to the curves at low B but reveals an excess contribution (shaded in the curve at 25 kbar) at large B, identified with ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{\mathit{A}}$, that increases with B. (C) Ratio ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{\mathit{A}}/{\mathit{n}}_{\mathrm{H}}$ (see fits in the Supplementary Materials) versus P in samples A1 and A2 (x = 0.5). The ratio, which is proportional to 〈Ω_z〉, shows a sharp increase at P₁, followed by a milder variation in the metallic phase. (D) Effect of B on the Weyl node separations (viewed along [¯1¯1¯1]). In zero B (left), the Weyl nodes are equal in size and symmetrically located about L₁ (Ω vanishes). A finite Zeeman field (right) increases the separation and Fermi energy of the pair ${\mathit{w}}_1^{\pm }$ while decreasing them in ${\mathit{w}}_2^{\pm }$. The explicit breaking of TRS leads to a finite ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{\mathit{A}}$.

The total (observed) Hall conductivity σ_xy is the sum of the conventional Hall and anomalous Hall conductivities, ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{\mathit{N}}$ and ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{\mathit{A}}$, respectively (Fig. 3B). With ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{\mathit{N}}$ given by the Drude expression, we find that a good fit to σ_xy is achieved if we assume ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{\mathit{A}}={\mathrm{\sigma }}_{\text{AHE}}^0\mathit{g}(\mathit{x})$, where ${\mathrm{\sigma }}_{\text{AHE}}^0$ is the AHE amplitude and g(x) is the smoothed step function 1/(e^−x + 1), with x being a reduced field (Supplementary Materials). In terms of Ω, ${\mathrm{\sigma }}_{\text{AHE}}^0$ is given by (16)

$${\mathrm{\sigma }}_{\text{AHE}}^0=\frac{\mathit{e}}{{(2\mathrm{\pi })}^3}{\displaystyle \int }{\mathit{d}}^3\mathit{k}{\mathrm{\Omega }}_{\mathit{z}}(\mathbf{k}){\mathit{f}}_{\mathbf{k}}^0=\mathit{e}\langle {\mathrm{\Omega }}_{\mathit{z}}\rangle {\mathit{n}}_{\text{tot}}$$ (1)

where ${\mathit{f}}_{\mathbf{k}}^0$ is the Fermi-Dirac distribution, 〈Ω_z〉 is the Berry curvature averaged over the FS, and n_tot is the total carrier density. From the fits at each P, we can track the variation of $\langle {\mathrm{\Omega }}_{\mathit{z}}\rangle ~{\mathrm{\sigma }}_{\text{AHE}}^0/{\mathit{n}}_{\text{tot}}$ versus P. As shown in Fig. 3C, the curvature 〈Ω_z〉 is negligible below P₁ but becomes large in the metallic phase, consistent with the Weyl scenario.

In Fig. 3B, we plot the observed σ_xy (solid curves) together with the Drude curve for ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{\mathit{N}}$ (dashed curves). Their difference is ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{\mathit{A}}$ (shaded region in the curve at 25 kbar). Similar results are obtained in A2 and E1 (Supplementary Materials). ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{\mathit{A}}$ grows quite abruptly at an onset field B_A close to where the system enters the lowest (n = 0) LL. Above B_A, the increasing dominance of the AHE current accounts for the abrupt bending of ρ_yx already noted in Fig. 3A, as well as the sharp increase above B_A in ρ_yx/Be in Fig. 2C. The observation that ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{\mathit{A}}$ is most prominent within the n = 0 LL (which is strictly chiral for Weyl fermions) suggests to us that it is intimately related to the chirality of the nodes.

Each Weyl node acts as a source (χ = 1) or sink (χ = −1) of Ω. As mentioned, in zero B, TRS requires the net sum of Ω over each pair of Weyl nodes to vanish (Fig. 3D). The ab initio calculations (Supplementary Materials) reveal how this cancellation is spoiled when TRS is broken in finite field B. A finite Zeeman field λ shifts the band energies, depending on their spin texture. This increases the k-space separation and Fermi energy of one pair of nodes, say ${\mathit{w}}_1^{\pm }$, while reducing them in the other ${\mathit{w}}_2^{\pm }$ (Fig. 3D). The unbalancing creates a finite Ω (hence, ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{\mathit{A}}$) that grows with B (Supplementary Materials).

Giant MR

Perhaps the most marked feature in Pb_1−xSn_xTe is the appearance of giant negative MR at pressures just above P₂. In Fig. 4A, we show the MR curves in sample Q1 for selected T with P fixed at 28 kbar (roughly 3 kbar above P₂). At 4.3 K, ρ_xx decreases by a factor of 30 as B increases to 10 T (aside from a slight dip feature below 0.5 T). In Fig. 4B, similar curves for E1 (at pressure P = 25.4 kbar) show an even larger negative MR (the weak-B dip feature is more prominent as well). The large negative MR is steadily suppressed as we increase P beyond the P₂ boundary. The negative MR magnitude is similar in magnitude in both the transverse MR and longitudinal MR geometries (B || $\widehat{\mathbf{z}}$ and B || $\widehat{\mathbf{x}}$, respectively). This implies a Zeeman spin mechanism. Finally, we note that, in both Q1 and E1, ρ_xx measured at 10 T decreases as T →5 K (that is, the system is metallic).

Fig. 4. Large, negative MR.

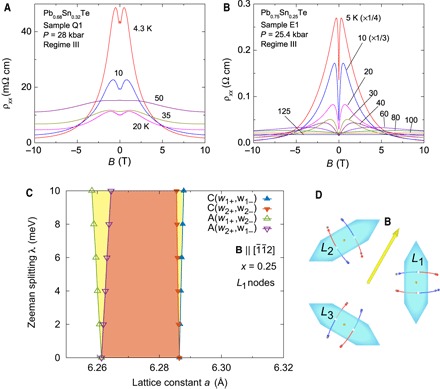
A large isotropic MR is observed when P is fixed just above P₂ in samples Q1 and E1. (A) ρ_xx versus B in Q1 (x = 0.32) at selected T, with P = 28 kbar. At P > P₂, both samples are insulators at B = 0 T. However, at B = 10 T, both are metallic (ρ_xx decreases with T). In (B), similar curves show an even larger negative MR in sample E1 (x = 0.25). (C) Ab initio phase diagram (Supplementary Materials) in the plane of a versus λ at L₁ for B || [¯1¯12]. With increasing λ, the Weyl node annihilation boundary (left V-shaped wedge shaded yellow) expands. A weaker expansion occurs at the creation boundary. (D) Effect of B (yellow arrow) on the locations of the Weyl nodes around L₁, L₂, and L₃.

DISCUSSION

The anomalously large changes in ρ_xx imply that the insulating state (at zero B) is converted to a metallic state in finite B. This is confirmed in the ab initio calculation (Supplementary Materials). A large λ favors the Weyl phase (the left V-shaped yellow region in Fig. 4C). As the phase boundary now tilts into the insulating side, the metallic phase is reentrant in increasing B. The observation of the giant negative MR provides further evidence in support of the Weyl node scenario.

As predicted in previous studies (1–4), gap closing in materials lacking inversion symmetry leads to a metallic phase that is protected by the distinct chirality of Weyl nodes. Pb_1−xSn_xTe is an instructive first example. Increasing pressure P drives an IM transition at P₁, with ρ (at 5 K) falling by four to seven orders of magnitude. Above P₁, the growth of the FS calipers is tracked by large SdH oscillations. The number of nodes (12) is consistent with the appearance of four Weyl nodes at each of the 3 L₁ points on the BZ surface. The Berry curvature, rendered finite in B, leads to an AHE that is most prominent in the n = 0 LL. Finally, we find that the boundary P₂ is shifted in finite B. The reentrance of the metallic phase leads to a marked decrease in ρ_xx by a factor of 30 to 50.

MATERIALS AND METHODS

Crystal growth

Single crystals of Pb_1−xSn_xTe were grown by the conventional vertical Bridgman technique. High-purity elements (5N) with the targeted values of x were sealed in carbon-coated quartz tubes under a high vacuum of ~10⁻⁵ mbar. The ampoules were heated at 1050°C for 12 hours. To ensure homogeneous mixing of the melt and to avoid bubble formation in the bottom, we stirred the ampoules. The ampoules were slowly lowered through the crystallization zone of the furnace, at the rate of 1 mm/hour. High-quality single-crystal boules of length ~10 cm were obtained. The crystal boules were cut into segments of 1 cm to investigate the bulk electronic properties along the boule length. The crystals were easily cleavable along different crystallographic planes.

A major difficulty in the rock salts is having to ensure that the chemical potential of the alloy lies within the bulk gap (otherwise, the pressure-induced changes to the gap will not be observable). To achieve this goal in crystals with Sn content x = 0.5, we have found it expedient to dope the starting material with indium [at the 6% level, with composition (Pb_0.5Sn_0.5)_1−yIn_yTe, with y = 0.06]. Indium doping has previously been carried out and investigated by several groups to understand the superconducting phase in Pb_1−xSn_xTe (17–19). Zhong et al. (19) have reported that In-doped Pb_1−xSn_xTe (x = 0.5) induces an insulating behavior. However, in our judgment, the precise role of In doping in the Pb-based rock salts is not well understood and merits further detailed investigation.

The x-ray diffractograms recorded for two powdered specimens of two typical samples are shown in fig. S4. The grown crystals were single-phased. The diffraction peaks were in very close agreement with the rock salt crystal structure of space group Fm$\overline{3}$m.

Some of the parameters measured in the four samples investigated (A1, A2, E1, and Q1) are reported in Table 1. The mobilities in E1 (p-type) and Q1 (n-type) were very high (500,000 and 4.2 × 10⁶ cm²/Vs, respectively). Although the samples with x = 0.50 (A1 and A2) had lower mobilities (18,000 and 29,000 cm²/Vs, respectively), clear SdH oscillations were observed above P₁.

Measurement of dielectric constant

We provide more details on the measurements of the relative dielectric constants ε₁. We adopted the (modified) Sawyer-Tower method (20, 21). The circuit of the original Sawyer-Tower method is shown in Fig. 5A. Figure 5B shows the modified method using an operational amplifier (op-amp) (21).

Fig. 5. Measurement of dielectric response.

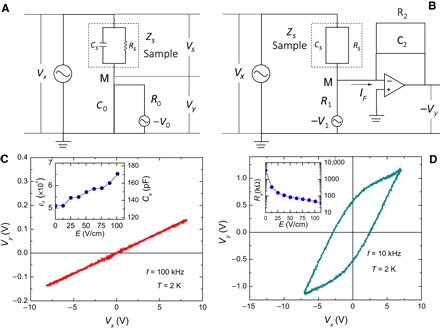
(A) Electrical circuit for measuring the relative dielectric constant ε₁ of the sample. The voltage V_y ~ V_xC_s/C₀ < V_x is proportional to the dielectric displacement D. By contrast, the applied voltage V_x is proportional to the electrical field E in the sample. Therefore, the curve of V_x versus V_y gives the relation between E and D, yielding the relative dielectric constant ε₁ as a function of applied electric field E. (B) Modified electrical circuit of (A). The op-amp forces the point M to act as a virtual ground. The integration circuit yields V_y = V_xC_s/C₂ when the relation V₁/R₁ = V_x/R_s is satisfied. Because C₂ does not have to satisfy C₂ ≫ C_s in (B), a large value for V_y can be realized. (C) Curve relating E and D (V_x versus V_y), which yields a relative dielectric constant ε₁ as large as 5 × 10⁴ even in the limit E→0 (inset). This implies that the system is in the FE state. (D) Apparent nonlinear relation between V_x and V_y caused by nonlinearity in the resistive component R_s of the sample. The inset shows how R_s varies with increasing E.

For the setup shown in Fig. 5A, the sample with a capacitance component C_s and a resistance component R_s was connected in a series with a known reference capacitance C₀ ≫ C_s. The reference capacitance C₀ was connected in parallel with a fixed resistor R₀ in series with an adjustable voltage source V₀ (or, equivalently, a variable resistor R_c) that was set such that the voltage V_y is inphase with voltage V_x, where V_x and V_y represent the voltages across the whole electrical circuit and the reference capacitor C₀, respectively. Because C₀ ≫ C_s was satisfied, the following relations hold: V_s ~ V_x, V_y ~ V_xC_s/C₀ ≪ V_x. Here, V_s is the voltage applied across the sample. This means that point M in the figure can be treated as a virtual ground. This yields the condition V₀/R₀ ~ V_x/R_s.

The setup in Fig. 5B is the same as that in Fig. 5A except that the op-amp is used to provide a more stable virtual ground at point M. From point M, current I_F was driven to the op-amp connected to C₂ and R₂ in parallel. Here, a large resistor R₂ (R₂C₂ ≫ 1/ω) was connected in parallel as the leak resistor so that the capacitor C₂ does not become overloaded. The integration circuit yielded the equation ${\mathit{V}}_{\mathit{y}}={\mathit{C}}_2^{-1}{\displaystyle \int }{\mathit{I}}_{\mathit{F}}(\mathit{t})\mathit{d}\mathit{t}$. If the adjustable voltage source V₁ is set to cancel the current I_s flowing into the sample, that is, if V₁/R₁ = V_x/R_s is satisfied, then the current I_F equals the current flowing into the capacitive component of the sample I_s = dQ/dt = d(C_sV_x)/dt. This gives V_y = V_xC_s/C₂, similar to the expression obtained for the case in Fig. 5A.

The advantage of using the op-amp is that one can choose any value of C₂ (as long the condition R₂C₂ >> 1/ω is satisfied) to attain a larger signal V_y than possible in the case in Fig. 5A. In general, the two setups in Fig. 5 (A and B) worked well. However, because the working frequency range of our op-amp (LF356N) was between 30 Hz and 30 kHz, we used setup A above 30 kHz. For frequencies below 30 kHz, both setups A and B were used. We confirmed that the two setups yielded the same results.

The measured results of the relative dielectric constants are plotted in Fig. 5C for f = 100 kHz and in Fig. 5D for f = 10 kHz. Figure 5C shows that V_y = V_xC_s/C₂ = DS/C₂ is proportional to V_x = Et. Here, E is the electric field in the sample, D is the dielectric displacement, and S and t are the area and the thickness of the sample, respectively. Using the values S = 0.234 mm² and t = 0.79 mm, we found the relative dielectric constants ε₁ ~ 5 × 10⁴ (shown in the inset of Fig. 5C). Unfortunately, the sample suffered dielectric breakdown above E ~ 100 V/cm, which prevented us from observing the saturation of dielectric displacement D at higher electric fields as should be expected from the FE behavior. This large relative dielectric constant ε₁ ~ 5 × 10⁴ observed in the limit E→0 strongly implies that the system is in the FE state.

We remark that the nonlinear behavior shown in Fig. 5D, previously interpreted by Möllmann et al. (22) as evidence for the FE state, is actually not the manifestation of the FE state. Rather, it arises from the fact that the resistive component of the sample R_s is strongly E-dependent, as shown in the inset. Because R_s is nonlinear, it is not possible to compensate the current I_s flowing through the resistive component R_s because V₁/R₁ = V_x/R_s cannot be satisfied for every V_x, unless V₁ is changed nonlinearly. Therefore, if V₁ is set to compensate the R_s at some fixed value of V_x (7 V in the case of Fig. 5D), then other parts of V_x cannot be compensated. As a result, they produce a nonlinear behavior that looks like the saturation expected in the FE state. The way to avoid this is to use a higher frequency f so that a larger portion of the current flows into the capacitive component C_s rather than into the resistive component R_s. This is precisely the case shown in Fig. 5C (f = 100 kHz).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/5/e1602510/DC1

section S1. Ab initio band calculations

section S2. Field-induced anomalous Hall effect

fig. S1. Calculated k-space trajectories of Weyl nodes in Pb_1−xSn_xTe (x = 0.5) under applied pressure in zero magnetic field.

fig. S2. Phase diagram of the Weyl phase in Pb_1-xSn_xTe (x = 0.25) and orbit parameters.

fig. S3. Phase diagram of the Weyl phase in Pb_1−xSn_xTe (x = 0.25) in the α-λ plane with applied B || [¯1¯12].

fig. S4. X-ray diffractograms of two powdered specimens of Pb_1−xSn_xTe taken from the crystal boules.

fig. S5. Supplemental data of (Pb_0.5Sn_0.5)_1−yIn_yTe for samples A1 and A2.

fig. S6. Supplemental data of Pb_0.75Sn_0.25Te for sample E1.

References (23–33)