Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 May 31.
Published in final edited form as: Phys Procedia. 2016;87:132–138. doi: 10.1016/j.phpro.2016.12.020

Design of HIFU transducers to generate specific nonlinear ultrasound fields

Vera A Khokhlova a,b,*, Petr V Yuldashev b, Pavel B Rosnitskiy b, Adam D Maxwell a, Wayne Kreider a, Michael R Bailey a, Oleg A Sapozhnikov a,b
PMCID: PMC5451200  NIHMSID: NIHMS861673  PMID: 28580038

Abstract

Various clinical applications of high intensity focused ultrasound (HIFU) have different requirements on the pressure level and degree of nonlinear waveform distortion at the focus. Applications that utilize nonlinear waves with developed shocks are of growing interest, for example, for mechanical disintegration as well as for accelerated thermal ablation of tissue. In this work, an inverse problem of determining transducer parameters to enable formation of shocks with desired amplitude at the focus is solved. The solution was obtained by performing multiple direct simulations of the parabolic Khokhlov–Zabolotskaya–Kuznetsov (KZK) equation for various parameters of the source. It is shown that results obtained within the parabolic approximation can be used to describe the focal region of single element spherical sources as well as complex transducer arrays. It is also demonstrated that the focal pressure level at which fully developed shocks are formed mainly depends on the focusing angle of the source and only slightly depends on its aperture and operating frequency. Using the simulation results, a 256-element HIFU array operating at 1.5 MHz frequency was designed for a specific application of boiling-histotripsy that relies on the presence of 90–100 MPa shocks at the focus. The size of the array elements and focusing angle of the array were chosen to satisfy technical limitations on the intensity at the array elements and desired shock amplitudes in the focal waveform. Focus steering capabilities of the array were analysed using an open-source T-Array software developed at Moscow State University.

Keywords: HIFU, nonlinear waves, shocks, transducer design, boiling histotripsy

1. Introduction

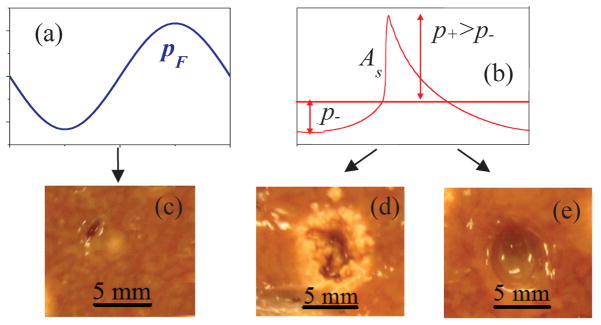
High Intensity Focused Ultrasound (HIFU) is an emerging medical technology developed for noninvasive surgery applications. The method utilizes focused ultrasound waves that propagate from the external transducer through the skin to the targeted location to either thermally or mechanically ablate an unwanted tissue within the patient body. In conventional HIFU treatments that operate at moderate in situ intensity levels of about several hundred W/cm2, ultrasound waves of nearly harmonic shape (Fig. 1(a)) generate purely thermal lesions at the focus (Fig. 1(c)). Higher intensities, up to several kW/cm2, can be used to accelerate treatments. At increased intensities, nonlinear propagation effects accumulate on the way from the transducer leading to formation of high-amplitude shocks in the ultrasound waveform at the focus (Fig 1(b)). When shocks are present, tissue heating is significantly stronger than heating by harmonic waves of the same pressure magnitude; boiling temperatures can be reached at the focus in milliseconds (Canney et al., 2008). Thermal lesions with a vaporized core can be rapidly generated when shock-induced boiling occurs (Fig. 1(d)). Short ultrasound pulses with shocks can be also used to generate purely mechanical liquefaction of tissue (histotripsy) (Fig 1(e)) (Hoogenboom et al., 2015, Khokhlova V. et al., 2015). Recently, two histotripsy methods have been developed. Both methods use a pulse-periodic irradiation protocol with a low duty factor of <1% to avoid accumulation of heating in tissue. Cavitation cloud histotripsy uses microsecond long pulses that generate a cavitation cloud in the focal region (Parsons et al., 2006), and boiling histotripsy (BH) uses millisecond-long pulses that induce localized boiling of tissue within each pulse (Khokhlova T. et al., 2011). Different methods of histotripsy require specific pressure levels and shock amplitudes at the focus. In general, higher peak pressures and therefore shock amplitudes are required for the cavitation cloud histotripsy method as compared to boiling histotripsy (Maxwell et al., 2012). To evaluate nonlinear ultrasound fields of existing transducers or to develop transducers optimized for specific shock-based applications, an inverse problem to determine transducer parameters capable of generating a desired shock amplitude or peak pressures at the focus should be solved.

Fig. 1.

Fig. 1

Open in a new tab

One cycle of a typical linear waveform (a), and nonlinearly distorted waveform with a shock (b) at the focus used in HIFU to generate a (c) purely thermal lesion, (d) thermal lesion with boiling, and (e) mechanical lesion in tissue.

In this work, multi-parametric calculations based on the KZK equation are performed to solve this problem for the case of a single-element spherically-shaped source. The modelling results were applied for designing a multi-element phased array for boiling histotripsy applications. Geometric parameters of the array that provide developed shock fronts of 90–100 MPa amplitude at the focus were determined. Focus steering capabilities of the array were analysed using an open-source T-Array software developed at Moscow State University.

2. Method

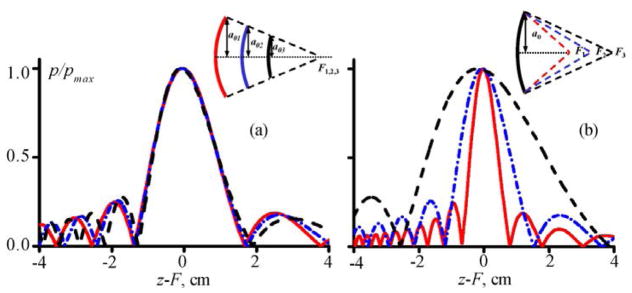
The hypothesis of the study was the fact that pressure levels in the focal waveform at which shocks are developed are mainly determined by the transducer focusing angle characterized by its Fnumber = F/2a0, where F – is the focal length of the source and a0 – is its radius. For transducers of different aperture but same Fnumber, the shape and the length of the main focal lobe on the beam axis in case of linear focusing are very close to each other (Fig. 2(a)). For transducers with different Fnumber, i.e. different focusing angles, the length of their focal lobes are significantly different (Fig. 2(b)). Nonlinear effects accumulate with propagation distance; this accumulation is the strongest over the propagation across the main focal lobe of the beam because there the pressure amplitude is highest and thus most of the nonlinear effects occur. Hence, for beams with the same focusing angle (same Fnumber), i.e. the same length of the main focal lobe (Fig. 2(a)), shocks should be formed at the focus at the same pressure level. On the contrary, for sources with higher focusing angle (lower Fnumber) that have shorter length of the focal lobe, higher pressures will be needed to develop shocks and vice versa for less focused sources (higher Fnumber) (Fig. 2(b)).

Fig. 2.

Fig. 2

Open in a new tab

Linear axial pressure amplitude distributions p/pmax normalized to their maximum values generated by spherically shaped focused transducers (a) with the same or (b) different values of their Fnumber = F/2a0. Here, a0 is the transducer radius, F is its focal distance, and z is the coordinate along the transducer axis. Examples are given for transducers with 1.5 MHz frequency and (a) F = 8, 12, 16 cm; Fnumber = 1.5; and (b) F = 8, 12, 16 cm; Fnumber = 1, 1.5, 2.

To confirm this hypothesis and to obtain a relation between pressure levels of the shocked focal waveform and the Fnumber of the source, simulations were performed using the parabolic Khokhlov–Zabolotskaya–Kuznetsov (KZK) equation with weak viscosity (Zabolotskaya et al., 1969; Rosnitskiy et al., 2015). The boundary condition to the KZK equation was set as a flat circular source with a uniform pressure amplitude distribution. Focusing was accomplished by changing the phase along the source surface according to the parabolic law as a function of the radial coordinate. In the earlier study (Rosnitskiy et al., 2016) an analytical relationship was shown between the solutions of the parabolic model for a flat disc and the solution of the full diffraction model for a spherical bowl in the focal region of the beam. Given that a single-element source in the shape of a spherical segment is more applicable for practical applications, the results of this study are represented in terms of the parameters of such a spherical source with a uniform distribution of vibrational velocity over its surface.

The KZK equation and the boundary condition were written in dimensionless form (Bessonova et al., 2008):

∂∂θ(∂P∂σ-NP∂P∂θ-A∂2P∂θ2)=14GΔ⊥P,P(σ=0,R,θ)={sin(θ+GR2),R≤10,R>1. (1)

Here P = p/p0 is the acoustic pressure normalized to the pressure amplitude at the transducer p0, θ = ω0 (t–z/c0) is the dimensionless retarded time, σ = z/F is dimensionless axial coordinate normalized to focal length of the equivalent source F, R = r/a is the radial coordinate normalized to the equivalent source radius a0, N = 2πFf0βp0/c0ρ0 is the dimensionless nonlinear parameter, G=πf0a02/c0F is the diffraction parameter (the linear coefficient of pressure amplification with respect to the pressure amplitude on the surface of the transducer), A=Fδω02/2c03 is the absorption parameter, and c0, β, ρ0 and δ are the ambient sound speed, nonlinearity coefficient, density, and diffusivity of sound of the medium, respectively.

The value of the absorption coefficient is very small when focusing in water is considered, A ≪ 1, thus the KZK equation solution depends only on two dimensionless parameters: linear focusing gain G and nonlinear parameter N. To solve the inverse problem of determining the transducer parameters that provide certain nonlinear fields at the focus, a multi-parametric solution of the KZK equation was obtained for a wide range of the values of G and N. Simulations were performed for the parameter G ranging from 10 to 100 with the step of 5, and for the parameter N ranging from 0 to 1.5 (75 points). Using the results of such multiple simulations, the relationship between the parameters of nonlinear field at the focus and the source was established.

3. Results

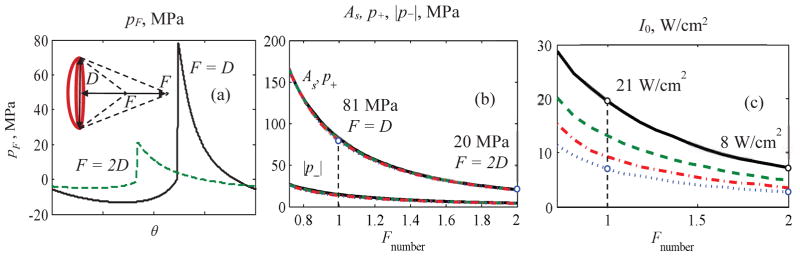
As noted earlier, histotripsy applications require irradiation regimes with high-amplitude shocks at the focus. The regime of focusing at which fully developed shock forms in a focal waveform has been introduced recently (Rosnitskiy et al., 2015). In this regime, the ratio of the shock amplitude in the focal waveform to the source pressure is the maximum that corresponds to the maximum focusing gain (As/p0) = max for the amplitude of the shock relative to the initial pressure amplitude. Characteristic pressure focal waveforms pF (θ) with a fully developed shock for strongly and weakly focused sources are illustrated in Fig. 3(a). Fig. 3(b) shows the dependence of the focal waveform parameters (shock amplitude As and the peak pressures p+ and p−) on the transducer Fnumber for different values of its radius a0 =3, 3.5, 4, and 4.5 cm. The transducer is considered to operate at 1 MHz frequency. It is seen, that the parameters of the focal waveform with a developed shock indeed depend only on the source Fnumber: the curves obtained for different values of the source radius a0 are virtually indistinguishable. Hence, the desired shock amplitude can be obtained at the focus by varying the focusing angle of the transducer. For example, if a developed shock of 80 MPa is necessary, the transducer with focal length equal to the diameter (F = D) or Fnumber = 1 should be chosen. If a shock of smaller amplitude is needed, say 20 MPa, a less focused transducer is optimal: F = 2D or Fnumber = 2 (Fig. 3(b)). The output intensity I0=p02/2ρ0c0 at the source at which fully developed shock is formed at the focus (Fig. 3(c)) depends both on the source aperture and its Fnumber. With the same Fnumber, higher intensity is required for transducer with smaller aperture to provide the same pressure levels in the focus required for shock formation condition; with the same aperture but different Fnumber, lower intensity I0 is needed for less focused transducers where nonlinear effects accumulate over longer focal lobe (Fig. 2).

Fig. 3.

Fig. 3

Open in a new tab

(a) Characteristic focal waveforms with a fully developed shock for a strongly focused (F = D, solid curve) and weakly focused (F = 2D, dashed curve) transducers of 1 MHz frequency. (b) Dependencies of the parameters of the focal waveform with a fully developed shock (As, p+, and p−) and (c) initial intensity, required to obtain a fully developed shock at the focus on the Fnumber of the transducer for different values of its radius: a0= 3 cm (solid curve), 3.5 cm (dashed curve), 4 cm (dash-dotted curve), 4.5 cm (dotted curve).

The results, shown in Fig. 3, were used to design a multi-element HIFU array for boiling histotripsy applications (Khokhlova V. et al., 2015). Some parameters of the array were predefined from the earlier studies. The array consisted of 256 elements that corresponded to the number of channels in the ultrasound (US) power supply; the frequency of 1.5 MHz frequency was determined from multi-frequency BH experiments (Khokhlova T. et al., 2015), a central opening of 40 mm was included to fit an ultrasound imaging probe, and a compact spiral layout of uniformly-sized elements was chosen for maximizing the power output of the array (Gavrilov et al., 2015) (Fig. 4(a)). The goal of this study was to determine the diameter of each array element and the focusing angle of the array so that a developed shock of 90–100 MPa is formed at the focus in water at the intensity of I0<3.75 W/cm2 at the array elements. The last requirement can be explained by technical limitations for the maximum intensity at the array elements (30 W/cm2) when focusing in tissue assuming a 9 dB increase for the source output to compensate for absorption losses in tissue (Bessonova et al., 2010).

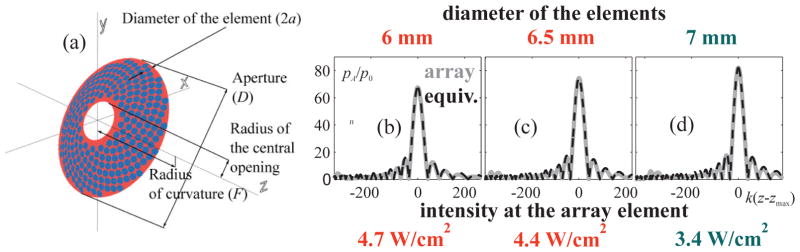
Fig. 4.

Fig. 4

Open in a new tab

(a) A sketch and general parameters of the considered array. An example of determination of the array element diameter is given for the cases of 6 mm (b), 6.5 mm (c), and 7 mm (d) sized elements. The linear axial fields of the arrays, pA/p0, calculated analytically using the Rayleigh integral (solid curves), and the fields of the equivalent spherical sources (dashed curves) are shown. Initial intensities at the array elements, necessary to obtain a fully developed shock at the focus are listed at the bottom of the figure.

Although the results shown in Fig. 3 were obtained for the model of a single element spherical source, they can be successfully used to describe the nonlinear field at the focus of a multi-element array. Indeed, the array can be replaced by an equivalent single element spherical source by varying the radius and the focal length of such a source to match the axial distributions of the linear pressure field of the equivalent source and the array. The hypothesis is that if a good match of the axial fields in the focal region is achieved resulting in the same accumulation of nonlinear effects, the equivalent spherical source will generate the same nonlinear focal field at the focus as the multi-element array.

The procedure of designing the array therefore consisted of several steps. First, the curves for the shock amplitude dependence on the Fnumber of the transducer (Fig. 3(b)) were analyzed. The results showed that in order to obtain the developed shock of 90–100 MPa at the focus, the equivalent spherical source with Fnumber = 0.9 is needed. Then, it was found, by calculating parameters of the equivalent source for different arrays with spiral elements distribution, that the Fnumber of the array is on the average about 8% less than the one of the spherical source. Thus, the Fnumber of the array was chosen as Fnumber = 0.83.

The next step was the choice of the array element diameter. Smaller element size can provide better focus steering capabilities of the array (Ilyin et al., 2015). However, small elements require unattainably high element intensities to produce a shock at the focus (Fig. 3(c)). The diameter of the array elements was increased to reach the value at which the initial intensity I0 is less than 3.75 W/cm2. Three representative cases of the element diameters considered here are shown in Fig. 4: 6 mm, 6.5 mm, and 7 mm. The equivalent source was found for each array, and the initial intensity at the elements, necessary to provide fully developed shock at the focus, was calculated (Fig, 4(b–d)). It is seen, that the case of 7 mm diameter of the element corresponds to initial intensity of 3.4 W/cm2, that is less, than the technical limitation value (I0<3.75 W/cm2).

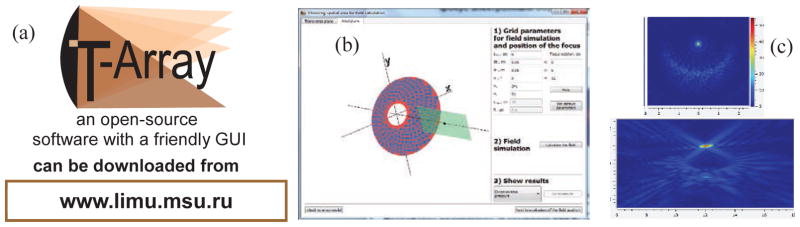
The last step of the array design was evaluating its dynamic focusing capabilities whether they are acceptable for creating volumetric boiling histotripsy lesions in tissue. To perform such evaluation, an open source software package “T-Array” (Fig. 5), developed at Moscow State University was employed (www.limu.msu.ru). The software performs multiple calculations of the array field with different locations of the focus using electronic steering. Two diffraction effects influence the spatial structure of the ultrasound field with electronic steering of the focus. Secondary grating lobes form and focal intensity decreases when the array focus is shifted away from the center of the geometrical curvature of the array. Evaluation of these effects showed that the spatial area of safe (grating lobes are less than 10% of the focal intensity) and efficient (focal intensity decreases is less than 50% of its maximum reachable value) focus steering was determined: ±19 mm along the array axis and ±9 mm transverse, which is acceptable to create volumetric lesions.

Fig. 5.

Fig. 5

Open in a new tab

(a) T-Array software package for fast field simulations and evaluation of the field quality when steering the focus of multi-element arrays. (b) A window of the program for setting parameters of the array, position of the focus, spatial window for simulations, and grid steps for calculating the field with a 3D visualization of the array and calculation area. (c) Windows of the program showing field simulation results.

A photo of the array transducer that has been manufactured (Imasonic, Voray Sur L’ognon, France) based on the proposed design is shown in Fig. 6. The final parameters of the array are: 1.5 MHz frequency, 144 mm aperture, 120 mm focal length (Fnumber = 0.83), 256 elements of 7 mm diameter positioned with 0.5 mm gaps in 16-arm spiral configuration, and 40 mm central opening for a P4-2 ultrasound imaging probe.

Fig. 6.

Fig. 6

Open in a new tab

Photo of the 256-element array transducer designed using the proposed method to generate shocks of 90 – 100 MPa at the focus. The final parameters of the array are: 1.5 MHz frequency, 144 mm aperture, 120 mm focal length (Fnumber = 0.83), 256 elements of 7 mm diameter positioned with 0.5 mm gaps in 16–arm spiral configuration, and 40 mm central opening for a P4-2 ultrasound imaging probe.

4. Discussion and Conclusion

In this study, an inverse problem of determining transducer parameters to provide the desired shock amplitude at the focus was solved. It was shown, that the focusing angle of the source is the main parameter that determines pressure levels in the focal waveform with fully developed shock. A multi-element HIFU array for boiling histotripsy applications was designed using the proposed method. The focusing angle of the array and the diameter of its elements were determined to satisfy technical limitations on the intensity level at the array elements as well as the required shock amplitudes at the focus. The T-Array software package developed to analyze steering capabilities of HIFU arrays was used to evaluate the region of the safe and efficient focus steering for the array design. In general, the results for pressure levels achievable at the focus in a shock-formation regime for different focusing angles of the source can be used for guiding transducer design for various HIFU applications.

This array and the process of designing HIFU probes aiming for the presence of shocks or for avoiding shocks described here will be used for many applications in the future. For example, the design process will help in developing lithotripters that specifically avoid shocks (Maxwell et al., 2015). It also fits well with the techniques described to derate nonlinear and shock waveforms measured in water to waveforms in tissue (Bessonova et al., 2010, Khokhlova et al., 2011). In another example, the array will be used for investigation of repositioning kidney stones (Sapozhnikov et al., 2013) via “tractor beam” (Sapozhnikov et al., 2014; Baresch et al., 2016).

Acknowledgments

That authors thank Bryan Cunitz at CIMU and Rémi Berriet and Simon Esteve at Imasonic for helpful discussions on the details of the array design. Work was supported by NIH grants EB007643 and DK043881, National Space Biomedical Research Institute through NASA NCC 9-58, and RSF grant 14-12-00974.

References

  1. Baresch D, Thomas JL, Marchiano R. Observation of a single-beam gradient force acoustical trap for elastic particles: acoustical tweezers. Physical Review Letters. 2016;116:024301. doi: 10.1103/PhysRevLett.116.024301. [DOI] [PubMed] [Google Scholar]
  2. Bessonova OV, Khokhlova VA, Bailey MR, Canney MS, Crum LA. Focusing of high power ultrasound beams and limiting values of shock wave parameters. Acoust Phys. 2009;55(4–5):463–473. doi: 10.1134/S1063771009040034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bessonova O, Khokhlova V, Canney M, Bailey M, Crum L. A derating method for therapeutic applications of high intensity focused ultrasound. Acoustical Physics. 2010;56(3):354–363. doi: 10.1134/s1063771010030140. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Canney MS, Bailey MR, Crum LA, Khokhlova VA, Sapozhnikov OA. Acoustic characterization of high intensity focused ultrasound fields: A combined measurement and modeling approach. J Acoust Soc Am. 2008;124(4):2406–2420. doi: 10.1121/1.2967836. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Gavrilov LR, Sapozhnikov OA, Khokhlova VA. Spiral arrangement of elements of two-dimensional ultrasonic therapeutic arrays as a way of increasing the intensity at the focus. Bulletin of the Russian Academy of Sciences: Physics. 2015;79(10):1232–1237. [Google Scholar]
  6. Hoogenboom M, Eikelenboom D, Den brok MH, Heerschap A, Futterer JJ, Adema GJ. Mechanical high-intensity focused ultrasound destruction of soft tissue: working mechanisms and physiologic effects. Ultrasound Med Biol. 2015;41(6):1500–1517. doi: 10.1016/j.ultrasmedbio.2015.02.006. [DOI] [PubMed] [Google Scholar]
  7. Ilyin SA, Yuldashev PV, Khokhlova VA, Gavrilov LR, Rosnitskiy PB, Sapozhnikov OA. Analytical method for evaluating the quality of acoustic fields radiated by a multielement therapeutic array with electronic focus steering. Acoustical Physics. 2015;61(1):51–59. [Google Scholar]
  8. Khokhlova T, Canney M, Khokhlova V, Sapozhnikov O, Crum L, Bailey M. Controlled tissue emulsification produced by high intensity focused ultrasound shock waves and millisecond boiling. J Acoust Soc Am. 2011;130(5):3498–3510. doi: 10.1121/1.3626152. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Khokhlova TD, Maxwell AR, Haider Y, Khokhlova VA. Comparison of boiling histotripsy lesions generated at different ultrasound frequencies. Program of the 15th International Symposium for Therapeutic Ultrasound; April 15–18, 2015; Utrecht, Netherlands. 2015. p. 215. [Google Scholar]
  10. Khokhlova VA, Fowlkes JB, Roberts WW, Schade GR, Xu Z, Khokhlova TD, Hall TL, Maxwell AD, Wang YN, Cain CA. Histotripsy methods in mechanical disintegration of tissue: Towards clinical applications. Int J Hyperthermia. 2015;31(2):145–162. doi: 10.3109/02656736.2015.1007538. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Maxwell A, Sapozhnikov O, Bailey M, Crum L, Xu Z, Fowlkes B, Cain C, Khokhlova V. Disintegration of tissue using high intensity focused ultrasound: Two approaches that utilize shock waves. Acoustics Today. 2012;8(4):24–36. [Google Scholar]
  12. Maxwell AD, Cunitz BW, Kreider W, Sapozhnikov OA, His RS, Harper JD, Bailey MR, Sorensen MD. Fragmentation of renal calculi in vitro by focused ultrasound bursts. J Urol. 2015;193(1):338–44. doi: 10.1016/j.juro.2014.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Parsons J, Cain C, Abrams G, Fowlkes J. Pulse, cavitational ultrasound therapy for controlled tissue homogenization. Ultrasound Med Biol. 2006;32(1):115–129. doi: 10.1016/j.ultrasmedbio.2005.09.005. [DOI] [PubMed] [Google Scholar]
  14. Rosnitskiy PB, Yuldashev PV, Khokhlova VA. Effect of the angular aperture of medical ultrasound transducers on the parameters of nonlinear ultrasound field with shocks at the focus. Acoustical Physics. 2015;61(3):301–307. [Google Scholar]
  15. Rosnitskiy PB, Yuldashev PV, Vysokanov BA, Khokhlova VA. Setting boundary conditions to the Khokhlov–Zabolotskaya equation for modeling ultrasound fields generated by strongly focused transducers. Acoustical Physics. 2016;62(2):151–159. [Google Scholar]
  16. Sapozhnikov OA, Bailey MR. Radiation force of an arbitrary acoustic beam on an elastic sphere in a fluid. J Acoust Soc Am. 2013;133(2):661–676. doi: 10.1121/1.4773924. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Sapozhnikov O, Maxwell A, Kreider W, Bailey M. Solid particle transverse trapping at the focus of 1.5-MHz vortex beam radiated by 12-sector ultrasonic array. Abstract book of the 2014 IEEE Int. Ultrasonics Symp; Chicago, Illinois, USA. September 3–6, 2014; 2014. p. 296. [Google Scholar]
  18. Zabolotskaya EA, Khokhlov RV. Quaziplane waves in nonlinear acoustics of bounded beams. Acoustical Physics. 1969;15(1):40–47. [Google Scholar]

RESOURCES