Computational Sensing Using Low-Cost and Mobile Plasmonic Readers Designed by Machine Learning

Abstract

Plasmonic sensors have been used for a wide-range of biological and chemical sensing applications. Emerging nano-fabrication techniques have enabled these sensors to be cost-effectively mass-manufactured onto various types of substrates. To accompany these advances, major improvements in sensor read-out devices must also be achieved to fully realize the broad impact of plasmonic nano-sensors. Here, we propose a machine learning framework which can be used to design low-cost and mobile multi-spectral plasmonic readers that do not use traditionally employed bulky and expensive stabilized light-sources or high-resolution spectrometers. By training a feature selection model over a large set of fabricated plasmonic nano-sensors, we select the optimal set of illumination light-emitting-diodes needed to create a minimum-error refractive index prediction model, which statistically takes into account the varied spectral responses and fabrication-induced variability of a given sensor design. This computational sensing approach was experimentally validated using a modular mobile plasmonic reader. We tested different plasmonic sensors with hexagonal and square periodicity nano-hole arrays, and revealed that the optimal illumination bands differ from those that are ‘intuitively’ selected based on the spectral features of the sensor, e.g., transmission peaks or valleys. This framework provides a universal tool for the plasmonics community to design low-cost and mobile multi-spectral readers, helping the translation of nano-sensing technologies to various emerging applications such as wearable sensing, personalized medicine, and point-of-care diagnostics. Beyond plasmonics, other types of sensors that operate based on spectral changes can broadly benefit from this approach, including e.g., aptamer-enabled nanoparticle assays and graphene-based sensors, among others.

Graphical abstract

Localized Surface Plasmon Resonance (LSPR) is at the heart of a class of biological and chemical sensors which operate by supporting resonances of collective electron oscillations that respond to changes of refractive index within their near field. ^1–3 In these types of sensors, plasmonic resonances occur when light interacts with sub-wavelength metal nanostructures and can be interrogated via far-field optics in the visible part of the spectrum. Typically, a characteristic Lorentzian peak or trough in the reflection or transmission spectrum can be tracked in response to changes in the near-field refractive index. ^3–5 For example, when a target analyte such as a protein or a virus is brought into the near-field of the plasmonic sensor structure, the effective refractive index is altered, and the characteristic peak undergoes a spectral shift. This resonance shift is particularly sensitive to surface binding events, making it a powerful tool to probe biological or chemical interactions near or at the sensor surface. LSPR sensors have already extensively been demonstrated in the literature as effective biological and chemical sensors, used for e.g., measuring DNA hybridization, heavy metal ion concentration, cancer bio-marker detection, quantification of protein concentration, and even viral load measurement in unprocessed blood samples. ^6–21 Furthermore, recent advances in nano-fabrication technologies such as colloidal self-assembly, soft lithography, and imprint molding have enabled high-throughput, low-cost, and scalable production of flexible, large-area, plasmonic sensors with a variety of different 2D and 3D nanostructure designs including nano-hole arrays, dome arrays, cross arrays, and many other exotic geometries. ^8,22–32 This recent and exciting trend now extends the applications of plasmonic sensors beyond laboratory settings for use as wearable sensors or as disposable point-of-care sensors, and also permits their integration into existing medical equipment such as intravenous tubes, syringes, blood bags, bandages, or medical garments. ^5,30,33–37

However, with the proliferation of these low-cost and flexible LSPR-based sensors, alternative designs for the corresponding read-out devices must also be considered. Field portability, low-cost, ease-of-use, and network connectivity are all desired features for ensuring widespread adoption of these sensing systems. ^33,38,39 Currently, the most common read-out and quantification scheme for LSPR sensors employs a stable, broad-band light source for illumination and a high resolution optical spectrometer for recording the transmission or reflection spectra. ^3,6,40–43 Alternatively, a tunable light source and a single photodiode can be used to obtain the same spectral information. Although a ‘peak/valley tracking’ based detection approach is quite effective in accurately registering and quantifying the sensor response, it requires optical hardware which can retrieve comprehensive spectral information, over a broad wavelength range of e.g., 400-700 nm. The inclusion of the above mentioned optical components can result in spectral read-out devices which are prohibitively bulky and expensive for many applications, especially in field and resource limited settings. Therefore, in an effort to engineer cost-effective and mobile plasmonic read-out devices, inexpensive optical components such as LEDs, complementary metal–oxide–semiconductor (CMOS) imagers or single photodiodes along with mobile-phone based designs can be considered. Some recent work has showcased such design considerations. ^44,45 However, in designing these mobile devices, one must select a strategic set of bands to be able to sensitively register the spectral response of the plasmonic sensor design. This LED selection process is crucial to the performance of the plasmonic read-out device, and is influenced by many factors such as the spectral location of the plasmonic resonances, as well as the responsivity of the CMOS imager or the photodiode. Additionally, the optical signal resulting from the selected set of LEDs must contribute to a mathematical sensing model that is tolerant to the inherent fabrication variability of the plasmonic chips, which is unavoidable especially when using some of the emerging large-area, low-cost nano-fabrication techniques. ^46,47 Finally, these LSPR sensors should be ‘plug and play’ and not need an individualized calibration procedure per sensor chip that is often performed in the literature.

In this work we demonstrate a machine-learning based computational sensing framework which can be used to design the most optimum and yet cost-effective plasmonic read-out device that is suitable for various mobile sensing applications in field and resource-poor settings (see Fig. 1). Our computational sensing framework implements a statistical approach to determine the optimal set of illumination LEDs needed to create a minimum error refractive index prediction model by taking into account the varied spectral responses as well as the fabrication variability of the plasmonic sensor design of interest. To demonstrate this approach, ‘training data’ were taken over a statistically significant number of individual sensors (N>30) for two different plasmonic sensor designs (hexagonal and square periodicity nano-hole arrays, see Fig. 2), fabricated using a large-area nano-imprint molding approach, to learn the spectral response of each plasmonic design due to refractive index changes. This data set was then used to train a machine learning algorithm with pre-defined constraints in order to form a computational model which accurately predicts the bulk refractive index of unknown test samples, without the need for an individualized calibration procedure per test.

Figure 1.

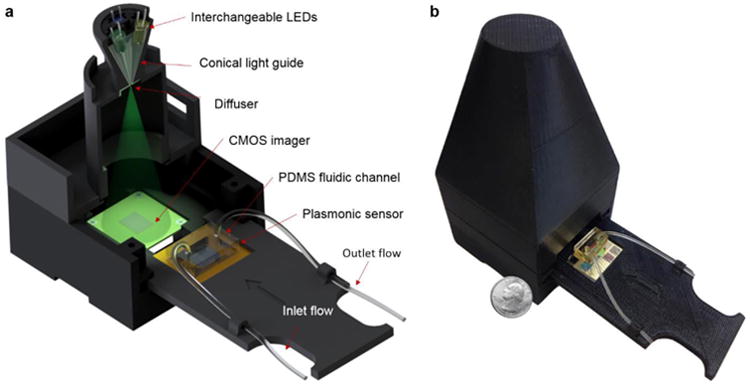
Modular design of our mobile, multi-spectral plasmonic reader. (a) Schematic illustration of the components of the reader. (b) 3D-printed prototype of the plasmonic reader used in this work.

Figure 2.

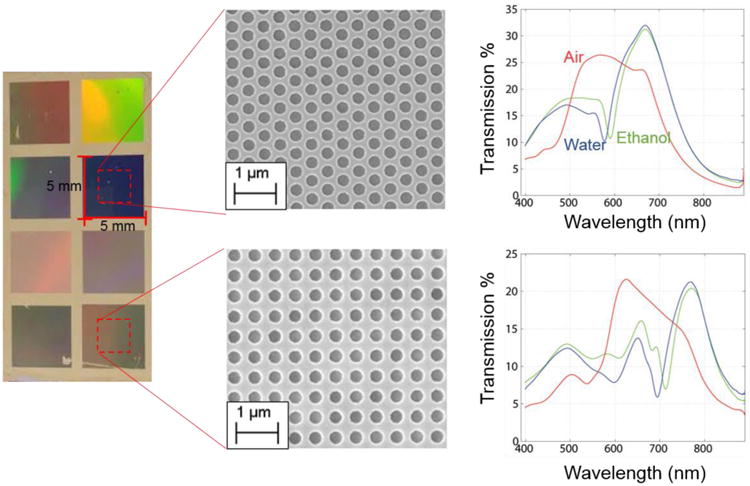
Optical (left) and SEM images (middle) of the plasmonic sensors consisting of hexagonal and square array of nano-holes and their corresponding transmission spectra in differing refractive index environments (right).

This proposed computational sensing framework can be generally used by the plasmonic sensing community to design optimized LSPR read-out devices which aim for cost-effectiveness, mobility, and robustness. Our approach can be broadly applied to any LSPR sensor geometry, and can accommodate any set of practical design constraints. Beyond the scope of LSPR sensors, this computational sensing and design framework can also be employed by any type of biochemical sensor which operates via a spectrum change or shift. Emerging sensing elements such as aptamer-enabled nanoparticle assays, plasmonic interferometers, dynamically tunable plasmonic sensors, and graphene-based materials, with engineered physical properties and responses can similarly be analyzed by this framework in order to determine the optimal mobile read-out and computational sensing scheme. ^24,48–54 Taken together, this proposed framework can be used as a robust engineering tool to design next generation plasmonic read-out and sensing devices for e.g., wearable and embedded sensing systems, personalized medicine applications, and point-of-care diagnostics, among various others.

Results and Discussion

Computational sensing and design framework for multi-spectral mobile plasmonic read-out using machine learning

The machine learning approach used in this work selects the optimal sub-set of LEDs from a pre-defined library, and aims to produce the minimum error refractive index prediction model for a given plasmonic nano-structure design and nano-fabrication method. To generate the initial ‘training data’ set, our plasmonic sensors, equipped with fluidic channels, were placed on a transmission stage and illuminated by a fiber-coupled broadband stabilized light source (Thor Labs, SLS201) as outlined in Figure 3. This training process needs to be performed only once for a given plasmonic sensor design and nano-fabrication method, and it aims to infer the statistical spectral variations of the sensor design, as a function of bulk refractive index as well as fabrication tolerances and imperfections. After a ‘spectral stack’ was recorded for every chip in the training set (N = 33 for both the hexagonal and square periodicity nano-hole arrays, Fig. 2), each spectrum was normalized to its ‘reference spectrum’, which in this case was taken to be the plasmonic transmission spectrum in de-ionized water (RIU = 1.3325). It is important to note that the resulting normalized ‘contrast spectra’, as shown in Figure 4, were normalized to their own characteristic references. A global reference would not properly zero the contrast information from the LEDs for every trained chip and therefore was not used. Next, a custom-built LED library (refer to the Materials and Methods Section for details) was utilized to simulate every possible LED transmission through the sensor. By defining the spectral output of each LED in terms of the peak wavelength and line-width specified in their respective data sheet, the overlap integral of the LED spectra with the plasmonic contrast spectra was numerically calculated. Applying this procedure for each sensor in the training data set yielded a matrix, X_Lib. which contained the simulated contrast values of all the LEDs in the pre-defined LED library for each bulk refractive index that was sampled during the training experiments (see Fig. 4). Specifically, the number of rows in this matrix is defined by the product of the number of plasmonic nano-sensors trained (N=33) and the number of transmission spectra sampled per sensor during the bulk refractive index modulation, which for our data set was 13, i.e., 33 × 13 = 429 rows exist in X_Lib. The number of columns is defined by the number of LED contrast features (i.e., the number of entries in our LED library, denoted with n in Fig. 4) plus one, where an additional column of ones is concatenated onto the LED contrast feature matrix to provide a constant term in the linear model. Quite importantly, X_Lib contains spectral data from multiple plasmonic sensor chips, and therefore has the appropriate statistical information of how each sensor's spectral response varies due nano-fabrication variability and imperfections.

Figure 3.

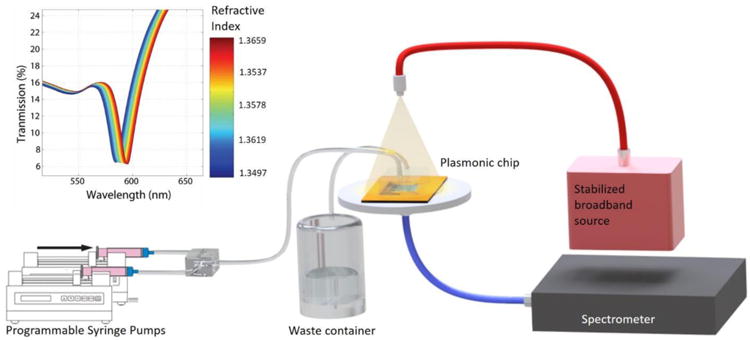
Schematic illustration of the fluidics set-up for collecting training data. The inset shows a representative transmission spectrum shift as the surrounding bulk refractive index was increased.

Figure 4.

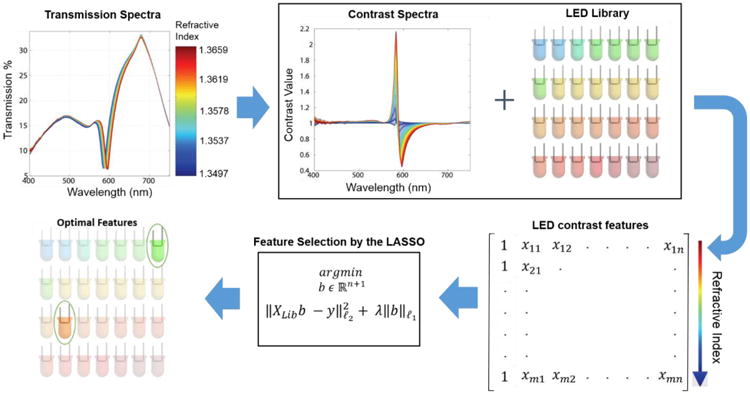
Schematic illustration of the machine learning framework.

This training data matrix, X_Lib, was then used as an input into an L1-norm regularization algorithm (i.e., LASSO, least absolute shrinkage and selection operator) which aims to find a regularized least-squares solution between the output of a linear model and the measured ‘gold-standard’ refractive index values, y, i.e. ^55–58

$$b^{\ast }=\underset{b\in {\mathbb{R}}^{n+1}}{\mathit{\text{argmin}}}{\Vert X_{\mathit{\text{Lib}}}b-y\Vert }_{{\ell }_2}^2+\lambda {\Vert b\Vert }_{{\ell }_1}$$ Eq. 1

where the vector b is the variable which is solved for, b* being the optimal solution for computational sensing, corresponding to the n + 1 optimal coefficients, which define the linear model. λ is the regularization parameter, which in this work is typically set to be between 10^-4 and 10^-7, as further discussed later in the manuscript.

Based on the above described statistical framework, in order to determine the optimal set of LEDs to be used in our computational mobile plasmonic reader, we used a ‘leave-one-sample-out cross validation’ (LOOCV) procedure with the training data set (N=33). For each iteration, the 33 samples were partitioned; 32 samples as training data and 1 sample being used a testing sample. The regularization parameter was selected by performing a nested LOOCV within that iteration's set of 32 training samples, revealing what range of parameters yielded the minimum error model, which for these training sets was typically between 10^-4 and 10^-7. It is also important to note that as the regularization parameter is varied over this range, the mean-squared-error of the nested LOOCV remains within one standard deviation of the minimum error and the features with corresponding non-zero coefficients in the linear models remain constant (see Supplementary Figure 2). This analysis indicates that no large bias or over-fitting permeates the linear models with this selection of the regularization parameter.

During this LED selection process and LOOCV procedure, 33 different linear models were generated using the LASSO (Eq. 1) and all the non-zero coefficients in each resulting b* solution were recorded every iteration, revealing which LEDs were statistically favored out of our LED library for forming the optimal linear model. The top four LEDs utilized most in these linear models were then selected for the testing process. A detailed ranking of these LEDs is shown in Supplementary Figure 3. For the case of the square periodicity nano-hole array (see Fig. 2), the fourth ranked LED (λ_peak = 735 nm) was replaced by an LED with λ_peak = 660 nm so that in the blind validation step we could directly compare our optimal linear model to a model created with LEDs directly to the left and right of the dominant plasmonic spectral feature as discussed later.

After this LED selection process, the optimal set of LEDs that we inferred were installed into our field-portable plasmonic reader device (Figure 1), the modular optical hardware of which will be detailed in the next sub-section. To ensure an accurate refractive index prediction model, the exact output spectra of the selected LEDs were also measured and used in our computational sensing step to mitigate any error which might occur due to slight differences between the modeled and actual spectra of the selected LEDs. The final refractive index prediction model was then generated by inputting the entire training data set into the same L1-norm regularized LASSO algorithm, this time with the training data matrix, X_optLED, consisting of 5 columns (4 columns corresponding to the optimal set of 4 LEDs installed in the portable reader, plus the column of ones as before), i.e.,

$$b_{\mathit{\text{mobile}}}^{\ast }=\underset{b_{\mathit{\text{mobile}}}\in {\mathbb{R}}^{n+1}}{\mathit{\text{argmin}}}{\Vert X_{\mathit{\text{optLED}}}{b}_{\mathit{\text{mobile}}}-y\Vert }_{{\ell }_2}^2+\lambda {\Vert b_{\mathit{\text{mobile}}}\Vert }_{{\ell }_1}$$ Eq. 2

where the regularization parameter (λ) was determined to be 1.15 × 10^-6 and 4.78 × 10^-7 for the hexagonal and square periodicity implementation of the algorithm, respectively. This selection was based off a secondary LOOCV, which determined the λ needed to achieve the minimum error solution over the training set. This secondary cross-validation step also elucidates the degree to which over-fitting might occur with the final linear model. Parametrically sweeping the regularization parameter over a logarithmic range of 10^-7 to 10⁰ assures that there is no over-fitting with the selection of a small regularization parameter in the range 10^-7 to 10^-4. This is because our set of LED contrast features are highly correlated to the change in the refractive index, especially given the optimal set of LEDs that exclude the features yielding the highest variance from chip to chip. The optimal solution for our mobile plasmonic reader design, $b_{\mathit{\text{mobile}}}^{\ast }$ was then used as the vector of coefficients in the final computational sensing step to predict the refractive index (RIU) of the sample using the mobile reader device, i.e.,

$${\mathit{\text{RIU}}}_{\mathit{\text{prediction}}}={\mathrm{X}}_{\mathit{\text{test}}}{b}_{\mathit{\text{mobile}}}^{\ast }$$ Eq. 3

where each row of X_test refers to an independent sensing measurement or multi-spectral test made with our mobile plasmonic reader.

Modular optical design of a low-cost and mobile multi-spectral plasmonic reader

Figure 1 shows the LED-based mobile multi-spectral plasmonic reader hardware used to validate our framework. This modular device is compact (6.5 × 6.5 × 7.5 cm), light weight (< 160 g), and cost effective, utilizing multiple LEDs for illumination and a CMOS imager (Basler dart series, daA1280-54µm USB 3.0) for the capture of the transmitted light from a plasmonic sensor of interest. An Arduino micro-controller was programmed to sequentially power on the LEDs and trigger the camera for image capture. The resulting device was prototyped via 3-D printing, and can be powered either through a USB cable or by battery. This device was specifically designed to accommodate interchangeable LEDs (up to a maximum of 4), consisting of a detachable 3-D printed cap which holds the selected LEDs and allows for convenient substitution of each LED depending on the design of the plasmonic chip. In this work, we used plasmonic nanostructures in the form of hexagonal and square array of holes with periodicity, relief depth, and hole diameter of 500 nm, 300 nm, and 380 nm, respectively, as shown in Figure 2. These plasmonic sensors were fabricated using soft imprint lithography, a process that is low-cost, scalable, and high-throughput, as detailed in the Materials and Methods section. During the device operation, the LEDs are turned on sequentially and their output light is guided through a conical light-guide onto a diffuser and then into a 1 mm pinhole. This design allows for up to four LEDs to mutually illuminate the LSPR sensor at approximately normal incidence angle. Additionally, this design records multi-pixel optical transmission information over a field of view of >17 mm², as opposed to the hyper-spectral yet single-pixel information obtained by a traditionally employed spectrometer. This difference in our field portable design allows for a multiplexed sensor read out, simultaneously reading transmission information from multiple surface functionalized regions targeting e.g., a panel of analytes. For the purposes of this study and to illustrate the proof-of-concept of our proposed computational sensing framework, we calculated a single transmission value from each CMOS image for a given illumination LED and bulk refractive index by averaging the pixel intensity of a centrally located binned region (i.e., 100 × 100 pixels). Lastly, the incorporation of a CMOS imager provides a robust, easy-to-align and yet compact design with simple light-coupling as a result of the in-line lensless imaging-based computational detection scheme.

Blind testing and validation of the machine learning and computational sensing framework using a modular mobile plasmonic reader

For independent validation of our computational sensing framework, our low-cost and field-portable plasmonic reader was used to blindly test a set of LSPR sensors, i.e., the plasmonic sensors being tested had not previously been used in our training data, preventing any sort of data contamination or artificial overfitting in the final linear model. Eight chips (N = 8) were tested with M=13 refractive index measurements sampled for each plasmonic chip, using the same fluidics mixing set-up illustrated in Figure 3. To illustrate the generality of this framework, both the hexagonal and square periodicity nano-hole arrays were tested (see Fig. 2), and the mean error of the RIU predictions resulting from our computational sensing framework (Eq. 3) was calculated using,

$$\mathit{\text{Mean Error}}=\frac{1}{NM}{\sum }_{p=1}^N{\sum }_{i=1}^M|{\mathit{\text{RIU}}}_{{\mathit{\text{prediction}}}_i^p}-y_i^p|$$ Eq. 4

Where, ${\mathit{\text{RIU}}}_{{\mathit{\text{prediction}}}_i^p}$ and $y_i^p$ represent the predicted and the gold standard refractive index values, respectively, for a given measurement, I, and a given testing chip, p.

Figure 5 compares three distinct linear models for our plasmonic sensors, for both the hexagonal (Fig. 5 a-c) and square nano-hole array designs (Fig. 5 d-f). The first linear model (dark blue) uses a single LED feature closest to the dominant plasmonic spectral feature (located at 590 nm and 700 nm for the hexagonal and square periodicity nano-hole arrays, respectively). The second linear model (light blue) uses a pair of LEDs directly to the right and left of the dominant plasmonic spectral feature. Lastly, the third linear model (green) uses the LEDs chosen through the feature selection process based on our machine learning framework. Previously published LED based field-portable plasmonic reader designs often use the second linear model (i.e., a ratio-metric approach) to measure and quantify sensor responses (45). However, this type of a design does not necessarily provide the most accurate results. For example, in the case of the hexagonal nano-hole array LSPR sensor, a linear model using LEDs that are closest to the main spectral feature, i.e., 595 nm and 527 nm LEDs to the right and to the left of the LSPR peak, respectively, resulted in ˜5 times higher mean error compared to a linear model using LEDs (525 nm and 611 nm) selected based on our machine learning approach (see Fig. 5). This reduction in mean error enabled by our machine learning approach is largely due to the inherent fabrication variability of large-area, low-cost, and scalable nano-fabrication techniques. This fabrication variability can be evidenced by varied microscopic and macroscopic defect rates, differing cured photo-polymer thickness, non-uniform topography, which might cause slight deviations from perfectly normal illumination thus altering the coupling conditions, as well as deformation of the desired cylindrical non-hole array structure. The advantages gained in scalability and cost-effectiveness of nano-fabrication can adversely result in subtle differences in peak locations of the main LSPR resonance from chip to chip (1-2 nm difference in peak location) as well as varying line-widths of the resonance. Therefore, when LEDs are ‘intuitively’ chosen based on their proximity to the dominant spectral features of the plasmonic sensor, they can yield large variances in their contrast values during the analyte-induced spectral shift. Therefore, such features should be avoided when designing a robust read-out model, especially when dealing with a large number of sensors that will naturally exhibit fabrication-related variations in their spectral response, as detailed earlier. Here we also illuminate an important trade-off in which signal strength (i.e., absolute LED contrast) is sacrificed for features which yield lower variance from chip to chip. In other words, more stable features exist from LEDs which only have partial spectral overlap (and thus less contrast) with the dominant spectral features. Our machine learning-based computational sensing approach ultimately selects the optimal compromise in this trade-off for a given plasmonic design and fabrication method.

Figure 5.

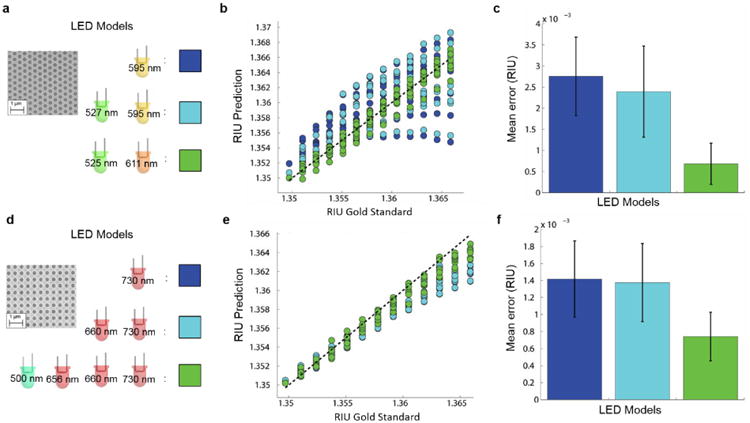
Comparison of different LED linear models. LEDs used in linear models (a), (d) for the two plasmonic sensors; hexagonal and square periodicity nano-hole arrays, respectively. (b), (e) Comparison between the refractive index prediction and gold standard values for the three models used in (a) and (d), respectively. Each LED model is color coded for better visualization, and the third linear model (green) uses the LEDs chosen through the feature selection process based on our machine learning framework. Mean error comparison is provided in (c) and (f) for the three linear models. Please refer to the Supplementary Information for additional performance comparisons among different models.

In the case of the hexagonal plasmonic sensor, the feature selection property of the L1-norm regularized LASSO algorithm recognized the large variance of the 595 nm LED contrast values and therefore forced this coefficient in the linear model to zero, instead selecting the 611 nm LED as a more stable spectral feature. A similar, albeit less dramatic effect, can be seen with the square periodicity plasmonic sensor. For this testing data, a model which utilized four LED contrast features proved more robust than using the two ‘intuitive’ LEDs located to the right and left (730 nm and 656 nm, respectfully) of the dominant LSPR spectral feature. Of particular importance is the inclusion of the 500 nm LED into the optimal model which reduced the refractive index prediction error in the testing data by 50%. This LED would not necessarily have been chosen by intuition because it is almost completely removed from the main LSPR spectral feature.

In summary, by ‘learning’ from the training data, which needs to be performed only once for a given plasmonic chip design and fabrication method, this machine learning and computational sensing framework identifies the spectral regions with a consistent response, differentiating them from the spectral regions with a varied response, and accordingly adjusts the computational sensing linear model to select the most stable features by divulging the optimal set of spectral bands (LEDs) and their corresponding weights. For completeness, the testing errors corresponding to all the possible linear models which could be made with the 4 selected LEDs and training data sets were also calculated and compared to each other for both of our plasmonic sensor designs (see Supplementary Tables 1-2.) In this comparison, we selected linear models which are solutions of the L-1 norm LASSO regularization, the L-2 norm Tikhonov regularization,⁵⁹ and a multivariable least squares solution based on QR decomposition, which contains no regularization term.⁶⁰ As detailed in our Supplementary Information, Supplementary Tables 1-2 not only compare the performances of the linear models solved using these three techniques, but also illustrate comprehensively how our ‘optimal model,’ $b_{\mathit{\text{mobile}}}^{\ast }$ compares to other linear models made with all the combinations of the LEDs that could be installed in our modular mobile plasmonic reader. It is evident from the testing data reported in Supplementary Tables 1-2 that the Tikhonov regularization, similar to LASSO, is effective in designing low error computational sensing models. However, it should be noted that the Tikhonov regression cannot replace the feature selection properties of LASSO, and therefore cannot explicitly be used to determine an optimal subset of features from a larger non-sparse set of features.

Lastly, in an effort to realistically address the role of future plasmonic read-out devices for various emerging sensing applications it must be emphasized that the plasmonic sensors used in this study were fabricated with techniques which allow for high-throughput, low-cost, and scalable sensor production. For example, the vapor deposited ‘non-stick’ layer on the silicon master (detailed in the Materials and Methods section) lasts for many iterations of the fabrication procedure, only needing to be reapplied after every 30-40 uses as a mold. Although the production of the initial silicon master requires the use of conventional photolithography tools and procedures, each silicon master can be used indefinitely with proper care and treatment, producing hundreds to thousands of soft molds, thereby dramatically reducing the fabrication cost of each quasi-3D nanostructure. Additionally, the subsequent imprint molding process can be performed by individuals with minimal training and equipment, requiring only basic tools and a standard UV lamp. This process can also be highly parallelized, only being limited by the number of silicon masters available for the initial soft mold fabrication. Each soft mold can be used upwards of 20 times without incurring significant defects. The metal deposition is the only step in this procedure which requires a clean-room facility, however, each metal deposition run can produce thousands of plasmonic sensors, depending on the tool configuration. For example, with the metal deposition tool (CHA Solution Electron Beam Evaporator) used in this work, approximately 1,400 plasmonic sensors can undergo metal deposition at once, assuming each sensor has an area of 5×5 mm and seven four-inch wafers can be loaded into the evaporator per run (as in our case). The material costs are also minimal, with ˜0.4 grams of gold being used per run for a 50 nm coating.

Conclusions

We developed and validated a universal machine learning and computational sensing framework, which brings mobility and cost-effectiveness to plasmonic sensor read-out device design. This computational sensing approach is especially valuable in designing multi-spectral readers where the selection of optimal low-cost illumination bands is critical. This framework is truly a ‘black-box’, compatible with any arbitrary plasmonic sensor geometry, and any illumination library based off of user-defined design constraints. As a result of this, the presented framework can be extended to broadly benefit any optical sensor which operates based on spectral changes in its transmission or reflection response. Also, because any illumination library can be used, more targeted libraries which include the spectral output from combinations of filters and LEDs can be explored along with the rolling addition of emerging illumination sources. Taken together, we believe this framework can be used by the plasmonic sensing community to design and optimize low-cost mobile readers for quantification of e.g., protein concentration, ion detection, and even whole-virus quantification with minimum error. Furthermore, coupled with the advances in scalable and low-cost plasmonic sensor fabrication techniques, our computational sensing approach holds significant potential to advance emerging applications for wearable sensors, personalized medicine, and point-of-care diagnostics.

Materials and Methods

Nano-fabrication of plasmonic sensors

The fabrication process of our plasmonic sensors (depicted in Supplementary Figure 1) involved first generating a silicon ‘master,’ through a one-time photo-lithography process, which contained the desired nanostructures such as our hexagonal and square periodicity nano-hole arrays. Next, a monolayer of Tridecafluoro, 1, 1,2,2-Trtrahydrooctyl-1-trichlorosilane (Gelest, Inc.) was deposited via vapor deposition to form a ‘non-stick’ layer for the subsequent nano-imprint molding process. The masters were then used as molds by casting a drop of UV curable polyurethane acrylate (PUA-311RM, Minuta Technology, Inc.) onto the surface. A flexible cellulose-acetate film was used to disperse and flatten the liquid droplet over the silicon master, before being placed under a UV lamp (UV-A, 4W, 800 μW/cm², Thermo Fisher) for 2 hours to cure. After UV curing, the cellulose-acetate film was peeled from the master, completing the fabrication process of the ‘soft mold’. These soft molds therefore consist of the inverse geometries of that on the silicon master, and must be used for a secondary imprint molding process in order to recover the desired nano-hole array structure. The soft mold was then used to imprint its relief features onto liquid precursor of photo-curable polymer (NOA 81) deposited onto an oxygen plasma cleaned glass slide. After 25 minutes of curing time under the UV lamp, the soft mold was peeled away from the glass backed photo-polymer, completing the fabrication process of the desired quasi-3D nano-hole array. Finally, a bi-layer of 5 nm chromium and 50 nm gold was deposited onto the nanostructures by Electron Beam Evaporation (CHA Solution Electron Beam Evaporator) at a deposition rate of 2 Å/s and 3 Å/s, respectively, to complete the fabrication of the plasmonic sensor. Once the final plasmonic sensor was fabricated, a fluidic channel made of Polydimethysiloxane (PDMS) with a 300 μm height and 3 mm width was placed onto the surface with inlet and outlet holes to allow for unidirectional flow over the plasmonic sensor surface.

Experimental training data

A high resolution spectrometer (Ocean Optics, HR2000+) was used to continuously capture the transmission spectra of the plasmonic sensors as the bulk refractive index in the fluidic channel was modulated over time. To ensure accurate and consistent bulk refractive index modulation during the training experiments, two programmable syringe pumps were employed (Chemyx, Fusion 100 Infusion). The first syringe pump contained filtered de-ionized water, and the second contained 0.3 g/mL glucose solution in water. The syringe pumps each fed into a T-connector where their contents were combined and mixed through diffusion in a fluidic channel with a length of 60 cm. During the course of these training experiments, the combined flow rate of the two syringe pumps was held constant at 30 µL/min, while the flow rate of the first syringe pump containing water was programmatically decreased and the flow rate of the second syringe pump containing the glucose solution was programmatically increased, ensuring a continuous and consistent gradient of bulk refractive index over the plasmonic sensor surface. These continuous spectral measurements of the transmission formed a ‘spectral stack’ which describes the individual plasmonic sensor's spectral evolution in response to increasing bulk refractive index. To ensure the bulk refractive index modulation was appropriately being executed, bulk refractive index samples were taken at the experimental time-points and verified with a refractometer (Bausch and Lomb, Abbe refractometer). For each plasmonic nano-structure design, we measured the transmission spectra of N = 33 individual plasmonic sensors, which provided sufficient statistical information on spectral variations due to fabrication tolerances, as already discussed in the Results and Discussion section.

Formation of the LED library

A library of possible illumination LEDs was generated by applying constraints to the available LEDs in the ‘LED Indication-Discrete’ database on the Digi-Key website (i.e., ˜21,000 LEDs).⁶¹ The on-line database was filtered using the following design constraints: 465 nm < λ_peak < 700 nm, millicandela rating > 10,000 mCd, and a requirement of through-hole mounting type. These design constraints ensured that the necessary plasmonic spectral region was covered, and that each LED had sufficient brightness for image capture. The following surface mount LEDs were also added to our LED library ad-hoc to cover the spectral region to the right of the dominant plasmonic feature of the square periodicity sensor: 656 nm (DigiKey part number: 475-3008-1-ND), 660 nm (DigiKey part number: 1214-1436-1-ND), 730 nm (DigiKey part number: 1214-1440-1-ND), 735 nm (DigiKey part number: 1416-1913-1-ND). Our final LED library consisted of 28 LEDs as depicted with color representation in Figure 4.