Solitonic conduction of electrotonic signals in neuronal branchlets with polarized microstructure

Abstract

A model of solitonic conduction in neuronal branchlets with microstructure is presented. The application of cable theory to neurons with microstructure results in a nonlinear cable equation that is solved using a direct method to obtain analytical approximations of traveling wave solutions. It is shown that a linear superposition of two oppositely directed traveling waves demonstrate solitonic interaction: colliding waves can penetrate through each other, and continue fully intact as the exact pulses that entered the collision. These findings indicate that microstructure when polarized can sustain solitary waves that propagate at a constant velocity without attenuation or distortion in the absence of synaptic transmission. Solitonic conduction in a neuronal branchlet arising from polarizability of its microstructure is a novel signaling mode of electrotonic signals in thin processes (<0.5 μm diameter).

Introduction

Motivation

The dynamic structure of electrical activity in the nervous system is information-rich¹ with action potentials considered by most neuroscientists to form the basis of electrical signaling². Action potentials are electrical spikes quantitatively described through a system of nonlinear equations developed by Alan Hodgkin and Andrew Huxley³ (hereafter H-H). The H-H model treats the nerve as an electrical cable upon which a propagating action potential is driven by dynamics. It is inscribed in a porous medium where currents leak through resistors and the membrane is a dielectric represented by a classical capacitor. Remarkably, the H-H model provides a quantitatively accurate description of electrical phenomena in neurons through properties of solitary waves. In particular, the nerve impulse, which is a solitary wave, is localized and remains stable, but destabilizes after collision with other action potentials⁴. Indeed, this has been understood as a golden rule of cable theory for neurons without microstructure⁵.

Conferring with the H-H model, colliding action potentials will annihilate due to the in-activation of the sodium conductance (the refractory period). However, there are also studies with the findings that two colliding action potentials will not lead to their mutual annihilation right away. Instead, they reflect from one another and eventually they annihilate, thereby projecting solitonic properties, see refs ^{6, 7}. Nevertheless, action potentials are solitary pulses and not solitons since they do not preserve their shape and velocity after collision. In other words, the crucial test for solitary pulses to be solitons is robustness to collision.

The early work of Aizawa and colleagues⁸ proved the existence of solitons in dissipative media referred to as ‘dissipative solitons’, which are dubbed quasi-solitons as dissipation is evident after collision. Although quasi-solitons (or soliton-like) behavior has been observed in many excitable systems⁹, the existence of solitons in reaction-diffusion systems was first shown by Tuckwell^{10, 11}. A reaction-diffusion system describes the concentration of charged ions which is mathematically equivalent to the conduction of current as flow of electrical charges in an electrical cable model. For example, a hybrid model developed by Meier and colleagues¹² proposed a voltage-dependent Nernst potential in a reaction-diffusion system where the membrane potential exhibited solitonic properties on an assumption that H-H model behaved like an electrochemical, reaction-diffusion system.

The H-H model excludes microstructure and simply assumes a homogenized resistive fluid for the interior of the giant axon of Loligo. Earlier cable modeling efforts treated the intracellular medium of neurons to be a homogeneous resistive fluid of 70 Ωcm as measured for electrolyte solution only, see ref. 13. Meier and colleagues¹² observed in neurons with radii several orders of magnitude smaller than that of the giant axon of Loligo, to have significant intracellular charge depletion. For these reasons, a cable model is required that specifically addresses electrotonic signal propagation in small neuronal processes with microstructure^{14, 15}. Modeling efforts by Shemer and colleagues¹⁶ have explicitly considered endoplasmic reticulum encased within a core-conductor. However, such cytoplasmic inhomogeneity in the microstructure does not explicitly take into consideration intracellular capacitive effects due to charge flow of molecular ions as a result of protein polarization¹⁷ or include capacitive effects only in the extracellular space¹⁸.

A cable model with passive membrane that includes the diffusion of free charge was derived in which it was confirmed that the diffusion of free charge contributes through the conduction of current flow arising from capacitive charge-equalization and axial capacitive effects¹⁹. The model was further developed by including polarization current due to dispersion of bound charge on the surface of endogenous structures in the cytoplasm²⁰. This resulted in polarization current arising from electrostatic interactions between charges/dipoles in the cytoplasm at slow varying electric fields (e.g., quasi-electrostatic conditions) causing self-excitability with a variety of different electrical signaling patterns created by charges held by the microstructure.

Gonzalez-Perez and his colleagues²¹ had shown experimentally how a collision between two electrical pulses did not result in their annihilation. This contrasts to the collective idea of annihilation due to the existence of a refractory period in the H-H model^{4, 5}, implying that active conduction is not universal for all types of nerve fibers after all. They proposed that their results can be explained in terms of a soliton model^{22, 23} based on the assumption that changes in lateral density of the membrane are proportional to changes in voltage. And mechanical signals propagate in phase with electrical pulses²⁴, so that a thermodynamic theory of a nerve impulse could be seen as complementary, which is nonelectrical and consistent with an adiabatic wave (e.g. sound wave), see ref. 25. Mechanical changes during an action potential can produce a self-sustaining and localized density pulse propagating over long distances without loss of energy with minimum propagation speed of 100 m/s, see ref. 26. However, Gonzalez-Perez and his colleagues²¹ experimental result have shown electrical pulses (which they presumed to be action potentials) of less than 10 mV in axons with diameter of lateral giant (Lumbricus terrestris) axons between 4 to 100 μm with velocities well under 10 m/s. Therefore their results are not compatible with a mechanical soliton model. In this paper, we introduce an alternative signaling mechanism based on solitonic conduction of electrotonic potentials that is compatible with their experimental results.

Methods

Intracellular capacitive effect of microstructure

Microstructure contains a dense meshwork of cytoskeletal structures made up of neutrally charged macromolecules assembled from amino-acids using information encoded in genes in a polypeptide chain linked by peptide bonds. At random orientations, the arrangement of charges in some macromolecules are static when no electric field is present, but in the presence of an electric field, macromolecules become polarized and separate by orienting the dipole moments of polar molecules resulting in the formation of permanent dipoles which attract surface charge densities (so-called bound charge densities) causing a displacement of charge. These bounded charges produce intracellular capacitive effects that can contribute to ionic current flow arising from the dispersion (fluctuation) of bound charge by affecting the voltage created by charge flow of molecular ions in the intracellular fluid.

One way to increase the densities of electrical charges within a neuronal branchlet (i.e., thin dendrite or thin axon that is under half a micron in diameter) is to polarize microstructure in the presence of quasistatic electric field (see Fig. 1). For example, the flux generated by electrical conduction of a polarized current in the longitudinal direction (along the cable length) arising from polarizability of its microstructure. In Fig. 1 the branchlet is shown to be tapering, while the model to be derived is intended to represent only for nontapered cylindrical representation.

Figure 1.

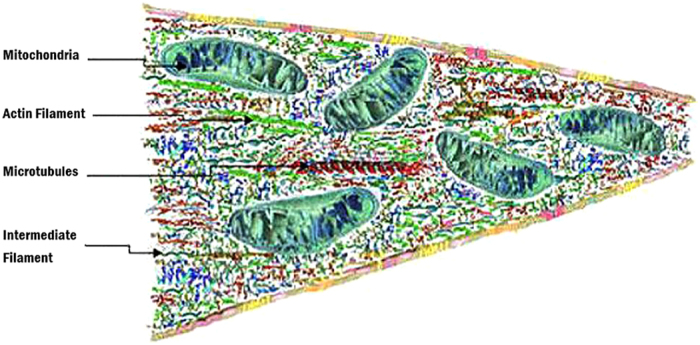
A schematic illustration of a longitudinal section of the neuronal branchlet with microstructure showing cytoskeletal structures (interlinking actin filaments, intermediate filaments, and microtubules) and closely compressed accumulated membranous organelles that extend to distal part of a branchlet. The cytoskeleton is a network of connected actin and intermediate filaments, and microtubules including mitochondria in neurons causing a gradual tapering towards one end. The microstructure constitutes a fissured domain of the cytosol (fluid that contains organelles, comprising the cytoplasm). The mitochondrial membrane is the largest organelle (∼0.2 μm) within the microstructure and dominates the constituency of the cytoskeletal structures since endoplasmic reticulum does not enter into branchlets below a micron.

The cytosol (fluid that contains orgenelles, comprising the cytoplasm) is a porous medium of the intracellular fluid assumed to be homogeneous and purely conducting, i.e., the electrical behavior of the medium is entirely characterized by a homogeneous electrical conductivity representing ionic homogeneity for all macromolecules. This is a simplification that suffices for the conduction process, focusing on homogeneous dielectric polarization²⁰ without exploring the physicochemical nature of excitation. Consequently in the context of conduction process, ionic polarizability of individual molecules is not taken into account, but instead a continuum of molecular ions with macroscopic charge densities are used as a phenomenological description of the electrostatic interactions and transfer of information due to the interactions among the molecular ions in a fluid environment within neuronal branchlets.

Cable model with homogenous microstructure

A homogenous microstructure is represented electrically in terms of intracellular capacitive effects that contribute to dielectric absorption, and nonlinear (voltage-dependent) transfer of macroscopic charge densities leading to inherent waveforms of electrical depolarization. Phenomenological description of quasi-electrostatic interactions of macroscopic charge densities held by the microstructure are modeled as flux generated by electrical contribution of polarization current in a homogenous core- conductor representation of a neuronal branchlet, assuming extracellular isopotentiality, spatial and ionic homogeneity and negligence of currents due to ionic concentration gradients among molecular ions in an electrolytic microenvironment.

Cable models of electrical activity in neurons assume a one-dimensional description of neuron geometry for describing the process of conduction⁵. In our cable model, we consider the microstructure to be a homogeneous dielectric of constant conductivity and permittivity in space and time and isotropic (same in x/y directions). We ignore anisotropic electrical properties, compare with refs ^{27, 28}, assume the polarization current is restricted longitudinally along the cable length, and extracellular isopotentiality and quasi-electrostatic conditions prevail. Therefore in the context of conduction process, ionic polarizability of individual macromolecules is not taken into account, but rather macroscopic charge densities are used as a phenomenological description of the electrostatic interactions between charges/dipoles held by the microstructure (i.e., charge ‘soakage’). Our model includes a homogenous microstructure of a cable representation of a branchlet as an approximation to an inhomogeneous microstructure of an electrolytic cable representation of a branchlet (see Fig. 2).

Figure 2.

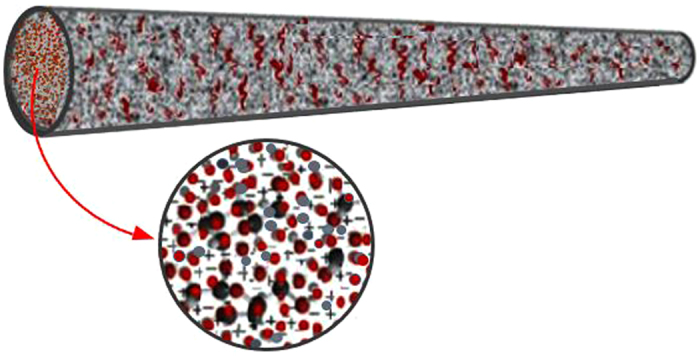
A schematic illustration of ionic inhomogeneity in a porous medium of a neuronal branchlet. The microstructure is indicative of macromolecules in an electrolyte solution (excluding subcellular membranes of mitochondria). The inset shows molecular ions in an electrolytic microenvironment within the neuronal branchlet.

Basic equation of the model

The membrane potential distribution can be derived from conservation of electric charge in a volume of cylindrical cable over a differential distance Δx as shown in Fig. 3 (top); see ref. 29. The cable has a radius (r), cross-sectional area (πr²) and perimeter around the membrane (2πr). If the conductivity of the extracellular medium is high, leaving the extracellular medium isopotential (i.e., V_e = 0) then the effect of the external potential on membrane potential (i.e., V = V_i − V_e) is negligible.

Figure 3.

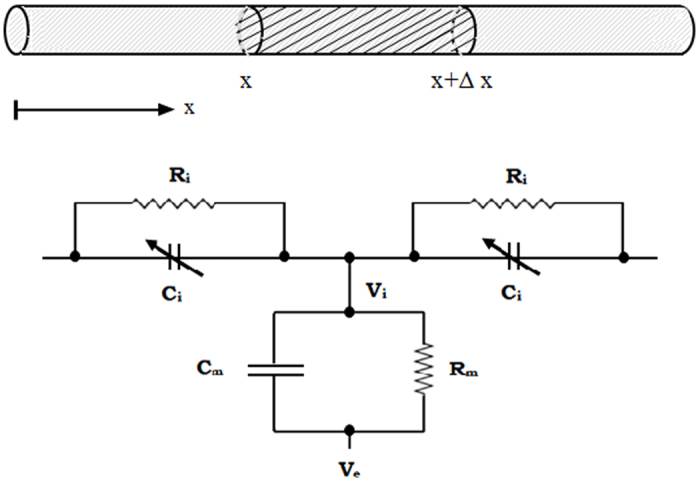
A segment of a neuronal branchlet as a cylindrical cable that supports the formation and propagation of electrical solitons reflective of the movement of macroscopic charge densities arising from polarizability of the microstructure, whose capacitance changes with voltage along a cable. The description of the ‘macroscopic’ electric parameters as a representation of a line charge in the branchlet caused by quasi-electrostatic interactions consists of infinitely long, infinitely thin distribution of charges uniformly distributed and denoted as charge per unit length of cable Q(x, t) (C/cm). The length increment Δx is shown where arrow indicates the convention that positive charge is in the direction of increasing x, which is the physical distance along the cable. It is assumed the cable is a homogeneous conductor with radial currents ignored. Below is an equivalent series-parallel RC circuit representing a patch of passive membrane in series with the intracellular medium represented by a voltage-dependent longitudinal (axial) capacitance C_i(V) = C_i C(V_i) of the cable (F/cm) in parallel with the intracellular resistivity (R_i) of the cable (Ωcm). Definitions of electrical terms are: R_m = 2πrr_m is the membrane resistivity or resistance across a unit area of passive membrane (Ωcm²), C_m = c_m/2πr is the membrane capacitance per unit area of membrane (F/cm²), C_i = c_i/πr² is the voltage-independent longitudinal capacitance (intracellular capacitance) per unit length of cable (F/cm), and c_i is the axial capacitance across unit length c_i = 2 ε_o πr² (Fcm). See text for other definitions of electrical terms.

If the membrane potential (V) in a neuronal branchlet is equal to the intracellular potential (V_i) together with passive membrane as shown in Fig. 3 then the nonlinear cable equation with polarized microstructure can be written as ref. 20:

$$\mathrm{V}+\partial \mathrm{V}/\partial \mathrm{T}={\partial }^2\mathrm{V}/\partial {\mathrm{X}}^2+\mathrm{\gamma }{\partial }^3\mathrm{V}/\partial \mathrm{T}\partial {\mathrm{X}}^2+\mathrm{\kappa }\partial \left\{\mathrm{C}(\mathrm{V})\mathrm{V}\right\}/\partial \mathrm{T}$$ 1

where V is the membrane potential (mV), γ = τ_ρ/τ_m ≪ 1 and κ = γ (λ²/πr²) are both positive constants (dimensionless), τ_p = 2ε_rε_o/σ < 1msec (Maxwell’s time constant), ε_r = 81 is the relative permittivity of sea water (dimensionless), ε_o = 7 × 10^—12 F/cm is the fluid permittivity, τ_m = c_mr_m (passive membrane time-constant in msec), λ = √(r_m/r_i) (electrotonic space-constant in cm), dimensionless time T = t/τ_m and dimensionless space X = x/λ, r_i is the core-resistance (or intracellular resistance) per unit length r_i = 1/(πr²σ) (Ω/cm), r_m is the membrane resistance across a unit length of passive membrane cylinder (Ωcm), c_m is the membrane capacitance per unit length of cylinder (F/cm). Note the core-resistance (or intracellular resistance) per unit length differs slightly from the intracellular resistivity R_i = 1/(2σ) (Ωcm) or volume resistivity of the intracellular medium, also referred to as specific resistance (1/σ) where σ is the electrical conductivity (S/cm).

Equation (1) contains two additional terms in the classical cable equation; see refs ^{5, 30, 31}, which reflect the intracellular capacitive effects due to polarization current. A physical interpretation of these new terms requires quantitative verification that is lacking even when γ is small and hence κ is small, yet the intracellular capacitive effects do form a significant dielectric, and not simple passive RC filter properties. The first new term γ ∂³V/∂T∂X² is a linear dissipative term due to surface-charge equalization between polarized intracellular free charges on endogenous structures within the microstructure¹⁹. The other new term ∂{C(V)V}/∂T is the charge ‘soakage’ due to polarization current within the microstructure produced by the bounded charges on endogenous structures²⁰. In a neuronal branchlet with microstructure, voltage created by charge ‘soakage’ produces intracellular capacitive effects. Charge ‘soakage’ is the tendency of a capacitor to recharge itself after being discharged and the nonlinear capacitance-voltage characteristic C(V) is approximated by a linear polarization capacitance-voltage characteristic of the microstructure (dimensionless):

$$\mathrm{C}(\mathrm{V})=2\mathrm{\alpha }\mathrm{V}$$ 2

where α > 0 is the ‘soakage’ parameter (mV⁻¹) determined from the quantity of electrical charges held in the capacitance of the microstructure. It represents the capacity to hold more electrical charge or electrical energy than a linear capacitor. Inherent in the assumption of the nonlinear voltage-dependent capacitance of the microstructure is that charge ‘soakage’ reflects a density of electric charges in the microstructure irrespective if charge flow of molecular ions is from mitochondrial inactive membrane channel³² or the cytoskeleton. The ‘soakage’ parameter α is zero only in the absence of microstructure and so there is no voltage-independent intracellular capacitance, that is, C(V) ≠ 1 + 2αV; otherwise it is positive (α > 0). The ‘soakage’ parameter should not be confused with the ‘feedback’ parameter³³ (β) for charge storage in the plasma membrane capacitance, which is negative (β < 0), that is C(V) = 1 + βV.

The nonlinear capacitor C_i(V) = C_i C(V) possesses voltage-dependence at slow varying electric fields (e.g., under quasi-electrostatic conditions) giving the capacity to hold more electric charge than a linear capacitor, which can result in non-dissipative electrical signaling. The polarized macromolecules attract bound charge densities within the microstructure which are stored in the nonlinear capacitor providing a physical basis of C(V). We can glean a quantitative understanding of C(V) which can be extracted from experimental data^{34, 35}. For example, if a quadratic capacitance-voltage characteristic C(V) = 2αV² is used instead of (2) then a ‘kink’ shaped soliton solution (i.e., waveform) results upon solving (1); see ref. 20. Therefore C(V) is the main source of nonlinearity responsible for both shape and stability of the electrotonic signal.

The capacitance in an electrostatic system represents a way to hold electric charges. Most nonlinear capacitors are defined as C_i(V) = dQ/dV and upon integration yields the charge-voltage relationship:

$$\mathrm{Q}={\mathrm{C}}_{\mathrm{i}}\mathrm{C}(\mathrm{V})\mathrm{V}$$

where Q is the electrical charge of the microstructure per unit length of cable (C/cm) and C_i is the linear voltage-independent longitudinal capacitance (F/cm). Also ∂Q/∂t = C_i ∂{C(V)V}/∂t is the polarizing current underlying the charge ‘soakage’. If α = 0 then no charge is stored due to the absence of microstructure. However, the contribution of microstructure to the generation of the voltage-dependent charge transfer excludes the changes in capacitance reflected through electrocompressive forces of the plasma membrane where the voltage-dependent charge transfer in the squid axon dQ/dV follows a quadratic relationship³⁴. Given that the nonlinear capacitance derived from electrostriction is less than 1% of the total charge in squid axons³⁵, and endogenous structures are active during the linear phase, therefore C(V) is linearly proportional to V; see e.g. ref. 32. In general, however, quadratic nonlinearity in C(V) is linked to electrocompressive forces³³ and not the result of charge ‘soakage’ in the microstructure.

Equation (1) represents a phenomenological description of nonlinear electrostatic diffusion of charges (conduction of electric current) in a cable reduced from Maxwell’s equations¹⁹. When κ = 0 implies no charge ‘soakage’ is stored due to the absence of microstructure and (1) reduces to a generalized linear cable equation; compare with refs ^{19, 29, 36}. If γ = 0 and κ = 0 then (1) reduces to electrotonic conduction of current in a “lossy” cable¹³. Finally it can be shown that the dispersion relation (see Supplementary data) is complex, and therefore the nonlinear cable equation without polarization current is dispersionless and dissipative as evident when T → ∞, so that the voltage pulse dissipates as it propagates. However, in our model, the electrotonic signals are self-generating due to the charge ‘soakage’ and they dissipate only in the absence of microstructure. This reflects upon the self-excitable nature of the model as opposed to a non-quiescent model²⁸ where solitary waves are observed due to excess charge on top of plasma membrane ionic channel proteins at discrete localizations.

Given that the parameters α and κ both require quantifying, we can alleviate this problem by expressing the normalized membrane potential in non-dimensional terms via U → ακV and therefore (1) becomes a third-order non-evolutionary equation:

$$\mathrm{U}+\partial \mathrm{U}/\partial \mathrm{T}={\partial }^2\mathrm{U}/\partial {\mathrm{X}}^2+\mathrm{\gamma }{\partial }^3\mathrm{U}/\partial \mathrm{T}\partial {\mathrm{X}}^2+2\partial {\mathrm{U}}^2/\partial \mathrm{T},0<\mathrm{X}<\mathrm{L}$$ 3

This equation is combined with a variety of boundary conditions at X = 0 and X = L (see Table 1). The only parameter γ = 0.001 is known from cable theory^{19, 20}. The non-dimensionalization of the membrane potential has clear advantages that allows for the electrotonic signals to be enhanced since under normal experimental situations they are rarely encountered due to their small amplitude, possibly buried in noise during electrophysiological recordings. Equation (2) expressed in non-dimensional membrane potential leaves the dissipation term small, while the charge ‘soakage’ term which is the only nonlinear term that is not small. Given that both α and κ are small parameters, the peak amplitude of the dimensional voltage V can be found from the inverse product (1/ακ). Although α and κ are removed through the normalization process, experimentally observed electrotonic signals of around V = 5 mV; see ref. 21, can be a way to crudely estimate α for any given κ.

Table 1.

Method of images solution coefficients for a finite neuronal branchlet.

Type of Boundary Condition	αn	βn
UX(0, T) = UX(L, T) = 0	1	1
U(0, T) = UX(L, T) = 0	(−1)n	−(−1)n
UX(0, T) = U(L, T) = 0	(−1)n	(−1)n
U(0, T) = U(L, T) = 0	1	−1

Results

Approximate traveling wave solutions in free space using the tanh-function expansion method

Traveling wave solutions assume a constant conduction velocity that relies on a Galilean transformation of the independent variables which reduces (3) to an ordinary differential equation: ξ = X − X_p1 − νT where X_p is the initial location of the electrotonic signal positioned along the cable and ν is the velocity of the electrotonic signal moving towards ξ → ∞. The solitary wave moving in the other direction ξ → − ∞, we would use ξ = X − X_p2 + νT. For convenience, we use the solitary wave ansatz U*(X, T) = Ω(ξ) where U* is the free space version of U on an infinite interval (−∞, ∞), with the following identities:

$$\begin{array}{l}\partial {\mathrm{U}}^{⁎}/\partial \mathrm{T}=-\mathrm{\nu }\mathrm{d}\mathrm{\Omega }/\mathrm{d}\mathrm{\xi },{\partial }^2{\mathrm{U}}^{⁎}/\partial {\mathrm{X}}^2={\mathrm{d}}^2\mathrm{\Omega }/{\mathrm{d}\mathrm{\xi }}^2,{\partial }^3{\mathrm{U}}^{⁎}/\partial \mathrm{T}\partial {\mathrm{X}}^2=-\mathrm{\nu }{\mathrm{d}}^3\mathrm{\Omega }/{\mathrm{d}\mathrm{\xi }}^3\mathrm{and}\hfill \\ \partial \left[{\mathrm{U}}^{⁎2}\right]/\partial \mathrm{T}=-\mathrm{\nu }\mathrm{d}\left[{\mathrm{\Omega }}^2\right]/\mathrm{d}\mathrm{\xi }=-2\mathrm{\nu }\mathrm{\Omega }(\mathrm{d}\mathrm{\Omega }/\mathrm{d}\mathrm{\xi })\hfill \end{array}$$ 4

Substitution of (4) into (3) yields

$$\mathrm{\nu }{\mathrm{\gamma }\mathrm{d}}^3\mathrm{\Omega }/{\mathrm{d}\mathrm{\xi }}^3-{\mathrm{d}}^2\mathrm{\Omega }/{\mathrm{d}\mathrm{\xi }}^2+\mathrm{\nu }(4\mathrm{\Omega }-1)(\mathrm{d}\mathrm{\Omega }/\mathrm{d}\mathrm{\xi })+\mathrm{\Omega }=0$$ 5

with the boundary conditions for electrotonic signals Ω(±∞) = 0.

The solution of (5) can be found numerically formulated as a two-point boundary value problem. Methods for numerical integration, such as shooting methods, can be used or alternatively a direct method can also be used to analytically solve (5). This has quantitative improvements over other methods that employ traveling wave fronts or phase-plane methods that require some numerical computation to estimate the velocity of the wave (e.g. shooting method); see e.g., ref. 37. One such direct method is the so-called tanh-function expansion method; see e.g., ref. 38, where a new independent variable is introduced:

$$\mathrm{y}=\tanh (\mathrm{\xi })$$

with

$$\begin{array}{lll}\hfill \mathrm{d}\mathrm{\Omega }/\mathrm{d}\mathrm{\xi }& \hfill =\hfill & [(\mathrm{1}-{\mathrm{y}}^2)\mathrm{d}f/\mathrm{dy}]\hfill \\ \hfill {\mathrm{d}}^2\mathrm{\Omega }/{\mathrm{d}\mathrm{\xi }}^2& \hfill =\hfill & [-2\mathrm{y}(1-{\mathrm{y}}^2)\mathrm{d}f/\mathrm{dy}+{(1-{\mathrm{y}}^2)}^2{\mathrm{d}}^{2}f/{\mathrm{dy}}^2]\hfill \\ \hfill {\mathrm{d}}^3\mathrm{\Omega }/{\mathrm{d}\mathrm{\xi }}^3& \hfill =\hfill & [2(1-{\mathrm{y}}^2)(3{\mathrm{y}}^2-1)\mathrm{d}f/\mathrm{dy}-6\mathrm{y}{(1-{\mathrm{y}}^2)}^2{\mathrm{d}}^{2}f/{\mathrm{dy}}^2+{(1-{\mathrm{y}}^2)}^3{\mathrm{d}}^{3}f/{\mathrm{dy}}^3]\hfill \end{array}$$

where Ω(ξ) → ƒ(y) and ƒ(±1) → 0.

Substituting the above new variables into (5) results in the following expression:

$$\begin{array}{lll}\hfill f-\mathrm{\nu }(1-{\mathrm{y}}^2)\mathrm{d}f/\mathrm{dy}& \hfill =\hfill & \left[-2\mathrm{y}(1-{\mathrm{y}}^2)\mathrm{d}f/\mathrm{dy}+{(1-{\mathrm{y}}^2)}^2{\mathrm{d}}^{2}f/{\mathrm{dy}}^2\right]\hfill \\ \hfill & \hfill & -\mathrm{\gamma }\mathrm{\nu }[2(1-{\mathrm{y}}^2)(3{\mathrm{y}}^2-1)\mathrm{d}f/\mathrm{dy}-6\mathrm{y}{(1-{\mathrm{y}}^2)}^2{\mathrm{d}}^{2}f/{\mathrm{dy}}^2\hfill \\ \hfill & \hfill & +{(1-{\mathrm{y}}^2)}^3{\mathrm{d}}^{3}f/{\mathrm{dy}}^3]-4\mathrm{\nu }f(1-{\mathrm{y}}^2)\mathrm{d}f/\mathrm{dy}\hfill \end{array}$$ 7

Note: For a variable width of the solitary wave, a more generalized tanh-function expansion method can be used with y = tanh (μξ) where μ donotes the width of the solitary wave³⁸.

The tanh-function expansion method admits the use of a finite expansion of the form ƒ(y) = ∑a_nyⁿ where n is a positive integer to be determined by equating the powers of y in the resultant equation upon its substitution into (7). To determine the parameter n, we balance the highest order linear terms with the highest order nonlinear terms, which gives n = 2. Therefore the solution takes the form:

$$f(\mathrm{y})={\mathrm{a}}_{\mathrm{o}}+{\mathrm{a}}_{\mathrm{o}}({\mathrm{a}}_{\mathrm{1}}-1)\mathrm{y}-{\mathrm{a}}_{\mathrm{1}}{\mathrm{a}}_{\mathrm{o}}{\mathrm{y}}^2$$ 8

Unlike a perturbation expansion, (8) represents a finite expansion and so no higher-order terms are required. As a result, there is no test of convergence that is required to be undertaken as expected when using perturbation methods. If y →  −1 then from (8) and the boundary condition ƒ(−1) → 0 yields a₁ = 1 and the solution takes the form:

$$f(\mathrm{y})={\mathrm{a}}_{\mathrm{o}}(\mathrm{1}-{\mathrm{y}}^2)$$ 9

If y → 1 then from (9) upon substituting into (7) and the boundary condition ƒ(1) → 0 yields the velocity of the wave:

$$\mathrm{\nu }=(3/2)\left[1/(1-4\mathrm{\gamma })\right]$$

Substitution of y = tanh(ξ) into (9) yields the traveling wave solution for a solitary wave of unitary width and moving at speed ν :

$${\mathrm{U}}^{⁎}(\mathrm{X},{\mathrm{X}}_{\mathrm{p}};\mathrm{T})={\mathrm{a}}_{\mathrm{o}}{\mathrm{sech}}^{\mathrm{2}}(\mathrm{X}-{\mathrm{X}}_{\mathrm{p}}-\nu \mathrm{T})$$ 10

where a_o is the dimensionless amplitude determined to be a_o ≈ 3γ + 3/(4ν) (see Supplementary data). Therefore the amplitude of the solitary wave decreases with distance from the initial position. Substituting the velocity ν into the dimensionless form of the traveling wave solution is given as

$${\mathrm{U}}^{\ast }(\mathrm{X},{\mathrm{X}}_{\mathrm{p}};\mathrm{T})\approx (3/8)[2-1/\nu ]{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2(\mathrm{X}-{\mathrm{X}}_{\mathrm{p}}-\nu \mathrm{T})$$ 11

The approximate traveling wave solution governed by (11) is known as a solitary-wave solution (or quasi-soliton) corresponding to an electrotonic signal propagating at a constant speed ν > 0.5. The solitary-wave solution is only an approximate solution of (3) that is shown to be stable based on local stability analysis (see Supplementary data).

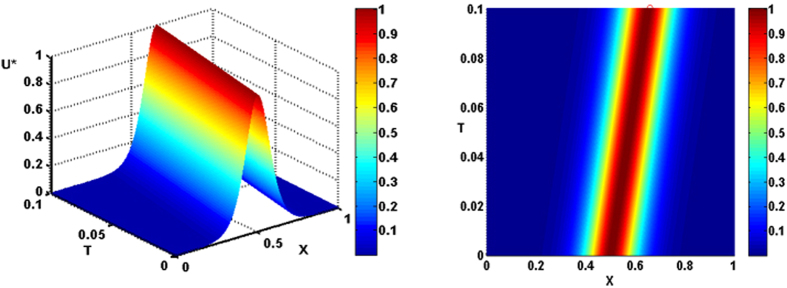
The results presented in Fig. 4 show a quasi-soliton as the spatiotemporal evolution of the normalized membrane potential U*(X, X_p;T)/U*(X_p, X_p;0) in non-dimensional terms along an infinite cable (in free-space) implemented in Matlab software package. The quasi-solitons are insensitive to the initial location of their positioning X_p as the hyperbolic secant function reaches a maximum value of unity when X = X_p. These solitary waves are not chaotic since they exhibit globally regular amplitudes and a constant velocity of propagation. The results are presented for a spatially homogeneous medium where the solitary waves propagate with a constant velocity and amplitude that is independent of their initial position. This quasi-soliton possesses no energy loss due to charge ‘soakage’ as charge keeps coming out of the capacitor of the polarized microstructure, which is absent in energy consuming action potentials. As shown in Fig. 4 (right-hand-side), the velocity of the quasi-soliton is inversely proportional to the slope of this graph. As can be seen the co-ordinate for the first and last points are (X₁, T₁) = (0.5, 0) and (X₂, T₂) = (0.6506, 0.1), respectively. Thus slope = (T₂ − T₁)/(X₂ − X₁) = (0.1 − 0)/(0.6506 − 0.5) = 0.6641 and the dimensionless velocity is inversely proportional to this slope 1/0.6641 ≈1.506.

Figure 4.

A propagating quasi-soliton expressed in terms of spatiotemporal evolution of normalized membrane potential U*(X, X_P; T)/U*(X_P X_P; 0) as a function of electronic distance (X) and dimensionless time (T) along an infinitely long neuronal branchlet obtained from (11). Parameters used were: ν = 1.506, γ = 0.001 and X_p = 0.5.

Solitonic properties

The solitonic property of a solitary wave (or quasi-soliton) is that asymptotically it preserves its shape and velocity on collision with other quasi-solitons³⁹. The linear superposition of electrotonic signals is assumed to approximate the collision:

$${\mathrm{U}}^{\ast }(\mathrm{X},{\mathrm{X}}_{\mathrm{p}1}+{\mathrm{X}}_{\mathrm{p}2};\mathrm{T})\approx (3/8)[2-1/\nu ]\{{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2(\mathrm{X}-{\mathrm{X}}_{\mathrm{p}1}-\nu \mathrm{T})+({\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2(\mathrm{X}-{\mathrm{X}}_{\mathrm{p}2}+\nu \mathrm{T})\}$$ 12

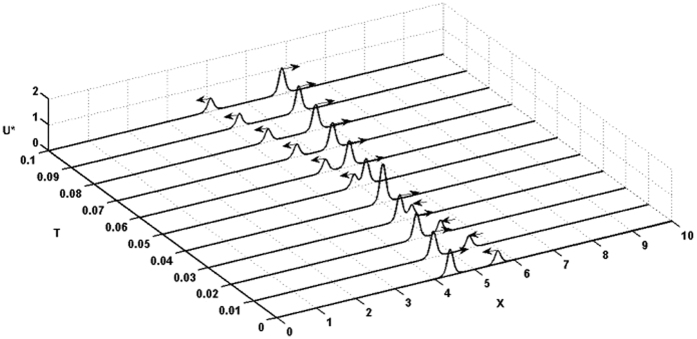
We illustrate the collision between two quasi-solitons with identical velocities in order to test their responses after collision. The electrotonic signal has fixed velocity and is not amplitude-dependent. The result of the head-on collision of two quasi-solitons is simulated resulting in an elastic interaction with electrotonic signals remaining unchanged after collision. The simulated result for the two quasi-solitons (solitary waves) approaching each other with the one moving to the right having a normalized amplitude of U*(X_{p 1}, X_{p 1} + X_{p 2}; 0) and the other moving to the left having a half-normalized amplitude of 2U*(X_{p 2}, X_{p 1} + X_{p 2}; 0) is shown in Fig. 5. The elastic interaction of quasi-solitons stems from the absence of recovery processes known to be the major cause of collapse of colliding spikes⁴. The elastic interaction between two quasi-solitons preserves their shape, amplitudes and velocities. Velocities are parameter-dependent on the ratio of the Maxwell’s time-constant and the membrane time-constant. The dynamics of electrotonic signals are shown to interact during collision, although no annihilation of electrotonic signals due to conservation of energy. The time of collision occurs at T = (X_p2 − X_p1)/2ν which is 0.04 with X_p1 = 0.5–4ν/100 = 0.4398 and X_p2 = 0.5 + 4ν/100 = 0.5602 as shown in Fig. 5.

Figure 5.

Two oppositely directed quasi-solitons (solitary waves) along an infinitely long neuronal branchlet result in a head-on collision. The collision occurred by linear superposition of the solitary waves. To differentiate the amplitudes of the traveling wave solutions expressed in terms of the membrane potential U*(X, X_{p 1} + X_{p 2}; T) obtained from (12) as a function of electrotonic distance (X) and dimensionless time (T), the quasi-soliton moving to the right was normalized by U*(X_{p 1}, X_{p 1} + X_{p 2}; 0) and the quasi-soliton moving to the left was half-normalized by 2U*(X_{p 2}, X_{p 1} + X_{p 2}; 0). Both quasi-solitons propagate with a dimensionless conduction velocity of ν = 1.506. Parameters used were: γ = 0.001, X_{p 1} = 4.398, X_{p 2} = 5.602.

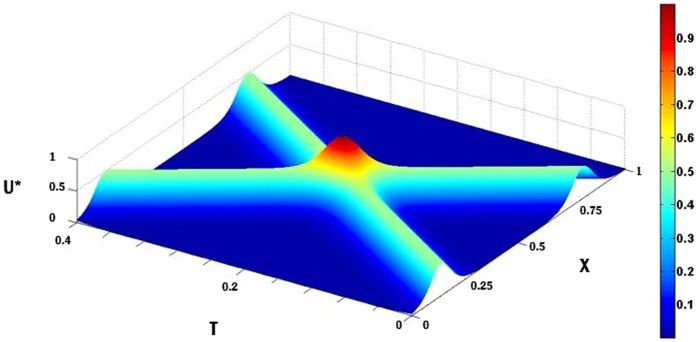
If the collision between two solitary waves is elastic (i.e. preserves their shape and velocities) then it can be described as being solitonic. This is the major property of soliton as a self-reinforcing solitary wave. In a non-dispersive medium, solitons are dissipative, but only in the sense that in the presence friction, they gradually decelerate and become smaller and they will eventually decay as T → ∞, but only when dissipative energy is not fueled by the reservoir of electrical charges held by the intracellular capacitance and which in turn releases stored energy for maintenance of the electrotonic signal. In a linear dissipative medium the dynamics of soliton collisions appear to be absorbing one another, i.e., solitons pass through one another⁴⁰. This is shown more clearly in Fig. 6 where two quasi-solitons undergo linear superposition at collision. The time of collision occurs at T = (X_p2 − X_p1)/2ν which is 0.234 (see Fig. 6). The simulation shows that the two electrotonic signals pass through one another and are not deformed after collision, preserving their shape, amplitude and velocity. More importantly, after the interaction they continue to propagate without dissipating, thus providing unequivocal support for quasi-solitons to be solitons. The defining condition for solitons is that they pass through one another and not merely reflect from one another. The simulation shows the existence of a point where there is only a single peak, suggesting that the solitons absorb one another during the collision. Also the traveling wave solution U*(X, T) = Ω(ξ) can be shown to satisfy the following conditions³⁸: Ω′(ξ) = Ω″(ξ) = Ω′″(ξ) = 0 where prime denotes differentiation with respect to ξ, further reinforcing the electrotonic signals as solitons.

Figure 6.

An elastic interaction between two oppositely directed quasi-solitons after a head-on collision along an infinitely long neuronal branchlet. Traveling wave solution in terms of a normalized membrane potential U*(X, X_p1 + X_p2; T)/(1 + 2γ) obtained from (12) as a function of electrotonic distance (X) and dimensionless time (T). Both quasi-solitons propagate with a dimensionless conduction velocity of ν = 1.506. The interaction between quasi-solitons occurred by linear superposition of quasi-solitons. Parameters used were: γ = 0.001, X_{p 1} = 0.15, X_{p 2} = 0.85.

The effect of boundaries

The method of images technique^{30, 31} can be employed to determine the appropriate spatiotemporal evolution of membrane potential on a finite domain for small values of time. On a finite interval, the effect of boundaries causes reflections to occur, which must be added to the original free space solitary wave U*(X, X_p;T) solution. Therefore, the solitary wave in a finite cable of electrotonic length L is expressed by

$$\mathrm{U}\left(\mathrm{X},\mathrm{T}\to 0\right)=\sum _{\mathrm{n}=-\infty }^{\infty }\left\{{\mathrm{\alpha }}_{\mathrm{n}}{\mathrm{U}}^{⁎}\left(\mathrm{X},2\mathrm{nL}-{\mathrm{X}}_{\mathrm{p}};\mathrm{T}\to 0\right)+{\mathrm{\beta }}_{\mathrm{n}}{\mathrm{U}}^{⁎}\left(\mathrm{X},2\mathrm{nL}+{\mathrm{X}}_{\mathrm{p}};\mathrm{T}\to 0\right)\right\}$$ 13

where α_n and β_n depend on boundary conditions and are given in Table 1.

The boundary condition U_X = 0 characterizes a reflecting boundary, where the conduction of current is reflected often called a “sealed-end” boundary condition. The boundary condition U = 0 represents an absorbing boundary, where the conduction of current is grounded to its resting state (or voltage –clamped if not zero) often called “killed-end” or “short-circuit” boundary condition. Additional boundary conditions not included in Table 1 are a combination of the two denoted as a “leaky-end” boundary condition where conduction of current is transmitted through a resistance representing a gap-junction⁴¹. Another common boundary condition is the “natural” boundary condition where a time derivative U_T is used in addition to the “leaky–end” reflecting an isopotential structure expressed electrically in terms of a RC circuit that is added to the cable at both ends, resulting in a dumbbell cable⁴². Both “leaky-end” and “natural” boundary conditions introduce an additional term in (13) upon use of the method of images technique⁴³.

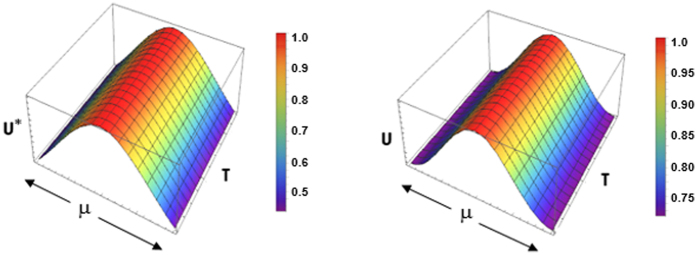
The simulations with finite cables are indistinguishable from the free space solutions. One reason is that the zero term dominates the expansion in (13), which governs the free space solution at small times. Therefore no damping of the electrotonic signals occurs due to the effects of the boundaries. The marginal differences in the normalized Gaussian profile can be seen if a more generalized tanh-function expansion method is employed³⁸. As indicated in Fig. 7 the normalized Gaussian profile appears to have a lower variance in the curved profile compared to the free space solution, which is attributed to the reflection of non-zero terms from the sealed-ends boundary conditions.

Figure 7.

The effect of sealed-end boundary conditions on the quasi-soliton profile showing the apex with a variable width. A generalized tanh-function expansion method with y = tanh (μξ) where μ donotes the width of the profile as a normalized Gaussian curve. The spatiotemporal evolution of the normalized membrane potential U(X_P , T)/U(X_P , 0) in non-dimensional terms obtained from (13) with n = 0 (left-hand side) and n = ±10 (right-hand side).

Discussion

A model of a neuronal branchlet that included a phenomenological description of polarized microstructure in terms of intracellular capacitive effects was shown to be capable of influencing subcellular electrical signal propagation under quasi-electrostatic conditions (slow moving electric field). The resultant intracellular capacitive effect of polarized microstructure gives rise to self-excitability due to charge ‘soakage’ held in voltage-dependent capacitance of the microstructure invoking traveling wave pulses instead of traveling wave fonts, as one would expect without any recovery processes inherent in the model.

These traveling wave pulses were shown to be conducted through a novel mode of conduction exclusively for branchlets with microstructure. The stable electrotonic signals propagated due to stored energy in the microstructure. The crucial test for solitary waves to be electrical solitons is robustness to collision. Electrical solitons do not undergo nonlinear amplitude modulation during collision because linear superposition of solitary waves is assumed in a linear dissipative medium⁴⁰. Based on linear superposition simulating interaction, the tanh-function expansion method enabled to directly procure approximate traveling wave solutions (quasi-solitons); their collision dynamics remained unchanged as they passed through one another, providing support for solitary waves to be electrical solitons. To the best of our knowledge, our model provides a first attempt at describing electrotonic signals denoting the direct spread of current in branchlets by means of solitonic conduction based on cable theory as opposed to transmission line theory (electrical lattices)⁴⁰ or reaction-diffusion theory^{10, 11}.

Traveling waves conducted as stereotypical action potentials are energy consuming⁴⁴. Therefore action potentials dissipate with time and annihilate upon collision⁴. Electrical solitons dissipate, but because of microstructure and the resultant distribution of charge ‘soakage’, the dissipative energy was shown to be conserved. Furthermore, electrical solitons did not annihilate upon collision because unlike action potentials with the refractory period, the electrotonic signals are maintained by the flux associated with the polarization current flowing through the miscrostructure. Therefore, the model possess attributes like stability and elastic interaction upon head-on collision that differ significantly from stereotypical action potentials attributed to the gating currents through the plasma membrane, including unstable pulses serving as threshold conditions for igniting these stereotypical action potentials⁴⁵.

What might be the function of electrotonic signals propagating along fine distal branchlets? Electrotonic signals without recovery are suitable in transmitting information through physical interaction of electrical charges held by microstructure and not synaptic inputs⁴⁶. The stable non-decremented electrotonic signals originating in branchlets could play a functional role in heterosynaptic plasticity. Also electrical solitons conserve energy and so they can decode local information permanently. The stable dynamics of electrotonic signals provide a mechanistic explanation to retrieve long-term memories⁴⁷. Our view is that backpropagating action potentials⁴⁸ are unencumbered by solitonic conduction for the reason that they become erratic and unpredictable prone to propagation failures at diameters smaller than 0.5 μm⁴⁹. Based on the permanence of these electrical solitons, it is unlikely that backpropagating action potentials are involved in higher brain functions such as in conceptual tasks. While for those action potentials that are initiated in thin dendrites (see ref. 50 for a review) we propose two specialized interdependent signals in local information processing: (1) dendritic spikes for encoding/imprinting information and (2) solitons for decoding/retrieval information in distal most dendrites of cortical neurons.

The function of solitonic conduction in branchlets may differ in thin axons and thin dendrities. Plasma membrane ion channel noise causes action potential reliability to be significantly diminished in their information carrying capacity in thin axons (<0.5 μm diameter)⁵¹. The lower limit to axon diameter is about 80 nm⁵². Experiments revealed very thin pyramidal cell axons can conduct action potentials reliably⁵³ and simulations show that action potentials in very thin axons are unlikely to fail to propagate due to ion channel noise⁵¹. This suggests conduction of action potentials in thin axons is not localized in the axonal branchlets. If neurons are designed for presynaptic information processing of local information to thin dendritic branchlets and not available at the site of spike initiation then electrotonic potentials can be locally integrated within the branchlets and then integrated again at one or more main intrinsic action potential initiation zones^{54, 55}.

Our view, however, is that in the presence of microstructure, solitons in thin distal dendrites are the agglomeration of electrical charge densities arising as a result of electrotonic signal interactions. If the non-stereotypical spike is a composite of soliton interactions then the propagation of non-stereotypical spikes could carry dynamically-rich information generated by propagation of localized soliton resonant interactions that occur and influence the generation of ionic flow in neuronal branchlets. The presence of localized electrotonic signals reinforces preferentially local integration in different parts of the neuron and can lead to meaningful electrotonic information processing (see for example ref. 56). To test our hypothesis of solitonic conduction in branchlets designed exclusively for local electrotonic information processing, the minute intracellular volumes that go beyond the limiting spatial resolution of confocal microscopes and two-photon laser scanning fluorescence microscopy⁵⁷ will need to be investigated with new technology that would enable to record and image the electrotonic signals in fine distal branchlets of neurons at higher spatial resolutions using dielectric scanning microscopy on neurons^{58, 59}.

In their experimental study, Gonzalez-Perez and colleagues²¹ observed pulses under 10 mV in amplitude that did not annihilate upon collision. Although their reference to solitons as ‘action potentials’ leads to confusion they further resorted to an electromechanical explanation without a clear indication as to why a purely electrical phenomenon should be re-packaged in terms of electromechanical pulses. Recently, El Hady and Machta⁶⁰ suggested that mechanical surface waves may be caused by charge separation leading to changes in capacitance due to compressive forces on the membrane (electrostriction), yet it is known that the nonlinear capacitance derived from electrostriction is expected to contribute less than 1% of the total capacitance³⁵. Therefore, any electromechanical traveling waves would be negligible. In accordance with the result of Gonzalez-Perez and colleagues²¹, our model supports their experimental findings without considering adiabatic phenomena during a nerve pulse, but through charge reservoirs within the neuronal microstructure, thus reconciling the difference between electrophysiological models and thermodynamic postulates without the need for postulating mechanical soliton models.

Author Contributions

R.R.P. Derived the mathematical model. L.A.C. Wrote the manuscript and prepared the figures. Y.M.S. Wrote the computing code. J.A. Supervised the project and the physics of the research. M.B. Validated the computing code. P.Y. Analyzed the data and reconciled with the coding. J.Y. Contributed through discussion and revision of the manuscript.

Competing Interests

The authors declare that they have no competing interests.