Abstract
Glomerular hypertension and hyperfiltration in early diabetes are associated with development and progression of diabetic kidney disease. The tubular hypothesis of diabetic hyperfiltration proposes that it is initiated by a primary increase in sodium (Na) reabsorption in the proximal tubule (PT) and the resulting tubuloglomerular feedback (TGF) response and lowering of Bowman space pressure (PBow). Here we utilized a mathematical model of the human kidney to investigate over acute and chronic timescales the mechanisms responsible for the magnitude of the hyperfiltration response. The model implicates that the primary hyperreabsorption of Na in the PT produces a Na imbalance that is only partially restored by the hyperfiltration induced by TGF and changes in PBow. Thus secondary adaptations are needed to restore Na balance. This may include neurohumoral transport regulation and/or pressure-natriuresis (i.e., the decrease in Na reabsorption in response to increased renal perfusion pressure). We explored the role of each tubular segment in contributing to this compensation and the consequences of impairment in tubular compensation. The simulations indicate that impaired secondary downregulation of transport potentiated the rise in glomerular hypertension and hyperfiltration needed to restore Na balance at a given level of primary PT hyperreabsorption. Therefore, we propose for the first time that both the extent of primary PT hyperreabsorption and the degree of impairment of the distal tubular responsiveness to regulatory signals determine the level of glomerular hypertension and hyperfiltration in the diabetic kidney, thereby extending the tubule-centric concept of diabetic hyperfiltration and potential therapeutic approaches beyond the proximal tubule.
Keywords: diabetic hyperfiltration, glomerular hypertension, diabetic kidney disease, mathematical model
the glomerular filtration rate (GFR) is elevated in early diabetes in many patients (1, 65), and this hyperfiltration has been associated with the development and progression of diabetic kidney disease (29, 42). Our understanding of the mechanisms responsible for hyperfiltration and subsequent renal injury is currently incomplete but may be critical for developing approaches to prevent diabetic kidney disease. Primary changes in the vasculature and the glomerulus, including those to the afferent and efferent arteriole, mesangial cells, the filtration barrier, and podocytes, play important roles in the pathophysiology of the diabetic kidney (23, 58). The tubulo-centric concept of diabetic hyperfiltration (51, 54, 64) proposes that hyperfiltration is initiated by a primary increase in sodium (Na) reabsorption in the proximal tubule (PT) (17, 55, 60). The primary hyperreabsorption of Na is due to tubular growth (49) and coupled reabsorption with glucose through Na glucose cotransporters (SGLT) (60) and increases GFR through changes in Bowman space pressure (PBow) and the tubuloglomerular feedback (TGF) mechanism (54, 60, 63, 64). Indeed, inhibition of tubular growth in diabetic rats (49) or inhibition of SGLT2 in rodent models of diabetes (50, 56, 62) as well as in diabetic patients (6) has been shown to reduce or eliminate hyperfiltration independent of effects on blood glucose.
The renal response to a primary change in proximal Na reabsorption likely involves multiple mechanisms. Much of our understanding comes from acute studies that measure the response to inhibition of PT Na reabsorption, either in the presence or absence of diabetes (21, 47, 52, 60). Measurements in diabetic animals (2, 52, 56, 60, 62) and humans (9, 17) have also provided insight on the chronic functional state of the kidney during hyperfiltration. However, a more complete understanding of the relationship between the acute and chronic renal response, as well as the relative contributions of the driving mechanisms, especially in the chronic state, is needed to better understand how diabetic hyperfiltration is initiated and, in particular, maintained, as the latter might contribute to diabetic kidney disease progression and provide new therapeutic options.
Mathematical models of physiological systems provide a framework for integrating first principles, accumulated knowledge of physiology, and experimental data to predict the temporal response of a system, including the response of variables that are not easily measureable experimentally. Such models can be used to evaluate the relative effects of contributing mechanisms, evaluate physical feasibility of hypothesized mechanisms, and propose new hypotheses. Beginning with Arthur Guyton (14), models of renal function have been developed and used to gain insight into mechanisms of renal physiology and disease (3, 16, 24, 26, 27, 32). In this study, we utilized an integrated mathematical model of the renal vasculature, tubular Na and fluid handling, and systemic blood volume regulation to investigate the potential mechanisms involved in both the acute and chronic GFR response to increased PT Na reabsorption in diabetes.
We first evaluated the hypothesis that changes in TGF and PBow mediate the initial hyperfiltration response to a primary increase in PT reabsorption in the early diabetic kidney. Based on the findings that these mechanisms only partially restore the Na imbalance introduced by a primary increase in PT reabsorption, we further tested the hypothesis that secondary tubular transport regulation is a critical factor in restoring Na balance and determining the degree of hyperfiltration and glomerular hypertension in the early diabetic kidney.
METHODS
The scope of the model used in this analysis is illustrated schematically in Fig. 1. In brief, the model describes the pressures, resistances, and blood flow throughout the renal vasculature; the filtration and reabsorption of Na and water along the tubule; the relationships among Na and water excretion and plasma Na concentration, cardiac output, total peripheral resistance, and blood pressure; vasopressin control of water reabsorption; whole body autoregulation of cardiac output; and TGF.
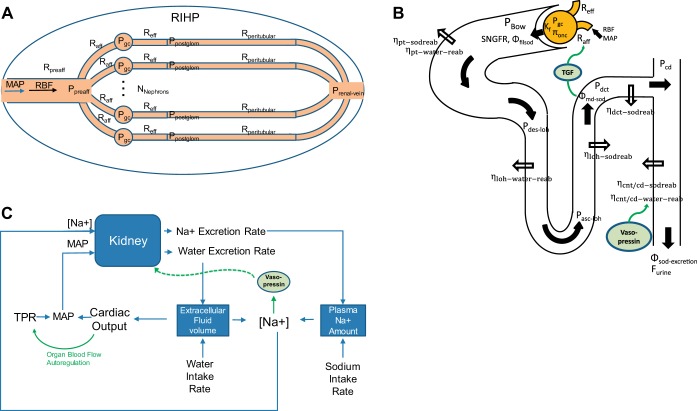
Fig. 1.
Schematic representation of the model of renal function, volume regulation, and feedback mechanisms. A: the renal vasculature is modeled by a single preafferent resistance vessel flowing into N parallel nephrons. B: Na and water filtration through the glomerulus is modeled according to Starling’s law. Na is reabsorbed at different fractional rates in each segment of the tubule, and water follows at the same fraction, except in the connecting tubule and collecting duct (CNT/CD), where water reabsorption is modulated by vasopressin. Based on tubular dimensions and flow rates, pressures are determined at the entrance to each tubular segment. C: Na and water excretion rates determined from the nephron model (B) affect extracellular fluid volume, plasma Na, cardiac output, and mean arterial pressure (MAP). Vasopressin secretion is modeled as a function of plasma Na concentration. Cardiac output is controlled by organ blood flow autoregulation. MAP and Na+ concentration then feed back into the kidney model (A and B). TGF, tubuloglomerular feedback; RBF, renal blood blow; PBow, Bowman space pressure; RIHP, renal interstitial hydrostatic pressure; SNGFR, single nephron glomerular filtration rate. See text and Table 1 for additional definitions.
In modeling a complex system such as the kidney, one must balance the incorporation of complexity with the utility of the model. In other words, the model should be fit-for-purpose. To that end, the model presented here is not meant to be a complete and perfect description of renal physiology, but rather a sufficient description of renal function and volume regulation to allow us to understand the specific problem at hand: the determinants of glomerular hypertension and hyperfiltration in response to a primary increase in PT Na reabsorption. As with all models, the assumptions and simplifications made should be kept in mind when interpreting the results or when attempting to extend the model to new research questions. We have tried when possible to point out the limitations and implications of the assumptions we make.
Model Equations
Renal vasculature and glomerular filtration.
As illustrated in Fig. 1A, glomeruli are assumed to sit in parallel with each other and in series with the preafferent (interlobar, interlobular, and arcuate arterioles) and peritubular vasculature. Thus, renal vascular resistance RVR is given by:
| (1) |
Rpreaff and Rperitubular are the total resistances of the preafferent and peritubular circulation, respectively. Raa and Rea are the resistances of a single afferent or efferent arteriole, respectively. Nnephrons is the number of functioning nephrons. In the current model all nephrons are assumed identical. As such, the model does not account for spatial heterogeneity or nephron cross-talk within the kidney.
Renal blood flow (RBF) is a function of the pressure drop across the kidney and RVR:
| (2) |
Pressure in the renal vein (Prenal-vein) is treated as constant. Determination of mean arterial pressure (MAP) is given later in Eq. 26. The second term in this equation is necessary to account for lower flow through the efferent arterioles due to GFR. As an approximation, all filtrate is assumed reabsorbed back into the peritubular capillaries, so that peritubular capillary blood flow is the same as afferent flow. The effect of loss of fluid through urine is ignored, since it is a very small fraction of GFR.
The hydrostatic pressure in the glomerular capillaries is determined by pressure drop across the renal vasculature before the glomerular capillaries:
| (3) |
Single nephron glomerular filtration rate (SNGFR) is defined according to Starling’s equation, where Kf is the glomerular ultrafiltration coefficient, Pgc is the glomerular capillary hydrostatic pressure, PBow is the pressure in the Bowman’s space, and πgo-avg is the average glomerular capillary oncotic pressure (ignoring any glomerular filtration of protein).
| (4) |
| (5) |
Determination of PBow is described later (Eq. 23).
The oncotic pressure is calculated using the Landis Pappenheimer equation, where Cprot is the concentration of protein at the point of interest. Plasma protein (Cprot-plasma) is treated as a constant. Protein concentration at the distal end of the glomerulus (Cprot-glom-out) is determined from plasma protein concentration, RBF, and GFR.
| (6) |
| (7) |
Glomerular capillary oncotic pressure πgo-avg is approximated as varying linearly along the length of the capillary, so that the average glomerular capillary oncotic pressure is the average of the oncotic pressure at the entrance and exit of the glomerular capillary, calculated using plasma protein concentration and protein concentration at the distal end of the glomerulus. The current model does not account for filtration equilibrium, which occurs in some species.
Tubular Na and water reabsorption and flow rates.
The proximal tubule reabsorbs a constant fraction of filtered Na load: the glomerulotubular balance phenomenon. Na reabsorption along the PT involves multiple transporters whose expression varies across the different segments of the PT. For this analysis, we approximate PT Na reabsorption as homogenous along its length, so that the reabsorption rate per unit length Rpt is related to the fractional rate of PT Na reabsorption ηpt and the length of the proximal tubule Lpt by:
| (8) |
We have found, through additional analysis not presented here, that incorporating different rates of reabsorption in different portions of the PT has minimal numerical effect on the simulation results presented in this analysis, and does not affect the conclusions. Thus we present here only the simpler model with homogeneous reabsorption. Under the simplifying assumption of uniform reabsorption along the tubule, at a given point along a tubule, the Na reabsorption dΦNa,pt over a length of tubule dx is given by:
| (9) |
Integrating, we obtain the Na flow along the length of the tubule:
| (10) |
ΦNa,pt(0) is the filtered Na load or SNGFR times the plasma Na concentration CNa.
Water is reabsorbed isoosmotically in the PT, so that flow rate along the PT is given by:
| (11) |
While the PT exhibits glomerulotubular balance, the degree of transport flow dependence in the loop of Henle (LoH), distal convoluted tubule (DCT), and connecting tubule and collecting duct (summarized as CNT/CD) is less well established, although there is evidence of flow dependence in each segment, particularly for the DCT and CNT/CD (25, 37, 43, 44). For the LoH, the fractional Na reabsorption rate was found to decrease only slightly in response to moderate (30%) increases in flow (59) but decreased significantly in response to large flow increases (>2-fold) (71).
For this analysis, we approximate Na reabsorption in each segment as distributed uniformly along the length, and the rate of reabsorption per unit length is formulated so that the degree of flow dependence can be varied. For a given segment, the nominal rate of reabsorption per unit length Ri,0 is given by the following, where η is the baseline fractional rate of reabsorption, ΦNa,0(0) is the amount delivered to the segment under baseline conditions, and L is the segment length.
| (12) |
where i is the ascending LoH (ALH), DCT, or CNT/CD.
The actual rate per unit length Ri,0 is then the nominal rate augmented by a flow-dependent component, as shown in Eq. 13. The coefficient B determines the degree of flow-dependence: for B = 0, there is no flow dependence; for B = 1, changes in reabsorption are directly proportional to flow. Experimental data suggest a value for B of 0.85 for changes in flow (for flow perturbations into the LoH of 30%) (59), although an earlier study using a flow increase of 300% indicated a value of 0.5 (71). This suggests that flow-dependent effects on transport may become weaker as flow increases. However, for this study, changes in LoH flow were never greater than 30%. Thus, we use a value for B of 0.85 (59).
| (13) |
Na flow along each segment is then:
| (14) |
ΦNa,i(0) is obtained from the Na flow out of the preceding tubule segment.
In the LoH, water is reabsorbed in the water-permeable descending LoH (DLH) due to the osmotic gradient created by active pumping of Na out of water-impermeable ascending limb (ALH). To model this countercurrent mechanism, we borrow from the work of Hoppensteadt and Peskin (20), who in turn borrowed from work by Layton et al. (40). We assume the descending limb is impermeable to Na, while the ascending limb is impermeable to water. The descending limb is assumed to quickly equilibrate with the interstitium. We also assume that all reabsorbed water and Na is picked up by the peritubular capillaries locally and that Na follows water into the peritubular capillaries at its local concentration. With these assumptions, the Na concentration along the length of the descending loop of Henle (CNa,DLH) and in the surrounding interestium (CIS) is given by Ref. 20:
| (15) |
CNa,DLH(0) and FDLH(0) (the Na concentration and fluid flow rate into the DLH) are the flow rates out of the PT, as given in Eqs. 10 and 11.
Water flow rate through the DLH is then given by:
| (16) |
Since the ascending limb is impermeable to water, flow through the ascending limb is equal to flow at the exit (x = L) of the descending limb.
| (17) |
The DCT is modeled as impermeable to water, such that water flow through the DCT equals flow out of the ascending LoH.
Fine regulation of water reabsorption occurs in the CNT/CD, through the cell membrane expression of aquaporins, regulated by vasopressin. Water reabsorption through aquaporin is represented as a nominal fractional rate, modulated by the normalized vasopressin level (μvasopressin). The vasopressin level is controlled by plasma Na concentration, as described below (Eq. 36).
| (18) |
Urine flow rate Furine is then given by the product of the flow out of the distal tubule, the total number of nephrons, and 1 minus the fractional rate of collecting duct water reabsorption.
| (19) |
Tubular hydrostatic pressure.
The model for tubular hydrostatic pressure was adapted from Jensen et al. (22). Once the flow rates along the tubule are known, the pressure at any point in the tubule can be determined. The change in intratubular pressure dP* over a length of tubule dx can be defined according to Poiseuille’s law as:
| (20) |
The tubules are compliant, and the relationship between transtubular pressure P and tubular diameter D can be defined by Eq. 21, where Dc is the diameter at some control pressure Pc and β is the exponent of tubular distensibility, previously estimated to be 0.2–0.4 (22).
| (21) |
Substituting and assuming uniform interstitial pressure throughout the kidney, we obtain:
| (22) |
Integrating over the length of a segment of tubule, we obtain the inlet pressure as a function of the outlet pressure and the flow rate:
| (23) |
The pressure calculated at the inlet to the PT is used as PBow in Eq. 4 above.
Because the diameter of the CNT/CD changes as nephrons coalescence, calculating pressure along this segment is challenging. Under normal conditions, pressure drops 5–7 mmHg across the CNT/CD (22). Thus an effective control diameter was calculated to give this degree of pressure drop under base case conditions.
Tubuloglomerular feedback.
Tubuloglomerular feedback (TGF) provides a signal that induces inverse changes in afferent arteriole diameter when macula densa (MD) Na, chloride, and potassium delivery changes. We focus on changes in Na, which we assume changes in parallel with chloride and potassium. The TGF effect is defined as:
| (24) |
The basal afferent arteriole resistance Raa is then multiplied by μTGF to obtain the ambient afferent arteriolar resistance. The setpoint CNa,MD,0 is the Na concentration out of the LoH and into the DCT in the baseline state at normal salt intake. The parameter mTGF determines the steepness of the TGF effect. This parameter is unknown, but sensitivity analysis has been performed to determine a reasonable range. STGF is the maximal response as Cmd-sod goes to ∞. Thus μTGF can take values between 1 − STGF/2 and 1 + STGF/2 and will equal 1 when MD Na concentration CNA,MD equals the setpoint. Since this parameter is unknown but may be important in determining the response to changes in PT Na reabsorption, in this paper we explore the impact of different values for this parameter.
Systemic hemodynamics.
While the primary focus of this model is renal function, renal and systemic hemodynamics are integrally linked, and thus it is necessary to connect the loop among blood volume, cardiac output, mean arterial pressure, and Na and water excretion. For this purpose, we have adapted Guyton’s simplistic but sufficient model of cardiovascular function (14, 24).
Systemic water and Na are modeled using a two-compartment model of blood and extracellular fluid (ECF), where exchange occurs along a concentration gradient. In the current model, exchange with intracellular space is ignored. Na amount in the blood (MNa,blood) is determined by the time integral of the difference between the rate of Na intake and excretion, as well as transfer to the ECF down a concentration gradient. For this analysis, the rate constant QNa was set to 1.
| (25) |
| (26) |
Blood volume (Vb) is determined by the time integral of the difference between the rate of water intake and urinary flow rate and the transfer of water between the blood and ECF compartments. Similarly, ECF volume (Vecf) is determined by the transfer of water between the ECF and blood. For the current simulations, we assume intracellular fluid volume remains constant. The blood Na concentration (CNa,blood) is then the blood Na amount divided by blood volume, and ECF Na concentration (CNa,ecf) is the ECF Na amount divided by ECF volume. For this analysis, the rate constant Qwater was set to 1.
| (27) |
| (28) |
| (29) |
| (30) |
The mean cardiac filling pressure (Pmf) is a function of blood volume and venous compliance cvenous.
| (31) |
Cardiac output (ΦCO) is mean filling pressure divided by resistance to venous return (Rvr).
| (32) |
Total peripheral resistance (TPR) is determined by treating the systemic and renal vasculatures as parallel resistances, in series with venous resistance:
| (33) |
Mean arterial pressure (MAP) is then:
| (34) |
Regulation of cardiac output in the face of changes in blood volume and/or blood pressure is a complex phenomenon, likely involving multiple mechanisms over different time scales. Detailed modeling of regulation of cardiac output is beyond the scope of the current analysis. For the purpose of this modeling study, we include only the mechanism of total body autoregulation: the intrinsic ability of organs to adjust resistance to maintain constant flow. Thus the effect of cardiac output on systemic vascular resistance (SVR) is represented by a proportional-integral controller, such that cardiac output is controlled to its setpoint CO0 at steady state. The gain values in this controller (Ki-svr, GCO-svr) were set so that after a perturbation, cardiac output returned to the setpoint over the course of a few days without overshoot or oscillations. The gain values in this controller (Ki-svr, GCO-svr) were set so that after a perturbation, cardiac output returned to the setpoint over the course of a few days without overshoot or oscillations.
| (35) |
Control of plasma Na concentration by vasopressin.
To sustain life, Na concentration must be controlled within a very tight range. Na and water intake are variable, and for a given amount of Na excretion, the kidney must be able to excrete exactly the right amount of water to maintain this ideal concentration. While water is reabsorbed passively along the tubule, fine control of tubular water reabsorption/excretion occurs in the CNT/CD through the action of vasopressin on aquaporin 2. Vasopressin is secreted by the posterior pituitary gland, in response to changes in plasma osmolality. To reproduce this effect, the effect of plasma Na concentration on vasopressin secretion is modeled by a proportional-integral controller, which ensures that plasma Na concentration is maintained at its setpoint CNa,0 at steady state. The normalized vasopressin concentration is given by:
| (36) |
The setpoint CNa,0 is the normal plasma Na concentration of 140 mEq/l. The parameters GNa-vp and Ki-vp are gains of proportional and integral control, respectively. The gain values in this controller were set so that after a perturbation, plasma Na concentration returned to the setpoint as quickly as possible without overshoot or oscillations. Vasopressin then affects the fractional rate of water reabsorption in the CNT/CD, as described above in Eq. 18.
While we do not attempt to model all the various neurohumoral effects that play a role in the kidney, the ability to maintain a constant plasma sodium concentration is critically dependent on the ability to regulate the reabsorption of water separate from Na, and thus modeling the action of vasopressin is critical to obtain a stable plasma sodium concentration in the model.
Linking blood pressure to natriuresis.
In the normal kidney, tubular Na reabsorption is responsive to changes in the neurohumoral milieu and renal perfusion pressure (the “pressure-natriuresis mechanism”), with increases in pressure leading to increased excretion with minimal changes in glomerular filtration. The signals that drive the pressure-natriuresis mechanism, and their relative contributions, remain uncertain, but the likely involve both intrinsic and neurohumoral signals, including but not limited to renal interstitial hydrostatic pressure, angiotensin II/aldosterone, and renal sympathetic nerve activity, and are modulated by autocrine and paracrine systems like prostaglandins and nitric oxide. As part of this study, we aimed to evaluate the role of compensatory changes in Na reabsorption on the renal response to a primary increase in PT Na reabsorption. However, because the precise mechanisms and their relative contributions remain incompletely understood, the influence of the neurohumoral and pressure-natriuresis system was represented through a direct effect of MAP on tubular Na reabsorption. This allows us to explore the consequences of alterations in these systems, without claiming to fully understand the exact mechanisms.
In addition to uncertainty regarding the mechanisms involved in regulation of tubular Na reabsorption, there is also uncertainty regarding the nephron segments most involved (73). Different regulatory signals may affect each tubular segment to varying degrees. Therefore, the model was structured to include an effect of MAP on Na reabsorption in each tubular segment that could be independently modulated or turned off. The relationship between MAP and the fractional Na reabsorption rate η of each tubular segment was modeled using the logistic relationship:
| (37) |
where i = PT, LoH, DCT, or CNT/CD. ηi Is the nominal fractional rate of reabsorption for that tubule segment. MAP0 defines the setpoint, and is determined from MAP at the baseline state at normal salt intake. SP-N,i defines the maximal response as MAP goes to ∞ and was used to vary the magnitude of the effect on each segment or to turn it off completely. For the simulations presented below, these effects were turned off (SP-N set to zero for each segment) unless stated otherwise.
Model Parameters and Species Scaling
Model parameters used to represent either human and rat physiology are given in Table 1. While we are ultimately interested in understanding human renal function, much experimental data on diabetic hyperfiltration have been collected in rats. Thus, for this analysis, we identified a subset of model parameters that can be changed to reflect either human or rat physiology. For instance, humans have ~2 million nephrons, while an adult rat has ~50,000. Tubular segments are shorter in rats. Water and Na intake rates are much lower in rats than humans (even though these rates are much higher relative to body weight). Cardiac output is also much lower in rats, and since cardiac output is controlled by whole body autoregulation, the setpoint (CO0) must be changed to represent the species difference. Other parameters were assumed conserved across species. For example, glomerular ultrafiltration coefficient (Kf), tubular diameters, etc. were all assumed similar across human and rats. Some parameters were calculated based on other parameter values and known typical steady state values for functional variables [e.g., nominal systemic vascular resistance (SVR0) was calculated from nominal baseline cardiac output and MAP].
Table 1.
Model parameters for human and rat
| Parameter | Definition | Human | Rat | Units |
|---|---|---|---|---|
| CNa,0 | Target sodium concentration | 140 | 140 | mEq/l |
| CNa,MD,0* | Macula densa sodium flow setpoint for TGF response | 39 | 39 | mEq/l |
| CO0 | Cardiac output setpoint | 5 | 0.4 | l/min |
| Cprot | Plasma protein concentration | 7 | 6.2 | g/dl |
| cvenous | Venous compliance | 0.134 | 37.2 | mmHg/l |
| Dc,cd | Effective CNT/CD diameter | 17 | 17 | um |
| Dc_dt | DCT tubule diameter | 17 | 17 | um |
| Dc_loh | LoH diameter | 17 | 17 | um |
| Dc_pt | PT diameter | 27 | 27 | um |
| Fwater-in | Water intake rate | 2 | 0.025 | l/day |
| GCO-svr | Cardiac output autoregulation gain | 2 | 2 | |
| GNa-vasopressin | Vasopressin controller gain | 1 | 1 | |
| Kf | Ultrafiltration coefficient | 3.9 | 3.9 | nl·min−1·mmHg−1 |
| Ki_vp | Integral gain for vasopressin controller | 0.1 | 0.1 | |
| Ki-svr | Integral gain for systemic vascular resistance controller | 100 | 100 | |
| Lcd | Length of the CNT/CD | 10 | 3 | mm |
| Ldt | Distal tubule length | 5 | 3 | mm |
| Lloh_asc | Ascending LoH length | 10 | 3 | mm |
| Lloh_des | Descending LoH length | 10 | 3 | mm |
| Lpt | PT length | 14 | 5 | mm |
| MAP0 | Mean arterial pressure setpoint | 85 | 100 | mmHg |
| mTGF | TGF effect slope | 0.5 | 0.5 | |
| Nnephrons | Number of nephrons | 2.00E+06 | 50000 | |
| QNa | Rate constant: sodium transfer between blood and ECF | 1 | 1 | |
| Qwater | Rate constant: water transfer between blood and ECF | 1 | 1 | |
| Pc_asc_loh | Ascending LoH control pressure | 7 | 8 | mmHg |
| Pc_cd | CNT/CD control pressure | 5 | 5 | mmHg |
| Pc_des_loh | Descending LoH control pressure | 8 | 10 | mmHg |
| Pc_dt | DCT control pressure | 6 | 6 | mmHg |
| Pc_pt | PT control pressure | 19.4 | 13.6 | mmHg |
| Pmf,0 | Baseline mean filling pressure | 30 | 30 | mmHg |
| Ppelvic | Pelvic pressure | 0 | 0 | mmHg |
| Pvenous | Venous pressure | 4 | 4 | mmHg |
| RBF0 | Nominal renal blood flow | 1 | l/min | |
| Rperitubular,0* | Peritubular resistance | 5.66 | 537 | mmHg·min−1·l |
| Rpreaff,0 | Baseline preafferent resistance | 14 | 3,500 | mmHg·min−1·l |
| Rvr | Resistance to venous return | 1.3 | 170 | mmHg·min−1·l |
| RVR0* | Nominal renal vascular resistance | 81 | 8,727 | mmHg·min−1·l |
| STGF | TGF maximal response as Φmd-sod goes to infinity. | 0.6 | 0.6 | |
| SP-N,LoH | Max effect on LoH sodium reabsorption as MAP goes to infinity | 0 | 0 | |
| SP-N,DCT | Max effect on DCT sodium reabsorption as MAP goes to infinity | 0 | 0 | |
| SP-N,CD | Max effect on CNT/CD sodium reabsorption as MAP goes to infinity | 0 | 0 | |
| SVR0* | Nominal systemic vascular resistance | 13.6 | 2,100 | mmHg·min−1·l |
| VECF(0) | Initial extracellular fluid volume | 15 | 0.06 | liter |
| Vb(0) | Initial blood volume | 5 | 0.018 | liter |
| β | Tubular compliance | 0.2 | 0.2 | |
| ηblood | Blood viscosity | 5.00E-07 | 5.00E-07 | mmHg/min |
| ηcd* | Nominal CNT/CD fractional rate of reabsorption | 0.724 | 0.724 | |
| ηdt | Nominal DCT fractional sodium reabsorption rate | 0.5 | 0.5 | |
| ηloh | Nominal LoH fractional sodium reabsorption rate | 0.88 | 0.88 | |
| ηpt | Nominal PT fractional sodium reabsorption rate | 0.7 | 0.7 | |
| φsodin | Sodium intake rate | 100 | 2 | mmol/day |
MAP, mean arterial pressure; TGF, tubuloglomerular feedback; CNT/CD, connecting tubule and collecting duct; DCT, distal connecting duct; PT, proximal tubule; LoH, loop of Henle; ECF, extracellular fluid; SNGFR, single nephron glomerular filtration rate.
Parameters that were calculated based on other parameter values.
Nominal renal vascular resistance (RVR0) was calculated based on normal pressure drop across the kidney and normal renal blood flow (RBF0). The peritubular vascular resistance value required to give typical renal blood flow was calculated based on the RVR0 and values specified for preafferent, afferent, and efferent resistances. Similarly, the value for CNT/CD fractional Na reabsorption rate (ηcnt/cd,0) was calculated for a given equilibrium GFR, plasma Na concentration, and plasma Na intake, as well as upstream fractional Na reabsorption rates, based on the fact that at equilibrium, Na excretion must equal Na intake.
There is substantial variability in experimental measurements of fractional Na reabsorption rates for each tubular segments. PT Na fractional reabsorption (ηpt,0) has been reported across the range of 40–78% (28, 47, 49, 55, 61). Under normal flow conditions, LoH fractional Na reabsorption (ηloh,0) has been reported from 85 to 93% (59, 71). For this analysis, fractional Na reabsorption rates in the PT, LoH, and DCT were set to 0.70, 0.88, and 0.5, respectively, and CNT/CD fractional reabsorption rate was calculated to be 0.724. As shown in Table 2, these rates correspond to 70, 26, 1.8, and 1.3% reabsorption as a percentage of filtered load for the PT, LoH, DCT, and CNT/CD, respectively. Textbooks and manuals on renal physiology typically state the contribution to Na reabsorption as a fraction of filtered load in each segment as about 65, 20, 10, and 5% for the PT, LoH, DCT, and CNT/CD, respectively. However, references supporting this distribution are difficult to locate. On the other hand, some studies have shown reabsorption rates of 95–97% up to the early distal tubule in normal rats (57, 60). Therefore, we believe the parameters given in Table 2 represent one set of physiologically reasonable parameter.
Table 2.
Calculation of Na delivery and reabsorption along the tubule, using typical human values for GFR, plasma Na concentration, and Na intake rate of 100 ml/min, 140 mEq/l, and 0.07 mEq/min (or 100 mEq/day), respectively
| Tubular Segment | Fractional Reabsorption Rate, η | Na Delivery, mEq/min | Na Reabsorption, mEq/min | Reabsorption as %Filtered Load |
|---|---|---|---|---|
| PT | 0.7 | 14.000 | 9.800 | 70% |
| LoH | 0.88 | 4.2 | 3.7 | 26.4% |
| DCT | 0.5 | 0.50 | 0.25 | 1.8% |
| CNT/CD | 0.724* | 0.25 | 0.18 | 1.3% |
| Urine excretion rate | 0.07* |
Significant difference.
To ensure that the model produces physiologically reasonable outputs for both rats and humans, the simulated steady-state model outputs were compared with key measurements of cardiovascular and renal function in rats and humans (Table 3).
Table 3.
Simulated model outputs at steady-state baseline fall within the typical clinically observed range for key measurements of cardiovascular and renal function
| Human |
Rat, 300 g |
|||
|---|---|---|---|---|
| Output, units | Typical Value | Model | Typical Value | Model |
| CO, l/min | 5 | 5 | 0.04 | 0.04 |
| MAP, mmHg | 80–100 | 85 | 100 | 100 |
| Blood volume, liter | 5 | 4.95 | 0.015–0.021 | 0.018 |
| ECF, liter | 15 | 14.6 | 0.06 | 0.059 |
| TPR, mmHg·min−1·l | 16 | 16.7 | 2,000–2,500 | 2479 |
| GFR, ml/min | 100–120 | 102.4 | 2–3 | 2.65 |
| SNGFR, nl/min | 50–60 | 51.2 | 40–60 | 53 |
Values are presented for both the human and rat model parameterization.
Software Implementation
The model was implemented in a free open-source programming language and software (R 3.1.2). It utilizes the RxODE package (66). A web-based user interface is available at http://qsp.engr.uga.edu:3838/DiabeticHyperfiltration, utilizing R’s Shiny Package (41). This interface allows the user to reproduce the simulations described here in real time, as well as to simulate additional scenarios and to explore the effects on all variables in the system, rather than the limited ones presented here. We invite the reader to explore this online companion. Model code is provided in the Supplemental Material (Supplemental Material for this article is available online at the Journal website).
Simulation Approach
Much of the available data on the renal response to changes in PT Na reabsorption come from experimental inhibition of PT Na reabsorption with infusion of agents such as carbonic anhydrase inhibitors (21, 73). It is important to first show that the model can reproduce these experiments. In addition, these experiments help inform values for some parameters around which there is uncertainty. However, we are ultimately interested in simulating the chronic renal response to increased PT Na reabsorption in diabetic humans. Thus we conducted two sets of simulations. Set 1 explored both the acute response to pharmacologic inhibition of PT Na reabsorption in rats. A step decrease in PT fractional rate of reabsorption of 40% was simulated to mimic the experimental pharmacologic inhibition of PT reabsorption (21, 73). Simulations were conducted for 10 min of simulation time, and the rat parameterization was used, since the available data for comparison was in rats. To understand the role of and to characterize the magnitude of the TGF response, simulations were conducted using a range of parameter values for the strength of the TGF effect (STGF).
Simulation set 2 explored the acute and chronic response to increased PT Na reabsorption in diabetic humans. A 15% step increase in PT fractional rate of reabsorption was used to mimic the diabetic state, in which PT fractional reabsorption has been shown to be increased by 5–25% in humans (17) and animals (2, 55). Simulations were conducted for 10 min and for 30 days of simulation time, to understand both the acute and chronic response to this change. The human model parameterization was used for these simulations. We also explored the impact of the ability of the nephron to compensate for proximal changes in reabsorption. For the 30-day simulation, we first performed simulations without allowing compensatory changes in tubular reabsorption rates. We then repeated the simulation, allowing an effect of MAP (as a convenient surrogate representing the composite effect of all regulatory effects contributing to pressure-natriuresis) on PT, LoH, DCT, or CNT/CD Na reabsorption, at a range of strengths (S in Eq. 37).
RESULTS
Simulation Set 1: Simulation of Experimental Inhibition of PT Na Reabsorption
Inhibition of PT Na reabsorption has been used experimentally to investigate the acute GFR response to primary changes in PT reabsorption (21, 41, 73). Leyssac et al. (28) reported that when PT reabsorption was inhibited with acetazolamide infusion (producing a 40% reduction in fractional PT reabsorption), the drop in GFR observed was associated with an increase in Bowman space pressure, which decreased net filtration pressure. Similar results have been observed by others (41, 60, 61). In Leyssac’s experiment, Bowman space pressure peaked at 2 min after the start of acetazolamide infusion and then settled to 2 mmHg above the control level. The settling in tubular pressure was attributed to the effects of TGF.
To reproduce this experiment, we simulated the acute renal response to a step 40% decrease in the fractional rate of PT Na reabsorption [representing the inhibition observed with acetazolamide (28)] and used Leyssac’s findings to validate our model predictions and identify constraints on parameters describing the TGF response. As shown in Fig. 2 and in agreement with Leyssac’s observations, the model predicted that single nephron GFR would fall, while PBow peaked and then settled to a lower level but still above baseline over the first 10 min. The initial peak in PBow is due to increased fluid flowing into the distal nephron when PT reabsorption is reduced, and results in a very fast fall in net filtration pressure and GFR. The magnitude of change in PBow relative to change in flow out of the PT was 0.3 mmHg·nl−1·min, consistent with observations by Holstein-Rathlou (0.2 mmHg·nl−1·min) (19), Vallon et al. (0.25–0.3 mmHg·nl−1·min) (61), and Thomson and Blantz (0.1–0.3 mmHg·nl−1·min) (48).
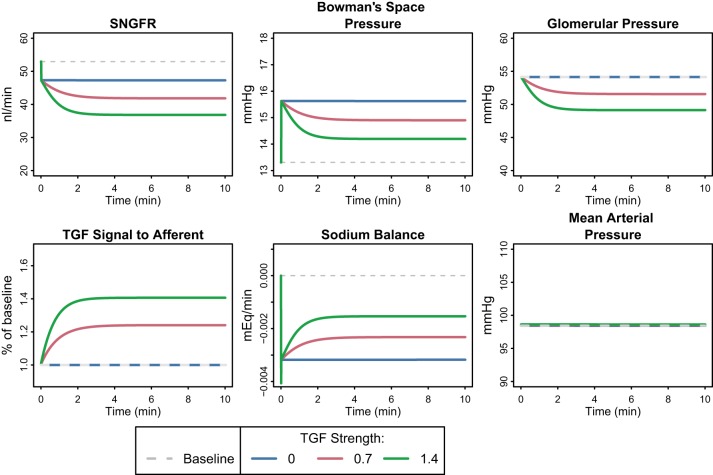
Fig. 2.
Acute response to a 40% step decrease in proximal tubule (PT) fractional Na reabsorption rate, with varying degrees of TGF feedback. PBow spikes initially, causing a very fast fall in net filtration pressure and glomerular filtration rate (GFR). Over the next few minutes, TGF constricts the afferent arteriole, reducing glomerular hydrostatic pressure, further lowering SNGFR while partially restoring PBow. The decrease in PT Na reabsorption causes a Na imbalance that is only partially restored by the decrease in SNGFR due to TGF and PBow.
The settling in PBow is a function of the TGF response. We performed the simulation at varying levels of TGF strength, as defined by the parameter STGF in Eq. 24. The values chosen for STGF (0, 0.7, and 1.4) correspond to a fractional compensation of 0, 0.5, and 1 [fractional compensation is a measure of TGF homeostatic efficiency (55)]. The TGF response constricted the afferent arterioles, reducing glomerular pressure and decreasing GFR further. This further decrease in GFR mitigated the initial increase in distal fluid delivery, lowering PBow toward control levels. Thus the degree of PBow settling depended on the magnitude of the TGF effect, with a strong effect (STGF = 1.4, fractional compensation = 1) returning PBow to near baseline, while removal of TGF (STGF and fractional compensation = 0) eliminated the PBow lowering. An intermediate level of TGF (STGF = 0.7, fractional compensation = 0.5) resulted in settling to a pressure of 2 mmHg above baseline, in agreement with Leyssac et al. and others (28, 52, 60). This level of fractional compensation is also consistent with previous measurements that showed fractional compensation in the range of 0.4–0.75 in normal and 0.2–0.4 in diabetic rats (55). Thus this level was assumed to be a reasonable choice for TGF strength and is used in all further simulations. At this level, the TGF response and PBow increase contributed nearly equally to the fall in GFR.
A critical observation from this simulation is that the combined effect of PBow and TGF on GFR was not able to normalize Na delivery to the distal tubule or urine thereby inducing negative Na balance (even at the highest TGF strength). A negative Na balance is not sustainable chronically. Thus additional changes beyond the acute response must occur to return homeostasis long term.
Simulation Set 2: Simulation of Increased PT Na Reabsorption in Diabetes
Acute and chronic response in the absence of regulation of tubular Na transport.
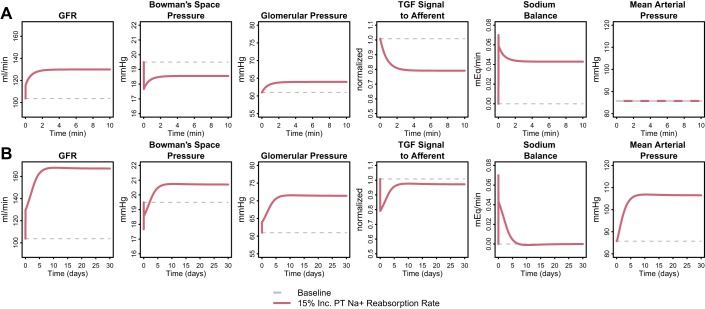
In diabetes, PT fractional Na reabsorption is increased 5–25% (2, 17, 55) presumably due to increased Na reabsorption through SGLT2 when filtered glucose is elevated. Diabetes-induced tubular growth also contributes. To investigate the hemodynamic impact of increased PT Na reabsorption, we simulated a step 15% increase in PT fractional Na reabsorption rate. For these simulations, we used the human model parameterization (We also conducted simulations using the rat parameterization, and observed consistent trends). Figure 3A shows the acute 10 min response. GFR increased very quickly by 12 ml/min or 12% due to a fall in PBow of 1.8 mmHg (the fall in net filtration pressure difference was 1.4 mmHg, due to a small rise in πonc-avg (0.3 mmHg, not shown) associated with the increase in GFR. Over the next few minutes, TGF signaling dilated the afferent arteriole, increasing glomerular pressure by 3.0 mmHg and driving SNGFR up an additional 14.3 ml/min (14%), while PBow recovered partially. Over this time period, as expected, MAP remained constant.
Fig. 3.
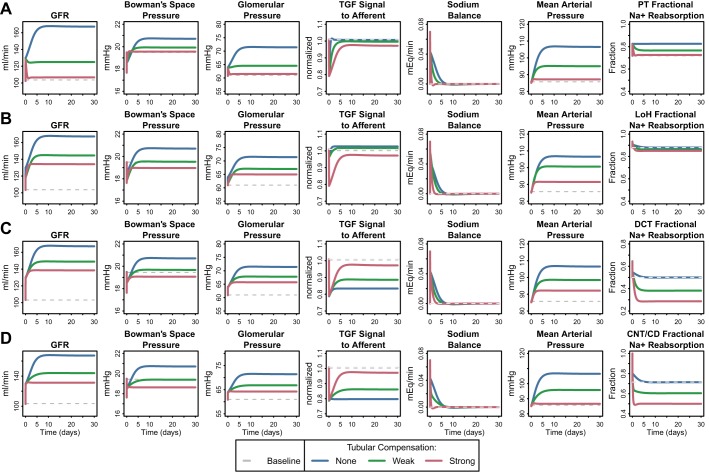
Acute 10-min (A) and chronic 30-day (B) response to a 15% step increase in PT fractional Na reabsorption rate, in the absence of any regulatory effects on tubular Na reabsorption (SP-N,i = 0 for all segments). Acutely, GFR increases very quickly due to a fall in PBow, and over the next few minutes, increases further as TGF signaling dilates the afferent arteriole, increasing glomerular pressure. The Na imbalance generated by the step increase in PT Na reabsorption is only partially restored by the combined effects of TGF and PBow on GFR. Thus, even though the changes in these variables have plateaued by 10 min, the system is not at steady state. Chronically, in the absence counterregulatory effects on tubular Na reabsorption, the Na imbalance causes Na and water retention that drives up mean arterial pressure and glomerular pressure, increasing GFR even further until Na excretion again matches intake and Na balance is returned.
Importantly, the simulations showed that the combined effects of TGF and PBow on GFR were not sufficient to return Na balance (Fig. 3A, Na Sodium). Thus, even though the changes in these variables have plateaued by 10 min, the system cannot be at steady state, and other changes must occur over time to return the system to Na balance. Assuming that Na intake remains constant, there are only two ways to restore balance: either tubular reabsorption of Na must decrease, or glomerular filtration must increase, until Na excretion again matches intake.
Figure 3B shows the chronic (30 day) response to a 15% increase in PT fractional Na reabsorption rate in the absence of regulatory effects on tubular Na reabsorption. Since tubular rates of Na reabsorption were constant, the only remaining way that Na balance could be returned was through an increase in filtration. As the simulations show, an additional increase in GFR of 37 ml/min on top of the initial 26 ml/min increase (total increase of 61%) was required to return Na balance. At steady state, the increase in GFR was driven by a large increase in both blood pressure and glomerular capillary hydrostatic pressure (15 mmHg). Thus, in the absence of tubular compensation, excessive glomerular hypertension is required to return Na balance. Such glomerular hypertension might be expected to have pathophysiological consequences (34, 38).
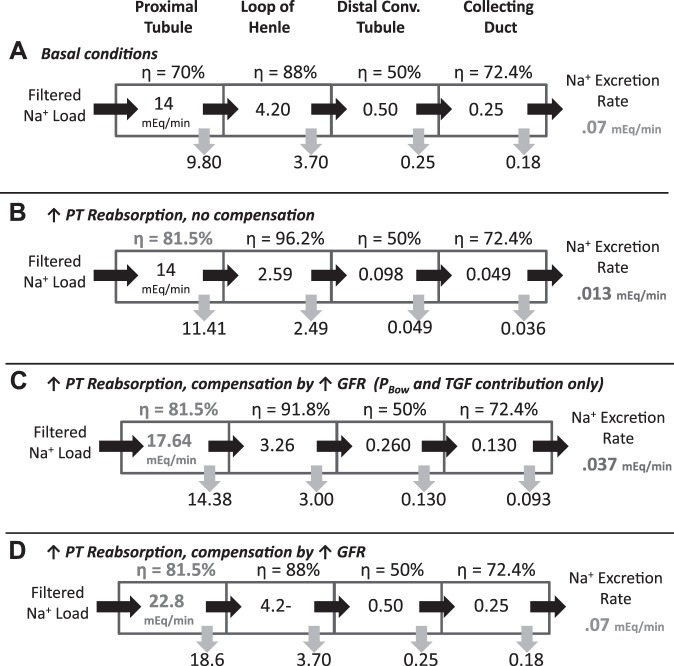
The necessity of the large increase in GFR to return Na balance after an increase in PT fractional Na reabsorption (in the absence of distal regulation) can be understood further from simple calculations illustrated in Fig. 4. Figure 4A shows Na delivery and reabsorption rates along the tubule under normal conditions, for a GFR of 100 ml/min, plasma Na concentration of 140 mEq/l, and Na intake (and thus excretion) of 0.07 mEq/min (100 mEq/day). Figure 4B illustrates that a 15% increase in PT fractional Na reabsorption would result in Na excretion that is ~80% less than intake (0.013 vs 0.07 mEq/min) if no other changes in filtration or reabsorption occurred. Figure 4C shows that the increase in GFR and filtered Na load due to TGF and decreased PBow restores Na balance partially but not fully (0.037 vs 0.07 mEq/min). Figure 4D shows that, if distal reabsorption rates remain constant, filtered Na load would have to increase from 14 to 22.8 mEq/min (which corresponds to an increase in GFR to 163 ml/min, as predicted by the model) to achieve the required 0.07 mEq/min Na excretion.
Fig. 4.
Na delivery and reabsorption rates along the tubule for a GFR of 100 ml/min, plasma Na concentration of 140 mEq/l, and Na intake of 0.07 mEq/min (100 mEq/day). Assumes perfect flow-dependent transport in the PT (i.e., fractional reabsorption not altered by load), and partial flow-dependent transport in the loop of Henle (LoH) (B = 0.85) A: basal conditions produce Na excretion that matches intake. B: a 15% increase in PT fractional Na reabsorption, without other changes in filtration or reabsorption, results in Na excretion that is much less than intake (0.013 vs. 0.07 mEq/min or 19%). C: TGF and PBow-induced increase in GFR of 26 ml/min (as predicted by the model) increases filtered load from 14 to 17.64 mEq/min, but is insufficient to return Na balance. D: increasing filtered Na load further to 22.8 mEq (63% increase in GFR from baseline) returns Na balance (0.07 mEq/min Na excretion) without changes in distal reabsorption. Na delivery to all segments downstream of the PT are returned to normal.
Note that in Fig. 4, B and C, the fractional reabsorption in LoH increases, since LoH Na delivery is decreased from the basecase (Fig. 4A), and flow dependence was assumed to be imperfect, so that as flow decreases, a higher fraction of delivered Na is reabsorbed. However, in Fig. 4D, Na delivery to the LoH is restored to normal due to increased GFR, so the fractional LoH reabsorption rate returns to baseline also.
Impact of regulation of tubular Na transport.
Up to this point, we have ignored the effects of tubular regulation of Na reabsorption. Figure 5 shows the response to a 15% increase in PT fractional Na reabsorption rate when the Na reabsorption in the PT (Fig. 5A), LoH (Fig. 5B), DCT (Fig. 5C), or CNT/CD (Fig. 5D) is allowed to compensate. As described above, MAP is used in the model to provide the signal for compensatory Na reabsorption. The intermediate mechanisms by which changes in MAP and thus renal perfusion pressure are transmitted to changes in tubular Na reabsorption are beyond the scope of this study. Rather, we seek to understand the effects of tubular Na regulation and the consequences of its impairment on hyperfiltration and glomerular hypertension, without regard to the specific mechanism by which it is achieved. Since there is uncertainty regarding the relative degree of regulation of each tubular segment, we explored the impact of compensatory changes in each tubular segment separately. From Fig. 5, we can first observe that, in all cases, the initial GFR rise (26 ml/min) resulting from the (fast) TGF and PBow response was consistent. Second, regardless of the tubular segment involved, as the degree of compensatory reduction in tubular Na reabsorption rate was increased, the additional GFR augmentation and associated increase in glomerular and mean arterial pressure required to achieve sodium balance was reduced. Tubular compensation also increased the speed at which Na balance was returned. Thus, tubular compensation allows Na balance to be achieved more quickly at lower pressures and GFR. Or alternatively, impairment of compensatory changes in tubular Na reabsorption required larger increases in blood pressure and glomerular hypertension to restore Na balance.
Fig. 5.
Chronic response to a 15% step increase in PT fractional Na reabsorption rates, when a regulatory effect of MAP on Na transport (represented by SP-N,i in Eq. 37) in the PT (A), LoH (B), distal collecting tubule (DCT; C), or CNT/CD (D) was included in the model (using baseline fractional reabsorption rates given in Table 2). In all cases, GFR rose initially due to the (fast) TGF and PBow response, and compensatory reduction in tubular Na reabsorption rate allowed Na balance to be returned more quickly. Strong PT compensation restored GFR nearly to normal. Strong compensation in all other segments prevented a further rise in GFR beyond the acute response. For the LoH, a small reduction in fractional Na reabsorption were sufficient to compensate but was predicted to increase macula densa (MD) Na concentration, inconsistent with experimental data (57, 60). Compensation through the DCT or CNT/CD prevented additional GFR increase while maintaining a reduced MD Na concentration.
Figure 5A shows the consequences of regulatory compensation through the PT alone. If the compensatory signal to PT Na reabsorption is strong enough, GFR can be restored nearly to normal. These simulations suggest that the degree to which the PT is able to compensate for diabetes-driven increases in Na reabsorption through other mechanisms will directly determine the degree of hyperfiltration. The PT is an important location for regulation of Na reabsorption (30). However, the fact that increases in PT reabsorption have been observed in diabetic patients and animals (2, 17, 55) suggests that the PT is not in fact able to fully compensate or that PT compensation is impaired in diabetes. If the PT compensation is insufficient or impaired, then either the distal nephron must compensate or GFR must increase further.
Figure 5B shows the consequences of a regulatory effect of MAP on the LoH alone. Despite the initial small increase in LoH fractional reabsorption (due to reduced delivery and imperfect flow-dependent reabsorption), small MAP-driven compensatory reductions in LoH reabsorption (<10%) are subsequently able to compensate and return Na balance, without a further increase in GFR beyond the acute response (orange line). The reduction in LoH Na reabsorption required is small partially because the baseline rate is so high [88% (59, 71)], so small reductions result in large increases in the amount delivered distally. However, the simulations also predict that a compensatory decrease in LoH Na reabsorption would cause MD Na concentration to increase and actually settle above baseline, resulting in a reversal of the TGF signal. Thus, while in this case TGF initially contributes to a rise in GFR, its signal would subsequently be reversed and it would act to counter the further rise in GFR. This is inconsistent with experimental data showing that early distal Na concentration, and thus the signal for TGF, is decreased, not increased, in diabetic animals (57, 60). Therefore, while the LoH may be capable of efficiently compensating, it seems unlikely that this actually happens in the diabetic kidney to a significant extent.
Figure 5, C and D, shows the consequences of compensation through the DCT or CNT/CD alone, respectively. Larger changes in fractional reabsorption are required in these segments (50% in DCT or 28% in the CNT/CD) to provide sufficient compensation to prevent an additional increase. While neither segment counters the acute increase due to TGF and PBow, in both cases, MD Na concentration is reduced from baseline (from 39 to 30 mEq/l), consistent with experimental data in early distal Na concentration (38–42 mEq/l in controls compared with 25–35 mEq/l in STZ rats) (57). Thus, distal tubular compensation is able to prevent further rises in GFR and glomerular hydrostatic pressure beyond those induced by PBow and TGF.
Role of TGF and myogenic regulation.
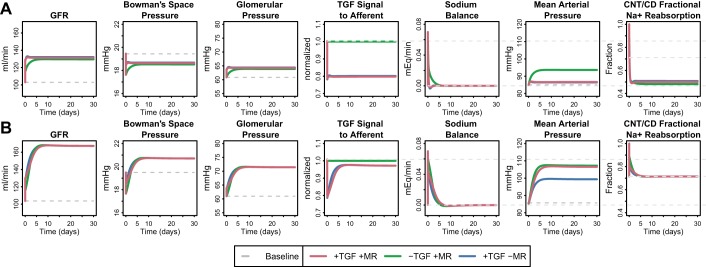
Both TGF and myogenic regulation may be modestly attenuated in diabetes (4, 18, 55). To investigate the impact of this blunting, we considered the extreme case where either the TGF or myogenic regulation is completely absent. Figure 6A shows these results when strong distal compensation is included in the model (as in Fig. 5D, red line). Removal of TGF resulted in a smaller acute increase in GFR but did not impact the chronic change in GFR. However, without TGF, a higher MAP was required to achieve this GFR. For comparison, Fig. 6B shows the extreme case where there is no distal compensation and when TGF is removed from the model. In this case, removal of TGF had little effect on the ultimate state. This is because without distal compensation, GFR and MD Na flow increases were large, and the ability of TGF to help restore sodium balance was already reduced. In other words, these simulations suggest that TGF and distal regulation normally work together to achieve homeostasis with little change in blood pressure, and impairment in either of these mechanisms may result in higher blood pressure.
Fig. 6.
Effect of TGF and myogenic regulation on the response to a 15% step increase in PT fractional Na reabsorption rate, when distal regulation of tubular Na reabsorption is strong (A) and when regulation of tubular Na reabsorption is absent (B). When distal regulation is strong (A), removing TGF does not affect the degree of increase in GFR but rather increases the MAP required to achieve this GFR. Removing distal regulation (B) reduces the ability of TGF to limit the rise in blood pressure, suggesting that TGF and distal regulation normally work together to achieve homeostasis with little change in blood pressure, and impairment in either of these mechanisms may result in higher blood pressure. Removing myogenic regulation while distal compensation was strong (A) had little impact, but when distal regulation was impaired (B), removal of myogenic regulation actually reduced the MAP level required for homeostasis.
When myogenic regulation was removed while distal compensation was strong (Fig. 6A), there was very little impact on either the acute or chronic response. Since little increase in MAP was required to return Na balance to begin with, there was a minimum myogenic response, and thus removing it had little effect. However, when distal regulation was absent from the model (Fig. 6B), a larger increase in MAP was required to restore sodium balance. Since myogenic regulation resists the transmission of blood pressure to the glomerulus, removal of myogenic regulation actually reduced the MAP level required for homeostasis.
DISCUSSION
In this study, we utilized a mathematical model of renal function and hemodynamics to explore potential mechanisms involved in diabetic glomerular hypertension and hyperfiltration, particularly the renal response to a primary increase in PT Na reabsorption. First, we mathematically tested the hypothesis that this single mechanism, increased PT Na reabsorption at elevated glucose levels, can provide an explanation for diabetic hyperfiltration, confirming and extending previous modeling studies (69). The model implicates that changes in both PBow and TGF drive the acute response (within minutes) and contribute to the chronic response (over 1 mo), but alone are not sufficient to correct the Na imbalance generated by the primary increase in PT Na reabsorption. Our simulations suggest that chronically, the degree of glomerular hyperfiltration and of the associated glomerular hypertension is determined by the ability (or lack thereof) of the kidney to secondarily compensate for diabetes-induced increased PT Na reabsorption through the inhibition of tubular reabsorption by endogenous mechanisms (e.g., neurohumoral or pressure-natriuresis).
Increased PT Na Reabsorption as a Causative Mechanism for Diabetic Hyperfiltration
Our analysis demonstrated mathematically what has been observed experimentally: that diabetes-driven increases in PT Na reabsorption can directly cause hyperfiltration. Mathematical modeling of this phenomenon then allowed investigation of the relative contribution of different hypothesized mechanisms that determine the magnitude of the hyperfiltration response to PT Na reabsorption, over both acute and chronic time scales, something that is difficult to do experimentally.
The model confirms that the hyperfiltration response to increased PT reabsorption is at least in part mediated by decreased PBow and TGF-induced afferent dilation. Increased/decreased PT reabsorption lowers/raises PT Na concentration and Bowman space pressure, and the simulated PBow response is consistent with experimental data (28, 52, 60, 61), providing confidence that the simulations are realistic.
Moreover, a key finding from our simulations was that a diabetes-induced increase in PT Na reabsorption causes a Na imbalance that cannot be fully rectified by the increase in GFR that occurs due to decreased PBow and the TGF response. Even when the strength of the TGF response was increased well beyond the level that produced PBow changes consistent with experimental observations, Na balance was not completely restored.
A positive Na balance in diabetes may seem counterintuitive, since diabetes is associated with episodes of polyuria, resulting from glucosuria accompanied by osmotic diuresis. One might actually expect a negative Na balance in this case. However, osmotic diuresis and polyuria are not stable features of diabetes but, rather, occur only when plasma glucose levels (and thus filtered glucose) are high enough to exceed the reabsorptive capacity of the proximal tubule. In humans, for plasma glucose levels up to around 230 mg/dl (for which most diagnosed and treated diabetics will fall below), nearly all filtered glucose is reabsorbed (8). Osmotic diuresis and polyuria only occur when glucose levels rise above this level. Therefore, there is a large space between normal glucose control and 240 mg/dl, when PT glucose and Na reabsorption are increased in diabetes (through increased reabsorption by SGLT and tubular growth (64), without being countered by osmotic diuresis. The threshold for glucose reabsorption seems even higher in rats and mice (>300–400 mg/dl). Thus our modeling covers the typical clinical situation and most rodent studies that prevent excessive hyperglycemia. The findings also apply when glucose levels increase further although in this setting the osmotic diuresis facilitates fluid and Na excretion, which is expected to attenuate to some extent the upregulation of GFR needed to restore Na balance.
Compensatory Downregulation of Tubular Na Reabsorption Is Necessary to Prevent Excessive Hyperfiltration and Glomerular Hypertension in Early Diabetes
Over the long-term Na balance must be precisely established: no steady-state error is permitted, or fluid volume would increase/decrease over time. Thus, to return Na balance after a primary increase in PT reabsorption in diabetes (due to SGLT2 or tubular growth), either tubular reabsorption through other mechanisms must decrease, or glomerular filtration must increase further. Our simulations demonstrate that if tubular Na reabsorption is reduced through regulatory mechanisms, then the hyperfiltration response will be limited to the acute effects through TGF and PBow. If this regulation is impaired, then much greater increases in glomerular pressure and GFR will be necessary to establish Na balance (Fig. 5).
The conclusion that tubular compensation (or lack thereof) determines the degree of hyperfiltration and glomerular hypertension is independent of the mechanism driving this compensation. Any mechanism that reduces tubular reabsorption when PT reabsorption is increased will prevent excess hyperfiltration, and impairment in these mechanisms will then require additional hyperfiltration/glomerular hypertension. In our simulations, we used MAP as the driving signal linking changes in volume to changes in tubular transport, without defining the precise mechanisms by which this pressure-natriuresis is achieved, since these mechanisms and their relative contributions remain incompletely understood. Changes in perfusion pressure may be transmitted to the interstitium, where renal interstitial hydrostatic pressure (RIHP) may alter Na transport through changes in Starling forces (45), or changes in tubular Na transporters (30) mediated by nitric oxide (15, 33, 36), prostaglandins (39), atrial natriuretic peptide (31), or mineralocorticoid receptors (35), or other mechanisms. Renal sympathetic nerve activity and the renin-angiotensin-aldosterone system are likely involved as well, and the compensation achieved may be the net effect of multiple mechanisms. The goal of this study was to analyze the consequences of such regulation. Analysis of the drivers of tubular transport regulation is left for a future analysis.
As Guyton has described previously, feedback control of volume status involves both proportional and integral feedback mechanisms (13). In control theory, proportional control mechanisms help to quickly eliminate large deviations in the variable being controlled but are not able to eliminate steady-state errors, since as the error signal is reduced, the feedback signal also diminishes. In this system, TGF and PBow act as proportional controllers of Na balance, acting quickly to limit the Na imbalance. Downregulation of tubular Na reabsorption also allows Na balance to be returned much more quickly, essentially acting as an additional but slower proportional controller.
On the other hand, integral feedback control begins at zero but grows larger over time as long as an error signal exists. Because of this, integral control mechanisms are ineffective for short-term control but can completely eliminate steady-state error. Pressure-driven filtration provides integral control of Na balance. The driving signal (increased renal perfusion pressure) grows larger over time if any Na imbalance persists, increasing filtration until Na balance is returned.
Thus pressure-driven regulation of tubular Na reabsorption, as well as the effects of TGF and PBow, likely speed the return to Na balance with smaller increases in blood pressure and glomerular hydrostatic pressure. Pressure-dependent filtration then essentially provides a back-up integral controller of Na balance. Without sufficient tubular compensation, Na and water begin to accumulate, increasing MAP and renal perfusion pressure, driving up GFR. This process ultimately returns Na balance but over a longer period and at much higher MAP, glomerular pressure, and GFR. The increase in blood pressure is consistent with clinical data showing that greater hyperfiltration is associated with higher blood pressure (72).
Role of Each Nephron Segment in Tubular Compensation
Based on our simulations, we suggest that 1) compensation through the PT would in theory be capable of fully compensating but is likely insufficient or impaired in diabetes; 2) while the regulation of the LoH would be able to compensate efficiently, simulations combined with experimental data suggest this is not the case in diabetes; and 3) the distal nephron may be critical in providing compensation to limit hyperfiltration and glomerular hypertension in diabetes.
The proximal tubule is responsive to multiple regulatory signals, including angiotensin (7, 46), renal sympathetic nerve activity (5), dopamine (10), prostaglandins (39), and changes in starling forces (45). Our simulations show that, as may be expected, the diabetes-driven increase in PT reabsorption could be fully compensated if PT reabsorption is sufficiently downregulated (essentially, a 15% compensatory reduction could fully compensate for the 15% increase, regardless of the mechanism). However, if there is no net change in PT reabsorption, then there would also be no change in distal delivery (and thus TGF), tubular pressure, or GFR at steady-state. However, the decreased early distal NaCl delivery and increased PT Na reabsorption observed in diabetes (17, 55, 57) suggests that this is not the case: that either PT regulation is insufficient to fully compensate or impaired in diabetes.
Our results suggest that quite small changes in LoH reabsorption could provide sufficient compensation but that this compensation would actually cause a net increase in MD Na concentration (Fig. 5B), in contradiction of experimental findings of decreased MD Na concentration in diabetes (55, 57).
If the PT and LoH are not able to fully compensate, the remaining compensation must necessarily occur in the distal nephron. Na transport in the DCT and CNT/CD is regulated by atrial natriuretic peptide (31), angiotensin II, and aldosterone (35) and may also be affected by renal sympathetic nerve activity and nitric oxide (15, 33, 36). Compensation through these segments can return Na balance while sustaining a decrease in early distal Na concentration/delivery (Fig. 5, C and D), in agreement with experimental data.
In summary, our simulations suggest that when the Na imbalanced produced by increased PT reabsorption diabetes is incompletely compensated in the PT (due to insufficient or impaired mechanisms), compensation through distal segments is required. The CNT/CD is the most likely location for this regulation, and the efficiency of the CNT/CD to compensate increases as the assumed LoH fractional reabsorption rate decreases. Impairment in the ability of the distal nephron to compensate will result in additional hyperfiltration and glomerular hypertension, until Na balance is restored. These conclusions are insensitive to assumptions regarding flow-dependent transport.
TGF and Myogenic Responsiveness Participate but Are Not Absolutely Necessary for a Hyperglycemia-Induced Increase in GFR
TGF and myogenic responsiveness of the preglomerular vasculature are key regulators of glomerular pressure. Both of these mechanisms may be modestly attenuated or impaired in diabetes. Our results suggest that while these mechanisms, when present, participate in the hemodynamic response to increased PT Na reabsorption, neither may be absolutely necessary for GFR to increase in the diabetic setting. This is expected when PT Na reabsorption is increased and not compensated for distally, and the system has the ability to restore Na balance by increasing GFR through other mechanisms. Our simulations suggest that TGF, when present, determines the acute increase in GFR, speeds the chronic GFR response, and helps minimize the increase in blood pressure.
As Na is retained and blood pressure increases, the myogenic response will constrict the preglomerular vasculature and increase the pressure drop from the renal artery to the glomerulus. Impairment in myogenic responsiveness then means that changes in MAP are more directly transmitted to the glomerulus, and thus smaller changes in MAP are needed to achieve the same (necessary) increase in GFR (Fig. 6B). One could even speculate whether a proposed partial loss of myogenic autoregulation in diabetes could be an adaptive response that facilitates the needed increase in GFR (to achieve Na balance) with lesser increases in MAP.
Primary Increase in PT Na Reabsorption Plus Impaired Secondary Na Transport Downregulation as Determinants of Diabetic Glomerular Hypertension: Implications for Diabetic Kidney Disease
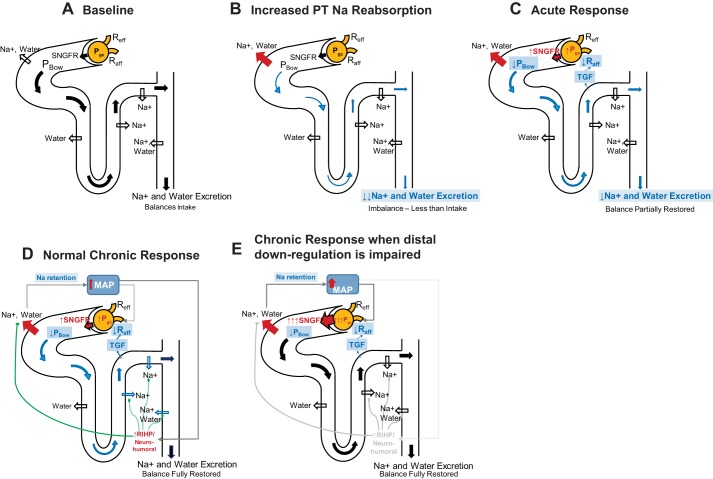
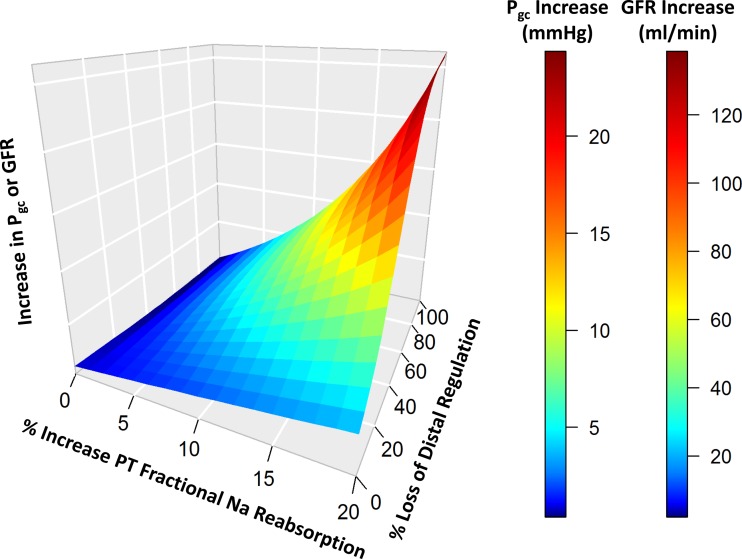
Taken together, our simulation results suggest for the first time that the coupling of these two mechanisms, the primary increase in PT reabsorption and impaired tubular Na counterregulation, is critical in determining the degree of glomerular hypertension and hyperfiltration in the diabetic kidney. The overall concept is illustrated in Fig. 7. The quantitative effect of coupling these two mechanisms is illustrated in Fig. 8. Alone, the diabetes-induced primary increase in PT Na reabsorption will cause some degree of hyperfiltration with a small TGF-driven increase in glomerular hydrostatic pressure. However, coupled with impaired tubular regulation, a much higher degree of glomerular hypertension and hyperfiltration results. These findings may be relevant and contribute to the prevalent salt sensitivity of blood pressure in diabetes, which is indicative of impaired distal tubular transport regulation (21, 53).
Fig. 7.
Summary of proposed mechanisms determining the degree of glomerular hyperfiltration and hypertension in diabetes. A: baseline. B: increased PT Na and water reabsorption initially reduces distal flow and Na delivery, reducing Na excretion and causing a Na imbalance. C: acute response: reduced tubular flow reduces PBow. Reduced MD Na delivery dilates the afferent arteriole through TGF. These two factors increase GFR, but do not completely restore distal delivery and Na excretion to baseline levels, so a Na imbalance remains. This Na imbalance results in Na and water retention which over time will tend to increase in MAP. D) Normal chronic response: Normally, small increases in MAP drive increases in renal interstitial hydrostatic pressure (RIHP), and/or neurohumoral changes that downregulate distal (and possibly proximal) Na reabsorption. This returns Na balance without further increases in MAP, glomerular hydrostatic pressure, or GFR. E: impaired chronic response: If distal (and possibly proximal) downregulation is impaired, Na will be retained and MAP will increase much further, driving up glomerular hydrostatic pressure, and GFR. This will continue until the increase in filtration is sufficient to overcome the increase in PT reabsorption and to restore distal Na+ flow, Na excretion, and Na balance.
Fig. 8.
The degree of glomerular hypertension and hyperfiltration is a function of both the primary increase in PT reabsorption and the impaired distal Na regulation or compensation. Loss of distal regulation alone will not cause glomerular hypertension. Increased PT reabsorption alone will cause only a small increase in GFR and glomerular hypertension. But the coupling of the two greatly increases the rise in both GFR and glomerular hydrostatic pressure. [For this simulation, fractional PT Na reabsorption ηpt varied from 0.7 to 0.84; SP-N,i varied from 1 (normal) to 0 (complete loss of regulation) for all distal segments: LoH, DCT, and CNT/CD.]
We speculate that the excessive glomerular hypertension (or glomerular hydrostatic pressure gradient) that occurs due to these two combined mechanisms may initiate and sustain a cascade of glomerulosclerosis, podocyte damage, proteinuria, and tubular fibrosis. Mitigation of these two mechanisms may be critical in preventing diabetic kidney disease. Mechanisms that reduce the diabetes-induced increase in PT Na reabsorption would be expected to reduce glomerular hypertension and prevent or slow the progression of kidney dysfunction. Indeed, this is supported by the recent results of the EMPA-REG trial, which demonstrated an impressive effect of the SGLT2 inhibitor empagliflozin in improving not only cardiovascular outcome in patients with high cardiovascular risk (74) but also slowing the decline in renal function (67).
The mechanisms responsible for impairment of tubular transport regulation in diabetes remain to be fully elucidated. Diabetes is associated with inflammation and endothelial dysfunction, which may over time affect the structures involved in transmitting pressure from the peritubular capillaries to the interstitium or in signaling to the tubular epithelial cells. Loss or thickening of peritubular capillaries (11), impairment in nitric oxide release (36), enhanced sympathetic tone (9), and increased intrarenal RAS activity (12) are some of the mechanisms that may play a role. Genetic and environmental influences also likely play a role. A better understanding of the pathophysiologic changes involved in impaired pressure natriuresis and transport regulation may allow identification of approaches to prevent or correct glomerular hypertension in diabetes.
Limitations
Regulation of tubular Na reabsorption in the current model was intentionally represented simplistically, since the goal was to evaluate the consequence of regulation, not the mechanisms involved. Thus the effects of any neurohormonal or local autocrine or paracrine system or pressure-natriuresis system that mediates or modulates the interaction between blood pressure and natriuresis were considered part of a black box. Future modeling may expand on the current work by investigating the relative contributions of these various mechanisms.
The model presented here represents tubular reabsorption along the nephron as a fractional rate for each tubular segment that represents the cumulative effect of the various transporters in that segment. We do not attempt to model the contribution of various transporters in detail. This has been done quite elegantly by others (26, 27, 32, 68–70). We believe that the current representation is sufficient to explore the questions addressed here and that in this case the simpler model may have been advantageous in elucidating the major determinants of the magnitude of hyperfiltration and glomerular hypertension in the diabetic kidney.
GRANTS
This research was supported by Astrazeneca Pharmaceuticals (to K. M. Hallow), National Institute of Diabetes and Digestive and Kidney Diseases Grants R01-DK-56248 and R01-DK-106102 (to V. Vallon), the University of Alabama at Birmingham/University of California San Diego O'Brien Center for Acute Kidney Injury Research Grant P30-DK-079337 (to V. Vallon), and the Department of Veterans Affairs (to V. Vallon). Over the past 12 mo, K. M. Hallow has received grant support for investigator-initiated research from Astrazeneca and Takeda Pharmaceutical. Over the last 12 mo, to V. Vallon has served as a consultant for Boehringer Ingelheim, Janssen Pharmaceutical, Eli Lilly, and Merck and received grant support for investigator-initiated research from Boehringer Ingelheim, Astra-Zeneca, Fresenius, Janssen, and Bayer.
DISCLOSURES
G. Helmlinger is employed by Astrazeneca Pharmaceuticals.
AUTHOR CONTRIBUTIONS
K.M.H. performed experiments; K.M.H. and Y.G. analyzed data; K.M.H., Y.G., G.H., and V.V. interpreted results of experiments; K.M.H. prepared figures; K.M.H. drafted manuscript; K.M.H., Y.G., G.H., and V.V. edited and revised manuscript; K.M.H., Y.G., G.H., and V.V. approved final version of manuscript.
Supplementary Material
REFERENCES
- 1.Bank N. Mechanisms of diabetic hyperfiltration. Kidney Int 40: 792–807, 1991. doi: 10.1038/ki.1991.277. [DOI] [PubMed] [Google Scholar]
- 2.Bank N, Aynedjian HS. Progressive increases in luminal glucose stimulate proximal sodium absorption in normal and diabetic rats. J Clin Invest 86: 309–316, 1990. doi: 10.1172/JCI114700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Beard DA, Mescam M. Mechanisms of pressure-diuresis and pressure-natriuresis in Dahl salt-resistant and Dahl salt-sensitive rats. BMC Physiol 12: 6, 2012. doi: 10.1186/1472-6793-12-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bell TD, DiBona GF, Wang Y, Brands MW. Mechanisms for renal blood flow control early in diabetes as revealed by chronic flow measurement and transfer function analysis. J Am Soc Nephrol 17: 2184–2192, 2006. doi: 10.1681/ASN.2006030216. [DOI] [PubMed] [Google Scholar]
- 5.Bello-Reuss E, Colindres RE, Pastoriza-Muñoz E, Mueller RA, Gottschalk CW. Effects of acute unilateral renal denervation in the rat. J Clin Invest 56: 208–217, 1975. doi: 10.1172/JCI108069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cherney DZ, Perkins BA, Soleymanlou N, Maione M, Lai V, Lee A, Fagan NM, Woerle HJ, Johansen OE, Broedl UC, von Eynatten M. Renal hemodynamic effect of sodium-glucose cotransporter 2 inhibition in patients with type 1 diabetes mellitus. Circulation 129: 587–597, 2014. doi: 10.1161/CIRCULATIONAHA.113.005081. [DOI] [PubMed] [Google Scholar]
- 7.Cogan MG. Angiotensin II: a powerful controller of sodium transport in the early proximal tubule. Hypertension 15: 451–458, 1990. doi: 10.1161/01.HYP.15.5.451. [DOI] [PubMed] [Google Scholar]
- 8.Devineni D, Curtin CR, Polidori D, Gutierrez MJ, Murphy J, Rusch S, Rothenberg PL. Pharmacokinetics and pharmacodynamics of canagliflozin, a sodium glucose co-transporter 2 inhibitor, in subjects with type 2 diabetes mellitus. J Clin Pharmacol 53: 601–610, 2013. doi: 10.1002/jcph.88. [DOI] [PubMed] [Google Scholar]
- 9.DiBona GF. Physiology in perspective: The wisdom of the body. Neural control of the kidney. Am J Physiol Regul Integr Comp Physiol 289: R633–R641, 2005. doi: 10.1152/ajpregu.00258.2005. [DOI] [PubMed] [Google Scholar]
- 10.Du Z, Yan Q, Wan L, Weinbaum S, Weinstein AM, Wang T. Regulation of glomerulotubular balance. I. Impact of dopamine on flow-dependent transport. Am J Physiol Renal Physiol 303: F386–F395, 2012. doi: 10.1152/ajprenal.00531.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Granger JP, Alexander BT, Llinas M. Mechanisms of pressure natriuresis. Curr Hypertens Rep 4: 152–159, 2002. doi: 10.1007/s11906-002-0040-3. [DOI] [PubMed] [Google Scholar]
- 12.Granger JP, Schnackenberg CG. Renal mechanisms of angiotensin II-induced hypertension. Semin Nephrol 20: 417–425, 2000. [PubMed] [Google Scholar]
- 13.Guyton AC, Coleman TG, Cowley AW, Manning RD, Norman RA, Ferguson JD. A systems analysis approach to understanding long-range arterial blood pressure control and hypertension. Circ Res 35: 159–176, 1974. doi: 10.1161/01.RES.35.2.159. [DOI] [Google Scholar]
- 14.Guyton AC, Coleman TG, Granger HJ. Circulation: overall regulation. Annu Rev Physiol 34: 13–46, 1972. doi: 10.1146/annurev.ph.34.030172.000305. [DOI] [PubMed] [Google Scholar]
- 15.Haas JA, Khraibi AA, Perrella MA, Knox FG. Role of renal interstitial hydrostatic pressure in natriuresis of systemic nitric oxide inhibition. Am J Physiol Renal Fluid Electrolyte Physiol 264: F411–F414, 1993. [DOI] [PubMed] [Google Scholar]
- 16.Hallow KM, Lo A, Beh J, Rodrigo M, Ermakov S, Friedman S, de Leon H, Sarkar A, Xiong Y, Sarangapani R, Schmidt H, Webb R, Kondic AG. A model-based approach to investigating the pathophysiological mechanisms of hypertension and response to antihypertensive therapies: extending the Guyton model. Am J Physiol Regul Integr Comp Physiol 306: R647–R662, 2014. doi: 10.1152/ajpregu.00039.2013. [DOI] [PubMed] [Google Scholar]
- 17.Hannedouche TP, Delgado AG, Gnionsahe DA, Boitard C, Lacour B, Grünfeld JP. Renal hemodynamics and segmental tubular reabsorption in early type 1 diabetes. Kidney Int 37: 1126–1133, 1990. doi: 10.1038/ki.1990.95. [DOI] [PubMed] [Google Scholar]
- 18.Hayashi K, Epstein M, Loutzenhiser R, Forster H. Impaired myogenic responsiveness of the afferent arteriole in streptozotocin-induced diabetic rats: role of eicosanoid derangements. J Am Soc Nephrol 2: 1578–1586, 1992. [DOI] [PubMed] [Google Scholar]
- 19.Holstein-Rathlou NH. A closed-loop analysis of the tubuloglomerular feedback mechanism. Am J Physiol Renal Electrolyte Physiol 261: F880–F889, 1991. [DOI] [PubMed] [Google Scholar]
- 20.Hoppensteadt FC, Peskin CS. Modeling and Simulation in Medicine and the Life Sciences. New York: Springer, 2002. doi: 10.1007/978-0-387-21571-6 [DOI] [Google Scholar]
- 21.Imanishi M, Yoshioka K, Okumura M, Konishi Y, Okada N, Morikawa T, Sato T, Tanaka S, Fujii S. Sodium sensitivity related to albuminuria appearing before hypertension in type 2 diabetic patients. Diabetes Care 24: 111–116, 2001. doi: 10.2337/diacare.24.1.111. [DOI] [PubMed] [Google Scholar]
- 22.Jensen PK, Christensen O, Steven K. A mathematical model of fluid transport in the kidney. Acta Physiol Scand 112: 373–385, 1981. doi: 10.1111/j.1748-1716.1981.tb06833.x. [DOI] [PubMed] [Google Scholar]
- 23.Kanwar YS, Sun L, Xie P, Liu FY, Chen S. A glimpse of various pathogenetic mechanisms of diabetic nephropathy. Annu Rev Pathol 6: 395–423, 2011. doi: 10.1146/annurev.pathol.4.110807.092150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Karaaslan F, Denizhan Y, Kayserilioglu A, Gulcur HO. Long-term mathematical model involving renal sympathetic nerve activity, arterial pressure, and sodium excretion. Ann Biomed Eng 33: 1607–1630, 2005. doi: 10.1007/s10439-005-5976-4. [DOI] [PubMed] [Google Scholar]
- 25.Kunau RT Jr, Webb HL, Borman SC. Characteristics of the relationship between the flow rate of tubular fluid and potassium transport in the distal tubule of the rat. J Clin Invest 54: 1488–1495, 1974. doi: 10.1172/JCI107897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Layton AT, Vallon V, Edwards A. Modeling oxygen consumption in the proximal tubule: effects of NHE and SGLT2 inhibition. Am J Physiol Renal Physiol 308: F1343–F1357, 2015. doi: 10.1152/ajprenal.00007.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Layton AT, Vallon V, Edwards A. Predicted consequences of diabetes and SGLT inhibition on transport and oxygen consumption along a rat nephron. Am J Physiol Renal Physiol 310: F1269–F1283, 2016. doi: 10.1152/ajprenal.00543.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Leyssac PP, Karlsen FM, Holstein-Rathlou NH, Skøtt O. On determinants of glomerular filtration rate after inhibition of proximal tubular reabsorption. Am J Physiol Regul Integr Comp Physiol 266: R1544–R1550, 1994. [DOI] [PubMed] [Google Scholar]
- 29.Magee GM, Bilous RW, Cardwell CR, Hunter SJ, Kee F, Fogarty DG. Is hyperfiltration associated with the future risk of developing diabetic nephropathy? A meta-analysis. Diabetologia 52: 691–697, 2009. doi: 10.1007/s00125-009-1268-0. [DOI] [PubMed] [Google Scholar]
- 30.McDonough AA. Mechanisms of proximal tubule sodium transport regulation that link extracellular fluid volume and blood pressure. Am J Physiol Regul Integr Comp Physiol 298: R851–R861, 2010. doi: 10.1152/ajpregu.00002.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Mizelle HL, Hall JE, Hildebrandt DA. Atrial natriuretic peptide and pressure natriuresis: interactions with the renin-angiotensin system. Am J Physiol Renal Fluid Electrolyte Physiol 257: R1169–R1174, 1989. [DOI] [PubMed] [Google Scholar]
- 32.Moss R, Layton AT. Dominant factors that govern pressure natriuresis in diuresis and antidiuresis: a mathematical model. Am J Physiol Renal Physiol 306: F952–F969, 2014. doi: 10.1152/ajprenal.00500.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nakamura T, Alberola AM, Salazar FJ, Saito Y, Kurashina T, Granger JP, Nagai R. Effects of renal perfusion pressure on renal interstitial hydrostatic pressure and Na+ excretion: role of endothelium-derived nitric oxide. Nephron 78: 104–111, 1998. doi: 10.1159/000044889. [DOI] [PubMed] [Google Scholar]
- 34.Neuringer JR, Brenner BM. Glomerular hypertension: cause and consequence of renal injury. J Hypertens Suppl 10, Suppl 7: S91–S97, 1992. doi: 10.1097/00004872-199212000-00011. [DOI] [PubMed] [Google Scholar]
- 35.Nishimoto M, Fujita T. Renal mechanisms of salt-sensitive hypertension: contribution of two steroid receptor-associated pathways. Am J Physiol Renal Physiol 308: F377–F387, 2015. doi: 10.1152/ajprenal.00477.2013. [DOI] [PubMed] [Google Scholar]
- 36.O’Connor PM, Cowley AW Jr. Modulation of pressure-natriuresis by renal medullary reactive oxygen species and nitric oxide. Curr Hypertens Rep 12: 86–92, 2010. doi: 10.1007/s11906-010-0094-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Palmer LG, Schnermann J. Integrated control of Na transport along the nephron. Clin J Am Soc Nephrol 10: 676–687, 2015. doi: 10.2215/CJN.12391213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Riser BL, Cortes P, Zhao X, Bernstein J, Dumler F, Narins RG. Intraglomerular pressure and mesangial stretching stimulate extracellular matrix formation in the rat. J Clin Invest 90: 1932–1943, 1992. doi: 10.1172/JCI116071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Roman RJ, Lianos E. Influence of prostaglandins on papillary blood flow and pressure-natriuretic response. Hypertension 15: 29–35, 1990. doi: 10.1161/01.HYP.15.1.29. [DOI] [PubMed] [Google Scholar]
- 40.Roy DR, Layton HE, Jamison RL. Countercurrent mechanism and its regulation. In: The Kidney: Physiology and Pathophysiology (3rd ed.). Philadelphia, PA: Lippincott Williams & Wilkins, 2000. [Google Scholar]
- 41.RStudio Shiny: Web Application Framework for R (R Package Version 0.10.1 ed.) (Online). https://cran.r-project.org/web/packages/shiny/index.html, [15 March 2017].
- 42.Ruggenenti P, Porrini EL, Gaspari F, Motterlini N, Cannata A, Carrara F, Cella C, Ferrari S, Stucchi N, Parvanova A, Iliev I, Dodesini AR, Trevisan R, Bossi A, Zaletel J, Remuzzi G; GFR Study Investigators . Glomerular hyperfiltration and renal disease progression in type 2 diabetes. Diabetes Care 35: 2061–2068, 2012. doi: 10.2337/dc11-2189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Satlin LM, Carattino MD, Liu W, Kleyman TR. Regulation of cation transport in the distal nephron by mechanical forces. Am J Physiol Renal Physiol 291: F923–F931, 2006. doi: 10.1152/ajprenal.00192.2006. [DOI] [PubMed] [Google Scholar]
- 44.Satlin LM, Sheng S, Woda CB, Kleyman TR. Epithelial Na+ channels are regulated by flow. Am J Physiol Renal Physiol 280: F1010–F1018, 2001. [DOI] [PubMed] [Google Scholar]
- 45.Schafer JA. Transepithelial osmolality differences, hydraulic conductivities, and volume absorption in the proximal tubule. Annu Rev Physiol 52: 709–726, 1990. doi: 10.1146/annurev.ph.52.030190.003425. [DOI] [PubMed] [Google Scholar]
- 46.Schuster VL, Kokko JP, Jacobson HR. Angiotensin II directly stimulates sodium transport in rabbit proximal convoluted tubules. J Clin Invest 73: 507–515, 1984. doi: 10.1172/JCI111237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Thomson SC, Bachmann S, Bostanjoglo M, Ecelbarger CA, Peterson OW, Schwartz D, Bao D, Blantz RC. Temporal adjustment of the juxtaglomerular apparatus during sustained inhibition of proximal reabsorption. J Clin Invest 104: 1149–1158, 1999. doi: 10.1172/JCI5156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Thomson SC, Blantz RC. Homeostatic efficiency of tubuloglomerular feedback in hydropenia, euvolemia, and acute volume expansion. Am J Physiol Renal Fluid Electrolyte Physiol 264: F930–F936, 1993. [DOI] [PubMed] [Google Scholar]
- 49.Thomson SC, Deng A, Bao D, Satriano J, Blantz RC, Vallon V. Ornithine decarboxylase, kidney size, and the tubular hypothesis of glomerular hyperfiltration in experimental diabetes. J Clin Invest 107: 217–224, 2001. doi: 10.1172/JCI10963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Thomson SC, Rieg T, Miracle C, Mansoury H, Whaley J, Vallon V, Singh P. Acute and chronic effects of SGLT2 blockade on glomerular and tubular function in the early diabetic rat. Am J Physiol Regul Integr Comp Physiol 302: R75–R83, 2012. doi: 10.1152/ajpregu.00357.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Thomson SC, Vallon V, Blantz RC. Kidney function in early diabetes: the tubular hypothesis of glomerular filtration. Am J Physiol Renal Physiol 286: F8–F15, 2004. doi: 10.1152/ajprenal.00208.2003. [DOI] [PubMed] [Google Scholar]
- 52.Thomson SC, Vallon V, Blantz RC. Reduced proximal reabsorption resets tubuloglomerular feedback in euvolemic rats. Am J Physiol Regul Integr Comp Physiol 273: R1414–R1420, 1997. [DOI] [PubMed] [Google Scholar]
- 53.Tuck M, Corry D, Trujillo A. Salt-sensitive blood pressure and exaggerated vascular reactivity in the hypertension of diabetes mellitus. Am J Med 88: 210–216, 1990. doi: 10.1016/0002-9343(90)90144-3. [DOI] [PubMed] [Google Scholar]
- 54.Vallon V, Blantz RC, Thomson S. Glomerular hyperfiltration and the salt paradox in early [corrected] type 1 diabetes mellitus: a tubulo-centric view. J Am Soc Nephrol 14: 530–537, 2003. doi: 10.1097/01.ASN.0000051700.07403.27. [DOI] [PubMed] [Google Scholar]
- 55.Vallon V, Blantz RC, Thomson S. Homeostatic efficiency of tubuloglomerular feedback is reduced in established diabetes mellitus in rats. Am J Physiol Renal Fluid Electrolyte Physiol 269: F876–F883, 1995. [DOI] [PubMed] [Google Scholar]
- 56.Vallon V, Gerasimova M, Rose MA, Masuda T, Satriano J, Mayoux E, Koepsell H, Thomson SC, Rieg T. SGLT2 inhibitor empagliflozin reduces renal growth and albuminuria in proportion to hyperglycemia and prevents glomerular hyperfiltration in diabetic Akita mice. Am J Physiol Renal Physiol 306: F194–F204, 2014. doi: 10.1152/ajprenal.00520.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Vallon V, Huang DY, Deng A, Richter K, Blantz RC, Thomson S. Salt-sensitivity of proximal reabsorption alters macula densa salt and explains the paradoxical effect of dietary salt on glomerular filtration rate in diabetes mellitus. J Am Soc Nephrol 13: 1865–1871, 2002. doi: 10.1097/01.ASN.0000016441.41118.57. [DOI] [PubMed] [Google Scholar]
- 58.Vallon V, Komers R. Pathophysiology of the diabetic kidney. Compr Physiol 1: 1175–1232, 2011. doi: 10.1002/cphy.c100049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Vallon V, Osswald H, Blantz RC, Thomson S. Potential role of luminal potassium in tubuloglomerular feedback. J Am Soc Nephrol 8: 1831–1837, 1997. [DOI] [PubMed] [Google Scholar]
- 60.Vallon V, Richter K, Blantz RC, Thomson S, Osswald H. Glomerular hyperfiltration in experimental diabetes mellitus: potential role of tubular reabsorption. J Am Soc Nephrol 10: 2569–2576, 1999. [DOI] [PubMed] [Google Scholar]
- 61.Vallon V, Richter K, Huang DY, Rieg T, Schnermann J. Functional consequences at the single-nephron level of the lack of adenosine A1 receptors and tubuloglomerular feedback in mice. Pflugers Arch 448: 214–221, 2004. doi: 10.1007/s00424-004-1239-8. [DOI] [PubMed] [Google Scholar]
- 62.Vallon V, Rose M, Gerasimova M, Satriano J, Platt KA, Koepsell H, Cunard R, Sharma K, Thomson SC, Rieg T. Knockout of Na-glucose transporter SGLT2 attenuates hyperglycemia and glomerular hyperfiltration but not kidney growth or injury in diabetes mellitus. Am J Physiol Renal Physiol 304: F156–F167, 2013. doi: 10.1152/ajprenal.00409.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Vallon V, Schroth J, Satriano J, Blantz RC, Thomson SC, Rieg T. Adenosine A(1) receptors determine glomerular hyperfiltration and the salt paradox in early streptozotocin diabetes mellitus. Nephron Physiol 111: 30–38, 2009. doi: 10.1159/000208211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Vallon V, Thomson SC. Renal function in diabetic disease models: the tubular system in the pathophysiology of the diabetic kidney. Annu Rev Physiol 74: 351–375, 2012. doi: 10.1146/annurev-physiol-020911-153333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Vora JP, Dolben J, Dean JD, Thomas D, Williams JD, Owens DR, Peters JR. Renal hemodynamics in newly presenting non-insulin dependent diabetes mellitus. Kidney Int 41: 829–835, 1992. doi: 10.1038/ki.1992.127. [DOI] [PubMed] [Google Scholar]
- 66.Wang W, Hallow KM, James DA. A Tutorial on RxODE: simulating differential equation pharmacometric models in R. CPT Pharmacometrics Syst Pharmacol 5: 3–10, 2016. doi: 10.1002/psp4.12052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Wanner C, Inzucchi SE, Lachin JM, Fitchett D, von Eynatten M, Mattheus M, Johansen OE, Woerle HJ, Broedl UC, Zinman B; EMPA-REG OUTCOME Investigators . Empagliflozin andpProgression of kidney disease in type 2 diabetes. N Engl J Med 375: 323–334, 2016. doi: 10.1056/NEJMoa1515920. [DOI] [PubMed] [Google Scholar]
- 68.Weinstein AM. A mathematical model of rat proximal tubule and loop of Henle. Am J Physiol Renal Physiol 308: F1076–F1097, 2015. doi: 10.1152/ajprenal.00504.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Weinstein AM. A mathematical model of the rat nephron: glucose transport. Am J Physiol Renal Physiol 308: F1098–F1118, 2015. doi: 10.1152/ajprenal.00505.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Weinstein AM. A mathematical model of the rat proximal tubule. Am J Physiol Renal Fluid Electrolyte Physiol 250: F860–F873, 1986. [DOI] [PubMed] [Google Scholar]
- 71.Wright FS, Schnermann J. Interference with feedback control of glomerular filtration rate by furosemide, triflocin, and cyanide. J Clin Invest 53: 1695–1708, 1974. doi: 10.1172/JCI107721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Yang GK, Maahs DM, Perkins BA, Cherney DZ. Renal hyperfiltration and systemic blood pressure in patients with uncomplicated type 1 diabetes mellitus. PLoS One 8: e68908, 2013. doi: 10.1371/journal.pone.0068908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Zhao D, Navar LG. Acute angiotensin II infusions elicit pressure natriuresis in mice and reduce distal fractional sodium reabsorption. Hypertension 52: 137–142, 2008. doi: 10.1161/HYPERTENSIONAHA.108.111435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Zinman B, Wanner C, Lachin JM, Fitchett D, Bluhmki E, Hantel S, Mattheus M, Devins T, Johansen OE, Woerle HJ, Broedl UC, Inzucchi SE; EMPA-REG OUTCOME Investigators . Empagliflozin, cardiovascular outcomes, and mortality in type 2 diabetes. N Engl J Med 373: 2117–2128, 2015. doi: 10.1056/NEJMoa1504720. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.