Abstract
How tension modulates cellular transport has become a topic of interest in the recent past. The effect of tension on clathrin assembly and vesicle growth continues to remain less understood. Here, we use the classical Helfrich theory to predict the energetic cost clathrin is required to pay to remodel membrane at different stages of vesicle formation. Our study reveals that this energetic cost is highly sensitive to not only the tension in the membrane but to the instantaneous geometry of the membrane during the shape evolution. Our study predicts a sharp reduction in clathrin coat size in the intermediate tension regime (0.01 − 0.1 mN/m). Remarkably, the natural propensity of the membrane to undergo bending beyond the Ω shape causes a significant decrease in the energy needed from clathrin to drive vesicle growth. Our studies in mammalian cells confirm a reduction in clathrin coat size in increased tension environment. In addition, our findings suggest that the two apparently distinct clathrin assembly modes, namely coated pits and coated plaques, observed in experimental investigations might be a consequence of varied tensions in the plasma membrane. Overall, the mechano-geometric sensitivity revealed in this study might also be at play during the polymerization of other membrane remodeling proteins.
1 Introduction
How physical properties of the membrane control membrane-protein interactions that lead to structural remodeling during numerous cellular processes is a fundamental open question in biology1. One such vital and evolutionary conserved physical process is clathrin-mediated endocytosis (CME) that living cells use to uptake extracellular molecules through the formation of clathrin-coated pits (CCPs) and subsequent internalization into intracellular vesicles2,3. CME is important for the exchange of lipids and proteins between the plasma membrane and organelles and is critical for maintaining the organization of the plasma membrane and regulating signal transduction pathways. While clathrin was discovered several decades ago, how clathrin polymerizes and remodels membranes is still a subject of active investigation4.
For example, recent studies have demonstrated the impact of a key physical parameter, tension in the plasma membrane, on CME. In low-tension environment, vesicle formation in mammalian cells is primarily driven by clathrin polymerization and is actin-independent5–7. In contrast, in high-tension environment, either due to the polarized nature of cells or due to mechanical manipulation of cells, vesicle formation becomes actin-dependent8,9. Along similar lines, CME in yeast cells, which experience high membrane tension due to large internal turgor pressure, is known to be actin-dependent5,10–13. The impact of cortical tension on CCPs dynamics has also been shown within single cells14. This has led to a natural question as to how tension impacts CCP dynamics.
The in vitro studies by Saleem et al. showed that vesicles subjected to increased tension exhibited reduced clathrin polymerization15. The work by Tan et al. showed that CCPs in cells subjected to increased cell spreading size exhibit increased short-lived CCPs and initiation rate16. These experimental studies are complimented by the modeling work by Walani et al. which suggests that an increase in tension should lead to smaller clathrin coat in order to match experimentally observed shapes observed in mammalian and yeast cells17. In addition, stochastic models have given fundamental insights into clathrin self-assembly18,19 and dynamic rearrangements in clathrin lattices20–22. In particular, curvature generation by indentation has been shown to promote solid to fluid phase transition in a planar clathrin lattice21.
While these studies have provided fundamental insights into the the different aspects of CCP dynamics, how membrane curvature and tension simultaneously regulate clathrin polymerization during vesicle growth is not yet well understood. Here, we use continuum mechanics to estimate the polymerization energy needed to bend the membrane during the shape evolution under different homeostatic tension conditions. Our study reveals that the vesicle growth is associated with a highly nonlinear energy demand which clathrin has to pay in order to bend the membrane. Remarkably, the energetic demand reaches its peak at a critical geometric point beyond which curvature energy contributes to vesicle growth and necking. Our study reveals a reduction in CCP size in the intermediate tension regime and formation of coated plaques in high tension regime. The former finding is supported by our experimental studies in mammalian cells.
2 The basic setup
We model bilayer as a 2D surface and use the well-known Helfrich theory to model clathrin-induced membrane remodeling. The strain energy for the membrane is given by , where H is the mean curvature, K is the Gaussian curvature, C is the effective spontaneous curvature imposed by the clathrin coat, and are the bending moduli23–27. Since we do not model topological changes, the second term in the energy does not contribute to the energetics of the shape evolution due to the Gauss-Bonnet theorem. We do not take into account the effects of other membrane remodeling proteins such as actin and BAR (in case of yeast cells) to isolate the impact of tension and geometry on clathrin polymerization. Such an insight is valuable to understand the extent of clathrin-induced membrane remodeling in high tension regime. In addition, since membranes only undergo a minimal areal dilation of 2 − 3%, we impose areal incompressibility.
We explore equilibrium solutions in the axisymmetric domain parametrized by meridional arc length s and the azimuthal angle θ. For this system the equilibrium equations reduce to
| (1) |
and
| (2) |
where λ is the surface tension, Δ(·) is the surface Laplacian and ()′ is the partial derivative with respect to the arclength. We solve these equations along with the geometric equations
| (3) |
and
| (4) |
to compute the equilibrium shapes. Above, r(s) is the radius from axis of revolution, z(s) is the elevation from a base plane and ψ(s) is the angle which the tangent makes with the radial vector.
In the coated domain, we assume that the clathrin coat imposes a spontaneous curvature C0 = 1/R0, where R0 = 50 nm is the preferred radius of curvature of the clathrin coat28,29, and an effective membrane stiffness ten times higher than that of the uncoated membrane30. To model these spatial variations, we prescribe
| (5) |
and
| (6) |
where κ0 = 20kBT is the bending modulus of the uncoated membrane, β = 12 is a constant that determines the sharpness of the tanh function and s0 is the prescribed domain of the clathrin coat in terms of the arc length. The spatial variation in κ and C in the uncoated and coated domains for a typical vesicle geometry is shown in Fig 2. As shown for the first time in Agrawal and Steigmann31, such a spatial heterogeneity in membrane properties can potentially lead to a variable surface tension field in the membrane.
Fig. 2.
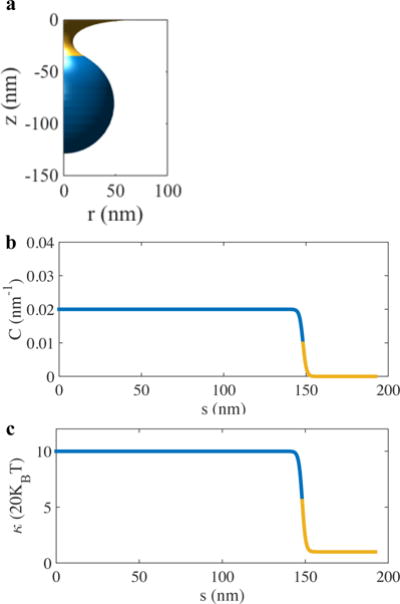
Effect of clathrin coat on the membrane properties. a) A typical shape of a vesicle during the shape evolution. The blue domain indicates the clathrin coated region. b and c) The spatially varying spontaneous curvature and bending modulus fields for the vesicle geometry shown in (a).
We integrate the differential equations with the appropriate boundary conditions to compute the CCP shapes (Fig. 3). At the pole of the CCP, lying on the axis of revolution, we require r = 0, ψ = 0 and L = r[κ(H−C)]′ = 0. The last condition, L = 0 where L represents the transverse shear force in the membrane, is associated with the requirement that there is no applied point load at the pole32. At the outer periphery, we impose z = 0, ψ = 0, and λ = λ0, the prescribed tension in the membrane. We use the coat area of as the reference area. This corresponds to the maximum (100%) area that a coat can have at zero tension. We vary the coat area and compute the equilibrium shapes for a fixed resting tension in the membrane. In order to have a handle on the coat area, we switch to area as the independent variable. The procedure is presented in32. In addition, we use R0 as the lengthscale to normalize the equations. As a consequence, the qualitative nature of our results are valid for any arbitrary radius preferred by the clathrin coat.
Fig. 3.
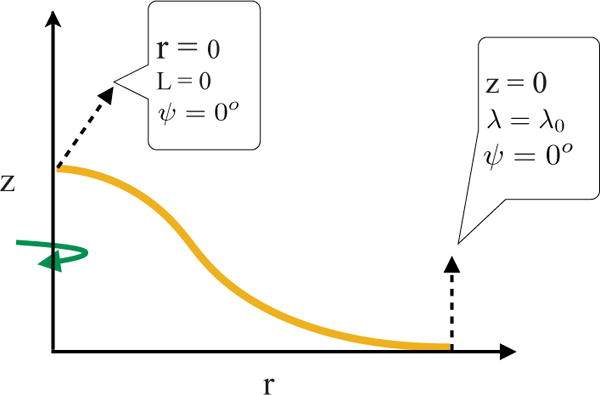
The key variables and the boundary conditions employed in the axisymmetric model to compute vesicle geometry.
The mathematical framework mentioned above has been used extensively to investigate endocytosis and nanoparticle uptake17,31,33–40 (for more studies on endocytosis of nanoparticles, see references in39). In this study, we use the same framework to simulate vesicle shapes but we ask a different question. What is the energy clathrin is required to pay to bend the membrane during shape evolution? In other words, if we start from a planar patch of membrane, how much energy clathrin trikelions have to impart to bend the membrane and turn it into a bud. We can investigate this problem by computing the work done to go from a planar state to an invaginated state. This work done comprises of two components. The first is the energy required to bend the bare membrane. In the framework of Helfrich theory, this energy would be given by the integration of κH2. The second contribution comes from pulling the membrane against the resting tension towards the endocytic site.
A simple thought experiment could provide additional insight in these energetic contributions. Let’s assume we start with a planar membrane at zero tension. Let’s further assume that clathrin polymerizes onto the membrane and transforms it into a nearly spherical bud. Under this scenario, H = C. If we compute the bending energy of the composite membrane-clathrin system, it is equal to zero. However, it does not imply that clathrin did not do any work in bending the membrane. In fact, the bending energy of a sphere is equal to 4πκ which is supplied by the clathrin coat. It is for this reason, we compute the bending energy of the uncoated membrane. A similar idea was employed in41 to compute the cost to form a vesicle. Since the resting tension is zero, no work is done in pulling membrane with a surface area equal to area towards the endocytic site (R0 is the radius of the clathrin coat and C = 1/R0).
We compute the energy for the entire shape evolution and then compute the rate of change of energy per unit clathrin coat area. This ‘energy density ε’ is the polymerization energy that newly added clathrin coat is required to supply at any stage in order to drive vesicle growth further. If the polymerization energy of clathrin, εc, at any stage is equal to or less than this required ε, clathrin can polymerize and bend the membrane. If not, clathrin polymerization and vesicle growth will stall. This approach differs from the notion of computing the average polymerization energy obtained from the ratio of the required bending energy 4πκ with the spherical coat area (as in41). Here, the polymerization cost is predicted as a function of the vesicle geometry during the shape evolution.
3 Results
The key results, the required polymerization energy ε (rate of change of energy per unit clathrin coat area) computed during the shape evolution at different resting tension values are presented in Fig. 4. The total energy plots for the corresponding cases are presented in Fig. S1. The plots exhibit four different patterns. Fig. 4a presents ε in very low tension regimes-λ0 < 0.015 mN/m. First, ε increases at a rapid rate till clathrin reaches 6 – 7% coat area. Next, it increases at a reduced rate until it reaches a maximum around 60% coat area. Beyond this critical point, ε drops rapidly and plateaus in the rest of the area domain. This behavior reveals interesting physics associated with membrane geometry. Up till the critical point (~ 60% coat area), a monotonically increasing polymerization energy is required to drive invagination. However, beyond this critical point, the geometry itself favors closure of the vesicle and as a result the energy required from clathrin undergoes a reduction. Thus, membrane geometry plays a critical role in determining the energetic input required from the protein to drive vesicle growth.
Fig. 4.

Rate of change of energy with respect to clathrin coat area in different tension (λ) regimes (a through d). This is the required polymerization energy that clathrin should possess in order to drive vesicle growth. This energy density shows high sensitivity to both membrane geometry and tension. The insets show the bud morphology at the critical junctures during the shape evolution. All the insets have the same axis allowing a direct comparison between bud profiles at different coat areas and membrane tension. The golden domain indicates the bare membrane and the blue domain indicates the clathrin-coated domain.
Fig. 4b shows the energy requirement in the next higher tension domain- 0.015 − 0.05 mN/m. Here, the plots exhibit similar behavior as before till the critical point (~ 70% coat area) which corresponds to an Ω shaped CCP. However, beyond the critical point, the vesicle undergoes a snapthrough instability and the curves undergo a sharp decline. This trend is a scaled-up version of the very low tension response. The effect of geometry is stronger, and the membrane has a much higher propensity to undergo necking. In the next higher tension regime (0.075 − 0.1 mN/m), ε increases monotonically and smoothly till 80% clathrin coat area (Fig. 4c). However, ε undergoes a rapid increase beyond 70% clathrin coat area which corresponds to an Ω shaped CCP. Interestingly, in this regime, even a 80% clathrin coat area is only able to create a partial vesicle. For higher coat areas, intriguingly, no converged solutions are obtained. Our speculation is that for higher coat area, there are two competing effects. While on one hand the vesicle wants to close up as in Fig. 4b, on the other hand, the coat size is large enough for the vesicle requiring the coat to go into the neck region. Since this would entail significant energetic cost due to curvature frustration, the vesicle does not achieve a closed geometry as in Fig. 4b and gets stalled in the Omega-shaped geometry. Finally, in the high tension regime, > 0.1 mN/m, there is a trend reversal (Fig. 4d). The required polymerization energy (ε) first increases till a critical point around 10% coat area and then decreases smoothly in the rest of the area domain. In this regime, due to very high tension, even a 90% coat area is unable to drive vesicle growth and the membrane stalls at a very shallow CCP.
While the required polymerization energy plots show different trends, the corresponding CCP invagination depths show similar behavior in all the tension regimes (Fig. 5). The depth increases monotonically with an increase in the area and decreases with an increase in the tension. Only in the low tension regime, contrary to intuition, depth decreases beyond 70% coat area. This effect most likely results from the closure of the vesicle which tends to pull the entire CCP towards the planar membrane.
Fig. 5.
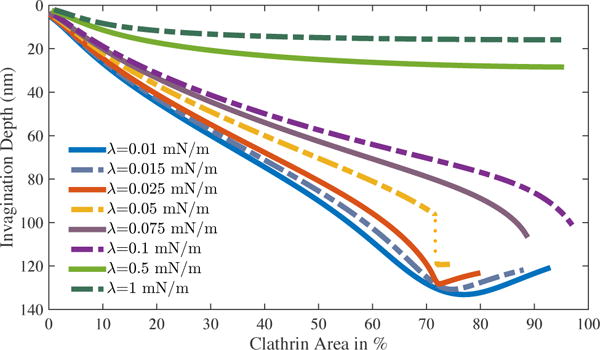
CCP invagination depth obtained in different tension regimes for different clathrin coat domains. Under most scenarios, depth increases monotonically. In low tension regime, vesicle retracts marginally due to necking and CCP closure.
So, what conclusions can be drawn about the size of the clathrin coat from the results presented in Fig. 4? If we assume that the clathrin has a fixed polymerization energy εc, we can determine the maximum coat area corresponding to this value from the ε plots presented in Fig. 4. For example, clathrin is able to form nearly spherical coats in mammalian cells that have an estimated tension in the order of ∼0.01 mN/m41–43. Fig. 4a then suggests that if clathrin has εc = 0.065 mN/m, it would be able to meet the highest energy demand and form a full spherical coat. If we assume that this polymerization energy remains constant under different mechanical environment, we can determine the clathrin coat area corresponding to ε = εc = 0.065 mN/m at different tension values. This yields a plot of clathrin coat area as a function of tension presented in Fig. 6a (red curve). The plot reveals a sharp decline in the clathrin coat area with an increase in the membrane tension. Remarkably, the coat area drops drastically by almost 95% till the tension reaches 0.2 mN/m. Beyond 0.2 mN/m, the coat area becomes insensitive to tension and remains constant.
Fig. 6.

a) Predicted clathrin coat area as a function of membrane tension for two different clathrin polymerization energies εc. The predicted clathrin coat area decreases rapidly in the intermediate tension regime. For εc ≥ 0.1 mN/m, our study predicts formation of coated plaques (nearly planar CCPs) of arbitrary size in high tension regime. Here, we cap the maximum area to 100% (dotted line). b) Corresponding CCP invagination depths for the predicted clathrin coat area. Despite a vast variation in the clathrin coat areas for the two polymerization energies, CCP invagination depth shows a monotonic decline with an increase in membrane tension.
To gain a deeper understanding into the relationship between the polymerization energy and the predicted coat area, we consider another scenario. We compute clathrin coat areas corresponding to a polymerization energy equal to 0.1 mN/m. The blue curve in Fig. 6a shows the coat areas for εc = 0.1 mN/m. Interestingly, the plot shows a very different trend compared to the red curve (corresponding to εc = 0.065 mN/m). For εc = 0.1 mN/m, the clathrin coat area first decreases rapidly till 0.1 mN/m and reaches a value of ∼ 45%. Remarkably, it then begins to increase smoothly till ∼ 0.35 mN/m and reaches a value of ∼ 90%. After ∼ 0.35 mN/m, the polymerization energy is higher than the required values suggesting that any arbitrary coat area greater than 100% can polymerize. However, in Fig. 6a, we cap the polymerized area to a maximum of 100% (dotted blue curve).
While the predicted clathrin coat area is sensitive to the polymerization energy clathrin possesses, the maximum invagination depth of the CCP shows a robust trend. The invagination depths corresponding to the two curves in Fig. 6a are presented in Fig. 6b. In both the scenarios, the invagination depth monotonically decrease with an increased tension. It is important to note that despite large variations in the coat areas in the medium to high tension regimes for the two cases, the invagination depths remain small and comparable. This reveals a tension-dependent decoupling between the polymerized coat area and the CCP invagination depth. In fact, prescribing a higher coat area (> 100%) in the high tension regime for εc = 0.1 mN/m has minimal impact on the invagination depth. Thus, our choice of capping the coat area to a maximum of 100% has no physical consequence on vesicle growth.
Our modeling results suggest that there is an inverse relationship between CCP size and tension in the low to intermediate tension regimes. It was shown previously that cells spread on large fibronectin micropatterned substrates had higher tension compared to small micropatterned substrates16. In order to directly observe CCP sizes on different sized micropatterned substrates, we performed superresolution imaging by stochastic optical reconstruction microscopy (STORM). Endogenously expressed clathrin heavy chain molecules were immunolabeled with Alexa Fluor 647 conjugated antibodies and imaged and analyzed as described previously44,45. As shown in Fig. 7, CCPs were clearly larger in a cell on small micropatterned substrate, consistent with our modeling result. Furthermore, the average correlation lengths computed from autocorrelation functions of the resultant superresolution localization data for the small and large micropatterns were 73 ± 4.2 nm and 54 ± 3.8 nm45, respectively, indicating a larger CCP size in cells with lower tension. These results support the modeling predictions.
Fig. 7.
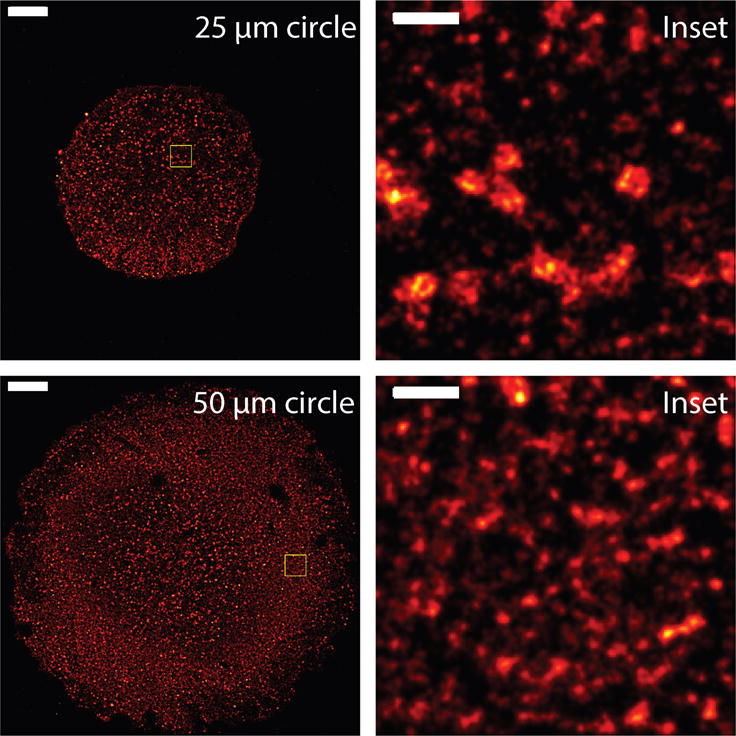
Superresolution images of CCPs of retinal pigment epithelial cells on 25 micron (top) and 50 micron (bottom) circle micropatterns. Insets of yellowed boxed regions are shown on the right. Images are blurred with 2D Gaussian at a radius of 50 nm and 20 nm for full and inset images, respectively. Scale bars are 5 micron and 500 nm for the full and inset images, respectively.
4 Discussion
In this study, we have used the Helfrich theory to model the energetics of clathrin-membrane interaction. Our results reveal that the polymerization energy required to transform a planar membrane into a vesicle shows a highly nonlinear trend determined synergistically by both the geometry and the tension of the membrane. The study shows that the Ω shaped geometry of the CCP is a critical point, beyond which much less work is needed from clathrin to drive vesicle growth. This effect of geometry is reminiscent of the drop in the force observed during pulling of a tubule from a planar membrane or a vesicle17,46,47. In addition, our study shows that the coat size shows extreme sensitivity to membrane tension and decreases rapidly in the low to intermediate tension regimes. Finally, our study presents a counterintuitive finding that the clathrin coat size could reach arbitrarily large values in high tension regimes if clathrin possesses a polymerization energy ∼ 0.1 mN/m. However, despite the increased coat size, the CCP remains nearly flat (Fig. S2).
The experimental findings in mammalian cells performed in this study show the predicted decrease in the CCP size in increased tension environment. The in vitro study by Saleem et al.15 also revealed a reduction in clathrin polymerization on vesicles subjected to hypoosmotic conditions. These experimental findings are aligned with the modeling predictions in the low to intermediate tension regimes. In our experimental setup, we were limited by the degree of cell spreading on the micropatterned substrates, and we found that cells were unable to reliably spread beyond 50 micron diameter circular patterns. Thus, while our other prediction that large shallow clathrin coats can form in high tension regime is not observed in these experiments, planar or moderately curved clathrin structures called ‘coated plaques’ have been observed on the adhered surfaces of mammalian cells48,49. Since cell-substrate adhesion can inhibit membrane bending in a manner similar to high membrane tension, the two scenarios can have similar energetics, giving rise to coated plaques of arbitrary sizes. Our study, therefore, suggests that geometrical constraint coupled with adequate polymerization energy could be a cause of coated plaque formation. Overall, our work reveals the interplay between geometry and elasticity associated with membrane-protein interactions that could regulate the polymerization of other scaffolding proteins such as COPI, COPII, caveolins and BAR proteins.
We would like to note that the notion of spontaneous curvature and polymerization energy for clathrin should be interpreted in a more broader context. While clathrin is known to bend and polymerize on the membrane, its interaction with the membrane is also associated with the recruitment of several accessory proteins3,50,51. These proteins can potentially have similar remodeling effect on the membrane and can alter the clathrin-membrane binding energy. As a result, the spontaneous curvature and the polymerization energy used in this study should be interpreted as effective parameters arising from a complex interplay between clathrin and the accessory proteins.
Lastly, our model assumes continuous polymerization of clathrin during vesicle growth. This mechanism is aligned with numerous experimental and modeling studies present in the literature16,17,31,35,36,52–54. However, the recent paper by Avinoam4 reveals an alternative mechanism in which the entire clathrin coat first polymerizes on a nearly planar membrane and then undergoes geometric remodeling driving vesicle formation. The factors that regulate the clathrin coat size in this model are currently unknown. Furthermore, how membrane tension would inhibit clathrin polymerization on a planar membrane in this model remains to be seen and will be a subject of future study.
Supplementary Material
Fig. 1.

The problem. a) The focus of the study is to predict the clathrin coat (red lattice) area that would polymerize under different membrane tension conditions. To this end, we employ the classic Helfrich theory to estimate the instantaneous energy clathrin monomers would have to provide during the shape evolution to drive vesicle growth.
Acknowledgments
A.A. acknowledges support from NSF Grants CMMI 1437330 and CMMI-1562043. A.P.L. acknowledges help from Xinyu Tan and Hanqing Liu for preparation of samples for superresolution imaging. A.P.L acknowledges support from NSF CMMI-1561794. S.L.V. acknowledges support from R01GM110052.
References
- 1.Diz-Muñoz A, Fletcher DA, Weiner OD. Trends in cell biology. 2013;23:47–53. doi: 10.1016/j.tcb.2012.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Conner SD, Schmid SL. Nature. 2003;422:37–44. doi: 10.1038/nature01451. [DOI] [PubMed] [Google Scholar]
- 3.McMahon HT, Boucrot E. Nature reviews Molecular cell biology. 2011;12:517–533. doi: 10.1038/nrm3151. [DOI] [PubMed] [Google Scholar]
- 4.Avinoam O, Schorb M, Beese CJ, Briggs JA, Kaksonen M. Science. 2015;348:1369–1372. doi: 10.1126/science.aaa9555. [DOI] [PubMed] [Google Scholar]
- 5.Girao H, Geli MI, Idrissi FZ. FEBS letters. 2008;582:2112–2119. doi: 10.1016/j.febslet.2008.04.011. [DOI] [PubMed] [Google Scholar]
- 6.Fujimoto LM, Roth R, Heuser JE, Schmid SL. Traffic. 2000;1:161–171. doi: 10.1034/j.1600-0854.2000.010208.x. [DOI] [PubMed] [Google Scholar]
- 7.Engqvist-Goldstein ÅE, Drubin DG. Annual review of cell and developmental biology. 2003;19:287–332. doi: 10.1146/annurev.cellbio.19.111401.093127. [DOI] [PubMed] [Google Scholar]
- 8.Boulant S, Kural C, Zeeh JC, Ubelmann F, Kirchhausen T. Nature cell biology. 2011;13:1124–1131. doi: 10.1038/ncb2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hyman T, Shmuel M, Altschuler Y. Molecular biology of the cell. 2006;17:427–437. doi: 10.1091/mbc.E05-05-0420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Aghamohammadzadeh S, Ayscough KR. Nature cell biology. 2009;11:1039–1042. doi: 10.1038/ncb1918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rodal AA, Kozubowski L, Goode BL, Drubin DG, Hartwig JH. Molecular biology of the cell. 2005;16:372–384. doi: 10.1091/mbc.E04-08-0734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kishimoto T, Sun Y, Buser C, Liu J, Michelot A, Drubin DG. Proceedings of the National Academy of Sciences. 2011;108:E979–E988. doi: 10.1073/pnas.1113413108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kukulski W, Schorb M, Kaksonen M, Briggs JA. Cell. 2012;150:508–520. doi: 10.1016/j.cell.2012.05.046. [DOI] [PubMed] [Google Scholar]
- 14.Liu AP, Loerke D, Schmid SL, Danuser G. Biophysical journal. 2009;97:1038–1047. doi: 10.1016/j.bpj.2009.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Saleem M, Morlot S, Hohendahl A, Manzi J, Lenz M, Roux A. Nature communications. 2015;6:6249. doi: 10.1038/ncomms7249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tan X, Heureaux J, Liu AP. Integrative Biology. 2015;7:1033–1043. doi: 10.1039/c5ib00111k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Walani N, Torres J, Agrawal A. Proceedings of the National Academy of Sciences. 2015;112:E1423–E1432. doi: 10.1073/pnas.1418491112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Banerjee A, Berezhkovskii A, Nossal R. Biophysical journal. 2012;102:2725–2730. doi: 10.1016/j.bpj.2012.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Banerjee A, Berezhkovskii A, Nossal R. Physical biology. 2016;13:016005. doi: 10.1088/1478-3975/13/1/016005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cordella N, Lampo TJ, Mehraeen S, Spakowitz AJ. Biophysical journal. 2014;106:1476–1488. doi: 10.1016/j.bpj.2013.11.4505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cordella N, Lampo TJ, Melosh N, Spakowitz AJ. Soft matter. 2015;11:439–448. doi: 10.1039/c4sm01650e. [DOI] [PubMed] [Google Scholar]
- 22.Mehraeen S, Cordella N, Yoo JS, Spakowitz AJ. Soft Matter. 2011;7:8789–8799. [Google Scholar]
- 23.Canham PB. Journal of Theoretical Biology. 1970;26:61–81. doi: 10.1016/s0022-5193(70)80032-7. [DOI] [PubMed] [Google Scholar]
- 24.Helfrich W. Zeitschrift fur Naturforschung - Section C Journal of Biosciences. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 25.Jenkins James T. SIAM Journal on Applied Mathematics. 1977;32:755–764. [Google Scholar]
- 26.Steigmann DJ. Archive for Rational Mechanics and Analysis. 1999;150:127–152. [Google Scholar]
- 27.Deserno M. Chemistry and Physics of Lipids. 2015;185:11–45. doi: 10.1016/j.chemphyslip.2014.05.001. [DOI] [PubMed] [Google Scholar]
- 28.Duwe H, Kaes J, Sackmann E. Journal de Physique. 1990;51:945–961. [Google Scholar]
- 29.Faucon J, Mitov M, Méléard P, Bivas I, Bothorel P. Journal de physique. 1989;50:2389–2414. [Google Scholar]
- 30.Jin AJ, Prasad K, Smith PD, Lafer EM, Nossal R. Biophysical journal. 2006;90:3333–3344. doi: 10.1529/biophysj.105.068742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Agrawal A, Steigmann DJ. Biomechanics and modeling in mechanobiology. 2009;8:371–379. doi: 10.1007/s10237-008-0143-0. [DOI] [PubMed] [Google Scholar]
- 32.Agrawal A, Steigmann DJ. Continuum Mechanics and Thermodynamics. 2009;21:57–82. [Google Scholar]
- 33.Gao H, Shi W, Freund LB. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:9469–9474. doi: 10.1073/pnas.0503879102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Liu J, Kaksonen M, Drubin DG, Oster G. Proceedings of the National Academy of Sciences. 2006;103:10277–10282. doi: 10.1073/pnas.0601045103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Liu J, Sun Y, Drubin DG, Oster GF. PLoS Biol. 2009;7:e1000204. doi: 10.1371/journal.pbio.1000204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Agrawal NJ, Nukpezah J, Radhakrishnan R. PLoS Comput Biol. 2010;6:e1000926. doi: 10.1371/journal.pcbi.1000926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dmitrieff S, Nédélec F. PLoS Comput Biol. 2015;11:e1004538. doi: 10.1371/journal.pcbi.1004538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Richards DM, Endres RG. Proceedings of the National Academy of Sciences. 2016;113:6113–6118. doi: 10.1073/pnas.1521974113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhang S, Gao H, Bao G. ACS nano. 2015;9:8655–8671. doi: 10.1021/acsnano.5b03184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Agudo-Canalejo J, Lipowsky R. Biophysical Journal. 2016;110:189a. doi: 10.1016/j.bpj.2016.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Stachowiak JC, Brodsky FM, Miller EA. Nature cell biology. 2013;15:1019–1027. doi: 10.1038/ncb2832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hochmuth F, Shao JY, Dai J, Sheetz MP. Biophysical journal. 1996;70:358. doi: 10.1016/S0006-3495(96)79577-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dai J, Sheetz MP, Wan X, Morris CE. The Journal of neuroscience. 1998;18:6681–6692. doi: 10.1523/JNEUROSCI.18-17-06681.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Stone MB, Veatch SL. Nature communications. 2015;6:7347. doi: 10.1038/ncomms8347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Veatch SL, Machta BB, Shelby SA, Chiang EN, Holowka DA, Baird BA. PloS one. 2012;7:e31457. doi: 10.1371/journal.pone.0031457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Derényi I, Jülicher F, Prost J. Physical review letters. 2002;88:238101. doi: 10.1103/PhysRevLett.88.238101. [DOI] [PubMed] [Google Scholar]
- 47.Koster G, Cacciuto A, Derényi I, Frenkel D, Dogterom M. Physical review letters. 2005;94:068101. doi: 10.1103/PhysRevLett.94.068101. [DOI] [PubMed] [Google Scholar]
- 48.Saffarian S, Cocucci E, Kirchhausen T. PLoS Biol. 2009;7:e1000191. doi: 10.1371/journal.pbio.1000191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kirchhausen T. Trends in cell biology. 2009;19:596–605. doi: 10.1016/j.tcb.2009.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Taylor MJ, Perrais D, Merrifield CJ. PLoS Biol. 2011;9:e1000604. doi: 10.1371/journal.pbio.1000604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Larson BT, Sochacki KA, Kindem JM, Taraska JW. Molecular biology of the cell. 2014;25:2084–2093. doi: 10.1091/mbc.E14-02-0771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kirchhausen T. Current Opinion in Structural Biology. 1993;3:182–188. [Google Scholar]
- 53.Loerke D, Mettlen M, Yarar D, Jaqaman K, Jaqaman H, Danuser G, Schmid SL. PLoS Biol. 2009;7:e1000057. doi: 10.1371/journal.pbio.1000057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Liu AP, Aguet F, Danuser G, Schmid SL. The Journal of cell biology. 2010;191:1381–1393. doi: 10.1083/jcb.201008117. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


