Abstract
We use a new high-accuracy all-dimensional potential to compute the cross second virial coefficient B12(T) between molecular hydrogen and carbon monoxide. The path-integral method is used to fully account for quantum effects. Values are calculated from 10 K to 2000 K and the uncertainty of the potential is propagated into uncertainties of B12. Our calculated B12(T) are in excellent agreement with most of the limited experimental data available, but cover a much wider range of temperatures and have lower uncertainties. Similar to recently reported findings from scattering calculations, we find that the reduced-dimensionality potential obtained by averaging over the rovibrational motion of the monomers gives results that are a good approximation to those obtained when flexibility is fully taken into account. Also, the four-dimensional approximation with monomers taken at their vibrationally averaged bond lengths works well. This finding is important, since full-dimensional potentials are difficult to develop even for triatomic monomers and are not currently possible to obtain for larger molecules. Likewise, most types of accurate quantum mechanical calculations, e.g., spectral or scattering, are severely limited in the number of dimensions that can be handled.
I. Introduction
Mixtures containing molecular hydrogen and carbon monoxide are of significant industrial interest. The well-known water gas-shift reaction produces H2 and CO from combining steam with coal or another source of carbon; the resulting synthesis gas is widely used in industry. H2 and CO are also prominent in the proposed advanced gasification power cycles that enable capture of CO2.1–3 In both of these cases, the primary interest for thermodynamic modeling is in gas-phase properties at moderate pressures. Such modeling is made more accurate if the second cross virial coefficient B12(T), representing the first deviation from the ideal-gas law due to the two-body interaction between H2 and CO molecules, is known at the temperature of interest.
Experimental thermodynamic data for this mixture are scarce, largely because both H2 and CO present major safety hazards in the laboratory. The few available vapor-liquid4–6 and vapor-solid7,8 equilibrium data are at cryogenic temperatures far from the conditions of most industrial interest. The available gas-phase data9–15 will be discussed in Section IV C.
The H2–CO molecular interaction is also of interest in astrophysics. The main reason is that CO spectra are easy to observe, in contrast to H2 which is spectroscopically invisible, in particular in interstellar molecular clouds. If cross-sections for collision of H2 with CO are known, the observed intensities of CO rotational transitions can be used to infer properties of interstellar media. H2–CO has been the subject of numerous spectroscopic investigations, partly due to its astrophysical importance. These measurement were reviewed by Jankowski et al.16
The importance of H2–CO has led to several efforts to produce pair potentials for this interaction. A detailed study was published by two of the present authors with collaborators,16,17 who studied the intermolecular potential on a set of points in six dimensions (6D), i.e., the H-H and C-O bond lengths were varied. From the 6D ab initio data, two four-dimensional (4D) analytic potential energy surfaces (PES) were derived by averaging over the vibrations of the H2 and CO molecules, corresponding to the two lowest (ν = 0 and ν = 1) vibrational states of CO, with H2 in the ground vibrational state in both cases. These vibrationally-averaged surfaces were used to compute infrared and microwave spectra,16,17 which showed excellent agreement with experimental data and helped to interpret such data.
However, some question about the adequacy of the PES remained because of an apparent disagreement16 between computed B12(T) and an experimental datum at low temperature (near 77 K). It was shown in Ref. 16 that this discrepancy is unlikely to be due to the residual errors in the 4D surface. One reason for this disagreement could be the semiclassical approximation used by Jankowski et al.16 to compute B12(T). Another possible reason could be an approximate description of the intramolecular degrees of freedom which were taken into account only indirectly by using the vibrationally averaged surfaces. Thus, to investigate these problems, one should employ both a fully quantum method to calculate the virial coefficients and an interaction energy surface depending explicitly on all degrees of freedom.
In this work, we use the path-integral Monte Carlo method (PIMC) to fully incorporate the quantum effects in the calculation of the second virial coefficient. A new, 6D interaction energy surface, applied in scattering calculations and partly described by Faure et al.,18 is used in our work without any approximations, i.e., the PIMC calculations are also six-dimensional. The uncertainty of the pair potential was carefully estimated and additional PIMC calculations were performed to determine the uncertainty in B12(T). The result is values of B12, with uncertainties, covering the range from 10 K to 2000 K.
Yang and coworkers19,20 recently developed a 6D potential for H2-CO and used it in scattering calculations. The cross-sections were generally in qualitative agreement with experiment for low-energy scattering, but this agreement was not as good as that for cross-sections calculated from the 4D potential of Refs. 16 and 17; see the discussion of these issues in Ref. 18. Faure et al.18 performed similar calculations with their new 6D potential and obtained very good agreement both with experiment and with the cross-sections from the 4D potential. In this work, we will examine whether the comparative performance between these two potentials also extends to the predicted second virial coefficient.
The determination of the uncertainties of the 6D surface required extensive investigations of its properties as described in Secs. II A–II C. The PIMC calculations probe a wide range of variables, therefore it was necessary to precisely characterize the range of variables for which the fitted potential energy function is reliable, as described in Sec. II D. We have also investigated, Sec. II E, characteristic points on the surface. The PIMC methodology is described in Sec. III. The results of full-dimensional treatment are presented in Sec. IV A and virials resulting from approximate treatments in Sec. IV B. We compare to experimental data in Sec. IV C and to values computed with the potential of Yang et al.19,20 in Sec. IV D.
II. H2–CO Potential
The development of a new full-dimensional interaction energy surface for H2–CO (denoted as V15) has been partly described in Ref. 18. In the present paper, we will first briefly summarize the most important information about this surface and then discuss some features of the surface that were not investigated in Ref. 18. Special attention will be given to the uncertainties of the surface which determine, together with the statistical uncertainties of the PIMC calculations, the uncertainties of the virial coefficients.
To describe the dependence of the interaction energy of H2–CO on the geometry of the complex, we use the intermolecular coordinates X = (R, θ1, θ2, ϕ) and the intramolecular coordinates Y = (r, s), where R denotes the distance between the centers of mass (COM) of monomers (the COM of H2 is placed at the origin of the coordinate system and the COM of CO at z = R), θ1 (θ2) denote the angles between the ẑ axis and the vectors starting at the appropriate COM and ending up in H (C), ϕ is the dihedral angle between these vectors, whereas r and s are the interatomic separations in H2 and CO, respectively. The surface has been fitted to the ab initio interaction energies calculated on a 6D grid of dimer geometries applying the following hybrid approximation:21–23
| (1) |
where Eint,H and Eint,B denote the interaction energies calculated at the “high” and “base” levels of theory, respectively, and (rc, sc) = (1.474, 2.165) bohr (1 bohr ≈ 0.52917721 × 10¬10 m). Eint,B is defined as
where is the interaction energy calculated at the Hartree-Fock level using the aug-cc-pVQZ basis set (we use aug-cc-pVXZ basis sets from Ref. 24 with cardinal number X taking values 2 (denoted by D), 3 (T), 4 (Q), and 5), whereas denotes the correlation contribution to the interaction energy calculated using the coupled-cluster method including up to perturbative triple excitations, CCSD(T), with the complete basis set (CBS) 1/X3 extrapolations25 from the calculations in the aug-cc-pVTZ and aug-cc-pVQZ basis sets. The CCSD(T) calculations performed to obtain correlated all electrons. Eint,H is defined as
| (2) |
where
is the correction obtained using an increased-size basis set, aug-cc-pV5Z, whereas
accounts for the electron correlation effects at the level of the coupled-cluster method with up to perturbative quadruple excitations, CCSDT(Q), computed in the aug-cc-pVDZ basis set using the frozen-core approximation (in this case, the CCSD(T) calculations also utilized this approximation). The hybrid approximation defined by Eq. (1) requires one to perform the expensive calculations of Eint,H only for the four-dimensional grid, with the intramolecular distances frozen at the (rc, sc) values. Thus, the hybrid approximation enables us to enhance the overall accuracy of the PES since the most important region near (rc, sc) is represented at a very high level of theory. At the same time, the costs of calculations remain reasonable since only a fraction of grid points are computed at the high level of theory. The analytic form and the procedure of fitting a 6D analytic surface to the hybrid interaction energies are discussed in more detail in Ref. 18.
If we use the full-dimensional description of the interacting complex, we need to employ the total PES Utot(R, θ1, θ2, ϕ, r, s) to find a geometry of the complex corresponding to the minimum energy. Thus, if we have the V surface representing only the interaction energy of the H2 and CO molecules, we need to add the one-dimensional, monomer potentials:
| (3) |
We used the VH2 potential for H2 from Ref. 26 and the VCO potential for CO from Refs. 27 and 28. These monomer potentials have minima at r = 1.4011 bohr and s = 2.1322 bohr, respectively. We will use the symbol Utot,15 to denote the PES that includes V15.
In this paper, we will also discuss four-dimensional approaches to calculating virial coefficients that require the interaction energies averaged over the vibrational motion of both molecules. We could have averaged the 6D potential on a set of intermonomer grid points and then fit a 4D surface to averaged interaction energies at these points, but instead we have performed the averaging on the fly, i.e., in each step of PIMC. Since the direct procedure would be time consuming, we have employed an approximate method based on the Taylor expansion of the interaction energy with respect to the intramolecular degrees of freedom, as described in Refs. 16 and 29.
To estimate uncertainties of computed observables, one has to know the uncertainties of the fitted surfaces. The latter uncertainties come from the following sources: (a) uncertainties of ab initio interaction energies at the highest level of theory; (b) uncertainties due to the use of the hybrid approximation; (c) uncertainties due to fitting. The source (a) has already been analyzed in Ref. 16, but only near equilibrium intramonomer separations. We will extend this analysis for large extensions of intramonomer separations where single-determinant-based methods that we use may converge poorly. The source (b) was analyzed in Ref. 18 and we will only recapitulate the results. The source (c) will be investigated in the present work.
A. Accuracy of computed interaction energies
The accuracy of the ab initio calculations at the Eint,H level has been estimated in Ref. 16 to be about 0.6 cm−1 (relative to the exact interaction energies for a given nuclear configuration) in the vicinity of the global minimum with the monomers at (⟨r⟩0, ⟨s⟩0) = (1.449, 2.14) bohr. To get the estimates, calculations were performed for 8 grid points in inter-molecular coordinates: two distances and four combinations of the angles (one of the points was close to the global minimum and another one to the local minimum). For each point, CCSD(T) interaction energies were computed in several basis sets, including the basis set aug-cc-pV6Z with X larger by one than used in calculations of Eint,H and bases with midbond functions. Analysis of basis set convergence including the convergence of CBS extrapolated values gave estimates of uncertainties of resulting from basis set truncations amounting to 0.4 cm−1 in the well region and 0.6% for the whole PES. For the contribution, the basis convergence was investigated by performing calculations with all electrons correlated in the aug-cc-pVDZ basis and extending the basis set to the aug-cc-pVTZ size at the frozen-core level. The effect of freezing the core was found to be completely negligible. The extension of basis set size gave changes of the order of 0.1 cm−1. The authors of Ref. 16 also computed the contribution of the iterated quadruple excitations to the interaction energy at four grid points. They found that the effect of such iterations on interaction energies, , is below 0.1%. Accounting for the uncertainties due to basis set incompleteness of and the neglect of , the overall uncertainties of the Eint,H interaction energies were estimated as 0.5 cm−1 in the well region and 0.7% for the whole surface. Since the total quadruples contribution to the interaction energy is of the order of only 1%, whereas that of triples is 19%, clearly the effects of higher excitations are well below the estimated uncertainties. Similarly, the adiabatic corrections and relativistic effects, evaluated in Ref. 30, are of the order of 0.1 cm−1. The authors of Ref. 16 concluded that the uncertainties of Eint,H relative to exact interaction energies at the adiabatic level with inclusion of relativistic effects are 0.6 cm−1 or 0.8%.
While the investigations of Ref. 16 were performed for (〈r〉0, 〈s〉0), the estimates should be valid for (rc, sc) used in calculations of Eint,H since these coordinates differ by only about 0.02 bohr. However, the estimates will likely not hold if Eint,H were computed for (r, s) departing significantly from this range. Information about such uncertainties is needed in order to obtain estimates of the accuracy of interaction energies in 6D. The authors of Ref. 18 computed Eint,H for the intermonomer coordinates fixed at the near minimum values (R,θ1,θ2,ϕ)=(8.0,0°,180°,0°) and sweeping the whole range of (r, s). We now will estimate the uncertainties of these values. The convergence in basis set should not change with (r, s), but the convergence in the number of excitations may. This is due to the well-known fact that methods based on a single-reference determinant start to converge more slowly for stretched chemical bonds. To examine this issue, we have performed calculations of the interaction energy at the CCSDTQ level for the set of grid points with R = 8 bohr used in Ref. 18. The results are presented in Table I. The correction, calculated in the aug-cc-pVDZ basis set with frozen core, is compared to the other post-CCSD(T) corrections, and , and the total interaction energy calculated in the same basis set. One can see that for (r, s) ≈ (rc, sc), the value of is −0.051 cm−1, which amounts to 2% of the contribution and 0.07% of . This is only slightly larger than the corresponding contribution of 0.06% at (〈r〉0, 〈s〉0) computed in Ref. 16. The contribution is even smaller for smaller values of r and s. However, for the most stretched intramolecular distances, (2.05, 2.45) bohr, the value of is as large as −0.89 cm−1 which amounts to 1.4% of . Thus, for this configuration the uncertainty of Eint,H has to be increased to about 2%, more than a factor of two compared to the region near equilibria of (r, s). For most points in Table I, the original estimate of 0.8% holds and only for points in the lower right corner of this table [and the point (0.95,2.45)] must it be increased to some value between 0.8% and 2%. Table I shows that it is the increase of r that is mainly responsible for the increase of . This is partly due to the fact that the H-H bond is maximally stretched by 46% versus only 15% for the C-O bond. As an aside, one may mention that for the isolated H2, the CCSD method is equivalent to the full configuration interaction method, i.e., is exact in a given basis set for any r. Thus, it may be surprising that depends so strongly on r. This is partly accidental, due to the fact that crosses zero around r = 1.2 bohr and therefore relative changes are large. The absolute changes related to r and s are not that different: 0.98 cm−1 for r changing from 0.95 to 2.05 bohr at s = 2.45 bohr and 0.58 cm−1 for s changing from 1.90 to 2.45 bohr at r = 2.05 bohr.
Table I.
Values of the , , , and contributions compared with the total interaction energy , calculated for the intermolecular geometry defined by (R,θ1,θ2,ϕ)=(8.0,0°,180o,0°) and the grid of values of the intramolecular geometries (r, s). For one more intramolecular geometry tested, (rc, sc) = (1.474, 2.165) bohr, the values of , , , , and are equal to −74.399, −1.804, −0.835, −0.051 and −77.089 cm−1, respectively. The aug-cc-pVDZ basis set and frozen core has been used in these calculations. The distances are given in bohr, energies in cm−1.
| r\s | 1.90 | 1.99 | 2.13 | 2.30 | 2.45 | ||
|---|---|---|---|---|---|---|---|
| 0.95 | -48.693 | -46.317 | -42.259 | -36.761 | -31.421 |
|
|
| -0.868 | -0.858 | -0.831 | -0.780 | -0.718 |
|
||
| -0.335 | -0.395 | -0.498 | -0.638 | -0.772 |
|
||
| +0.005 | +0.013 | +0.032 | +0.060 | +0.092 |
|
||
| -49.892 | -47.556 | -43.557 | -38.119 | -32.819 |
|
||
| 1.20 | -69.012 | -65.118 | -58.521 | -49.685 | -41.222 |
|
|
| -1.224 | -1.223 | -1.212 | -1.180 | -1.133 |
|
||
| -0.442 | -0.515 | -0.640 | -0.807 | -0.963 |
|
||
| -0.014 | -0.006 | +0.010 | +0.033 | +0.053 |
|
||
| -70.691 | -66.861 | -60.363 | -51.640 | -43.266 |
|
||
| 1.40 | -86.460 | -81.123 | -72.114 | -60.115 | -48.702 |
|
|
| -1.592 | -1.605 | -1.618 | -1.619 | -1.598 |
|
||
| -0.538 | -0.619 | -0.756 | -0.934 | -1.097 |
|
||
| -0.042 | -0.038 | -0.029 | -0.024 | -0.027 |
|
||
| -88.633 | -83.384 | -74.517 | -62.691 | -51.423 |
|
||
| 1.67 | -109.620 | -101.998 | -89.177 | -72.197 | -56.154 |
|
|
| -2.267 | -2.313 | -2.384 | -2.466 | -2.519 |
|
||
| -0.685 | -0.769 | -0.906 | -1.073 | -1.215 |
|
||
| -0.112 | -0.119 | -0.135 | -0.176 | -0.243 |
|
||
| -112.685 | -105.198 | -92.602 | -75.911 | -60.130 |
|
||
| 2.05 | -136.289 | -124.787 | -105.507 | -80.108 | -56.259 |
|
|
| -3.725 | -3.863 | -4.096 | -4.401 | -4.664 |
|
||
| -0.936 | -0.994 | -1.075 | -1.143 | -1.169 |
|
||
| -0.311 | -0.356 | -0.452 | -0.637 | -0.887 |
|
||
| -141.262 | -130.000 | -111.130 | -86.289 | -62.980 |
|
The analysis presented above shows that if the whole 6D PES were computed at the Eint,H level, the accuracy of the predictions from this surface would be determined by uncertainties of PES for near-equilibrium intermonomer separations since this uncertainty extends to quite a broad range of (r, s) coordinates and the regions where uncertainties become large is only lightly sampled in typical applications in spectroscopy, scattering, and thermodynamics. However, Eint,H was computed only at (rc, sc), whereas for other (r, s) the hybrid approximation was used. The error of Eint,B is mainly due to the neglect of the post-CCSD(T) contributions and is therefore of the order of 3% for near-equilibrium monomers. The hybrid approximation makes the PES accurate to 0.8% near (rc, sc), but is not guaranteed to reduce errors at large monomer deformations. This issue was investigated in Ref. 18 on the same set of grid points discussed above and in addition for an analogous set located in the region of the local minimum with R = 7 bohr (see Sec. I and Table I in Supplementary Information of that work). It was shown there that the hybrid approximation reduces uncertainties at 78% of the grid points, i.e., the errors of Eint,hyb relative to Eint,H are smaller than the errors of Eint,B. In the region where both r and s are large, the errors of Eint,hyb are about 3%, i.e., are larger than the uncertainties of Eint,H (due to the neglect of ) in this region. Thus, the final conclusion from these investigations is that the reduced rate of convergence for stretched bonds leads to smaller additional uncertainties than those that result from the use of the hybrid approximation in this region. One may also notice in Table SI-I of Ref. 18 that the CCSD(T) approximation deteriorates with increasing r and s similarly as CCSDT(Q) does. At R = 8 bohr, the error of less than 3% near equilibrium values becomes as large as 6% at (2.05,2.45). The 78% “success rate” listed above for the hybrid approximation is partly due to this deterioration since Eint,B inherits this deterioration.
B. Accuracy of fitting
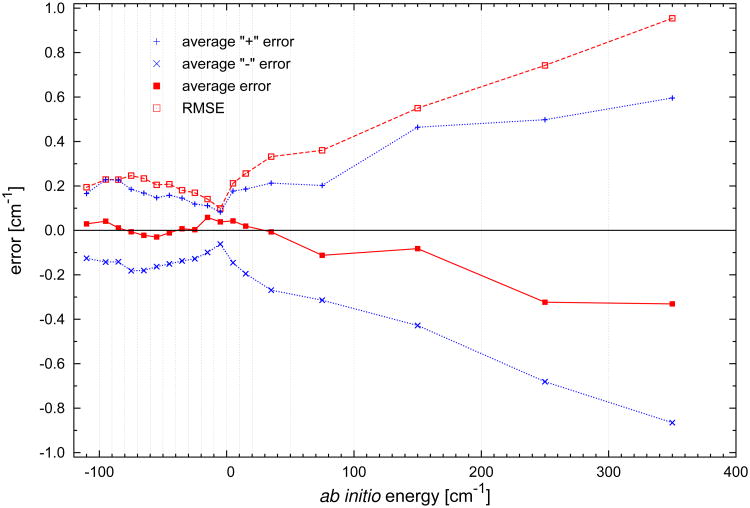
The analytic form of the fit should be at the same time flexible enough to describe subtle features of the potential and not too flexible to prevent undulating behavior between grid points. Clearly, the fitting errors should be smaller than the errors originating from the ab initio calculations. The errors of the V15 fit with respect to the training set of ab initio interaction energies were briefly discussed in Ref. 18. The root-mean-square error (RMSE) is 0.63 cm−1 for all 27 132 grid points used in the final fit. For the 22 668 energies belonging to the interaction potential well, the RMSE is 0.16 cm−1, and for the 4464 positive energies smaller than our threshold of 1000 cm−1, the RMSE is 1.51 cm−1. We will now present a more detailed description of this issue. Figure 1 shows the average, signed average, and RMSE errors of the V15 surface with respect to the ab initio data computed for several energy intervals. One can see that the average “+” and “−” errors have a rather stable amplitude in all intervals within the potential well and only slightly exceed 0.2 cm−1. Moreover, these errors cancel each other to a great extent and the average error is close to zero. For the (−10, 0) cm−1 interval of the energy, the errors are especially small, which is due to the large number of small energies calculated for geometries belonging to this interval with relatively large values of R. The values of RMSE are also very similar for all energy intervals within the potential well and barely exceed 0.2 cm−1. This finding shows that the accuracy of the fit in terms of RMSE is very uniform for all negative energies and the overall RMSE of 0.16 cm−1 is a good representation of the accuracy of the fit everywhere in this region. For the positive energies, the absolute values of the averaged energies increase, but the relative ones still remain at a very reasonable level. The cancellation of the “+” and “−” errors is also very good, e.g., for the (50, 100) cm−1 interval their difference is −0.11 cm−1 which is less than about 0.2% of the energies in this range. The RMSE in this interval is 0.36 cm−1, which amounts to 0.7% of the smallest energies from this interval. As one can see, the value of RMSE behaves linearly for increasing values of energies. This is consistent with our weighting function (see Ref. 18), which enforces the fit to be of uniform accuracy within the whole potential well and to have a stable relative error in the repulsive part of the surface. This function included the product of three factors depending on the interaction energy and on the deformation of the H2 and CO molecules. The latter two factors were introduced to enhance the quality of the fit for the grid points with intramolecular distances in the vicinity of the monomer's equilibrium separations.
Fig. 1.
The average and RMS errors of the interaction energies of H2–CO predicted by V15 calculated with respect to the ab initio values for 27 132 geometries with R ≤ 12 bohr. The errors are calculated in the intervals of energy indicated by the vertical dotted lines, except that the points corresponding to the lowest energy range represent the errors calculated for all energies lower then −100 cm−1. The abscissas of the symbols are taken in the middle of these intervals. There are also plotted, for both surfaces, the average values of the positive and the negative errors.
The dependence of the fit accuracy on intramonomer separations is presented in Table II, which shows the values of RMSE separately for each (r, s) pair used and divides them into three energy ranges: (−∞, 0), (0, 1000), and (−∞, 1000) cm−1. As already seen in Fig. 1, RMSEs for negative energies are small: 3-6 times smaller than the ab initio uncertainty of about 0.6 cm−1 in the van der Waals minimum region. This demonstrates that the fit is more than sufficiently accurate there. The increase of RMSE for (r, s) far from (rc, sc), imposed by our weighting function, is fairly weak, only up to 44% for negative energies and up to a factor of 4 for the positive ones. In fact, for some values of (r, s), RMSEs are slightly smaller than for (rc, sc), most likely just due to numerical fluctuations. While RMSEs either increase slowly with s or fluctuate, there is an overall clear increase with r. One reason is, of course, the greater variation of r as discussed earlier. Another reason can be an increase of the anisotropy of the interaction energy as r increases. The anisotropy is governed by the electrostatic component of the interaction energy, and the leading term in the asymptotic expansion of this component depends on the quadrupole moment of H2, equal to 0.256, 0.483, and 0.770 a.u.31 at r = 1.0, 1.4, and 2.0 bohr, respectively, a rather large increase.
Table II.
The values of the RMSE of the fit with respect to to ab initio energies calculated for the given values of the intermolecular coordinates (r, s) and for three intervals of the interaction energy. The only point from the intermolecular grid not given in the table is (rc, sc) = (1.474, 2.165) bohr. In this case the calculated RMSE values are 0.16, 0.81, and 0.35 cm−1 for (−∞, 0], (0, 1000), and (−∞, 1000) ranges of the interaction energy, respectively. All energies are given in cm−1 and distances in bohr.
| r\s | 1.90 | 1.99 | 2.13 | 2.30 | 2.45 |
|---|---|---|---|---|---|
| energy range (−∞, 0) | |||||
|
| |||||
| 0.95 | 0.16 | 0.13 | 0.11 | 0.11 | 0.15 |
| 1.20 | 0.14 | 0.13 | 0.12 | 0.11 | 0.11 |
| 1.40 | 0.16 | 0.15 | 0.14 | 0.13 | 0.12 |
| 1.67 | 0.19 | 0.19 | 0.18 | 0.17 | 0.16 |
| 2.05 | 0.24 | 0.23 | 0.22 | 0.22 | 0.23 |
|
| |||||
| energy range (0, 1000) | |||||
|
| |||||
| 0.95 | 0.97 | 0.91 | 1.00 | 0.93 | 1.07 |
| 1.20 | 1.13 | 1.12 | 1.11 | 1.12 | 1.09 |
| 1.40 | 1.15 | 0.95 | 0.82 | 0.78 | 0.74 |
| 1.67 | 1.48 | 1.54 | 1.61 | 1.49 | 1.44 |
| 2.05 | 2.32 | 2.03 | 2.26 | 2.53 | 3.29 |
|
| |||||
| energy range (−∞, 1000) | |||||
|
| |||||
| 0.95 | 0.41 | 0.39 | 0.42 | 0.39 | 0.46 |
| 1.20 | 0.48 | 0.47 | 0.46 | 0.47 | 0.46 |
| 1.40 | 0.49 | 0.41 | 0.36 | 0.34 | 0.32 |
| 1.67 | 0.62 | 0.65 | 0.67 | 0.62 | 0.60 |
| 2.05 | 0.98 | 0.85 | 0.96 | 1.05 | 1.34 |
We will use in calculations of virials a 4D surface denoted as V15(r0) obtained from V15 by setting the intramolecular distances at the vibrationally averaged values r0 = 〈r〉0 = 1.4487 bohr and s0 = 〈s〉0 = 2.1399 bohr for H2 and CO, respectively. We cannot directly evaluate the accuracy of this surface since no calculations have been done at (r0, s0). However, we computed the full set of ab initio intermolecular energies at (rc, sc) = (1.474, 2.165) bohr, very close to (r0, s0). Clearly, based on the evidence in Sec. II A, the accuracy of the V15(r0) surface should be very close to that of V15 calculated at (rc, sc). The appropriate values of RMSE are given in the caption of Table II and are 0.16, 0.81, and 0.35 cm−1 for the (−∞, 0), (0, 1000), and (−∞, 1000) cm−1 ranges of the interaction energy, respectively.
It is more difficult to estimate the uncertainty of another 4D PES that will be used in calculations of virial coefficients, the 〈V15〉0 surface obtained by averaging V15 over the ground-state vibrations of the monomers. However, this surface should be very similar to the 4D V12 surface16,17. While the value of 〈V15〉0 at an arbitrary point X = (R, θ1, θ2, ϕ) is obtained by integrating out the (r, s) coordinates from the 6D PES (no 4D fitting is involved), V12 was fitted to the set of averaged ab initio interaction energies at all X grid points. The average used interaction energies Taylor expanded around (rc, sc), with the values at the expansion point computed at the Eint,H level and the derivatives computed at the Eint,B level, which is equivalent to using our hybrid approach. Therefore, we can evaluate the errors of 〈V15〉0 on this set of points. Such RMSEs are presented in Table III for both PESs. To make a fair comparison with V12, the intervals (−∞, 400) cm−1 and (0, 400) cm−1 used in Ref. 16 are also included. Table III shows that the RMSE of 〈V15〉0 for negative interaction energies is very small, 0.2 cm−1, showing that the 6D fitting did not introduce any spurious errors. However, in all intervals below 400 cm−1, V12 has about twice smaller RMSE than 〈V15〉0. This could be expected, since the reference data set is the training set for V12. The larger RMSE of 〈V15〉0 does not indicate, however, that it is the inferior of the two 4D surfaces. In fact, it is likely that the opposite is true, since 〈V15〉0 employed a much wider range of (r, s) in the averaging over intramonomer distances than V12. One has, however, to also admit an (unlikely) possibility that the increased errors of ab initio points at extreme values of (r, s) might have had a negative effect on the accuracy of 〈V15〉0. For the intervals containing energies larger than 400 cm−1, the relations are opposite and the RMSEs of V12 are about twice as large as those of 〈V15〉0. The obvious reason is the neglect of such energies in fitting V12.
Table III.
The values of RMSE calculated for several intervals of interaction energy for the 〈V15〉0 surface with respect to the set of the ab initio vibrationally averaged interaction energies used to fit the V12 surface.16,17 For comparison, the values of RMSE calculated for V12 are also given. All energies are in cm−1 and distances in bohr.
| range | 〈V15〉0 | V12 |
|---|---|---|
| (0, 1000) | 0.935 | 2.320 |
| (0, 400) | 0.394 | 0.156 |
| (−∞, 0) | 0.145 | 0.077 |
| (−∞, 400) | 0.193 | 0.090 |
| (−∞, 1000) | 0.373 | 0.865 |
C. Overall uncertainty of fitted surface
The overall uncertainty of our fit surface V15 is a combination of the uncertainties from sources (a)–(c) discussed earlier in this section. The uncertainty (a) of Eint,H, i.e., the most accurate of our interaction energies computed only at (rc, sc) (and at a few test points) is 0.6 cm−1 in the region of the potential well and 0.8% in all other regions. The source (b), the use of the hybrid approximation, introduces only negligible errors in a fairly broad range of (r, s) around (rc, sc), whereas the errors at the maximally stretched bonds are about 3% relative to the Eint,H level. The deterioration of the CCSDT(Q) approximation as intramonomer bonds are stretched was estimated to amount to only 1.4%, increasing the total basis set and theory level truncation uncertainty to 2%, so it is of secondary importance. Source (c), the errors of the fit, are about 0.2 cm−1 for negative interaction energies (for all values of r and s) which gives 0.2% error near the bottom of the well. If we add the uncertainties in quadrature for the region around (rc, sc), i.e., 0.6 and 0.2 cm−1, the overall uncertainty is still 0.6 cm−1. At largest (r, s), simply adding the relative errors mentioned above: 2%, 3%, and 0.2%, we get an overall uncertainty of about 5%. We approximated this uncertainty (in percent) by the function 0.8 + 8|r − rc| + 15|s − sc| − 10|r − rc||s − sc|. For the maximally stretched configuration (r, s) = (2.05, 2.45) bohr, this expression gives a relative uncertainty of 8%. We interpret this uncertainty in the potential as an expanded uncertainty with coverage factor k = 2, roughly corresponding to a 95% confidence interval.
D. Validity ranges of coordinates
The analytic form of the surface is constructed from the long- and short-range parts, which ensure the proper physical behavior of the resulting surface, i.e., the inverse-power dependence on R at long range and the exponential growth of the interaction energy for small R. The long-range part is damped, but the damping is not perfect and all surfaces of such form suffer problems when the values of R are very small since the negative 1/Rn terms tend to dominate the positive exponential terms in this region. To test the performance of the V15 surface for small R, we calculated values of V15 on the same grid of (θ1,θ2,ϕ,r,s) points as used in the ab initio calculations18. The angular part is composed of 241 points and the intramolecular part of 26 points, giving 6266 points total. We used three values of R: 4.00, 3.75, and 3.50 bohr, and for each point (θ1,θ2,ϕ,r,s) from the grid, we checked whether the interaction energy increases as R decreases. In only three cases, the interaction energy slightly decreased when R changed from 3.75 to 3.50 bohr. Thus, we can assume that the V15 interaction energy potential has no “holes” for R ≥ 3.5 bohr and can be used for such intermolecular distances. It should also be stressed that the smallest value of the interaction energy calculated for the test grid at R = 3.5 bohr was 7894 cm−1, so this value of R corresponds to the highly repulsive part of the interaction energy surface.
The range of the r and s variables is defined by the intervals of values used in the ab initio calculations, i.e., (0.95, 2.05) and (1.90, 2.45) bohr, respectively. Outside of these ranges, the interaction energy is extrapolated by our PES, but one cannot expect that the extrapolated values are reliable far outside the ranges. Thus, the potential should not be used for r or s far from the recommended region. This should not be needed for most physical applications, since these intervals include the classical turning points for the v = 2 (v = 3) vibrational state of H2 (CO) (for H2, the outer v = 2 classical turning point is slightly outside the range). Although quantum mechanical wave functions do probe the region beyond classical turning points, the probabilities of particles to penetrate far into these regions are negligible, so the reduced accuracy of the PES there is inconsequential. Thus, V15 can be used with full confidence in applications where the vibrational excitations of H2 and CO include states with v = 2 and v = 3 states, respectively. This means that the constraints on the values of (r, s) do not introduce limitation for a wide range of prospective applications.
E. Features of potential energy surface
The positions and values of the global and local minima on the Utot,15 PES are given in Table IV. We use two ways of specifying the depth at a minimum. One is the vertical interaction energy (Vmin) which is computed with respect to monomers at the same intramonomer separation as in the dimer. The other one is the stabilization energy32 (Utot,min) which is the difference between the total energy at the minimum and the sum of the monomer energies at their equilibria. Thus, the two definitions differ by the energies needed to deform monomers from their equilibrium configuration to that assumed in the minimum dimer. Table IV shows that, at the global minimum found for the linear HH–CO arrangement, the vertical interaction energies are very close to the stabilization energies. The reason is that even small departures from (re, se) give large positive contribution to the interaction energy from the monomer energies in Eq. (3). Thus, at the global minimum such deviations are only of the order of 0.001 bohr and the sum of deformation energies is only 0.055 cm−1. The local minimum of the PES has been found for the linear HH–OC arrangement with R 0.76 bohr shorter than for the global minimum, which is partly due to the COM of CO being closer to O than to C. This minimum is 19 cm−1 shallower than the global minimum. The deformation energies are even smaller than in the case of the global minimum.
Table IV.
Comparison of some characteristic points of the H2–CO PES. The distances are given in bohr and energies in cm−1.
| R | rH2 | rCO | VH2(rH2) | VCO(rCO) | Vmin | Utot,min | |
|---|---|---|---|---|---|---|---|
| (θ1,θ2,ϕ)=(0°,180°,0°) | |||||||
| Utot,15a | 7.8977 | 1.4021 | 2.1319 | 0.0419 | 0.0139 | -91.1649 | −91.1091 |
| Yang et al.b | 8.0000 | 1.4011 | 2.1359 | −85.937 | |||
| Utot,Yc | 8.0000 | 1.4011 | 2.1359 | 0.0000 | 1.8023 | −79.626 | |
| Utot,15 | 8.0000 | 1.4011 | 2.1359 | 0.0000 | 1.8023 | -90.2631 | −88.4607 |
| Utot,Ya,c | 7.9156 | 1.4025 | 2.1319 | 0.0814 | 0.0139 | -80.4394 | −80.3441 |
| (θ1,θ2,ϕ)=(0°,0°,0°) | |||||||
| Utot,15d | 7.1398 | 1.4016 | 2.1325 | 0.0108 | 0.0103 | -72.1001 | −72.0789 |
| Utot,Yc,d | 7.1858 | 1.4015 | 2.1325 | 0.0070 | 0.0103 | -69.1956 | −69.1782 |
The positions and values of the minima of V15 cannot be directly compared with the corresponding values of V12,16 since the latter surface was fitted to the interaction energies averaged over the vibrations of the monomers. However, one can compare the V12 and 〈V15〉0 surfaces. Such a comparison is presented in Table V. We have also included the V0429 potential. As we can see, the positions of the global minima for 〈V15〉0 and V12 are very close to each other and differ by only 0.002 bohr. The interaction energy at the minimum is higher by 0.162 cm−1 in the case of 〈V15〉0. This difference is consistent with the uncertainties of the two fits discussed in Sec. II B. For the local minimum, the relations are similar.
Table V.
The positions, Rmin, and values, Vmin, of the global and local minima of the 〈V15〉 and V15(r0) surfaces. The corresponding values obtained for the earlier surfaces V0441 and V1216,17 are also given for comparison. The distances are given in bohr and energies in cm−1.
Comparison of Tables IV and V shows that the vertical minimum interaction energy of the 6D potential is smaller in magnitude by 2.77 cm−1 than the minimum interaction energy of 〈V15〉0. This happens at almost identical values of intermonomer coordinates. Such a large energetic difference is due to the fact that the monomer coordinates are very close to (re, se) in the former case whereas the average performed in the latter case tends to favor larger (r, s) which correspond to more negative interaction energies. The latter interaction energy is very close, within 0.3 cm−1, to the minimum energy of V15(r0), for the same reason. Interestingly, the difference is larger for the local minimum, where it amounts to 0.6 cm−1. Thus, the potentials 〈V15〉0 and V15(r0) are quite similar near the minima. However, we will see that 〈V15〉0 performs slightly better in calculations of virial coefficients, so that the significantly larger effort needed to obtain this PES is not wasted.
We have also computed the minima for the Yang et al.19,20 PES using the (original) intermonomer potential subroutine from the Supporting Information of Ref. 20 and adding to it the same intramonomer potentials as used in Utot,15. The results presented in Table IV show that these minima are significantly above our minima: by 10.77 and 2.90 cm−1 for the global and local minimum, respectively. The value of the global minimum on Utot,Y may appear to be in contradiction with the interaction energy equal to −85.937 cm−1 published by Yang et al.19 The reason is that this value is an ab initio computed interaction energy. The Utot,Y fit gives −79.626 cm−1 for this point on the surface.
III. Path-Integral Calculations of the Second Virial Coefficient
We calculated the second virial coefficient of the H2–CO system using the path-integral formulation of quantum statistical mechanics. In this section, we will briefly summarize the principal ideas behind this calculation. Our method has been described in detail in previous papers both for rigid-rotor22,33 and fully flexible34 models for the molecules.
From statistical mechanics, the second virial coefficient B(T) is given by
| (4) |
where is the partition function of monomer a, is the partition function of the dimer, and V denotes the volume of the box enclosing the system, with the limit V → ∞ to be taken at the end of the calculations. Starting from Eq. (4), one can derive the general expression
| (5) |
where the meaning of the effective potential Veff(…) as well as the meaning of the average 〈⋯〉 and the coordinate R depend on both the assumed description of the molecules involved (e.g., rigid or flexible) and the level of theory used to calculate the virial coefficient (e.g., classical or quantum mechanics).
If the molecules are considered to be classical rigid linear rotors, then the effective potential Veff(…) appearing in Eq. (5) is the actual intermolecular potential, R is the distance between the centers of mass of molecules a and b, and the average is performed over molecular directions uniformly distributed on a sphere.35 If the molecules are assumed to be quantum rigid linear rotors, then it is convenient to evaluate the partition functions in Eq. (4) using the path-integral method. This procedure results in a mapping of the quantum partition function of two linear rigid rotors into an equivalent classical partition function of two ring polymers with P monomers. Each replica of a monomer, identified by an index p = 1, …, P, is a rigid rotor whose center of mass is connected by a harmonic potential to the centers of mass of two adjacent neighbors, those labeled by the indices p − 1 and p + 1, with the ring condition implying that p = P + 1 is equivalent to p = 1. The orientational degrees of freedom between adjacent monomers are also coupled via a quasi-harmonic potential. The path-integral formulation provides an expression for the spring constant connecting the centers of mass, as well as a (numerical) expression of the potential that couples the rotational degrees of freedom. At the end, it can be shown22,33 that the path-integral expression for B(T) also has the form of Eq. (5) where:
The coordinate R is the relative distance between the centers of mass of two beads with the same index (p = 1, say) on the molecules a and b.
The effective potential appearing in the exponential is the average of the original intermolecular potential V(⋯) performed on the pairs of beads of the two molecules having the same index p.
The average 〈⋯〉 is performed on the configurations that the two ring polymers corresponding to molecules a and b have when they do not interact.
A fully flexible model also results in an expression for B(T) in the form of Eq. (5). In the classical case, the average in Eq. (5) is taken over the distribution of bond lengths of isolated molecules, as well as their orientations. When the two-body partition function of flexible molecules is calculated according to the path-integral formulation of quantum-statistical mechanics, one again obtains a mapping of the quantum system into an equivalent classical system of ring polymers.34 In this case, a ring polymer is associated with every atom of both molecules and, again, the quantum expression for B(T) has the form of Eq. (5). The average 〈⋯〉 is now performed on configurations of isolated molecules where each atom is substituted by a P-bead ring polymer. The ring polymers corresponding to atoms within the same molecule interact among themselves with a potential energy that is the average of the intramolecular potential on the P configurations characterized by the same value of the index p. Analogously to the rigid-rotor case, the effective potential Veff(…) appearing in Eq. (5) becomes the average of the original intermolecular potential on the P configurations with the atoms of both molecules having same index p.
As is well known, molecular hydrogen exists in two types, depending whether the nuclear spins are in a singlet state (para-H2) or in a triplet state (ortho-H2). Their thermodynamic properties are only significantly different at very low temperatures (where the para form is energetically favored). Since the simulation of ortho-H2 is plagued by a sign problem that would make Monte Carlo sampling much more laborious, in this work we limited ourselves to considering para-H2 only. Details on the method can be found in Ref. 22 for the rigid case and in Ref. 34 for the flexible case.
In our calculations, we evaluated the integral in Eq. (5) using the VEGAS algorithm36 with 10 000 integration points. In evaluating the average 〈⋯〉 for each value of the sampled coordinate R, we used 12 independent ring-polymer configurations for each of the molecules a and b. These configurations were sampled with a dedicated Monte Carlo routine, which included uniformly distributed random overall rotations. The path-integral mapping is exact in the limit P → ∞. In practice, however, a finite value of P is sufficient to reach converged results. The value of P for which convergence is reached depends on the specific system and model under consideration, as well as on the temperature of the simulation and the required accuracy of the calculation; P is in general higher when quantum effects are more pronounced (usually, when the temperature decreases and for smaller masses).
In the case of rigid rotors, we observed well converged results by choosing P as a function of the temperature T according to the relation P = (2800 K)/T + 7. In the case of flexible molecules, however, the “quantumness” of the system is largely determined by the fact that atoms are confined in molecules. In the H2–CO system, the requirement to properly describe the quite extensive zero-point motion of hydrogen atoms confined in H2 molecules makes the dependence of P on the temperature less pronounced. We observed convergence in the results by taking P = 48, independent of the temperature. In all cases, B(T) was calculated by analyzing the results of 16 independent simulations at each temperature.
The Utot,15 PES described in Section II was used in PIMC calculations. Since a calculation of virial coefficients (unlike the scattering calculations reported in Ref. 18) requires evaluation of the potential at all values of R, care had to be taken regarding the short-range behavior of V15 (and, consequently, Utot,15), which may become unphysical at very small values of R. V15 was developed using grid points down to R ≥ 4.5 bohr, but as described in Sec. II D, it behaves reasonably (increasing positive values with decreasing R) for R > 3.5 bohr. Further investigation revealed that if r and s are close to rc and sc, respectively, which is the case in construction of all 4D surfaces derived from V15 and studied here, the resulting surfaces can be used for any point with R ≥ 0.15 nm ≈ 2.8 bohr. At shorter R, we imposed a hard core. For the fully flexible calculations, criteria based on atomic positions are necessary; our cutoffs in this case were 0.1 nm for the C-H distance and 0.09 nm for the O-H distance, with a hard core imposed if either distance was smaller than the cutoff.
IV. Results and Discussion
A. Virials from full-dimensional calculations
In Table VI, we give values of B12 calculated from Utot,15 as described above over the temperature range from 10 K to 2000 K. The expanded uncertainty U(B12) (coverage factor k = 2, approximately corresponding to a 95% confidence interval) has two contributions. The first results from the uncertainty in the pair potential. To get this contribution, we calculated B12 for the “plus” and “minus” perturbations of V15, obtained by adding and subtracting the uncertainty described in Sec. II C. We assume these perturbed potentials to correspond to an expanded (k = 2) uncertainty. The contribution to the expanded uncertainty is then simply half the difference between B12 calculated from the “plus” and “minus” potentials. The second contribution comes from the statistical uncertainty in the PIMC calculations. These two contributions are added in quadrature to obtain U(B12). At the conditions investigated here, the uncertainty in the pair potential is the dominant contribution to the overall uncertainty.
Table VI.
Calculated values of B12 (in cm3/mol) as a function of temperature T, calculated with the fully flexible model Utot,15 = V15 + VH2 + VCO and at various levels of approximation. All calculations use PIMC except for the classical (cl) and semiclassical (semi) results reported in the last two columns. The expanded uncertainty U(B12) in the third column, in cm3/mol and reported with coverage factor k = 2, is for the fully flexible calculation and incorporates both contributions from the uncertainty of the pair potential and the statistical uncertainty of the PIMC calculation.
| T (K) | V15 +VH2 +VCO | U(B12) | V15(re) | V15(r0) | 〈V15〉0 | 〈V15〉T | 〈V15〉0 (cl) | 〈V15〉0 (semi) |
|---|---|---|---|---|---|---|---|---|
| 10 | −4296 | 313 | −4132 | −4572 | −4518 | −4519 | −101765 | −1325 |
| 15 | −1364 | 68.2 | −1343 | −1445 | −1434 | −1434 | −5819 | −616 |
| 20 | −722.9 | 30.5 | −712.0 | −757.6 | −752.4 | −752.0 | −1684.4 | −491.0 |
| 25 | −470.9 | 17.2 | −461.6 | −487.6 | −485.3 | −485.0 | −834.2 | −387.4 |
| 30 | −339.2 | 11.4 | −331.8 | −349.4 | −347.8 | −347.8 | −521.5 | −307.0 |
| 40 | −207.2 | 6.5 | −202.3 | −212.4 | −211.4 | −211.5 | −277.8 | −203.3 |
| 50 | −142.8 | 4.6 | −138.7 | −145.5 | −144.9 | −144.9 | −179.2 | −143.7 |
| 60 | −104.3 | 3.7 | −101.3 | −106.4 | −105.9 | −105.9 | −126.9 | −106.3 |
| 80 | −61.61 | 2.46 | −59.50 | −62.80 | −62.52 | −62.51 | −72.78 | −63.37 |
| 100 | −38.67 | 1.85 | −36.98 | −39.35 | −39.17 | −39.17 | −45.38 | −39.82 |
| 125 | −21.68 | 1.47 | −20.32 | −22.04 | −21.86 | −21.91 | −25.78 | −22.33 |
| 150 | −11.04 | 1.15 | −9.88 | −11.20 | −11.09 | −11.10 | −13.81 | −11.40 |
| 175 | −3.81 | 1.00 | −2.84 | −3.89 | −3.80 | −3.81 | −5.80 | −3.99 |
| 200 | 1.44 | 0.88 | 2.24 | 1.37 | 1.46 | 1.41 | −0.15 | 1.30 |
| 225 | 5.38 | 0.74 | 6.03 | 5.28 | 5.37 | 5.33 | 4.06 | 5.24 |
| 250 | 8.40 | 0.69 | 8.93 | 8.30 | 8.38 | 8.33 | 7.28 | 8.29 |
| 275 | 10.75 | 0.62 | 11.22 | 10.69 | 10.76 | 10.71 | 9.84 | 10.68 |
| 300 | 12.70 | 0.59 | 13.06 | 12.60 | 12.68 | 12.64 | 11.86 | 12.61 |
| 350 | 15.51 | 0.50 | 15.82 | 15.47 | 15.53 | 15.50 | 14.88 | 15.48 |
| 400 | 17.48 | 0.46 | 17.75 | 17.46 | 17.52 | 17.49 | 17.01 | 17.49 |
| 450 | 18.91 | 0.41 | 19.13 | 18.92 | 18.96 | 18.94 | 18.53 | 18.94 |
| 500 | 20.00 | 0.38 | 20.16 | 19.99 | 20.04 | 20.01 | 19.66 | 20.01 |
| 600 | 21.43 | 0.32 | 21.53 | 21.42 | 21.46 | 21.45 | 21.17 | 21.45 |
| 700 | 22.27 | 0.31 | 22.33 | 22.28 | 22.31 | 22.29 | 22.10 | 22.30 |
| 800 | 22.79 | 0.28 | 22.81 | 22.78 | 22.82 | 22.81 | 22.65 | 22.82 |
| 900 | 23.10 | 0.26 | 23.09 | 23.09 | 23.12 | 23.12 | 22.96 | 23.12 |
| 1000 | 23.28 | 0.27 | 23.24 | 23.26 | 23.30 | 23.28 | 23.15 | 23.28 |
| 1200 | 23.39 | 0.23 | 23.30 | 23.35 | 23.37 | 23.39 | 23.26 | 23.37 |
| 1400 | 23.30 | 0.20 | 23.19 | 23.26 | 23.27 | 23.29 | 23.20 | 23.28 |
| 1600 | 23.09 | 0.22 | 22.99 | 23.07 | 23.09 | 23.12 | 23.01 | 23.09 |
| 1800 | 22.87 | 0.22 | 22.75 | 22.83 | 22.85 | 22.90 | 22.78 | 22.85 |
| 2000 | 22.64 | 0.20 | 22.48 | 22.58 | 22.59 | 22.65 | 22.54 | 22.59 |
B. Virials from approximate treatments
In previous work on hydrogen,34 we described several levels of approximation to the full 6D PES that one might consider to simplify the calculation of B12. Results from these approximations are given in Table VI.
First, we consider a rigid-rotor model in which flexibility is completely ignored by fixing the intramolecular bond lengths at their equilibrium values re and se. We denote this potential as V15(re) and the resulting B12 are tabulated in Table VI.
Second, we consider the potential V15(r0), in which we fix the bond lengths at the values r0 and s0 obtained as the expectation values over the ground-state rovibrational wave functions. As argued for the first time in Ref. 37, monomers are on average in their average geometries, rather than in their equilibrium geometries, so a better agreement with experiment or with all-dimensional theory should be obtained using such averaged geometries.
Third, we consider the surface 〈V15〉0, proposed originally in Ref. 38, obtained by averaging the full-dimensional interaction energy over the product of ground-state rovibrational wave functions of the two monomers. 〈V15〉0 is a 4D potential (same dimensionality as rigid-rotor potential), but it does not correspond to any fixed values of (r, s). A PES averaged in this way was shown in Ref. 38 to perform better compared to full-dimensional calculations than a reduced-dimensionality potential computed at r0.
Finally, we consider the “improved rigid rotor” surface 〈V15〉T, which we have used previously22,34 for the H2 dimer. This surface is like 〈V15〉0, except that the monomer wave functions used in averaging over intramonomer coordinates are not only the ground-state wave functions, but instead are the full set of monomer rovibrational wave functions (more accurately, all those contributing beyond a small threshold of significance) weighted according to their Boltzmann factors at the temperature of the calculation. In the low-temperature limit, 〈V15〉T reduces to 〈V15〉0, but it should be more accurate at higher temperatures where excitations above the ground state become important.
In order to examine the magnitude of quantum effects and the adequacy of a first-order treatment of those effects, the last two columns of Table VI contain results from a classical calculation and from a semiclassical calculation of B12(T). For the semiclassical calculation, we use the effective potential approach of Takahashi and Imada,39 implemented as described by Schenter,40 the same methods as used in the calculations of Ref. 23. Both the classical and semiclassical calculations are performed with the potential 〈V15〉0, so it is that column in the table to which those approximations should be compared.
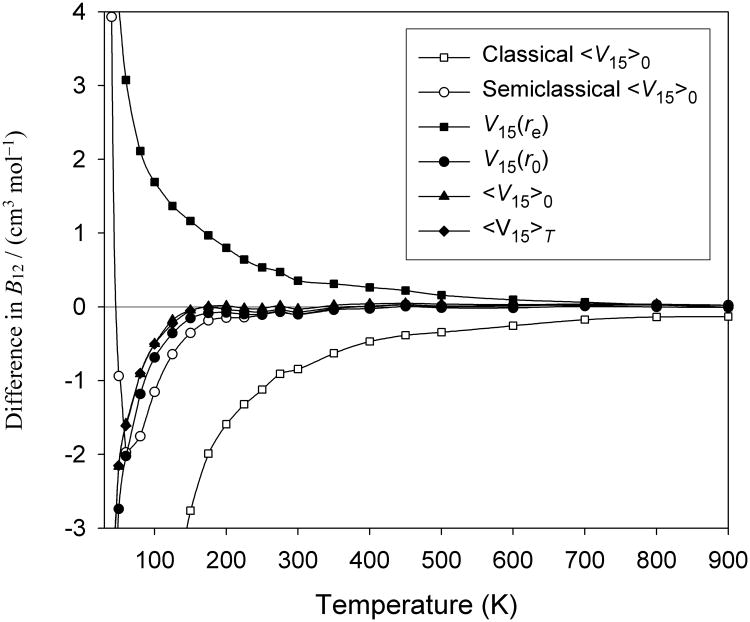
In Table VI and in Fig. 2, we see that the three 4D approaches that incorporate flexibility in some way, V15(r0), 〈V15〉0, and 〈V15〉T, give virials very close to each other and to the rigorous 6D calculation at most of the temperatures studied. Below about 125 K, the approximations begin to underestimate the fully flexible result, but in relative terms these errors are still small, reaching a maximum at 10 K of about 5% for 〈V15〉0 and 〈V15〉T and a little over 6% for V15(r0). These deviations at lower temperatures are probably due to increased importance of quantum effects. Quantum calculations explore PESs globally and can be expected to be sensitive to actual couplings of inter- and intramolecular degrees of freedom which are only present in Utot,15. As expected, the “improved rigid rotor” approach 〈V15〉T is better at high temperatures where excited rovibrational states are more populated, but the improvement over 〈V15〉0 and even over the rigid-rotor surface V15(r0) is only slight, because those simpler 4D surfaces already produce quite accurate B(T) as can be seen in Fig. 2. Also as expected, the error of B(T) computed from the potential V15(re), in which vibrational motion in monomers is completely ignored by fixing the bond lengths at their equilibrium values, is larger than the errors of the approximations that incorporate these vibrations in some way.
Fig. 2.
Deviations of approximate virials from the virials computed using the full-dimensional approach with flexible potential Utot,15.
The classical approximation with the 〈V15〉0 potential agrees very well with the full-quantum calculations using the same potential for T > 1000 K. For lower T, the agreement gradually deteriorates, but it is still good down to about 500 K, and is reasonable down to perhaps 200 K. The semiclassical approach is much better, with near-perfect agreement above 200 K and still very good agreement (within about 1 cm3/mol) down to about 50 K, finally producing large errors below about 30 K.
We have also compared with virials computed from the 4D potentials V04 from Ref. 41 and V12 of Ref. 16, fully accounting for quantum effects with PIMC. The agreement with values obtained from our present rigid-rotor potential V15(r0) is excellent (within 0.5% except near where B(T) crosses zero) throughout the entire range of temperatures. This shows that the improvements of the level of ab initio theory since 2004 lead to negligible changes of virials. The improvement made since that time was almost entirely due to the increased dimensionality and complete accounting for quantum effects.
Finally, we note that, to our knowledge, the semiclassical approach can only be applied to the 4D potentials; see a derivation of this approach in Ref. 23. Incorporation of flexibility, which is inherently a quantum effect, requires the PIMC method. Therefore, the semi-classical approach is only a viable simplification if the 〈V15〉0 approximation or the 〈V15〉T approximation is considered to be adequate.
C. Comparison with experimental data
B12 cannot be measured directly; it is inferred from experiments with mixtures and knowledge of the pure-component values B11 and B22. When necessary in our data analysis, we used values of B from the equation of state of Leachman et al.42 for H2 and of Lemmon and Span43 for CO.
Brewer12 measured the “excess” second virial coefficient at 0 °C, defined as the difference between B12 and the arithmetic mean of the pure-component second virials:
| (6) |
can be obtained by measuring the pressure change upon mixing equal volumes of pure gases at constant temperature (or the volume change upon mixing at constant temperature and pressure). Brewer converted his measured value of to B12 = 10.13 cm3 mol−1, but current values of the pure-component virials yield B12 = 9.7 cm3 mol−1. Between the uncertainty of the experiments and of the pure-component virials, the uncertainty of this value of B12 is probably on the order of 1–2 cm3 mol−1. Michels and Boer-boom11 performed a volume-of-mixing experiment at 25 °C whose result is equivalent to , yielding B12 = 12.6 cm3 mol−1; the uncertainty in B12 is probably similar to that for Brewer's result.
Dymond and Smith44 analyzed the volumetric data for H2–CO mixtures of three different compositions taken by Scott9 at 25 °C and by Townend and Bhatt10 at 0 °C and 25 °C. The resulting values of B12 scattered over approximately 2 cm3 mol−1; we used the average in our comparisons.
Schramm et al.13 used an expansion technique to derive B12 at four temperatures from 77.3 K to 213.15 K. It appears that their values were obtained by a relative technique with the room-temperature results of Townend and Bhatt10 as derived by Dymond and Smith44 used as a baseline.
It is also possible to extract B12 from data for the solubility of solid CO in gaseous H2 at moderate pressure, as described previously for the He–H2 system.45 The solubility measurements of Dokoupil et al.8 were analyzed by Reuss and Beenakker,46 who derived B12 at seven temperatures from 36 K to 60 K. The measurements of Verschoyle7 were mostly at pressures too high for analysis at the second virial level to be appropriate, but we were able to derive three values at approximately 63 K and one value at approximately 58 K.
In principle, the measurements of hydrogen fugacity in H2–CO mixtures of varying compositions by Bruno and Schroeder14 from 403 K to 463 K could yield B12. However, our analysis of these measurements found widely different B12 at different compositions, which is unphysical and indicates that these data are not precise enough to use for the purpose of deriving B12. The density data of Cipollina et al.15 are at pressures too high to be able to extract virial coefficients.
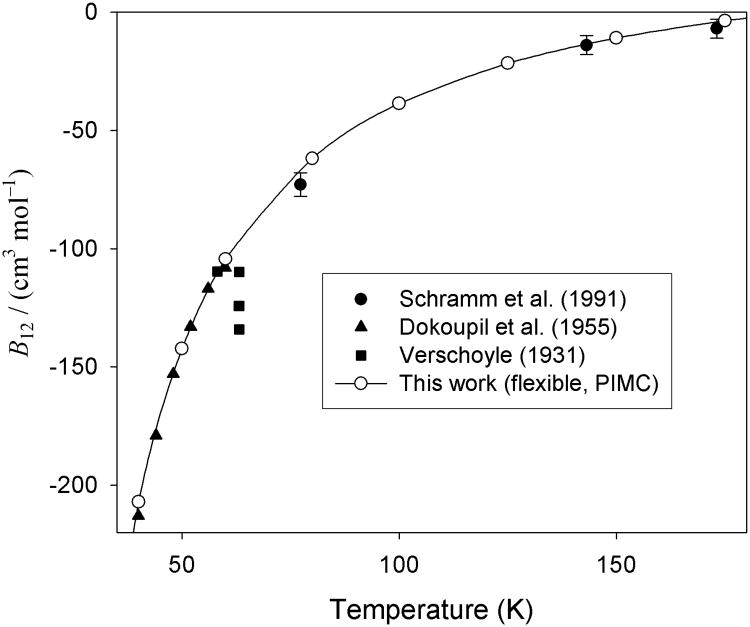
In Fig. 3, we plot our calculated results along with the available experimental data at cryogenic temperatures. Error bars are plotted for those data sources where uncertainties were reported or could be estimated from the information given in the reference. The uncertainties in our results (see Table VI) are smaller than the symbols on the plot for all but the four lowest temperatures. We do not plot the various simplifying approximations discussed above, because the differences would be too small to see on the scale of the plot. Agreement with the B12(T) data of Dokoupil et al.8 and Schramm et al.13 is excellent, and the calculated results are at least consistent with the more scattered data of Verschoyle.7
Fig. 3.
Values of B12 for H2 with CO at low temperatures, calculated with full consideration of flexibility and quantum effects with the PIMC approach, and compared with experimental data. Uncertainties for the calculations are smaller than the size of the symbols except for the four lowest temperatures. The virials computed from the V15(r0) potential are not shown since they would be nearly indistinguishable from those computed from the Utot,15 potential.
The B12 datum near 77 K reported by Schramm et al.13 has been problematic for theory. Although estimates both from theory and from comparisons with spectral data suggested uncertainties of the V04 PES of the order of 1 cm−1 in the well region, in order to get agreement with this datum (which was the lowest temperature experimental virial used in that comparison), the PES had to be scaled by a factor of 1.042 which implies a 4 cm−1 error at the minimum. In 2012, Chefdeville et al.47 had to use a similar scaling to obtain agreement with their scattering data. However, at about the same time, two of us and coworkers demonstrated16,17 that the estimate of the uncertainty of the V04 PES was correct and no scaling was needed. Indeed, later it was found48 that the discrepancies seen in Ref. 47 were due to an experimental error. The authors of Ref. 17 wrote that the difference between their B12 calculated semiclassically and the datum of Schramm et al.13 near 77 K may be due to inadequacy of the semiclassical calculation of quantum effects at low temperatures. This opinion was supported by the fact that for the H2–H2 dimer at 75 K the fully quantum result is by a factor 1.25 larger in magnitude than the semiclassical one.33 Our results do not support that conjecture. In Table VI, it can be seen that the difference between the semiclassical result and the fully quantum PIMC result is still small at 77 K, only about 1 cm3/mol, and in fact that fully incorporating quantum effects shifts the calculated B12 slightly further away from that datum, resulting in a discrepancy of about 5 cm3/mol. In conjunction with the other results shown in Fig. 3, we believe it is likely that this reported experimental point was slightly too low, and/or had greater uncertainty than the authors estimated. However, the two results are consistent to within mutual uncertainties.
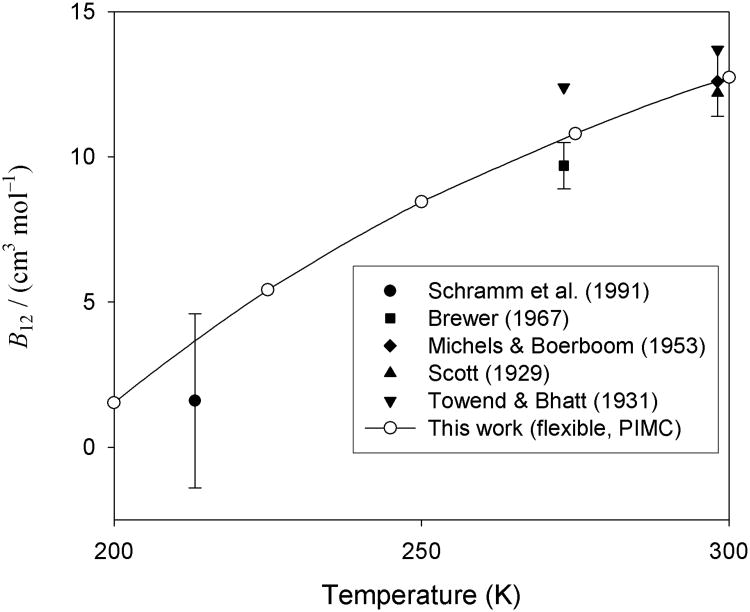
Figure 4 similarly compares our calculations to experimental data at higher temperatures, including near room temperature where there have been several investigations. Once again, our results are consistent with the experimental data but have smaller uncertainties. In Fig. 4, we did not plot the curves for the virials obtained with the V15(r0), 〈V15〉0, and 〈V15〉T PESs, since these curves would be indistinguishable from the one shown in the plotted range of temperatures (cf. Fig. 2).
Fig. 4.
Values of B12 for H2 with CO at high temperatures, calculated with full consideration of flexibility and quantum effects with the PIMC approach, and compared with experimental data. The virials computed from the V15(r0) potential are not shown since they would be nearly indistinguishable from those computed from the Utot,15 potential.
D. Comparison with potential of Yang and coworkers
We also attempted to perform calculations of B12(T) with the recent VY pair potential of Yang et al.19,20 We found this to be impossible for two reasons. The first problem is with the long-range behavior of that potential, which fails to decay to zero at long range if the intramolecular distances r and s differ from their equilibrium values.
The second issue is more subtle. The potential of Yang et al.19,20 was fitted for values of r between 1.01 and 1.81 bohr, which was adequate for their scattering calculations. However, the flexible calculation of B12(T) requires evaluating the potential over the entire probability distribution for the bond lengths of the H2 and CO molecules. Because of the highly quantum nature of the H atom, even for the ground-state vibration the fraction of states outside the limits of the VY potential is several percent (a similar issue arises with the 6D potential of Ref. 16; this was part of the motivation for developing V15 which covers a wider range of r). In order to avoid evaluating the potential of Yang et al. at conditions where it is not valid, we consider it in a four-dimensional form similar to our V15(r0), as rigid rotors with the intramolecular distances fixed at r0 and s0, denoted as VY(r0).
The problem with the long-range behavior of the potentials of the type used by Yang et al. is well known.49 In order to correct it, we constructed a combination potential in which VY(r0) was used at short and medium distances, but V15(r0) was used when the intermolecular distance R exceeded 9 bohr. We refer to this asymptotically corrected potential as VY,AC(r0).
Points calculated with the PIMC method from VY,AC(r0) are plotted on Figs. 3 and 4. It can be seen that VY,AC(r0) overestimates B12 throughout the temperature range by an amount that, while not too large, is clearly inconsistent with our results and with the available experimental data. The discrepancy is not due to the approximation of the potential of Yang et al. by a 4D form; comparison of the V15 and V15(r0) columns in Table VI shows that full inclusion of flexibility would make B12 slightly more positive (less negative), which is the opposite direction from that needed to reconcile the VY,AC(r0) results with experiment.
After analyzing the behavior of VY,AC(r0) in comparison to V15, cf. Table IV, we believe the reason for the discrepancy is that the potential of Yang et al.19,20 gives interaction energies that lie too high (too positive or insufficiently negative) at most configurations. This was already noted by Faure et al.18 for the minimum-energy configuration, where the difference was attributed to the lower level of theory used by Yang et al. Now we see from Table IV that inaccuracy in the fit also contributes to this deviation. The relative differences between our B(T) and that calculated from Yang's et al. potential are larger than the comparison of Table IV might suggest. The reason is that in the region very close to the minimum the agreement is better than in other regions (there are points with negative interaction energies where discrepancies exceed 30 cm−1.)
V. Conclusions
A flexible (six-dimensional) potential for the interaction of H2 and CO developed at a high level of theory [up to CCSDT(Q)] and with large basis sets has been analyzed to determine its uncertainties. Using the results from Ref. 16, performing additional calculations, and analyzing the errors of the fit, we determined the uncertainties to be about 0.8% for the monomers near equilibria, increasing to about 8% for monomers at their maximum deformations. The range of monomer bond lengths included in the set of grid points for the ab initio calculations was sufficiently wide to support the quantum-mechanical probability distribution of intramolecular distances (which is wider than that of the corresponding classical vibration, especially for H2). This feature is important to avoid spurious results in PIMC calculations that incorporate flexibility. Similarly, the range of R values that the analytic fit is valid for was determined.
The agreement of full-dimensional calculations with most of the available experimental virial coefficients is excellent, and theoretical virials have generally smaller uncertainties than virials from these experiments. For all the experimental virials published with uncertainties, the experimental and theoretical error bars overlap or nearly overlap. We believe that the theoretical virials can be the benchmark data for modeling gas-phase thermodynamics in these systems. The few experimental data points that do not agree well with theory also disagree with other data, and probably have unrecognized errors. The excellent agreement with a large subset of data also confirms the high accuracy of the V15 potential.
We have examined the performance of various approximations of our procedures. The low-energy scattering results reported for V15 by Faure et al.18 established that the four-dimensional 〈V15〉0 potential was adequate to reproduce low-energy scattering data. In the present work, we have established a similar result for the interaction second virial coefficient B12. The 〈V15〉0 potential produces second virial coefficients that remain within uncertainties of the fully flexible quantum treatment except at very low (below 50 K) temperatures. We explain the larger discrepancies at very small T by the overwhelming quantum character of virials in that regime. The use of the simpler 4D potentials V15(r0) and V15(re) result in larger discrepancies, but V15(r0) performs almost as well as 〈V15〉0, in contrast to the performance on spectra.38 The fact that the reduced dimensionality approaches give satisfactory agreement with experiment is an important finding, since for larger molecules full-dimensional treatment is not possible at the present time. We have also compared our virials to those computed using the potentials V0429 and V1216 and found that the latter virials are in very good agreement with those computed from 〈V15〉0. This shows that the increased levels of ab initio theory applied in development of consecutive potentials do not bring significant improvements in accuracy of virials with the present accuracies of experiments. Furthermore, a semiclassical calculation of the second virial coefficient from 〈V15〉0 is sufficient to account for quantum effects as long as the temperature is not below approximately 50 K.
Supplementary Material
Acknowledgments
This work was partly supported by the National Science Foundation (NSF) Grant CHE-1566036. G.G. acknowledges support from FBK via the Mobility programme. The calculations of the virial coefficients were performed on the KORE computing cluster at Fondazione Bruno Kessler.
Footnotes
Partial contribution of the National Institute of Standards and Technology, not subject to copyright in the United States
Supplementary Material: See supplementary material for a FORTRAN routine that calculates the V15 PES and a sample program using it.
References
- 1.Figueroa JD, Fout T, Plasynski S, McIlvried H, Srivastava RD. Int J Greenhouse Gas Control. 2008;2:9. [Google Scholar]
- 2.Kapetaki Z, Ahn H, Brandani S. Energy Procedia. 2013;27:2196. [Google Scholar]
- 3.Harvey AH. Tech Rep 1015542. Electric Power Research Institute; Palo Alto, CA: 2008. Thermodynamic data to support high-temperature syngas quench design: Vapor-liquid equilibrium calculations. [Google Scholar]
- 4.Tsang CY, Street WB. Fluid Phase Equilib. 1981;6:261. [Google Scholar]
- 5.Hong JH, Kobayashi R. Adv Cryo Eng. 1982;27:849. [Google Scholar]
- 6.Kremer H, Knapp H. Fluid Phase Equilib. 1983;11:289. [Google Scholar]
- 7.Verschoyle TTH. Phil Trans R Soc London A. 1931;230:189. [Google Scholar]
- 8.Dokoupil Z, Soest GV, Swenker MDP. Appl Sci Res A. 1955;5:182. [Google Scholar]
- 9.Scott GA. Proc R Soc London A. 1929;125:330. [Google Scholar]
- 10.Townend DTA, Bhatt LA. Proc R Soc London A. 1931;134:502. [Google Scholar]
- 11.Michels A, Boerboom AJH. Bull Soc Chim Belg. 1953;62:119. [Google Scholar]
- 12.Brewer J. Tech Rep 67-2795. AFOSR; 1967. Determination of mixed virial coefficients. [Google Scholar]
- 13.Schramm B, Elias E, Kern L, Natour G, Schmitt A, Weber C. Ber Bunsenges Phys Chem. 1991;95:615. [Google Scholar]
- 14.Bruno TJ, Schroeder JA. Int J Thermophys. 1988;9:525. [Google Scholar]
- 15.Cipollina A, Anselmo R, Scialdone O, Filardo G, Galia A. J Chem Eng Data. 2007;52:2291. [Google Scholar]
- 16.Jankowski P, Surin LA, Potapov AV, Schlemmer S, Mc Kellar ARW, Szalewicz K. J Chem Phys. 2013;138:084307. doi: 10.1063/1.4791712. [DOI] [PubMed] [Google Scholar]
- 17.Jankowski P, McKellar ARW, Szalewicz K. Science. 2012;336:1147. doi: 10.1126/science.1221000. [DOI] [PubMed] [Google Scholar]
- 18.Faure A, Jankowski P, Stoecklin T, Szalewicz K. Sci Reports. 2016;6:28449. doi: 10.1038/srep28449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yang B, Zhang P, Wang X, Stancil PC, Bowman JM, Balakrishnan N, Forrey RC. Nature Comm. 2015;6:6629. doi: 10.1038/ncomms7629. [DOI] [PubMed] [Google Scholar]
- 20.Yang B, Balakrishnan N, Zhang P, Wang X, Bowman JM, Forrey RC, Stancil PC. J Chem Phys. 2016;145:034308. doi: 10.1063/1.4958951. [DOI] [PubMed] [Google Scholar]
- 21.Leforestier C, Szalewicz K, van der Avoird A. J Phys Chem. 2012;137:014305. doi: 10.1063/1.4722338. [DOI] [PubMed] [Google Scholar]
- 22.Garberoglio G, Jankowski P, Szalewicz K, Harvey AH. J Chem Phys. 2012;137:154308. doi: 10.1063/1.4757565. [DOI] [PubMed] [Google Scholar]
- 23.Jankowski P, Murdachaew G, Bukowski R, Akin-Ojo O, Leforestier C, Szalewicz K. J Phys Chem A. 2015;119:2940. doi: 10.1021/jp512847z. [DOI] [PubMed] [Google Scholar]
- 24.Kendall RA, Dunning TH, Jr, Harrison RJ. J Chem Phys. 1992;96:6796. [Google Scholar]
- 25.Halkier A, Klopper W, Helgaker T, Jørgensen P, Taylor PR. J Chem Phys. 1999;111:9157. [Google Scholar]
- 26.Pachucki K. Phys Rev A. 2010;82:032509. [Google Scholar]
- 27.Le Floch A. Mol Phys. 1991;72:133. [Google Scholar]
- 28.Song L, van der Avoird A, Groenenboom GC. J Phys Chem A. 2013;117:7571. doi: 10.1021/jp402470b. [DOI] [PubMed] [Google Scholar]
- 29.Jankowski P. J Chem Phys. 2004;121:1655. doi: 10.1063/1.1766293. [DOI] [PubMed] [Google Scholar]
- 30.Noga J, Kallay M, Valiron P. Mol Phys. 2006;104:2337. [Google Scholar]
- 31.Komasa J, Thakkar AJ. Mol Phys. 1993;78:1039. [Google Scholar]
- 32.Szalewicz K, Jeziorski B. J Chem Phys. 1998;109:1198. [Google Scholar]
- 33.Patkowski K, Cencek W, Jankowski P, Szalewicz K, Mehl J, Garberoglio G, Harvey AH. J Chem Phys. 2008;129:094304. doi: 10.1063/1.2975220. [DOI] [PubMed] [Google Scholar]
- 34.Garberoglio G, Jankowski P, Szalewicz K, Harvey AH. J Chem Phys. 2014;141:044119. doi: 10.1063/1.4890440. [DOI] [PubMed] [Google Scholar]
- 35.Hirschfelder JO, Curtiss CF, Bird RB. Molecular Theory of Gases and Liquids. John Wiley & Sons; 1954. [Google Scholar]
- 36.Lepage GP. VEGAS: An adaptive multi-dimensional integration program. 1980 Tech Rep (Cornell preprint CLNS 80-447. [Google Scholar]
- 37.Mas EM, Szalewicz K. J Chem Phys. 1996;104:7606. [Google Scholar]
- 38.Jeziorska M, Jankowski P, Szalewicz K, Jeziorski B. J Chem Phys. 2000;113:2957. [Google Scholar]
- 39.Takahashi M, Imada M. J Phys Soc Jpn. 1984;53:3765. [Google Scholar]
- 40.Schenter GK. J Chem Phys. 2002;117:6573. [Google Scholar]
- 41.Jankowski P, Szalewicz K. J Chem Phys. 2005;123:104301. doi: 10.1063/1.2008216. [DOI] [PubMed] [Google Scholar]
- 42.Leachman JW, Jacobsen RT, Penoncello SG, Lemmon EW. J Phys Chem Ref Data. 2009;38:721. [Google Scholar]
- 43.Lemmon EW, Span R. J Chem Eng Data. 2006;51:785. [Google Scholar]
- 44.Dymond JH, Smith EB. The Virial Coefficients of Pure Gases and Mixtures. Clarendon Press; Oxford: 1980. [Google Scholar]
- 45.Garberoglio G, Patkowski K, Harvey AH. Int J Thermophys. 2014;35:1435. [Google Scholar]
- 46.Reuss J, Beenakker JJM. Physica. 1956;22:869. [Google Scholar]
- 47.Chefdeville S, Stoecklin T, Bergeat A, Hickson KM, Naulin C, Costes M. Phys Rev Lett. 2012;109:023201. doi: 10.1103/PhysRevLett.109.023201. [DOI] [PubMed] [Google Scholar]
- 48.Chefdeville S, Stoecklin T, Naulin C, Jankowski P, Szalewicz K, Faure A, Costes M, Bergeat A. Astrophys J Lett. 2015;799:L9. [Google Scholar]
- 49.Braams BJ, Bowman JM. Int Rev Phys Chem. 2009;28:577. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.