ModelFinder: Fast Model Selection for Accurate Phylogenetic Estimates

Abstract

Model-based molecular phylogenetics plays an important role in comparisons of genomic data, and model selection is a key step in all such analyses. We present ModelFinder, a fast model-selection method that greatly improves the accuracy of phylogenetic estimates. The improvement is achieved by incorporating a model of rate-heterogeneity across sites not previously considered in this context, and by allowing concurrent searches of model-space and tree-space.

Model-based molecular phylogenetic analysis plays a key role in comparative genomics and evolutionary biology, allowing us to annotate genomes more accurately¹, test our understanding of the evolution of species, genomes and genes^2–6, and determine the likely origins and routes of dispersal of pathogens and pests^7,8. Selecting an optimal model of sequence evolution (SE) is a critical step in all such analyses. Here we introduce ModelFinder, a model-selection method that combines substitution models used in other popular model-selection methods^9,10 with a flexible rate-heterogeneity-across-sites (RHAS) model, and show that its use often leads to substantial improvements in the fit between tree, model and data.

Model selection is used to identify the best-fitting model of SE that led to the available data. Several methods for doing so are available for DNA⁹ and protein¹⁰. It is even possible to do so when different models are required for analysis of different sets of sites in an alignment¹¹.

Finding an optimal model of SE for a given sequence alignment entails finding the best-fitting substitution model and the best-fitting model of RHAS. Usually, this means comparing three models of RHAS that assume: (i) all sites evolved at the same rate, (ii) some sites evolved at the same rate whilst the others were invariable (I), or (iii) RHAS follows a probability distribution, like the popular discrete Γ distribution¹².

The discrete Γ distribution is parameterized using k rate categories, each comprising a rate (r_i) and a weight (w_i), where r_i > 0, w_i = 1/k, and $1={\Sigma }_{i=1}^k{r}_i{w}_i.$ Doing so imposes two constraints on the model: it is assumed RHAS can be modeled accurately by a Γ distribution, and that the probability that a site belongs to rate category i equals 1/k. These assumptions may be unrealistic and bias phylogenetic estimates.

One solution to this problem is to infer the weights from the data, as proposed by Yang¹³. The advantage offered by this probability-distribution-free (PDF) model of RHAS is that the distribution of rates-of-change across sites may take any shape, implying that estimates of rates and weights should be more accurate than those obtained under a Γ distribution. Until now, however, the PDF model was not available in the context of model selection.

To meet this need, we developed ModelFinder, a model-selection method for alignments of nucleotides, codons, amino acids, or other discrete data. ModelFinder is implemented in IQ-TREE¹⁴ and offers many features, including the choice of comparing models of SE inferred on the same tree (default) or on different trees (advanced). When the advanced option is used, ModelFinder searches tree space for every model of SE considered and, therefore, may find superior models of SE. ModelFinder incorporates 22 and 36 substitution models for DNA and protein, respectively, and 13 models of RHAS, including the PDF model with k = 2, … , k_max rate categories. By default, k_max = 10 but it can be increased if needed. Each PDF model, henceforth labelled R_k, is a family of RHAS models. The user can also specify the numbers and types of models to compare. In summary, ModelFinder considers models of RHAS that are more complex than those considered by other model-selection methods^9–11.

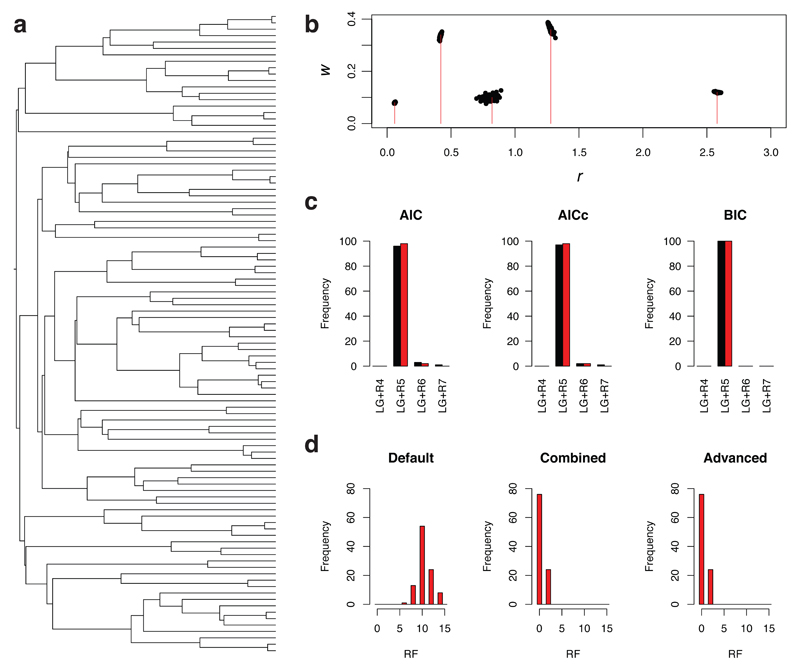
The PDF model is more parameter-rich than the discrete Γ model, so parameter estimation is a challenge. To tackle this challenge, ModelFinder uses the expectation-maximization (EM) algorithm¹⁵ to estimate the parameters for every R_k model, and an algorithm to identify the optimal value of k for the PDF model (Online Methods). The accuracy of ModelFinder was assessed by analysis of 100 amino-acid alignments generated on a 100-tipped tree (Fig. 1a). Alignments with 10,000 sites were generated using INDELible¹⁶ and the LG¹⁷+R₅ model of SE. A bimodal distribution of RHAS was used. Figure 1b shows that ModelFinder estimated the model parameters accurately when the data were analyzed using the correct tree and model. Figure 1c shows that ModelFinder is accurate regardless of the optimality criterion (AIC, AICc, or BIC) and search option (default or advanced) used. When AIC or AICc were used, a 2-3% bias towards more parameter-rich RHAS models was found. The high success rate of BIC is noteworthy because the optimal model of SE was inferred even when the best tree found differed from the true tree. Figure 1d shows the distribution of Robinson-Foulds (RF) distances¹⁸ between the true tree and: (a) the parsimony tree (found using the default search option), (b) the tree inferred using the best model of SE found using the default search option, and (c) the tree found using the advanced search option. The RF distances ranged from 0 to 14, implying, in the best cases, that the trees were identical and, in the worst cases, that 7 of the 97 internal edges differed between the trees. In summary, ModelFinder is accurate and can identify models of SE that other model-selection methods are unable to detect.

Figure 1. Assessment of the accuracy of phylogenetic estimates obtained using ModelFinder.

(a) The rooted 100-tipped tree, with a root-to-tip distance of 0.5 substitutions/site, that was used to generate the simulated data. (b) Plot showing the true values of r_i and w_i (red lines; r_i = (0.06, 0.42, 0.82, 1.28, 2.58) and w_i = (0.08, 0.34, 0.10, 0.36, 0.12)) and the estimated values of (r_i, w_i) for the 100 simulated data sets (black dots). (c) Histograms showing the number of times different models of SE were identified under different criteria (AIC, AICc and BIC) using the default (black) and advanced (red) search options. (d) Graphs showing the distribution of Robinson-Foulds (RF) distances between the true tree and (a) the tree used during the default model search (Default), (b) the tree found, given the optimal model of SE found using the default model-search option (Combined), and (c) the tree found during the advanced model search (Advanced) (the BIC optimality criterion was used in this example).

The benefits of using ModelFinder are illustrated with an analysis of the alignment of amino acids that formed the basis for a genomic encyclopedia of Bacteria and Archaea¹⁹. The data were originally analyzed using the WAG+I+Γ₅ model. The optimal model of SE was the same (LG+R₁₄) for the two search options but the advanced option led to a better-parameterized model (BIC = 3,855,048) than the default option (BIC = 3,858,039) (when BIC scores differ by more than 10 (ΔBIC > 10) there is strong evidence against the model with the higher BIC score²⁰). The large difference between these BIC scores (ΔBIC = 2,991) concurs with a large difference between the corresponding trees (RF = 138), implying that the default search option relied on a suboptimal tree. Doing so may lead to the selection of a suboptimal model of SE; that did not occur here, but it is a risk to consider when the default search option is used.

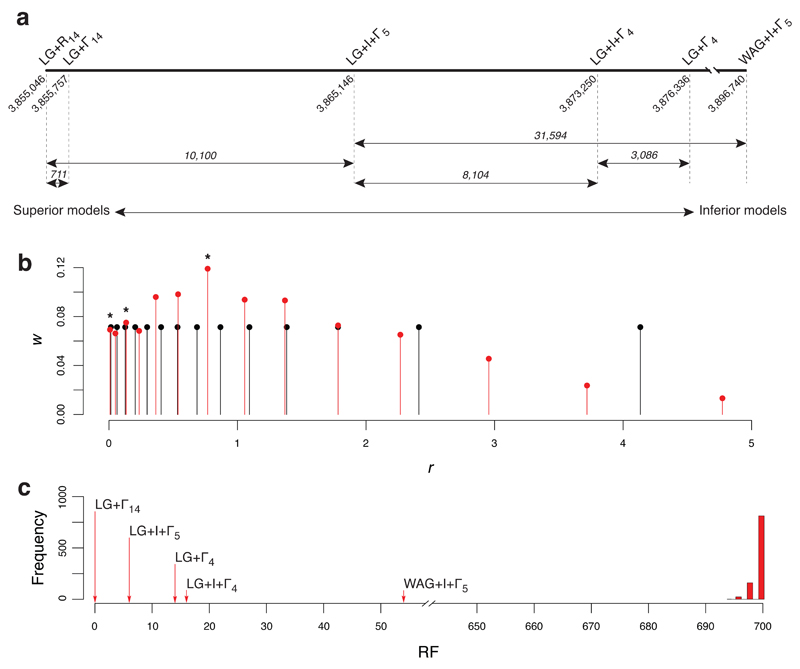
We then did a phylogenetic analysis to compare the estimates for selected models. Figure 2a confirms that the LG+R₁₄ model is the best. Factors contributing to its superior fit include changes in substitution model (WAG+I+Γ₅→LG+I+Γ₅:ΔBIC = 31,954) and the RHAS model (LG+I+Γ₅→LG+R₁₄:ΔBIC = 10,100). Other models considered reveal the effects of the I model of RHAS (LG+Γ₄→LG+I+Γ₄:ΔBIC = 3,086) and the number of rate categories used to model the Γ distribution (LG+I+Γ₄→LG+I+Γ₅:ΔBIC = 8,104). Given this last result, we wondered whether the LG+Γ₁₄ model might fit the data better than the LG+R₁₄ model, but this was not the case (ΔBIC = 711). Figure 2b shows the estimates of r_i and w_i for the R₁₄ and Γ₁₄ models. Unlike the Γ₁₄ model, the R₁₄ model is trimodal and has a larger maximum/minimum rate ratio (r_max/r_min = 575 for R₁₄ and 274 for Γ₁₄). In summary, for these data, RHAS is best modeled by the R₁₄ model.

Figure 2. Illustration of the advantages provided by ModelFinder.

(a) One-dimensional plot showing the BIC scores of selected models of SE, given the alignment of amino acids used by Wu et al.¹⁹ The models are listed above the line. Numbers drawn at a 45° angle are the BIC scores and those shown in italics are the ΔBIC scores. The relative position of each model of SE is shown on the axis, with the worst model on the right and the best model on the left. (b) Plot showing the values of r_i and w_i obtained under the R₁₄ model of RHAS (red lines and balls) and the Γ₁₄ model of RHAS (black lines and balls) for the alignment analyzed by Wu et al.¹⁹ Stars (*) indicate local peaks in the R₁₄ model of RHAS. (c) Plot showing the RF distances between the most likely tree inferred under the LG+R₁₄ model of SE and the most likely trees inferred under the LG+Γ₁₄, LG+Γ₄, LG+I+Γ₄, LG+I+Γ₅ and WAG+I+Γ₅ models of SE. For comparison, a histogram with the distribution of 1,000 RF distances is included; each of these distances was obtained by comparing the most likely tree inferred under the LG+R₁₄ model of SE to a randomly-generated tree with the same number of leaves.

Finally, we wanted to see whether the optimal tree for these data was model-dependent. Figure 2c shows the RF distances between the most likely tree inferred under the LG+R₁₄ model and those inferred under the other models. The RF distances ranged from 0 to 54, so the optimal tree for these data is clearly model-dependent. Interestingly, although the trees inferred under the other models differ from that inferred under the LG+R₁₄ model, they are still significantly more like the tree inferred under the LG+R₁₄ model than random trees are, so the other models are not too misleading. That said, the best explanation for these data is provided by the tree inferred under the LG+R₁₄ model.

Similar results emerged from analyses of other phylogenetic data (Table 1). In each of these cases, the best model of SE involved the PDF model of RHAS, and the best tree inferred using this model often differed from that found using the best model identified using other model-selection methods. Clearly, using ModelFinder can lead to a significant improvement in the fit between tree, model, and data irrespective of the source and type of data. A survey of 130 other data sets from TreeBASE²¹ reinforces this conclusion (Supplementary Table 1): in 122 of the cases, the fit between tree, model, and data improved (in 111 cases significantly), and in 118 of the cases, the tree topology changed. When the default and advanced search options were compared, a better fit between tree, model, and data was found using the advanced search option in 75 of the 130 cases. In 46 of these 75 cases, the models of SE differed, and in every one of these 46 cases the optimal trees differed; hence, the advanced search option provides a significant advantage over the default search option.

Table 1.

Results from analyses of five other data sets. For each data set is shown: the numbers of sequences in the alignment, the number of sites in the alignment, the optimal models of SE identified using ModelFinder and IQ-TREE’s implementations of jModelTest⁹ and ProtTest¹⁰ (Other Methods), and the differences in terms of the ∆BIC score and RF distance between phylogenetic estimates inferred using these optimal models of SE.

Data type, source & origin	Sequences	Sites	ModelFinder	BIC	Other Methods	BIC	∆BIC	RF
DNA, Lassa virus7	179	3,186	SYM+R5	131,325	SYM+I+Γ4	131,540	215	16
DNA, mitochondrial, mammals3	274	7,370	GTR+R8	681,837	GTR+I+Γ4	684,469	2,632	16
DNA, nuclear, birds4	200	394,684	GTR+R8	18,891,706	GTR+I+Γ4	18,969,054	77,348	4
Protein, plastids, green plants5	360	19,449	JTT+F+R10	2,830,471	JTT+F+I+Γ4	2,838,957	8,486	4
Protein, nuclear, yeast6	23	634,530	LG+F+R7	25,629,204	LG+F+I+Γ4	25,638,043	8,839	0

ModelFinder is fast and more flexible than other model-selection methods^9–11 and can detect models of SE that the other methods are unable to detect (e.g., multi-modal distributions of RHAS). Based on surveys of simulated and real data, ModelFinder proved accurate (Fig. 1) and often outperformed other model-selection methods in terms of the fit between tree, model and data (Table 1, Supplementary Table 1). Fears of over-parameterization have traditionally led users of model-based phylogenetic methods to avoid parameter-rich models of SE, but the use of the BIC, AIC and AICc criteria should alleviate this concern. Although the accuracy and benefits of ModelFinder were demonstrated using proteins generated under time-reversible conditions, the method is also suitable to other data that have evolved under such conditions. If, however, the data have evolved under more non-time-reversible conditions, then ModelFinder is not suitable for model selection. When data have evolved under non-time-reversible conditions, model selection is a challenge because different edges in the tree may require different models of SE. In practical terms, the HAL-HAS model²² addresses this need for nucleotides but a similar solution for other data is not yet available.

Software

ModelFinder is implemented in IQ-TREE version 1.5.4 (http://www.iqtree.org).

Data

Data and scripts used in this study are available from http://www.iqtree.org/ModelFinder/.

Online Methods

ModelFinder is included in IQ-TREE version 1.5.4. and available from http://www.iqtree.org. ModelFinder complements other methods for identifying the optimal model of SE^{9–11,23–30} for data comprising alignments of nucleotides or amino acids, but it differs from most of these other methods in three important ways:

• ModelFinder considers alignments of nucleotides, codons, amino acids, and other discrete data (e.g., binary and morphological data). Like the methods cited above, but not PartitionFinder¹¹, ModelFinder defines the alignment as a single partition of sites;

• ModelFinder includes the PDF model of RHAS proposed by Yang¹³, thus increasing the variety of models of RHAS that are considered during model selection. The PDF model has since been used elsewhere³¹, but its suitability is not yet widely recognized;

• ModelFinder allows the tree topology to vary during the search for an optimal model of SE, thus reducing the chance of entrapment in local optima during model selection. This search strategy has been used previously²⁸, but its suitability is under-recognized.

ModelFinder uses three algorithms to search model space. Algorithm 1 (default search option), uses the following steps:

• 0.Given an alignment of characters (D);
• 1.Find a reasonable tree T (inferred using parsimony);
• 2.Obtain L(D|T, S_i, H_i) over i and j, where S_i is a list of substitution models and H_j is a list of RHAS models;
• 3.Identify (S_opt,H_opt) using AIC, AICc or BIC (default).

where L(D|T, S_i, H_j) denotes the likelihood of the data, given a tree, T, the i-th substitution model and the j-th model of RHAS, S_opt denotes the optimal substitution model, and H_opt denotes the optimal RHAS model. Algorithm 2 (advanced search option), uses the following steps:

• 0.Given an alignment of characters (D);
• 1.Obtain L(D|T_h, S_i, H_j) over h, i, and j, where T_h is a list of trees (generated by IQ-TREE), S_i is a list of substitution models and H_j is a list of RHAS models;
• 2.Identify (S_opt,H_opt) using AIC, AICc or BIC.

Algorithm 3 identifies the optimal PDF model of RHAS and is a key component of Algorithm 1 and Algorithm 2 (it is used whenever the PDF model of RHAS is considered). In the example given below, the BIC optimality criterion is used (but the AIC and AICc optimality criteria can be used if the user chooses to do so):

• 0.Given an alignment of characters (D), a tree (T), and a substitution model (S);
• 1.Set k = 2;
• 2.Obtain L(D|T, S, R_k) and L(D|T, S, R_k+1);
• 3.If BIC(L(D|T, S, R_k)) > BIC(L(D|T, S, R_k+1)),
• 4.Increment k by one unit, and go to 2;
• 5.Else stop, and report R_k as the optimal PDF model.

In practice, Algorithm 1 is invoked with this command (given here for an alignment of amino acids):

iqtree -s data.fst -st AA -m MF

while Algorithm 2 is invoked using:

iqtree -s data.fst -st AA -m MF -mtree

IQ-TREE includes several other options (Supplementary Table 2) that will cause ModelFinder to conduct the search under different constraints. For example, the -m TEST and -m TESTONLY options cause ModelFinder to operate like jModelTest⁹ and ProtTest¹⁰ while the -m TESTMERGE and -m TESTMERGEONLY options cause it to operate like PartitionFinder¹¹. However, none of these options consider the PDF model of RHAS. To do so, it is necessary to use the -m MF and -m MFP options.

When the PDF model is used, it is often necessary to optimize more than two parameters (the I+Γ₄ model is parameterized using two parameters). To ensure that these parameters are estimated as accurate as possible, we initially compared parameter estimates obtained using two parameter optimization procedures: the expectation-maximization (EM) algorithm¹⁵ (see subsection below) and the quasi-Newton BFGS algorithm³². We found the EM algorithm to be most accurate (results not shown).

ModelFinder is fast. For example, when benchmarking time required by the standard model-selection procedure of ModelFinder, we saw a 39- to 289-fold speedup when compared with jModelTest⁹ (based on 70 alignments of DNA) and a 16- to 52-fold speedup when compared to ProtTest¹⁰ (based on 45 alignments of amino acids).

Model selection for the alignment used by Wu et al.¹⁹ (i.e., 6,597 sites and 353 species) was done using two commands:

iqtree -s data.fst -st AA -m MF -msub nuclear -cmax 20

iqtree -s data.fst -st AA -m MF -msub nuclear -cmax 20 -mtree

Having found the optimal model of SE for the data, phylogenetic analyses were done under six models of SE using the following commands:

iqtree -s data.fst -st AA -m WAG+I+G5

iqtree -s data.fst -st AA -m LG+I+G5

iqtree -s data.fst -st AA -m LG+I+G4

iqtree -s data.fst -st AA -m LG+G4

iqtree -s data.fst -st AA -m LG+R14

iqtree -s data.fst -st AA -m LG+G14

Each of these analyses was repeated 100 times to reduce the likelihood of being caught in local optima. The fact that the fit between tree, model and data varied across the 100 results for each of these models of SE shows that this problem is an issue to consider, as done here.

Model selection for the alignments considered in Table 1 was done using commands like those above, albeit with some variations to accommodate, for example, the type of data.

Model selection for the data considered in Supplementary Table 1 was done using two commands:

iqtree -s data.fst -m MF -mtree

iqtree -s data.fst -m TEST

The first command causes IQ-TREE to run the advanced version of ModelFinder; the second command causes IQ-TREE to run its implementation of jModelTest⁹ or ProtTest¹⁰, followed by a phylogenetic analysis under the optimal model of SE.

The PDF model is available in three other phylogenetic programs (i.e., PhyML³³, PhyTime³⁴, and BEAST³⁵), so users of ModelFinder are not limited to using IQ-TREE to solve their phylogenetic questions.

Practical considerations

When using ModelFinder, it is important to remember that it optimizes the likelihood of the tree and model, given the data, whenever it searches for the optimal values of parameters considered. Therefore, it is possible that the search algorithms may become trapped in local optima. To reduce the chance of this occurring, we strongly recommend model selection be repeated many times for each data set, as noted above. Doing so may entail using much more computing time, especially when long, species-rich alignments are considered or the advanced search option of ModelFinder is used. Therefore, when the alignment is very long, we recommend the following set of strategies to reduce the amount of time used on model selection:

• If the computational resources allow distributed computing, invoke the –nt x option to spread the processes over x threads;

• If the data are characters encoded by a specific type of genome (e.g., mitochondrial), invoke the –msub source option to limit the search to this specific type of data;

• If the optimal model turns out to include the R₁₀ model of RHAS, we recommend the analysis be rerun with both the –cmin x and –cmax y options invoked (e.g., –cmin 8, –cmax 20). Doing so will ensure that PDF models with k = 8, 9, … , 20 are considered (i.e., lower values of k are ignored). The program will stop when the optimal value of k has been found, even if this value turns out to be 10.

• Use the default search option to find the optimal model of SE. Having identified this model, use the advanced search option with the optimal substitution model selected (e.g., –mset LG) to search for the optimal model of RHAS. While there is no guarantee that this approach will identify the optimal model of SE, our experience suggests that the choice of RHAS model is highly influenced by the topology of the tree while that of the substitution model is not.

The EM algorithm to estimate PDF model parameters

Let $\Theta$ = {W₁, …, W_k, r₁, …, r_k} be the weights and rates of the PDF model R_k that we want to estimate. First, we initialize $\Theta$ using a discrete Γ_k model¹² (i.e., the initial values of $\widehat{w_1}=\cdots =\widehat{w_k}=1/k$ and $\widehat{r_1},\dots ,\widehat{r_k}$ are derived from the discrete Γ distribution with k categories and a shape parameter α = 1). This becomes the current estimate $\widehat{\Theta }$. The EM algorithm iteratively performs an expectation (E-) step and a maximization (M-) step to update the current estimate until a (local) maximum in likelihood is reached.

E-step:

For the i-th site in the alignment D_i and the j-th category compute the posterior probability $\widehat{p_{ij}}$ of D_i belonging to category j based on the current estimate $\widehat{\Theta }$:

$$\widehat{p_{ij}}=\frac{\widehat{w_j}L\left({\mathbf{\text{D}}}_i|T,S,\widehat{r_j}\right)}{{\displaystyle {\sum }_{c=1}^k\widehat{w_c}L\left({\mathbf{\text{D}}}_i|T,S,\widehat{r_c}\right)}}$$

where $L\left({\mathbf{\text{D}}}_i|T,S,\widehat{r_j}\right)$ is the likelihood of the tree T, substitution model S, and relative rate $\widehat{r_j}$ for the alignment site D_i.

M-step:

For each category j the log-likelihood function:

$$\text{log}L={\displaystyle \sum _{i=1}^N\widehat{p_{ij}}\text{log}L\left({\mathbf{\text{D}}}_i|T,S,r_j\right)}$$

is maximized to obtain the next ${\widehat{r_j}}^{NEW},$ where N is the number of sites in the alignment. This can be done with standard numerical optimization such as Brent’s method³⁶. The weights are updated using:

$${\widehat{w_j}}^{NEW}=\frac{1}{N}{\displaystyle \sum _{i=1}^N\widehat{p_{ij}},}$$

that is, the new weight for category j is the mean posterior probability of each alignment site belonging to class j. This completes the proposal of the new estimate ${\widehat{\Theta }}^{NEW}$. If the likelihood of ${\widehat{\Theta }}^{NEW}$ is higher than that of $\widehat{\Theta }$, then $\widehat{\Theta }$ is replaced by ${\widehat{\Theta }}^{NEW}$ and the E- and M-steps will be repeated. Otherwise, the EM algorithm stops and reports $\widehat{\Theta }$ as the maximum-likelihood estimates of the PDF model R_k.

This EM algorithm allows estimation of the parameters of the R_k model, given a fixed tree T and a substitution model S. ModelFinder then iteratively estimates branch lengths of T, model parameters of S, and R_k until the likelihood converges.