A computational model predicts adjunctive pharmacotherapy for cardiac safety via selective inhibition of the late cardiac Na current

Abstract

Background

The QT interval is a phase of the cardiac cycle that corresponds to action potential duration (APD) including cellular repolarization (T-wave). In both clinical and experimental settings, prolongation of the QT interval of the electrocardiogram (ECG) and related proarrhythmia have been so strongly associated that a prolonged QT interval is largely accepted as surrogate marker for proarrhythmia. Accordingly, drugs that prolong the QT interval are not considered for further preclinical development resulting in removal of many promising drugs from development. While reduction of drug interactions with hERG is an important goal, there are promising means to mitigate hERG block. Here, we examine one possibility and test the hypothesis that selective inhibition of the cardiac late Na current (I_NaL) by the novel compound GS-458967 can suppress proarrhythmic markers.

Methods and results

New experimental data has been used to calibrate I_NaL in the Soltis-Saucerman computationally based model of the rabbit ventricular action potential to study effects of GS-458967 on I_NaL during the rabbit ventricular AP. We have also carried out systematic in silico tests to determine if targeted block of I_NaL would suppress proarrhythmia markers in ventricular myocytes described by TRIaD: Triangulation, Reverse use dependence, beat-to-beat Instability of action potential duration, and temporal and spatial action potential duration Dispersion.

Conclusions

Our computer modeling approach based on experimental data, yields results that suggest that selective inhibition of I_NaL modifies all TRIaD related parameters arising from acquired Long-QT Syndrome, and thereby reduced arrhythmia risk. This study reveals the potential for adjunctive pharmacotherapy via targeted block of I_NaL to mitigate proarrhythmia risk for drugs with significant but unintended off-target hERG blocking effects.

1. Introduction

Cardiotoxicity is a common risk for drugs in development, often manifesting as prolongation of the QT interval in the ECG and an increased likelihood for life-threatening ventricular arrhythmias [1,2,3]. QT interval prolongation typically arises from hERG block in ventricular myocytes and hERG interaction must be analyzed for all drug candidates to determine their potential for proarrhythmia [4]. A limitation of this approach is that many potentially useful drugs are eliminated early in the drug discovery process and development because they block hERG and thereby may cause acquired Long-QT Syndrome. Numerous drugs with potential for high therapeutic value never make it to the market because of their hERG positive signal. Here we consider an alternative approach that involves addition of an additional drug that selectively blocks late Na current (I_NaL) in order to “cancel” the hERG blocking effect. This approach, if useful, may be warranted in instances where a hERG positive therapy is uniquely indicated for disease and no alternative therapies exist.

The exploration of adjunctive therapy to mitigate drug side effects is with strong precedent [5,6,7]. A longstanding example can be found in effective antiarrhythmic drugs, which while categorized by their primary mechanism of action, exhibit off-target effects that apparently mitigate proarrhythmia risk. Included in this group is the most effective therapeutic for treating cardiac ventricular arrhythmias, amiodarone, a dirty drug whose multiple off-target effects likely underlie its efficacy. Here we try to extend this idea to adjunctive therapy design to promote the concept of “virtuous promiscuity” [8].

In this study we explore the basis for a novel adjunctive therapy aimed at mitigating acquired Long-QT as associated arrhythmia risk by pharmacological targeting of late Na current (I_NaL) using GS-458967, a potent and selective inhibitor of this current [9]. The first studies on the preclinical compound GS-458967 in 2013 showed potent selective targeting of I_NaL (GS-458967, IC₅₀ for I_NaL = 130 nM, compared to Kd for tonic block of peak I_Na = 1500 μM [9]) allowing for specific therapeutic inhibition and study of the physiological and pathological role for I_NaL in the heart.

We evaluated arrhythmia vulnerability by integrating data-based drug channel models into virtual ventricular myocyte and tissue models. On this basis we can provide predictions of emergent drug effects that modify individual elements of the TRIaD. This approach yielded novel and potentially important insights into the proarrhythmia markers at the myocyte and/or tissue scales. Thus, it is based on the fundamental biophysical and molecular pharmacological mechanisms underlying drug induced arrhythmia and their influence on electrophysiological parameters. Gaining reliable insights that inform arrhythmia risk is the first necessary step that must be taken to ultimately lead to development of specific in silico screening test for both assessing risk and then implementing practical risk reduction measures.

Our model predictions illustrate that selective pharmacological targeting of I_NaL by inhibiting this current using GS-458967 improves all TRIaD related parameters in acquired Long-QT syndrome and consequently reduces arrhythmia risk.

2. Methods

2.1. Experimental methods

2.1.1. Recordings of late I_Na and action potentials using whole-cell patch-clamp technique

The conventional whole-cell configuration of patch clamp technique was used to record late I_Na in voltage-clamp mode and action potentials (APs) in the current-clamp mode. All whole-cell data were acquired using a Multiclamp 700B amplifier with pClamp 10.2 software (Molecular Devices, Sunnyvale, CA). Data was analyzed using pClampfit 10, Microcal Origin 8 (OriginLab Corporation, Northampton, MA), and GraphPad Prism 5 (GraphPad Software, Inc., La Jolla, CA) software programs. Patch pipettes were pulled from borosilicate glass (World Precision Instruments, Sarasota, FL) using a DMZ Universal Puller (Dagan Corporation, Minneapolis, MN). Current-clamp experiments were performed at 36 ± 1 °C using a temperature controlling system (TC-334B, Warner Instruments, Hamden, CT), whereas, the voltage-clamp experiments were done at 22 ± 1 °C. In all experiments, after a gigaseal was established in the whole-cell configuration, 5–10 min was allowed for stabilization before the experimental protocol was started.

In recordings of I_Na, myocytes were superfused with bath solution containing (in mM): 135 NaCl, 4.6 CsCl, 1.8 CaCl₂, 1.1 MgSO₄, 10 HEPES and 10 glucose supplemented with nitrendipine at a final concentration of 10 μM. The pH was adjusted to 7.4 with NaOH. The patch pipette resistances varied from 1.5–2 MΩ when they were filled with an internal solution containing (in mM): 120 aspartic acid, 20 CsCl, 1 MgSO₄, 4 ATPNa₂, 0.1 GTPNa₃ and 10 HEPES. The pH was adjusted to 7.3 with CsOH. Late I_Na was recorded during a 1500 msec ramp voltage-clamp command starting from −90 mV and depolarizing to 0 mV once every 20 s. Late I_Na was measured as the maximum inward current during each ramp depolarization.

For microelectrode intracellular recordings of action potentials (APs), myocytes were superfused with bath solution containing (in mM): 140 NaCl, 4 KCl, 1.8 CaCl₂, 1 MgCl₂, 0.33 NaH₂PO₄, 5 HEPES and 7.5 glucose. The pH was adjusted to 7.4 with NaOH. Pipette resistances were in the range of 2–2.5 MΩ when using an internal solution containing (in mM) the following: 60 K aspartate, 80 KCl, 8 NaCl, 5 Mg-ATP, 0.25 Tris-GTP, and 5 HEPES was used. The pH was adjusted to 7.3 with KOH. APs were elicited by 3–3.5 ms depolarizing current pulses adjusted to approximately 1.5 time the threshold and applied every 5 s (0.2 Hz). The APD was measured at 90% (APD₉₀) of full repolarization. Ten consecutive AP recordings were averaged for each experimental condition.

2.2. Simulation methods

2.2.1. Cellular simulations

A rabbit cardiac myocyte model was chosen in this study to align with the rabbit ventricular myocytes experimental data - unpublished and from [9]. The Soltis-Saucerman cardiac cell model [28] was modified as follows: The I_Na channel was replaced with Markov model described below and with full parameters in the accompanying supplement. The Na channel model structure was based on previously published models [11,12]. Recognizing that cardiac myocytes exhibit substantial variability in both current and action potential amplitudes and morphologies [13], we then empirically tuned the Ca²⁺ and K⁺ current amplitudes to simultaneously recapitulate a representative rabbit experimental current data [14,15,16] and action potential duration in experiments [9] are shown in Table 1.

Table 1.

Current density changes in cardiac ventricular cell model: the maximum conductances were tuned to approximate the experimentally measured current amplitudes during the action potential. An action potential duration that was within the experimental range was determined.

Ionic parameters	Scaling factors
pCa	0.7
Gtoslow	1.3
Gtofast	1.3
GK1	0.5

2.3. Optimization procedure for rabbit sodium channel

A computational Markov model of the drug-free (control) and GS-458967 drug channel interaction was formulated via numerical optimization from experimentally derived rate constants as previously described [11,17]. Five pacing protocols were optimized: steady state availability at test potentials from −130 mV to −50 mV followed by depolarization to −35 mV, steady state activation (the holding potential was −120 mV and the testing potentials ranged from −60 to 20 mV in 5-mV steps) [18], recovery from inactivation at a holding potential of −100 mV [18], I_Na time course current [9], and ramp pulses from Gilead Sciences, Inc. (Please see the section above on Recordings of late INa and action potentials using whole cell patch-clamp technique).

A cost function for each protocol was defined as the sum of squared differences between experiment and simulation. The total cost function (sum of the individual protocol errors) was then minimized and converged when a tolerance of 0.01 for the change of the cost function and 0.01 for the change in parameters was achieved.

All rate constants were allowed to change during the optimization. Post-optimization and Initial values are shown in Online Tables I and II, respectively.

2.4. Parameter optimization for drug-bound model

Simulations of GS-458967 dose-dependent effects on late Na current were optimized to fit the experimentally measured late Na⁺ current with GS-458967 concentrations of 0.03, 0.1, 0.3 and 1 μM. The drug-bound rate constants (αx2, α13n, α_22, β_33, K_on, K_inactive, K_closed) were optimized to fit the experimentally measured late Na⁺ current with GS-458967 concentrations of 0.03, 0.1, 0.3, 1 μM and 10 μM, and the peak Na⁺ value at 10 μM (Fig. 3A). The optimized rate constants are shown in Online Table IV. Because GS-458967 is highly non-basic and cannot be protonated at physiological pH, the post-optimization values (αx2, α13n, α_22, β_33, K_on, K_inactive, K_closed) are shown in Online Tables III, and initial guesses are shown in Online Tables IV.

Fig. 3.

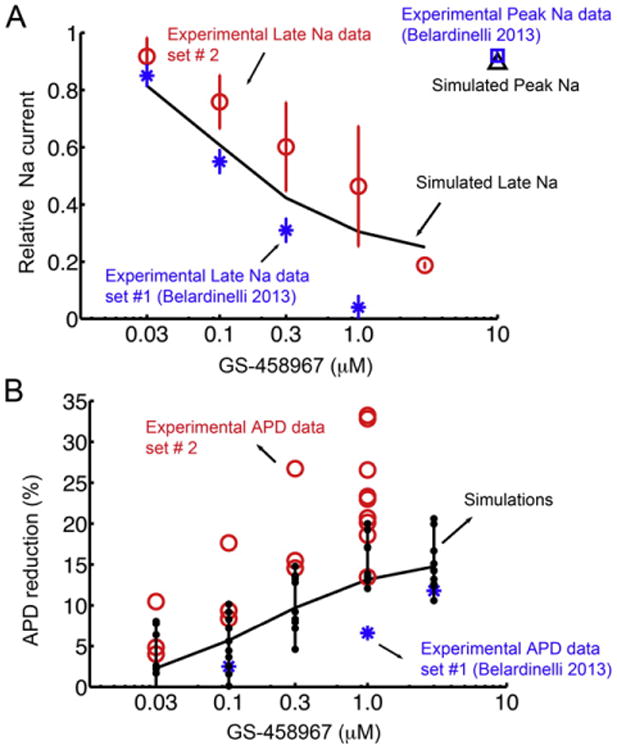
Experimentally measured and model predicted effect of GS-458967 on I_Na in rabbit ventricle. (A) Optimized model generated concentration-dependent data for GS-458967 on late Na current compared to two separate sets of experimental data - Blue asterisks indicate experimental data set #1 (n = 4) [9], and red circles are from experimental data set #2 (For 0 μM and 0.03 μM, n = 3. For 0.1 μM and 0.3 μM, n = 4. For 1 μM, n = 6. For 3 μM, n = 2). The effect of high concentration GS-458967 on peak I_Na is indicated for experiments (blue square), and simulated I_Na peak (black triangle). (B) Behavior of a myocyte ‘population’ was simulated by randomly varying the amplitude of maximal conductances for I_Na, I_CaL, I_Ks, I_Kr, I_K1, I_to, I_NaK, I_NaCa (to within 10% of their nominal values in the rabbit ventricular myocyte model). This approach allowed for efficient analysis of 100 distinct cell action potentials. APD₉₀ was calculated at 1 Hz for each case. These simulated myocyte properties were compared to experimental data set #1 (blue asterisks) and experimental data set #2 (red circles).

2.5. Introduction of variability in the cellular model to create cell populations

Simulated single action potentials (APs) were recorded at the 500th paced beat (BCL = 1000 ms). We have also simulated a cell ‘population’ by randomly varying the amplitude of maximal conductances for I_Na, I_CaL, I_Ks, I_Kr, I_K1, I_to, I_NaK, I_NaCa to within 10% (Fig. 3B) of their nominal values in the rabbit ventricular myocyte model, as is done in standard sensitivity analysis ([19,20,21]). This approach allowed for efficient analysis of 100 distinct cell action potentials. APD₉₀ was calculated at 1 Hz for each case. These simulated myocyte properties were compared to distinct experimental data sets #1 (blue asterisks) and #2 (red circles) as shown in Fig. 3.

The numerical method used for updating the voltage was forward Euler. All the simulations were encoded in C/C++ and run on Mac Pro 3.06 GHz 12-Core computers. Numerical results were visualized using MATLAB R2014a by The Math Works, Inc.

2.6. Simulated effects of ATX-II

We have also simulated a ‘population’ of 100 cells by randomly varying the amplitude of maximal conductances as in Fig. 3B. APD₉₀ was calculated at 0.2 Hz for each case in Fig. 5.

Fig. 5.

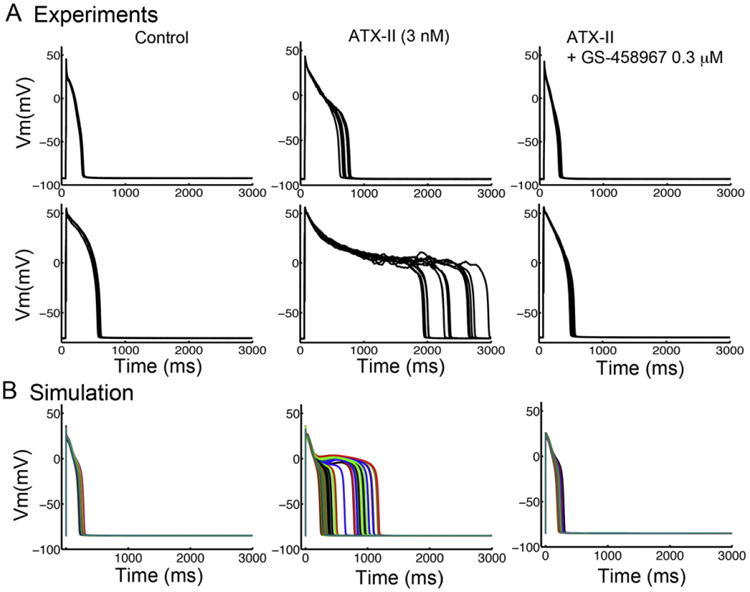
GS-458967 can effectively attenuate APD prolongation by ATX-II in rabbit ventricular myocytes. (A) Experimental data from two distinct data sets from rabbit ventricular myocytes showing drug free conditions (left), the effect of 3 nM ATX-II (middle) and the combination of 3 nM ATX-II with 0.3 μM GS-458967 (right). (B) Simulated effects on virtual rabbit ventricular myocyte showing drug free (left), simulated effect of ATX-II (middle) and ATX-II with co-treatment with GS-458967 0.3 μM (right).

In Fig. 6B and C, 1D cables were first paced at 1 Hz for 200 beats with simulated ATX-II effects only, added GS-458967 for next 10 beats at 1 Hz (s1) followed by a pause (3000 ms), and then applied a premature beat (s2).

Fig. 6.

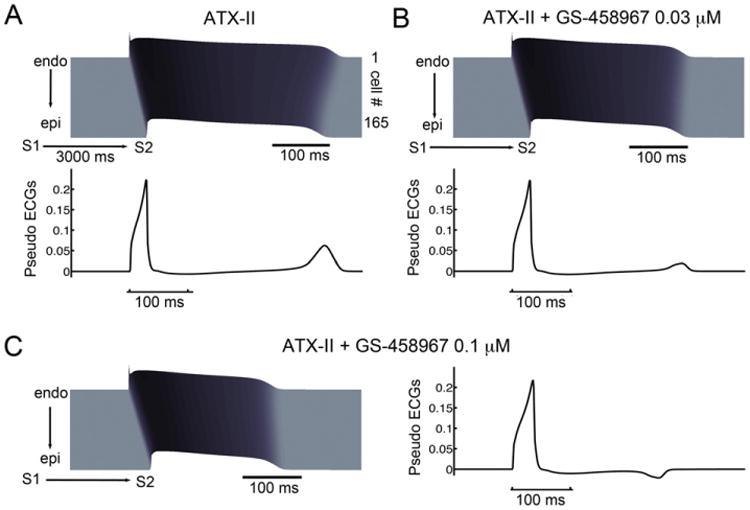
Simulations showing that GS-458967 can effectively reduce spatial APD dispersion caused by ATX-II. (A) Space-time plots of membrane potential (top) and pseudo ECGs (lower) computed from a 165-rabbit myocyte transmural cardiac preparation in the presence of ATX-II during a “short-long-short” pacing protocol. (B) 0.03 μM GS-458967 markedly diminishes QT interval prolongation and APD dispersion as indicated by reduced T-wave amplitude. (C) 0.1 μM GS-458967 further reduced QT interval prolongation and reversed the repolarization gradient as demonstrated by inversion of the T-wave.

2.7. Simulation of TRIaD in dofetilide and drug-free models

To simulate effects of dofetilide, we replaced the I_Kr channel with our previously published Markov model [22]. For the TRIaD simulations, simulations were conducted as follows: First, Triangulation was calculated as the repolarization time from APD₃₀ to APD₉₀ from 1000 simulated cell with noise currents. Reverse-use-dependence was measured APD₉₀ at steady state for each pacing cycle length (from 3 Hz to 0.5 Hz) and APD adaptation curves were constructed. Instability was simulated by applying small amplitude inward currents randomly between −0.1 to −0.2 pA/pF for 50 ms over the course of the action potential plateau at a pacing cycle length = 1000 ms. A small inward current was also applied randomly in time between 10 to 210 ms on the plateau phase for 1000 beats. We modeled beat-to-beat APD variability by adding noise currents into membrane potential calculations, and simulated 1000 cells action potentials. Using the equation from [23],

$$V_{t+\mathrm{\Delta }t}=V_t-\frac{I(V_t)\mathrm{\Delta }t}{C_m}+\xi n\sqrt{\mathrm{\Delta }t}$$

Where n is N(0,1) is a random number from a Gaussian distribution, and Δt is the time step. ξ is the diffusion coefficient, which is the amplitude of noise. In Fig. 7, ξ was set to 0.32 based on [23]. The noise current was generated and applied to membrane potential V_t throughout the whole simulated time course.

Fig. 7.

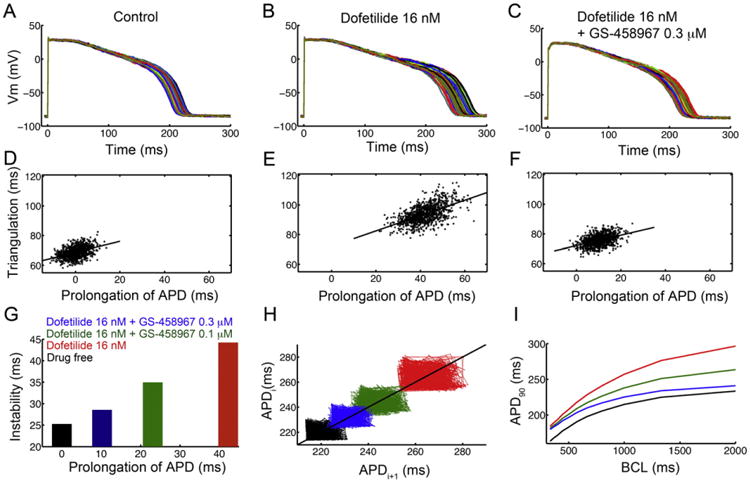
In silico pharmacological results suggesting that GS-458967 can reduce all proarrhythmia-linked parameters set out in the TRIaD approach: Triangulation, reverse use dependence, beat-to-beat instability of action potential duration, as well as temporal and spatial action potential duration dispersion. Predicted temporal action potential duration dispersion of 1000 simulated myocyte action potentials generated after incorporating physiological noise to induce beat-to-beat variability at 1 Hz in (A) the drug-free control case, (B) effects of simulated application of the I_Kr blocker Dofetilide (16 nM) and (C) predicted effects of 0.3 μM GS-458967 with Dofetilide 16 nM. Action potential triangulation as a function of APD prolongation for individual myocytes for (D) control (slope = 0.37), (E) Dofetilide 16 nM (slope = 0.52) and (F) Dofetilide 16 nM + GS-458967 0.3 μM (slope = 0.35). (G) Instability of APD was quantified as the difference between the maximum and minimum of 1000 individual myocytes in the presence of physiological noise current as a function of prolongation of APD (shown in panels A–C). (H) Simulated beat-to-beat instability of rabbit ventricular myocyte action potentials to small perturbations before and after application of drugs. Poincaré plots of sequential APD pairs indicating beat-to-beat instability are shown for each case. (I) GS-458967 improved dofetilide induced reverse use dependence: Action potential adaptation curves show APD₉₀ at various pacing frequencies in the presence or absence of drugs.

2.8. Transmural fiber simulations

The in silico transmural fiber was composed of 165 ventricular cells (Δx = Δy = 100 μm) connected by resistances to simulate gap junctions [28]. The fiber contains an endocardial region and epicardial region, which shown a linear decreased in APDs [24,25]. In the model, G_toSlow was monotonically increased from 0.0615 to 0.078, and G_toFast was linearly increased from 0.0095 to 0.026. The fiber was paced at BCL = 1000 ms for 200 beats. The stimulus is applied to the first cell.

2.9. ECG computation

Extracellular unipolar potentials (Φ_e) generated by the fiber in an extensive medium of conductivity σ_e, were computed from the transmembrane potential V_m using the integral expression as in Gima and Rudy [26]:

• In one-dimension:

  $$\begin{array}{c}{\Phi }_e(x^{\prime },y^{\prime })=\frac{a^2{\sigma }_i}{4{\sigma }_e}\int (-\nabla V_m)•[\nabla \frac{1}{r}]\mathit{\text{dx}}\mathit{\text{dy}}\\ r={[{(x-x^{\prime })}^2]}^{1/2}\end{array}$$
• In two-dimension:

  $${\Phi }_e(x^{\prime },y^{\prime })=\frac{a^2{\sigma }_i}{4{\sigma }_e}\int (-\nabla V_m)•[\nabla \frac{1}{r}]\mathit{\text{dx}}\mathit{\text{dy}}$$

r=[(x−x′)² + (y−y′)]^1/2 where ∇V is the spatial gradient of V_m, a is the radius of the fiber, σ_i is the intracellular conductivity, σ_e is the extracellular conductivity, and r is the distance from a source point (x, y, z) to a field point (x′, y′, z′). Φ_e was computed at an “electrode” site 2.0 cm away from the distal end along the fiber axis.

2.10. Transmural tissue simulations

We simulated a heterogeneous cardiac tissue assuming a 500 by 500 component grid Δx = Δy = 100 μm. This tissue was assumed to contain an endocardial region and epicardial region, with a linear decrease in APDs [24,25]. All ion channel conductances and gap-junctions parameters are same as in the one-dimensional simulations. Current flow is described by the following equation:

$$\frac{\partial V(x,y,t)}{\partial }=D_x\frac{{\partial }^{2}V(x,y,t)}{\partial x^2}+D_y\frac{{\partial }^{2}V(x,y,t)}{\partial y^2}-\frac{I_{\mathit{\text{ion}}}-I_{\mathit{\text{stim}}}}{C_m}$$

Where V is the membrane potential, x and y are distances in the longitudinal and transverse directions, respectively, D_x and D_y are diffusion coefficients in the x and y directions. I_stim is 500 mA/cm² for 1 ms. We also incorporated anisotropic effects by setting D_x and D_y such that the ratio of conduction velocity is 1:2 [27].

This ventricular tissue segment was first paced for 200 beats (S1) at BCL = 1000 ms on the entire length of one side of tissue. A premature stimulus (S2) was then delivered at 330 ms in control case (A) after S1 in a 2.5 cm × 2.5 cm area on the top edge of the endocardial region. (B) In ATX-II case, S2 paced at 450 ms, and at 465 ms in Dofetilide case (C) after S1 in a 2.5 cm × 2.5 cm area on the top edge of the endocardial region. With GS-458967 applications, S2 was applied at 420 ms in ATX-II (D) and at 430 ms (E) in Dofetilide cases (Fig. S2).

3. Results

The starting point for this study compared the simulated main currents and Ca²⁺ transient in the Soltis-Saucerman rabbit ventricular action potential model [28] during the AP to those recorded experimentally from individual rabbit ventricular myocytes (Fig. 1A–F). Next the Soltis-Saucerman model parameters for the maximum conductances for Ca²⁺ and K⁺ currents were tuned to match the experimental data from rabbit ventricular myocytes [14,15,16] including action potential durations [9]. Following these minor adjustments, the output of the model showed good agreement with the experimentally recorded currents.

Fig. 1.

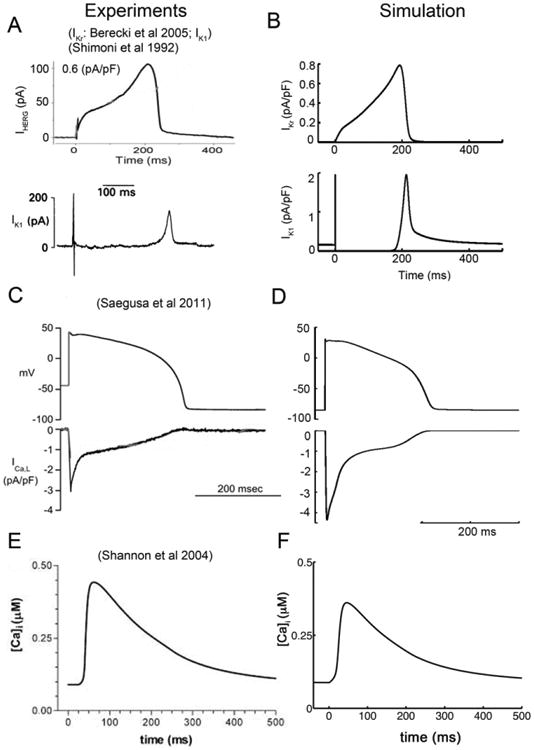
A comparison of experimentally recorded and model generated transmembrane ion currents from rabbit ventricular myocytes. (A) Experimentally measured I_Kr (upper) [55], and I_K1 (lower) [14]. (B) Simulated I_Kr (upper) and I_K1 (lower) compared. (C) Experimental action potential clamp waveform (upper) and corresponding L-type Ca²⁺ current (lower) from rabbit ventricular myocyte [56]. (D) Simulated rabbit ventricular myocyte action potential and model generated L-type Ca²⁺ current. (E) Experimentally recorded Ca²⁺ transient during the AP [15]. (F) Corresponding simulated Ca²⁺ transient.

We next modeled the rabbit ventricular Na⁺ current by re-optimizing the model parameters described in Moreno et al. [11] to reproduce the time-course and kinetics of I_Na that were experimentally recorded in rabbit ventricular myocytes patch clamping experiments. Fig. 2 shows the adjusted, post-optimized, model-generated I_Na (blue lines) superimposed on experimental records (black symbols). Fig. 2A shows the superimposition of model and experimentally generated voltage dependent activation curves. Panel (B) shows the steady-state Na⁺ channel availability (inactivation) relationship. Panel (C) shows the recovery time course of current (or reactivation) at −100 mV generated using a standard double pulse voltage clamp protocol. The time-course of I_Na is depicted in at low and high gain normalized to the peak I_Na value (panels D and E, respectfully). Panel F shows I_Na generated in response to a slow depolarizing voltage clamp ramp protocol. All protocols that are illustrated in the figure panels are described in detail in the Methods and Simulation methods section. It is interesting to note that rabbit ventricular myocytes exhibit a much smaller late I_Na component measured during a square wave voltage depolarizing pulse, when compared to the current measured in guinea pig ventricular myocytes [12].

Fig. 2.

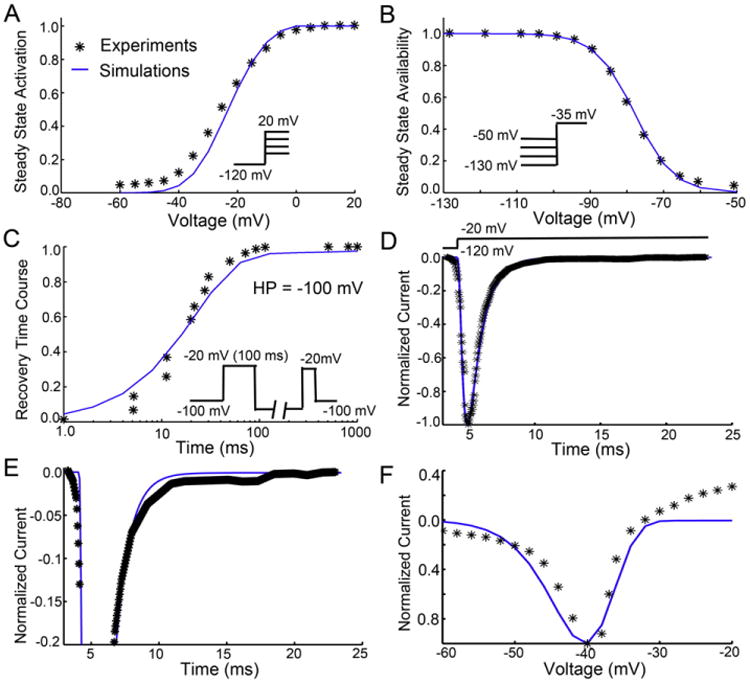
Experimental (symbols) and model optimized (lines) drug free Na⁺ current parameters in a rabbit ventricular myocyte. (A) Na⁺ current activation curve derived from data generated in response to depolarizing voltage clamp pulses [18]. (B) Steady-state inactivation [18]. (C) Recovery from inactivation at −100 mV [18]. (D) I_Na waveform in drug free conditions at low gain normalized to peak current [9]. (E) Drug free I_Na at high gain [9]. (F) Superimposition of model predicted and experimentally recorded drug free or baseline I_Na in response to a slow depolarizing ramp voltage protocol.

3.1. Concentration-dependent reduction in I_NaL and APD by GS-458967

GS-458967 selectively inhibits endogenous I_NaL and causes concentration-dependent shortening of APD in ventricular myocytes [9,29,30]. Two independent experimental data sets from rabbit ventricular myocytes have been used as the basis for our model optimization to simulate the effects of GS-458967 on experimental data for rabbit I_NaL during the AP and on APD. The blue asterisks indicate previously published experimental data set #1 [9], and red circles are from our new (unpublished) experimental data set #2. We incorporated our calibrated rabbit ventricular Na⁺ channel model from Fig. 2 into the Soltis-Saucerman rabbit ventricular model of the cardiac ventricular action potential and then optimized the drug model parameters to fall within the independent experimental data sets. The results are shown in Fig. 3. Panel 3A shows the simulated effects of a 10-fold changes in concentrations of GS-458967 and selective I_NaL block during the rabbit AP. The model accurately predicts the marked concentration-dependent shortening of the APD observed experimentally. Note that reduction of the large transient endogenous I_Napeak in the optimized model simulations is minimal even after a very high concentration of GS-458967 (10 μM). This was also observed experimentally in rabbit ventricular myocytes (compare blue open square to black open triangle). The selectivity for block of I_NaL compared to I_Napeak was a key goal in the drug discovery process that resulted in selection of GS-458967 as a potential candidate compound.

Fig. 3B shows a model prediction of the concentration dependence of the simulated effects of GS-458967 on the APDs in a rabbit ventricular myocyte population. These data were tracked in a population of 100 virtual myocytes generated by randomly varying the amplitude of maximal conductances for I_Na, I_CaL, I_Ks, I_Kr, I_K1, I_to, I_NaK, I_NaCa (to within (±) 10% of their nominal values in the rabbit ventricular myocyte model) prior to the upstroke of each action potential. APD₉₀ was calculated for each AP at a steady pacing frequency of 1 Hz. Note that the simulated APD₉₀ variability falls well within the range of experimentally recorded APD₉₀ from both data set #1 (blue asterisks) and data #2 (red circles).

Fig. 4A shows the simulated time-course of the rabbit AP waveform. These results reveal the concentration-dependent effects of GS-458967 on rabbit ventricular repolarization. Panel B shows the corresponding dose-dependent effects of GS-458967 on the time-course of the endogenous I_NaL. It is notable that although I_NaL in the rabbit ventricular myocyte is very small in response to voltage clamp square wave depolarizing pulses (Fig. 2E), there is a detectable I_NaL throughout the plateau of the AP. Note also that I_NaL slowly increases during repolarization as expected from the progressively increasing electrochemical driving force.

Fig. 4.

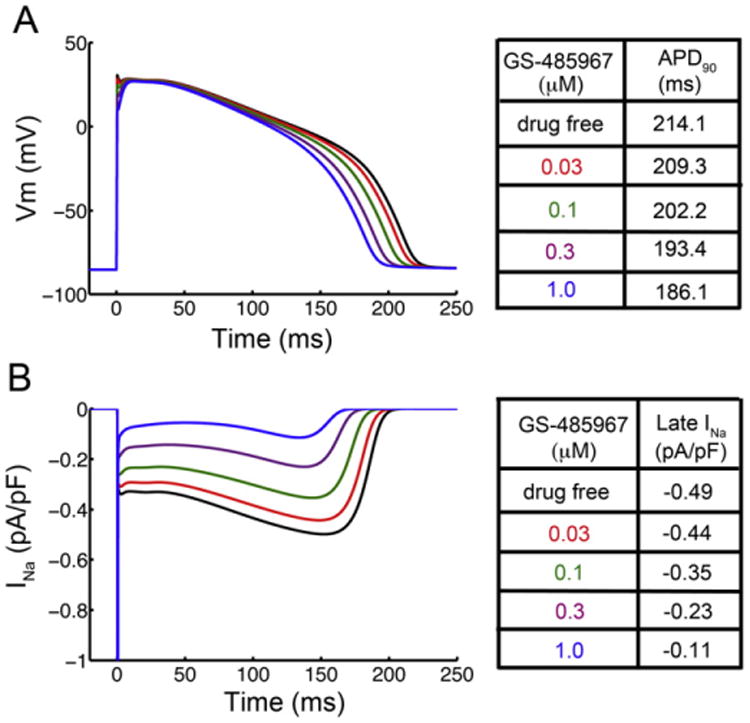
In silico prediction of GS-458967 induced reduction of I_NaL and concentration-dependent shortening of APD in rabbit ventricular myocytes. (A) Simulated effects of GS-458967 on rabbit ventricular myocyte AP and (B) the corresponding effects of GS-458967 on late I_Na.

3.2. GS-458967 normalizes drug induced APD prolongation

Our experimental data show that GS-458967 is very effective in reversing APD prolongation by agents/toxins that selectively enhance I_NaL (e.g. ATX-II). We used these data as a basis for comparisons for the computational model predictions. Specifically, we tested whether the selected drug concentrations would have similar effects when experimental data was compared to the model predictions, thereby acting as a model validation test and providing a basis for using the model for predictive testing. In Fig. 5 panel (A), experimental data from two different data sets from rabbit ventricular myocytes are shown in drug free conditions (left), and also following the application of 3 nM ATX-II (middle) as well as with combined 3 nM ATX-II with 0.3 μM GS-458967 application (right). Panel (B) shows the predicted effects of these same conditions in the virtual rabbit ventricular myocyte population constructed by randomly vary the amplitude of maximal conductances for I_Na, I_CaL, I_Ks, I_Kr, I_K1, I_to, I_NaK, I_NaCa to within (±) 10% of their nominal values in the rabbit ventricular myocyte model at a steady pacing frequency of 0.2 Hz with drug free (left), simulated effect of ATX-II (middle) and combined application of GS-458967 0.3 μM with ATX-II (right). This pattern of results clearly shows the same low concentration of GS-458967 is predicted to normalize the potent effect of ATX-II to prolong APD in the experiment and simulation (Table 2).

Table 2.

Simulated and experimental measured APD₉₀: To simulate enhancement of late I_Na with ATX-II, rate constant, μ2, was reduced by 40%.

BCL = 5000 ms Fig. 5	Experimental APD90 (ms) (mean values)		Simulated APD90 (ms) (mean values from 1000 APs)
	Cell 1	Cell 2
Control	258.8 (n = 11)	522 (n = 6)	240.91
ATX-II	625.2 (n = 10)	2305.2 (n = 12)	497.02
Relative change to ATX-II	58.6%	77.3%	51.53%

Having established that a reduction of I_NaL (by GS-458967) can be protective against APD prolongation during exposure to ATX-II, we focused on the effect of GS-458967 to normalize QT interval prolongation and reduce spatial dispersion of repolarization following application of ATX-II. Fig. 6 shows membrane potential space-time plots and simulated electrograms (lower) computed using a one-dimensional 165-rabbit ventricular myocyte transmural cardiac strand preparation. Panel A shows the effect of application of ATX-II alone during a short-long-short (S1-S2-S1) pacing protocol. Notice that ATX-II causes high amplitude T-waves on the computed electrograms following application of the S2. This is an indication of spatial APD dispersion. In (B), the effects of 0.03 μM GS-458967 both reduces QT interval prolongation and diminishes spatial APD dispersion as indicated by the marked reduction in T-wave amplitude. Panel (C) shows that an increase in GS-458967 concentration to 0.1 μM further reduced QT interval prolongation. The higher concentration of GS-458967 also reversed the repolarization gradient. This is illustrated by inversion of the T-wave. This effect is a result of repolarization of the endocardial myocytes before the epicardial myocytes. This is due to the larger effect of block of I_NaL on the background of smaller repolarizing currents intrinsic to the endocardial cells.

3.3. Reduction of I_NaL by GS-458967 reduces all proarrhythmia-linked parameters in the TRIaD

Detailed assessment of the effects of GS-458967 on the proarrhythmia parameters that form the TRIaD, systematic simulations to track each parameter were done (i) in the drug free control conditions, (ii) in the presence of dofetilide and (iii) with a combination of dofetilide and GS-458967. The results are shown in Fig. 7.

The effects of GS-458967 to improve temporal action potential duration dispersion were assessed first. We conducted a “computational experiment” using a myocyte sample consisting of 1000 action potentials generated after incorporating physiological noise [31] [23,32]. This produces quite pronounced beat-to-beat variability at 1 Hz pacing rate as shown in Fig. 7 (A) the drug-free control case (mean = 214.76 ms, standard deviation = 4.17 ms), (B) following simulated application of the I_Kr blocker dofetilide (16 nM) (mean = 256.27 ms, standard deviation = 6.89 ms) and (C) predicted effects of 0.3 μM GS-458967 with dofetilide 16 nM (mean = 236.87 ms, standard deviation = 5.24 ms). The noisy current was generated as described in [23] and in the Methods. Following pacing to steady-state at a stimulation frequency of 1 Hz, the physiological noise was applied throughout the duration of the ensuing simulation of 1000 paced beats. The action potentials for each beat during this noise protocol were recorded.

We next predicted the extent of action potential triangulation in silico as a function of APD prolongation in the myocyte population as described above for Fig. 7A–C. In Fig. 7 control (slope = 0.37) is shown in panel D. Panel E shows the effect of dofetilide 16 nM (slope = 0.52) and in (F) dofetilide 16 nM in combination with GS-458967 0.3 μM (slope = 0.35) is shown. Dofetilide increased both the APD₉₀ as indicated by the right shift and increase in area of the APD prolongation “cloud” (indicating more APD dispersion). In addition, dofetilide increased the triangulation slope, defined as APD₉₀ – APD₃₀. When dofetilide was applied in combination with GS-458967, the model predicted a return to baseline as measured by the APD₉₀ “cloud” and a reduction in triangulation.

The effect of the drugs on instability of APD (Fig. 7G) was detected and quantified as the difference between the maximum and minimum of 1000 individual cells with physiological noise current as a function of prolongation of APD shown in Fig. 7 panels A–C.

The beat-to-beat instability of rabbit ventricular myocyte action potential duration was assessed based on the sensitivity of virtual myocytes to small electrical perturbations before and after the application of drugs. A small inward current (between 0.1 and 0.2 pA/pF for 50 ms) was applied randomly during the AP plateau between 10–210 ms after AP initiation. Fig. 7H are Poincaré plots of sequential APD pairs indicating the beat-to-beat instability for each case. For the control case, shown in black, the mean APD₉₀ was 219.17 ms and the standard deviation was 4.75 ms, whereas the max and min APD₉₀ was 231.17 ms and 213.49 ms, respectively. The case for dofetilide 16 nM is shown in red with (mean = 263.31 ms, standard deviation = 7.67 ms, max APD₉₀ = 282.25 ms, min APD₉₀ = 252.37 ms). The case for dofetilide 16 nM in combination with 0.1 μM GS-458967 is shown in green and has APD₉₀ values as follows: mean = 242.91 ms, standard deviation = 6.12, max = 257.92 ms, min APD₉₀ = 232.33 ms. In blue is the effect of a higher concentration of GS-458967 (0.3 μM) in combination with 16 nM dofetilide resulting in a mean APD₉₀ of 230.41 ms, standard deviation of 4.84, max and min APD₉₀ = 242.76 ms and 222.47 ms, respectively.

Lastly, as shown in Fig. 7I, the potential for GS-458967 to decrease reverse use dependence induced by dofetilide was evaluated. The action potential adaptation curves were generated using APD₉₀ values from myocytes at steady-state at the indicated pacing frequencies. When dofetilide (red) was applied, there was a clear steepening of the APD adaptation curve compared to the baseline drug-free case (black). GS-458967 at 0.1 μM (green) flattened the curve, and the application of the higher dose of 0.3 μM of GS-458967 (blue) had a marked effect caused mainly by reducing the slow rate dependent APD prolongation.

Arrhythmia can be considered a fundamental emergent spatial phenomenon. Accordingly, simulations to determine whether GS-458967 could prevent reentrant arrhythmias in the setting of an in silico acquired Long-QT Syndrome were performed. In this study a two-dimensional heterogeneous anisotropic rabbit ventricular in silico tissue composed of (5 cm × 5 cm) myocytes was employed (Fig. 8). Simulations were conducted using a paired stimulus (S1-S2) protocol where the S2 was applied (following 200 paced beats initiated along the left endocardial edge of the tissue) following the preceding S1 in the computed vulnerable window for reentry. Time snapshots are shown on the left for phase maps [33]. These maps were constructed following the last planar wave (S1) (first panel) and throughout termination of the most persistent wave after S2 (last panel). Membrane voltages are indicated by the color gradient. The corresponding pseudo-ECGs are shown in the right panels. Panel A in Fig. 8 illustrates the control or drug-free baseline condition. In the absence of any drug, there was no persistent reentry. In panel (B) the effect of ATX-II is shown, which promoted a persistent reentrant arrhythmia. Panel (C) shows that ATX-II combined with 0.3 μM GS-458967 prevented the persistent reentry observed with ATX-II alone. When 16 nM dofetilide was applied (panel D), persistent reentry was induced, but this was prevented by co-treatment with 0.3 μM GS-458967 (panel E).

Fig. 8.

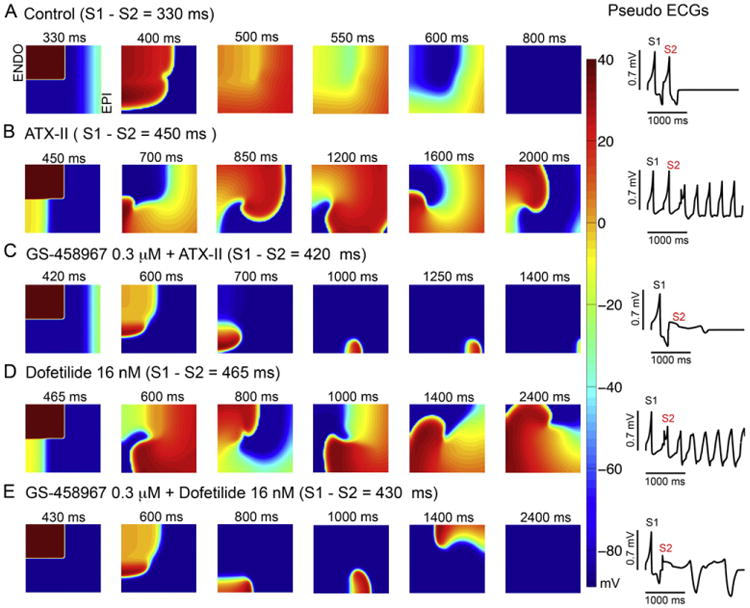
GS-458967 can prevent spiral wave reentry in the setting of acquired Long-QT Syndrome. A two-dimensional simulated heterogeneous anisotropic rabbit ventricular tissue was activated using a paired stimulus (S1-S2) protocol. (A) Shows the control or drug-free case, (B) with ATX-II, (C) with ATX-II and 0.3 μM GS-4589677, (D) 16 nM Dofetilide, or (E) 16 nM Dofetilide and 0.3 μM GS-458967. Tissues (5 cm × 5 cm) were stimulated (S1) along left edge (endocardium) and this followed by a premature stimulus (S2) applied in the vulnerable window (see Methods). Six snapshots obtained following application of GS-458967, dofetilide or both at selected time points. Corresponding pseudo-ECGs are in the right panels. Membrane voltage values are indicated by the color gradient.

4. Discussion

Recently, new chemical entities (NCEs) have been developed that specifically target the slowly inactivating component of the cardiac Na current, that is, the late Na current (I_NaL). Such compounds are now being evaluated as therapeutics in inherited and acquired cardiac diseases [34–40]. One promising preclinical candidate first described in 2013 is GS-458967. GS-458967 specifically and potently inhibits I_NaL (IC₅₀ for I_NaL = 130 nM) [9].

In order to begin to understand the potential for selective inhibition of I_NaL to mitigate arrhythmia risk associated with acquired Long-QT Syndrome, we have utilized experimental data describing the kinetics of the cardiac Na⁺ channel in rabbit ventricular cells models in order to modify the Soltis-Saucerman model of the rabbit ventricular myocyte action potential model. We then modeled the interaction of GS-458967 with the rabbit Na⁺ channel and the concentration-dependent effect of this novel preclinical compound to affect electrophysiological parameters in rabbit cells. Results of the simulations were in good agreement with experimental findings with both approaches showing potent concentration-dependent reduction in I_NaL and action potential duration. In these experiments and model simulations, GS-458967 did not affect myocyte excitability or conduction velocity in ventricular tissues, respectively [9]. Although I_NaL is small compared to peak (I_Napeak) (∼1–3%), the magnitude of this current is similar to that of other currents that are active during the action potential plateau phase, including I_Kr, the rapidly activated component of the delayed rectifier K⁺ current.

Abnormal cardiac electrophysiological activity is a common effect caused by block of hERG, the alpha subunit of I_Kr. Block of hERG leads to prolongation of the QT interval on the ECG, a phase of the cardiac cycle that corresponds to ventricular cell repolarization. Prolongation of the QT interval and proarrhythmia have been so strongly associated that the QT interval has become widely used as a surrogate marker for arrhythmia risk. Since 2005, the regulatory process for clinical drug candidates includes a dedicated clinical study in healthy volunteers, the so-called “Thorough QT Study”. A drug that causes greater than 5 ms QT prolongation above normal in healthy humans triggers a “regulatory concern”. In the present work, we asked the question, “Can we mitigate the risk of QT prolonging proarrhythmic drugs with targeted adjunctive therapy by the I_NaLinhibitor GS-458967”. In the current study, we undertook a combined modeling and experimental approach in an attempt to improve the rationale for predictive Cardiac Safety Pharmacology.

One way to prevent acquired Long-QT based arrhythmias is to screen and eliminate compounds that fail the Thorough QT test. An alternative solution is to identify derivative analogs of promising drugs that can retain therapeutic efficacy with reduced hERG block [41,42,43,44]. Another approach is to capitalize on the well-known fact that most effective antiarrhythmic drugs are “dirty” - they exhibit multiple channel effects [8]. By co-administering or co-formulating a specific I_NaL blocker in the setting of unintended hERG block, it may be possible to create a situation of “virtuous promiscuity”, where the two drug effects counter each and thus reduced or eliminate electrophysiological abnormalities, including prolongation of the action potential duration (APD) and lengthening of the QT interval [8,[45].

There is substantial precedent for the empirical mixing and matching of drugs to mitigate risk or reduce side effects [45,7]. Moreover, it is notable that the most successful on-market antiarrhythmic drugs exhibit multiple off-target or “dirty” effects. Examples include amiodarone, dronedarone and verapamil [1,2]. Here, we have expanded this concept in an attempt to develop a way to inform and predict the therapeutic benefit of mixing drugs to mitigate cardiotoxic side effects. We have focused on the common example of unintended hERG based cardiotoxicity. Our model predicts substantial reduction of all acquired Long-QT proarrhythmia-linked parameters through adjunctive administration using GS-458967 to specifically inhibit I_NaL and “cancel” or diminish the effect of hERG block.

We tested the potential for targeted inhibition of I_NaL by GS-458967 to improve cardiac safety in the setting of acquired long-QT Syndrome induced by dofetilide. Dofetilide is a prototype of the proarrhythmic class - associated with hERG block, QT prolongation and TdP [46]. We recently developed a detailed kinetically based model of the hERG blocker dofetilide by extending the consensus five-state Markov chain model that includes three closed states (C₃, C₂ and C₁), a conducting open state and (O) an inactivation state (I) [22,47,48,49]. This expanded I_Kr model that includes dofetilide interactions was incorporated into the Soltis-Saucerman rabbit ventricular action potential (AP) models [28]. Dofetilide has a distinct structure activity relationship that underlies drug-channel interaction kinetics that promotes the TRIaD: Triangulation, reverse use dependence, beat-to-beat instability of action potential duration, temporal and spatial action potential duration dispersion. Thus, we simulated the effects of dofetilide as a “positive control” against which we could systematically predict effects of GS-458967 on each parameter of the TRIaD linked proarrhythmia.

In our previous study [13], we carried out a simulation showing the effects of GS-458967 application on Na loading at different frequencies. We also showed the effect of the nominal changes to intracellular Na concentration on the amplitudes of the NCX and NaK currents during the action potential. These effects were minimal. Our results are not surprising. Previous studies have suggested that even pathological increases in late I_Na are not sufficient to account for substantial Na loading and that other mechanisms must also be contributing to Na loading during pathological states like heart failure [50,51,11].

There is a critical need to identify a more efficient and better approach for preclinical drug screening that is both specific and sensitive, and that also identifies actual “proarrhythmia”, rather than surrogate markers [52]. Here, we applied a multiscale modeling approach based on experimentally determined drug-channel interactions and kinetics intended to predict drug safety or electro-toxicity in the heart. Electrophysiological measurements were used to inform the kinetic parameters for functional scale Markov models of drug interactions with cardiac ion channels. Drug-channel models were then integrated into virtual cardiac cell and tissue level models to predict emergent drug effects to promote specific elements of the TRIaD, comprising the proarrhythmia markers that emerge at cell and tissue levels. Experiments were then used to test and validate the predictions of the model. Such a combined analysis could be used along with the proposed early QT assessment [53] in order to replace the so-called thorough QT study.

We suggest that the in silico TRIaD analysis performed here may be useful to finally remove some of the “art” that has been implicit in defining experimental conditions and ensuing tests that have been used to provoke arrhythmic responses [54]. Not only does the systematic application of the TRIaD tests allow the tracking of numerous proarrhythmic parameters, this approach also accounted for cell-to-cell variability and physiological noise that likely contribute to the random and rare amalgam of conditions that must be concomitantly present to allow a rare arrhythmia event to occur. The in silico screen presented in this study can be readily expanded with low cost and high efficiency to comprehensively examine any number of arrhythmia provoking conditions or additional electrophysiological parameters for preclinical drug testing.