Abstract
Current drug delivery devices (DDD) are mainly based on the use of diffusion as the main transport process. Diffusion-driven processes can only achieve low release rate because diffusion is a slow process. This represents a serious obstacle in the realization of recent successes in the suppression of lymphatic metastasis and in the prevention of limb and organ transplant rejection. Surprisingly, it was overlooked that there is a more favorable drug release mode which can be achieved when a special DDD is implanted near lymphatics. This opportunity can be realized when the interstitial fluid flow penetrates a drug delivery device of proper design and allows such fluid to flow out of it. This design is based on hollow fibers loaded with drug and whose hydrodynamic permeability is much higher than that of the surrounding tissue. The latter is referred to as hollow fiber of high hydrodynamic permeability (HFHP). The interstitial flow easily penetrates the hollow fiber membrane as well as its lumen with a higher velocity than that in the adjacent tissue. The interstitial liquid stream entering the lumen becomes almost saturated with drug as it flows out of the HFHP. This is due to the drug powder dissolution in the lumens of HFHP which forms a strip of drug solution that crosses the interstitium and finally enters the lymphatics. This hydrodynamically-driven release (HDR) may exceed the concomitant diffusion-driven release (DDR) by one or even two orders of magnitude. The hydrodynamics of the two-compartment media is sufficient for developing the HDR theory which is detailed in this paper. Convective diffusion theory for two compartments (membrane of hollow fiber and adjacent tissue) is required for exact quantification when a small contribution of DDR to predominating HDR is present. Hence, modeling is important for HDR which would lead to establishing a new branch in physico-chemical hydrodynamics. The release rate achieved with the use of HFHP increases proportional to the number of hollow fibers in the fabric employed in drug delivery. Based on this contribution, it is now possible to simultaneously provide high release rates and long release durations, thus overcoming a fundamental limitation in drug delivery. Perhaps this breakthrough in long-term drug delivery has potential applications in targeting lymphatics and in treating cancer and cancer metastasis without causing the serious side effects of systemic drugs.
Keywords: Hydrodynamically-driven drug release (HDR), Diffusion-driven drug release (DDR), Hollow fiber of high hydrodynamic permeability (HFHP), Rate of HDR, Duration of HDR, Lymphatic targeting
1. Introduction
Drug release kinetics and related pharmaceutical drug delivery applications [1,2] are largely based on the principles of surface and colloid science, in particular, colloidal transport in porous adsorbing media, diffusion processes, lipophilic/hydrophilic balance and membrane wetting. The broad application of colloid and interface science has been successfully employed to describe lymphatic targeting with drugs [3,4]. The above principles have been further used to control the delivery of immunosuppressive drugs to prevent limb and organ transplant rejection, and to treat cancer or prevent cancer metastasis. There is evidence in the literature that when tacrolimus (FK-509) is injected subcutaneously in the form of a hydrogel, it could suppress limb rejection in rats for more than 100 days [3,4].
Clinical experience has demonstrated that long-term drug delivery by means of daily injection is not convenient for patients. A cardinally new development to achieve long-term drug delivery without daily injection can be based on the implantation of a drug delivery device (DDD) near the initial lymphatics, mainly near the ensembles of initial lymph capillaries (ILCs). This new device could provide a permanent drug stream along the initial lymphatics to lymph nodes (LNs) which are located downstream of the interstitial fluid flow. Since LNs are the main site where leukocytes/lymphocytes reside and where circulating/released cancer cells are transported, their targeting with drug will suppress the local immune system, kill cancer cells or provide other forms of therapy.
A similar strategy in drug delivery may be suitable to suppress cancer metastasis when the tumor is close to and draining into local lymphatics. Currently, there is central recognition that lymphatic targeting with immunosuppressant and cytotoxic drugs can be used to prevent or decrease cancer metastasis [5]. In this particular application, similar to tacrolimus (KF-509) [3,4], long-term drug release can be employed to suppress tumors. To achieve this goal, simultaneously a high-release rate is required to provide drug concentration within LNs (Cln) above the minimum inhibitory concentration (MIC) of the drug. MIC is the minimal drug concentration needed to achieve effective therapy. Simultaneously providing high release rates, dictated by the MIC value of the drug, and a long release duration will be possible if a rather large amount of drug is stored in a DDD in the form of solid particles or powder. This DDD may be a hollow fiber with a porous wall having a sufficiently large pore radius and where a large amount of drug can be stored in the lumen of the fiber to provide for long-term release. In this DDD, the wall of the hollow fiber functions as a membrane to transport the drug loaded in the fiber lumen to the surrounding tissue.
If pore wetting of the hollow fiber wall membrane of the DDD is provided, significant flow of interstitial fluid flow in the pores takes place. This process leads to the filling of fiber lumen with interstitial liquid and to the gradual dissolution of the drug. After a short relaxation time, the onset of steady drug diffusion from the fiber lumen through the membrane (fiber wall) into adjacent tissue occurs.
This mechanism corresponds to the accepted understanding of drug release when the walls of the device are porous. We will define this mechanism as diffusion-driven drug release (DDR). There is a serious constraint in this mechanism caused by the low diffusivity of drug molecules in adjacent tissue Dti. Dti is only 6.10−8 cm2/sec, as for example in the Tenofovir (HIV drug) case [6].
The drug delivery from the DDD to the lymphatics is a two-stage process: (i) short-range transport from DDD to adjacent tissue (drug release), and (ii) further long-range transport along the tissue to the lymphatics. Although the characteristic distance for the second stage of transport may be orders of magnitude larger than the first, its duration may be orders of magnitude shorter. This occurs because there is interstitial fluid flow to the lymphatics and this involves the released drug during this movement (convective transport).
In spite of the very low velocity of interstitial flow [7], about 1 micron/sec, the second stage of transport takes less than 20 min (time required to cover a distance of about 1 mm between the hollow fiber of the DDD and the lymphatics at a velocity of 1 micron/sec).
According to this much faster transport mechanism, the convection affects drug diffusion transport from the hollow fiber into the interstitial flow. At a much smaller distance than fiber radius Rf, diffusion predominates in the thin diffusion layer δ. At a distance larger than δ, convective flow predominates. Nevertheless, we accounted for diffusion enhancement due to convection in this work and found that the diffusion-controlled drug release rate is too slow to provide drug concentration in the lymph node (Cln) higher than MIC. Hence, the inevitable weakness of the diffusion-controlled drug release mechanism represents a serious constraint for lymphatic targeting by means of a DDD implanted near the lymphatics.
Fortunately, DDD in the form of hollow fibers with a porous wall offers an opportunity to realize a cardinally different and surprisingly stronger mechanism for drug release. As there is no relevant information available in the literature, we call this new and promising mechanism of drug release “hydrodynamically-driven drug release (HDR)”.
Two conditions are needed to realize the HDR mode. The first condition for the onset of HDR is the placement of the DDD near initial lymphatics in order to provide a stable and a not weak interstitial flow in the fiber vicinity. The second condition for the onset of HDR relates to the property of the hollow fiber membrane, namely: its pore diameter and porosity need to be sufficiently large to provide hydraulic permeability of the membrane (and fiber) much higher than that of the tissue. Correspondingly, this kind of hollow fiber may be called hollow fiber of high permeability (HFHP). Although increasing the pore size leads to an increase in drug diffusivity of the membrane Dm, this does not by itself cause overall drug release because the latter is controlled by lower diffusivity in the tissue Dti.
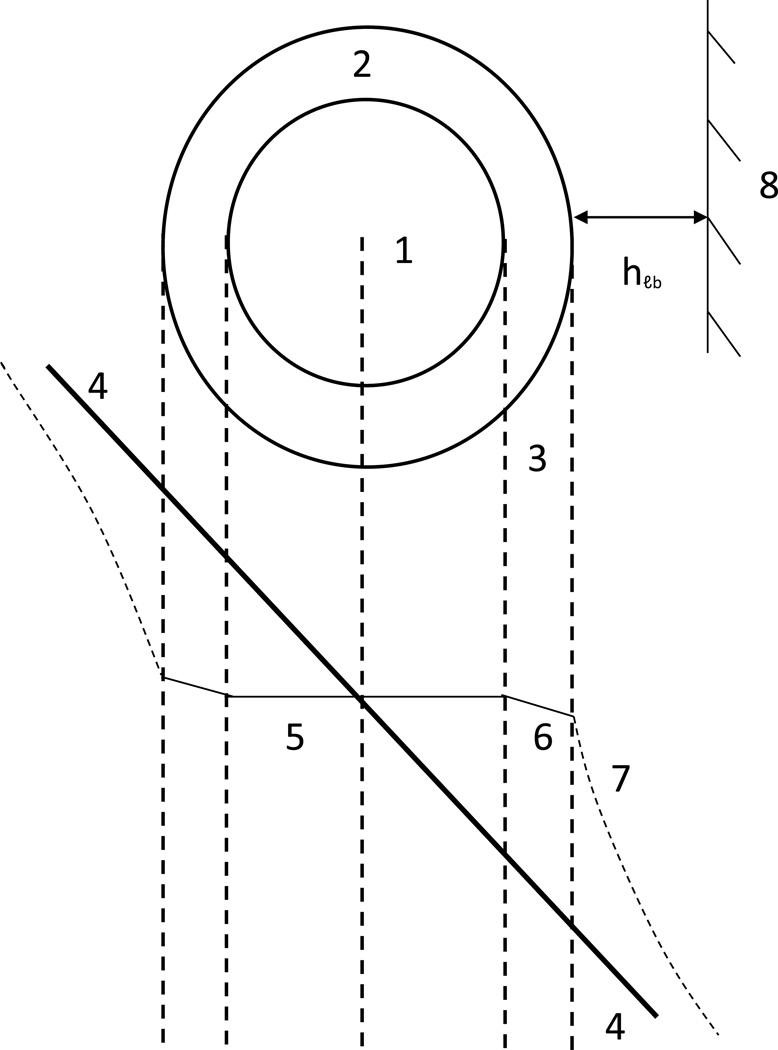
The unique and valuable characteristics of HFHP are the strong penetration of interstitial fluid flow through the fiber membrane into the fiber lumen and the achievement of permanent flow through the HFHP. This interstitial fluid flow through the lumen of HFHP, filled with drug powder, may be considered one central premise for achieving HDR. Moreover, the interstitial fluid flow concentrates within HFHP because such flow meets a smaller resistance in the tissue space occupied by the fiber as depicted in Fig. 1.
Fig. 1.
Schematic illustrating: a) drug strip caused by hydrodynamically-driven drug release which encounters a small portion of disk-like lymphatic bed (LB). 1) Disk-like LB, 2) Hollow fiber with high hydrodynamic permeability (HFHP), 3) Drug convective strip, 4) Streaming lines; b) 1) membrane of hollow fiber, 2) drug powder, 3) lumen
It is known that the interstitial flow is very slow and consequently, the liquid flow through the fiber lumen moves at a similarly slow velocity. This means that the residence time of liquid crossing the lumen is rather long. It may be estimated as 2Rfi/Vl, where Rfi is the internal radius of fiber and Vl is velocity in the lumen whose difference from interstitial velocity before fiber implantation is not very large and will be quantified later in this paper. As the liquid entering the fiber lumen is clean (drug-free), drug dissolution into the slow liquid flow takes place. As the residence time is rather long inside the lumen, the interstitial fluid flow crossing the fiber will almost achieve the saturation concentration of the drug.
Hence, the portion of the interstitial fluid flow which penetrates the hollow fiber becomes saturated with the drug. If the volumetric velocity of this portion is nominated qf, the amount of drug released from a single fiber per unit of time (drug release rate, Jc) equals
| (1.1) |
where
| (1.2) |
where 2Rflf is the area of the axial cross-section of fiber of length lf.
One concludes that the release rate in this case may be quantified without taking into account diffusion because it is mainly controlled by convective transport. Hence, this is considered a special mode of drug release, which qualitatively differs from the conventionally known diffusion-controlled drug release.
The latter, diffusion-controlled drug release, occurs when the pore dimension and porosity of the membrane are smaller than those of the tissue. Although interstitial hydrodynamic flow penetrates the hollow fiber in this case as well, convective transport is very weak in comparison with diffusion, which controls the diffusion rate. Since a typical tissue comprises both initial lymphatics and venules, the hydrodynamically-driven drug release may be employed to deliver drugs to many tissues and organs.
Because experiments with device implantation in animals or humans are expensive and time consuming, especially when investigating long-term release, employing mathematical modeling becomes mandatory. It is clear that identification of velocity in Eq. (1.2) in the fiber with the interstitial velocity before fiber implantation is over simplification. The theory has to predict the velocity distribution inside the hollow fiber and in its vicinity when the local velocity is known before implantation. In addition, the flow in the fiber lumen has to be considered. Hence, three compartments have to be included in the modeling, namely: fiber lumen, fiber membrane and adjacent tissue.
The hydrodynamics for closed membrane was systematically elaborated by Professor Starov’s group [8]. However, there is an essential difference between [8] and the case when a hollow fiber with a porous wall is considered. First, cylindrical symmetry has to be introduced for the case of porous hollow fiber, while impermeable spherical particles covered by a spherical porous shell was elaborated in [8]. Another difference is that a two-compartment problem was studied in [8] compared to the three-compartment problem detailed in the present study. The hydrodynamic flow in [8] comprised a spherical membrane and an external flow while the spherical particle was hydrodynamically impermeable. The most essential difference between [8] and our case is that the external compartment in unconfined liquid in [8] dictates the application of the Navier-Stokes equation. In contrast, all three compartments for implanted hollow fiber consider porous media with different levels of hydraulic permeability; one of the three compartments is the porous hollow fiber. Accordingly, the present study considers a new problem relevant to both general hydrodynamics of porous media and membrane science.
Fortunately, there is mathematical similarity between this new problem and other classical mathematical problems in many areas of physics. Examples of the latter include electrical conductivity, thermal conductivity, magnetic susceptibility and diffusion in disperse systems [9,10]. These classical problems address two-compartment systems with spherical or cylindrical symmetry; however, the geometry of the hollow fiber did not attract attention. Nevertheless, the similarity found has provided a mathematical approach which allowed us to elaborate the hydrodynamics of porous hollow fiber case in this study (Section 4). In turn, this result enabled us to derive a more rigorous equation for the hydrodynamically-driven drug release (HDR).
To design a drug-delivery implant, it is not only sufficient to consider the release rate but the pharmacokinetics also need to be considered as well. This is required in order to determine if Cln > MIC could be achieved. In addition, it is necessary to consider what release duration can be obtained and what drug has to be used especially with respect to its saturation concentration (Cs). The latter is needed to provide designs and formulations to achieve desirable release duration. In addition to addressing the hydrodynamics of porous hollow fiber, the present contribution achieves the following objectives:
Consideration of the hydrodynamics of the ensemble of ILCs called the lymphatic bed (LB) – Sections 3 and 5.
Development of an equation for the release rate for hollow fibers and hollow fiber fabric implanted near the LB – Sections 7 and 8.
Development of an equation for the release duration from implanted hollow fibers and/or fiber fabric- Section 9.
2. Coupling between lymph hydrodynamics and hydrodynamics in interstitium
2.1. Transport properties
Transport properties were addressed in connection with the composition of the interstitium (collagen, glycosaminoglycan, etc.) in [11]. Interstitium composition involves hydration of the tissue, and as a consequence the calculated pore radius can double resulting in about three to five times increase in the interstitial fluid volume [11]. The concept of the interstitium as a static structure predominates in the description of transport properties and this would thus influence the modeling which is primarily based on the Darcy law [12]. Specifically, 1.5 · 10−9 cm4 dyne−1 sec−1 [11] and 5 · 10−12 cm4 dyn−1 sec−1 were reported for the hydraulic conductivity of a normally hydrated tissue.
2.2. Pre-nodal lymphatics
The lymphatic system is composed of a network of vessels, termed lymphatics, which include lymph nodes and lymphoid organs. Pre-nodal lymphatics consist of initial lymphatics, pre-collecting lymphatics and collecting lymphatics. Interstitial fluid enters through the small lymph capillaries (also called initial or terminal lymphatics) that gradually combine to form larger diameter vessels, namely the pre-collectors that combine to form collectors.
2.3. Mechanisms of interstitial fluid mobilization
Interstitial fluid originates when blood plasma leaves the arterioles and flows into tissue, where it becomes tissue fluid, also known as interstitial fluid. When this interstitial liquid enters the initial lymph capillaries, it is called “lymph,” and this transition process is called the lymph formation. Oncotic pressure caused by the gradient of protein concentration and hydrostatic pressure may contribute to lymph formation. However, there are many unanswered questions regarding the role of oncotic pressure in lymph formation which still need to be answered [7, 11].
The hydrostatic pressure theory of lymph formation relies on the development of hydrostatic pressure differences between the interstitium and the lumen of the initial lymphatic (Fig. 2). This theory relies on the contraction/compression and relaxation cycle of either the extrinsic or intrinsic lymph pump in initial or collecting lymphatics, and on the function of one-way valves in the initial lymphatics [7]. These one-way valves allow for the transient entry of fluid into the initial lymphatics during the expansion/relaxation phase and prevent fluid loss during the contraction/compression phase [7]. In turn, interstitial flow is connected with lymph formation. One concludes that interstitial flow depends on the contractile activity of lymphangions [7] as well as the action of extrinsic forces.
Fig. 2.
- Schematic showing the decreased pressure inside an ILC and the axial dependence of pressure.
- Interstitial fluid flow towards an initial lymph capillary; Jr(R,Z) is the flux density in the radial direction around the ILC with axial symmetry.
2.4. Mathematical models
Recent investigations explored the delivery of protein drugs to lymphatics via subcutaneous injection as the primary delivery route [7]. Since there is no subcutaneous injection in our case, it was shown [13, 14] that this will lead to an essential modification of the task when considering both the movement of interstitial liquid and convective transport. Nevertheless, the fundamentals in our approach cannot essentially differ from those described in the literature [7]. The bases for our modeling are: i) the conservation laws which govern the transport of interstitial fluid and drug molecules, ii) the transport properties of the interstitium, iii) the hydrodynamics of afferent (pre-nodal) lymphatics, and iv) the equations which interconnect lymph flow and the flow of interstitial liquid, as follows:
The conservation law for incompressible fluids is:
| (2.1) |
where v is superficial velocity distribution in space.
The conservation law for momentum is the Darcy law for the interstitium
| (2.2) |
where p is pressure distribution in space, η is viscosity of the interstitial fluid and Kti is the hydraulic conductivity of the interstitium.
The conservation law for the momentum for propulsion in the initial capillaries is the Navier-Stokes equation. The flow potential ψ satisfies the Laplace equation which follows from Eq. (2.2) and the equation for fluid conservation (Eq. (2.1)).
| (2.3) |
i.e.,
| (2.4) |
3. The interstitial velocity distribution around a lymphatic bed
While the hollow fiber diameter considered is about 300 micron, the diameter of the ILC is only about 20 micron. The placement of a hollow fiber at a small distance from an ILC is surgically difficult to achieve. On the other hand, the velocity generated with a single ILC is too weak at a large distance from the ILC, where the hollow fiber placement is surgically possible. Fortunately, the velocity at a distance of about one fiber diameter is a superposition of velocities originated by numerous ILCs attached to pre-collecting collectors, which in turn are attached to single collectors (Fig. 5). We may assume linear superposition if a liquid stream of a certain ILC is not affected by the interstitial stream generated by adjacent ILCs. This is possible if the shortest distance between an adjacent ILC is not large. This ensemble of ILCs is called the “lymphatic bed” (LB).
Fig. 5.
Schematic for prenodal lymphatics - Axial cross-section of 3D structure: 1 afferent capillary (collector); 2 precollector; 3 ILCs
The velocity distribution around the LB at the shortest distance between the fiber surface and the LB surface is required to quantify the hydrodynamic flow penetrating the hollow fiber. However, it is important to define the LB surface. We consider the LB surface as an imaginary surface whose shape is the shape of the ILCs ensemble. The above definition of LB surface simplifies the modeling due to its large characteristic dimension in comparison with the ILC dimension. Naturally, the roughness of this imaginary surface may be at least about one ILC in length, i.e., lic ~ 0.05cm. This roughness may be neglected when the LB dimension is much larger. The LB may consist of one layer of ILC. The LB surface may be imagined as a surface comprising the entire length of this layer. This definition may preserve when, in addition to this layer, a deeper layer or layers of ILCs are present. This definition also assumes a convex shape of the ILCs layer. A more general definition of the LB shape is required if the concave portion of the surface is not small. A certain ambiguity of the notion of LB surface plays a minor role in modeling when the velocity is quantified at a distance from the LB, which essentially exceeds lic.
In our preceding work [13,1], it was shown that the pressure drop in the interstitium exceeds essentially the pressure drop along an ILC. This means that pressure change along the LB surface is considered very small and consequently, the tangential velocity is also very small in comparison with the normal flow velocity and hence, it may be neglected.
Consequently, the LB as an outlet and generator of interstitial flow may be characterized by distribution of the normal component of velocity along the LB surface. This distribution can be found in the solution of the Laplace Eq. (2.4) with boundary condition p=const over the LB surface. When the LB surface is rather simple (spherical, cylindrical, disk-like), Vn along the surface is uniform. The product and surface area of the LB Slb is the total flow through the LB which upstream flows through the collector (afferent vessel), i.e.,
| (3.1) |
where Qaf is the measurable volumetric velocity in the afferent vessel which is unknown and is difficult to measure. Consequently, it is expressed through Qaf and Slb and is amenable for measurement
| (3.2) |
4. Application of the Darcy law and the Laplace equation for quantification of hydrodynamic flow through implanted porous hollow fiber
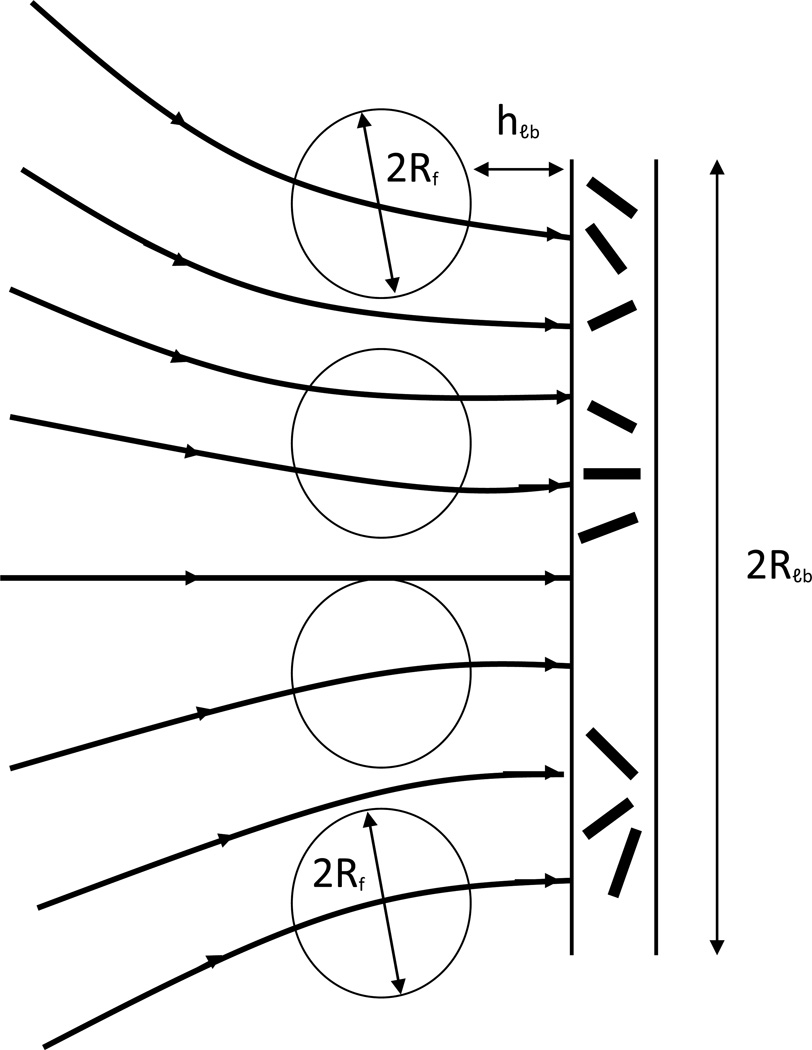
Although the velocity distribution around the LB is non-uniform (for example, it decreases when the distance between the fiber and LB increases), it can be approximately considered as uniform within an area whose linear dimensions are much smaller than the LB dimension. The fiber diameter is much smaller than the LB dimension. When a hollow fiber is implanted at a certain distance from the LB surface, the velocity distribution inside the lumen and in the fiber vicinity depends only on the velocity distribution which existed at the same distance before implantation. As the linear dimension of this area is about 2Rf and consequently, is much smaller than the LB dimension, the implanted fiber can be considered as placed into uniform interstitial flow with velocity V(hlb). This simplification may be called locally uniform approximation. This approximation is used in the present study in formulating the problem addressed to modeling the local velocity distribution after fiber placement.
Identification of liquid flow velocity through a fiber with local velocity V(hlb), which existed before fiber placement not far from the LB, is used as only the first and rather crude approximation. Even without quantification, it is clear that the velocity in the lumen Vl exceeds Vlb. As the fiber’s Darcy constant essentially exceeds Kti, the streaming lines concentrate (Fig. 1) within the lumen, which leads to an increase in the hydrodynamically-driven release. For this purpose, the velocity distribution has to be quantified in three compartments, namely: in tissue, in membrane and in lumen taking into account the interconnection between them. This may be done without the use of a complicated three-compartment model Kl ≠ Km ≠ Kti, where Kl, Km and Kti are hydrodynamic permeability in lumen, membrane and tissue, respectively, taking into account that the pores between the drug powder particles in the lumen are much larger than those in the membrane itself, even at condition Km >> Kti. This means that Kl >> Km. As this is so, even a small pressure drop is sufficient enough to drive the interstitial liquid across the fiber lumen. This pressure drop may be neglected. An approximately uniform pressure in the lumen may be identified with the locally uniform pressure before fiber implantation, i.e., pressure in cross-section θ = π/2. A schematic of the pressure distribution within the three compartments is presented in Fig. 3.
Fig. 3.
Schematic showing pressure distribution arising after placement of hollow fiber into interstitial flow generated by lymphatic bed (LB). The fiber axis is parallel to the LB surface. 1) fiber lumen; 2) hollow fiber membrane wall; 3) tissue. The straight line; 4) shows the linear pressure distribution Pext, existed before fiber placement; 5) pressure distribution in lumen with small gradient because Kℓ >> Km; 6) pressure distribution with membrane with higher pressure gradient because Km >> Kti; 7) pressure distribution inside adjacent tissue with high pressure gradient near membrane surface because of Kti << Km, pressure gradient gradually decreases approaching at a large distance to initial pressure gradient; 8) LB surface
There are two boundary conditions at the interface between tissue and membrane
| (4.1) |
| (4.2) |
The pressure drop across the membrane is larger than that through the lumen, but is much smaller than that across the tissue. In addition, the membrane thickness is rather small. This allows us to consider linear dependence on r within the membrane. As to the pressure distribution outside the fiber, a proper solution of the Laplace equation, written in the cylindrical system of coordinate
| (4.3) |
is required. In order to satisfy the conditions of uniform and given pressure gradient, namely, gradpext (approximation of locally uniform velocity distribution) and the boundary condition of the fiber surface, the solution may be sought in the form of linear superposition |gradpext| rCosθ and a second function, which is proportional to Cosθ and tends to go to zero at infinity. The function Cosθ/r satisfies the Laplace equation and tends to zero at infinity and is proportional to Cosθ. There is one unknown coefficient in this superposition and one unknown coefficient in the pressure distribution within the membrane. These two unknown coefficients are determined with the use of two boundary conditions (1) and (2): The substitution of the aforementioned superposition with unknown coefficients in boundary conditions (4.1) and (4.2) yields a system of two linear algebraic equations with two unknown coefficients. This system is easy to solve and substitution of the found coefficients yields
| (4.4) |
| (4.5) |
where Rmi is the lumen radius (internal radius of the fiber) and plb is pressure in the lumen, which is almost uniform. Hence, pressure on the boundary between lumen and membrane, i.e., pm(Rmi,θ) has to be uniform as well, which is accounted for in Eq. (4.5).
The formation of the diffusion layer on the fiber surface is affected by the tangential and normal components of velocity on the external surface of the fiber, i.e., at r=Rf
| (4.6) |
where plb(r,θ) is the pressure distribution caused by the LB before fiber placement. The vector Vlb may be formally characterized by θ and r components
| (4.7) |
Combining equations for and Vlb yields
| (4.8) |
where |Vlb|Cosθ is .
At the used condition Km >> Kti, the coefficient in Eq. (4.8) is approximately 2. Hence, the accomplished quantification revealed that hollow fiber placement in tissue leads to twice an increase in the local velocity. This in turn leads to a twice stronger HDR. A similar procedure yields for
| (4.9) |
It is noteworthy that a rather small multiplier 2lm/Rf appeared in the expression for tangential velocity. The physical reason for this is due to smaller angular dependencies of pressure in the lumen and in the membrane. This is caused by large Kl and small lm.
A five times decrease in tangential velocity leads to weaker convective diffusion with a concomitant decrease in its role in comparison with HDR.
Vθ(Rf,θ) and Vr(Rf,θ) are present in the Levich equation [15] for convective diffusion of the hydrodynamically-impermeable sphere as well. Their angular dependencies are Cosθ and Sinθ, respectively, as well. However, the amplitudes of the velocity component in the Levich case are almost the same, i.e., Vθ(θ = π/4)~Vr(θ = π/4). In contrast, the strong hydrodynamic permeability of the fiber leads to two (2) fundamental differences in the velocity components. The permeability leads to a decrease in tangential velocity by a factor of Rf/2lm in comparison with external velocity Vlb. In the meantime, the smaller Vθ(Rf,θ) is, the weaker is the convection influence on diffusion. As δ becomes thicker, weaker diffusion is predicted in this case. Vθ(Rf,θ) decreases 5 times (lm = 15 micron) leading to Pe decrease of 5 times and to δ increase Pe0.5=100.5~3.16 in comparison with Levich equation.
The mathematical problem, including the Laplace equation and boundary conditions, similar to (4.1) and (4.2) for the two-compartment system, is a classical task in many areas of physics: electric conductivity, dielectric phenomena, diffusion, etc. Correspondingly, analogs of the Darcy law are the differential Ohm law, Fick law and Fourier law. This mathematical analogy allows us to introduce this general principle of similarity, the application of which is discussed in [9]. If the task under consideration is mathematically solved for a certain branch of physics, this solution can be used for other branches as well. It is sufficient to replace the main characteristics, for example, to replace the differential conductivity σ by diffusivity D in the found distribution for electric potential and to obtain the concentration distribution in the diffusion task. Naturally, this is possible if the geometries of the compartment tasks are identical. It is surprising that the problem of pressure distribution in the two-compartment porous media was not discussed earlier in the framework of the generalized principle of similarity. Unfortunately, it is impossible to apply this principle to interconnect pressure distribution arising after implantation of a porous hollow fiber. To our knowledge, the geometry of porous hollow fiber has not attracted attention.
5. A model for the lymphatic bed and the interstitial flow around it
The axial lymph flow inside the ILC initiates the flow of interstitial fluid towards its external surface (Fig. 1). As the diameter of the ILC is very small (about 20 micron), this axially symmetrical flow may decrease in orders of magnitude in distance from the ILC hlb about the fiber radius (Rf about 150 micron). In reality, this may not happen because many ILCs forming the LB contribute to the interstitial flow at a long distance. In the meantime, the interstitial velocity at a long distance is of interest with respect to drug release from the hollow fiber because its placement at a small distance to the ILC is problematic due to surgical limitations. Hence, the distribution of interstitial velocity at a long distance from the LB is of interest in achieving effective drug release from the hollow fiber.
According to a well-known review [16], the microanatomy of pre-nodal lymphatics is organ specific in contrast to the mechanism of lymph formation and mobilization (valves, primary and secondary, etc.), which is universal. Initial lymphatics, pre-collecting lymphatics and collecting lymphatics constitute the main portions of pre-nodal lymphatics (Figs. 4 and 5). Interstitial fluid enters through the small initial capillaries 20 micron in diameter that gradually combine to form larger diameter vessels, namely the pre-collectors (150 micron in diameter,) and the latter further join to form the collectors (500 micron in diameter). There are data in the literature [17] about the characteristic length of initial capillaries (500 micron), pre-collectors (1000 micron) and collectors (3000 micron). The authoritative reviews [16, 17] do not provide more detailed information, in particular about the number of pre-collectors npc per one collector and the number of initial capillaries nic per one pre-collection. Both of these numbers are not large according to some brief remarks in the literature. In addition, schematic illustrations of very complex three-dimensional structures of pre-nodal lymphatics in the literature are not quantitative, for example, Fig. 1 in [17] (Fig. 4) for cardiovascular lymphatics.
Fig. 4.
The lymphatic system.
To render the modeling of drug release more clear, we illustrate the spatial structure of the pre-nodal lymphatic with an example (Fig. 5). The illustration assumes a rather regular structure with respect to angles and of rotation around the collector axis and pre-collector axis, respectively. Then the sequence of rotation around the axis of collector and pre-collector allows one to characterize the structure of pre-nodal lymphatics in three dimensions.
With respect to the transformation of interstitial fluid into the lymph, the fundamental difference between ILCs and pre-collecting and collecting lymphatics is that this process occurs only within the ILC wall, while there is no liquid flow through the walls of pre-collecting and collecting lymphatics. Hence, being interested in lymphatic flow, we may restrict our interest to ILC ensembles, which will be called the lymphatic bed (LB). On the other hand, the linear dimension for pre-collector and collector lymphatics allows to estimate the radius of the LB Rlb from below. It is seen that Rlb is about some millimeters which exceeds that in order of magnitude the thickness of the LB which is about the length of the ILC, i.e., about 0.5 mm. This allows us to model the LB shape as a thin disk with radius Rlb.
Unfortunately, there is large uncertainty regarding the Rlb value, which may only be evaluated from below and from above, using information about capillary length and radii.
| (5.1) |
where lpc and lic are lengths of pre-collector and collector lymphatics, respectively, αpc and αic are angles between the collector and pre-collector axis and between the axis of the ILC and the axis of the pre-collector, respectively. The absence of information about αpc and αic causes an uncertainty. The estimates from below and from above follow when αpc = αic = 0 or αpc = αic = π/2.
| (5.2) |
or 250 micron < Rlb < (250 + 1000 + 500) micron 250 micron < Rlb < 1750 micron
If αpc = αic= π/6, Rlb ~ 1000 micron. However, the disk is not thin in this case because 2Rlb = 2000 micron exceeds lic = 500 micron only 4 times.
The component is almost invariant and equal for two flat surfaces of disk. The larger the distance to the flat surface is, the larger is the variation of between the axis and the edge of the disk. This is illustrated in the schematic illustration of interstitial velocity distribution around a thin disk (Fig. 6). When the distance hlb to the flat surface of the disk-like LB is small in comparison with Rlb, namely hlb < Rlb, the velocity distribution is uniform and is approximately equal to .
Fig. 6.
Schematic for velocity distribution around disk-like lymphatic bed of initial lymph capillaries
The volumetric velocity of the entire interstitial flow which enters both flat surfaces of the LB is ), where is difficult to measure. This interstitial flow transforms into lymph flow in the collector with volumetric velocity about , where Vaf and Qaf are linear and volumetric velocities, respectively, through the afferent vessel, which is an alternative term for collector. Some information about Vaf in the literature exists. Hence, the unknown may be calculated as , that yields . This equation allows one to eliminate the unknown from the equation for the release rate: .
While the linear velocity inside the ILC was measured by many research groups, the data about velocity along the afferent capillary is scarce. There is consensus about the velocity along the ILC 10 < Vic < 50 micron/sec [7]. Hence, the value given in [18], namely 0.02 micron/sec, which is 3 orders of magnitude smaller than the results of many groups, is a misprint or refers to a different animal model (mouse model). Indeed, mm/sec instead of printed micron/sec yields for the ILC a reasonable value Vic = 0.02 mm/sec = 20 micron/sec instead of the erroneous 0.02 micron/sec. Then, the unaccepted velocity value for the afferent vessel Vaf = 0.2 micron/sec has to be replaced by Vaf = 0.2 mm/sec = 200 micron/sec.
Although there was a possibility of using values for the linear interstitial velocity from the literature [7], we prefer to introduce Vaf and Rlb for to various reasons. It is not to be excluded that a different Rlb and consequently, a different Vint are possible at the same Vaf. Perhaps this is the reason that the measured Vint varies in a broad range. On the other hand, both Rlb and Vaf are measurable, which allows one to clarify whether the correlation between Vaf and Rlb exists or not. If it exists, Vint is predetermined with Rlb values, whose measurement is easier. On the other hand, information about Rlb is required to specify the dimension of hollow fiber fabric (Section 8).
6. Suppression of convective diffusion under the condition of hydrodynamically-driven drug release. Influence of a normal component of velocity
The illustration in Fig. 7 for the angular dependence of pore velocity shows that there are no conditions for diffusion in the angle range π/2 < θ < π because the liquid that enters the pores is already saturated with drug and there is no concentration gradient along the streaming line. In contrast, clean liquid enters the pores in an angle range 0 < θ < π/2, while downstream in the lumen, the liquid is saturated with drug. Hence, drug diffuses at this angle range from the lumen into the pores when 0 < θ < π/2.
Fig. 7.
Schematic illustration distribution along fiber surface of normal component of velocity on membrane surface.
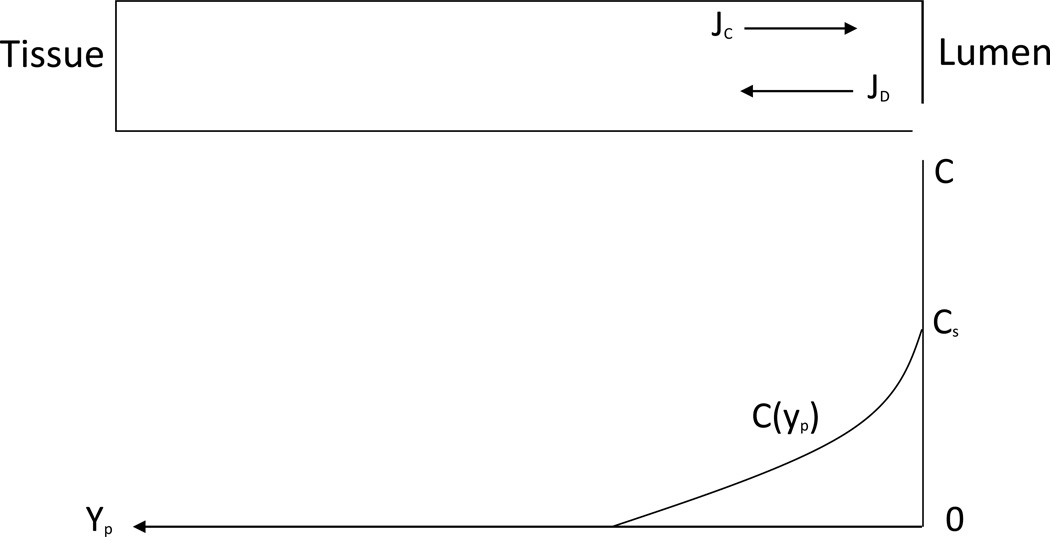
A straight pore as in the case of a nucleopore membrane is shown in Fig. 8. With coordinate yp, while yp(0) corresponds to the internal surface of the membrane wall, where the concentration equals approximately Cs. Within a straight pore, liquid moves with mean velocity
| (6.1) |
where ε is the membrane porosity towards the lumen, while the diffusion proceeds in the opposite direction. After the first onset of steady state, the velocity profile is determined by the condition that the diffusion flux in any cross-section is equal to convective flux.
| (6.2) |
whose solution shows the exponential decay in the direction of the tissue.
| (6.3) |
Fig. 8.
Schematic to mechanism of preventing drug diffusion from lumen into tissue due to opposite liquid flow in a single isolated straight pore (hollow fiber membrane).
The characteristic length l of drug penetration into the pore opposite to the convection direction is
| (6.4) |
| (6.5) |
There is no essential release from the pores located on the fiber at θ < θb. This occurs because for smaller θ(smaller than θb), the convective flow prevents diffusional penetration through the entire length of the membrane. There is exponentially small drug penetration outside the membrane. This small amount of drug is involved in the tangential flow that causes an exponentially small contribution to the diffusional drug release. As C(Rf,θ) is not zero, there is penetration of the drug in the tangential flow around the surface. This means that the flux I along the pore has to be accounted for in differential equation (6.2).
One boundary condition Cp(yp=0)=Cs is not sufficient to determine both I and the concentration distribution. In the meantime, the formulation of the boundary condition for yp = lf is problematic. When I is small, taking this into account in the differential equation leads to a small correction. The possibility of disregarding I in the equation follows from the accomplished consideration without taking into account for I.
At a small angle, the pore velocity may be sufficiently high to decrease C(Rf,θ) to values much smaller than Cs. With increasing θ, the velocity decreases, which leads to the onset of concentration C(Rf,θb) = Cse−1. It may not be sufficiently small and may affect the derivation of the equation for θb. Nevertheless, the introduction of θb is useful for the clarification of the mechanism of suppression diffusion driven release, when the hydrodynamic driven release is strong.
When the difference between θb and π/2 is rather small, the portion of the surface area in the vicinity of θ = π/2, where the diffusion release is not retarded essentially by liquid inflow into the lumen, is rather small. This is a sufficient condition to disregard the diffusion contribution to the hydrodynamically-driven release. Naturally, there is a matter of convention in the choice for the θb value. It is shown schematically in Fig. 9 that the radial velocity in the pores decreases to 0 as θ approaches π/2, which makes it possible for diffusion penetration in the tangential stream solute, which diffuses opposite to the radial velocity. Diffusion flux in the pores transforms in the tangential convective flux after the drug exits the pores. The accomplished primitive quantification provided here allows to formulate quantitative criterion, when the diffusion contribution into the hydrodynamically-driven release may be disregarded because drug diffusion penetration from the lumen into the tangential interstitial flow around the membrane surface occurs within a narrow vicinity of θ = π/2.
| (6.6) |
Fig. 9.
Schematic for angular dependence for radial Vr and tangential VӨ components of liquid velocity on surface of hollow fiber which affect drug diffusion from lumen into tissue (drug-release). Large radial velocity and small tangential velocity at Ө < Өb suppress diffusion. The diffusion becomes noticeable in vicinity of Ө = π/2 where normal velocity decreases fast while the tangential velocity is at its maximum.
As drug molecular weight varies in a broad range, D dependence on r is required to apply criterion (6.6) for drugs. D depends on water viscosity η and macromolecule radius r. This dependence is described by the Stokes-Einstein equation
| (6.7) |
where K is the Boltzman constant, T is absolute temperature. r increases with molecular weight (MW) and 100 < MW < 500 g/mole. Examples are given in Table 1 below:
Table 1.
Diffusion coefficient values of model drugs in water and in membrane
| Drug | MW (g/mol) | D (cm2/s) Aqueous | Dm = 0.25D |
|---|---|---|---|
| Caffeine | 194.2 | 4.9 × 10−6 | 1.5 × 10−6 |
| Insulin | 41,000 | 8.3 × 10−7 | 2.5 × 10−7 |
The known molecular weight allows one to determine the hydrodynamic radius r according to equation
| (6.8) |
where N is the Avogadro number, ρ is approximately 1 g/cm3.
Afterwards, substitution of r into the Stokes-Einstein equation yields:
| (6.9) |
7. Comparison of hydrodynamically-driven drug release and diffusion-driven release. Influence of decreased tangential velocity on diffusion
Considering membranes with decreasing hydrodynamic permeability, transition occurs from the mode of hydrodynamically-driven release to the mode of diffusion- controlled release. The maximal possible diffusion flux in “sink approximation” is Dm/lm, where Dm and lm are diffusivity within the membrane and its thickness, respectively. Its comparison with the release rate which is controlled by hydrodynamics, namely, Jc = CsVl, where Vl is velocity in the lumen, reveals an increase in the release rate due to the transition to strong penetration in the lumen of the hydrodynamic flow
| (7.1) |
Naturally, this ratio may essentially decrease if the hydrodynamic permeability of the membrane Km decreases in comparison with Kti with a concomitant decrease of Vl. However, comparison of the maximal possible values for hydrodynamically-driven release and diffusion-driven release is of practical importance.
Maximal release rates for both mechanisms are achieved when the dimension of the pores and porosity are sufficiently large. These conditions satisfy Km >> Kti. This means that the comparison is of interest for the proposed HFHP with respect to hydrodynamically-driven release. The maximal diffusion-driven release occurs in the case of HFHP as well because diffusivity achieves its maximal value with the increasing diameter of membrane pores.
When the diameter of pores essentially exceeds the molecule dimension, Dm may be presented as a product of 3 multipliers: diffusivity in water D, membrane porosity ε and tortuosity t0; . The maximal porosity is about 0.5. Taking into account tortuosity t0 = 2, Dm ~ 0.25D. V has to be replaced by 2Vlb when the condition 2Rlb >> Rf is valid and the fiber is placed at a small distance from the LB. Hence, Jc/JD~4Vlblm/D represents the case of HFHP. As to lm, its minimal value is desirable for the maximal diffusion case.
The decrease of lm below 15 micron may worsen the mechanical properties of the hollow fiber. The unknown Vlb may be expressed through the characteristics of the afferent vessel using the result in Section 5. This yields
| (7.2) |
The ratio
| (7.3) |
may be called the index or coefficient of hydrodynamically-driven release efficiency. This equation underestimated E because the diffusion flux is overestimated when the concentration on the boundary between fiber membrane and tissue Cm is replaced by zero. This is the well-known sink approximation, which is valid when the concentrations drop between Cm and zero in the liquid stream is neglected. But zero concentration in the interstitial flow is realized at some distance δ. This distance is called the diffusion layer thickness δ [15]. The diffusion flux through the tissue adjacent to the fiber surface is equal to the diffusion flux through the membrane, when the steady transport is under consideration. This dictates a certain value for Cm. An equation for Cm follows from the condition that locally the flux through the membrane is equal to the flux through the tissue. Such a rather simple approach is valid when the diffusion layer is thin: δ << Rf. In turn, this condition is valid if the so-called Peclet number Pe=Vl/D is large.
The physical sense of the Peclet number is that it characterizes the ratio of convection flux to diffusion flux. A large Peclet number means strong predomination convection over diffusion. When dissolution of solid spherical particles is under consideration in the classical Leveque-Levich theory, both normal and tangential components of velocity are equal to zero on the solid surface. Hence, the diffusion predominates near the surface due to hydrodynamic stagnation. But convection starts to predominate with increasing distance to the surface because velocity increases. In the meantime, along the liquid trajectories within pure convective transport, the concentration does not change [19]. As a result, the concentration drop within tissue is located within a thin diffusion layer δ. Correspondingly, the diffusion flux may be expressed as
| (7.4) |
The diffusion through the tissue may be slower when Dti << Dm, which is our case when pores in the membrane are much wider than those in the tissue. According to general kinetic regularity, the slower stage determines the flux in a two-stage process, namely, the stage of diffusion through the membrane and the stage of diffusion through the tissue.
The second general regularity is that the larger portion of the total concentration drop (Cs in our case) occurs when the process is slower (in the tissue in our case). Hence, Cm >> (Cs − Cm). This allows one to replace Cm by Cs in the equation for .
The condition for this approximation is
| (7.5) |
The replacement of larger Dm/lm by smaller Dti/δ in the equation for the efficiency index leads to its smaller value:
| (7.6) |
With respect to broad pores of the membrane in the case of HFHP
| (7.7) |
which is illustrated in Table 2.
Table 2.
Calculated efficiency values according to equation (7.15) for 3 drugs
|
Dti (cm2/sec) → |
1.5 × 10−6 Z−1 | 2.5 × 10−7 Z−1 | Tenofovir 6.10−8 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Rf/Rlb↓ | E | E | E | ||||||
| 1/7 | 4 | 2.6 | 24 Z−1 | 8.4 Z−0.5 | 100 | 22 | |||
As tissue pores are rather narrow, an additional factor decreases Dti in comparison with Dm at the same drug molecule dimension ddr. With the approach of ddr to dp, i.e., with increasing ratio ddr/dp, Dti decreases in comparison with diffusivity when pores are broad. Hence, a multiplier Z(ddr/dp) < 1 has to be introduced in the equation which interconnects diffusivity in narrow pores with diffusivity in broad pores.
| (7.8) |
Although detailed information about Z(ddr/dp) is absent, it is clear qualitatively that Z→0 when ddr/dp→1 and Z→1 when ddr/dp exceeds 1 essentially. In fact, Z(ddr/dp) has to be accounted for in the denominator of the equation for E. This will lead to a further increase of the Peclet number:
| (7.9) |
in the case when the condition (7.5) is valid.
The definition
| (7.10) |
is used in Eq. (7.8).
Dti is measured for tenofovir [6]. This allows one to transform Eq. (6.9) into an equation for the determination of the Z values for drugs, for which Dti is measured, for example, Tenofovir and tacrolimus.
While the Levich equation [15] was derived for an impermeable sphere, we need a similar equation for the permeable cylinder, i.e., hollow fiber. To our knowledge, this topic has not been considered in the literature. However, the traditional problem of convective diffusion for the case of a solid cylinder in flow has attracted much attention. The so-called HEPA filters were a large achievement in aerosol filtration with respect to most penetrating particles. Their high efficiency is caused by the high efficiency of the capture of most penetrating particles from a contaminated air stream. The regularities of diffusion from the laminar flow of air and liquid are identical. This allows one to use the equation for δ, as used in aerosol filtration. However, Eq. (12.46) in [20] yields the so-called collection efficiency
| (7.11) |
where the Pe definition is similar to Eq. (7.9).
ηD is defined as the rate (by mass) with which particles are removed by impacting with the collecting drop (sphere Dc) divided by the mass flow rate of particles in a stream tube of a cross-sectional area equal to that of the collecting sphere:
| (7.12) |
where V is the speed of the gas stream relative to the collector and C0 is the concentration of contaminant particles in the gas stream approaching the collector.
In the cylinder case, πD2/4 has to be replaced by the axial cylinder cross-section per unit length l. Then the mass removal rate in our case is the total diffusion flux ID of the drug into the interstitial flow stream obviating a fiber
| (7.13) |
where Eq. (7.9) is used.
The total convective flux through the fiber membrane which is enhanced due to concentrating streaming lines within the lumen is
| (7.14) |
One obtains for HDR efficiency:
| (7.15) |
The Peclet number is calculated using Eq. (7.10) for one Vlb values and 3 drugs. These results are presented in Table 2. E is calculated according to according to Eq. (7.15) for the same values of argument.
As the Peclet number decreased, the Levich theory for δ and its modification for the cylinder, used in the derivation for E, is valid only for Pe = 24 and 100. For Pe = 4 in the Table, the convection influence on diffusion may be weak. To our knowledge, the equation for δ, when Pe is not sufficiently large, is unknown. This causes uncertainty in estimating the E values for Pe = 4.
It must be taken into account that the equation (7.10) derived for the impermeable cylinder does not account for 2 effects, which suppress diffusion, when the cylinder is permeable: decreased tangential velocity and liquid stream, opposite to diffusion. The real diffusion transport is weaker and E is really higher.
Taking into account the 2 times increase in Vn and a concomitant increase in convective flux, and for a smaller Vθ and a concomitant decrease in enhancement of the diffusion flux due to tangential convection reveal a small contribution of diffusion flux under the condition of hydrodynamic-driven drug release.
The diffusivity decrease in tissue pores is an important factor which contributes to the predominating HDR. This is seen in the example of Tenofovir (Table 2). Dti for Tenofovir equals 6×10−8 cm2/sec in tissue, according to [6]. The molecular weight determines the diffusivity within unconfined water according to Eq. (6.9). It may be assumed that other drugs whose molecular weight does not differ essentially from Tenofovir are characterized with Dti as that of Tenofovir. Consequently, almost the same high HDR efficiency is possible for them. This conclusion assumes that r is the single factor affecting Dti, as it is valid for D.
8. Downstream dilution of drug and advantage of the hollow fiber fabric
Estimates accomplished in Sections 6 & 7 have shown that HDR may provide a much higher release rate than DDR. This predetermines the advantages of HDR in practical applications. This will be shown in this and the next sections.
Maximal possible release rate is of practical importance to achieve effective therapy, which requires the achievement of Cln > MIC. Only a portion of this flow is affected by the fiber and is leaded loaded with drug, while the major portion of the flow is not affected by the drug release from the fibers, i.e., does not contain drug (Fig. 1). When these two portions of radial interstitial flow enter the LB, they are mixed in the lymph flow. Hence, there is dilution of the drug stream produced by fiber drug release in the interstitial flow after entering the lymphatics. As a result, the drug concentration in the afferent capillary and in the LN Cln may be much lower than that in the initial stream of drug. This dilution, i.e., decrease in Cln is harmful because Cln has to exceed MIC.
This harmful dilution may be suppressed when a fabric of hollow fiber is implanted instead of a single hollow fiber. The total release rate caused by numerous fibers of fabric may exceed that caused by a single fiber by orders of magnitude. This leads to an significant increase of Cln which is favorable for achieving therapeutically effective condition, Cln > MIC.
The fabric placed parallel to the flat surface of the disk-like LB at distance hlb is shown in Fig. 10. As Rlb is rather large, the condition hlb << 2Rlb can be satisfied. This means that liquid velocity at this distance before fabric placement is uniform and is approximately equal to Vlb. The placement of the fabric with fibers having lower hydrodynamic permeability than that of the tissue would decrease the Vn(hlb) until its values become essentially lower than Vlb. Since we are interested in hydrodynamically-driven release, an opposite case, namely HFHP, is of interest. In this case, Vn(hlb) = Vlb. If the distance between parallel fibers of fabric hf exceeds Rf, hydrodynamic fields of adjacent fibers overlap only slightly, i.e., the release of any fiber does not depend essentially on the presence of adjacent fibers. One obtains for the release rate from any fiber
| (8.1) |
Fig. 10.
Schematic illustrating disposition of hollow fiber fabric and disk-like lymphatic bed (LB). At small hlb << 2Rlb, the interstitial flow through the fabric is almost uniform.
The length of a square fabric of fibers for targeting lymphatics can be reasonably chosen as equal to 2Rlb and this fabric would in principle provide uniform drug flux over the entire flat surface of the LB. This choice specifies the above written equations for qf
| (8.2) |
because lf = 2Rlb and where Vn(hlb) = 2Vlb
The stream saturated with drug through one flat surface of the LB and an equal stream of clean liquid through the opposite flat surface of the LB are mixed. Hence, the dilution is rather small (about 50%) in the case of fabric as distinct from the unacceptable high dilution in the case of a single hollow fiber. The release rate for fabric can be obtained as product Jc and Nfab (fiber amount in fabric) because there is no essential difference in the release rate for fibers. In turn, Nfab may be expressed through the fabric dimension 2Rlb and (2Rf+hf)
| (8.3) |
The substitution Rlb=7Raf yields
| (8.4) |
This yields for fabric
| (8.5) |
The substitution Rlb = 7Raf yields
| (8.6) |
9. Hydrodynamically-driven release (HDR) from a fabric of hollow fibers allows the achievement of a unique strong drug release of long duration
To design an effective HDR implant, it is not only sufficient to satisfy the release rate requirement but satisfying the pharmacokinetics is also required to deliver effective therapy at Cln > MIC. In order to accomplish long-term release from an HDR implant, it is also necessary to know the solubility of the drug at saturation (Cs). To achieve effective therapy, a high release rate is required (Cln >> MIC) even when considering lymph dilution with a predominating stream Qlb of interstitial fluid. For prolonged treatment inside the LN and outside the afferent capillary, a long release time is necessary. Meanwhile, the release duration decreases with increasing release rate because a larger portion of drug stored in the device is consumed due to high release rates. Satisfying the parameters constitutes fundamental difficulties for perfecting long-term therapy.
If the distance between skin in the LB hlb is large, increasing the fiber diameter allows an increase in the stored amount of drug proportional to . This approach fails if hif is not sufficiently long.
The use of a fabric formed from hollow fibers to make the drug delivery device (Fig. 10) allows us to increase the release rate and to simultaneously achieve long duration therapies. In the case of a fabric-based delivery device, the release from a certain hollow fiber is not affected by the release of an adjacent fiber if hf > Rf. Hence, the release time Tf for a single fiber determines the total release time Tfab of the entire fabric drug delivery device: Tfab = Tf. The amount of drug lost by a single fiber per unit time equals Jc. The drug loss is invariant in time before release abruptly stops. As a result, the release terminates at time Tf, when the total released amount of drug JcTf is equal to the amount of drug stored in the fiber where Rif is the internal fiber radius, ρ is the density of solid drug, lf = 2Rlb. Using this equality and equation (8.2), Tfab can be calculated
| (9.1) |
where Cs is the saturated weight concentration.
Although at first glance the fabric application does not appear to extend the release duration, the real situation is the opposite one. It is questionable whether the release rate providing Cln >> MIC is required because the side effects of the drug increase with Cln increase much above MIC. We assume that this therapeutic release rate provides Cln > MIC, but using a condition when Cln exceeds MIC is not essential. On the other hand, Cs has essentially exceeded MIC in the case of a single fiber because of dilution with a predominating stream of clean interstitial fluid. In favorable contrast, Cs may be chosen only slightly above MIC in the fabric case because the dilution is almost eliminated.
It can be concluded that a drug delivery device (DDD) in the form of a fabric offers an additional degree of freedom (Nfab), which allows one to solve the central problem in drug release, i.e., allowing for a simultaneous increase in the release rate and release duration. This constitutes an essential premise for the development of a new branch in implant therapy, namely, “long-term implant therapy.”
Eq. (9.1) does not take into account more than 50% dilution in the fabric case. In addition, Cln has to exceed MIC, for example, at least twice. This means that Cs has to exceed MIC at least 4 times.
| (9.2) |
This allows us to express Tfab through the known MIC as follows:
| (9.3) |
Examples of calculations according to this equation are given in Table 3 for Rlb/Rf = 7. The substitution Rf = 1.3 · 10−2 cm, Vaf=2.10−2 cm/sec, Rlb/Raf=7 into Eq. (9.3) yields Tfab dependence on MIC, characterized in Table 3.
Table 3.
The release time (sec) as a function of MIC for Vaf = 0.02 cm/sec
| MIC, gm/ cm3 → | 10−3 | 10−4 | 10−5 |
| Tfab, sec | 1.2 · 104 | 1.2 · 105 | 1.2 · 106 |
10. Requirement arising at the practical application of hydrodynamic-driven drug release
The polymer selected to fabricate the HFHP has to satisfy two main requirements. First, the fibers have to be biocompatible because a drug delivery device should not cause inflammation or irritation during long-term implantation. Second, the fiber has to be hydrophilic because the pores of the membrane have to be filled with water in order to provide the required high hydraulic permeability needed to make successful HDR implants. When the pores are hydrophilic, they become filled with water due to spontaneous imbibition. [21]
Filling of the fiber lumen with drug powder may be achieved by means of axial flow of the drug suspension with a filter installed at the lumen outlet. The latter will allow the particles to be retained in the lumen while the suspending liquid will pass through the filter. As the lumen is filled with drug suspension, the membrane pores become filled with water due to imbibition. On the other hand, the pores would remain dry if the polymer used to make the fiber is hydrophobic. In addition, the polymer used to make the fiber has to provide the necessary mechanical strength in spite of the presence of large pores and high porosity which are needed for higher hydraulic permeability. The ability to achieve the needed porous structure of the membrane may be provided by proper selection of the polymer and by the process of manufacturing. Manufacturing polymer membranes and hollow fibers is well established in the industry.
Contact angle is normally smaller when surfactant solutions are used. Inclusion of surfactants in drug formulation allows us to simultaneously achieve higher hydraulic permeability and to provide imbibition from the drug suspension stored in the fiber lumen. Accordingly, wetting of the membrane with surfactant solutions has to be taken into account when such surfactants are used in drug formulations [21].
Many existing drugs have favorable properties to consider them as candidates for implant therapy. Their saturation concentration Cs is known. With respect to achieving therapeutic concentrations with implants, the concentration of the drug in serum and in the target tissue/organ must be achieved without inducing systemic toxicity.
In the past 40–50 years, low molecular weight anticancer drugs have been the main treatment modality of many cancers at advanced stage, but have offered no improvement in the cure rate. The biggest limitation of these therapeutic agents is their overwhelming toxicity due to lack of selectivity. Scientists realized this fact finally towards the end of the 20th century and thus, cancer selective targeting became one of the most important goals. Theoretically, in drug development, a molecular target drug is considered more ideal not only in cancer but also in other diseases such as inflammation, primarily to avoid side effects. One example of drug targeting includes the delivery from nanoliposomes into cancer cells [25].
Although lymphatic targeting with nanoparticle systems (nanospheres, nanoemulsions, nanoliposomes) have become mainstream in current lymphatic targeting, their utility in achieving effective therapy remains limited. In our opinion, this does not mean that anticancer therapies cannot be further perfected.
Intravenous injection of large doses of chemotherapeutic drugs requires their passive accumulation in cancer cells which is not acceptable due to toxicity. However, a high decrease in side-effects may be possible when the administration of the same drug is accomplished via lymphatic targeting. This could not be done earlier because a large release rate and long duration therapy are required simultaneously and could not be achieved. At the same time, there was no drug delivery device to achieve this purpose. The HDR-HFHP system described in this paper represents a suitable vehicle to achieve this goal.
Although drug molecules eventually enter the blood stream during lymphatic targeting, a large advantage of HDR lies in that the required drug amount needed to achieve effective therapy may be significantly smaller compared to traditional systemic therapy.
In conventional anticancer therapy, high drug concentration in cancer cells is necessary to provide effective therapy. Chemotherapeutic cancer drugs are highly toxic to patients and in many cases they cannot provide effective high concentration in cancer cells without causing systemic toxicity. Accordingly, the HDR-HFHP local drug therapy is a promising technology that deserves further investigation and clinical studies.
An example of the HFHP potential application in preventing cancer metastasis is when the interstitial flow from the tumor containing circulating cancer cells terminates on the LB as illustrated in Fig. 11. If the distance between the tumor and the LB exceeds the thickness of the HFHP fabric (about 500 micron), it may be installed between the tumor and the LN. As the LB dimension (about 5–10 mm) exceeds the tumor dimension (millimeters), the fabric dimension has to be about the size of the LB dimension. At this condition, streaming lines originating from the tumor terminate on the LB. The circulating cancer cells involved in the interstitial flow occur within the convective drug strip where drug concentration can be essentially higher than MIC. This may provide inactivation of the circulating cancer cells in spite of the rather short residence time within the strip (about 102 sec). This duration corresponds to the distance between the HFHD fabric and LB of about 100 micron and the interstitial velocity of about 1 micron/sec. This example demonstrates the necessity of strong drug release required for high concentration in the strip and for long term release because long term prevention of metastasis is required.
Fig. 11.
HFHP fabric (1) which prevents transport of circulating / released cancer cells from tumor (2) into lymphatic bed (3). HFHP fabric is placed between tumor and LB where convective drug strip is formed and is shown in the figure as the shaded area.
Although the concentration within the strip has to essentially exceed MIC, this perhaps may not cause inflammation of the tissue between the tumor and the LB due to the known phenomenon that cancer cells consume drugs at a higher rate than normal cells. Naturally, more consistent analysis is required taking into account the complicated regularities of the metastasis process [26].
11. Discussion
Local application of drugs decreases their systemic toxicity and harmful side effects. Loco-regional drug delivery (e.g., topical) has become important when long-term treatment is required, for example in preventing infection such as viral transmission, treating cancer, decreasing cancer metastasis and administering immune suppressants. Drug delivery implants are especially advantageous for local and topical therapies. In particular, drug delivery devices (DDD) which could provide a high rate of release to achieve therapeutic concentrations to local or regional sites are required, i.e., Cln > MIC. In principle, simple analysis shows that often this task cannot be solved because current drug release technologies rely on the accepted diffusional mechanism of release. This is because diffusion in tissue is a very slow process especially with respect to high molecular weight drugs. In the meantime, high molecular weight drugs and biologics are promising as anticancer drugs and for immunotherapies [4]. The constraints caused by low diffusivity of high molecular weight drugs are unavoidable because any change in diffusion-controlled DDD designs is not fruitful. Low value of diffusivity, Dti, occurs within tissue because of the small width of its pores. Meanwhile, DDD modification is helpless because faster diffusion inside DDD will not improve the effective release rate which is controlled by slow diffusion in adjacent tissue especially when targeting drug delivery to the lymphatics.
The above limitations dictate the necessity of supplementing the current paradigm of diffusion-driven release with new ideas. The new direction detailed in this paper and related inventions show that these limitations can be overcome, at least when lymphatic targeting is required, because interstitial flow towards and around the lymphatics exists as recognized in physiology. We show that it is sufficient to use drug-filled hollow fibers with high hydrodynamic permeability higher than that of the tissue to achieve effective drug delivery to lymphatics. In this situation, the interstitial flow will penetrate into the drug-filled fiber lumen, with concomitant drug dissolution and sufficient drug loading in penetrating the liquid stream. The convective flow of drug solution from fiber lumen in the drug delivery mode is called hydrodynamically-driven drug release (HDR), which does not depend on drug diffusion. In contrast to traditional diffusion-controlled release, HDR is considered as a new mode and as a new paradigm in drug release that can be applied to achieve new treatments, especially with respect to lymphatics targeting and treatment of cancer metastasis among others.
At first glance, this large delay in the invention of HDR cannot be explained. This may have been caused by low interest regarding the role of convection in drug delivery and by overlooking the importance of long-range drug transport in drug delivery research. We wrote earlier [14], that the majority of published reviews in drug release are focused on diffusion, while in reality such processes are dominated by convective diffusion. This trend proceeds in spite of the fruitful activity of Professor M. Swartz’s group [7] which was dedicated to convective transport in interstitium.
The invention of HDR technology may be viewed as the synthesis of two components or two findings in drug release. It was proclaimed in [14] that nanoparticle transport from the vagina to lymphatics may occur without their diffusion, which was confirmed by experiments in animal models. Nanoparticles may be involved in the convective flow from the vagina to lymphatics, which is possible due to our discovery of foci (natural nano-holes in the epithelial barrier), and this flow is driven by the natural and well-known contractile activity of lymphangions. However, drug release due to convection was not covered in our previous research [14].
A proper DDD in the form of hollow fibers filled with drug powder was elaborated due to systematical investigations at the NovaFlux company in Princeton, NJ; such research is protected by several patents [22,23]. Although the initial modeling of drug release from the hollow fiber DDDs was based on the accepted paradigm of diffusion release, this modeling was not in vain because further analysis revealed the weakness of the diffusion mechanism compared to HDR, especially with respect to drug delivery to lymphatics and other applications, including cancer metastasis. The need for targeted release to lymphatics promoted the search for alternative modes of drug release that can achieve effective therapies.
The next stage in the design and development for HDR was the recognition for the need to include hollow fiber fabrics in the design. The main unsolved problem in the development of long-term drug release drug delivery implants can be solved by the use of fabric of hollow fibers loaded with drug powder. The possibility of achieving high drug release rates and long release duration, in spite of controversial requirements to achieving both at the same time, was accomplished by means of HDR in combination with HFHP fabric for the first time, as shown in Section 9.
The cardinal difference between diffusion-driven release and hydrodynamically-driven release is clarified in Fig. 12, which illustrates the significant principle difference in convective diffusion between two cases: a) the dissolution of a large solid cylinder and b) small solid drug particle dissolution in the lumen of the hollow fiber. Drug transfer from the large solid cylinder into the tangential liquid stream occurs due to diffusion, while convection plays a secondary role enhancing diffusion. The released drug strip, behind the solid cylinder forms due to the outward hydrodynamic flow at θ > π/2. On the other hand, the released drug strip from the hollow fiber downstream consists of two portions of different origins: (i) the internal portion of the strip originating from convection in the lumen which has the form of a slab parallel to external flow, and (ii) an external portion of strip in the form of two external slabs adjacent to an internal slab which is created by the involvement of the diffusion layer formed within angle range 0 < θ < π/2 in the external convective tangential stream as shown in Fig. 12.
Fig. 12.
a) Schematic for angular dependence of diffusion layer thickness δ in case of hydrodynamically impermeable fiber. The δ extension at Ө > π/2 is caused by outward velocity and is not relevant in our analysis of diffusion, focused on Ө < π/2; b) A schematic for angular dependence for δ when the fiber is hydrodynamically permeable. The hydrodynamic flow opposite to diffusion retards diffusion departure of solute from fiber lumen. At Ө ~ π/2, diffusion layer separates from membrane and forms two slab-like external convective drug strips adjacent to internal slab-like convective strip originated due to convection through the lumen. The diffusion layer within 0 < θ < π/2 is much broader in case of permeable fiber because tangential velocity near surface decreases when fiber is permeable. In spite of the increase of δ(π/2) with increasing fiber hydrodynamic permeability, the convective drug flux in cross-section between (Rf, π/2) and (Rf + δ(π/2), π/2) caused by diffusion downstream within θ range (0, π/2) decreases due to decrease of tangential velocity.
Fig. 12 clarify the cardinal difference between the HDR mechanism and the DDR mechanism. DDR occurs due to diffusion from the membrane in the tangential stream. HDR occurs due to dissolved drug involvement in the convective flow inside the lumen. Fig. 12 show that diffusion always contributes to HDR, but its role may be negligible when the Pe number, i.e., VnRf/Dti, is large because the Pe numerator grows with Vn increase, and the Pe denominator grows with Dti increase. In the meantime, Dti is very low for high molecular weight drugs, and the accomplished estimate (Sections 6 and 7) demonstrates the huge predomination of HDR.
The predicted phenomenon of HDR cardinally differs from convection enhanced release described in the literature, devoted to traditional diffusion release from hydrodynamically impermeable DDD. In this well-known case, convective diffusion replaces diffusion in stagnant media, being faster.
HDR relates to a completely other class of DDD, namely hydrodynamically permeable ones. The diffusion mechanism may predominate when local interstitial velocity is sufficiently weak. As HDR is caused by convective transport and consequently, proportional to velocity in the lumen Vl, it decreases with Vl, i.e., with Vlb and becomes weaker than diffusion transport at sufficiently small Vint (local interstitial velocity). How small Vint has to be for DDR to predominate is difficult to state. Some tissues do not possess lymphatics. DDR in those tissues plays a role. Whether DDR may predominate when lymphatic is present is not clear even for a large distance from the LB because interstitial flow arises due to many other mechanisms, known as the extrinsic pump [11,13].
Another factor which influences the relative role of DDR and HDR is drug molecular weight (MW). When it is high (macromolecular drug, 103 < MW < 106), diffusivity D and especially diffusivity in tissue Dti may be very small (Dti < (10−8–10−7) cm2/sec), DDR is very weak and HDR may always predominate even when Vint << Vlb ~ 1 micron/sec but more than 0.1Vlb.
For low molecular weight drugs (MW < 103), the DDR role increases, especially when MW < 200, because the diffusivity Dti ~ D and is not so small. The DDR theory for this case of a not large Peclet number is absent because the diffusion layer is not thin. It may be stated that the contribution of DDR and HDR into release rate may be comparable for MW < 200 to 1000.
We may acknowledge that DDR is a more universal phenomenon because it does not require external interstitial flow and its penetration into the fiber lumen takes place. It preserves its significance for tissues, where lymphatics are absent or when the velocity is very low in comparison with a typical velocity of 1 micron/sec [7]. In contrast, DDR cannot compete with HDR when the implanting therapy addresses tissues possessing lymphatics, or in other words, when lymphatics are involved in the therapy. Although there is DDR contribution in the latter, it is practically negligible.
Further theoretical analysis is required when drug MW is low, as in the caffeine case, and when Pe is not sufficiently large. The accomplished estimate of DDR contribution taking into account the role either only Vr(Section 6) or only Vθ (Section 7) is not sufficient in this case. More rigorous analysis is required based on the two-dimensional equation of convective diffusion [15]. In fact, a new direction in physico-chemical hydrodynamics [15] has to be developed to elaborate these processes. While the theory of convective diffusion [15] is usually addressed concerning the single compartment system, HDR requires theory generalization over the two compartment system: fiber membrane and adjacent tissue. Even larger difficulties arise due to not large Pe values.
Diffusophoresis and capillary osmosis [24] may contribute to the release of charged drug macromolecules if the drug suspension is prepared with the use of deionized and distilled water that promote high zeta potential of drug macromolecules and pores of membrane and tissue. At the value of the electro-diffusional potential [24] 25 mV and lm = 15 micron, the electric field in the membrane pores achieves 200 V/cm. At such a high electric field, velocities of electrophoresis and electro-osmosis may essentially exceed the interstitial velocity of 1 micron/sec.
12. Conclusions
An essential limitation of diffusion-driven drug release (DDR) for lymphatic targeting with high molecular weight drugs or biologics is that the release rate is too low. In contrast, the rate of hydrodynamically-driven release (HDR) is high and may provide drug concentration in lymph nodes Cln above MIC value. This may be achieved with the use of porous hollow fibers of high hydrodynamic permeability (HFHP) (much higher than that of tissue). In spite of the decrease in release time with increasing release rate, application of a fabric consisting of HFHP allows one to simultaneously provide high release rate and long release duration due to the unique advantages of HDR. Perhaps the practical development of DDD as a fabric of HFHP may lead to a breakthrough in lymphatic targeting with anticancer or immuno-suppressant drugs either for cancer treatment or in preventing cancer metastasis.
Table 4.
Relative role of HDR and DDR dependence on drug molecular weight and Vint, when Km >> Kti or Km ~ Kti.
| Conditions | Mode of Drug Release |
|---|---|
| MW > 103, Vint > 0.1 micron/sec | HDR predominate |
| Vint = 0 or Vint < 0.1 micron/sec | DDR plays role |
| MW < 103 | Contributions of HDR and DDR in drug release are comparable |
Highlights.
Invention of hydrodynamically-driven drug release (HDR)
Advantage of hollow fiber with high hydrodynamic permeability of wall (HFHP)
Hydrodynamics of HFHP, implanted near lymphatics
Unique strong release rate and simultaneously unique long release time for fabric of HFHP
Estimate for tiny contribution of diffusion release to predominating HDR
Abbreviations
- DDD
Drug Delivery Device
- DDR
Diffusion-Driven Drug Release
- HDR
Hydrodynamically-Driven Drug Release
- HFHP
Hollow Fiber of High Hydrodynamic Permeability
- MIC
Minimum Inhibition Concentration
- MW
Molecular Weight
- LB
Lymphatic Bed
- LN
Lymph Node
- ILC
Initial Lymph Capillary
- Pe
Peclet Number
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Frontiers in Formulation Science. Selected Papers from 5th International Conference on Formulation Technology; November 2007; Potsdam, Germany, Colloids Surf.. 2008. p. A331. [Google Scholar]
- 2.Park K, Stowell JG. Controlled Drug-delivery Systems. Stripes Publishing, LLC; 2005. [Google Scholar]
- 3.Hawley AE, Davis SS, Illum L L. Advanced Drug Delivery Reviews. 1995;17(1):129–148. [Google Scholar]
- 4.Maeda H, Bharate GY, Daruwalla J. Eur. J. Pharm. Biopharm. 2009;71(3):409–419. doi: 10.1016/j.ejpb.2008.11.010. [DOI] [PubMed] [Google Scholar]
- 5.Ruoslahti E, Bhatia SN, Sailor MJ. The Journal of Cell Biology. 2010;188(6):759–768. doi: 10.1083/jcb.200910104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gao Y, Katz DF. PLoS ONE. 2013;8(9):1–1.1. doi: 10.1371/journal.pone.0074404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wiig H, Swartz MA MA. Physiol. Rev. 2012;92(3):1005–1060. doi: 10.1152/physrev.00037.2011. [DOI] [PubMed] [Google Scholar]
- 8.Vasin SI, Filippov AN, Starov VM. Adv. Colloid Interface Sci. 2008;139(1–2):83–96. doi: 10.1016/j.cis.2008.01.005. [DOI] [PubMed] [Google Scholar]
- 9.Dukhin SS, Shilov VN. Dielectric Phenomena and the Double Layer in Disperse Systems and Polyelectrolytes. New York: Wiley; 1974. [Google Scholar]
- 10.Dukhin SS, Labib ME. Colloids Surf. A. 2012;409:10–20. doi: 10.1016/j.colsurfa.2012.04.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Aukland K, Reed RK. Physiol. Rev. 1993;73:1–78. doi: 10.1152/physrev.1993.73.1.1. [DOI] [PubMed] [Google Scholar]
- 12.Happel J, Brenner K. Low Reynolds Number Hydrodynamics. Prentice Hall; 1965. [Google Scholar]
- 13.Dukhin SS, Labib ME. Adv. Colloid Interface Sci. 2013;199–200:23–43. doi: 10.1016/j.cis.2013.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dukhin SS, Ballou B, Hope TJ, Labib ME. In: Colloid and Interface Science in Pharmaceutical Research and Development. Ohshima H, Makino K, editors. Elsevier; 2014. [Google Scholar]
- 15.Levich VG. Physico-chemical Hydrodynamics. Englewood Cliffs, NJ: Prentice Hall; 1962. [Google Scholar]
- 16.Schmid-Schonbein GW. Physiological Reviews. 1990;70(4):987–1028. doi: 10.1152/physrev.1990.70.4.987. [DOI] [PubMed] [Google Scholar]
- 17.Margaris KN, Black RA. J. R. Soc. Interface. 2012;9(69):601–612. doi: 10.1098/rsif.2011.0751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Freitas RA., Jr . Nanomedicine, Vol. IIA: Biocompatibility. Georgetown, TX: Landes Bioscience; 2003. [Google Scholar]
- 19.Fan LT, Singh SK, editors. Controlled Release – A Quantitative Treatment. Berlin Heidelberg: Springer-Verlag; 1989. [Google Scholar]
- 20.Heinsohn RJ, Kabel RL. Source and Control of Air Pollution. Upper Saddle River, NJ 07458: Prentice Hall Inc.; 1999. [Google Scholar]
- 21.Lee KS, Ivanova N, Starov VM, Hilal N, Dutschk VM V. Adv. Colloid Interface Sci. 2008;144(1–2):54–65. doi: 10.1016/j.cis.2008.08.005. [DOI] [PubMed] [Google Scholar]
- 22.Labib ME, Dukhin SS. Fabric for drug release. 62/197,814. US Patent Application No. (Filed: July 28, 2015)
- 23.Labib ME, Dukhin SS, Materna P, Robertson J, Lai C-Y, Tabani Y. Implants and constructs including hollow fibers and hollow fiber fabrics for drug delivery and applications thereof. 62/196,289. US Patent Application No. (Filed: July 23, 2015)
- 24.Prieve DC. Adv. Colloid Interface Sci. 1982;16:321. [Google Scholar]
- 25.Dimitrov DS. Coll. and Surf. A. 2006;282–283:8–10. [Google Scholar]
- 26.Geiger TR, Peeper DS. Biochimica et Biophysica Acta. 2009;1796(2):55–332. doi: 10.1016/j.bbcan.2009.07.006. [DOI] [PubMed] [Google Scholar]