Iterative Shrinkage Algorithm for Patch-Smoothness Regularized Medical Image Recovery

Abstract

We introduce a fast iterative shrinkage algorithm for patch-smoothness regularization of inverse problems in medical imaging. This approach is enabled by the reformulation of current non-local regularization schemes as an alternating algorithm to minimize a global criterion. The proposed algorithm alternates between evaluating the denoised inter-patch differences by shrinkage and computing an image that is consistent with the denoised inter-patch differences and measured data. We derive analytical shrinkage rules for several penalties that are relevant in non-local regularization. The redundancy in patch comparisons used to evaluate the shrinkage steps are exploited using convolution operations. The resulting algorithm is observed to be considerably faster than current alternating non-local algorithms. The proposed scheme is applicable to a large class of inverse problems including deblurring, denoising, and Fourier inversion. The comparisons of the proposed scheme with state-of-the-art regularization schemes in the context of recovering images from undersampled Fourier measurements demonstrate a considerable reduction in alias artifacts and preservation of edges.

I. Introduction

The recovery of images from noisy measurements acquired using an ill-posed measurement scheme is a central problem in many medical imaging modalities such as magnetic resonance imaging (MRI), positron emission tomography (PET), and computed tomography (CT) [1]. Several regularized optimization schemes were introduced to make the recovery of images well-posed [2], [3]. We focus on patch based regularization in this paper, which is motivated by non-local algorithms. Non-local means (NLM) denoising algorithms recover each pixel as a weighted linear combination of all pixels in the noisy image; the inter-pixel weights were estimated as the similarity between patch neighborhoods [4], [5], [6]. This algorithm was extended to deblurring problems [7], [8], [9] by posing the recovery as an optimization scheme. However, this algorithm is not readily applicable to MRI recovery from undersampled data since the weights estimated from aliased images preserve alias patterns. Some authors have iterated between denoising and weight estimation steps [10]. However, this scheme had limited success in heavily undersampled Fourier inversion problems. This alternating NLM scheme has been recently shown to be a majorize-minimize algorithm to solve for a penalized optimization problem, where the penalty term is the sum of unweighted robust distances between image patches [11], [12], [13]. While convex distance metrics such as ℓ₁ distances may be used, non-convex metrics that correspond to the classical NLM choices are seen to provide significantly improved image quality [11]. The availability of the global cost function enabled homotopy continuation strategies to encourage the convergence to global minima, when non-convex metrics are used [11]. The main challenge associated with the implementation in [11] is the high computational complexity of the alternating minimization algorithm.

The main focus of this paper is to introduce an iterative nonlocal shrinkage (NLS) algorithm, which directly minimizes the robust non-local criterion in [11]. This algorithm alternates between (a) evaluating the denoised inter-patch differences by shrinkage, and (b) computing an image that is consistent (in least-square sense) with the denoised inter-patch differences and measured data. This approach is based on additive half quadratic majorization of the patch based penalty term [14], [15], [16], [17]. Unlike the majorization used in our previous work [11], the weights of the quadratic terms are identical for all patch pairs, but now involve new auxiliary variables that may be interpreted as the denoised inter-patch differences. We derive analytical shrinkage expressions for approximate versions of a range of distance functions that are relevant for non-local regularization; this generalizes the shrinkage formulae derived by Chartrand in the context of ℓ_p penalties [18]. The proposed approximations are the same as the Huber-like corner-rounded penalties [19], [20], [21], [22]. However, the key difference with our approach is that the corner-rounded approximations emerge as convex relaxations, which shows that this approximation is indeed the best possible one for the original distance function that allows a valid quadratic majorization. Note that each step of the iterative shrinkage algorithm is fundamentally different from classical non-local schemes that solve an weighted quadratic optimization at each step [4], [5], [6], [7], [8], [9]. The direct evaluation of the patch shrinkages are computationally expensive. We propose to exploit the redundancies in the shrinkages at adjacent pixels using separable convolution operations, thereby considerably reducing computational complexity. Computing the image that is consistent with the measured data and the denoised inter patch differences is a quadratic subproblem. We re-express the penalty involving the sum of patch differences as one involving sum of pixel differences, which enables us to solve for the quadratic sub-problem analytically.

We validate the proposed scheme in the context of recovering MR images from undersampled measurements. This is an active research area with several applications [23], [24], [25] and several algorithms [2], [3]. In this context, Akcakaya et al., proposed to form clusters of patches, which are denoised using hard-thresholding in appropriate transform domain; these denoised patches are later averaged to provide the recovery [25]. This approach implicitly uses different basis sets for different clusters and hence is conceptually similar to [26] and recent methods that exploit low-rank structure of patch clusters [27], [28]. While these methods are very powerful, they are also considerably more complex than the proposed scheme. In addition, since the above alternating schemes lack a global energy function, their convergence properties cannot be commented upon. Wong et al., uses the similarity of nearby pixels using homotopic ℓ₀ minimization [29], which is also related to non-local means regularization used in [30]. The proposed optimization strategy also has similarities to the recent approach for regularized reconstruction based on nonlocal operators [31].

The rest of this paper is organized as follows. We briefly describe the background in Section II. The proposed iterative non-local shrinkage algorithm is detailed in Section III, while the details of the implementation are outlined in Section IV. Section V demonstrates the utility of the algorithm in the context of recovering MR images from undersampled Fourier measurements.

II. Background

A. Problem Formulation

We consider the recovery of a complex image f : Ω → ℂ from its measurements b. Here, Ω ⊂ ℤ² is the spatial support of the complex image. We model the acquisition scheme by the linear degradation operator A:

$$\mathbf{b}=\mathbf{Af}+\mathbf{n}.$$

For example, A ∈ ℂ^M×N corresponds to a convolution in the deconvolution setting, a Fourier matrix in the case of Fourier inversion, or identity matrix in the case of denoising. Here, f ∈ ℂ^N is a vector obtained by the concatenating the rows in a 2-D image f(x) and b ∈ ℂ^M is the vector of measurements. We assume n to be Gaussian distributed white noise process of a specified standard deviation σ.

B. Unified Non-Local Regularization

The iterative algorithm that alternates between classical non-local image recovery [32] and the re-estimation of weights was shown [11] to be a majorize-minimize (MM) algorithm:

$$\widehat{\mathbf{f}}=arg\underset{\mathbf{f}}{min}\underset{\mathcal{C}(\mathbf{f})}{\underbrace{{\Vert \mathbf{Af}-\mathbf{b}\Vert }^2+\lambda \mathcal{G}(\mathbf{f})}},$$ (1)

where ||Af − b||² is the data fidelity term, and the regularization functional 𝒢(f) is specified by:

$$\mathcal{G}(\mathbf{f})=\sum _{\mathbf{x}}\sum _{\mathbf{y}\in \mathbf{x}+\mathcal{N}}\phi (P_{\mathbf{x}}(\mathbf{f})-P_{\mathbf{y}}(\mathbf{f})).$$ (2)

Here φ is an appropriately chosen potential function and P_x(f) is a patch extraction operator which extracts an image patch centered at the spatial location x from the image f; i.e. P_x(f) can be written as f(x + p), where p ∈ ℬ which denotes the indices in the patch. For example, if we choose a square patch of size (2N + 1), the set ℬ = [−N, ..., N] × [−N, ..., N]. Similarly, 𝒩 are the indices of the search neighborhood; the patch P_x(f) is compared to all the patches whose centers are specified by x + 𝒩. For example, if we choose a square shaped neighborhood of size 2M + 1, the set 𝒩 = [−M, ..., M] × [−M, ..., M]. The shape of the patches and the search neighborhood may be easily changed by re-defining the sets 𝒩 and ℬ.

In this paper, we focus on potential functions of the form

$$\phi (\mathbf{g})=\varphi (\Vert \mathbf{g}\Vert ),$$ (3)

where ϕ : ℝ⁺ → ℝ⁺ is an appropriately chosen distance metric and ||g||² = Σ_p∈ℬ|g(p)|².

C. Solution Using Iterative Reweighted Algorithm

We showed in [11] that (1) can be solved using a majorize-minimize algorithm, where the regularization term is majorized by the weighted sum of patch differences:

$$\mathcal{G}(\mathbf{f})\le \underset{{\mathcal{G}}_n(\mathbf{f})}{\underbrace{\sum _{\mathbf{x}}\sum _{\mathbf{p}\in \mathcal{N}}{w}_n(\mathbf{x},\mathbf{x}+\mathbf{p}){\Vert P_{\mathbf{x}}(\mathbf{f})-P_{\mathbf{x}+\mathbf{p}}(\mathbf{f})\Vert }^2}}.$$ (4)

The above relation is essentially the classical multiplicative half-quadratic majorization [15], [16], [33] of the penalty in (1). The weights w_n(x, x + p) in (4) are specified by:

$$w_n(\mathbf{x},\mathbf{y})=\frac{{\varphi }^{\prime }(\Vert P_{\mathbf{x}}({\mathbf{f}}_n)-P_{\mathbf{y}}({\mathbf{f}}_n)\Vert )}{2\Vert P_{\mathbf{x}}({\mathbf{f}}_n)-P_{\mathbf{y}}({\mathbf{f}}_n)\Vert }.$$ (5)

Here, f_n is an image vector at the n^th iteration. Each iteration of the MM algorithm involves the minimization of the criterion

$${\mathbf{f}}_{n+1}=arg\underset{\mathbf{f}}{min}{\Vert \mathbf{Af}-\mathbf{b}\Vert }^2+\lambda {\mathcal{G}}_n(\mathbf{f}).$$ (6)

Note from (4) that 𝒢_n is a weighted linear combination of patch differences, where the weights w_n(x, x + p) are spatially varying. This makes it difficult to develop a closed form expression to solve (6). As discussed above, one of the main challenges of the algorithm is its high computational complexity. Specifically, the conjugate gradients algorithm to solve (6) converges slowly, especially as the weights increase.

III. Proposed Algorithm

A. Majorization of the Penalty Term

In this work, we will consider the additive half-quadratic majorization [14], [17], [33] of the potential function φ, specified by

$$\phi (\mathbf{t})\triangleq \underset{\mathbf{s}}{min}\left\{\psi (\mathbf{s})+\frac{\beta }{2}{\Vert \mathbf{s}-\mathbf{t}\Vert }^2\right\}$$ (7)

This additive half-quadratic majorization scheme was originally introduced for edge preserving gradient regularization; using this scheme has not been reported in patch regularization to the best of our knowledge. With additional simplifications below, using this scheme results in a fast algorithm. The function ψ in (7) depends on φ and β, while s is an auxiliary variable. Since φ is the minimum of $\psi (\mathbf{s})+\frac{\beta }{2}{\Vert \mathbf{s}-\mathbf{t}\Vert }^2$, we will also solve for s along with t, as shown in Section III-B. Note that unlike (4), the quadratic term on the right hand side of (7) is weighted by the scalar β/2, which is the same for all spatial locations. The spatial invariance of the weights enables us to analytically solve a key subproblem as shown in Section III-C, which is not possible with (4). Using (7), we express the original problem in (1) as:

$$\widehat{\mathbf{f}}=arg\underset{\mathbf{f}}{min}\underset{\{{\mathbf{s}}_{\mathbf{x},\mathbf{q}}\}}{min}{\Vert \mathbf{Af}-\mathbf{b}\Vert }^2+\lambda \sum _{\mathbf{x}}\sum _{\mathbf{q}\in \mathcal{N}}\psi ({\mathbf{s}}_{\mathbf{x},\mathbf{q}})+\lambda \frac{\beta }{2}\sum _{\mathbf{x}}\sum _{\mathbf{q}\in \mathcal{N}}{\Vert P_{\mathbf{x}}(\mathbf{f})-P_{\mathbf{x}+\mathbf{q}}(\mathbf{f})-{\mathbf{s}}_{\mathbf{x},\mathbf{q}}\Vert }^2.$$ (8)

Note that the solution involves the minimization with respect to both f and the variables {s_x,q}. We use an alternating minimization algorithm, where we alternate between two steps. In the first step, we minimize (8) with respect to {s_x,q}, assuming f to be fixed. In the second step, we solve for f, assuming {s_x,q} to be fixed. We show in Section III-B and Section III-C that these steps can be solved analytically. The efficient implementation of these subproblems is the main reason why the proposed algorithm is faster than the iterative reweighted implementation. Similar speed-ups were reported with using the half-quadratic regularization scheme in the context of other regularization penalties [14], [17], [33].

B. The s Sub-Problem: solve for s_x,q, assuming f fixed

We focus on minimizing (8) with respect to the auxiliary variables {s_x,q}, assuming f to be a constant in this subsection. In this case, determining each of the auxiliary variables s_x,q corresponding to different values of x and q can be treated independently:

$${\overline{\mathbf{s}}}_{\mathbf{x},\mathbf{q}}=arg\underset{{\mathbf{s}}_{\mathbf{x},\mathbf{q}}}{min}\frac{\beta }{2}{\Vert P_{\mathbf{x}}(\mathbf{f})-P_{\mathbf{x}+\mathbf{q}}(\mathbf{f})-{\mathbf{s}}_{\mathbf{x},\mathbf{q}}\Vert }^2+\psi ({\mathbf{s}}_{\mathbf{x},\mathbf{q}}).$$

We will show in the subsection III-D (see (21)) that with a convex hull approximation of the function β|t|²/2 − φ(t), we can analytically determine s_x,q as a shrinkage for all penalties of interest:

$${\overline{\mathbf{s}}}_{\mathbf{x},\mathbf{q}}=[P_{\mathbf{x}}(\mathbf{f})-P_{\mathbf{x}+\mathbf{q}}(\mathbf{f})]\nu (\Vert P_{\mathbf{x}}(\mathbf{f})-P_{\mathbf{x}+\mathbf{q}}(\mathbf{f})\Vert ),$$ (9)

where ν : ℝ⁺ → ℝ⁺ is a function that depends on the distance metric ϕ. Note that the structure of the algorithm is exactly the same for different choices of distance function; only the analytical expressions for the shrinkage steps will change depending on the specific choice. We will determine the shrinkage rules corresponding to the useful penalties in Section III-D.

C. The f Sub-Problem: solve for f, assuming s_x,q fixed

In this subsection, we focus on minimizing (8) with respect to f, assuming the auxiliary variables {s_x,q} to be fixed. We show that this quadratic sub-problem can be solved analytically in the Fourier domain for several measurement operators.

Minimizing (8) with respect to f, assuming {s_x,q} fixed, simplifies to:

$$\widehat{\mathbf{f}}=arg\underset{\mathbf{f}}{min}{\Vert \mathbf{Af}-\mathbf{b}\Vert }^2+\frac{\lambda \beta }{2}\underset{\mathcal{R}(\mathbf{f})}{\underbrace{\sum _{\mathbf{x};\mathbf{q}\in \mathcal{N}}{\Vert P_{\mathbf{x}}(\mathbf{f})-P_{\mathbf{x}+\mathbf{q}}(\mathbf{f})-{\mathbf{s}}_{\mathbf{x},\mathbf{q}}\Vert }^2}}$$ (10)

The above quadratic penalty may be solved using the conjugate gradients algorithm. However, we will now simplify it to an expression that can be solved analytically, which is considerably more efficient. The quadratic penalty term involves differences between multiple patches in the image, each of which is a linear combination of quadratic differences between image pixels. The differences between two specific pixels are thus involved in different patch differences. We show in Appendix A that the pixel differences from several patches can be combined to obtain the following pixel-based penalty:

$$\widehat{\mathbf{f}}=arg\underset{\mathbf{f}}{min}{\Vert \mathbf{Af}-\mathbf{b}\Vert }^2+\lambda \frac{\beta }{2}\sum _{\mathbf{q}\in \mathcal{N}}{\Vert {\mathbf{D}}_{\mathbf{q}}\mathbf{f}-{\mathbf{h}}_{\mathbf{q}}\Vert }^2.$$ (11)

Here, D_q is the finite difference operator

$$({\mathbf{D}}_{\mathbf{q}}\mathbf{f})(\mathbf{x})=\mathbf{f}(\mathbf{x})-\mathbf{f}(\mathbf{x}+\mathbf{q}).$$ (12)

The images h_q(x), q ∈ 𝒩, are obtained from the patch shrinkages in Section III-B as:

$${\mathbf{h}}_{\mathbf{q}}=({\mathbf{D}}_{\mathbf{q}}\mathbf{f})●{\mathbf{v}}_{\mathbf{q}}.$$ (13)

Here, ● denotes the entrywise multiplication of the vectors, and v_q is obtained by summing the shrinkage weights of nearby patch pairs

$${\mathbf{v}}_{\mathbf{q}}(\mathbf{x})=\sum _{\mathbf{p}\in \mathcal{B}}\underset{{\mathbf{u}}_{\mathbf{q}}(\mathbf{x})}{\underbrace{\nu (\Vert P_{\mathbf{x}+\mathbf{p}}(\mathbf{f})-P_{\mathbf{x}+\mathbf{p}+\mathbf{q}}(\mathbf{f})\Vert )}}.$$ (14)

We solve (11) in the Fourier domain for measurement operators A that are diagonalizable in the Fourier domain, as shown section IV.

D. Determination of Shrinkage Rules

The existence of an analytical solution to (6) is key to the fast implementation of the alternating minimization scheme. In this subsection, we determine analytical shrinkage rules for a larger class of potential functions. The main idea is to use properties of convex conjugate functions to derive the dual function ψ(s) in (7), which is required for the solution of (6). However, this approach requires certain convexity requirements which are not met by many potential functions of practical interest. Therefore, we propose a procedure for approximating potential functions that yields an analytical shrinkage rule. This quality of this approximation is controlled by a parameter β, becoming exact as β → ∞.

We rewrite (7) as:

$$\phi (\mathbf{t})=\underset{\mathbf{s}}{min}\left\{\psi (\mathbf{s})+\frac{\beta }{2}\left({\Vert \mathbf{s}\Vert }^2-2\mathfrak{R}(\langle \mathbf{s},\mathbf{t}\rangle )+{\Vert \mathbf{t}\Vert }^2\right)\right\},$$

where ℜ (x) is the real part of x. The above equation is further rearranged as:

$$\underset{r(\mathbf{t})}{\underbrace{\frac{{\Vert \mathbf{t}\Vert }^2}{2}-\frac{1}{\beta }\phi (\mathbf{t})}}=\underset{\mathbf{s}}{max}\left\{\mathfrak{R}(\langle \mathbf{s},\mathbf{t}\rangle )-\underset{g(\mathbf{s})}{\underbrace{\left(\frac{1}{\beta }\psi (\mathbf{s})+\frac{{\Vert \mathbf{s}\Vert }^2}{2}\right)}}\right\}$$ (15)

From the theory in [34], the above relation is satisfied when r(t) is a convex function, in which case g = r^*, the Legendre-Fenchel dual (or convex conjugate) of r:

$$r^{\ast }(\mathbf{s})=\underset{\mathbf{t}}{max}\{\mathfrak{R}(\langle \mathbf{s},\mathbf{t}\rangle )-r(\mathbf{t})\}.$$ (16)

However, the function r is not convex for most penalties φ that we are interested in, especially for small values of β. When r is not convex, we propose to approximate r by a convex function r̂ so that relation (15) is satisfied. We choose r̂ such that the epigraph of r̂ is the convex hull of the epigraph of r; r̂ is thus the closest convex function to r (see Fig. 2.b). For φ functions of the form (3), we have r(t) = q(||t||), where the function q : ℝ⁺ → ℝ⁺ is specified by q(t) = t²/2 − ϕ(t)/β. In all the cases we consider in this paper (see Appendix B), we can obtain the convex hull approximation of r as

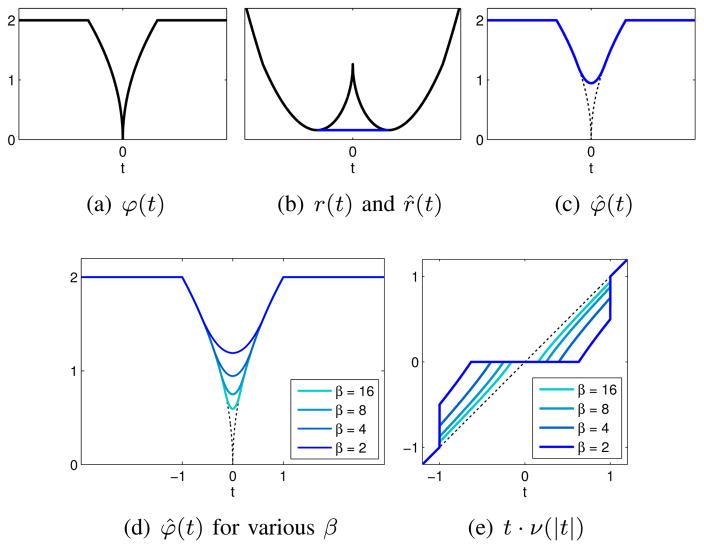
Fig. 2.

Approximation of the potential function: (a) shows the original potential function φ(t) in 1-D, which is the truncated ℓ_p; p = 0.5 penalty, T = 1. (b) indicates the corresponding $r(t)=t^2/2-\frac{1}{\beta }\phi (t)$ function with β = 2, shown in black. Note that this function is non-convex. Hence, we approximate this function by r̂ (t) shown in blue, which is the best convex approximation of r(t). The corresponding modified potential function is shown in blue in (c). (d) indicates the approximations for different values of β. Note that the approximations converge uniformly to φ. (e) shows the corresponding shrinkage rules. The potential functions and shrinkage rules for different penalties are shown in Fig. 1.

$$\widehat{r}(\mathbf{t})=\{\begin{array}{ccc}q(\Vert \mathbf{t}\Vert )& \text{if}& q^{\prime }(\Vert \mathbf{t}\Vert )>0\\ c& \text{else}& \end{array},$$ (17)

where c is an appropriately chosen constant to ensure continuity of r̂; see Fig. (2 b) for an example.

The convex hull approximation of r(t) is equivalent to approximating the original penalty φ(t) as:

$$\widehat{\phi }(\mathbf{t}):=\beta \left(\frac{{\Vert \mathbf{t}\Vert }^2}{2}-\widehat{r}(\mathbf{t})\right);$$

see Fig. (2 c). For the potentials considered in this paper, this “Huber-like” approximation:

$$\widehat{\phi }(\mathbf{t})=\{\begin{array}{ll}\frac{\beta {\Vert \mathbf{t}\Vert }^2}{2}-c\hfill & \text{if}\Vert \mathbf{t}\Vert <L\hfill \\ \varphi (\Vert \mathbf{t}\Vert )\hfill & \text{else}\hfill \end{array},$$ (18)

amounts to approximating the cusp of the original potential function at the origin by a quadratic function. Note that L = L(β) → 0 as β → ∞, when the approximation of φ by φ̂ is exact. In particular we have φ̂ → φ uniformly as β → ∞; see Fig. (2 d). This approximation enables us to derive the analytical solution for (6), which is termed as a shrinkage rule.

The shrinkage rule in (6) involves computing s̄ specified by:

$$\overline{\mathbf{s}}(\mathbf{t})=arg\underset{\mathbf{s}}{min}\left\{\psi (\mathbf{s})+\frac{\beta }{2}{\Vert \mathbf{s}-\mathbf{t}\Vert }^2\right\}$$

which is often called the proximal mapping of ψ. The above equation can be simplified as

$$\begin{array}{l}\overline{\mathbf{s}}(\mathbf{t})=arg\underset{\mathbf{s}}{min}\left\{\beta \left(\frac{1}{\beta }\psi (\mathbf{s})+\frac{{\Vert \mathbf{s}\Vert }^2}{2}+\frac{{\Vert \mathbf{t}\Vert }^2}{2}-\langle \mathbf{s},\mathbf{t}\rangle \right)\right\}\\ =arg\underset{\mathbf{s}}{max}\left\{\langle \mathbf{s},\mathbf{t}\rangle -\underset{{\widehat{r}}^{\ast }(\mathbf{s})}{\underbrace{\left(\frac{{\Vert \mathbf{s}\Vert }^2}{2}+\frac{1}{\beta }\psi (\mathbf{s})\right)}}\right\}\end{array}$$ (19)

Differentiating the right hand side of (19) with respect to s and setting it to zero, we obtain t − ∂r̂^*(s̄) ∋ 0, or equivalently,

$$\overline{\mathbf{s}}(\mathbf{t})\in {(\partial {\widehat{r}}^{\ast })}^{-1}(\mathbf{t}).$$

Since the subgradients of Legendre-Fenchel duals satisfy (∂r̂^*)⁻¹(t) = (∂r̂)(t), we have

$$\overline{\mathbf{s}}(\mathbf{t})\in \partial \widehat{r}(\mathbf{t}).$$ (20)

Considering the expression for the convex hull approximation of r̂ in (17), we have:

$$\overline{\mathbf{s}}(\mathbf{t})=\{\begin{array}{ccc}{q}^{\prime }(\Vert \mathbf{t}\Vert )\frac{\mathbf{t}}{\Vert \mathbf{t}\Vert }& \text{if}& q^{\prime }(\Vert \mathbf{t}\Vert )>0\\ 0& \text{else.}& \end{array}$$

Setting q(t) = t²/2−ϕ(t)/β in the above equation, we obtain the shrinkage rule as:

$$\begin{array}{l}\overline{\mathbf{s}}(\mathbf{t})=\frac{\mathbf{t}}{\Vert \mathbf{t}\Vert }{\left(\Vert \mathbf{t}\Vert -\frac{1}{\beta }{\varphi }^{\prime }(\Vert \mathbf{t}\Vert )\right)}_{+}\\ =\mathbf{t}\underset{\nu (\Vert \mathbf{t}\Vert )}{\underbrace{{\left(1-\frac{{\varphi }^{\prime }(\Vert \mathbf{t}\Vert )}{\beta \Vert \mathbf{t}\Vert }\right)}_{+}}},\end{array}$$ (21)

where (·)₊ := max{·, 0}. Here, ν (||t||) is a scalar between 0 and 1, which when multiplied by t will yield the shrinkage of t. Setting t = P_x(f) − P_x+q(f) in the above equation, we obtain the shrinkage rules to be used in (9). Note that the above approach can be adapted to most penalties. We determine the shrinkage rules and the associated ν functions for common penalty functions φ in non-local regularization in Appendix B. Figure (1) shows the penalty functions for different metrics and the corresponding shrinkage weights. We observe that the derived shrinkage rule for the s_x,q sub-problem is only exact for the convex hull approximation r̂ in (17). However, note the Huber-like approximations of the penalties corresponding to r̂ specified by (18) approach the original penalty as β → ∞.

Fig. 1.

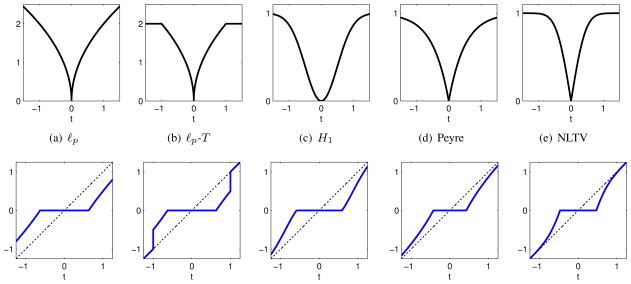
Distances functions ϕ(t) that are relevant in non-local regularization (first row) and the associated shrinkage rules t · ν (|t|) (second row); see Appendix B for the corresponding formulas that relies on a convex hull approximation (see Fig. 2) of the original penalty. Here we illustrate the shrinkage rules in 1-D for the parameter choices β = 2, p = 0.5, T = 1, and σ = 0.5. The approach introduced in the paper enables evaluating the shrinkage rules for a much larger class of penalties, generalizing the results in [18] for ℓ_p penalties shown in the first column.

IV. Implementation

We now focus on the implementation of the sub-problems. Specifically, we show that all of the above steps can be solved analytically for many penalties and measurement operators A that are diagonalizable by the Fourier domain (e.g. Fourier sampling, deblurring). This enables us to realize a computationally efficient algorithm. We also introduce a continuation scheme to improve the convergence of the algorithm.

A. Analytical Solution of (10) in the Fourier Domain

The Euler-Lagrange equation for (11) is given by:

$$\left(2{\mathbf{A}}^H\mathbf{A}+\lambda \beta \sum _{\mathbf{q}\in \mathcal{N}}{\mathbf{D}}_{\mathbf{q}}^H{\mathbf{D}}_{\mathbf{q}}\right)\mathrm{f}=2{\mathbf{A}}^H\mathbf{b}+\lambda \beta \sum _{\mathbf{q}\in \mathcal{N}}{\mathbf{D}}_{\mathbf{q}}^H{\mathbf{h}}_{\mathbf{q}}$$ (22)

Here B^H denotes the Hermitian transpose of matrix B. We now aim to solve for f, assuming h_q; q ∈ 𝒩 in the left hand side of (22) to be pre-determined from the previous iterate f_n−1. Thus, this step involves the solution to a linear system of equations. Motivated by analytical solutions to similar problems in the context of total variation minimization [35], we propose to solve for (22) in the Fourier domain. Specifically, the measurement operator A is diagonalizable in the Fourier domain in many inverse problems of interest (e.g. Fourier sampling, deblurring). In these cases, we may write A^HA as a pointwise multiplication in the Fourier domain. For instance, in the particular case when A is a Cartesian Fourier undersampling operator, we may write

$${\mathbf{A}}^H\mathbf{Af}={\mathcal{F}}^{-1}(\mathbf{a}●\mathcal{F}(\mathbf{f}))$$ (23)

where ℱ discrete Fourier transform and a is a vector of ones and zeros corresponding to the Fourier sample locations. It is well-known that the operators ${\mathbf{D}}_{\mathbf{q}}^H{\mathbf{D}}_{\mathbf{q}}$ are circulant under periodic boundary conditions on f (see [35] for example) and hence are diagonalizable in the Fourier domain as

$${\mathbf{D}}_{\mathbf{q}}^H{\mathbf{D}}_{\mathbf{q}}\mathbf{f}={\mathcal{F}}^{-1}({\mid {\mathbf{d}}_{\mathbf{q}}\mid }^2●\mathcal{F}(\mathbf{f})),$$ (24)

where |d_q|² is the pointwise modulus squared of the Fourier multiplier d_q corresponding to D_q. Hence, taking the DFT of both sides of (22) we have

$$\left(2\mathbf{a}+\lambda \beta \sum _{\mathbf{q}\in \mathcal{N}}{\mid {\mathbf{d}}_{\mathbf{q}}\mid }^2\right)●\mathcal{F}(\mathbf{f})=2{\mathbf{b}}_0+\lambda \beta \mathcal{F}\left(\sum _{\mathbf{q}\in \mathcal{N}}{\mathbf{D}}_{\mathbf{q}}^H{\mathbf{h}}_{\mathbf{q}}\right)$$

where b₀ = ℱ (A^Hb) ∈ ℂ^M is a zero-padded version of the Fourier samples b ∈ ℂ^N. Solving for f gives

$$\widehat{\mathbf{f}}={\mathcal{F}}^{-1}\left[\frac{2{\mathbf{b}}_0+\lambda \beta \mathcal{F}\left({\sum }_{\mathbf{q}\in \mathcal{N}}{\mathbf{D}}_{\mathbf{q}}^H{\mathbf{h}}_{\mathbf{q}}\right)}{2\mathbf{a}+\lambda \beta {\sum }_{\mathbf{q}\in \mathcal{N}}{\mid {\mathbf{d}}_{\mathbf{q}}\mid }^2}\right]$$ (25)

where the division occurs entrywise. Note that we have omitted the iteration step n from the above equation. Strictly speaking, it is an update for f̂, assuming h_q to be determined from f_n−1.

In inverse problems such as non-Cartesian MRI and parallel MRI, where the measurement operator A is not diagonalizable in the Fourier domain, we solve (22) efficiently using conjugate gradient (CG) algorithm [36]. A few CG steps at each iteration are often sufficient for good convergence since the algorithm is initialized by the previous iterate.

B. Efficient Evaluation of Shrinkage Weights

We now focus on the efficient evaluation of v_q(x); ∀ q ∈ 𝒩 in (14). Note that u_q(x) involves the comparison of the patches P_x(f) and P_x+q(f); since these quantities have to be computed for all spatial locations x and different shifts q, the direct evaluation of (14) is computationally expensive. We propose to exploit the redundancies between v_q(x) to considerably accelerate their computation. From (14), we have

$${\mathbf{u}}_{\mathbf{q}}(\mathbf{x})=\nu \left(\sqrt{\underset{({\mid {\mathbf{D}}_{\mathbf{q}}\mathbf{f}\mid }^2\ast \eta )(\mathbf{x})}{\underbrace{\sum _{p\in \mathcal{B}}{\Vert \mathbf{f}(\mathbf{x}-\mathbf{p})-\mathbf{f}(\mathbf{x}-\mathbf{p}+\mathbf{q})\Vert }^2}}}\right).$$ (26)

Here η is a moving average filter with the size of the patch. The above equation implies that computing u_q(x); ∀x can be obtained efficiently by simple pointwise operations and a computationally efficient convolution operation. Combining the above result with (14), we obtain

$${\mathbf{v}}_{\mathbf{q}}=\underset{{\mathbf{u}}_{\mathbf{q}}}{\underbrace{\left[\nu \left(\sqrt{{\mid {\mathbf{D}}_{\mathbf{q}}\mathbf{f}\mid }^2\ast \eta }\right)\right]}}\ast \eta$$ (27)

We realize the convolutions |D_qf|²*η and u_q *η using separable moving average convolution operations. This approach has some similarities to [37], where moving average filters were used to speed up the non-local means algorithm.

C. Continuation Strategy to Improve Convergence

The quality of the majorization in (7) depends on the parameter β. It is known that high values of β results in poor convergence. However, since we require the convex-hull approximation of the original penalty (see Section III-D) for the majorization, the solution of the proposed scheme corresponds to that of the original problem only when β → ∞. Hence we use a continuation strategy to improve the convergence rate, where β is initialized with a small value and is increased gradually to a high value [11]. As discussed in [11], we use homotopy continuation on the penalties to encourage convergence to global minima. For example, with truncated penalties we start with a large threshold T and gradually decrease it until it attains a small value. In all the experiments, we initialize β to 1e-2 and set β_incfactor = 2 while we set T_decfactor = 1.1. The pseudo-code of the algorithm is shown below.

Algorithm IV.1.

NonLocal Shrinkage(A, b, λ)

Input : b = k-space measurements
β = βinit; T = Tinit;
while i < # Outer Iterations
do		while j < # Inner Iterations
		do		Shrinkage: Compute vq using (27)
				Compute hq using (13)
				Update f using (25)
		β ← β * βincfactor
		T ← T * Tdecfactor
return (f)

We observe that the proposed algorithm is similar in structure to our previous algorithm [11], shown below.

Algorithm IV.2.

Reweighted MM (A, b, λ, σ)

Input : b = k-space measurements
T = Tinit;
while i < # Outer Iterations
do		while j < # Inner Iterations
		do		Update wx,y using (16) in [11]
				Compute γx,y using (20) in [11]
				Update f by solving (26) in [11]
		T ← T * Tdecfactor
return (f)

Note from the pseudo-code that the non-local shrinkage algorithm requires two moving-average convolution operations per q value to evaluate (27). For a 3 × 3 neighborhood, this translates to 16 moving convolution operations. In addition, evaluating f according to (25) requires one FFT and one IFFT. We typically need 10 – 20 inner iterations and about 30 – 40 outer iterations for the best convergence and recovery.

All the experiments were performed in MATLAB 2012 on a Linux Intel Xeon workstation machine with four cores, 3.2 GHz CPU and 32 GB RAM.

V. Results

We focus on the application of this scheme for the recovery of MR images from undersampled measurements. All the datasets used in this paper were acquired on the Siemens 3T Tim Trio scanner at the University of Iowa. The datasets were collected under a protocol approved by the Institutional Review Board (IRB) at the University of Iowa and an informed consent was obtained from the subjects prior to the scan.

A. Convergence Rate

We first compare the proposed scheme with our previous iterative reweighted non-local algorithm [11]. We considered the recovery of an MR brain image used in Fig. 4 from its retrospectively undersampled Fourier measurements using a variable density random sampling pattern (see Fig. 4.(e) for an example). The regularization parameters of both algorithms were set to λ = 10⁻⁴; this parameter was chosen to obtain the best possible reconstructions. The number of inner iterations and outer iterations in both the algorithms were set to 5 and 45, respectively. The maximum number of CG iterations to solve each quadratic subproblem in IRW scheme was set to 10. The tolerance values for all loops in both algorithms were set to 1e-8.

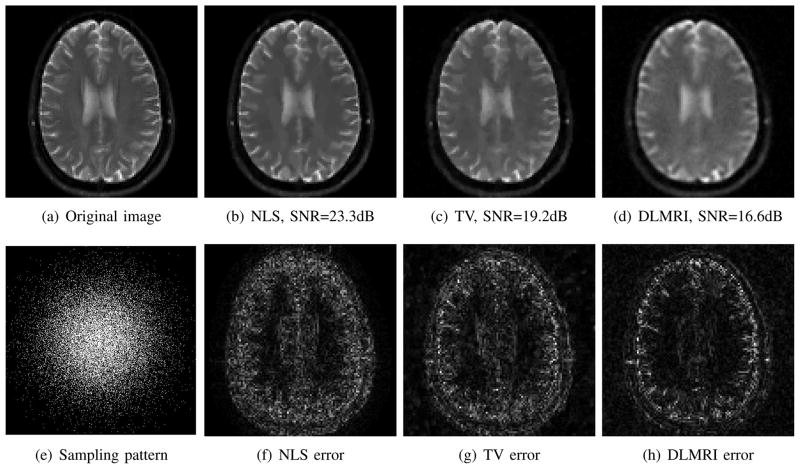
Fig. 4.

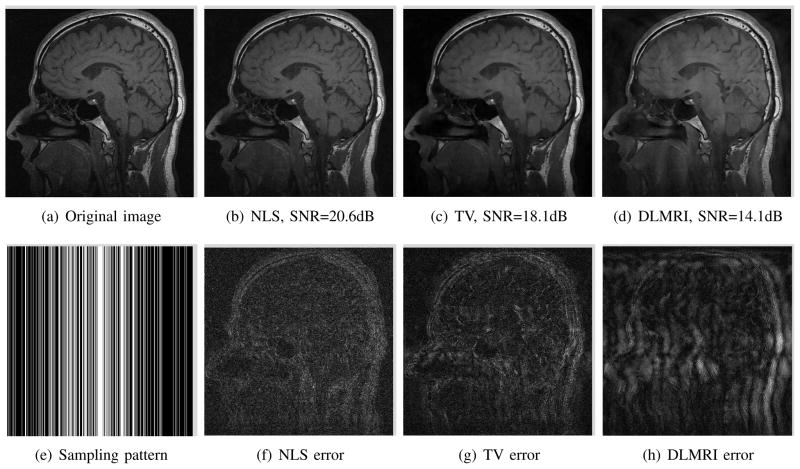
Comparison of the algorithms in the absence of noise. We consider the recovery of a 128×128 MR brain image from 5 fold undersampled Fourier samples, acquired using a random sampling pattern shown in (e) using non-local shrinkage scheme (NLS), DLMRI and local TV. The reconstructions are shown in (b)-(d). The corresponding error images, scaled by a factor of 5 for better visualization, are shown in the bottom row. The reconstructions show that the NLS scheme is capable of better preserving the edges and details, resulting in less blurred reconstructions. Note that this example was used as an illustration; the proposed 2-D under sampling pattern on the dataset acquired using a 3-D sequence is not very realistic. We also used a high acceleration factor to demonstrate differences between the methods; thus the resulting images may not be of diagnostic quality.

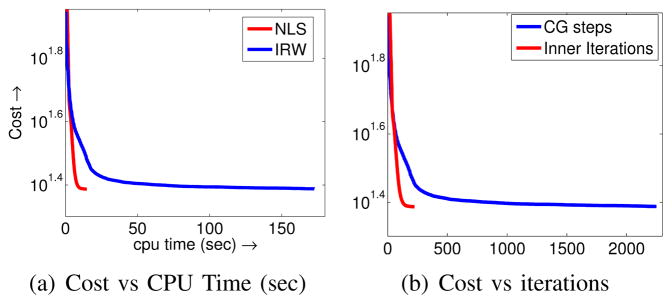
The convergence plots of the two algorithms as functions of computation time and number of iterations are shown in Fig. 3. We observe that both algorithms converge to almost the same final cost. However, the non-local shrinkage (NLS) algorithm is around ten times faster than the iterative reweighted (IRW) scheme in terms of computation time; the NLS scheme took around 17 seconds, while the IRW required 172 seconds to converge. All the weight updates in IRW together took a total of 9.4 seconds, while the shrinkage steps in NLS took a total of 12.0 seconds. The main difference in complexity between the algorithms can be attributed to the analytical solution of f in the NLS scheme, which took only 0.4 seconds for all 225 inner iterations. At the same time, solving the quadratic subproblems in IRW using CG took around 163 seconds for all 225 inner iterations. We observe that the condition number of the quadratic subproblem in iterative reweighting [11] grows with iterations, resulting in slow convergence of the CG algorithms especially in later iterations. The speedup offered by using an additive half-quadratic majorization specified by (7) is consistent with using this method in non-patch regularization schemes [33].

Fig. 3.

Comparison of the convergence rate of the iterative reweighted (IRW) algorithm and the proposed iterative non-local shrinkage (NLS) algorithm. The plots indicate the evolution of the cost function in (1) as functions of (a) the CPU time and (b) number of inner iterations in NLS and CG steps in IRW. Both NLS and IRW algorithms converged in around 225 inner iterations. However, the IRW scheme needed around 9 CG steps/inner iteration on average, requiring a total of 2200 (see Algorithms IV.1 and IV.2). Since each inner iteration in NLS is considerably faster than the corresponding one in [11], we obtain a speedup of approximately ten fold.

B. Impact of the Distance Metric

The proposed scheme can be adapted to most non-local distance metrics by simply changing the shrinkage rule. The shrinkage rules for different non-local penalties are shown in Fig. 1. In Table I we compare the different metrics in the context of recovering three MR images from five fold randomly undersampled data. Here we quantify the reconstruction quality by the signal-to-noise ratio (SNR), defined as

TABLE I.

(SNR in dB) Impact of the distance metric on the reconstructions. We compare the reconstructions obtained using the non-local shrinkage algorithm using ℓ₁, H₁, NLTV, thresholded ℓ₁ and thresholded ℓ_p; p = 0.5 metrics. All the metrics, except the convex ℓ₁ scheme are saturating priors. We observe that saturation is key to good performance of non-local algorithms. Among the different metrics, the thresholded ℓ_p penalty is observed to provide the best results in all the examples.

Image	ℓ1	H1	NLTV	ℓ1-T	ℓp-T
Brain1	19.8	22.8	23.0	21.4	23.4
Brain2	18.0	20.2	21.1	19.5	22.9
Head	19.1	19.2	19.5	19.3	19.9

$$\text{SNR}=20{log}_{10}\left(\frac{{\Vert {\mathbf{\Gamma }}_{\text{orig}}\Vert }_F}{{\Vert {\mathbf{\Gamma }}_{\text{rec}}-{\mathbf{\Gamma }}_{\text{orig}}\Vert }_F}\right),$$

where Γ_orig is the original image, Γ_rec is the recovered image, and ||·||_F is the Frobenius norm. The parameters of all the algorithms are optimized to provide the best possible SNR. The first column corresponds to the convex ℓ₁ differences between patches. The second and third columns correspond to alternating H1 and NLTV penalties [11], respectively.

All of the penalties saturate with inter-patch distances except the ℓ₁ distance function. This explains the poor performance of the convex ℓ₁ penalty compared to the non-convex counterparts. Unlike local total variation, which only compares a particular pixel with a few other pixels, several pixel comparisons are involved in non-local regularization. Saturating priors are needed to avoid the averaging of dissimilar patches, which may result in blurring. Since the saturating ℓ_p metric provides the best overall reconstructions, we use this prior for remaining comparisons.

C. Comparisons With State-of-the-Art Algorithms

We compare the proposed scheme with local total variation regularization (TV) and the dictionary learning MRI (DLMRI) scheme [26] using retrospectively undersampled MRI data. Specifically, the Fourier samples of the images on the specified sampling mask are used for reconstruction using different algorithms. These reconstructions are compared to the original image. We relied on the MATLAB implementation of DLMRI available from the authors webpage, which was adapted to account for complex MR images. The regularization parameters of all the algorithms have been optimized to yield the best SNR. The comparison of the above methods in the context of random sampling with 5 fold undersampled data in the absence of noise is shown in Fig. 4. This fully sampled 128×128 MR brain image was acquired using a Turbo spin echo (TSE) sequence, FOV=22x22 cm², slice thickness=5.0 mm. The under sampling pattern in (e) was generated using a Monte-Carlo algorithm [2], which may be realized in 3D imaging by choosing the readout to be orthogonal to the image plane. We observe that the proposed non-local algorithm provides better preservation of edge details. The quantitative comparisons of different methods on the retrospective under sampling of more MR images in the absence of noise and five fold random undersampling are reported in Table II. We observe that NLS provides a consistent 1–4 dB improvement over other methods.

TABLE II.

(SNR in dB) Quantitative comparison of the proposed iterative non-local shrinkage (NLS) algorithm using the saturating ℓ_p; p = 0.5 penalty with dictionary learning MRI (DLMRI) [26] and local total variation regularization (TV) schemes in the absence of noise. We considered five-fold random undersampling.

Image	DLMRI	TV	NLS
Brain	16.6	19.3	23.4
Brain2	17.5	21.0	22.9
Thigh	16.3	22.0	24.0
Calf	19.1	21.2	22.5
Head	18.6	19.6	19.9

D. Performance with noise

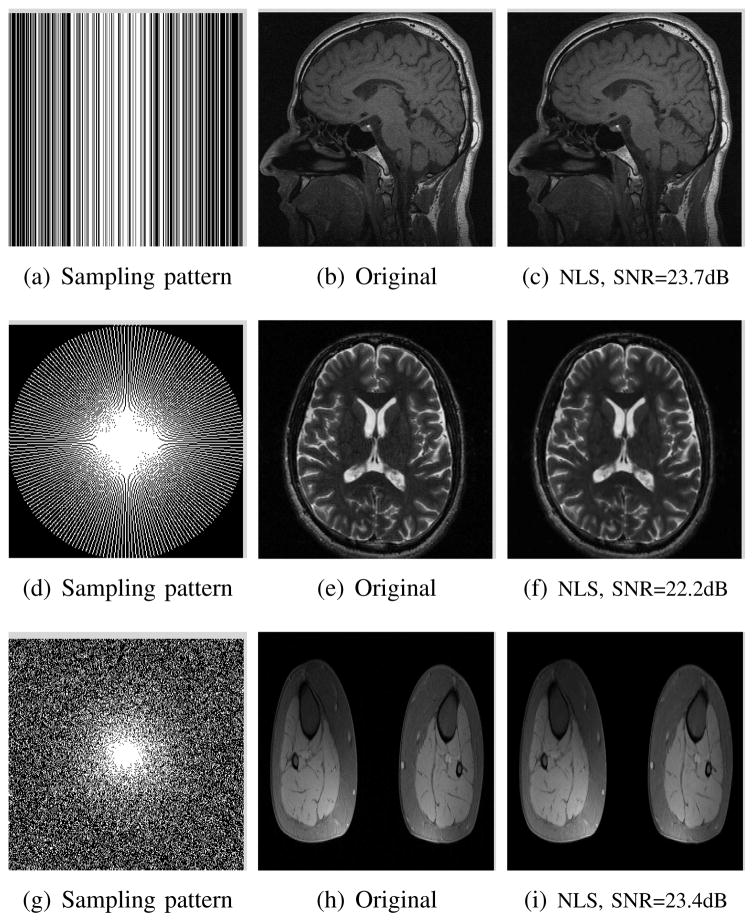
We study the performance of the proposed algorithm in the context of recovering MR images from their retrospectively undersampled measurements using different sampling trajectories in the presence of noise. The reconstructions of 512×512 MR head complex image from its three-fold Cartesian retrospectively undersampled Fourier data, corrupted with zero mean complex Gaussian noise are shown in Fig. 5. The SNR of the noisy measurements was 25.0 dB. This is a really challenging case since the 1-D downsampling pattern is considerably less efficient than 2-D random sampling. We observe that the non-local algorithm provides better reconstructions than the other schemes. Specifically, the TV scheme results in patchy artifacts and are over-smoothed. The DLMRI results in blurring and loss of details. By contrast to the classical algorithms, the degradation in performance of the non-local algorithm is comparatively small. The quantitative comparisons of the algorithms on this setting using different MR images are shown in the top section of Table III.

Fig. 5.

Comparison of the algorithms in the presence of noise. We consider the recovery of a 512×512 MR head complex image from three-fold undersampled k-space data, acquired using a Cartesian sampling pattern contaminated by zero mean complex Gaussian such that the SNR value after adding the noise is 25.0 dB. The top row shows the original and reconstructed images using non-local shrinkage scheme (NLS), DLMRI and local TV. The reconstructions are shown in (b)-(d). The corresponding error images as well as the sampling pattern are shown in the bottom row. This is a challenging case due to the high 1-D undersampling factors and noise. We observe that the NLS scheme provides better reconstructions with minimal aliasing artifacts. Note that this example was used as an illustration; the proposed 2-D under sampling pattern on the dataset acquired using a 3-D spin-echo sequence is not very realistic. Note that we used a high acceleration factor to demonstrate differences between the methods. The resulting images may not be of diagnostic quality.

TABLE III.

Quantitative comparison of the algorithms in the presence of noise. The top part shows the SNR of the reconstructions obtained from 3 fold Cartesian undersampled data. The bottom part shows the SNR of the reconstructions from radial undersampled data with 70 spokes. Both experiments are contaminated by zero mean complex Gaussian noise such that the SNR of the noisy images are reported in the table. The quantitative results show that the proposed iterative NLS scheme provides consistently better reconstructions for the above cases.

Image	k-space SNR	DLMRI	TV	NLS
Brain	12.9	13.9	15.0	16.8
Brain2	18.7	15.9	16.1	18.5
Thigh	23.7	12.6	18.7	21.7
Calf	21.6	15.9	18.5	20.6
Head	25.0	14.1	18.1	20.3
Brain	11.6	14.6	17.6	17.3
Brain2	17.4	17.0	17.7	18.0
Thigh	22.4	13.8	17.2	20.0
Calf	20.3	9.3	16.7	19.0
Head	23.4	17.9	18.1	18.2

We also consider the recovery of five various MR images from their pseudo-radial samples acquired with 70 spokes/frame, which approximately corresponds to an acceleration factor of 4.2. The radial samples are approximated by the nearest Cartesian samples. The quantitative results in this setting for those MR images are shown in the bottom section of Table III. The Fourier measurements are corrupted with zero mean complex Gaussian noise of a specific variance. The SNR of the corresponding k-space measurements is reported in the second column. All methods are observed to result in loss of subtle image features since the acceleration factor and the noise level are high. But we also observe that the NLS scheme provides better recovery than the competing methods. The SNR improvement offered by NLS over the other methods in this experiment is not as high as in the previous cases, mainly due to the considerable noise in the data and the high acceleration. All of the above experiments were conducted at high acceleration factors to demonstrate the performance improvement offered by the proposed scheme. We show in Fig. 6 the recovery of three MR images from Fourier samples corresponding to low accelerations, contaminated with zero mean complex Gaussian noise. These experiments show that the NLS scheme can be used to obtain good quality reconstructions at moderate acceleration factors and noise levels.

Fig. 6.

Comparison of three different MR images using NLS scheme in the presence of noise. The Fourier samples are contaminated by zero mean complex Gaussian noise such that the SNR of the data corresponding to the head, brain2 and calf images are 32.3, 24.7 and 27.6 dB, respectively. The top row shows the recovery from 2 fold acceleration using the Cartesian sampling pattern, while the middle one shows the recovery from 100 radial spokes (≈3 fold acceleration). The bottom row shows the recovery from 3 fold acceleration using random pattern. We observe that the NLS scheme is capable of preserving the key image details.

E. Validation using non-Cartesian MRI data

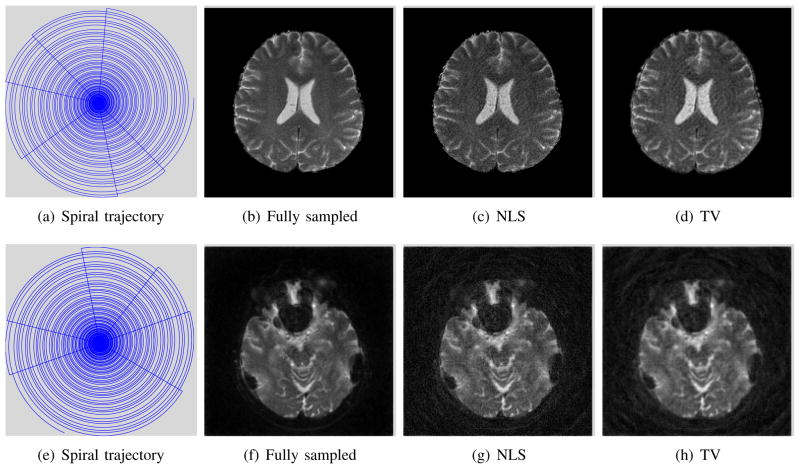
We consider the recovery of multichannel multi-shot spiral MRI data using the proposed scheme and TV regularization in this subsection. These datasets were acquired using a spin-echo variable density multi shot spiral acquisition with 22 interleaves, 192×192 matrix and a 12 channel head array. The fully sampled dataset is recovered from all 22 interleaves and four of the important coils using total variation regularization. Specifically, each of the channels were reconstructed independently from the measured k-space data and the coil sensitivities were estimated from them. These coil sensitivities were used to recover the images from undersampled data. The forward and backward models are implemented using the non-uniform fast Fourier transform (NUFFT) [38], [39]. Since the forward model is a non-Cartesian Fourier transform, we are no longer able to use the analytical solution (25). We instead use the conjugate gradient algorithm (CG) to solve (22). We set the maximum number of CG iterations to 20 and the the previous iterate was set as the the initial guess. We observe that very few CG iterations (average of 3–4) are needed in each inner iteration, thanks to the good conditioning of (22), especially at later iterations.

The undersampled data was recovered from the measured k-space data corresponding to a random subset of 7 interleaves of the above four channels. We recovered the images using the different algorithms. The forward model in this case is the non-Cartesian Fourier transform of the coil sensitivity weighted images, using the coil sensitivities estimated from fully sampled data¹. We use the CG algorithm with the same settings as above to solve (22). We did not use any pre-conditioners in the present study; we expect to further reduce the computational complexity in the future using efficient preconditioners. We only compare our recovery against TV as it was difficult to modify the DLMRI scheme to the non-Cartesian setting. We show the acquisition from two subjects in Fig. 7. The trajectories corresponding to the datasets are shown in the first column. The data from the second subject (bottom slice) had considerable off-resonance losses since the slice was close to the frontal sinuses and the ear regions. In addition, it also suffered from inter-shot motion that resulted in inconsistencies between the interleaves. The comparisons clearly show the benefit of the proposed scheme in a practical setting. Specifically, the NLS reconstructions preserve fine details better than TV regularization.

Fig. 7.

Comparison of MR brain images using NLS and TV algorithms from undersampled multichannel multi-shot spiral data. The fully sampled data was acquired using a multishot spiral sequence with 22 interleaves acquired using 12 channels. All the interleaves were used to recover the fully sampled datasets, while only 7 randomly chosen interleaves were used to recover the undersampled datasets. The retained interleaves are shown in the first column. We only used the data corresponding to four important coils for the recovery. The two rows corresponds to two slices in the acquisition. The recovery of the lower slice was considerably challenging due to field inhomogeneity losses and subtle physiological motion between interleaves; this explains the poor recovery of the datasets. The two rows show the spiral trajectory, original and reconstructed images. Both the proposed and TV regularized reconstructions are seen to have lower SNR, mainly due to decreased number of measurements. However, we observe that the proposed scheme provides sharper reconstructions.

VI. Conclusion

We introduced a fast iterative non-local shrinkage algorithm to recover MR image data from undersampled Fourier measurements. This approach is enabled by the reformulation of current non-local schemes as an iterative re-weighting algorithm to minimize a global criterion [11]. The proposed algorithm alternates between a non-local shrinkage step and a quadratic subproblem, which can be solved analytically and efficiently. We derived analytical shrinkage rules for several penalties that are relevant in non-local regularization. We accelerated the non-local shrinkage step, whose direct evaluation involves expensive non-local patch comparisons, by exploiting the redundancy between the terms at adjacent pixels. The resulting algorithm is observed to be considerably faster than our previous implementation. The comparison of different penalties demonstrated the benefit in using distance functions that saturate with distant patches. The comparisons of the proposed scheme with state of the art algorithms show a considerable reduction in alias artifacts and better preservation of edges.

Appendix A: Simplification of Eq (10)

Using the formula for the shrinkage from (9), specified by

$${\mathbf{s}}_{\mathbf{x},\mathbf{q}}=(P_{\mathbf{x}}(\mathbf{f})-P_{\mathbf{x}+\mathbf{q}}(\mathbf{f}))\nu (\Vert P_{\mathbf{x}}(\mathbf{f})-P_{\mathbf{x}+\mathbf{q}}(\mathbf{f})\Vert ),$$

we obtain

$$\mathcal{R}(\mathbf{f})=\sum _{\mathbf{x};\mathbf{q}\in \mathcal{N}}{\Vert P_{\mathbf{x}}(\mathbf{f})-P_{\mathbf{x}+\mathbf{q}}(\mathbf{f})-{\mathbf{s}}_{\mathbf{x},\mathbf{q}}\Vert }^2.$$ (28)

Expanding the above expression:

$$\mathcal{R}(\mathbf{f})=\sum _{\mathbf{x}:\mathbf{q}\in \mathcal{N}}\sum _{\mathbf{p}\in \mathcal{B}}{\mid f(\mathbf{x}+\mathbf{p})-f(\mathbf{x}+\mathbf{q}+\mathbf{p})-{\mathbf{s}}_{\mathbf{x},\mathbf{q}}(\mathbf{p})\mid }^2$$ (29)

We use a change of variables x = x + p to obtain:

$$\begin{array}{l}\mathcal{R}(\mathbf{f})=\sum _{\mathbf{x};\mathbf{q}\in \mathcal{N}}\sum _{\mathbf{p}\in \mathcal{B}}{\mid \stackrel{e(\mathbf{x},\mathbf{q})}{\overbrace{f(\mathbf{x})-f(\mathbf{x}+\mathbf{q})}}-{\mathbf{s}}_{\mathbf{x}-\mathbf{p},\mathbf{q}}(\mathbf{p})\mid }^2\\ =\sum _{\mathbf{x};\mathbf{q}\in \mathcal{N}}{\mid e(\mathbf{x},\mathbf{q})\mid }^2-2\sum _{\mathbf{x};\mathbf{q}\in \mathcal{N}}e(\mathbf{x},\mathbf{q})\underset{h_{\mathbf{q}}(\mathbf{x})}{\underbrace{\sum _{\mathbf{p}\in \mathcal{B}}{\mathbf{s}}_{\mathbf{x}-\mathbf{p},\mathbf{q}}(\mathbf{p})}}+c\\ =\sum _{\mathbf{x};\mathbf{q}\in \mathcal{N}}{\mid f(\mathbf{x})-f(\mathbf{x}+\mathbf{q})-h_{\mathbf{q}}(\mathbf{x})\mid }^2+c-d.\end{array}$$ (30)

In the above equations, c = Σ_{x;q∈𝒩;p∈ℬ}|s_x−p,q(p)|² and d = Σ_x;q∈𝒩|h_q(x)|². Since the solution to (10) does not depend on the constants, we ignore these terms. Thus, (29) can be rewritten using (30) as

$$\mathcal{R}(\mathbf{f})=\sum _{\mathbf{x};\mathbf{q}\in \mathcal{N}}{\Vert \underset{{\mathcal{D}}_{\mathbf{q}}f}{\underbrace{f(\mathbf{x})-f(\mathbf{x}+\mathbf{q})}}-h_{\mathbf{q}}(\mathbf{x})\Vert }^2$$

Here, 𝒟_qf(x) = f(x + q) − f(x) is the finite difference operator. We observe that the expression for h_q(x)

$$h_{\mathbf{q}}(\mathbf{x})=\sum _{\mathbf{p}\in \mathcal{B}}{\mathbf{s}}_{\mathbf{x}-\mathbf{p},\mathbf{q}}(\mathbf{p}),$$ (31)

can be further simplified. From (9), we have the patch s specified as

$${\mathbf{s}}_{\mathbf{x},\mathbf{q}}=(P_{\mathbf{x}}f-P_{\mathbf{x}+\mathbf{q}}f)\underset{u_{\mathbf{q}}(\mathbf{x})}{\underbrace{\nu (\Vert P_{\mathbf{x}}f-P_{\mathbf{x}+\mathbf{q}}f\Vert )}}$$

Here, u_q(x) = ν(||P_xf − P_x+qf||) is the factor between 0 and 1, which is multiplied by the patch to get the shrinked patch. Hence,

$${\mathbf{s}}_{\mathbf{x},\mathbf{q}}(\mathbf{r})=[f(\mathbf{x}+\mathbf{r})-f(\mathbf{x}+\mathbf{q}+\mathbf{r})]·u_{\mathbf{q}}(\mathbf{x});\mathbf{r}\in \mathcal{B}.$$

Thus, we have

$${\mathbf{s}}_{\mathbf{x}-\mathbf{p},\mathbf{q}}(\mathbf{p})=[f(\mathbf{x})-f(\mathbf{x}+\mathbf{q})]u_{\mathbf{q}}(\mathbf{x}-\mathbf{p}).$$ (32)

Substituting in (31), we get

$$h_{\mathbf{q}}(\mathbf{x})=(f(\mathbf{x})-f(\mathbf{x}+\mathbf{q}))\underset{v_{\mathbf{q}}(\mathbf{x})}{\underbrace{\sum _{\mathbf{p}\in \mathcal{B}}{u}_{\mathbf{q}}(\mathbf{x}-\mathbf{p})}}.$$ (33)

Appendix B: Shrinkage rules for useful non-local distance functions

1) Thresholded ℓ_p; p ≤ 1 metric

We now consider the saturating ℓ_p metric, specified by

$$\varphi (t)=\{\begin{array}{ccc}{\mid t\mid }^p/p& \text{if}& \mid t\mid <T\\ T^p/p& \text{else}& \end{array}$$ (34)

Computing the shrinkage rule for this mapping according to (21), we obtain

$$\nu (t)=\{\begin{array}{ccc}0& \text{if}& \mid t\mid <{\beta }^{1/(p-2)}\\ 1-\frac{1}{\beta }{\mid t\mid }^{p-2}& \text{if}& {\beta }^{1/(p-2)}\le \mid t\mid <T\\ 1& \text{else}& \end{array}$$ (35)

Setting T = ∞ we get the shrinkage rule for the unthresholded ℓ_p metric as

$$\nu (t)=\{\begin{array}{ccc}0& \text{if}& \mid t\mid <{\beta }^{1/(p-2)}\\ 1-\frac{1}{\beta }{\mid t\mid }^{p-2}& \text{else}& \end{array},$$ (36)

which is consistent with [18].

2) Penalty corresponding to alternating H₁ non-local scheme

We now consider the H₁ metric, specified by

$$\phi (t)=1-exp\left(-\frac{t^2}{2{\sigma }^2}\right).$$ (37)

From (21) we obtain

$$\nu (t)=\{\begin{array}{ccc}0& \text{if}& exp\left(-\frac{t^2}{2{\sigma }^2}\right)>\beta {\sigma }^2\\ 1-\frac{exp\left(-\frac{t^2}{2{\sigma }^2}\right)}{\beta {\sigma }^2}& \text{else}& \end{array}$$ (38)

3) Penalty corresponding to Peyre’s non-local scheme

We now consider the penalty corresponding to Peyre’s alternating scheme [11], [40]:

$$\varphi (t)=1-exp\left(-\frac{t}{\sigma }\right).$$ (39)

From (21) we obtain

$$\nu (t)=\{\begin{array}{ccc}0& \text{if}& exp\left(-\frac{t}{\sigma }\right)>\beta \sigma t\\ 1-\frac{exp\left(-\frac{t}{\sigma }\right)}{\beta \sigma t}& \text{else}& \end{array}$$ (40)

4) Penalty corresponding to alternating non-local TV scheme

The penalty function for the alternating non-local TV scheme is specified by [11], [41]:

$$\varphi (t)=\text{erf}\left(\frac{t}{\sigma }\right).$$ (41)

From (21) we obtain

$$\nu (t)=\{\begin{array}{ccc}0& \text{if}& \frac{2}{\sqrt{\pi }}exp\left(-\frac{t^2}{{\sigma }^2}\right)>\beta \sigma t\\ 1-\frac{2}{\sqrt{\pi }}\frac{exp\left(-\frac{t^2}{{\sigma }^2}\right)}{\beta \sigma t}& \text{else}& \end{array}$$ (42)