An extension of stochastic hierarchy equations of motion for the equilibrium correlation functions

Abstract

A traditional stochastic hierarchy equations of motion method is extended into the correlated real-time and imaginary-time propagations, in this paper, for its applications in calculating the equilibrium correlation functions. The central idea is based on a combined employment of stochastic unravelling and hierarchical techniques for the temperature-dependent and temperature-free parts of the influence functional, respectively, in the path integral formalism of the open quantum systems coupled to a harmonic bath. The feasibility and validity of the proposed method are justified in the emission spectra of homodimer compared to those obtained through the deterministic hierarchy equations of motion. Besides, it is interesting to find that the complex noises generated from a small portion of real-time and imaginary-time cross terms can be safely dropped to produce the stable and accurate position and flux correlation functions in a broad parameter regime.

I. INTRODUCTION

Equilibrium correlation functions (ECF) have long stood as the central and fundamental issue in quantum dynamics, largely on account of their ability to encode an abundance of dynamical information, such as the reactive flux rate constants,^1–7 the emission spectra,^8–13 and various transport coefficients.^14–17 Out of its importance, great endeavours have been devoted in this area that blossom out into a number of impressive analytical and numerical methodologies.^{3,5,12,18–27}

It has already been verified that the accurate evaluations of equilibrium correlation functions rely significantly on the exact treatment of quantum Boltzmann operator of the whole Hamiltonian including system and bath, as well as their interaction,^11,21,27 for which the imaginary-time path integral technique combined with the Monte Carlo sampling scheme is the best-suited.²⁸ Based on this technique and molecular dynamics, ring polymer molecular dynamics (RPMD)^20,21,29 and centroid molecular dynamics (CMD)^22,30–34 have earned their fame due to their versatile applications. However, they are challenged in the cases, where the real-time quantum coherence effects play a crucial role, such as in the low temperature and the small friction strength regimes. Although the path integral Monte Carlo could be straightforwardly extended into the real-time regime, it is beset by the highly oscillatory nature of integrand, namely, the sign problem, and then limited to the very short time simulation.³⁵

Makri and co-workers have creatively proposed an accurate and efficient quasi-adiabatic propagator path integral (QUAPI) methodology.^36–38 The triumph principally contributes to an advanced partitioning strategy of the Hamiltonian in the time evolution propagator that leads to the substantial reduction of time slices in the discretized path integral formalism.³⁹ Besides, the usage of system-specific discrete variable representation can result in the contraction of quadrature grid points.⁴⁰ Furthermore, a tensor multiplication scheme allows an iterative algorithm for the long time simulations of the equilibrium correlation functions and is raised on the basis of the observation that the nonlocality of the bath response function spans finitely along any direction in the complex time plane.^41,42 In reality, by employing QUAPI, they were able to provide the long-awaited numerical exact results for quantum rate constants.^23,43 But the numerical requirements for the convergence grow formidably fast when it is applied to large-size systems with long memory length.

A different routine toward the numerically exact solutions is offered by the hierarchy equations of motion (HEOM). Instead of the direct evaluation of the path-integral density matrix, the HEOM introduces an infinite number of auxiliary density operators to obtain the Markovian dynamics in the full space, but maintain the quantum-mechanical nonlocality in the zeroth-order. On the foundation of a factorized initial state between the system and bath, the real-time HEOM has arisen as a standard non-perturbative and non-Markovian method to promise us a deeper and wider insight into numerous problems in various fields over the past few decades, as shown in Ref. 44 and the references therein. In its extension for calculating equilibrium correlation functions, it is conventional to propagate the arbitrary state from the distant past to make sure that all the elements of auxiliary density matrices reach their equilibrium at the initial moment.^9,45 Nevertheless, this practice is, most of the time, computationally heavy and might turn into an impossible task at extreme cases without dynamical dissipation, specifically speaking under the influence of a few underdamped harmonic oscillators. Until recently, Tanimura has established the deterministic imaginary-time HEOM to prepare the initial values for the real-time propagation upon a transformation.^24,25 In addition, the imaginary-time HEOM bears another benefit of the accessibility to the partition function and thereafter a great variety of related thermodynamical properties, such as entropy and heat capacity. Following up on that, by stochastically unravelling the pure imaginary-time nonlocality in the influence functional, Song and Shi developed the stochastic imaginary-time HEOM to provide another choice for the initial conditions without the effort of an additional transformation.⁴⁶ But the virtues of these formalisms are often exhausted by a plethora of auxiliary density matrices in the low temperature regime where many Matsubara or Padé frequencies are needed.

Actually, the harmonic bath in its nature allows for the usage of Gaussian stochastic fields in both real and complex time regimes.^12,47–49 For instance, Cao and co-workers⁴⁷ have put forward an effective numerical strategy to sample the paths of every harmonic mode and then propagate the system under quantum fluctuations. Stockburger and co-workers⁴⁸ unravel the total influence functional by introducing two correlated complex Gaussian stochastic processes to obtain a strikingly simple stochastic Liouville-von Neumann equation (SLN) for ECF. Shao⁴⁹ also provides an alternative derivation. The quantum-mechanical nonlocality is now rooted in the interaction with the stochastic fields and then is only perceivable after implementing the ensemble average. As a result, for every realization of random sampling, SLN is memory free. It is also commendable that SLN makes no discrimination on all kinds of spectral density functions, including the realistic one. Unfortunately, the numerical performance deteriorates fast when it is subjected to slightly larger system-bath coupling strength and longer simulation time. Despite this fact, Moix and Cao showed that it still works well with regard to the dipole-dipole correlation function of the emission spectra, because the absence of the real-time forward system path results in an accelerating decay speed.¹²

Following the spirit, delivered by many real-time stochastic hierarchy equations of motion (sHEOM) methodologies,^44,50–54 that all the temperature-dependent part of the influence functional should be stochastically unravelled so as to circumvent Matsubara or Padé frequency decomposition, while the temperature-free part is handled with the help of the hierarchical technique to ameliorate the statistical errors, and we would like to provide an alternative stochastic hierarchy equations of motion for the equilibrium correlation functions in this paper. The rest of the sections are arranged as follows: Section II provides derivation details about the proposed method. The numerical applications in the dimer emission spectra and spin-boson model are shown in Sec. III to demonstrate the validity and efficiency of the method. Besides, an extremely accurate approximation is invoked upon the proposed method. Some concluding remarks are given in Sec. IV.

II. METHOD

Although the realistic environment might be rather complex, it is still a reasonable protocol to replace it with a bath that is composed of infinite harmonic oscillators and is coupled linearly to the systems of interest.⁵⁵ To this end, the total Hamiltonian is written as

$$Ĥ=\frac{{\widehat{p}}_x^2}{2}+V\left(\widehat{x}\right)+\sum _j\left\{\frac{{\widehat{P}}_j^2}{2}+\frac{1}{2}{\omega }_j^2{\left({\widehat{Q}}_j-\frac{c_j\widehat{x}}{{\omega }_j^2}\right)}^2\right\},$$ (1)

where $\widehat{x}$ and ${\widehat{p}}_x$ are mass-weighted position and momentum operator of the system, respectively, while ${\widehat{Q}}_j$ and ${\widehat{P}}_j$ are those of the jth oscillator with the frequency ${\omega }_j$. The strength of the system-bath coupling is characterized by the coefficient {c_j}. For the sake of simplicity, the Boltzmann constant k_B and the reduced Planck constant ℏ are set to 1 in the whole context.

Since many dynamical properties are related to ECF which take the general form

$$C_{AB}\left(t\right)=Q_{\beta }^{-1}Tr\left[Âe^{iĤt}\widehat{B}{e}^{-iĤt}{e}^{-\beta Ĥ}\right].$$ (2)

Here $Â$ and $\widehat{B}$ denote arbitrary system-pertaining operators, such as the flux operator, the transition dipole moments, and so on. $Q_{\beta }=Tr\left[e^{-\beta Ĥ}\right]$ is the canonical partition function at the given inverse temperature $\beta =1∕T$. Making use of the permutation invariance under the trace operation, it would be technically favorable to recast the above expression as the average of the operator $\widehat{B}$ in the system subspace with respect to the disguised reduced density operator

$${\widehat{\rho }}_A\left(t,\beta \right)=Q_{\beta }^{-1}{Tr}_b\left[e^{-iĤt}{e}^{-\beta Ĥ}Âe^{iĤt}\right].$$ (3)

Here, Tr_b denotes tracing over all bath degrees of freedom, which could be fulfilled analytically in the Feynman path integral formalism to yield the elegant functional integral representation of the reduced density matrix elements⁵⁶

$$\begin{array}{rcl}{\rho }_A\left(x_f,x_f^{\prime },t,\beta \right)& =& Q_{\beta }^{-1}\iint \iint \mathrm{d}{x}_i^{+}\mathrm{d}{x}_i^{-}\mathrm{d}{\overline{x}}_i\mathrm{d}{\overline{x}}_f{\rho }_0\left(x_i^{+},x_i^{-},{\overline{x}}_i,{\overline{x}}_f\right)\\ & & \times {\int }_{x_i^{+}}^{x_f}\mathcal{D}{x}^{+}\left(t\right){\int }_{x_i^{-}}^{x_f^{\prime }}\mathcal{D}{x}^{-}\left(t\right){\int }_{{\overline{x}}_i}^{{\overline{x}}_f}\mathcal{D}\overline{x}\left(\tau \right)\\ & & \times exp\left\{i{S}_0\left[x^{+}\left(t\right)\right]-i{S}_0\left[x^{-}\left(t\right)\right]-S_0^E\left[\overline{x}\left(\tau \right)\right]\right\}\\ & & \times F\left[x^{+}\left(t\right),x^{-}\left(t\right),\overline{x}\left(\tau \right)\right],\end{array}$$ (4)

with ${\rho }_0\left(x_i^{+},x_i^{-},{\overline{x}}_i,{\overline{x}}_f\right)=A\left({\overline{x}}_i,x_i^{-}\right)\delta \left({\overline{x}}_f,x_i^{+}\right)$. From now on, t is designated as the real-time variable originating from 0, and τ is the imaginary-time variable with a definite interval ranging from 0 to β. S₀[x⁺(t)] and S₀[x⁻(t)] are the real-time action functionals for the forward path x⁺(t) and backward path x⁻(t), respectively, and $S_0^E\left(\overline{x}\left(\tau \right)\right)$ is the Euclidean action functional for the imaginary-time path $\overline{x}\left(\tau \right)$. The subscript “0” denotes the association with the bare system Hamiltonian. After the reduction, all the bath effects on the system dynamics are entirely merged into the term, so-called the influence functional $F\left[x^{+},x^{-},\overline{x}\right]=exp\left(\mathrm{\Theta }\left[x^{+},x^{-},\overline{x}\right]\right)$, with the influence phase specifically given as

$$\begin{array}{rcl}\mathrm{\Theta }\left[x^{+},x^{-},\overline{x}\right]& =& -{\int }_0^t\mathrm{d}s{\int }_0^s\mathrm{d}{s}^{\prime }\left(x^{+}\left(s\right)-x^{-}\left(s\right)\right)\\ & & \times \left[\alpha \left(0,s-s^{\prime }\right)x^{+}\left(s^{\prime }\right)-{\alpha }^{*}\left(0,s-s^{\prime }\right)x^{-}\left(s^{\prime }\right)\right]\\ & & +i{\int }_0^{\beta }\mathrm{d}\tau {\int }_0^t\mathrm{d}s{\alpha }^{*}\left(\tau ,s\right)\overline{x}\left(\tau \right)\left(x^{+}\left(s\right)-x^{-}\left(s\right)\right)\\ & & +{\int }_0^{\beta }\mathrm{d}\tau {\int }_0^{\tau }\mathrm{d}{\tau }^{\prime }\overline{x}\left(\tau \right)\alpha \left(\tau -{\tau }^{\prime },0\right)\overline{x}\left({\tau }^{\prime }\right).\end{array}$$ (5)

The bath response function, herein, is expressed in terms of both the real and imaginary time variables t and $\tau$ as

$$\begin{array}{rcl}\alpha \left(\tau ,t\right)& =& {\int }_0^{\infty }\mathrm{d}\omega \frac{J\left(\omega \right)}{\pi }\left[\frac{cosh\left(\frac{\beta \omega }{2}-\omega \tau \right)}{sinh\left(\frac{\beta \omega }{2}\right)}cos\left(\omega t\right)\right.\\ & & \left.-i\frac{sinh\left(\frac{\beta \omega }{2}-\omega \tau \right)}{sinh\left(\frac{\beta \omega }{2}\right)}sin\left(\omega t\right)\right]\\ & =& {\alpha }^R\left(\tau ,t\right)+i{\alpha }^I\left(\tau ,t\right),\end{array}$$ (6)

and the bath structure is encoded in the spectral density function

$$J\left(\omega \right)=\pi \sum _j\frac{c_j^2}{2{\omega }_j}\delta \left(\omega -{\omega }_j\right).$$ (7)

The direct evaluation of ${\rho }_A\left(x_f,{x^{\prime }}_f,t,\beta \right)$ is, at most occasions, prohibitively expensive because of the quantum-mechanical time-nonlocality in $F\left[x^{+},x^{-},\overline{x}\right]$. In quest of an accurate and efficient algorithm, we resort to the hybrid employment of stochastic unravelling and hierarchical techniques. The influence functional is predisposed as the product of three components $F=F_1\times F_2\times F_3$, so as to enable their own distinct treatments. The first component is allocated as

$$\begin{array}{rcl}{F}_1\left[x^{\times },\overline{x}\right]& =& exp\left\{-{\int }_0^t\mathrm{d}s{\int }_0^s\mathrm{d}{s}^{\prime }{x}^{\times }\left(s\right){\alpha }^R\left(0,s-s^{\prime }\right)x^{\times }\left(s^{\prime }\right)\right.\\ & & +i{\int }_0^{\beta }\mathrm{d}\tau {\int }_0^t\mathrm{d}s{\alpha }^R\left(\tau ,s\right)\overline{x}\left(\tau \right)x^{\times }\left(s\right)\\ & & \left.+{\int }_0^{\beta }\mathrm{d}\tau {\int }_0^{\tau }\mathrm{d}{\tau }^{\prime }\overline{x}\left(\tau \right)\alpha \left(\tau -{\tau }^{\prime },0\right)\overline{x}\left({\tau }^{\prime }\right)\right\},\end{array}$$ (8)

with the shorthand notation $x^{\times }\left(s\right)\equiv x^{+}\left(s\right)-x^{-}\left(s\right)$ that stands for the commutator ${\widehat{x}}^{\times }\widehat{\rho }=\left[\widehat{x},\widehat{\rho }\right]$ in the operator representation. Similarly, $x^{°}\left(s\right)\equiv x^{+}\left(s\right)+x^{-}\left(s\right)$ that will be encountered soon stands for the anticommutator ${\widehat{x}}^{°}\widehat{\rho }=\left\{\widehat{x},\widehat{\rho }\right\}$. In practice, F₁ can be reproduced by the following expression, often referred to as the well-known Hubbard-Stratonovich transformation:

$$\begin{array}{rcl}{F}_1\left[x^{\times },\overline{x}\right]=\iint W\left(\xi ,\overline{\xi }\right)\mathrm{d}\xi \mathrm{d}\overline{\xi }{e}^{-i{\int }_0^t\xi \left(s\right)x^{\times }\left(s\right)\mathrm{d}s-{\int }_0^{\beta }\overline{\xi }\left(\tau \right)\overline{x}\left(\tau \right)\mathrm{d}\tau },& & \end{array}$$ (9)

so long as the real Gaussian stochastic processes $\left(\xi \left(t\right),\overline{\xi }\left(\tau \right)\right)$ are of zero mean values and obey the following two-time correlation functions:

$$\left\{\begin{array}{ccc}{⟨\xi \left(t\right)\xi \left(t^{\prime }\right)⟩}_{W_{\xi ,\overline{\xi }}}\hfill & =\hfill & {\alpha }^R\left(0,t-t^{\prime }\right),\hfill \\ {⟨\overline{\xi }\left(\tau \right)\xi \left(t\right)⟩}_{W_{\xi ,\overline{\xi }}}\hfill & =\hfill & {\alpha }^R\left(\tau ,t\right),\hfill \\ {⟨\overline{\xi }\left(\tau \right)\overline{\xi }\left({\tau }^{\prime }\right)⟩}_{W_{\xi ,\overline{\xi }}}\hfill & =\hfill & \alpha \left(|\tau -{\tau }^{\prime }|,0\right).\hfill \end{array}\right.$$ (10)

The generation scheme for $\left(\xi \left(t\right),\overline{\xi }\left(\tau \right)\right)$ is relatively simple by virtue of filtering the white noises with the kernel obtained from the Cholesky decomposition of the covariance matrix constructed by Eq. (10).⁵²

The second component of the influence functional is given by

$$F_2\left[x^{\times },\overline{x}\right]=exp\left\{{\int }_0^{\beta }\mathrm{d}\tau {\int }_0^t\mathrm{d}s{\alpha }^I\left(\tau ,s\right)\overline{x}\left(\tau \right)x^{\times }\left(s\right)\right\},$$ (11)

which is temperature-dependent as well. So, following our central idea, we would like to employ the Hubbard-Stratonovich transformation for the second time,

$$F_2\left[x^{\times },\overline{x}\right]=\iint W\left(v,\overline{v}\right){\mathrm{d}}^{2}v{\mathrm{d}}^2\overline{v}{e}^{{\int }_0^{t}v\left(s\right)x^{\times }\left(s\right)\mathrm{d}s+{\int }_0^{\beta }\overline{v}\left(\tau \right)\overline{x}\left(\tau \right)\mathrm{d}\tau }.$$ (12)

Nevertheless, $W\left(v,\overline{v}\right)$ is an ill-defined probability density function as the covariance matrix constructed by the following two-time correlation functions

$$\left\{\begin{array}{ccc}{⟨v\left(s\right)v\left(s^{\prime }\right)⟩}_{W_{v,\overline{v}}}\hfill & =\hfill & 0,\hfill \\ {⟨\overline{v}\left(\tau \right)v\left(s\right)⟩}_{W_{v,\overline{v}}}\hfill & =\hfill & {\alpha }^I\left(\tau ,s\right),\hfill \\ {⟨\overline{v}\left(\tau \right)\overline{v}\left({\tau }^{\prime }\right)⟩}_{W_{v,\overline{v}}}\hfill & =\hfill & 0,\hfill \end{array}\right.$$ (13)

is negative-definite. As a consequence, only if $v\left(t\right)$ and $\overline{v}\left(\tau \right)$ are the complex Gaussian stochastic processes can the requirements in Eq. (13) be satisfied. The elaborate generation scheme for such a kind of stochastic process can be found in Refs. 12 and 51.

The rest component of the influence functional,

$$\begin{array}{rcl}{F}_3\left[x^{\times },x^{°}\right]=exp\left\{-i{\int }_0^t\mathrm{d}s{\int }_0^s\mathrm{d}{s}^{\prime }{x}^{\times }\left(s\right){\alpha }^I\left(0,s-s^{\prime }\right)x^{°}\left(s^{\prime }\right)\right\},& & \end{array}$$ (14)

is temperature-free and prefers the treatment in a hierarchical way, especially when the system-bath coupling is strong. To proceed, we substitute F₁ and F₂ in Eq. (4) with their stochastic counterparts shown in Eqs. (9) and (12) to yield

$$\begin{array}{rcl}{\rho }_A\left(x_f,x_f^{\prime },t,\beta \right)& =& Q_{\beta }^{-1}\iint \iint \mathrm{d}\xi \mathrm{d}\overline{\xi }{\mathrm{d}}^{2}v{\mathrm{d}}^2\overline{v}W\left(\xi ,\overline{\xi }\right)\\ & & \times W\left(v,\overline{v}\right){\rho }_{\xi ,v}^{\left(0\right)}\left(x_f,x_f^{\prime },t,\beta \right).\end{array}$$ (15)

Here, ${\rho }_{\xi ,v}^{\left(0\right)}\left(x_f,{x^{\prime }}_f,t,\beta \right)$ denotes the zeroth-order of the following predefined stochastic auxiliary density matrices:

$$\begin{array}{rcl}{\rho }_{\xi ,v}^{\left(n\right)}\left(x_f,{x^{\prime }}_f,t,\beta \right)& =& \iint \iint \mathrm{d}{x}_i^{+}\mathrm{d}{x}_i^{-}\mathrm{d}{\overline{x}}_i\mathrm{d}{\overline{x}}_f{\rho }_0\left(x_i^{+},x_i^{-},{\overline{x}}_i,{\overline{x}}_f\right){\int }_{x_i^{+}}^{x_f}\mathcal{D}{x}^{+}\left(t\right){\int }_{x_i^{-}}^{x_f^{\prime }}\mathcal{D}{x}^{-}\left(t\right){\int }_{{\overline{x}}_i}^{{\overline{x}}_f}\mathcal{D}\overline{x}\left(\tau \right)e^{i{S}_0\left[x^{+}\left(t\right)\right]-i{S}_0\left[x^{-}\left(t\right)\right]-S_0^E\left[\overline{x}\left(\tau \right)\right]}\\ & & \times e^{-i{\int }_0^t\left[\xi \left(s\right)+iv\left(s\right)\right]x^{\times }\left(s\right)\mathrm{d}s-{\int }_0^{\beta }\left[\overline{\xi }\left(\tau \right)-\overline{v}\left(\tau \right)\right]\overline{x}\left(\tau \right)\mathrm{d}\tau }{\left({\int }_0^t{\alpha }^I\left(0,t-s\right)x^{°}\left(s\right)\mathrm{d}s\right)}^n{F}_3\left[x^{\times }\left(t\right),x^{°}\left(t\right)\right],\end{array}$$ (16)

given the Debye-Lorentzian form of spectral density function

$$J\left(\omega \right)=\frac{2\mathrm{\lambda }\omega {\omega }_c}{{\omega }^2+{\omega }_c^2}$$ (17)

that results in a very simple exponential in the imaginary part of the bath response function

$${\alpha }^I\left(0,t\right)=-\mathrm{\lambda }{\omega }_c{e}^{-{\omega }_{c}t}.$$ (18)

Actually, the definition of the auxiliary density matrices is bath specific. Extension to all other kinds of spectral density function is accessible but more convoluted. In this paper, we will not go into details about this topic, but offer some valuable literature concerning this question. Meier and Tannor advocated that any kind of spectral density function could be parameterized by a few underdamped Lorentzian modes.⁵⁷ The fitting parameters for the frequently used Ohmic, super-Ohmic, and sub-Ohmic spectral density functions with exponential cutoff are available in Refs. 57–59, respectively.

The derivative of ${\rho }_{\xi ,v}^{\left(n\right)}\left(x_f,{x^{\prime }}_f,t,\beta \right)$ in Eq. (16) with respect to the real-time variable t reads

$$\begin{array}{rcl}\frac{\partial {\widehat{\rho }}_{\xi ,v}^{\left(n\right)}\left(t,\beta \right)}{\partial t}& =& \left(-i{L}_0-i\left(\xi \left(t\right)+iv\left(t\right)\right){\widehat{x}}^{\times }-n{\omega }_c\right){\widehat{\rho }}_{\xi ,v}^{\left(n\right)}\left(t,\beta \right)\\ & & -i{\widehat{x}}^{\times }{\widehat{\rho }}_{\xi ,v}^{\left(n+1\right)}\left(t,\beta \right)-n\mathrm{\lambda }{\omega }_c{\widehat{x}}^{°}{\widehat{\rho }}_{\xi ,v}^{\left(n-1\right)}\left(t,\beta \right).\end{array}$$ (19)

L₀ is the Liouvillian of system Hamiltonian. The above equation is in the similar structure to the real-time stochastic HEOM published in Refs. 44 and 50–53. It, in principle, consists of an infinite number of simultaneous differential equations, but one can often truncate it at a certain level L to obtain the numerical solutions within the desired accuracy. The initial values are zeros for all the elements of the auxiliary density matrix ${\rho }_{\xi ,v}^{\left(n\right)}\left(0,\beta \right)$ when $n>0$, which could be directly inferred from their definition given in Eq. (16). But to obtain ${\rho }_{\xi ,v}^{\left(0\right)}\left(0,\beta \right)$, one needs to integrate the following stochastic differential equation:

$$\frac{\partial {\widehat{\rho }}_{\xi ,v}^{\left(0\right)}\left(0,\tau \right)}{\partial \tau }=-\left(H_0+\left(\overline{\xi }\left(\tau \right)-\overline{v}\left(\tau \right)\right)\widehat{x}\right){\rho }_{\xi ,v}^{\left(0\right)}\left(0,\tau \right),$$ (20)

until the inverse temperature β, with the initial setting ${\widehat{\rho }}_{\xi ,v}^{\left(0\right)}\left(0,0\right)=\widehat{I}$. The unity matrix $Î$ could be interpreted as the thermal equilibrium population at the infinite temperature. There are some comments worth to note about Eq. (20). After the propagation to the finite temperature β and being multiplied by A from the right-hand side, it works as the initial values for Eq. (19) to obtain ${\rho }_A\left(t,\beta \right)$ and ultimately the equilibrium correlation function C_AB(t). Besides, the stochastically averaged $⟨{\rho }_{\xi ,v}^{\left(0\right)}\left(0,\beta \right)⟩$ itself is endowed with physical meaning, that is, the unnormalized exact equilibrium reduced density matrix. As such, it is open to a variety of equilibrium properties, for instance, the canonical partition function $Q_{\beta }=Tr\left[⟨{\rho }_{\xi ,v}^{\left(0\right)}\left(0,\beta \right)⟩\right]$. Last but not least, the computational resources invested on Eq. (20) are trivial compared to those on Eq. (19). In summary, the proposed new stochastic HEOM in Eqs. (19) and (20) is not only an unification but also an extension of the traditional real-time stochastic HEOM^44,50–53 and imaginary-time stochastic Bloch equation.⁶⁰

III. NUMERICAL SIMULATIONS

To start this section with the purpose of exemplifying the feasibility and validity of the proposed approach, it is advisable to calculate the steady-state emission line shape of the simplest aggregate model—homodimer,

$$E\left(\omega \right)=\frac{1}{2\pi }\mathfrak{R}\left\{{\int }_0^{\infty }⟨\widehat{\mathbf{\mu }}\left(t\right)\cdot \widehat{\mathbf{\mu }}{\rho }_e⟩e^{-i\omega t}\mathrm{d}t\right\},$$ (21)

where $\widehat{\mathbf{\mu }}={\sum }_{i=\mathrm{1,2}}{\mathbf{\mu }}_i\left(\left|\right.g⟩⟨{\pi }_i\left|\right.+\left|\right.{\pi }_i⟩⟨g\left|\right.\right)$ is the total transition dipole operator. As it is obviously seen in the above expression, the core of the problem lies in the calculation of the dipole-dipole correlation function $C_{\mu \mu }\left(t\right)=⟨\widehat{\mathbf{\mu }}\left(t\right)\cdot \widehat{\mathbf{\mu }}{\rho }_e⟩$. It is interesting to know that in the path integral expression of $C_{\mu \mu }\left(t\right)$, contrary to the absorption case where only the forward real-time system path is considered, the emission takes into account both the imaginary-time and backward real-time system paths.¹² As such, besides the dynamical coherence, the equilibrium correlation between the system and bath also plays a significant role in the exact simulation of emission spectra. This feature certainly increases technical difficulties and invalidates considerable approximation methods, such as cumulant expansion,¹⁰ time-local, and time-nonlocal generalized master equations.⁹ But emission spectra, in compensation, convey more information about the excited state properties that has facilitated many progresses, like the hybrid cumulant expansion scheme¹¹ and detailed-balance conditioned coherent potential approximation.¹³

In the following, our numerical calculations of emission line shapes are focused on the J-type homodimer, i.e., the transition energies ${𝜖}_1={𝜖}_2=0$ and the excitonic coupling between two excited states $\left|\right.{\pi }_1⟩$ and $\left|\right.{\pi }_2⟩$ is set to be J = −1. For simplicity, the orientations of ${\mathit{u}}_1$ and ${\mathit{u}}_2$ are chosen to be parallel and their magnitudes also to be the same. By varying the bath parameters, that is, the cutoff frequency ${\omega }_c$, the reorganization energy λ, and the inverse temperature β, we demonstrate the simulation results $E\left(\omega \right)$ obtained from Eq. (21) while $C_{\mu \mu }\left(t\right)$ are obtained through solving Eqs. (19) and (20), shown as the underlying black lines in Fig. 1. It is no wonder that the results are in line with those obtained from the deterministic HEOM⁹ (coloured balls in Fig. 1), as they are both numerically exact.

FIG. 1.

Emission line shapes of the homodimer calculated using the full-sHEOM (underlying black lines), trim-sHEOM (gray dashed lines), and deterministic HEOM⁹ (coloured balls). (a) $\beta =1$, $\mathrm{\lambda }=0.5$, and ${\omega }_c$ is varied; (b) $\beta =1$, ${\omega }_c=0.3$, and λ is varied; (c) same as (b) except at $\beta =3$. Some baselines are artificially lifted by certain values for the sake of clear visualization.

The proposed method inherits many merits from the traditional real-time sHEOM. The auxiliary density matrix number is free of the temperature and the truncation level should be smaller than the deterministic HEOM as a part of quantum nonlocality is transferred into the random noises.⁵² By its stochastic nature, the program is embarrassingly parallel and strongly scalable. These advantages might be more prominent in the lower temperature regime and in larger-size systems. However, one point different from the traditional real-time sHEOM is that the extra set of stochastic processes $\left(v\left(t\right),\overline{v}\left(\tau \right)\right)$ is complex. But it surprises us that, no matter in the presence or the absence of $v\left(t\right)$ in Eq. (19) and $\overline{v}\left(\tau \right)$ in Eq. (20), they give graphically indiscernible results of $C_{\mu \mu }\left(t\right)$ both regarding the real and imaginary parts, and then naturally lead to the same emission line shapes. To distinguish from the full version of sHEOM Eqs. (19) and (20) (full-sHEOM), we denote the approximation without the incorporation of $\left(v\left(t\right),\overline{v}\left(\tau \right)\right)$ as the trimmed stochastic HEOM (trim-sHEOM) and their numerical results are plotted as the gray dashed lines in Fig. 1.

From the standpoint of the computational cost and numerical performance, the trim-sHEOM is no doubt more appealing. Apart from saving efforts for generating $\left(v\left(t\right),\overline{v}\left(\tau \right)\right)$ in the simulation processes, its major benefit over the full-sHEOM is a considerably faster convergence speed to obtain the reliable results, especially in the cases with large bias, strong system-bath coupling, low temperature, and long simulation time. As in these cases, the full-sHEOM has to cope with the sign problem that generally demands an astronomical number of random sampling to assure the stochastic convergence. Furthermore, based on the fact presented in Sec. II that $\left(v\left(t\right),\overline{v}\left(\tau \right)\right)$ originate from a very small portion of the influence functional, merely a part of real-time and imaginary-time cross terms, it is plausible that they might play a rather trivial role. Therefore, it is interesting to explore under what conditions is trim-sHEOM reliable. As it is suggested by Moix and Cao,¹² the dipole-dipole correlation function decays faster than other kinds of dynamical properties, it might not be an appropriate model for our testing.

The spin-boson model, despite its simple appearance, sheds light on many essential physics in the condensed phase,^55,61 like low-temperature tunneling and quantum coherence. The Hamiltonian takes the form

$$H=𝜖{\sigma }_z+\mathrm{\Delta }{\sigma }_x+\frac{1}{2}\sum _j\left(P_j^2+{\omega }_j^2{Q}_j^2\right)-{\sigma }_z\sum _j{c}_j{Q}_j,$$ (22)

where $𝜖$ is the energy bias. In our simulations, the unbiased system $𝜖=0$ and the biased system $𝜖=1$ are both adopted. The electronic coupling is fixed at $\mathrm{\Delta }=1$, and ${\sigma }_z$ and ${\sigma }_x$ are Pauli spin matrices. The original version of the spin-boson model is a dissipative double well system considering only two grid points that reside at two local minima.⁵⁵ The position operator is $\widehat{x}={\sigma }_z$ such that the velocity operator reads $\widehat{v}=\frac{d}{dt}\widehat{x}=i\left[H,\widehat{x}\right]=2{\sigma }_y$ and the flux operator reads $ĵ=-{\sigma }_y$.

In the following, the quantities of specific interest are the position correlation function $C_{xx}\left(t\right)=\mathfrak{R}\left\{⟨{\sigma }_z\left(0\right){\sigma }_z\left(t\right)⟩\right\}$ and the flux correlation function $C_{jj}\left(t\right)=\mathfrak{R}\left\{⟨{\sigma }_y\left(0\right){\sigma }_y\left(t\right)⟩\right\}$. They are connected to each other according to the relation⁶² ${\ddot{C}}_{xx}\left(t\right)=-4C_{jj}\left(t\right)$. So in some cases where C_xx(t) tends to a non-vanishing stationary value at long time limits, C_jj(t) always tends to zero.

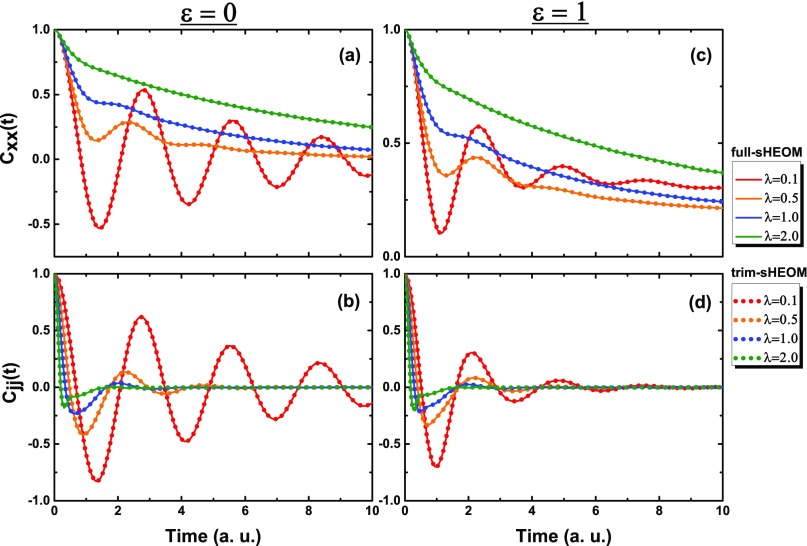
Figure 2 displays C_xx(t) and C_jj(t) for both biased and unbiased systems from the highly oscillatory regime to the damping regime, by varying the system-bath coupling strength, measured as the reorganization energy λ. It is worth to note that, when one enlarges the system-bath coupling λ, both the truncation level L and random trajectory number N_r should be increased accordingly to obtain the converged results. For the parameters chosen in Fig. 2, L ranges from 1 to 30 and N_r from 10⁴ to 10⁶ for the trim-sHEOM. It should be stressed that we brutally set deep-tier $\left(>L\right)$ auxiliary density matrices to zero in the propagation. A better truncation scheme should be effective in reducing L at a large reorganization energy value, but this subject is beyond the scope of this work. The full-sHEOM usually requires more random samplings, from the same scale at $\mathrm{\lambda }=0.1$ to three orders of magnitude at $\mathrm{\lambda }=2$ relative to the trim-sHEOM. At $\mathrm{\lambda }=2$, we are not able to obtain the converged results for C_jj(t) when $t>3\mathrm{\text{a.u.}}$ using the full-sHEOM even as many as a billion random trajectories are used, but it is no doubt that it would converge to 0 as those obtained by the trim-sHEOM.

FIG. 2.

Position correlation function C_xx(t) and flux correlation function C_jj(t) for both unbiased $𝜖=0$ and biased $𝜖=1$ systems at varied reorganization energies λ. Other bath parameters are fixed at $\beta =0.5$ and ${\omega }_c=0.5$.

In Fig. 3, the inverse temperature $\beta$ is varied when other bath parameters are fixed at $\mathrm{\lambda }=0.5$ and ${\omega }_c=0.5$. The truncation level L = 2 is sufficient for the high temperature and L = 15 for the lowest temperature. The random trajectory number N_r for the trim-sHEOM falls in between 10⁵ and 10⁷, and the latter is responsible for the lowest temperature condition in the biased systems, which poses greater difficulty for the full-sHEOM to obtain the converged results in a slightly long time domain even at the cost of a billion random trajectories. But except that, all the results are satisfactorily in agreement with those obtained from the trim-sHEOM. Finally, the cutoff frequency ${\omega }_c$ is altered in Fig. 4 from the adiabatic regime $\left({\omega }_c=0.1\right)$ to the non-adiabatic regime $\left({\omega }_c=2\right)$. Other parameters are fixed at $\mathrm{\lambda }=0.5$, $\beta =0.5$, L = 4, and N_r = 10⁶ for all parameter sets. When the cutoff frequency ${\omega }_c$ is small, it corresponds to a long response time of the bath to the feedback from the system. Such strong non-Markovian effects^25,63 are exhibited as slow relaxation and more oscillatory features in ECF.

FIG. 3.

Position correlation function C_xx(t) and flux correlation function C_jj(t) for both unbiased $𝜖=0$ and biased $𝜖=1$ systems at varied inverse temperatures β. Other bath parameters are fixed at $\mathrm{\lambda }=0.5$ and ${\omega }_c=0.5$.

FIG. 4.

Position equilibrium function C_xx(t) and flux correlation function C_jj(t) for both unbiased $𝜖=0$ and biased $𝜖=1$ systems at varied cutoff frequencies ${\omega }_c$. Other bath parameters are fixed at $\mathrm{\lambda }=0.5$ and $\beta =0.5$.

All in all, to learn about the accuracy and efficiency of the trim-sHEOM, we have performed the calculations of C_xx(t) and C_jj(t) in a pretty broad parameter space. It shows that the trim-sHEOM marvelously gives, graphically speaking, indistinguishable results to those obtained from the full-sHEOM with a cheaper computational expense. As such, we expect it to act as a powerful tool for our future studies in many basic dynamical properties, such as the carrier transport in a variety of novel and promising materials.

IV. CONCLUSION

Equilibrium correlation functions, because of their ability to produce a wealth of dynamical properties, are at the heart of the quantum dynamics. In this paper, a new stochastic hierarchy equations of motion approach is raised, based on the stochastic unravelling of temperature-dependent part and the hierarchical treatment of temperature-free part of the influence functional in the path integral formalism of the reduced density matrix, aiming at providing an accurate and efficient calculation of equilibrium correlation functions. Besides, a numerical strategy to neglect the complex noises that originate from a very small portion of real-time and imaginary-time cross terms gives stable and at the same time accurate results compared with those obtained without any approximation or the deterministic HEOM for emission line shapes of homodimers, position and flux correlation functions of the spin-boson model. In conclusion, the proposed method should be a very promising tool for future prospects of exploring many essential features in the condensed phase, such as the energy transfer and charge carrier transport in the natural and artificial photovoltaic devices.