Does Everyone’s Motivational Beliefs about Physical Science Decline in Secondary School?: Heterogeneity of Adolescents’ Achievement Motivation Trajectories in Physics and Chemistry

Abstract

Students’ motivational beliefs about learning physical science are critical for achieving positive educational outcomes. In this study, we incorporated expectancy-value theory to capture the heterogeneity of adolescents’ motivational trajectories in physics and chemistry from seventh to twelfth grade and linked these trajectories to science-related outcomes. We used a cross-sequential design based on three different cohorts of adolescents (N = 699; 51.5% female; 95% European American; M_ages for youngest, middle, and oldest cohorts at the first wave = 13.2, 14.1, and 15.3 years) coming from ten public secondary schools. Although many studies claim that physical science motivation declines on average over time, we identified seven differential motivational trajectories of ability self-concept and task values, and found associations of these trajectories with science achievement, advanced science course taking, and science career aspirations. Adolescents’ ability self-concept and task values in physics and chemistry were also positively related and interlinked over time. Examining how students’ motivational beliefs about physical science develop in secondary school offers insight into the capacity of different groups of students to successfully adapt to their changing educational environments.

Introduction

Students’ motivational beliefs about physical science learning are critical for bettering performance, increasing enrollment in advanced courses, and instilling a desire to pursue a college major or career in science, technology, engineering, and mathematics (STEM; Denissen, Zarrett, & Eccles, 2007; Maltese, Melki, & Wiebke, 2014; Osborne, Simon, & Collins, 2003). Although students’ academic motivations tend to decline throughout adolescence (Wigfield, Eccles, Scheifele, Roeser, & Davis-Kean, 2006), recent studies suggest that domain-specific motivational trajectories may not decline uniformly across all students. Yet, research on physical science learning fails to consider the substantial heterogeneity in developmental changes of student motivational beliefs throughout secondary school (Archambault, Eccles, & Vida, 2010; Wang & Peck, 2013). Moreover, heterogeneity in motivational trajectories in physical science and its implications for subsequent science outcomes have yet to be explored. Approaching physical science motivation as a dynamic process characterized by multiple developmental pathways would greatly enhance our understanding of why some students are motivated to further their science learning and why others are not. Examining heterogeneity in motivational change will also help to identify the nature and course of the developmental mechanisms involved in physical science learning, a critical step for designing targeted intervention programs for specific groups of students with the most detrimental trajectories of motivational declines (Archambault et al., 2010; Wang, Fredricks, Ye, Hofkens, & Schall, 2016).

In this study, we built upon expectancy-value theory as a conceptual framework by focusing on two important motivation indicators for physics and chemistry: ability self-concept and subjective task values. We investigated how ability self-concept and subjective task values in physics and chemistry changed from grades seven through twelve and whether distinct motivational trajectories predicted discrepancies in course grade, advanced science course enrollment, and science career aspirations during high school. We focused on both physics and chemistry for two reasons. First, they are both categorized as physical science fields and are considered among the most challenging school subjects by students (Farenga & Joyce, 1999; Huber, Häusler, Jurik, & Seidel, 2015). Research suggests that physics is perceived to be the most difficult subject, followed closely by chemistry, even among high achieving students (Havard, 1996). Second, the noted difficulty of high school physics and chemistry is found to result in declining course enrollment in physical science subjects (Osborne, Simon, & Collins, 2003; Lyons, 2006). Physics and chemistry are among the most disliked of all school subjects and, in contrast to biology, are considered by students to have far less relevance to their everyday lives (Osborne & Collins, 2000; Osborne et al., 2003). Accordingly, the focus on physics and chemistry will help us better understand how students’ general motivational trajectories regarding physical science change over time, particularly as they transition to secondary school.

Expectancy-Value Theory as the Developmental Framework

Expectancy-value theory (Eccles, 2009) posits that students’ educational choices are greatly influenced by their cognitive competencies, their ability self-concepts, and the subjective task values they attach to each subject or field. Ability self-concept refers to an individual’s expectations for success and confidence in the ability to succeed in a particular field of study. Subjective task values, on the other hand, refer to the values an individual places on pursuing a specific field, such as interest, utility value, and attainment value. When youth feel confident in their ability to learn and achieve success in particular subject areas, they are more likely to engage in deeper-level cognitive strategies, which, in turn, are associated with increased academic achievement and course-taking (Eccles, 2009). Task value beliefs are also predictive of academic achievement, and are even stronger predictors of educational choices and future aspirations (Wang, 2012). Thus, increasing both competence beliefs and subjective task values are essential for adolescents to excel in scientific learning.

Research tracking developmental changes from elementary to secondary school typically shows that ability self-concepts and task values decline, on average, over time, across numerous academic domains (Achambault et al., 2010; Fredricks & Eccles, 2002; Jacobs et al., 2002). Scholars have proposed several plausible explanations for the decline of academic motivation, primarily focusing on changes in cognition and environment (Eccles, 1999; Eccles, Lord, & Midgley, 1991). The cognitive processing approach reasons that academic motivation declines as a function of universal maturational changes in brain development (Stipek & Mac Iver, 1989). Because young children are unwaveringly optimistic in their perceived competence across a spectrum of abilities, they tend to rate themselves highly regardless of their actual performance (Eccles, Wigfield, & Schiefele, 1998). However, as children enter middle childhood and adolescence, their overly optimistic views become more realistic as they increase their use of social comparisons and evaluative feedback from parents and teachers to judge their own abilities (Eccles, 1999; Wigfield et al., 1997). Accordingly, based on the feedback that they receive, many youth may begin to lower their perceived competence in science, leading to declines in their interest and desire to pursue a science career. On the other hand, the contextual perspective emphasizes how changes in environmental demands during adolescence create a mismatch between adolescent developmental needs and the school environment (Eccles et al., 1993), reducing students’ capacity to feel motivated and engaged with their school work (Eccles, 1999). For example, students desire an environment that grants them more autonomy and connectedness as they progress through school. Unfortunately, the structure of many secondary school environments is often more isolating and controlling than elementary school, offering a clear discrepancy between the developmental needs of adolescents and the school’s expectations and assumptions regarding their behavior (Eccles et al., 1998; Eccles, 1999).

However, many studies that documented extensive declines in achievement motivation actually began tracking changes in student motivation in early elementary school and ended in secondary school (e.g., Achambault et al., 2010; Jacobs et al., 2002). The reported declines may be somewhat exaggerated or misleading. Since we know that early elementary school students struggle to accurately gauge their cognitive abilities and interests across a number of domains (Wigfield & Eccles, 2002), accordingly, first graders’ view of their abilities may not be comparable to their views in seventh grade. Given that ability and value ratings of young children differ qualitatively from those of older children (Wigfield et al., 2006), the previous studies tracking motivation from early elementary school until the end of secondary school may confound the mechanisms for these motivational declines with both maturational changes in cognitive reasoning and environmental changes in school settings.

In this study, we sought to examine heterogeneous developmental trends in physical science motivation. We selected seventh grade as the beginning point of the motivational trajectories for two reasons. First, students have already transitioned to middle school by seventh grade, potentially avoiding the confounding role of maturational changes in cognition that influences declines in motivation. Second, examining motivation from seventh through twelfth grade enables us to capture motivational changes in physical science during the transition to high school: a key time period when students’ task values and ability self-concepts in science reliably predict future educational choices (Maltese & Tai, 2011). By tracking heterogeneity in physical science motivational trends across the middle school and high school years, we hope to gain a more accurate picture of the extent that adolescents improve, decline, or maintain stability in their motivation.

Trajectories of Ability Self-Concept and Task Values in Science

Studies using variable-centered approaches to examine average sample trends have shown that, as they progress through their school careers, youth’s ability self-concept and task values in science learning decline over time. For example, researchers found average declines, from ages 9 to 17, in intrinsic motivation in science (Gottfried, Marcoulides, Gottfried, & Oliver, 2009). Specifically, interest in chemistry and physics continuously declined from ages 11 to 16, whereas an interest in biology increased between ages 11 and 14 and then decreased at age 16 (Bennett & Hogarth, 2009). Furthermore, cross-cultural data has shown global declines in perceived ability and expectancies for success in science during junior high school (Wilkins, 2004), while other studies have also shown that middle and high school students rate science as less valuable, important, and understandable than elementary school students do (Neathery, 1997).

Although average declines in science ability self-concept and task values have been documented, such trends do not necessarily mean that all students are declining at the same rate or experiencing homogeneous developmental changes (Gottfried et al., 2009). Focusing on average trends in student motivation masks potential variability in these developmental processes. Some students may, indeed, experience declines in motivation during adolescence, but others may experience increasing or even stable trajectories. Furthermore, the existence of divergent trajectory groups may contribute to discrepancies in grades, course enrollment, and STEM career aspirations.

In order to address this limitation, several studies have employed person-centered approaches to identify groups of high risk students that, in comparison to other groups, demonstrate stark declines in academic motivation over time (Ratelle, Guay, Larose, & Senécal, 2004). For example, engagement studies show that developmental changes in behavioral, emotional, and cognitive engagement are not uniform across all adolescents, and that these patterns are linked to differences in academic and psychosocial adjustment (Archambault, Janosz, Morizot, & Pagani, 2009; Li & Lerner, 2011). Similar growth mixture modeling techniques were applied to study the development of literacy motivation, in which joint trajectories of ability self-concepts and subjective task values in literacy were modeled across grades one through twelve (Archambault, Eccles, & Vida, 2010). Of the seven trajectory groups identified, all groups experienced declines. There were substantial differences in the rates of decline across groups and only a few experienced some recovery during the secondary grades. However, it is worth noting that the detection of uniform declines across all seven groups is not surprising given the selection of first grade as the starting point of the modeled trajectories. Examining motivational changes with a baseline in middle school may produce groups with fewer or far less dramatic declines over time.

In our review of the literature, only one study used semiparametric growth modeling to identify heterogeneity in science motivation. This study tracked changes in science self-efficacy (a global scale combining ratings of chemistry, physics, and biology courses) in a Canadian sample from the end of high school to the transition to college (Larose, Ratelle, Guay, Senécal, & Harvey, 2006). They identified three trajectory groups: a high stable group; an increasing group; and a decreasing group. The increasing and high stable groups were more likely to choose science careers and have higher science interests than the decreasing group. These empirical findings challenge the notion that adolescents experience a common developmental pattern of decline in science achievement motivation, and support the use of person-centered approaches to identify differential motivational trajectories. However, since the Larose et al. (2006) study relied on a sample of adolescents that had already chosen at age 17 to pursue science in college, there is still a need for person-centered research that examines how motivational beliefs in science (particularly physics and chemistry, the least popular of all the sciences; Osborne & Collins, 2000) develop during the formative years when youth are still exploring their academic identities and building educational experiences that may guide them toward either a STEM or non-STEM career. Our study, therefore, expands upon this research by tracking a sample of U.S. adolescents from seventh through twelfth grade to pinpoint divergent trends in motivational beliefs during this crucial time period of STEM career development.

Longitudinal Association between Ability Self-Concept and Task Values

Ability self-concept and task values have long been theorized to be reciprocally related (Ferry, Fouad, & Smith, 2000; Pajares, 2005; Wigfield & Eccles, 2002), although the strength of this relation is expected to increase as children age. Young children often start out with optimistic appraisals of their abilities across a diverse range of subjects (Wigfield & Eccles, 2002), but they temper their ratings of competence (often downward) as they begin to rely more heavily on feedback from teachers and parents to judge their own abilities (Wigfield et al., 1997). As they age, they have a better sense of how to coordinate their cognitions and behaviors to achieve their desired goals. They also adjust their task values to better coincide with their perceptions of their cognitive abilities (Denissen, Zarrett, & Eccles, 2007; Wigfield et al., 2006). For example, a longitudinal study found that the associations among ability self-concept and interest in English, math, and science became more stable from grades 1 through 12, indicating that, as they age, children’s perceived ability and interest in academic domains become increasingly interlinked and mutually reinforcing over time (Denissen et al., 2007). However, without capturing heterogeneity in trajectories, we still have limited understanding of how physical science self-concept and task values develop contemporaneously. We aim to determine if the increasing convergence patterns identified in previous studies will apply for students with different developmental trajectories.

Science Motivation and Learning Outcomes

In addition to identifying heterogeneity in longitudinal development of physical science motivation throughout adolescence, it is important to establish the extent to which changes in motivation are linked to important science outcomes toward the end of high school. Research has shown that ability self-concept and subjective task values are critical determinants of science learning outcomes during secondary school (Lau & Roeser, 2002; Simpkins, Davis-Kean, & Eccles, 2006). For example, studies found that students’ perceptions of science ability predicted their performance on standardized tests (Nagengast & Marsh, 2012; Wilkins, 2004), and science self-concept predicted their science course selection (Marsh & Yeung, 1997) and career aspirations in STEM (Nagengast & Marsh, 2012). Likewise, task values strongly predict academic performance and persistence in science. For example, perceived importance, interest, and usefulness of science were found to correlate with science achievement (Neathery, 1997) and to indirectly link to science achievement through greater time spent on academic activities (Singh, Granville, & Dika, 2002). While these findings highlight the importance of student ability self-concept, interest, attainment value, and utility value in subsequent educational choices, most studies have not examined how different developmental trajectories of ability self-concepts or task values are linked to science outcomes. Our study will address this gap in the literature by examining how heterogeneity in motivational changes throughout adolescence differentially predicts important science outcomes.

The Current Research

In this study, we incorporated expectancy-value theory to capture the motivational trajectories of adolescents in physics and chemistry and to link these trajectory groups to important learning outcomes in science. First, we aim to examine whether adolescents’ ability self-concept and subjective task values in physics and chemistry are characterized by divergent growth trajectories from seventh to twelfth grade. Specifically, if different growth trajectories can be identified, how many trajectory groups will emerge and what patterns will be identified? Second, we investigate how trajectory group membership is associated with subsequent educational outcomes in science (i.e., advanced course enrollment, course grades, and STEM career aspirations).

Because of the scarcity of empirical evidence on profiles of physical science motivation, we do not make predictions on the specific number of profile groups we might find. However, following the logic of our conceptual framing, we hypothesized that a minimum of four groups of students following continuously decreasing, stable high, and nonlinear trajectories would be identified. First, due to the misalignment between the school environment and adolescent needs during the transition to secondary school, we expect to find a group of students who experienced continuous declines in science motivation from seventh through twelfth grade. This group may demonstrate difficulty adjusting to the stress of a new learning environment by losing interest in school and confidence in their ability to succeed academically. Second, despite the stress of transitioning to secondary school, we hypothesize that not all students will experience difficulty adapting to the academic and social demands of the new learning environment. We hypothesize detection of a well-adjusted group distinguished by high and stable motivation in physical science. Subsequently, in line with prior literature on trajectory groups of intrinsic motivation in science (Larose et al., 2006), we expect that the stable group may represent the majority of students in the sample. Third and fourth, we anticipate the identification of two distinct groups of nonlinear trajectories. As the science curriculum becomes more specialized in high school, the transition from middle to high school may serve as a turning point for enhancing or undermining science self-concept and values in adolescents. One group, for example, may experience stark increases in physical science motivation at the transition to high school due to the emergence of a variety of science courses that can be taken as electives. For this particular group, we would expect that initial declines in science motivation leading up to ninth grade would eventually change over to increases in motivation as these students take advantage of their newfound ability to choose the physical science courses of greatest interest to them. Conversely, another group of students may feel overwhelmed by the complexity of the secondary science curriculum, or fall victim to ineffective teaching or poor relationships with teachers, or simply choose to opt out of science course electives altogether. We would expect this particular group of students to demonstrate initial increases in science motivation up until ninth grade, and then switch over to a steady decline until twelfth grade. Additionally, we expect that students with developmental trajectories characterized by increasing motivation or stable high motivation are more likely to have higher course grades and STEM career aspirations and to enroll in more advanced science courses.

Methods

Participants

We used data from the Childhood and Beyond Study, an ongoing longitudinal study following three cohorts of students through elementary school, junior high school, and senior high school adopting a cross-sequential cohort design (Eccles, Wigfield, & Blumenfeld, 1984). The purpose of this study was to investigate the development of students’ motivational beliefs in a variety of academic and nonacademic fields, and the influences of school and home factors on student motivational beliefs, activity choices, and performance. The study sampled ten elementary public schools located in the Midwestern United States.

The first wave of data collection was conducted when the three cohorts were in kindergarten, first grade, and third grade. Our analyses of students’ ability self-concept and task values for physics and chemistry utilized data from Wave 5 to Wave 7 collected when students were in seventh, eighth, and tenth grade (youngest, middle, and oldest cohorts, respectively; see Table 1). The combined cross-sequential sample provided information on students’ physical science ability self-concept and task values from seventh grade through twelfth grade. The sample consisted of 699 students (48.5% were boys; 95% were European American; 197, 202, and 300 from the youngest, middle, and oldest cohorts, respectively). The samples were mainly from middle and working class households (67.6% eligible for free/reduced lunch).

Table 1.

Number of Participants by Cohort and Grade at Each Wave of Data Collection

Cohort	Wave of Data
	Wave 5	Wave 6	Wave 7
Youngest (n = 197)	Grade 7	Grade 8	Grade 9
Middle (n = 202)	Grade 8	Grade 9	Grade 10
Oldest (n = 300)	Grade 10	Grade 11	Grade 12

Procedures

Students were recruited through their respective schools. Teachers provided letters describing the study, along with permission slips, to students’ families, of which 80% agreed to participate. Student data was collected during school hours in the spring of every data collection year. Students completed questionnaires assessing their ability self-concept and task values in physics and chemistry, and career aspirations in STEM fields. All the scales included in the student questionnaire were validated through cognitive testing procedure with middle school and high school students to ensure that the items were comprehended and interpreted as intended. Family annual income was provided by primary caregivers, and students’ science grades and advanced course enrollment were gathered from school records. Students and primary caregivers received small monetary compensation for their participation.

Measures

Ability self-concept in physics and chemistry

Physical science ability self-concept was calculated as the mean of three items measuring students’ perception of ability in physics and chemistry. The ability self-concept scale is well-validated with similar samples in prior studies (e.g., Simpkins, Davis-Kean, & Eccles, 2005). Students responded on a scale from 1 (not at all good) to 7 (very good) for the first and second items: “How good would you be at physics and chemistry?” and “How good do you think you would be in a career that requires physics and chemistry?” The third item asked “How well do you expect to do in physics and chemistry in high school?” This item was also rated on a 7-point scale (1= not at all well to 7 = very well). Scores on this scale demonstrated high estimated internal consistency reliability in this sample (αs = .88 ~ .94 across seventh to twelfth grade).

Subjective task values in physics and chemistry

Task values for physics and chemistry were calculated as the mean of four items assessing student interest, perceived importance, and usefulness of these subjects. We combined the four task value items into one single task value construct because they are highly correlated (Wave 5: .55– .77, Wave 6: .58–.82, and Wave 7: .66 to .81). These items have been validated with similar samples and used widely for measuring task values in different school subjects, such as math, reading, and sports (Jacobs, Lanza, Osgood, Eccles, & Wigfield, 2002; Wigfield et al., 1997). The items were: “In general, how useful is what you learn in physics and chemistry science (1 = not at all useful to 7 = very useful)?”, “For me, being good at physics and chemistry is… (1 = not at all important to 7 = very important)”, “I find working on physics and chemistry assignments… (1 = very boring to 7 = very interesting), and “How much do you think you will like doing physics and chemistry (1 = a little to 7 = a lot)?” Scores on this scale demonstrated high estimated internal consistency reliability in this sample (αs = .84 ~ .92 across seventh to twelfth grade).

High school science course grade

Students’ course grades in physics and chemistry from tenth to twelfth grade were collected from school record data (ranging from 1 = F to 16 = A+). A mean of course grades was created as an indicator of high school science achievement (M = 10.67, SD = 2.95, minimum = 1, maximum = 16).

Advanced placement (AP) science courses

The number of high school Advanced Placement (AP) science courses in physics and chemistry each student took was collected from school record data. The total number of AP physics and chemistry courses taken in high school was used to indicate advanced science course enrollment (M = 0.31, SD = 0.61, minimum = 0, maximum = 2) .

Aspirations for STEM-related jobs

At twelfth grade, students were asked to imagine and rate how likely they would consider pursuing STEM-related jobs which require a bachelor’s or master’s degree, such as an engineer or architect: a scale commonly used in national surveys (Jodl, Michael, Malanchuk, Eccles, & Sameroff, 2001). Responses were rated along a 7-point scale (1= very unlikely to 7 = very likely).

Covariates

We examined how a vector of important covariates were related to student motivation and achievement, including gender, family SES, prior science achievement, and cohort. We used annual family income reported by the primary caregivers as the SES indicator and responses were given on a 9-point scale (1 = under $10,000 a year, 9 = over $80,000). The mean of family income was 5.7 on this 9-point scale (SD = 1.92, minimum = 1, maximum = 9, skewness = −0.16, kurtosis = −0.54). Students’ yearly science course grades from first to sixth grade collected from school records were rated on a 16-point scale (ranging from 1 = F to 16 = A+). The mean of science course achievement between first and sixth grade was used to indicate prior science achievement (M = 10.06, SD = 2.19). We created two binary variables (with the youngest cohort as the reference group) to account for cohort effects.

Analytic Strategies and Missing Values

We conducted tests of measurement equivalence to ensure that the content of the repeated measures was perceived and interpreted in the same way over time. We found empirical support for measurement invariance of the underlying ability self-concept and task value constructs across time and within cohorts (see Table 2). We then used multiple-process growth mixture modeling (GMM) to identify distinct developmental trajectories of ability self-concept and task value in physics and chemistry. All models were estimated with Mplus 7.31 (Muthén & Muthén, 2015).

Table 2.

Models representing Different Degrees of Longitudinal Invariance for Ability Self-Concept and Task value within Cohort

Model	χ2	df	CFI	RMSEA	SRMR	Δχ2 (Δdf), p
Self-Concept (Young Cohort)
Model 1: Configural invariance	18.39	15	0.99	0.03	0.04	---
Model 2: Metric invariance	26.21	19	0.99	0.04	0.05	Compare with Model 1: 7.81 (4), p = n.s.
Model 3: Scalar invariance	35.07	23	0.99	0.05	0.06	Compare with Model 2: 9.86 (4), p = n.s.
Model 4: Strict measurement invariance	53.51	29	0.98	0.07	0.05	Compare with Model 3: 18.44(6), p < 0.01
Task Values (Young Cohort)
Model 1: Configural invariance	115.90	39	0.94	0.09	0.06	---
Model 2: Metric invariance	126.05	45	0.93	0.09	0.07	Compare with Model 1: 10.06 (6), p = n.s.
Model 3: Scalar invariance	189.30	51	0.93	0.09	0.07	Compare with Model 2: 56.25 (6), p < 0.01
Model 4: Strict measurement invariance	207.18	59	0.93	0.09	0.07	Compare with Model 3: 24.88 (8), p < 0.01
Self-Concept (Middle Cohort)
Model 1: Configural invariance	17.26	15	0.99	0.03	0.03	---
Model 2: Metric invariance	21.68	19	0.99	0.03	0.05	Compare with Model 1: 4.42 (4), p = n.s
Model 3: Scalar invariance	32.96	23	0.99	0.05	0.05	Compare with Model 2: 11.23, p < 0.05
Model 4: Strict measurement invariance	49.18	29	0.98	0.05	0.07	Compare with Model 3: 16.22, p < 0.01
Task Values (Middle Cohort)
Model 1: Configural invariance	89.41	39	0.96	0.08	0.05	---
Model 2: Metric invariance	97.35	45	0.99	0.08	0.07	Compare with Model 1: 7.94, p = n.s
Model 3: Scalar invariance	111.42	51	0.95	0.08	0.07	Compare with Model 2: 14.07, p < 0.05
Model 4: Strict measurement invariance	128.75	59	0.95	0.08	0.07	Compare with Model 3: 17.33, p < 0.01
Self-Concept (Old Cohort)
Model 1: Configural invariance	29.32	15	0.99	0.06	0.03	---
Model 2: Metric invariance	31.84	19	0.99	0.05	0.04	Compare with Model 1: 2.51, p = n.s
Model 3: Scalar invariance	38.40	23	0.99	0.05	0.04	Compare with Model 2: 6.56, p = n.s
Model 4: Strict measurement invariance	69.11	29	0.98	0.07	0.05	Compare with Model 3: 30.71, p < 0.01
Task Values (Old Cohort)
Model 1: Configural invariance	164.27	39	0.94	0.09	0.06	---
Model 2: Metric invariance	176.16	45	0.93	0.09	0.07	Compare with Model 1: 11.90, p = n.s
Model 3: Scalar invariance	189.30	51	0.93	0.09	0.07	Compare with Model 2: 13.14, p < 0.05
Model 4: Strict measurement invariance	207.18	59	0.93	0.09	0.07	Compare with Model 3: 17.88, p < 0.01

Note. Supported level of measurement invariance highlighted. df = degrees of freedom; CFI = comparative fit index; RMSEA = root mean square error of approximation; SRMR = standardized root mean square residual; p = probability.

To answer the first research question, a series of unconditional GMM models were conducted to classify the participants into subgroups based on their trajectories of physical science ability self-concept and task values. In each GMM model, we estimated the intercepts, linear slopes, and quadratic terms for both ability self-concept and task values. We tested one- to ten-class model solutions. Both bootstrap likelihood ratio tests (BLRT; McLachlan & Peel, 2000) and Lo–Mendell–Rubin likelihood ratio tests (LMR; Lo, Mendell, & Rubin, 2001) were used to determine if sequentially adding one more class to each model substantially improved the fit. In addition, a series of model fit indices, such as the Bayesian information criterion (BIC; Schwarz, 1978) and Akaike’s information criterion (AIC; Akaike, 1987) were also used to identify the optimal number of groups that best fit the data. Moreover, we used the entropy index of the optimal model to assess how accurately the optimal model classified participants into their respective trajectory groups (Muthén, 2004). While there appears to be no definitive criteria for determining optimal numbers of latent classes when estimating growth mixture models, researchers have recommended the use of multiple statistical indices, along with conceptual considerations and interpretability of the latent groups (Marsh, Hau, & Grayson, 2005; Marsh, Lüdtke, Trautwein, & Morin, 2009).

To answer the second research question, we specified two sets of conditional models based on the best-fitting GGM model identified in the previous step. A newly developed Mplus algorithm, the three-step approach (Asparouhov & Muthén, 2013), was employed to specify our conditional models. In the three-step conditional model, the statistical model simultaneously assigned individuals into trajectory groups and estimated if the trajectory groups differed across both the covariates (e.g., demographic characteristics) and the outcomes (e.g., course grade).

Approximately 80.2% of participants at Wave 5 participated in Waves 6 or 7. The amount of missing data ranged from 5.6% to 40.3%. Missing completely at random chi-square tests (Little, 1998) revealed that the missing data were missing completely at random for the youngest (χ² = 26.97, df = 21 p = n.s.), middle (χ² = 26.59, df = 21 p = n.s.), and the oldest (χ² = 20.18, df = 23 p = n.s.) cohorts. In addition, we conducted a series of t-tests to determine whether participants with complete data differed from those who had missing data within each cohort. Within the middle cohort, participants with complete data had slightly higher ability self-concept at 8^th and 10^th grade (mean differences = 0.42 and 0.49 on a 7-point scale, respectively), family income (mean difference = 1.06 on a 9-point scale), and prior science course grades (mean difference = 0.91 on a 16-point scale), than those with missing data. Within the oldest cohort, males were more likely than females to have missing data. No significant differences were found within the youngest cohort. We dealt with missing data through full-information maximum likelihood estimation, allowing us to include all available data and identify the parameter values that have the highest probability of producing the sample data (Baraldi & Enders, 2010). Models were estimated with a procedure (COMPLEX MIXTURE) to address violations of independence assumptions related to the clustering nature of the data, thereby achieving robust standard errors.

Results

Means, standard deviations, and correlations are presented in Table 3. No obvious deviations from normality were detected for either ability self-concept or task values, and all correlations between motivation, covariates, and outcomes were in the expected directions.

Table 3.

Means, Standard Deviations and Univariate Skewness of Ability Self-Concept and Task Values, and Their Correlations with Predictors and Outcomes

Variables					Correlations with Predictors			Correlations with Outcomes
	Mean	SD	Skewness	Kurtosis	Gendera	SES	Prior course grade	High school course grade	AP science course taken	Science/math job aspiration
Grade 7: Self-concepta	4.59	1.18	−0.08	−0.19	.04	.23**	.09	.25*	.29**	.21
Grade 8: Self-concepta	4.61	1.35	−0.28	−0.05	.13*	.08	.15*	.15	.35**	.38**
Grade 9: Self-concepta	4.75	1.36	−0.47	−0.13	.22**	.10	.18**	.21**	.46**	.36**
Grade 10: Self-concepta	4.48	1.52	−0.29	−0.42	.16**	.11	.23**	.49**	.54**	.38**
Grade 11: Self-concepta	4.37	1.56	−0.25	−0.42	.31**	.28**	.26**	.42**	.45**	.51**
Grade 12: Self-concepta	4.60	1.60	−0.50	−0.29	.29**	.18*	.18*	.51**	.17	.52**
Grade 7: Task valuesb	4.78	1.26	−0.49	−0.04	.05	.15	.01	.30**	.16	.15
Grade 8: Task valuesb	4.55	1.41	−0.42	−0.12	.07	.01	.13*	.18*	.23*	.30**
Grade 9: Task valuesb	4.59	1.40	−0.53	0.07	.14*	.09	.10	.24**	.34**	.32**
Grade 10: Task valuesb	4.26	1.56	−0.30	−0.68	.13**	.07	.13**	.36**	.36**	.32**
Grade 11: Task valuesb	4.11	1.50	−0.13	−0.65	.23**	.24**	.28**	.39**	.35**	.44**
Grade 12: Task valuesb	4.43	1.55	−0.51	−0.54	.21**	.18*	.14	.45**	.29**	.44**

Note.

^aFemale = 0; Male = 1.

^aResponses on 1 to 7 scale (higher scores = higher ability self-concept).

^bResponses on 1 to 7 scale (higher scores = higher task values).

^*p < .05.

^**p < .01.

We ran latent growth curve (LGC) analysis to compare the linear and curvilinear LGC models for ability self-concept and task values. For both constructs, the curvilinear models provided a better fit to the data than the linear models (ability self-concept: χ²_diff (4) = 12.51, p < 0.05; task values: χ²_diff (4) = 14.55, p < 0.01). Accordingly, the curvilinear specification was used in the subsequent GMMs for identifying physics and chemistry motivation trajectory groups. The means of the intercept, linear slope, and quadratic term were 4.60, −0.04 (p = n.s.), and 0.01 (p = n.s.) for self-concept trajectory, and were 4.75, −0.23 (p < 0.01), and 0.03 (p < 0.01) for task values trajectory. Importantly, the variance of intercept (0.97) and slope (0.70) for self-concept as well as intercept (0.85) and slope (0.75) for task values were statistically significant (p < .05), indicating the heterogeneity of motivation development among individuals.

Identification of Trajectory Groups of Ability Self-Concept and Task Values

The AIC, BIC, and entropy indices of the one- to ten-group solutions are summarized in Table 4. While AIC continuously decreased as the number of trajectory groups increased, BIC suggested that the seven-group model provided a better fit to the data: it decreased as the number of trajectory groups increased from one to seven groups, but increased as the number of trajectory groups changed from seven to eight groups. On the other hand, the LMR first became non-significant when the number of groups in the solution turned from three to four. The results of the BLRT for the ten models were non informative. Although continued adding to the number of groups in the solution might lead to a non-significant BLRT result, a solution with a large number of latent classes might statistically distinguish classes with little practical difference. The size of the groups might also become too small for meaningful interpretation.

Table 4.

Fit Statistics for Growth Mixture Models with Different Number of Trajectory Groups

No. of Group	No. of parameter	Log likelihood	AIC	BIC	Entropy	pBLRT	pLMR
1	18	−5632.68	11301.35	11383.25	---	---	---
2	25	−5139.69	10329.38	10443.12	0.76	0.00	0.00
3	32	−4943.14	9950.28	10095.87	0.79	0.00	0.01
4	39	−4859.00	9795.99	9973.43	0.75	0.00	0.22
5	46	−4807.90	9707.81	9917.09	0.73	0.00	0.03
6	53	−4773.98	9653.95	9895.08	0.72	0.00	0.84
7	60	−4743.38	9606.75	9879.73	0.75	0.00	0.05
8	67	−4721.31	9576.61	9881.44	0.72	0.00	0.22
9	74	−4702.94	9553.89	9890.56	0.72	0.00	0.62
10	81	−4686.12	9534.24	9902.76	0.72	0.00	0.11

Note. AIC = Akaike’s Information Criterion; BIC = Bayesian Information Criterion; pBLRT = p values for the bootstrap likelihood ratio test for K versus K − 1 classes; PLMR = Lo–Mendell–Rubin likelihood ratio test for K versus K − 1 classes.

Based on BIC and LMR tests, we narrowed down the best solution between the three- and the seven-group models. As Muthén (2001) suggests, the relative strength of LMR and BIC is not sufficiently well-understood though several recent studies do caution that LMR does not always function as a reliable indicator for deciding optimal solution (Diallo, Morin, & Lu, 2016a; 2016b). Accordingly, the decision on the number of classes should not be based solely on statistical measures but also on theoretical justification and interpretability. With that in mind, we concluded that the 7-group solution was more appropriate than the 3-group solution. The entropy value (.75) for the seven-group model was also considered good (Muthén, 2000), indicating that this solution provided appropriate classification into trajectory groups. Average probabilities of individual assignment into respective classes ranged from .78 to .90, further demonstrating the robustness of the seven-group solution.

Additionally, we conducted additional analyses to support the robustness of the seven group solution. These analyses suggested that the 7-class solution could be replicated even when science ability self-concept and subject task-values were analyzed separately in two series of growth mixture models. The three-group solution mainly showed the level differences in the trajectories (high, moderate, and low) without differentiating the slope differences, which appears to oversimplify the heterogeneity of the trajectory patterns.

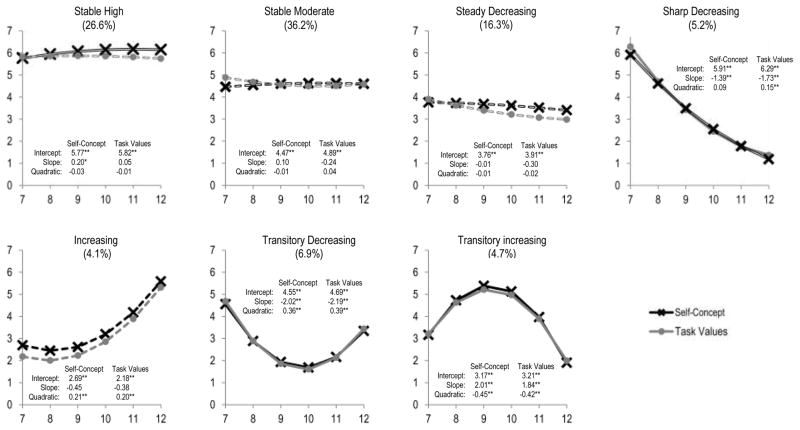
Figure 1 presents the means for ability self-concept and task values in physics and chemistry for the seven trajectory groups across seventh to twelfth grade. Overall, ability self-concept and task values in physics and chemistry followed similar patterns of longitudinal change within each group. To ensure the finding is not simply a measurement artifact of the two trajectories being estimated simultaneously, we conducted the growth mixture models for ability self-concept and task values separately and found that the number and nature of trajectory groups were consistent. According to the pattern of changes in science ability self-concept and task values, the seven groups were labeled as Stable High, Stable Moderate, Steady Decreasing, Sharp Decreasing, Increasing, Transitory Decreasing, and Transitory Increasing. Four major trajectory patterns could be summarized among these groups.

Figure 1.

Estimated means of ability self-concept and task values of the seven latent classes. Y-axis indicates the means of ability self-concept and task values. X-axis indicates the time (i.e., grades). Trajectories with significant slope and quadratic terms are indicated in solid line ( ). Trajectories with significant slope but non-significant quadratic terms are indicated in double line ( ). Trajectories with non-significant slope but significant quadratic terms are indicated in solid-dotted line ( ). Trajectories with non-significant slope and quadratic terms are indicated in double-dotted line ( ).

**p < .01.

Stable trajectories

Two trajectory groups, namely Stable High (26.6% of the sample) and Stable Moderate (36.2% of the sample), were characterized by rather stable levels of ability self-concept and task value across seventh to twelfth grade. As for Stable High, the means of the intercept, slope and quadratic terms were 5.77, 0.20 (p < .05), and −0.03 (p = n.s.) for self-concept trajectory, and the means of these growth factors were 5.82, 0.05 (p = n.s.), and −0.01 (p = n.s.) for task values trajectory. As for Stable Moderate, the means of the intercept, slope, and quadratic terms were 4.47, 0.10 (p = n.s.), and −0.01 (p = n.s.) for self-concept trajectory, and the means of these growth factors were 4.89, −0.24 (p = n.s.), and 0.04 (p = n.s.) for task values trajectory.

Unstable decreasing trajectories

The second category included the two trajectory groups characterized by longitudinal decreases in ability self-concept and task values: Steady Decreasing (16.3%) and Sharp Decreasing (5.2%). While ability self-concept and task value declined rather steadily for individuals in the Steady Decreasing group (means of intercept, slope, and quadratic terms = 3.76, −0.01 (p = n.s.), and −0.01 (p = n.s.) for self-concept trajectory, and 3.91, −0.30 (p = n.s.), and −0.02 (p = n.s.) for task values trajectory), the decline for Sharp Decreasing was more pronounced (means of intercept, slope, and quadratic terms = 5.91, −1.39 (p < .01), and 0.09 (p = n.s.) for self-concept trajectory, and 6.29, −1.73 (p < .01), and 0.15 (p < .01) for task values trajectory).

Unstable increasing trajectories

In contrast to the second category of trajectory groups, the third category included only one group, the Increasing trajectory group (4.1% of the sample), whose members experienced an increase in science motivation throughout their high school years (means of intercept, slope, and quadratic terms = 2.69, −0.45 (p = n.s.), and 0.21 (p < .01) for self-concept trajectory, and 2.18, −0.38 (p = n.s.), and 0.20 (p < .01) for task values trajectory). In the Increasing group, students’ ability self-concept and task values remained rather stable across seventh and ninth grade. After ninth grade, however, both ability self-concept and task values increased considerably until the end of high school.

Transitory decreasing and increasing trajectories

The last category included the last two trajectory groups, Transitory Decreasing (6.9% of the sample) and Transitory Increasing (4.7% of the sample). As for Transitory Decreasing, the means of the intercept, slope, and quadratic terms were 4.55, −2.02 (p < .01), and 0.36 (p < .01) for self-concept trajectory, and 4.69, −2.19 (p < .01), and 0.39 (p < .01) for task values trajectory. As for Transitory Increasing, the means of the intercept, slope, and quadratic terms were 3.17, 2.01 (p < .01), and −0.45 (p < .01) for self-concept trajectory, and 3.21, 1.84 (p < .01), and −0.42 (p < .01) for task values trajectory. These groups were characterized by self-concept and task value trajectories that reversed or changed direction around ninth grade, when students transitioned into high school. Youth in the Transitory Decreasing group reported a rapid decrease in both ability self-concept and task values across seventh to ninth grade. The decreasing trends leveled off during ninth and tenth grades and then increased from tenth to twelfth grade. Contrarily, Transitory Increasing exhibited an opposite trajectory pattern. For youth in this group, self-concept and task values increased from seventh to ninth grade and then reversed to a decreasing trend around ninth grade.

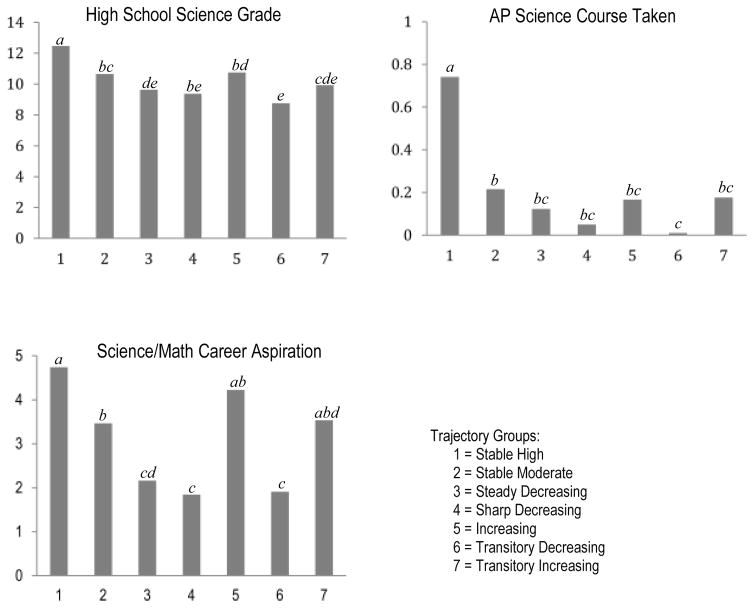
Comparing Science Outcomes Among the Different Trajectories

As shown in Figure 2, high school science grades for Stable High were higher than the other six trajectory groups. High school science grades for Stable Moderate and Increasing were similar and highest in magnitude after Stable High, followed closely by Transitory Increasing. Steady Decreasing and Sharp Decreasing also shared similar high school science grades, with Transitory Decreasing containing the lowest high school science grades among the sample.

Figure 2.

Results of the multinomial logistic regression comparing outcomes of the ability self-concept and task values trajectory groups. Y-axis indicates the means of each outcome. X-axis indicates the trajectory groups. Means sharing the same superscript (indicated on the top of each bar) are not significantly different at the p < .05 level.

Comparing the number of AP science courses taken for each trajectory group, Stable High again outweighed the other six groups. Similarly, Stable Moderate had the second highest number of courses taken. No significant differences in course taking were found among Increasing, Steady Decreasing, Sharp Decreasing, Transitory Decreasing, and Transitory Increasing.

As for STEM career aspirations, Stable High reported the highest mean score across all trajectory groups. However, there were no significant differences in STEM career aspirations between Stable High, Increasing, and Transitory Increasing. Increasing and Transitory Increasing did not differ significantly from Stable Moderate. Finally, Steady Decreasing, Transitory Decreasing, and Sharp Decreasing also did not significantly differ from one another, and Sharp Decreasing had the lowest STEM career aspirations out of the entire sample.

Discussion

Secondary school is a critical period to develop academic self-concept and interest in physical science. In order to keep up with challenging course material in STEM postsecondary programs, science career trajectories must begin early, with youth demonstrating motivation and proficiency in physical science and enrolling in advanced science courses throughout secondary school. In this study, we examined the joint developmental patterns of adolescents’ ability self-concept and subjective task values in physics and chemistry from seventh to twelfth grade. We aimed to identify groups of students with similar science motivation trajectories and examine how motivational trajectories predicted science learning outcomes. Although many studies claim that science motivation declines on average over time (e.g., Gottfried et al., 2009), we identified seven differential trajectories of motivational change from the beginning of middle school through the end of high school. Adolescents’ physics and chemistry ability self-concept and task values in each group were positively correlated over time. Additionally, we not only detected heterogeneity in patterns of physics and chemistry motivation, but also found differential associations with science achievement, advanced science course taking, and career aspirations across these trajectories.

The advantage of employing person-centered approaches is that they enable us to identify subgroups of individuals at heightened risk of experiencing continuous declines in ability self-concept and task values. These approaches will aid in the development of more nuanced strategies and individualized interventions to increase student motivation in physics and chemistry. When we focus on average trends across a sample of students, we risk overlooking the substantial diversity in student motivational trajectories, particularly for the students showing less typical developmental trends in motivation. Many students with different learning needs, as indicated by their motivational trajectories, may not receive the specialized support systems they need to improve their learning outcomes in physical science. Identifying students at higher risk for declining motivation and tailoring strategies to meet their individual needs is an important step in effectively reversing or slowing declines in physical science motivation over time. Therefore, while the seven groups identified vary in size, students classified in the smaller groups may actually need more attention and support than those following more common or typical developmental trajectories of stability.

Trajectory Groups of Ability Self-Concept and Task Values and Science Outcomes

We classified the seven developmental trajectories into four categories based on their similar developmental patterns: stable trajectories, unstable decreasing trajectories, unstable increasing trajectories, and transitory declining and increasing trajectories.

Stable trajectories

While studies of achievement motivation have found that the majority of students from elementary through secondary school experienced declining trajectories across subject domains (Wigfield et al., 2006), by examining change exclusively across middle and high school, we identified two stable trajectories of high and moderate levels of learning motivation in physics and chemistry, comprising a majority (63%) of students. This pattern could be considered the normative developmental course of physics and chemistry learning motivation in adolescence, although levels of stability did vary and were differentially associated with the outcomes of interest. For example, students belonging to the Stable High group were more likely than the Moderate Stable group to have higher science achievement, higher STEM career aspirations, and to enroll in more advanced placement science courses. However, despite significant outcome differences between the two stable groups, stability at either a high level or a moderate level was characterized by more consistently positive educational outcomes in comparison to the changing or unstable trajectory groups. These results indicate that maintaining a constant, positive perception of competence, interest, and value in physics and chemistry across middle and high school, may provide a number of long-term academic benefits for youth. For these students in particular, physics and chemistry motivation established in their early school years seems to set the stage for their later academic development.

The seemingly protective nature of stable-at-a-high-level or stable-at-a-moderate-level in physics and chemistry motivation underscores the importance of optimizing early science learning experiences to facilitate and maintain high levels of perceived ability and utility of physics and chemistry. Specifically, research suggests that personal interest in science could be triggered by formal and informal learning experiences throughout childhood (Maltese & Tai, 2010), and that science interests in eighth grade and the start of high school are strong predictors of future STEM degree attainment and career interest (Maltese & Tai, 2011; Sadler et al., 2012). While it is unclear exactly what sustained the motivational beliefs of these students over such an extended period of time, we can speculate that possibly having high quality learning experiences such as attending high quality schools or experiencing engaging hands-on instruction may be the driving mechanisms. Future research should investigate whether individuals with stable-at-a-high-level motivational trajectories in physics and chemistry have more high quality in-school and out-of-school science experiences than students in unstable trajectories.

Unstable and decreasing trajectories

Students in the Sharp Decreasing (16.3%) and Steady Decreasing trajectories (5.2%) demonstrated a continuous drop in physics and chemistry motivation over time, but the rate of decline varied across the school years. These students began seventh grade with above average motivational beliefs, with most reporting being good at physics and chemistry and finding them useful. Unfortunately, over time, motivational beliefs about physics and chemistry became progressively more negative. These findings are troubling, given that researchers have suggested that when students tend to report lower perceptions of their ability in a specific domain than their actual performance, their performance eventually begins to match their perceptions (Phillips & Zimmerman, 1990). It appears that self-perceptions of competence inform subsequent task performance, and because task values are closely tied to academic self-concepts, it follows that ability self-concepts and task values will continuously shape both each other and achievement over time (Assor & Connell, 1992). Our findings seem to support these pathways, as students in decreasing trajectory groups had lower STEM career aspirations than those in both stable trajectory groups, and lower science grades and advanced course enrollment than the Stable High group.

Given that our trajectories track adolescent development from middle to high school, changes in the structure of the educational environment may lead many students to feel less academically competent and experience stark declines in achievement motivation as they transition to secondary school (Fredricks & Eccles, 2002; Gottfried, Fleming, & Gottfried, 2001; Jacobs et al., 2002). However, consistent declines may also be indicative of strategies that students use to cope with poor quality schools, and unengaging instruction. Feedback from teachers may also play a role, as youth often have difficulty reengaging with material after receiving continuously negative feedback. While we do not have the sociocultural or contextual data to test these assumptions, it would be valuable for future research to examine whether changes in school structure, teacher quality, and parent behavior interactively result in continued declines in motivation from middle to high school.

Unstable and increasing trajectories

A third category of students demonstrated an unstable and increasing pattern of motivational development. This small group of students (4% of the sample) had below average motivation in physics and chemistry at the start of middle school and experienced little change until ninth grade, when their physics and chemistry motivation increased sharply. This group bucks the trend of declining motivation seen throughout developmental literature by demonstrating that, for a small group of students, science motivation actually increases throughout high school. This raises the question, however, of why these students maintained lower motivation until entering high school. Although we do not know the specific mechanisms that led to these motivational increases throughout high school, we can offer some probable suggestions. For instance, most students in middle school have a prescribed course load, while high school students have more options to choose physics and chemistry electives that might interest them. This may explain why achievement motivation in physics and chemistry increased dramatically for this small group of students at the beginning of high school.

In addition, while increases in science motivation may be seen as beneficial, the late start for this group may be somewhat problematic. For example, although these students performed relatively well in science and had relatively high career aspirations in STEM, their late interest in physics and chemistry may have impeded their ability to take as many advanced science courses as their stably motivated peers. This is evidenced by the smaller average number of AP courses taken by the Increasing group relative to the High Stable or Moderate Stable groups. Due to STEM degree programs requiring a strong foundation in advanced science coursework prior to entering college, development of science interests late in high school may delay students’ educational progress toward obtaining a STEM degree. Future research should investigate whether students who developed science interests late in high school, but ultimately major in a science field, have difficulty keeping up with the college course load relative to students who develop their science interests early.

Transitory declining and increasing trajectories

The fourth category represented two groups of unstable trajectories: one with a decreasing trajectory (Transitory Decreasing) that leveled out and then began to increase at ninth grade, and another with an increasing trajectory that transitioned to a steep decline upon entry into ninth grade (Transitory Increasing). For both transitory groups, ninth grade was a critical turning point in the subsequent development of ability self-concept and task values in physics and chemistry, aligning with prior findings that school transitions can be difficult for many students. In fact, stage-environment fit theory postulates that the incongruence between adolescent developmental needs and the environmental structure of secondary schools leads many students to feel alienated and less attached to their school (Eccles et al., 1993). Future research could examine whether contextual factors differ across these two groups resulting in opposite patterns of motivational trajectories over time.

Although these groups experienced opposite patterns of development over time, their developmental inconsistencies seemed to place these students at an academic disadvantage, with lower average AP science course enrollment and science academic performance, compared to most other groups. Indeed, the fluctuations in motivation detected for these two transitory groups may have reduced students’ likelihood of enrolling in advanced courses in science. This may explain why students in these groups were less likely to enroll in AP science courses, and as a result, may have been less academically prepared to pursue careers in science, as reflected by their lower average science grades. This finding corroborates our previous conclusion that high, stable patterns of ability self-concept and task values in physics and chemistry appear to be the optimal pattern of motivational beliefs to support and further enhance the development of scientific knowledge and ability.

The Longitudinal Relation between Ability Self-Concept and Task Values

As adolescents’ perception of their own competence and ability in physics and chemistry changed over time, their reported interest in physics and chemistry changed in tandem. This was true regardless of the initial level and shape of students’ developmental trajectories. Stability in ability self-concept was accompanied by stability in task value, while increases or decreases in ability self-concept were accompanied by increases or decreases in task value, respectively. These findings are consistent with the empirical and theoretical literature positing that academic self-concept and task value beliefs are reciprocally related and mutually reinforcing over time (Denissen et al., 2007; Wigfield & Eccles, 2002). According to expectancy-value theory, children are more interested in domains in which they feel more competent, and achieve greater competence in domains in which they have greater interest. While elementary school students are less likely to report ability self-concept and values that are similar in magnitude (Wigfield et al., 1997), older students become less optimistic about their performance, and become more adept at judging their own abilities (Eccles et al., 1998). In particular, as children progress from elementary through middle school they become more proficient at rating their ability and interest across specific subject domains (Eccles, 1999). As a result, ability self-concept and task value ratings of middle school and high school students are often lower and more closely related to each other than those of younger students (Eccles et al., 1993; Wigfield & Eccles, 1994).

Limitations and Future Research

Although this study has much to offer, some caveats need to be noted. First, the majority of our sample was White, limiting our ability to generalize the findings to other racial/ethnic populations. Some minority groups, such as African Americans and Latinos, are underrepresented in STEM fields and face a number of social challenges (e.g., prejudice, discrimination) that infrequently affect White middle-class populations (Wang & Degol, 2016). However, racial/ethnic minorities also have cultural strengths that they can build upon to help them succeed in STEM, such as African American girls viewing STEM careers as an important dimension of family (Hanson, 2007). It is important, therefore, that future research investigates the development of science motivation among Latino and African American youth, with a focus on the unique challenges and strengths that they face.

Second, we operationalized science motivation by combining physics and chemistry subject domains, yet it is likely that physics and chemistry have unique motivational trajectories. To address this limitation, future studies should evaluate physics and chemistry individually and examine whether our findings can be replicated in other science subject domains as well, such as biology and computer science. In addition, while we are confident that our measure of STEM career aspirations appropriately assesses twelfth graders’ inclination to pursue a STEM career, we acknowledge that having high aspirations in STEM does not necessarily translate to a future career in STEM. Additional follow-up analyses are needed to determine differences in actual career attainment across motivational trajectory groups.

Third, while a clear strength of our study is its focus on motivational changes during the middle school and high school years, which minimized the related cognitive maturational effect on motivation, modeling stability or change in motivation across the transition from elementary to middle school could help us determine if the transition to middle school is truly characterized by declines across all groups. Such analyses would also enable us to compare the transition to middle school with the transition to high school and determine if the high school transition stands out as a more critical turning point for the creation of divergent pathways of physical science motivation. These findings, therefore, may shed more light on the crucial role that high school plays in creating motivational discrepancies in science learning between different groups of students.

Fourth, given that the growth mixture modeling analysis procedure used in this study is newly developed, it is quite common that different modeling-fitting indices or statistical tests may not support the same decision as indicated in many studies (e.g., Diallo, Morin, & Lu, 2016b; Marsh et al., 2009). While there are no agreed-upon criteria for facilitating decisions about the number of classes in growth mixture modeling, future research should investigate whether our findings can be replicated across multiple studies (Nylund et al., 2007).

Fifth, although we identify the longitudinal relationships between motivation and achievement outcomes, the development of motivation and achievement could be bidirectional, with performance and course taking shaping science motivation over time and vice versa. It is therefore vital to consider the potential reciprocity among achievement and motivation to determine how strongly they influence each other longitudinally. Sixth, we used course grades and advanced course enrollment as our achievement measures. Although the participating schools were selected due to their comparable SES, grading rubric, curriculum design, and student academic performance, it is difficult to determine whether course grades are comparable across these schools and whether a similar number of AP courses were available to students enrolled in different schools. Future studies may want to use standardized test scores as the achievement measure and examine if the results can be replicated.

Finally, while we identified differential trajectory groups of physics and chemistry motivation, and related these groups to various educational outcomes, it is unclear what contextual or sociocultural factors led to these developmental patterns. These factors should be further investigated in order to construct a more holistic view of how adolescents’ physical science motivation is shaped and how contexts vary across trajectory groups. For example, despite the relative importance of educational experiences in determining motivational development, we were unable to control for school quality in modeling our trajectories or to determine if school quality varied significantly across our existing trajectory groups (Wang & Peck, 2013). Future research should examine whether educational contexts may distinguish stable from unstable trajectories of science motivation.

Implications for Practice and Research

Several implications for intervention and practice can be derived from the current study. This research validates substantial heterogeneity in the development of students’ achievement motivation in physics and chemistry from seventh through twelfth grade. Extant research has principally focused on average trends, which demonstrate constant declines in ability self-concept and task values (Fredericks & Eccles, 2002; Gottfried et al., 2007). Conversely, the majority of youth in our sample followed stable trajectories of motivational development; still other students demonstrated unstable patterns characterized by some increases and decreases in motivation over time. Relying solely upon average trends masks these developmental processes and forces both thriving students and struggling students into one general category of development (Wang & Degol, 2014). Person-centered approaches, on the other hand, enable us to identify subgroups of students who may need additional support to stay engaged in science learning. This work is therefore positioned to inform the development of individualized instructional techniques and strategies that help struggling students become more competent and interested in their academic endeavors.

Our findings support the domain specificity of achievement motivation and the importance of differentiating motivational changes across subject domains. In comparison to literacy motivation (Archambault et al., 2010), for example, it appears that literacy and physical science motivation trajectories follow distinctly different patterns of development. While seven groups of literacy motivation were identified, most of the groups shared declining patterns of motivation, and group differences centered on rates or time points of decline. Meanwhile, our findings suggest that physics and chemistry motivation varies individually, with developmental patterns that demonstrate stable, increasing, or decreasing trajectories. The majority of youth experienced general stability in physics and chemistry ability self-concepts and task values, presenting a diversity of heterogeneous patterns not observed in literacy. Another essential distinction between the two subject domains is that self-concept and task value in physics and chemistry followed the same relative pattern of development, while literacy self-concept and task value diverged more over time. It is worth noting that the differences detected may be attributed to our decision to focus solely on adolescent development, as opposed to development from early childhood to adolescence in the literacy study.

Conclusion

While increasing science performance and course enrollment for adolescents is an important endeavor, our study suggests that increasing learning motivation may not only promote achievement but career aspirations as well, activating multiple potential pathways to a successful career in STEM fields (Wang et al., 2015). For many students, secondary school is their first opportunity to choose physics and chemistry courses that may be of specific interest to them from a differentiated curriculum, and could therefore, potentially serve as a key turning point in maximizing or enhancing interests and career aspirations. Thus, examining how these motivational patterns develop during the high school transition will offer insight into the capacity of different groups of students to successfully adapt to their changing educational environments. Moreover, given the heterogeneity in developmental trajectories and their divergent outcomes, adopting a tailored trajectory-specific intervention strategy rather than a universal approach may facilitate the design of effective interventions for addressing physical science motivation. Special attention should be paid to the time points during which different groups of students experience the greatest risk of losing motivational interest in physics and chemistry so that we can identify optimal intervention points for buffering the declining trajectories in learning.

Biographies

Ming-Te Wang is an Associate Professor of Psychology and Education and Research Scientist of Learning Research and Development Center at University of Pittsburgh. He received his doctorate in Human Development and Psychology from Harvard University. His major research interests include motivation and engagement, risk and resilience, stereotype threat, and psychosocial interventions.

Angela Chow is an Assistant Professor of Public Health at Indiana University Bloomington. She received her doctorate in Education from University of Hong Kong. Her major research interests include motivational development and learning, transition from adolescence to adulthood, and longitudinal studies.

Jessica Lauren Degol is an Assistant Professor of Human Development and Family Studies at Penn State University Altoona. She received her doctorate in Applied Developmental Psychology from University of Pittsburgh. Her major research interests include child development, gender differences in STEM, and early childhood care.

Jacquelynne Sue Eccles is a Distinguised University Professor of Education at University of California Irvine and Distinguished University Professor of Psychology Emeritus at the University of Michigan, Ann Arbor. She received her doctorate in Psychology from UCLA. Her major research interests include adolescent development, expectancy-value theory, and school transitions.