Abstract
New software that performs Classical and Bayesian Instrument Development (CBID) is reported that seamlessly integrates expert (content validity) and participant data (construct validity) to produce entire reliability estimates with smaller sample requirements. The free CBID software can be accessed through a website and used by clinical investigators in new instrument development.
Demonstrations are presented of the three approaches using the CBID software : (a) traditional confirmatory factor analysis (CFA); (b) Bayesian CFA using flat uninformative prior; and (c) Bayesian CFA using content expert data (informative prior).
Outcomes of usability testing demonstrate the need to make the user-friendly, free CBID software available to interdisciplinary researchers. CBID has the potential to be a new and expeditious method for instrument development, adding to our current measurement toolbox. This allows for the development of new instruments for measuring determinants of health in smaller diverse populations or populations of rare diseases.
Keywords: instrument development methods, Bayesian methods, Free software
The overall purpose is to demonstrate a Bayesian approach to confirmatory factor analysis (CFA) using a free software program Classical and Bayesian Instrument Development (CBID), and to assess usability of the software. Additionally, we wish to disseminate an innovative method for Bayesian instrument development that integrates expert data with participant data collected for classical instrument development. Extending our previous research (Author-6 et al., 2012; Author-6, Author-4, & Author-1, 2015; Author-6 et al., 2013; Author-3 et al., 2015; Jiang et al., 2014; Pawlowicz et al., 2012), we use a framework grounded in long-standing and empirically-verified Bayesian analyses where content experts’ data are updated with data collected from participants to establish construct validity and to efficiently achieve a unified psychometric model.
Background
While Bayesian methods have been added to Mplus structural equation modeling (SEM) software (Muthén, 2010), no existing software has the ability to combine content validity and construct validity data. The present work addresses this shortcoming. We recently have developed a free software program (CBID) that performs both classical and Bayesian instrument development. CBID is designed for use by investigators and can be accessed and executed from a web browser (http://biostats-shinyr.kumc.edu/CBID/). The CBID software fits Markov chain Monte Carlo (MCMC) methods (Author-3 et al., 2015) and requires the user to specify a prior distribution in a form that can be “flat uninformative”, prior data, or content expert data.
While the nursing research community is well-versed in applying and fitting confirmatory factor analytic (CFA) models to validate instruments, most investigators are likely to encounter challenges in programming CBID using MCMC methods. Moreover, even if one could do so, it is a burdensome and time consuming process. In the background to the web browser, we have created the software package CBID in R 3.1.2 (R Core Team, 2013) programming language and in WinBUGS (Li & Baser, 2012) (both freeware). Instead of running from the browser, one alternately can download the software on their machine (http://www.kumc.edu/school-of-medicine/department-of-biostatistics/software/cbid.html).
CBID was applied retrospectively to instrument development studies from other investigators at our institution who had collected expert data for content validity and participant data for construct validity. Typically this is what one would use for classical approaches to instrument development. For the purposes of this paper we will apply CBID to an American Indian mammography satisfaction instrument (Engelman et al., 2010) and also provide readers step-by-step instructions for running the software using their own data. One of the most important practical contributions of the software is that we provide 95% credible intervals -along with a point estimate of score reliability (Jiang et al., 2014) that usually is not found in commercial software programs like Mplus. The intervals provide a level of uncertainty that reflects the sample size (Author-6, Author-4, & Author-1, 2015). This is an important contribution since the American Psychological Association strongly encourages the reporting of confidence (frequentist) or credible (Bayesian) intervals around point estimates (American Educational Research Association et al., 2014).
This paper is targeted towards clinical investigators as well as the statisticians with whom they work. Given the nature of research becoming increasingly interdisciplinary, we believe software such as CBID provides an important contribution allowing collaborations among researchers. Also, since CBID is open source and built upon R (also open source) this software supports the Open Science movement for transparency in research improving dissemination, sharing and reproducibility of research results. We are hopeful that this effort will allow other investigators free access to the CBID software via the following website: (http://www.kumc.edu/school-of-medicine/department-of-biostatistics/software/cbid.html). Additionally, the researchers can provide feedback on the usability of the software that will assist in improvements to the software.
CBID Software
CBID allows nursing researchers to conduct confirmatory factor analysis (CFA) and estimate score reliability along with the associated 95% credible intervals. Built via RStudio’s “Shiny” package, CBID is a free, accessible CFA-based application. It has a graphical user interface (GUI) (i.e., “point and click” environment similar to SPSS that often is not found in open source software) that allows researchers quickly to conduct a detailed classical CFA or Bayesian CFA/Item Response Theory (IRT) analysis without any prior programming knowledge.
Construct Validity Modeling
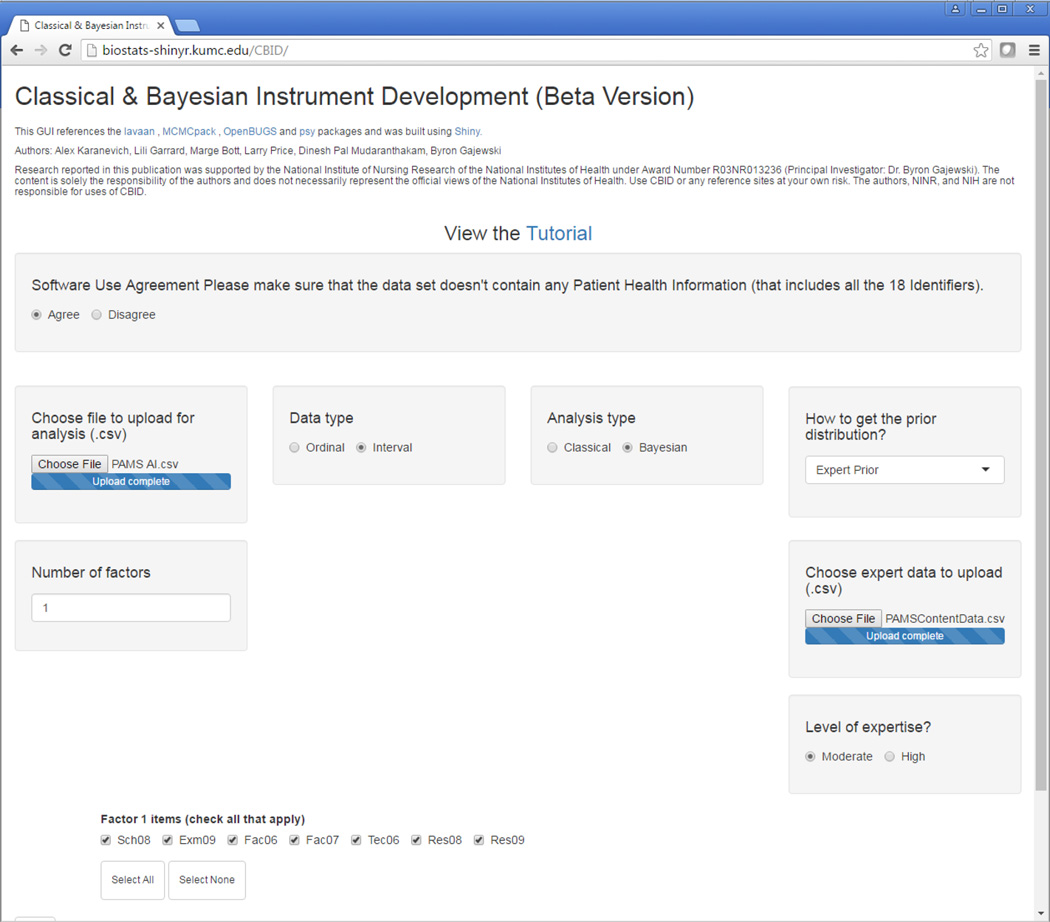
To conduct the validity testing, the CBID software can be accessed at the following website: http://biostats-shinyr.kumc.edu/CBID/. The first step prior to using the software is completing the software use agreement on the website by clicking on “agree” (Figure 1).
Figure 1.
Screen Shot of CBID Software Showing Classical Analysis Type
Data file preparation
To be compliant with the software use agreement, all patient health information identifiers must be removed from the data prior to converting the data set. To use CBID, a user converts the analysis data set (i.e., data collected from participants in a survey instrument) to a comma separate values (.csv) format (easily converted using programs such as Microsoft Excel or SPSS) and uploads the file to the CBID application. The first row of the participant data file is reserved for item names that should be descriptive and concise (see example in Table 1). Examples of good item names tend to be limited to about eight characters so they can fit on the webpage in one line. This of course depends on the number of items in a factor. These variables can begin with capital letters but not numbers. The current version of CBID requires complete (non-missing) data. For model identification purposes, at least three items are required per factor (Brown, 2014). Finally, all negatively worded items in the data set need to be reverse coded prior to converting and uploading the file.
Table 1.
Participant Data: The First 10 Rows of Data in the .csv Format, with Item Names
| Sch08 | Exm09 | Fac06 | Fac07 | Tec06 | Res08 | Res09 |
|---|---|---|---|---|---|---|
| 3 | 3 | 3 | 3 | 4 | 4 | 3 |
| 3 | 4 | 4 | 3 | 4 | 4 | 3 |
| 4 | 3 | 3 | 4 | 5 | 4 | 5 |
| 3 | 2 | 3 | 3 | 3 | 4 | 3 |
| 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 5 | 4 | 5 | 5 | 5 | 4 | 5 |
| 3 | 4 | 5 | 5 | 5 | 5 | 5 |
| 5 | 4 | 5 | 5 | 5 | 5 | 5 |
| 3 | 3 | 4 | 4 | 4 | 4 | 4 |
If the user wants to conduct the Bayesian analysis (for an introduction to Bayesian analysis see Carpenter et al., 2008) using prior data (i.e., previous participant or content expert data), this would require users to upload a separate .csv formatted data file. Again the item names must be placed in the first row and must match the names of items contained in the participant data file (see example in Table 2). Both prior participant data and current participant data files must contain the same number of columns whereas the number of rows/cases does not have to be the same between prior and current datasets. After successfully uploading the data set, CBID automatically extracts the item names from the first row of the data file.
Table 2.
Prior Data: Previous or Expert Data in the .csv Format, with Item Names
| Sch08 | Exm09 | Fac06 | Fac07 | Tec06 | Res08 | Res09 |
|---|---|---|---|---|---|---|
| 4 | 4 | 3 | 4 | 4 | 4 | 4 |
| 4 | 4 | 4 | 4 | 3 | 3 | 4 |
| 2 | 4 | 3 | 3 | 3 | 3 | 2 |
| 2 | 4 | 4 | 4 | 4 | 4 | 4 |
| 1 | 4 | 3 | 4 | 4 | 4 | 4 |
| 3 | 2 | 2 | 3 | 2 | 3 | 2 |
Approaches
Classical CFA Approach
To establish evidence of construct validity using the classical CFA approach, the user chooses to model their participant data as either ordinal (e.g. “very unlikely, “unlikely,” …) or interval (e.g. continuous data like BMI, weight, age), and selects the number of factors and which items should load on each factor. Our software can handle dichotomously scored items, which is a special case of ordinal (e.g. items that are correct of incorrect). For the ordinal case the responses are not assumed to be symmetrically distributed nor normally distributed. The CBID software allow for more flexibility than the usual factor analysis assumption of (a) continuous data and (b) multivariate normality. Users may select additional options, but otherwise can run CBID and obtain the CFA results. For classical CFA, CBID utilizes the R package lavaan (Yves, 2012). Output from CBID quickly can provide a detailed summary of CFA results for multiple factors using both interval and ordinal data along with Cronbach’s α. CBID also calculates the “entire reliability” (this is short for what Alonso et al., 2010 refer to as reliability of the entire scale) for single-factor models. Entire reliability (Alonso et al., 2010) is a more accurate measure of reliability than Cronbach’s α, since the latter is a lower-bound estimate of reliability (Sijtsma & van der Ark, 2015; Author-4, 2016).
Bayesian CFA Approach
For Bayesian CFA, CBID utilizes the R package called mcmcpack (Martin, Quinn, & Park, 2011). When analyzing single-factor models (for either ordinal or interval data), CBID can conduct a Bayesian analysis to determine estimates for the factor loadings and score reliability for the entire reliability instrument. Unlike the classical CFA analysis, this analysis reports 95% credible intervals for both the factor loadings and the entire reliability estimate. In the Bayesian framework, a 95% credible interval for a value x signifies that there is a 95% probability that x is in that interval. Many propose this is more intuitive than a confidence interval, which is a statement about how confident we are that the parameter of interest is in the interval (i.e., if we calculated this interval repeatedly with resampled data, we would cover the true parameter 95% of the time).
Bayesian analyses can be performed using a variety of priors (Carpenter et al., 2008). Choices of priors for CBID include a flat uninformative prior (uniform on the interval [0,1]), a prior automatically calculated from previous data: (a) informative data from a previous data collection from participants or (b) informative prior derived from subject experts’ relevancy rankings of the items to the construct of interest (i.e., content validity). For subject experts’ prior one can choose between experts having high or moderate expertise (Author-3 et al., 2015). For the purposes of this paper we choose the moderate expertise option.
Ordinal Data Examples in CBID
We now demonstrate CBID using three examples: (a) classical approach, (b) Bayesian approach with flat uninformative priors, and (c) Bayesian approach with (moderate) content expert data. We will analyze an ordinal data set using the short form (single factor with seven items) of the Patient Assessment of Mammography Services (PAMS) satisfaction survey (Engelman et al., 2010). Note: CBID can also run multiple factors at once for classical only and not Bayesian. This file has five-point Likert-type responses (poor [1] to excellent [5]) from 299 subjects on the items named: Sch08, Exm09, Fac06, Fac07, Tec06, Res08, and Res09 (Table 1). Additionally, content expert data were collected on the seven items on a scale of “content is not relevant” (1) to “content is very relevant” (4) from six experts (Table 2).
Classical Approach
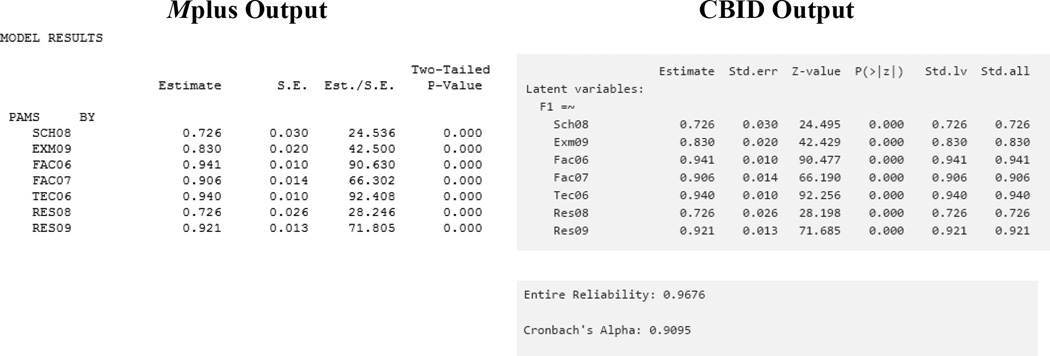
We treat the data as ordinal and conduct a classical CFA analysis using CBID (Figure 1). After clicking the “Go!” button, we obtain the output from the CBID analysis that can be compared to the Mplus output (Figure 2). Note that the standardized estimates and the standard errors are identical in both outputs; and the factor loadings can be interpreted directly as item-to-domain correlations. Using CBID, entire reliability (.97) and Cronbach’s α (.92) are reported.
Figure 2.
Comparison of Mplus Output to CBID output using Classical Approach
Bayesian Approach with Flat Uninformative Prior
After running the classical CFA, suppose one wants to further investigate factor one within a Bayesian framework. Using CBID, we change the analysis type to Bayesian (“Analysis Type” box – Figure 3), which will prompt the user to select a prior. For this example, we will use a flat uninformative prior (uniform on the interval between 0 and 1, inclusive). The output is displayed in Figure 4. Bayesian analysis only will report relevant results: (a) Markov chain Monte Carlo (MCMC) acceptance rates; (b) the factor loadings estimates and standard errors (std), along with the 95% credible intervals (CrI) for the factor loadings; and (c) the entire reliability estimate (along with std and 95% CrI). Desirable MCMC procedure acceptance rates are between 20–50% for each item (Gelman et al., 2004). In our example, the MCMC acceptance rates range from .38–.50. Because we are investigating a single factor, CBID outputs the entire reliability as both a point estimate and a 95% CrI. This feature is unique to CBID and, to our knowledge, unavailable in commercial software. Notice that even the lower bound of the entire reliability, reported as 0.96 (.95–.97), is higher than the point estimate Cronbach’s α (.91).
Figure 3.
Screen Shot of CBID Software Showing Bayesian Analysis Type with Flat Uninformative Prior
Figure 4.
Bayesian Analysis Output on Ordinal Data using Flat Uninformative Prior
Bayesian Approach with Expert Data
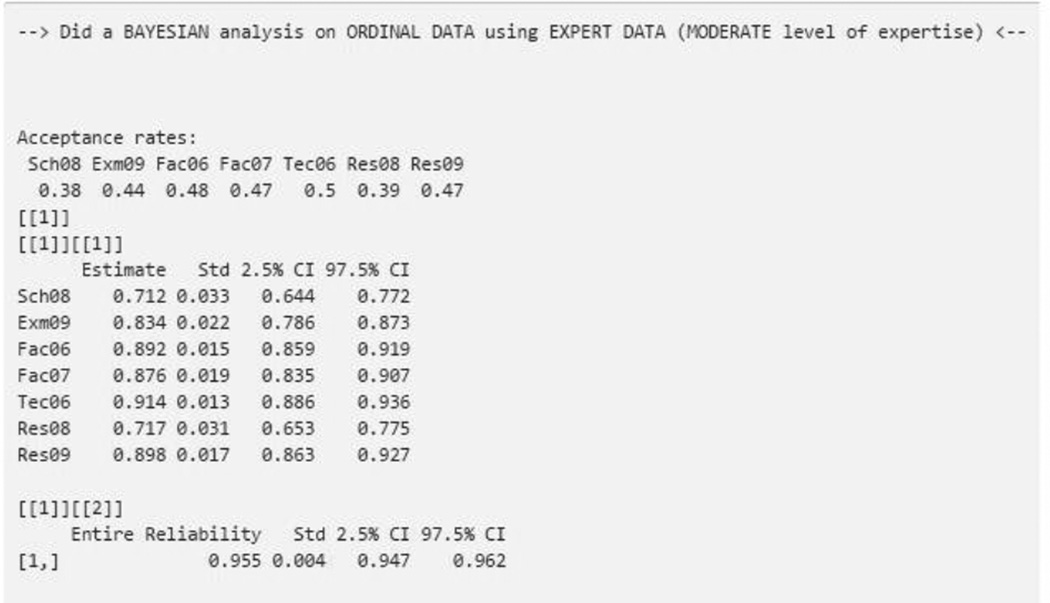
Since we have chosen the analysis type as Bayesian, we now select “expert” prior on the prompt, “how to get a prior distribution.” We will be prompted to upload the data set that contains experts’ relevancy rankings on each of the items, and asked for the level of expertise of the content experts (Figure 5). This decision is made by the researcher who chose the content experts. For this example, the content experts were deemed by the researcher to have “moderate” expertise. Since we are using the same seven items and one factor, we are ready to submit the “Go” button to complete the analysis (Figure 6). Compared with flat uninformative prior output, the analysis produces similar results for MCMC acceptance rates, and slightly lower estimates for the factor loadings (i.e., item-to-domain correlations) along with corresponding CrIs,. With the addition of prior information from content experts (informative priors), we find that the entire reliability is lower (.955) when compared to the analysis using flat uninformative priors (.961). However, the lower bound of the entire reliability, reported as .96 (.95–.96), is higher than Cronbach’s α (.91), that is considered the lower bound of reliability. Also notice that experts are supplying more information than the flat uninformative prior, resulting in a CrI width of .015 (.962−.947=.015) that is narrower than the CrI width supplied by the flat uninformative prior (.969−.952=.017).
Figure 5.
Screen Shot of CBID Software Showing Bayesian Analysis Type with Expert Informative Prior
Figure 6.
Bayesian Analysis Output using Expert Informative Prior with Moderate Level of Expertise
CBID Usability
In order to determine the accessibility of CBID, we conducted software usability testing (Lewis, 1995) with a convenience sample of ten researchers (five nurse scientists, three statisticians, and one psychologist). A 19-item, software usability survey (http://garyperlman.com/quest/quest.cgi) was available for the researchers to provide feedback after using the software. User responses are collected using the Research Electronic Data Capture (REDCap) web application (Harris et al., 2009). From our convenience sample of ten, 90 % of the respondents “agreed to strongly agreed” that they were overall satisfied with the software. Respondents did not score as favorably (60%) to items about the belief that they became productive quickly using this system (item 8) or the system gave error messages that clearly told them how to fix problems (item 9).
Discussion and Conclusions
Establishing evidence for the reliability and validity of scores produced on a measurement instrument is essential for nursing research. Having the access to appropriate software is critical for carrying out relevant psychometric analyses. We have introduced a free, open source, easily-accessible application called CBID that can conduct both classical and Bayesian CFA-based construct validity analyses and provide estimates of reliability measures. CBID has advantage over the commercial software as it can report 95% credible intervals for both factor loadings and -score reliability estimates for the entire instrument.
Acknowledgments
Research reported in this publication was supported by the National Institute of Nursing Research of the National Institutes of Health under Award Number R03NR013236 (Principal Investigator: Author-6). Please note that we used REDCap for surveying the usability (CTSA Award # UL1TR000001).
Footnotes
The authors declare that there are no conflicts of interest.
Disclaimer
This manuscript reflects the views of the authors and should not be construed to represent the FDA's views or policies. Author-3 completed this work as a PhD student in the Department of Biostatistics at the University of Kansas Medical Center.
Contributor Information
Marjorie Bott, University of Kansas Medical Center School of Nursing.
Alex G. Karanevich, University of Kansas Medical Center Department of Biostatistics.
Lili Garrard, Division of Biometrics III, OB/OTS/CDER, U.S. Food and Drug Administration
Larry R. Price, Texas State University College of Education and Department of Mathematics.
Dinesh Pal Mudaranthakam, University of Kansas Medical Center Department of Biostatistics.
Byron Gajewski, University of Kansas Medical Center Department of Biostatistics.
References
- Alonso A, Laenen A, Molenberghs G, Geys H, Vangeneugden T. A unified approach to multi-item reliability. Biometrics. 2010;66:1061–1068. doi: 10.1111/j.1541-0420.2009.01373.x. [DOI] [PubMed] [Google Scholar]
- American Educational Research Association, American Psychological Association, and National Council on Measurement in Education. Standards for educational and psychological testing. Washington, DC: American Educational Research Association; 2014. [Google Scholar]
- Brown TA. Confirmatory factor analysis for applied research. 2nd. New York: Guilford Publications; 2014. [Google Scholar]
- Carpenter J, Author-6 B, Teel C, Aaronson LS. Bayesian data analysis: Estimating the efficacy of Tai Chi as a case study. Nursing Research. 2008;57:214–219. doi: 10.1097/01.NNR.0000319495.59746.b8. [DOI] [PubMed] [Google Scholar]
- Engelman KK, Daley CM, Author-6 BJ, Ndikum-Moffor F, Faseru B, Braiuca S, et al. An assessment of American Indian women's mammography experiences. BMC Women's Health. 2010;10:34. doi: 10.1186/1472-6874-10-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Author-6 BJ, Coffland V, Boyle D, Author-1 MJ, Author-4 LR, Leopold J, Dunton N. Assessing content validity through correlation and relevance tools: A Bayesian randomized equivalence experiment. Methodology. 2012;8:81–96. [Google Scholar]
- Author-6 BJ, Author-4 LR, Author-1 MJ. Response to ‘Conceptions of reliability revisited, and practical recommendations.’. Nursing Research (invited) 2015;64:137–139. doi: 10.1097/NNR.0000000000000077. [DOI] [PubMed] [Google Scholar]
- Author-6, Author-4, Coffland V, Boyle D, Author-1 Integrated analysis of content and construct validity of psychometric instruments. Quality & Quantity. 2013;47:57–78. [Google Scholar]
- Author-3, Author-4, Author-1, Author-6 A novel method for expediting the development of patient-reported outcome measures and an evaluation of its performance via simulation. BMC Medical Research Methodology. 2015;15:77. doi: 10.1186/s12874-015-0071-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian data analysis. Texts in statistical science series. 2004 [Google Scholar]
- Harris PA, Taylor R, Thielke R, Payne J, Gonzalez N, Conde JG. Research electronic data capture (REDCap) - A metadata-driven methodology and workflow process for providing translational research informatics support. Journal of Biomedical Informatics. 2009;42:377–381. doi: 10.1016/j.jbi.2008.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Y, Boyle DK, Author-1, Wick JA, Yu Q, Author-6 Expediting clinical and translational research via Bayesian instrument development. Applied Psychological Measurement. 2014;38:296–310. doi: 10.1177/0146621613517165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis JR. IBM computer usability satisfaction questionnaires: Psychometric evaluation and instructions for use. International Journal of Human-Computer Interaction. 1995;7:57–78. [Google Scholar]
- Li Y, Baser R. Using R and WinBUGS to fit a generalized partial credit model for developing and evaluating patient-reported outcomes assessments. Statistics in Medicine. 2012 doi: 10.1002/sim.4475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin AD, Quinn KM, Park JH. MCMCpack: Markov Chain Monte Carlo in R. Journal of Statistical Software. 2011;42:1–21. [Google Scholar]
- Muthén B. Bayesian analysis in Mplus: A brief introduction. Technical Report. 2010 http://www.statmodel.com/download/IntroBayesVersion%203.pdf.
- Pawlowicz F, Author-6, Coffland V, Boyle D, Author-1, Dunton N. Application of bayesian methodology within an equivalence content validity study. Nursing Research. 2012;61:181–187. doi: 10.1097/NNR.0b013e318253341b. [DOI] [PubMed] [Google Scholar]
- Author-4 . Psychometric Methods: Theory into Practice. New York, NY: Guilford Publications; 2016. [Google Scholar]
- R Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2013. URL http://www.R-project.org/ [Google Scholar]
- Sijtsma K, van der Ark LA. Conceptions of reliability revisited, and practical recommendations. Nursing Research. 2015;64:128–136. doi: 10.1097/NNR.0000000000000077. [DOI] [PubMed] [Google Scholar]
- Yves R. lavaan: An R package for structural equation modeling. Journal of Statistical Software. 2012;48:1–36. URL http://www.jstatsoft.org/v48/i02/ [Google Scholar]