How Are You Feeling?: A Personalized Methodology for Predicting Mental States from Temporally Observable Physical and Behavioral Information

Abstract

It is believed that anomalous mental states such as stress and anxiety not only cause suffering for the individuals, but also lead to tragedies in some extreme cases. The ability to predict the mental state of an individual at both current and future time periods could prove critical to healthcare practitioners. Currently, the practical way to predict an individual’s mental state is through mental examinations that involve psychological experts performing the evaluations. However, such methods can be time and resource consuming, mitigating their broad applicability to a wide population. Furthermore, some individuals may also be unaware of their mental states or may feel uncomfortable to express themselves during the evaluations. Hence, their anomalous mental states could remain undetected for a prolonged period of time. The objective of this work is to demonstrate the ability of using advanced machine learning based approaches to generate mathematical models that predict current and future mental states of an individual. The problem of mental state prediction is transformed into the time series forecasting problem, where an individual is represented as a multivariate time series stream of monitored physical and behavioral attributes. A personalized mathematical model is then automatically generated to capture the dependencies among these attributes, which is used for prediction of mental states for each individual. In particular, we first illustrate the drawbacks of traditional multivariate time series forecasting methodologies such as vector autoregression. Then, we show that such issues could be mitigated by using machine learning regression techniques which are modified for capturing temporal dependencies in time series data. A case study using the data from 150 human participants illustrates that the proposed machine learning based forecasting methods are more suitable for high-dimensional psychological data than the traditional vector autoregressive model in terms of both magnitude of error and directional accuracy. These results not only present a successful usage of machine learning techniques in psychological studies, but also serve as a building block for multiple medical applications that could rely on an automated system to gauge individuals’ mental states.

Graphical Abstract

1. Introduction

Major mental illnesses such as schizophrenia, bipolar disorder, and chronic diseases do not just appear unexpectedly, but often gradually emit symptoms that can be externally observed in early stages [1]. Such illnesses might be prevented or managed more effectively if anomalous mental states are detected during the early stages of the disease, where special care and treatment could be provided. For example, intervention and careful observation could be provided by medical specialists to individuals who have high risk of mental health problems. Given that assessment of individuals’ mental states from their appearance or behavior is still advanced psychological science that has not yet been automated, most mental diagnosis solutions involve active participation of patients and medical experts [2, 3]. Although solutions that involve screening tests exist, such solutions would not be feasible for large populations due to financial and time constraints. Furthermore, diagnosis-based methods sometimes end up discouraging sick individuals from participating [4]. As a result, psychological disruptions often remain undetected, or under-treated.

Oftentimes, an individual’s mental state has direct impact on his/her behavioral outcomes, and vice versa. For example, a person may experience intense stress after losing a job, which may later cause him/her to consume extraordinary amounts of alcohol. Similarly, positive interactions with friends may decrease the level of one’s stress. It is our conjecture that an individual’s mental state can be inferred from his/her physical behaviors that can be objectively observed. A trivial, illustrative example would be the ability to predict whether someone is satisfied with life from his/her alcohol intake, hours of sleep, and social interactions. The ability to model the interplay between behavioral and emotional attributes could also shed light onto multiple psychological and healthcare applications. For example, a recommendation model could be built from the history of a patient who suffers from chronic stress to suggest proper actions to avoid encountering situations that may trigger emotional instability. As another example, a forecasting model could be generated to monitor an individual’s emotional state using his/her observable behavioral attributes as signals.

Existing literature has studied emotional and behavioral development at the aggregate level, where a mathematical model is developed to explain the phenomena for an entire population. While individual-level studies exist, such works rely on the data collected from specialized wearable devices that detect specific signals such as respiratory inductive plethysmograph (RIP) and electrocardiogram (ECG) [5, 6]. As a result, their methodologies are limited to users who wear such devices. In this paper, we pursue an individual-level approach, where a mathematical model is built to predict and forecast mental states for each individual using the personalized data that can be externally observed. In this research, a set of mathematical models are proposed for predicting individual mental states, using the information observable from daily activities. First, we frame the problem as a multivariate time series forecasting problem, where each individual is represented with a multivariate time series stream characterizing his/her quantifiable daily physical/behavioral statuses and activities. Each multivariate time series represents a set of attributes, each of which carries a temporal stream of (typically daily) values. An attribute is an individual measurable property of a phenomenon being monitored or collected. Attributes can be divided into two categories: observable and latent. An observable attribute quantifies the level of an observable physical activity or behavior. Examples of observable attributes include number of hours of sleep, number of drinks, and length of the recent conversation. On the contrary, a latent attribute quantifies the level of a specific dimension of an unobservable mental state, such as stress, concern, anxiety, etc. While observable attributes are relatively objective and can be easily observed by a third person (or an external monitor), latent attributes can be difficult to observe from outside without detailed evaluations from psychological experts or well established self-evaluation methods (e.g., the ones used to collect ground truth validation data in this work). Hence, the ability to infer and predict these latent attributes from the observable information could prove to be critical to multiple psychological-related applications, especially those involving the detection of mental anomalies. Multiple time series forecasting techniques are explored, including traditional vector autoregressive and machine learning models. A case study of 150 participants, whose observable and latent attributes were collected across 60 days, is used to validate and compare the efficacy of the forecasting models.

The multivariate time series forecasting problem involves the learning of historical multivariate information in order to predict the future values of an attribute of interest. Although traditional statistical based techniques for multivariate time series forecasting already exist (such as vector autoregression (VAR), its variant that allows exogenous variables (VARX), its periodic-aware variant Vector Autoregressive Integrated Moving Average (VARIMA), and State Space models), and are used in psychological studies [7, 8], these models are not always applicable due to the following reasons:

1. They are not well designed to handle high-dimensional time series data [9]. The multivariate time series data used in this paper is high-dimensional (i.e., having a large number of attributes), consisting of at least 132×l dimensions, where l is the lag and 132 is the number of attributes in our dataset. Such data could introduce too many variables that not only over-consume computational resources, but also induce false relationships among attributes that may impede the forecasting performance. Though preprocessing techniques exist that reduce the dimension (e.g., PCA) or select a subset of attributes, to project the high-dimensional data onto a lower dimensional one, such preprocessing techniques could eliminate useful information, allowing the time series models to capture the relationships from only partial data.

2. They have various assumptions regarding the characteristics of the data (e.g., stationary, linear relationship, white noise only, independency among attributes, etc. [10]). Our dataset is not always well-formed due to having missing data and being sparse, so the attributes are not guaranteed to be independent. These traditional multivariate time series techniques often do not match the characteristics of real-world data.

In the past decade, multiple machine learning algorithms have been developed and optimized. Prevalent applications of machine learning algorithms include classification, regression, and clustering. Though different machine learning algorithms have different advantages and disadvantages, some of these algorithms are known for the ability to deal with high-dimensionality, non-linear relationships, and flexibility in datasets (e.g., missing data and different data types including string and nominal) [11]. In this paper, we propose to use machine learning regression algorithms for the multivariate time series forecasting task. A comparison study of applying machine learning algorithms on psychological multivariate time series data that has high dimensionality and non-linear relationships shows that the relationship between observable and some latent attributes of an individual can be modeled. Furthermore, we find it is possible to infer or predict the values of latent attributes using only the observable information.

1.1. Problem Statement

Our goal is to generate person-specific individualized mathematical models capable of predicting particular latent attributes that represents individuals’ mental states, using only information that can be objectively observed. Such a problem is framed within the multivariate forecasting framework, in which a set of generalized algorithms is developed to generate prediction models. Let ℙ = {p₁, p₂, ..., p_K} be the entire population, where p_k represents an individual. Mathematically, an individual p_k ∈ ℙ is represented as a sequence of n attribute vectors (i.e. n data points), each of which has m attributes representing the attribute values at a specific time period. The individual p_k can be represented with a matrix notation as:

$$p_k=\left[\begin{array}{ccccc}{a}_1^{(1)}& a_2^{(1)}& a_3^{(1)}& \dots & a_m^{(1)}\\ a_1^{(2)}& a_2^{(2)}& a_3^{(2)}& \dots & a_m^{(2)}\\ a_1^{(3)}& a_2^{(3)}& a_3^{(3)}& \dots & a_m^{(3)}\\ \dots & \dots & \dots & \dots & \dots \\ a_1^{(n)}& a_2^{(n)}& a_3^{(n)}& \dots & a_m^{(n)}\end{array}\right]$$ (1)

In our setting, m is the number of attributes of a participant from whom the data was collected for n time periods. Hence, the attribute $a_i^{(j)}$ is the value of the attribute a_i collected on the j^th time period. In this paper, a time period is equivalent to one day, due to the nature of the data collected.

An attribute could be either observable or latent. An observable attribute pertains to a quantity that can be directly observed by other human or machine observers, such as number of drinks consumed in a single day, number of hours of exercise, number of friends in the recent conversation, etc. A latent attribute is a more subjective and less directly observable quantity estimated by either the individual him/herself or evaluated by psychological experts. Such attributes often represent feelings or mental states, such as an individual’s satisfaction with life, an individual’s feeling of success, an individual’s satisfaction with the weather, etc.

Each of the observable and latent attributes may be numeric or categorical. A numeric attribute is usually presented with a percentage or a natural number, while the value of a categorical attribute has to belong to a predefined class (such as education degree, day of week, ethnicity, etc).

Given an individual p_k, our task is to build an individualized forecasting model f (p_k, a_t, n, h) that learns from the individual’s data (i.e. p_k) of the past n days, and predicts the value of the target attribute $a_t^{(n+h)}$ of the next h days in advance (assuming that the current day is the n^th day). The value h is also called the horizon or forecast horizon throughout the paper. Note that, when the attribute a_t is designated as a target attribute, it is also treated as an exogenous (external) variable. That is, historical values of a_t are not included in the prediction model. The prediction at h = 0 means that it is made for today’s (current) value. Mathematically, given an individual p_k, associated n days of historical data, and a target attribute a_t, we would like to find a mathematical function f (p_k, a_t, n, h) that estimates the value of a_t in the next h days.

1.2. Main Contributions

This paper has the following main contributions:

• We present a methodology to identify a suitable individual-level prediction model to predict an individual’s mental state.

• We present a modification to traditional machine learning based regression algorithms so that they can be used for forecasting seasonal multivariate time series data. Specifically, the time-delay embedding algorithm is applied to the feature space as a preprocessing step to allow traditional machine learning algorithms to process the data in a temporally dependent manner.

• We find the best multivariate time series model that captures the temporal dependencies in the data by comparing the performance between multiple machine learning algorithms from different families and the traditional VARX model (baseline) that has been previously used to analyze attributes in psychological literature.

• We demonstrate with empirical evidence that latent attributes can be predicted using only information from the observable attributes.

The remainder of this paper is organized as follows: Section 2 discusses some background of the related literature. Section 3 describes the proposed machine learning based time series forecasting techniques used in this paper, along with the methods used to investigate the possibility of forecasting the latent attributes. Section 4 discusses the case study, the ground truth validation dataset, results, and related discussion. Section 5 discusses limitations and lists some of the potential applications that could build upon our work. Section 6 concludes the paper.

2. Background and Related Works

Although the computational psychology literature includes studies of the development of and relationship between multiple mental and physical attributes, most works have examined the phenomenon of interest at the aggregate level as opposed to at an individual level. Furthermore, these works tend to investigate relations (especially correlations) among a few focus attributes. On the contrary, the input to our proposed system comprises a large number of attributes that may or may not have direct impact on each other. The ability to generate a person-specific model would enable fine-grained prediction of individual mental states, which could potentially give rise to multiple personalized emotion based applications such as monitoring and recommendation systems. We aim to generate a person-specific model for each individual using his/her historical objectively observable information. In this section, relevant literature is discussed.

2.1. Predicting and Monitoring Behavioral and Emotional Attributes

The increasing health concern behooves the ability to monitor and predict certain health attributes so that appropriate actions or treatment can be provided in a proactive manner. Though diagnosis based methods exist that involve health practitioners evaluating potential patients, efforts have been made in the literature to supplement such human-based methods with automated ones to reduce costs and increase accuracy and consistency. In this work, our goal is to predict latent emotional attributes from various observable signals. Hence, we discuss some of the relevant research with similar applications.

Choudhury et al. proposed a method to detect depression in Twitter [12]. A number of features are extracted from a Twitter message including engagement, ego-network, emotion, linguistic style, and user engagement. A Support Vector Machine classifier is trained with these attributes to detect the level of depression in each Twitter message. Their methodology applies beyond microblogging data, but does not consider temporal change in the latent state. Hence their method only estimates the current depression level, but is not capable of predicting future states.

Litman and Forbes-Riley showed that acoustic-prosodic and lexical features can be used to automatically predict students’ emotions in computer-human tutoring dialogues [13]. They examined emotion prediction using a classification scheme developed for prior human-human tutoring studies (negative/-positive/neutral), as well as using two simpler schemes proposed by other dialogue researchers (negative/non-negative, emotional/non-emotional). Their methods were developed to handle transcribed (textual) data which is different from ours (time series). Furthermore, their method only indicates three polarities of emotions (i.e. negative, positive, and neutral), while our methods aim to quantify the level of a dimension of a mental state (i.e. level of stress, anger, happiness, etc.).

Korhonen et al. presented TERVA, a system for long-term monitoring of wellness designed for home usage [14, 15]. The system runs on a laptop and is able to monitor physiological attributes such as beat-to-beat heart rate, motor activity, blood pressure, weight, body temperature, respiration, ballistocardiography, movements, and sleep stages. In addition, self-assessments of daily well-being and activities are stored by keeping a behavioral diary. The accuracy of the system was reported to be 70–91%. This work had success in monitoring some observable attributes without the supervision of human experts. Though their methodology does not involve forecasting of mental states, but only monitoring physical attributes, in our future work, we could extend their system to build a monitoring system that collects the daily routines and observable behavior. This collected observable information can then be used to build a prediction model for target latent attributes. Wang et al. used passively perceived signals from smartphones such as accelerometer, microphone, light sensor, GPS/Bluetooth, along with self-evaluation questionnaire to assess mental health, academic performance, and behavioral trends of college students as part of the StudentLife project [16]. They later used the same smartphone sensing data to assess students’ GPA [17] and hunger levels [18]. In order to assess mental health (such as stress levels), their methods still rely on self-report information which is not passively obtained. Studies by Santosh Kumar’s research group have also investigated the possibility to use sensed data such as ECG, respiration, skin conductance, accelerometry, temperature, alcohol, etc., captured via wearable devices to assess craving, stress, and mood [19, 5, 20]. While their works involve prediction of some mental attributes, their methods are currently applicable to users who wear these specific devices, while our works aim to use external, passive information that can be observed without user engagement. Saeb et al. used logistic regression to model depression using the sensing data from smartphones including location, movement, and duration of home stay [21]. Our work differs from theirs in three aspects: 1.) our input data is routine behaviors that are externally observable, while their input data are spatial and temporal sensor-based data, 2.) our work aims to predict the mental state of an individual which includes many dimensions of emotion, while their work only targets the prediction of depression levels, 3.) their methodology created a single classifier that learns from the information of all the test subjects, while ours generates a personalized mental state predictor for each individual. However, since their work has illustrated a successful applicability of using passive sensor-based information for predicting a mental attribute, we could explore the possibility of incorporating such data into our models in the future investigation.

2.2. Techniques for Multivariate Time Series Prediction and Their Applications in Healthcare Domains

Many prediction problems have been translated into a time series forecasting problem so that the temporal dimension could be incorporated into the prediction model. In this paper, the individual mental state prediction problem is framed as a multivariate time series forecasting problem to also allow multiple attributes to be modeled together; hence, in this section, previous-works in healthcare and biomedical informatics that utilized time series forecasting techniques are discussed.

2.2.1. Vector Autoregression Based Techniques for Modeling Mental States

Vector Autoregression (VAR) [22] models, including regression analyses, have been successfully used to capture linear interdependencies among multiple univariate time series, and have been shown effective in forecasting tasks in financial [23, 24], meteorology [25, 26], biomedical [27, 28] domains, etc.

A VAR model describes the evolution of a set of m attributes over the same sample period (t = 1, ..., T) as a linear function of only their past values. The attributes are collected in a m×1 vector y^(t), whose i^th element, $y_i^{(t)}$, represents the time t observation of the i^th attribute. For example, if the i^th attribute is Number of Drinks, then $y_i^{(t)}$ is the number of drinks that the individual had on day t.

A l-th order VAR, denoted VAR(l), can be written as:

$$y^{(t)}=c+A_1{y}^{(t-1)}+A_2{y}^{(t-2)}+\dots +A_l{y}^{(t-l)}+e^{(t)}$$ (2)

Where c is a vector of constants (or intercepts), and A_i is a time-invariant coefficient matrix. During the initialization process, these parameters can be set at random starting values, after which they will be iteratively adjusted to minimize the error during the learning process [29]. Informally, VAR(l) predicts the value of y^(t) by modeling linear relationship among the attributes observed in the past l days, where l is the lag.

Latif et al. employed multivariate auto-regression to model a two-channel set of electromyography (EMG) signals from the biceps and triceps muscles [30]. The coefficients of the model are used to define the direct transfer function (DTF), which later is used as frequency domain features to train a Support Vector Machine classifier to classify an EMG into either extension or flexion classes.

Goode et al. used the correlation and regression analyses to generate the “Stress Process” model that predicts longitudinal changes in Alzheimer’s family caregivers [31]. Their model considers three psychological attributes as input, namely appraisals, coping responses, and social support. Their model was tested on 122 dementia caregivers which revealed that benign appraisals of stressors, the use of approach coping, and higher levels of social support were associated with more positive health outcome over time.

Ciarrochi et al. used regression analysis to find the relationship between stress and three mental variables, namely depression, hopelessness, and suicidal ideation in people with high emotional intelligence (EI) [32]. The findings revealed that people with high emotional perception tend to have higher levels of depression, hopelessness, and suicidal ideation than others when experiencing the similar sets of situations that induce stress.

All the previous works discussed in this section assume that the relationships among the attributes in the data are linear, while such an assumption is relaxed in the current work. Furthermore, the data studied in previous works involve a small number of dimensions (less than 10), while the time series models in the current work are developed to handle high-dimensional data.

2.2.2. Machine Learning Based Techniques for Modeling Mental States

Computational psychology has recently become more advanced and complex, requiring observational and experimental data from multiple participants, times, and thematic scales to verify hypotheses. This data grows not only in magnitude, but also in its dimension. While vector autoregressive models (and its variants VARX, VARIMA, VARIMAX models) have been widely used for modeling multivariate time series data, such models face the following drawbacks that prevent them from being generalized to high-dimensional, more complex data.

• They cannot model non-linear relationships among attributes. Linear models are not well adapted to many real-world applications [33]. As studies have revealed that human brains can no longer be modeled with a linear model [34], these vector autoregressive models may not be suitable for investigation of psychological phenomena. Although multiple computational psychology works have shown successful usage of VAR based models to capture linear relationships among attributes [35, 36, 37], these works may have failed to include necessary attributes that exhibit non-linear relationships.

• They have certain requirements of the data that must be met. Darlinton mentioned that certain requirements (such as completeness, stationary, and independency) in the dataset must be met so that VAR based models can be built [9]. Given that psychological experimental data are often noisy, nonstationary, and not always independent, these requirements are rarely satisfied. Despite the inappropriate uses of VAR based models in computational psychology works, multiple studies in various fields also discourage the use of these VAR based models in multivariate time series forecasting tasks [38, 39].

• They are not suitable for high-dimensional time series data. A VAR model of n attributes with the lag of l needs to keep track of at least (2+l)n+ln² variables. This number of variables can be handled in the case of small problems which involve only a few attributes (i.e. n is small, typically fewer than 10). However, VAR models can become very inefficient when dealing with high-dimensional data such as ours. In the future, the system proposed in this paper would have to handle many data points from multiple participants. In the era of big data, where the Internet of Things (IoTs) technology enables massive and heterogeneous data to be collected and available for processing in real time, VAR based models may not scale well in these real-time, data intensive applications.

Machine learning techniques have been widely investigated and developed in the past decade. A wide range of applications that emerge from such techniques make machine learning algorithms suitable and applicable for many problems that aim to discover knowledge from data such as clustering, classification, and regression. Recently, Bontempi proposed extensions to machine learning algorithms to add the capability to model time series dependencies [40]. However, their methods only handle univariate time series data. Hegger et al. proposed the time-delay embedding technique which modifies the traditional feature space of machine learning algorithms so that history of data can be taken into account, allowing the learners to capture temporal dependency in multivariate time series data [41]. This time-delay embedding technique was first implemented in the TISEAN¹ package for nonlinear time series analysis; however, such a package only processes univariate time series data. In this work, an extension is made to one of their methods to handle time series data with more than one dimension. Specifically, for a given lag of l time periods, an instance is represented with the most l + 1 recent sets of attribute values. Hence, the size of the feature space would become m × (l + 1). This time-delay embedding modification to expand the feature space to include historical data would allow the regressor to generate a regression model that also takes previous information into account, allowing temporal dependencies among multiple attributes to be modeled altogether.

3. Methodology

In this paper, we propose to apply the time-delay embedding technique [41] which modifies the traditional feature space of machine learning algorithms so that history of data can be taken into account, allowing the learners to capture temporal dependency in multivariate time series data. This chronology-capable feature space allows amachine learning based regressor to learn the temporal relationship among observable attributes and the target attribute, while optimizing the prediction performance in a resource-efficient manner.

This section starts by describing our implementation framework, including data preprocessing, feature engineering (time-delay embedding), training and forecasting steps. The efficacy of the system is tested against the well-known baseline VARX model. While a VAR model treats all the attributes as endogenous (i.e., the status of each attribute is relative to the specification of a particular model and causal relations among the independent attribute), a VARX model treats the target attribute as an exogenous variable (i.e., the value of the target attribute is wholly causally independent from other variables in the system) [42]. We treat the target attributes as exogenous because, in our study, they are mental attributes, whose values are difficult to quantify. Hence, the prediction models should not rely on the availability of the past values of such latent mental attributes.

Then, we investigate the possibility of inferring the latent characteristics of an individual person using only his/her observable information. The best configuration of the proposed time series forecasting methods are trained with three types of information: observable information only (O), latent information only (U), and both (OU). Then the performance is compared to make an empirical conclusion on the ability to predict mental states from only the observable information.

Figure 1 outlines the methodology presented in this paper. First, ground-truth data is acquired from participants. Since the raw data is not well-formed, a data preprocessing layer is applied to ensure that the data is in the proper multivariate time series format. The preprocessed data is then converted (i.e. featurized) into the format that machine learning algorithms can process. In this step, data points are generated, each of which represents one day of participant’s data. Then, the time-delay embedding technique is applied to allow an instance of the training data to take temporal dependency into account. Once the data is featurized, a number of advanced machine learning based regression models are tested for their compatibility and ability to model the data (Objective 1). Then, the best forecaster from Objective 1 is chosen to test the ability of the model to predict the latent attributes using only observable attributes. The ability to generate such a prediction model would then make it possible to implement a mental health monitoring system that only passively observes patients’ daily activities without interfering with their routines.

Figure 1.

The high-level diagram of the methodology.

3.1. Data Acquisition

Ground truth validation data for this investigation is collected from human participants via a series of questionnaires conveniently accessible on smartphone devices. The data is collected in bursts, where each burst is a data collection period. Two consecutive bursts are separated by a break period. The questionnaires aim to quantify and monitor each participant’s physical states, and establish the ground-truth validation data for this study. In particular, the values of each individual’s latent attributes were estimated using standard psychological self-report questionnaire items (see references in Table 1). Example questions are listed below:

Table 1.

Sets of questionnaires, each aiming to quantify particular observable and latent characteristics of the participant, along with their references (if any).

Group	ID	Name	# Raw Attr.	# Com Attr.	Description	Ref(s)
Once	DemoA	Demographics Visit 0	8	2	Background information such as gender, ethic, employment status, marital status, income status, and zip code.
	DemoB	Demographics Visit 2–4	2	0	Information pertaining to dentures and menopause regularity
	DemoC	Demographics Visit 4	21	1	Information about educational background, housing composition (especially children and their ages), medication (gastrointestinal and cardiovascular), height, and weight.	[43, 44]
Burst	CESD	Center for Epidemiologic Studies Depression Scale	20	1	20 questions used to measure the overall level of depression.	[45]
	BFI	Big Five Inventory	10	5	10 questions for self-measuring personality (Neuroticism, Extraversion, Openness, Agreeableness, and Conscientiousness)	[46]
	CONTROL	Control	9	1	Assessing sense of self-control and control over surrounding environments (relationship, finances, health, work, leisure, life).	[47]
	CVI	Cardiovascular Health	8	2	Assessment of cardiovascular symptoms	[48]
	GII	Gastrointestinal Health	12	2	Assessment of functional gastrointestinal disorders	[48]
	META	Metacognition Questionnaire	15	1	15 questions for self assessment of cognitive and neuropsychological impairment (distraction, focus, forgetfulness, etc.)	[49, 50]
	LES	Life Experiences	12	1	Assess of impacts of life changing events (i.e. relationship statuses, death of loved ones, illness, injuries, work status, finances, family members’ well-being, pregnancy, incarceration, increase in level of arguments, eating/sleeping habits, living condition, stressful events.)	[51, 52]
	SATIS	Overall Satisfaction with Life	6	1	Satisfaction with relationship, finances, health, work, leisure, and life.	[53, 54]
	SF36	Short Form 36-item Health Survey Questionnaire	36	8	36 questions to self-assess mental and physical health	[55, 56, 57]
Daily	LETQ	Leisure Time Questionnaire	3	1	Assessing level of today’s exercise (vigorous, moderate, mild)	[58]
	SLEEP	Sleep	3	0	Assessing last night’s sleep quality.	[59]
	WEATHER	Weather Enjoyment	1	0	Assessing weather enjoyment
	SE_d	Self Esteem	1	0	Level of self-esteem	[60]
	CONTROL_d	Perceived Control	1	0	Measuring the level of overall control over things.	[61]
	SAT_d	Satisfaction with Life and Health overall	2	0	Assessing levels of satisfaction with life and health.	[53]
	SHAME	State Shame and Guilt Scale	2	0	Assessing shame and guilt	[62]
	STRESS	Perceived Stress Scale	11	2	Justifying overall level of stress originated from environment such as interpersonal tensions, work/school, home, finances, health/accident, other people’s events, being evaluated, etc.	[63, 64]
	FEELINGS	Feeling States	27	6	27 Dimensions of feelings, i.e. Enthusiastic, Calm, Nervous, Sluggish, Happy, Peaceful, Embarrassed, Sad, Alert, Satisfied, Upset, Bored, Proud, Relaxed, Depressed, Excited, Content, Fatigued, Tense, Disappointed, Ashamed, Relieved, Angry, Grateful, Conceited, Snobbish, and Successful	[65, 66, 67, 68]
	PRIDE	State Pride Facets Scale	1	0	Today I felt successful	[69]
	TU	Time Use	3	4	How much time did you spend on work/school, leisure, and other obligation.	[70, 71]
	HB	Health Behaviors	9	2	Surveying health-related behaviors such as smoking, alcohol consumption, caffeine intakes, brushing, flossing, meals, and snacks.	[72]
	EMOTION	State Emotions	7	0	Physical pain, attitude towards physical and emotional health, and expectation for tomorrow.
Event contingent	Context variables	Event-contingent	15	0	Information about each interaction encountered, such as length, place, purpose, and interactants’ information (age, gender, relationship, acquaintanceship).
	Interpersonal Grid	Event-contingent	4	0	Assessing interpersonal perceptions such as friendliness and dominance of self and others in a conversation.	[73]
	Affect Grid	Arbitrary	2	0	Assessing how you act (pleasant or unpleasant) and how you feel (sleepy or aroused).	[65]
	Emotion Regulation	Event-contingent	2	0	Assessing the abilities to suppress and reappraise emotions during the conversation.	[74]
	Interaction Reflections	Event-contingent	7	2	Assessing empathy (understanding others’ feelings) and the ability to measure cost/benefit from the conversation.
	State Emotions	Event-contingent	5	0	Assessing current emotions, i.e. anger, sadness, pride, shame, and happiness.

• How many of the following [beer/glasses of wine/shots of liquor] did you consume today?

• How many hours of sleep did you get last night?

• I am satisfied with my life today. (agreement rated)

• Did you enjoy the weather today?

Note that, while it is true that self-reported data can have biases that result in inaccuracy in the ground-truth data, in this work, an assumption is made that all participants answer the questions accurately and honestly.

The questionnaires are chosen to quantify observable and latent attributes that have been shown in previous psychological literature to be effective and representative measures of mental and physical conditions of human participants. A response to a questionnaire may result in one or more values of attributes being collected. For example, the response to the question How many hours of sleep did you get last night? will result in a numeric value associated with the attribute S LPHRS d, which represents the number of hours of last night’s sleep. Note that attributes with the suffix d are daily attributes. Different questionnaires may be collected at different temporal intervals. For example, How old are you? may be asked once at the beginning of the data collection campaign, Did you exercise today? may be asked once per day, and How long did the conversation last? may be asked every time the participant finishes a social interaction. Listed below are the different temporal cadences at which specific questionnaires are issued:

• Once: The corresponding questionnaires are asked only once at the beginning of the data collection campaign. Most of these inquiries pertain to background information such as gender, age, number of kids, employment status, etc.

• Pre-burst: The pre-burst questionnaires are distributed to each participant at the beginning of each burst of data collection. These questions aim to gauge the general state, personality profile, and physical health of each participant before each data collection period.

• Post-burst: The post-burst questionnaires are the same as the pre-burst ones, and are used to measure changes in personality and physical health of each participant during a data collection period.

• Daily: A participant is asked to respond to these daily questionnaires once per day (evening). Most questions are designed to collect daily routines, and gauge daily mental and physical health.

• Event-contingent: A participant is asked to respond to these event-based questionnaires after each social interaction (conversations lasting longer than 5 minutes). These questions are designed to keep track of certain properties of interaction events (e.g., number of friends, how long, what time, purposes of the interaction, etc.). The intent of these social related questionnaires is to investigate how social interactions contribute to mental and physical well-being.

Table 1 lists all the sets of questionnaires, each of which is intended to quantify certain characteristics of a participant. Interested readers are encouraged to consult [75] for further detail regarding this survey. These sets of questionnaires can be categorized by their frequencies of response, namely once (background information), burst (pre/post burst visits), daily (daily information), and event-contingent (interaction/conversation information). Each set of questionnaires aims to quantify certain aspects of the participant. Each aspect is represented by a set of attributes. Response to each question will result in a value of a raw attribute. A composite attribute is calculated by combining certain relevant raw attributes. An example of a composite attribute includes the overall level of stress, which sums up the individual levels of stress from interpersonal tensions, work/school, home, finances, health/accident, other people’s (e.g., children’s) events, and stress that is a result of being evaluated. Most of these questionnaires have been approved and used extensively for self-quantification of mental and physical characteristics (see references in Table 1).

3.2. Data Preprocessing

Concretely, the data collected from a participant must be converted into the matrix format of multivariate time series data as illustrated in Equation 1 before further processing. From here on, it is assumed that a time unit is one day, so that the i^th row of data represents the snapshot of data corresponding to the i^th day. This data format would make sure that both traditional and newly-developed forecasting techniques can compatibly use the same data source, mitigating the bias (from data preparation) when comparing these algorithms. The subsequent subsections will describe how the raw data is preprocessed in this paper.

3.2.1. Heterogeneous Data Types and Ranges

Different kinds of questions and response options were provided to the participants. An answer to a question can be binary (e.g., true/false), multiple choices, nominal values (e.g., day of week), non negative integer (e.g., number of friends), and ranged value (e.g., percentage). While most forecasting techniques only understand numeric attributes, each of these data types must first be converted to appropriate numeric values.

If the value is already numeric (either bounded, or unbounded), then it remains the same. The unbounded number will not be an issue, since a normalization will be applied to the data before feeding it to the regression model. Hence, the values corresponding to each attribute would eventually be ranged to [0,1].

A value of each binary attribute (true or false) is replaced by either 0 or 1, based on the polarity. For example, true would be 1, and false would be 0.

A multiple choice or nominal attribute is first converted to a sequence of binary attributes, where the above solution for binary attributes can be applied. For example, a value of attribute A could be one of the days of week. A is first split into 7 sub-attributes: A.sun, A.mon, A.tue, A.wed, A.thu, A. f ri, and A.sat, each of which is a binary attribute. Hence, if the original value is Monday, then the sub-attribute A.mon would be 1, while the other sub-attributes become 0.

3.2.2. Heterogeneous Data Frequencies

As mentioned in Section 3.1, different attributes are collected at different temporal cadences (i.e. once, pre-burst, post-burst, daily, and event-contingent). While the values of each attribute must be available every day (since it is assumed that a time unit = one day), all attributes must be converted to daily attributes.

Since some attributes may be collected less or more than once a day, these attributes must be normalized so that their values are available on a daily basis. For attributes whose values are collected less than daily (i.e. once, pre-burst, and post-burst), their values are replicated on subsequent days, where applicable. For example, the pre-burst data is replicated on each day of the following data collection period, and the post-burst data is replicated on each day of the next data collection burst. For attributes whose values are collected more than once a day, their values corresponding to the same day are aggregated (by summation if numeric, and median or mode if nominal). These aggregated values are then used to represent daily values of the corresponding non-daily attributes.

3.2.3. Missing Values

Participants are not forced to answer the questions. Hence, it is inevitable that some or all questions on particular days may be left unanswered, resulting in missing values. As some forecasting techniques cannot handle missing values, they must be dealt with before further processing.

While multiple schemes have been used to deal with missing attribute values including using the default values (i.e., 0) and completely discarding the instances containing missing values [76], a number of works in computational psychology have used interpolation to deal with missing values [77, 78]. Hence, in this work, the missing values are cubic spline interpolated using the data available from the same participant. We use Apache Commons Math² implementation which implements the cubic spline interpolation algorithm described in [79]. If there is not enough data to interpolate the missing values, then they are set to default values. Note that a nominal attribute is converted to a series of numeric attributes before this step; hence, their missing values can be interpolated.

3.2.4. Discontinuous Data

The data corresponding to a participant is divided into three bursts, resulting in three discontinuous chunks of multivariate time series data. Since the forecasting models considered in this paper do not have ensemble capability (where multiple learners, each of which may learn each chunk of data, then make an ensemble prediction), these chunks of data need to be appropriately concatenated to produce a smooth single multivariate time series for each participant.

The sequence of days of week is preserved to allow the prediction models to take weekly activities into account. For example, some learners are able to predict that the set of situations that happen on a Friday would likely happen again on the next Friday. For each participant, the bursts of data are concatenated while preserving the sequence of the days of week. For example, if the first burst of data collection ends on Friday, while the beginning day of the second burst is Wednesday, then the last three days of the data of the first burst (i.e., Wednesday, Thursday, and Friday) are discarded. Note that, we choose to discard such data, rather than interpolate the gap, to minimize the use of synthetic data.

3.3. Feature Space Modification

The proposed machine learning based multivariate time series forecasting methodology in this work relies on the use of base machine learning regressors to train on the history of multi-variate time series data. However, traditional machine learners treat an instance (daily data) independently, which makes sense since most types of data points in traditional machine learning literature are assumed to be independent (e.g., images, documents, emails, etc.). However, in this work, each data point represents a snapshot of attribute values of a participant collected on each day, which can be dependent on the values of prior days, in terms of both seasonality and activity decay/growth. An example of seasonality would be that a participant may habitually drink heavily on Fridays, moderately on weekends, and not at all on the other week days. Hence, if such a participant happens to drink heavily on a work day, then the learner should be skeptical about possible mental anomalies. An example of activity decay would be the level of fever which can reduce in its magnitude in subsequent days. An example of activity growth would be the accumulative stress from final exams, which tends to gradually increase as the final exam week draws near.

In order to take the seasonality and activity decay/growth into account, an instance of data must incorporate the temporal relationship between the data point at a given day and the data points of the previous days. The number of previous days that a data point is relating to is referred to as lag. Equivalently, the i^th data point with lag l is the data point representing the set of attributes whose values are collected at the i^th day, along with the previous l days. A data point with lag 0 only represents current (today’s) values of attributes.

Here, the time-delay embedding algorithm is applied to the feature space by expanding the slots for previous data associated with the participant p_k. Mathematically, let the instance p_k(i) represents the data snapshot of the i^th day:

$$p_k(i)=\left[\begin{array}{ccccc}{a}_1^{(i)}& a_2^{(i)}& a_3^{(i)}& \dots & a_m^{(i)}\end{array}\right]$$ (3)

Then the time-delay embedded version of such an instance with lag = l, p_k(i, l), is defined as:

$$\begin{array}{llllll}{p}_k(i,l)=[\hfill & a_1^{(i)}\hfill & a_2^{(i)}\hfill & a_3^{(i)}\hfill & \dots \hfill & a_m^{(i)}\hfill \\ \hfill & a_1^{(i-1)}\hfill & a_2^{(i-1)}\hfill & a_3^{(i-1)}\hfill & \dots \hfill & a_m^{(i-1)}\hfill \\ \hfill & a_1^{(i-2)}\hfill & a_2^{(i-2)}\hfill & a_3^{(i-2)}\hfill & \dots \hfill & a_m^{(i-2)}\hfill \\ \hfill & \dots \hfill & \dots \hfill & \dots \hfill & \dots \hfill & \hfill \dots \hfill \\ \hfill & a_1^{(i-l)}\hfill & a_2^{(i-l)}\hfill & a_3^{(i-l)}\hfill & \dots \hfill & a_m^{(i-l)}]\hfill \end{array}$$ (4)

For each attribute $a_j^{(i)}$, the feature space also includes its previous l values.

For example, Table 2 illustrates an example of a participant’s partial daily data during a period of seven days. Each data point has four attributes (m = 4). The snapshot that represents the 5^th day of the data is then mathematically expressed as:

$$p_k(5)=\left[\begin{array}{llll}6\hfill & 2\hfill & 5\hfill & 3\hfill \end{array}\right]$$

Table 2.

Example of a participant’s partial data, collected during a 7-day period. SLPHRS d denotes the number of hours of last night’s sleep. MILEX d denotes the number of today’s mild exercises. EATS d denotes how many times the participant eats snacks today. DrinkTOT d denotes the total number of drinks the participant consumes today.

Day	SLPHRS_d	MILEX_d	EATS_d	DrinkTOT_d
1	7	5	3	1
2	7	8	5	1
3	8	2	4	4
4	8	0	4	3
5	6	2	5	3
6	6	4	4	2
7	6	3	5	1

After applying the time-delay embedding algorithm with the lag of three days (l = 3), the above data point would incorporate the values of the previous three days, thus becoming:

$$\begin{array}{lllll}{p}_k(5,3)=[\hfill & 6\hfill & 2\hfill & 5\hfill & 3\hfill \\ \hfill & 8\hfill & 0\hfill & 4\hfill & 3\hfill \\ \hfill & 8\hfill & 2\hfill & 4\hfill & 4\hfill \\ \hfill & 7\hfill & 8\hfill & 5\hfill & 1]\hfill \end{array}$$

Where p_k(5, 3) is a vector that represents the participant’s 5^th day of data along with his/her previous three days’ data. Once the feature space is modified according to the rules above, a regressor can then learn and predict using the conventional machine learning regression methodology.

3.4. Objective 1: Model Selection

In this work, we present amachine learning based forecasting methodology for multivariate time series data. We claim that such methodology is built upon machine learning algorithms, some of which are known to handle high dimensionality and non-linear relationships quite effectively [11]. In this paper, such claims are tested by comparing the forecasting efficacy of our proposed methods with the traditional VARX model.

Many time series forecasting techniques have been proposed for a wide range of forecasting problems. In this paper, 10 time series forecasting models are considered, including a variant of traditional vector autoregression (VARX) and multiple machine learning based regression techniques from different families such as function based, tree based, and lazy learning based methods. These models are listed in Table 3, along with their references. Note that, though Random Forest (RF) was originally designed for classification problems, here, the range of the class variable is discretized so that such an algorithm can be adopted for regression problems [93].

Table 3.

List of forecasting models considered, along with their references.

Acronym	Model Name	Algorithm Type
VARX	Vector Autoregression [22]	Regression
SVMR	Support Vector Machines for Regression [80, 81]	Machine Learning: Function Based
SLR	Simple Linear Regression [82]	Machine Learning: Regression
Based	RF Regression by Discretization using Random Forest [83, 84]	Machine Learning: Tree
Based	RBFN Radial Basis Function Networks for Regression [85]	Machine Learning: Function
Based	MPR Multi-layer Perceptron for Regression [86]	Machine Learning: Function
Based	M5P M5 Model Tree with Continuous Class Learner [87, 88]	Machine Learning: Tree
Based	LWL Locally Weighted Learning [89, 90]	Machine Learning: Lazy Learning Based
LR	Linear Regression [82]	Machine Learning: Function Based
IBK	K-nearest Neighbors [91]	Machine Learning: Lazy Learning Based
GPR	Gaussian Processes for Regression [92]	Machine Learning: Function Based

The objective is carried out in two stages: partial and comprehensive. In the partial stage, all forecasting models listed in Table 3 are trained with partial, dimension reduced data, and tested against each other. Participants with incomplete (missing) information are disregarded, and the remaining data is projected onto a lower dimension space (i.e. 10 dimensions) using the Principal Component Analysis algorithm [94]. Note that preprocessing the data with dimensional reduction techniques could eliminate necessary information that could have been captured by the time series models; however, in this stage, the dimension of the data is reduced to allow fair comparison between the VARX model and the machine learning based models. In particular, this dimension reduction is carried out because the VARX technique cannot handle data with large dimension³. Only complete data is chosen to ensure that the models are not tested on their ability to handle missing values. The goal of the partial stage is to identify the best forecasting models, in terms of prediction accuracy, applicable with the dataset used in this paper.

The comprehensive stage selects top forecasting models from the partial stage, then runs them on full data, with missing values and complete dimensionality. The goal of this stage is to find the best model for each target attribute, and for analysis of the results in the Objective 2.

3.5. Objective 2: Predicting Latent Attributes

This paper investigates the potential to generate a personalized forecaster that predicts the latent attributes (i.e., feelings and mental statuses that constitute a mental state) for each individual with only observable information. These latent attributes are difficult to quantify merely via external observation; hence, the ability to infer and forecast them could prove to be valuable in multiple computational psychology-related applications. The best forecaster from the Objective 1 is selected for the analysis in this objective. We prepare three types of training data: observable only (O), latent only (U), and both (OU). The forecaster is trained with each of these source types, then the forecasting performance of the select latent attributes is compared. We first investigate the impact of different data sources on the forecasting performance. Then, the lag parameter is varied to study what would be the appropriate amount of the history of data that the learner should keep track of.

4. Case Study

For each participant p_k, and each target attribute a_t, a forecasting model is trained with the history of data of p_k for the lag l days to predict the value of a_t on the next h days in the future. The history of a_t is treated as an external variable. That is, it is not included in the training data and its historical data is not used. Target attributes are made external variables because it is an assumption in this work that these attributes are not easily quantified through simple external observation. Hence, the ability to estimate these latent attributes accurately would be more valuable than simply predicting other observable attributes.

4.1. Ground Truth Validation Data

The ground-truth validation data was drawn from the Intra-individual Study of Affect, Health, and Interpersonal Behavior [75]. The data collection campaign was conducted with 150 participants from the Pennsylvania State University community, ages range from 18 – 90 years (mean = 47.10, standard deviation = 18.76). 51% of the participants are women, and 49% are men. 91% are Caucasian, 4% African American, 1% Asian American, 2%Other, 2%mixed (Asian, Hispanic/Latino, or American Indian + Caucasian), with 93% self-reporting as heterosexual, 6% Bisexual/Gay/Lesbian, and 1% declining to answer. Participants had, on average, 1.5 children (standard deviation 1.41, min 0, max 6).

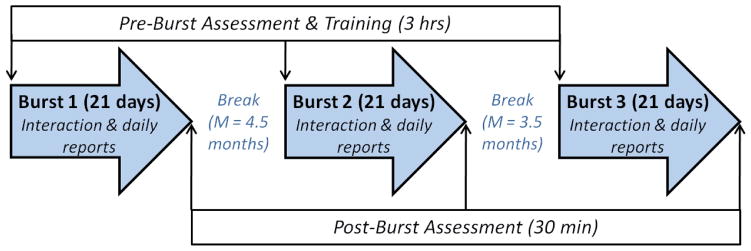
The data was collected in three bursts, each of which lasted for 21 days. On average, there was a 4.5 month break between the first and second bursts, and 3.5 month break between the second and third bursts. Each participant was required to participate in a pre-burst assessment and training session that provided an overview of the project and instructions to use the mobile app to respond to the questionnaires. Furthermore, each participant was also required to participate in a post-burst assessment session where they completed another set of questionnaires. Figure 2 illustrates the three bursts of data collection process. Table 4 breaks down the numbers of attributes from the dataset collected at different temporal cadences, classified by their observability. For further details about the data acquisition procedure, please refer to the iSAHIB project [75].

Figure 2.

Illustration of the three bursts during which the data was collected.

Table 4.

Data associated with different attributes are collected at different frequencies.

Attribute Type	Frequency
	Once	Pre-burst	Post-burst	Daily	Arbitrary
Observable	43	50	50	55	50
Latent	0	102	102	60	24

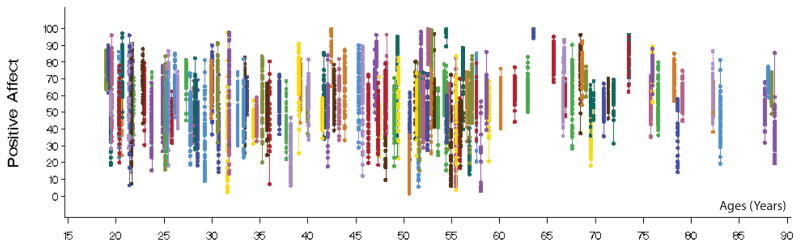
As an example of the collected attributes, Figure 3 plots the ranges of the Positive Affect (PosAffect_d) attribute against ages of all the 150 participants (without temporal relations). Each line/color is corresponding to a participant. There are roughly 60 dots in each line, each of which represents the positive affect level measured in a day. Each attribute leads to a new dimension in the time series data for each participant. From Figure 3, the majority of the participants have the ages around 45–60. Each participant also has a wide fluctuation of the positive affect levels during the data collection, urging a natural curiosity to investigate further into the temporal relationship across different attributes to explain such phenomena.

Figure 3.

Distribution of the Positive Affect (PosAffect_d) attribute of the 150 participants. The Y axis marks the level (0 to 100), and the X axis represents ages in years of the participants. Each line/color is corresponding to a participant. Each dot represents a daily positive effect level.

4.2. Selected Target Attributes

Table 5 lists the six target attributes used as test cases in this research. These attributes are all latent attributes that are commonly used in psychological studies (see references in Table 1). These 6 attributes are chosen as representative target attributes, that represent different aspects of a participant’s mental state. Note that if a composite attribute is chosen as the target attribute, then all the sub (raw) attributes used to produce it are not taken into the feature space to avoid the causality and dependency biases.

Table 5.

List of select target attributes along with their references. Refer to Table 1 for the comprehensive description of each attribute.

Name	Description
CONTROL_d	Perceived Control. (Did you have control over the things that happened to you today?) [61]
NegAffect_d	Net affect of negative emotional attributes such as nervousness, disappointment, boredom, etc. [65, 66, 67, 68]
PHYHEALTH_d	Perception of physical health. PosAffect d Net affect of positive emotional attributes such as pride, calm, happiness, etc. [65, 66, 67, 68]
SATHEALTH_d	Satisfaction with health. [53, 54]
SATLIFE_d	Satisfaction with life. [53, 54]

4.3. Implementation

Listed below are the major implementations by the authors of this paper during this paper (using Java as the main programming language):

1. Data import, cleaning, pre-processing, and conversion to the compatible multivariate time series data structure.

2. The time-delay embedding algorithm that flattens multivariate time series data onto a delay dependent feature space, with control parameter lag (l).

3. A wrapper that enables each base learner to incrementally learn new instances without having to retrain the whole model from scratch. This is useful when conducting the leave-one-out sliding evaluation protocol in which the current validation data is fed back to the forecaster’s training data to make the next prediction, until no ground truth data is available.

4. Experimental framework, including batch commands, result logging, and computation of evaluation statistics.

The experiments in this paper use the Matlab implementation of the VARX model⁴, and Weka’s implementation of all other base machine learning classification and regression algorithms⁵. Note that, though Weka⁶, a software package that implements a collection of machine learning algorithms, also offers a forecasting package, such a package would not facilitate our study for the following reasons:

1. If the user wants to model the dependency among multiple attributes, these attributes must be set as target attributes. The tool would then generate a multivariate model for each target attribute. In our setting that involves modeling hundreds of attributes, it would be computationally expensive to generate a model for each of them.

2. The tool does not offer leave-one-out sliding evaluation protocol. Though the user could set apart a certain portion of the training data for testing, the tool does not feed some of already-tested data to the training data. In our evaluations, we would like to feed the already-tested data back to the training data to predict further not-yet-tested values to see whether the error could be reduced by having more training data.

For these reasons, it was more efficient to implement our own multivariate time series framework for flexibility and future development purposes. The source code will be made available to others for research purposes (upon request).

4.4. Forecasting Evaluation Protocol

Leave-one-out sliding evaluation protocol is used to validate the forecasting models. Such an evaluation protocol is widely used to evaluate time series forecasting models in previous literature [95]. For each participant p_k, each target attribute a_t, lag l, and a given day i, the personalized forecasting model learns the history of the data from day (i − l) to (i), then makes the prediction for the target value of the next h days. In the experiment, the predictions are made for each of the 150 individuals’ most recent 14 values in the time series (roughly the latter half of the data in the 3rd burst), then the statistics of the predictions corresponding to all the individual participants are averaged.

4.5. Forecasting Evaluation Metrics

Five metrics are used to compare and quantify the forecastability of each model, including directional accuracy (DAC), mean average error (MAE), mean average percentage error (MAPE), mean square error (MSE), and root mean square error (RMSE). Such metrics have been successfully used to measure forecastability in multiple forecasting-related works [96, 97].

4.6. Objective 1: Model Selection

This section reports the results from comparing multiple forecasting models in order to select the best one for further experiments.

4.6.1. Stage 1: Partial Comparison

The analysis of three chosen attributes are shown (in Table 6). Note that the training times are not reported because the objective of the partial comparison focuses on the prediction accuracy of the models, rather than the efficiency in terms of running time. Each regressor is trained with dimension-reduced data using the Principal Component Analysis technique. It is apparent that the performance of machine learning based methods (especially Random Forest) outperform the baseline VARX model on all the three chosen attributes. It is interesting to see that the traditional VARX method that has been widely used for multivariate time series forecasting performs worse than the machine learning based algorithms. This could be not only because the data has more dimensions than the VARX model can effectively handle, but also because the relationship between the attributes may not be linear.

Table 6.

Comparison of the forecasting results of the three sample target attributes on the select forecasting models with lag l = 3 and forecasting horizon h = 1. The models are trained with partial training data (i.e. using dimension-reduced data with no missing values). DAC denotes directional accuracy, MAE denotes mean average error, MAPE denotes mean average percentage error, MSE denotes mean square error, and RMSE denotes root mean square error.

Target Attribute	Reg. Model	DAC	MAE	MAPE (%)	MSE	RMSE
NegAffect	VARX	0.5257	16.5378	28.4516	459.9315	18.2033
	SVMR	0.6327	6.3261	15.0258	84.4304	7.8731
	SLR	0.6749	6.3707	16.2492	79.7906	7.7339
	RF	0.6893	6.0867	16.9891	72.3964	7.4043
	RBFN	0.6862	6.6261	17.3026	87.6746	8.0549
	MPR	0.6348	8.1201	18.9394	137.1940	10.3114
	M5P	0.6646	6.3734	15.1783	80.4128	7.7991
	LWL	0.6759	6.5596	15.5309	88.7314	8.1442
	LR	0.6512	6.4480	15.2470	80.8905	7.8626
	Ibk	0.5874	7.5983	16.5657	118.1801	9.4736
	GPR	0.6564	6.1359	15.4226	74.1160	7.4966
PosAffect	VARX	0.5535	26.3600	71.0436	1095.0173	30.2500
	SVMR	0.6461	6.5107	15.4641	85.3383	8.2210
	SLR	0.6667	6.4836	16.5372	79.3142	8.0352
	RF	0.6842	5.8792	14.7563	66.5746	7.3716
	RBFN	0.6759	6.6577	17.3851	83.5140	8.1976
	MPR	0.6235	8.4115	19.6191	144.4885	10.6435
	M5P	0.6595	6.3026	15.0097	74.6272	7.8280
	LWL	0.6584	6.6242	15.6839	84.2575	8.1982
	LR	0.6533	6.3524	15.0209	74.7017	7.8534
	IBk	0.5710	7.6001	16.5697	117.0639	9.5517
	GPR	0.6615	6.1047	15.3441	72.4103	7.6512
Control	VARX	0.5288	29.4296	79.3165	1428.1814	33.4424
	SVMR	0.6759	8.6540	20.5549	162.4305	10.8847
	SLR	0.6759	8.4926	21.6613	149.1373	10.5181
	RF	0.6739	8.0625	20.8032	130.8079	9.9277
	RBFN	0.6656	8.8722	23.1677	156.0613	10.8053
	MPR	0.6183	11.1605	26.0310	285.8279	14.7689
	M5P	0.6718	8.5195	20.2893	150.1819	10.6231
	LWL	0.6708	9.0107	21.3344	184.7712	11.4806
	LR	0.6749	8.5829	20.2951	152.7628	10.6900
	IBk	0.5885	10.0613	21.9355	216.7923	12.6711
	GPR	0.6770	8.4783	21.3100	144.5252	10.4939

4.6.2. Stage 2: Comprehensive Comparison

In this section, the top eight regressors are chosen to test on the full data, without dimensionality reduction.

Table 7 lists the forecasting performance of top forecasting models from Stage 1, on the six select attributes. Red/bold figures are the best (lowest error, highest directional accuracy) evaluation scores among all the forecasting models. It is evident that Random Forest forecasters yield the lowest error (as measured by MAE, MAPE, MSE, and RMSE). This finding is also consistent with results from Stage 1, where all the forecasters were trained/tested on dimension reduced, partial data. Random Forest has been shown successful in many classification tasks [98, 99, 100, 101], due to its ability to deal with unbalanced data, avoid over-fitting, and automatically select useful features. In terms of directional accuracy (DAC), Random Forest performs the best only for the attributes CONTROL d and S ATHEALTH d, while Radial Basis Function Networks for Regression (RBFN) outperforms the other on the remaining four target attributes. However, Random Forest stands the second best in most of such attributes. Also, the DAC differences between the RBFN and the Random Forest are only marginal. Hence, in terms of forecasting performance, we believe the forecasters implementing the Random Forest algorithm are the most suitable ones for our dataset.

Table 7.

Average forecasting results of all the 150 participants using full data (L = 7 and H = 1) of forecasting models on the select six attributes. DAC denotes directional accuracy, MAE denotes mean average error, MAPE denotes mean average percentage error, MSE denotes mean square error, RMSE denotes root mean square error, and TrainTime denotes model training time.

Attribute	Model	DAC	MAE	MAPE	MSE	RMSE	Train Time (ms)
SATHEALTH_d	LR	0.6132	10.86	25.73	251.82	14.10	2272.28
	MPR	0.5936	11.24	26.36	268.82	14.64	2017.06
	GPR	0.6368	10.29	23.31	242.02	12.80	27.45
	M5P	0.6584	9.27	22.80	178.22	11.82	374.15
	RBFN	0.6749	8.47	22.71	145.26	10.40	40.15
	J48	0.6492	10.09	27.42	211.61	12.72	127.64
	RF	0.6872	8.12	21.56	134.05	10.04	458.31
	SMVR	0.6348	10.40	23.49	247.13	12.98	34.27
NegAffect_d	LR	0.5730	14.27	40.62	401.74	17.98	4355.01
	MPR	0.5710	12.96	38.82	340.00	16.39	2832.36
	GPR	0.5905	11.66	36.41	308.97	14.60	26.70
	M5P	0.6101	10.77	32.32	249.47	13.75	310.00
	RBFN	0.6492	10.44	35.83	261.73	12.81	38.87
	J48	0.6142	10.67	34.57	241.46	13.25	103.60
	RF	0.6440	9.11	31.22	174.03	11.24	389.56
	SMVR	0.5957	11.59	36.36	300.03	14.55	33.53
PosAffect_d	LR	0.6060	11.14	25.27	268.70	14.12	2873.44
	MPR	0.5638	11.35	26.62	273.51	14.17	2816.51
	GPR	0.5916	10.15	23.53	260.39	12.55	26.80
	M5P	0.6101	9.51	23.33	200.62	11.85	378.33
	RBFN	0.6152	9.60	24.28	184.27	11.24	40.54
	J48	0.6173	10.42	25.90	226.58	12.84	121.99
	RF	0.6286	8.37	20.94	140.32	10.02	451.94
	SMVR	0.5936	10.21	23.67	262.68	12.63	33.87
SATLIFE_d	LR	0.6276	8.22	83.94	139.99	10.40	1840.27
	MPR	0.6080	8.32	74.46	138.72	10.51	1862.34
	GPR	0.6481	7.72	74.31	176.24	9.74	24.26
	M5P	0.6502	6.96	70.73	98.93	8.67	340.22
	RBFN	0.6965	6.38	68.68	84.84	7.79	40.31
	J48	0.6615	7.30	68.39	108.83	9.07	135.65
	RF	0.6883	6.06	65.63	72.38	7.35	504.95
	SMVR	0.6440	7.81	75.87	182.38	9.85	32.46
CONTROL_d	LR	0.6039	8.95	22.00	169.22	11.42	7912.66
	MPR	0.5854	8.88	21.21	148.73	11.05	3642.25
	GPR	0.6029	8.02	18.41	166.55	9.96	27.98
	M5P	0.6451	7.29	17.19	106.12	9.17	383.06
	RBFN	0.6944	6.49	16.62	79.13	7.99	39.32
	J48	0.6183	7.68	19.31	111.20	9.52	128.10
	RF	0.6883	5.87	14.83	66.12	7.36	509.24
	SMVR	0.6008	8.09	18.56	169.12	10.04	36.81
PHYHEALTH_d	LR	0.6163	10.02	26.21	221.13	12.72	2350.12
	MPR	0.5751	10.93	25.48	243.56	13.69	2095.35
	GPR	0.6327	9.29	23.27	222.05	11.73	28.49
	M5P	0.6502	8.51	26.04	156.80	10.83	377.62
	RBFN	0.6842	7.91	24.46	129.36	9.73	39.49
	J48	0.6461	9.12	25.87	173.91	11.46	139.99
	RF	0.6811	7.26	22.09	113.20	9.14	466.79
	SMVR	0.6307	9.46	23.49	234.20	11.90	35.24

It may be the case that good performance comes at the cost of learning time. Though the training times of Random Forest are not as large as those of Linear Regression (LR) and Multi-layer Perceptron for Regression (MPR), due to not having built-in feature selection mechanism, they are still quite computationally expensive compared to other relatively good models, such as RBFN and M5P. This computational resource consumption is due to internal configuration of the Random Forest, which builds 300 atomic decision trees to make ensemble decisions. However, since the training process can be done off-line, we will stick with Random Forest for the analysis in the Objective 2. In future works, another implementation of Random Forest, Fast Random Forest⁷, which claims to improve upon the implementation used in this paper (speed is one of the major improvements) could be explored.

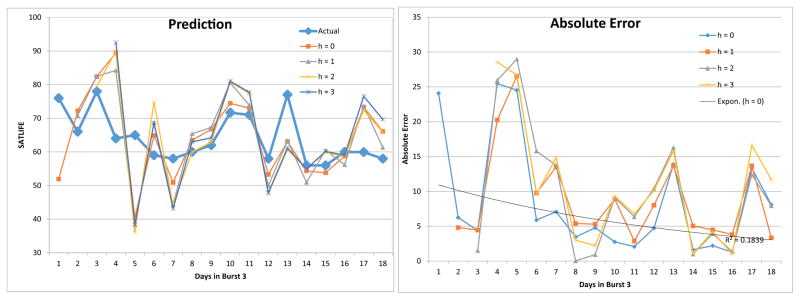
Figure 4 (Left) shows sample forecasting results of the actual values of a sample individual on the attribute Satisfaction in Life (S AT LIFE d). The forecasting model used here is based on the Random Forest algorithm, with the lag of 3 days (l = 3). The prediction horizons vary from 0 to 3. Note that h = 0 means the forecasting model is predicting today’s value of the target attribute. This particular example illustrates that the prediction accuracy decreases as the model predicts the values further ahead in the future. Figure 4 (Right) shows the absolute errors calculated from the predictions in the left figure. It is interesting to note that the absolute error decreases as the model predicts more recent values. This is because as the forecaster proceeds to predict the value in the next period, the current values are fed back to the training data, resulting in incrementally more historical data to learn from.

Figure 4.

(Left) Comparison of example forecasting results by RF with different horizons (i.e. h = 0, 1, 2, 3) against the actual values of the attribute S AT LIFE d of a participant. (Right) Comparison of absolute error of each horizon (i.e. h = 0, 1, 2, 3).

4.7. Objective 2: Predicting Latent Attributes

In this objective, we investigate whether it is possible to predict the latent attributes (target attributes) using only the observable information as training data. First the impact of different training data sources (i.e. observable only, latent only, and both) is investigated. Then we study the effect of different lags on the forecasting performance.

4.7.1. Impact of Different Sources of Information

The ability to predict and forecast latent attributes using the information from only observable attributes could prove crucial to multiple applications in mental and emotional anomaly detection. For each participant, a Random Forest forecaster is trained with each of the three data source modes: observable only (O), latent only (U), and both (OU). Recall that O-based, U-based, and OU-based forecasters are trained with only objectively and externally observable information, only subjective latent information, and both, respectively. For each source mode, the lags are varied between 1, 3, 5, and 7. The results from all the participants and lags are averaged for presentation and interpretation.

Figure 5 plots the mean absolute error (MAE) of the prediction at different horizons on the six selected latent attributes. The forecasters trained with only observable information (blue-circle) perform the best, as they achieve the lowest absolute error at every horizon for all the select attributes. Note that since each select latent attribute can take a value from [0 – 100], the magnitude of error can be thought of as percentage error (in the absolute sense). The magnitudes of error vary across different latent attributes. For instance, the forecasts for the attribute PHYHEALTH d have the absolute error fluctuating around [8.5 – 9], while those of NegAffect_d are fluctuating around [6.0 – 6.1]. Regardless, the errors are considered small and acceptable, suggesting that observable daily routine and behavior information can constitute good predictors for mental and emotion states, as evident in our case study. Surprisingly, the forecasters trained only with latent information (magenta-square lines) perform the worst. This suggests that the mental attributes could be the causal effects of the physical ones, making the relationship among latent attributes rather loose. In short, individuals exist in real contexts. It is interesting to note that the error magnitudes of the prediction of the forecasters trained with only latent information significantly and constantly decrease as the horizon increases, despite the intuition that further prediction should be less accurate. Regardless of which, the magnitudes of errors of these latent-only forecasters are quite large, compared to the observable-only ones. The forecasters trained with both observable and latent information perform somewhere in between. This is reasonable because, while the observable information is proven most useful, adding the latent information could taint the learned model, impeding the overall forecasting accuracy. Though Random Forest has a built-in feature selection mechanism, the effect of the addition of this less useful information may not be completely eliminated.

Figure 5.

Comparison of average mean absolute error (MAE) with error bars showing standard errors, produced by Random Forest forecasters trained with different information sources (i.e. OU = both observable and latent information, O = only observable information, U = only latent information) at each horizon (days ahead of prediction). Each prediction is an average of prediction using different lags (i.e. lags = 1, 3, 5, and 7). Each attribute value has a range of [0, 100].

Figure 6 shows the average directional accuracy of the forecasting of the select six latent attributes. Recall that directional accuracy quantifies the accuracy of the predicted polarity change (i.e., greater or less than the current value) of a particular attribute. Unlike the performance in terms of error magnitudes, where the observable-only forecasters all outperform other forecasters, the directional accuracy results indicate a mixed conclusion. The observable-only forecasters perform better than others on the attribute S ATHEALTH d, and on-par with the combined forecasters on the attributes CONTROL d, PHYHEALTH d, PosAffect_d, and S AT LIFE d. The directional accuracy of the observable only forecaster is worst on the attribute NegAffect_d. However, the observable only forecasters perform best when used to forecast most of the mental states up to three days in advance.

Figure 6.

Comparison of directional accuracy (DAC), range between [0, 1], produced by Random Forest forecaster trained with different information sources (i.e. OU = both observable and latent information, O = only observable information, U = only latent information) at each horizon (days ahead of prediction). Each prediction is an average of prediction using different lags (i.e. lags = 1, 3, 5, and 7).

In sum, we trained the Random Forest forecaster with three sources of information: observable only, latent only, and both. The results in terms of error magnitudes indicate a singular conclusion that it is possible to build a predictor for mental states that observe only physical actions and daily routines. This observable-only predictor not only yields good prediction results on its own, but its prediction performance (in terms of magnitudes of error) is also even better than the forecaster trained with both observable and latent information. However, some of the observable information used in this paper can still be cumbersome to capture in an automated manner (note that all observable information in the dataset were collected by having the participants manually respond to the questionnaires.). These observable attributes include number of sleep hours and number of drinks. In the next immediate step, this observable information would still be input to the forecaster manually either by human observers or the test subjects themselves, while we continue to investigate the possibility of obtaining this observable information in an automated, sensor-based manner.

4.7.2. Impact of Different Lags

It is often a natural question when implementing a time series forecaster: how much history does the forecaster need to take into account to achieve the optimal forecasting performance? In this section, the observable-only forecaster, which implements the Random Forest algorithm, is trained with observable information with different lags of 1, 3, 5, and 7 days. Mean absolute error and directional accuracy are measured from the average forecasting results of the horizons 0, 1, 2, ..., 7. Table 8 lists the results for all the select six attributes.

Table 8.

Comparison of the forecasting performance between Random Forest forecasters trained with data of different lags (i.e. L = 1, 3, 5, 7) on the select latent attributes. The predictions of each horizon (i.e. 0 to 7) are averaged.

Attribute	Mean Absolute Error (MAE)				Directional Accuracy (DAC)
	L1	L3	L5	L7	L1	L3	L5	L7
CONTROL_d	8.04343	8.10174	8.06407	8.09793	0.69186	0.68839	0.68703	0.68645
NegAffect_d	6.05397	6.07227	6.02823	6.00741	0.68670	0.68319	0.68530	0.68313
PHYHEALTH_d	8.80460	8.80975	8.78863	8.81821	0.66009	0.65672	0.65697	0.65696
PosAffect_d	6.07272	6.07991	6.06503	6.09752	0.68090	0.67917	0.67681	0.67753
SATHEALTH_d	8.23313	8.23469	8.19631	8.21561	0.61994	0.61706	0.61709	0.61722
SATLIFE_d	7.42245	7.43354	7.42356	7.43150	0.68136	0.67634	0.67763	0.67958

In terms of mean absolute error, the lag of one day yields the best performance on CONTROL d and S AT LIFE d, the lag of five days on PHYHEALTH d, PosAffect_d, and S ATHEALTH d, and the lag of seven days on NegAffect_d. Even though there is no single dominant consensus on the best lag that would yield the minimum error for all the attributes, the results illustrate that different attributes are dependent on different lengths of past data. For example, the most recent information is already good enough to determine the states of CONTROL d and S AT LIFE d, which represent the level of perceived control over surrounding environments and the level of satisfaction in life, respectively. While, more information is needed in the case of PHYHEALTH d, PosAffect_d, and S ATHEALTH d. In some cases where the attributes tend to exhibit seasonality (e.g., NegAffect_d) a lag of one week (7 days) would be the optimal. This particular case of NegAffect_d is quite intuitive since an individual may experience depression-induced events (meetings, homework dues, etc.) on a weekly basis.

It is, however, interesting to note that the lag of one day yields a dominant result in terms of directional accuracy. This suggests that the relational mental states in the next time period can be best predicted using the information in the most recent time period. The Random Forest forecaster yields the directional accuracy of roughly 68% on average. This means that, it can predict whether a particular mental attribute will be higher or lower than the current day with the accuracy of 68%. Though this number is not high enough to implement in the real system, this is a preliminary investigation that can be built upon.

5. Limitations and Potential Applications

Although the preliminary results suggest the potential of using the proposed machine learning based time-series models to develop a mental state prediction system from temporal, completely observable information, there is room for improvement that requires further study and research.

1. Currently, the ground-truth mental state data is collected from standard self-evaluation reports, which may raise doubts about subjectivity and bias. Hence, future evaluation should include opinions from psychological domain experts and objective evidence such as brain signals [102].

2. Though a forecasting model is built for each individual, the underlying machine learning algorithms still remain static across the entire population. That is, a forecaster that implements the same machine learning algorithm is generated for each individual. A variant of the methodology where the most appropriate machine learning algorithm is automatically selected for each individual, as part of the model selection process, could be investigated as future work.

3. The data collected from 150 participants may not be sufficient to be conclusive. Figure 4 (right) not only shows that prediction error decreases as more historical data is available, but also suggests that more data points and higher frequency of data collection would increase the predictive accuracy.

The ability to identify and forecast one’s mental states could prove useful not only in psychological applications already mentioned above, but also in other emergent and commercialization platforms. Some of the applications that could potentially be built upon this work include:

1. Tragedy Prevention. It is believed that mental anomalies may be the root causes of many tragedies and incidents [103, 104, 105]. For example, a recent plane crash was the collateral damage of a suicide incident committed by a co-pilot who was believed to have mental problems⁸. Lim et al. reported that 94.5% of suicidal incidents in Korea are caused by mental anomalies, especially stress [106]. Such suicides and suicide attempts not only cause sentimental damage to those living, but also impose financial burdens to the society. Approximately, $34.6 billion a year is spent on combined medical and work loss costs in the United States⁹. In addition to suicidal behaviors, mental anomalies can cause violence that often results in fatalities, including homicides. Neustatter described 7 different motives for murder, all of which involve mental distortion [107]. In more common scenarios, life changing events or critical incidents often leave mental strain on one’s mind that results in unhappiness or, in some cases, chronic mental diseases. Future works could extend our work presented here by allowing the machine learning forecasters to learn from historical information of the people who have been diagnosed with such severe mental diseases. The trained models could then be used to estimate the chances of such tragedies, and enable appropriate prevention and intervention.

2. Personalized Medicine. Although personalized medicine that provides treatment specific to each individual genome has been implemented [108], psychological practitioners could use our algorithms along with other auxiliary information such as social networks [109] to generate a mental profile for each mental patient so that personalized psychotherapeutic treatment could be designed.

3. Product Recommendation. Another dimension of possible applications would be recommendation systems that suggest products (songs, drinks, movies, etc.) based on users’ current emotions. While a number of research works have explored the use of user-generated content (such as social media, web-blogs, and product reviews) to infer customers’ preferences towards particular products /product features [110, 111, 112], limited works have investigated utilizing users’ mental states for such a purpose. Collaborative filtering techniques could be applied to cluster similar users so that an ensemble learning method could be used to make more accurate recommendations for each group of users based on their emotional profiles.

6. Conclusion and Future Direction

The research reported in this paper illustrates an emotion and mental state prediction framework that uses machine learning algorithms to analyze a set of psychological multivariate time series data. The problem is framed as a multivariate time series forecasting problem, in which multiple forecasting models are compared using standard forecasting evaluation protocols. The selected models comprise the traditional vector autoregression (VARX) and multiple variants of machine learning based regression algorithms modified for multivariate time series data. The first set of experiments shows that the Random Forest based forecaster was best suited for the dataset. In the second batch of the experiments, it was empirically shown that some of the latent attributes could be effectively predicted using only the observable information. These results not only provided primary, promising initial progress towards our ultimate goal, but also pointed out there is ample of room for improvement. Future research could include collecting more data and investigating automatic methods to collect participants’ information (e.g. using Microsoft Kinect¹⁰ or a wearable accelerometer to detect movements, and the Apple Health app ¹¹ to detect sleep pattern and other physical information). We could also investigate cases where data is passively sensed by smartphones and sensor beds. It would also be interesting to see if collaborative filtering techniques could be used to infer the mental state of a target user by learning auxiliary information from other similar users.

Highlights.

This paper has the following main contributions:

• We present a methodology to identify a suitable individual-level prediction model to predict an individual’s mental state.

• We present a modification to traditional machine learning based regression algorithms so that they can be used for forecasting seasonal multivariate time series data. Specifically, the time-delay embedding algorithm is applied to the feature space as a preprocessing step to allow traditional machine learning algorithms to process the data in a temporally dependent manner.

• We find the best multivariate time series model that captures the temporal dependencies in the data by comparing the performance between multiple machine learning algorithms from different families and the traditional VARX model (baseline) that has been previously used to analyze attributes in psychological literature.

• We demonstrate with empirical evidence that latent attributes can be predicted using only information from the observable attributes.