Mechanotransmission in endothelial cells subjected to oscillatory and multi-directional shear flow

Abstract

Local haemodynamics are linked to the non-uniform distribution of atherosclerosic lesions in arteries. Low and oscillatory (reversing in the axial flow direction) wall shear stress (WSS) induce inflammatory responses in endothelial cells (ECs) mediating disease localization. The objective of this study is to investigate computationally how the flow direction (reflected in WSS variation on the EC surface over time) influences the forces experienced by structural components of ECs that are believed to play important roles in mechanotransduction. A three-dimensional, multi-scale, multi-component, viscoelastic model of focally adhered ECs is developed, in which oscillatory WSS (reversing or non-reversing) parallel to the principal flow direction, or multi-directional oscillatory WSS with reversing axial and transverse components are applied over the EC surface. The computational model includes the glycocalyx layer, actin cortical layer, nucleus, cytoskeleton, focal adhesions (FAs), stress fibres and adherens junctions (ADJs). We show the distinct effects of atherogenic flow profiles (reversing unidirectional flow and reversing multi-directional flow) on subcellular structures relative to non-atherogenic flow (non-reversing flow). Reversing flow lowers stresses and strains due to viscoelastic effects, and multi-directional flow alters stress on the ADJs perpendicular to the axial flow direction. The simulations predict forces on integrins, ADJ filaments and other substructures in the range that activate mechanotransduction.

1. Introduction

This study investigates the impact of flow direction over the cardiac cycle simulating atherosclerotic disease prone and spared regions on forces transmitted to inter-/intracellular structures of endothelial cells (ECs) that mediate important mechanotransduction processes. The patchy distribution of atherosclerotic lesions preferentially localizes in vessel bifurcations, curvatures and points of blood flow recirculation and stasis [1–3]. In these susceptible areas, fluid shear stress (FSS) on the vessel wall is lower in magnitude and exhibits directional changes and possibly flow separation, features absent from areas of arteries generally spared from atherosclerosis [2,4]. Responses of ECs to haemodynamic forces play a significant role in vascular health and disease [3,4], and models of EC mechanics have evolved significantly since the early studies of Fung & Liu [5]. ECs transduce the FSS resulting from blood flow into intracellular signals that affect gene expression and cellular functions such as proliferation, apoptosis, migration, permeability, cell alignment and mechanical properties [6–12]. Numerous sites have been implicated in transducing mechanical stresses, including the plasma membrane [5,6,9,12–15] and its associated glycocalyx [12,16–19], focal adhesions (FAs) [10,12,20–26], the nucleus [27,28], the cytoskeleton [6,12,16,29,30], the cortical membrane [1,12,31,32] and the intercellular junctions [33–36]. However, detailed models of mechanotransmission in EC monolayers simulating disease-prone regions of arteries have not been described (table 1).

Table 1.

List of symbols.

ECs	endothelial cells
SFs	stress fibres
APL	apical layer
FAs	focal adhesions
ADJs	adherens junctions
WSS	wall shear stress
FSS	fluid shear stress
TAWSS	time average wall shear stress
OSI	oscillatory shear index
transWSS	transverse wall shear stress
PL	perpendicular
PP	parallel
SFsPP	stress fibres are perpendicular to the principal flow direction
SFsPL	stresses fibres are parallel to the principal flow direction

In this context, Dabagh et al. [12] developed a multi-scale, multi-component computational EC monolayer model to quantify the intra- and intercellular stresses generated upon initial exposure to steady shear stress. Such computational models are unique as no experiment can reveal the cellular force transmission in such detail. The model of Dabagh et al. [12] treated all cellular components as incompressible neo-Hookean materials; viscoelastic effects were not considered. Gouget et al. [37] developed a model of mechanical signal transmission within a cell by describing strains in a network of pre-stressed viscoelastic stress fibres following the application of a force to the cell surface. Barakat [38] developed a mathematical model for the shear stress-deformation of a flow sensor on the EC surface which was modelled with a viscoelastic formulation. Other potential mechanosensors involved in mechanotransmission in ECs were not included in these models. Several other models have been developed to study how ECs sense shear flow on the cell surface, how signals are transmitted within ECs and how certain signals regulate cell function [37–40]. However, these models either included only one or two mechanosensors in the model or did not treat the cellular components as viscoelastic structures.

On the other hand, the responses of vascular ECs to the magnitude and direction of shear stress have been studied experimentally [5–8]. Wang et al. [41] examined the effects of flow direction (0°—forward, 90°—transverse and 180°—reverse) on signalling pathways. They reported that flow parallel to the long axis of ECs (0° or 180°) activated endothelial nitric oxide synthase and the production of nitric oxide, whereas transverse flow preferentially activated reactive oxygen species and nuclear factor-κB. Yumnah et al. [9] compared maps of lesion prevalence around aortic branch ostia in immature and mature rabbits with maps of time average wall shear stress (TAWSS), oscillatory shear index (OSI) and transverse wall shear stress (transWSS) obtained from computational simulation. They observed the best correlation between transWSS and lesion prevalence. They suggested that oscillatory flow has pro-inflammatory effects when acting perpendicular to the EC axis.

This study will investigate the impact of flow direction on mechanotransmission to inter/intracellular structures of ECs through a comprehensive model. Our emphasis is on the FA plaques at the basal aspect of the cell where prominent integrin signalling is localized [1,10,12,21–26], and the adherens junction (ADJ) between cells where additional important signals originate [1,12,20,33–36]. We do not focus on the apical cell membrane where many additional mechanosensors are located [42]. A three-dimensional, viscoelastic, multi-component, multi-scale model of the EC monolayer will be developed to quantify the force transmission from cell surface to subcellular elements. Major cellular elements, several treated as viscoelastic structures, are incorporated in the model, including the glycocalyx layer, actin cortical layer, nucleus, FAs, cytoskeleton and ADJs. The impact of the flow direction on mechanotransmission will be examined by exposing ECs to low, oscillatory WSS parallel to the long axis of the cells and multi-directional, low, oscillatory WSS. These atherogenic WSS profiles will be compared with unidirectional shear with no reversal and with steady shear. Magnitudes of the simulated TAWSS, OSI and transWSS are in close agreement with data reported by Yumnah et al. [9] for multi-directional, oscillatory or purely forward shear waveforms. The results provide insight into the links between flow directionality and atherosclerosis by identifying the magnitudes of stresses on mechanosensors thought to be important in the disease process.

2. Methods

2.1. Geometric model

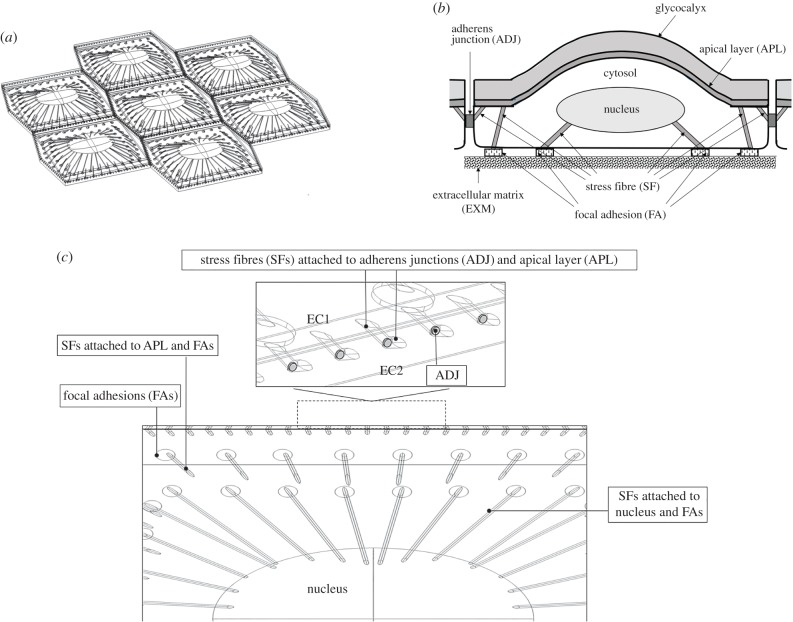
It has been well documented that ECs located in pro-atherosclerosic regions of arteries retain a polygonal morphology similar to that of their static counterparts [10]. ECs in these regions do not have any preferential orientation [11]. In this study, the ECs are modelled as hexagonal. The EC monolayer contains seven cells (figure 1a) where each EC consists of the following major subcellular load-bearing structures: the apical glycocalyx layer with thickness 500 nm [17–19] that is in direct contact with fluid flow; the apical cortex layer with thickness 100 nm [12,13]; the cytosol having length and width of 36 and 32.1 µm [12], respectively; the nucleus at the centre of each EC is located 1.25 µm above the cell base [14,27], taken as an ellipsoid with maximum radius of 8 µm (along x-axis) and minimum radius of 6 µm (along y-axis), and maximum height of 2.5 µm (along z-axis) [27,28]; the cytoskeleton linking the apical plasma membrane to FAs or the nucleus or intercellular junctions [12,20,21,26,27,39,40,43]; FAs providing the contact points with the extracellular matrix [1,12,21–26]; and ADJs binding ECs together across their lateral boundaries [12,33–36].

Figure 1.

(a) Geometry of EC monolayer and inter-/intracellular organelles. (b) Schematic side view of EC, its connection to neighbouring cells and subcellular structures. (c) Zoomed view of subcellular structures including SFs that attach the apical plasma membrane to FAs and intercellular junctions and SFs that attach the nucleus to FAs. Inset of c shows the ADJs between two cell (EC1 and EC2) with SFs from the plasma membrane attached to ADJs.

Each EC is represented by a hexagon at its base. The surface topology of each EC is prescribed as a sinusoid [6,14–16] given by equation (2.1) [6,15]:

2.1

where 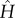is the amplitude of the surface contour. The streamwise and transverse wavenumbers α and β are given by, α = 2π/λ_x and β = 2π/λ_y where λ_x and λ_y are the surface undulation wavelengths assumed as 30 and 26.1 µm, respectively [6,14,15]. The maximum excursion of the surface undulation between peak height (over the nucleus) and minima (at intercellular junctions) is set to 4 µm [6,14]. The mean height to length ratio, 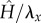, is taken as 0.133 and the aspect ratio, q = λ_x/λ_y (length divided by the width), is assumed as 1.15, which are characteristics of ECs in disturbed flow regions. Aligned cells in high-shear regions typically have aspect ratios greater than 2 [6,14,15,26]. The height of ECs at intercellular junctions is taken as 1 µm [6,12,14]. The perspective view of the EC monolayer is depicted in figure 1a and the side view of the central cell is presented in figure 1b.

Thoumine et al. [10] showed in vitro that confluent bovine aortic ECs exposed to an oscillatory shear stress, with polygonal morphology similar to that of control (static) cultures, possessed more central stress fibres than in static cells and exhibited a partial loss of peripheral bands of actin. The cytoskeleton, in this study, is modelled as a network of viscoelastic stress fibres (SFs) that are peripherally and centrally distributed, based on the observations of Thoumine et al. [10]. Other components of the cytoskeleton, most notably, microtubules and intermediate filaments, are not included in the model, but effective properties are used for the cytoplasm, which considers the influence of these components [12]. The arrangement of SFs is shown in figure 1c which demonstrates that SFs emanate from the apical plasma membrane and link to FAs or the nucleus or intercellular junctions. One SF connects each FA on the basal side of the cell to the apical plasma membrane; one SF connects each FA on the basal side of the cell to the nucleus; one SF connects each ADJ to the apical plasma membrane [12,20,26,27,39,40,43]. The mechanical linkage between the apical surface and the nucleus also exists through the effective viscoelastic properties used for the cytoplasm [12]. SFs are modelled as bundles with a circular cross-section of 200 nm in diameter [12,39,40,43].

Previous studies have shown that the cross-sectional area of each FA varies in the range of 0.5–10 µm² and the total area of all FAs in a cell covers approximately 2–5% of the complete cellular area [22,23]. In this study, FAs are modelled as cylinders with a radius of 0.4 µm and a thickness of 110 nm [24,26]. Seventy-two FAs are located in the basal aspect of each EC covering 4.2% of the cell's basal area.

ADJs, significant load bearing structures between cells, are included in the model as direct pathways for intercellular mechanotransmission. ADJs are modelled as finger-like structures, which grow perpendicular to the cell–cell interface, with an inter-finger distance of 1 µm and number density of 1 µm⁻² [33–36]. The fingers are modelled as cylinders with a radius of 100 nm located at 25% of the cleft depth or 250 nm from the apical surface [12,44]. A zoomed view of one EC and subcellular structures is displayed in figure 1c.

2.2. Constitutive equations

The SFs, nucleus, cytosol, FAs and cortical layer are treated as viscoelastic materials using the Kelvin–Voigt model [37–40,45]. The model can be represented by a purely viscous damper with viscosity η and purely elastic spring having a modulus E connected in parallel, leading to the well-known equation relating the stress (σ) and the strain (ɛ) [37–40]:

2.2

Equation (2.2) is applied to the normal stresses of a viscoelastic material. The relaxation time, t*, is defined as [37,39]:

2.3

The glycocalyx and ADJs are treated as incompressible neo-Hookean materials [34–36,46–48], whose strain energy function U is given by the equation:

2.4

where C₁₀ is a constant and λ₁, λ₂ and λ₃ are the principal stretches. The constant C₁₀ is related to Young's E modulus by C₁₀ = E/6.

All stress components are computed and applied to calculate the von Mises stress (σ_vM), a stress invariant usually referred as the effective stress [30]. The von Mises stress is computed by the equation:

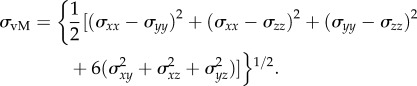2.5

The bending strain (ɛ_b) along any SF is calculated by the equation [43]:

2.6

L₀ is the un-deformed length of the SF which is obtained from the initial geometry and L the deformed length of the SF.

2.3. Boundary conditions

2.3.1. Imposed shear stress

The oscillatory shear stress distributions in the axial and transverse directions applied on the surface of EC monolayer are expressed as:

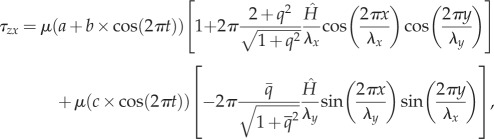2.7a

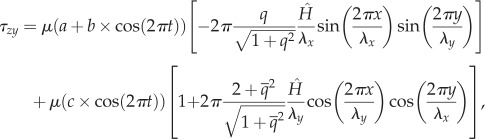2.7b

where μ is the dynamic viscosity of blood, t the time, q the aspect ratio (q = λ_x/λ_y), 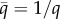and the amplitude of the surface contour, a the mean wall shear stress (WSS) imposed by the axial flow far from the endothelial surface, b the amplitude of the axial shear stress oscillation and c the amplitude of the transverse shear stress oscillation. Equation (2.7a) expresses the total axial shear stress applied over ECs. The first term in equation (2.7a) represents the axial shear stress induced by the far field axial component [9,12,15,38–40] and the second term in equation (2.7a) is the axial shear induced by the far field transverse flow [9,15]. Equation (2.7b) expresses the total transverse shear stress applied over the EC monolayer. The first term in equation (2.7b) is the transverse shear induced by the far field axial shear flow [9,12,15,38–40] and the second term in equation (2.7b) stands for the transverse shear stress induced by the far field transverse flow [9,15]. Additional details about the origins of equations (2.7a) and (2.7b) are presented in electronic supplementary material, appendix A.

In this study, four different shear flows are applied over the EC surfaces resulting in different values of TAWSS, OSI and transWSS as defined in equations (2.8)–(2.10) [9].

2.8

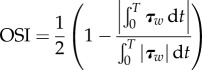2.9

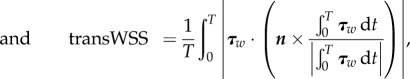2.10

where τ_w represents the instantaneous WSS vector and T the period of the cardiac cycle.

The magnitudes of a, b and c in equations (2.7a) and (2.7b) are assigned to achieve each of the following four shear flows: (a) the first shear regime is multi-directional, disturbed flow where μa = 0.01 Pa, μb = 1 Pa and μc = 0.31 Pa to achieve TAWSS = 1.0 Pa, transWSS = 0.3 Pa and OSI = 0.5 Pa. (b) The second shear regime is pulsatile flow with reversal where μa = 0.01 Pa, μb = 1.15 Pa and μc = 0.0 to achieve TAWSS = 1.0 PA, transWSS = 0.0, OSI = 0.5 Pa. (C) The third shear regime is pulsatile flow with no-reversal (purely forward flow) where μa = 0.75 Pa, μb = 0.3 Pa and μc = 0.0 to achieve TAWSS = 1.0 Pa, transWSS = 0.0, OSI = 0.0. (D) The fourth shear regime is steady flow where μa = 1.0 Pa, μb = 0.0 and μc = 0.0 were taken to achieve TAWSS = 1.0. Note that all cases have the same TAWSS of 1.0 Pa. Case C is pulsatile but with no reversing or transverse shear. Case B has reversing shear but no transverse shear, and case A has both reversing and transverse shear components present. It is important to note that TAWSS is an average of the magnitude of the WSS over the pulsatile flow cycle. It differs from the mean wall shear when there is flow reversal.

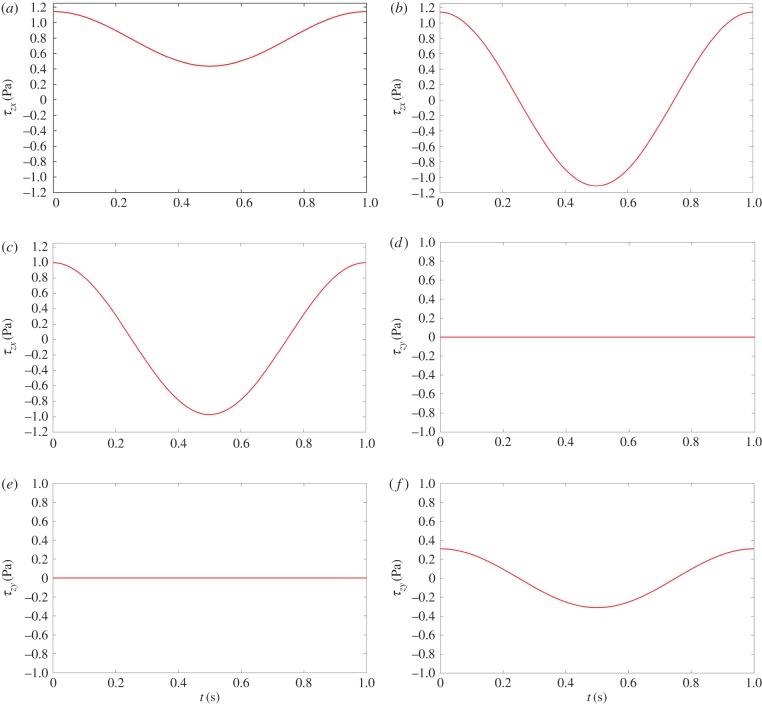
Figure 2 demonstrates the spatially averaged WSS components τ_zx (axial) and τ_zy (transverse) as a function of time over one cycle, based on equations (2.7a) and (2.7b), for different flow conditions. Figure 2a,d shows pulsatile flow with no-reversal. Figure 2b,e demonstrates pulsatile flow with reversal. Figure 2c,f shows multi-directional, disturbed flow. The fourth shear condition, steady flow, is not shown in figure 2.

Figure 2.

Sketches of the spatially averaged WSS components τ_zx (axial) and τ_zy (transverse) as a function of time over one cycle, based on equations (2.7a) and (2.7b). Left (a,d): pulsatile flow with no-reversal; middle (b,e): pulsatile flow with reversal; right (c,f): multi-directional, disturbed flow. Corresponding magnitudes of OSI, TAWSS and transWSS for each flow condition are also included. TAWSS: 1.0, 1.0, 1.0; OSI: 0.0, 0.5, 0.5; transWSS: 0.0, 0.0, 0.3. (Online version in colour.)

2.3.2. Additional boundary conditions

The apical integrin attachments, the cell base and cell membranes are subject to free displacement boundary conditions. The boundaries of basal FAs are constrained in all directions, while the boundaries of ADJs are interior boundaries which are connected to the neighbouring ECs.

2.4. Model parameters

All subcellular structures are assumed to be homogeneous materials. The test ranges and the reference values of geometric and mechanical parameters applied in the model are summarized in table 2.

Table 2.

Summary of parameters used for the multi-component, multi-cell model of the endothelium.

parameter	literature rang	our setting	references
α, m−1 (streamwise wavenumber)	1.2–2.3 × 105	2.09 × 105	[20,25,49,50]
β, m−1 (transverse wavenumber)	1.2–3 × 105	2.41 × 105	[20,25,49,50]
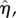m (amplitude of surface contour)	4.41 ± 0.7 × 10−6	5 × 10−6	[20,25,49,50]
λx, m (surface undulation wavelengths)	40 ± 13 × 10−6	30 × 10−6	[20,25,49,50]
λz, m (surface undulation wavelengths)	36 ± 15 × 10−6	26.1 × 10−6	[20,25,49,50]
q (aspect ratio)	1.12 ± 0.31	1.15	[20,25,49,50]
GSFs, Pa (shear modulus of SFs)	4–4.9 × 105	4.9 × 105	[13,39,40]
KSFs, Pa (bulk modulus of SFs)	3–4.8 × 107	4.8 × 107	[13,39,40]
ESFs, Pa (Young's modulus of SFs)	0.3–104 × 106	1.45 × 106	[13,39,40]
tSFs, s (relaxation time of SFs)	0.1–10 × 10−3	1 × 10−3	[4,37,39]
Eg, Pa (Young's modulus of glycocalyx)	390–1000	390	[13,33]
Gcytos, Pa (shear modulus of cytosol)	50–100	66	[50]
Kcytos, Pa (bulk modulus of cytosol)	20 000–30 000	25 830	[50]
tcytos, s (relaxation time of cytosol)	1–5	3.03	[50]
Ecytos, Pa (Young's modulus of cytosol)	500–1000	700	[27,28,30]
Gnuc, Pa (shear modulus of nucleus)	1500–2000	2000	[51]
Knuc, Pa (bulk modulus of nucleus)	0.1–0.2 × 106	199 980	[51]
tnuc, s (relaxation time of nucleus)	0.1–0.5	0.2	[51]
Enuc, Pa (Young's modulus of nucleus)	5000–6000	6000	[27,30,52]
Gcor, Pa (shear modulus of apical layer)	—	333	[31,32]
Kcor, Pa (bulk modulus of apical layer)	—	33 330	[31,32]
tcor, s (relaxation time of apical layer)	0.01–0.1	0.09	[31,32]
Ecor, Pa (Young's modulus of apical layer)	—	1000	[27]
lFA, m (height of the FA)	—	110	[53]
AFA, m2 (cross-sectional area of one FA)	0.5–10 × 10−12	0.5003 × 10−12	[53]
GFA, Pa (shear modulus of FA)	500–11 000	11 008	[53]
KFA, Pa (bulk modulus of FA)	1–2 × 106	1 093 324	[53]
tFA, s (relaxation time of FA)	0.1–1	0.5	[53]
EFA, Pa (Young's modulus of FA)	1650–32 000	32 803	[54]
AADJ, m2 (area of one ADJ)	—	7.854 × 10−15	[30,38]
EADJ, Pa (Young's modulus of ADJ)	5200–89 000	8102	[30,38]

2.5. Computational method

Several views of the EC monolayer consisting of the glycocalyx, cortical layer, cytosol, nucleus, SFs, FAs and ADJs, are demonstrated in figure 1a–c. A Matlab code (Matlab v. R2014a) is applied to generate the geometry of the cytosol, sinusoidal surface of ECs, nucleus, apical cortical layer and glycocalyx. Then the subcellular/intracellular components of ECs are created using the computer package Gambit (v. 2.4.6, Fluent Inc.). Model geometries are exported to the finite-element method solver via Comsol Multiphysics v. 5.1. All cellular components are assigned with material properties, mesh specifications and boundary conditions. The computational results for the von Mises stress, shear stress and strain are determined and examined for independence of mesh density. A computational mesh is employed in each EC consisting of 3.4 × 10⁵, 1.2 × 10⁵, 1.5 × 10⁴, 1 × 10⁵, 2000, 1300 and 900 tetrahedral elements for the cytosol, apical cortical layer, glycocalyx, nucleus, FA, SF and ADJ, respectively. The model is solved using a time-dependent solver for 30 cardiac cycles to achieve solutions converged in time. Simulations were performed on a Dell PRECISION T3600, 12 processor computer with 128 GB RAM. During the solution process for the entire domain of the seven-cell EC monolayer, there were approximately 18.5 × 10⁶ elements. Post-processed results for stress, strains and deformations are obtained using post-processing features of the Comsol Multiphysics v. 5.1 package.

3. Results

3.1. Influence of flow regime of cell deformation

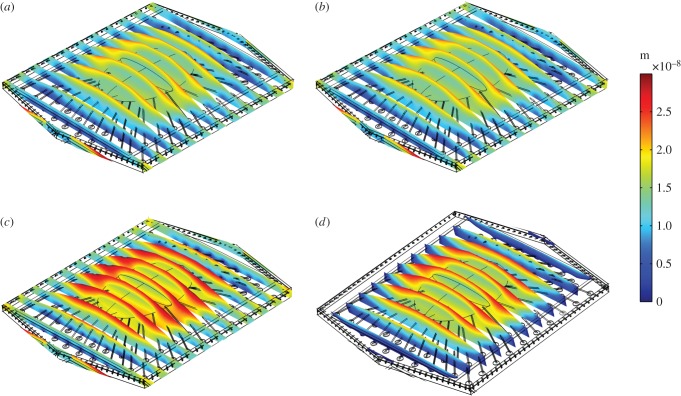
Figure 3 demonstrates the deformation of the middle EC of the monolayer in response to simulated fluid flow, at peak systole. Figure 3a shows the ECs exposed to multi-directional flow, while figure 3b–d corresponds to EC exposure to pulsatile flow with reversal, purely forward flow and steady flow, respectively. The cross-sectional views show how the displacement changes from the glycocalyx to the cell surface to the cytosol and from the centre to the boundaries of the cell. The mean deformation of the cytosol is 25 nm when the cell is exposed to steady flow. The magnitude of deformation is 30, 21 and 20 nm when the EC monolayer is exposed to purely forward flow, pulsatile flow with reversal or multi-directional flow, respectively.

Figure 3.

Displacement of the EC monolayer in response to different shear profiles. EC exposed to (a) multi-directional, disturbed flow, (b) pulsatile flow with reversal, (c) pulsatile flow with no-reversal and (d) steady flow. (Online version in colour.)

3.2. Influence of flow regime on the stress and strain distributions over stress fibres

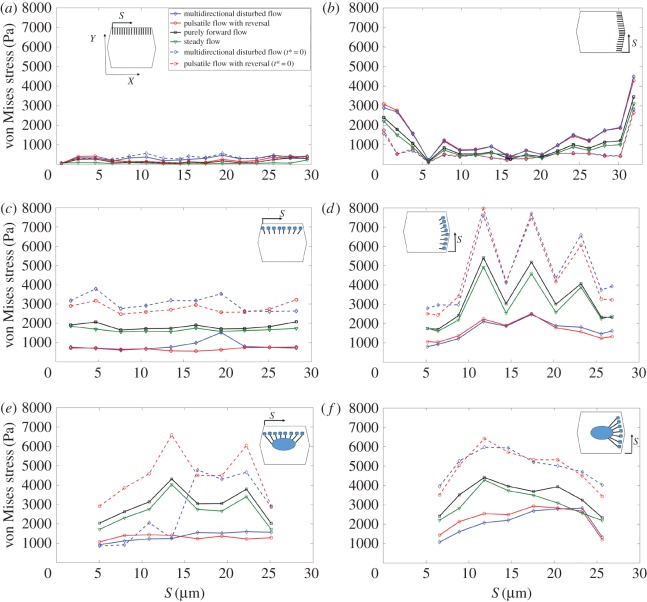
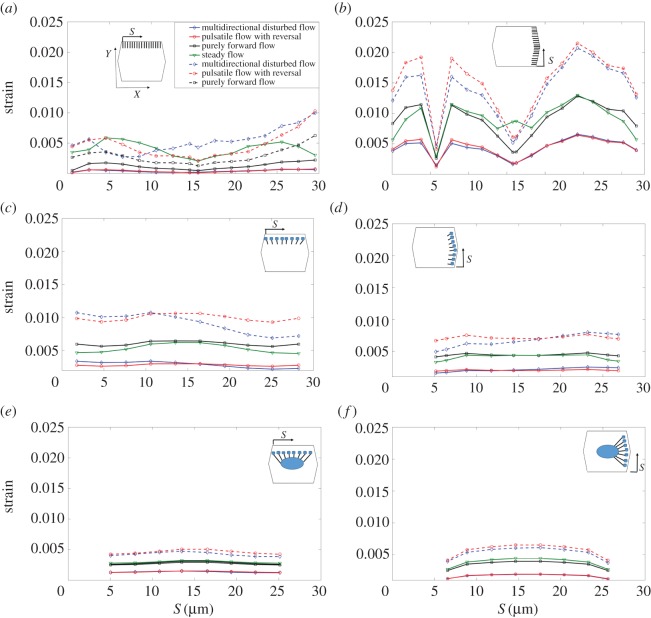
Figure 4 displays the time-averaged von Mises stress magnitude over SFs in the central cell of the EC monolayer exposed to different flow regimes. Note that the dashed curves correspond to the purely elastic results (t* = 0). Figure 4a shows stresses for SFs located perpendicular to the principal flow direction connecting the apical layer and ADJs. This is denoted by the abbreviation (SFsPP–APL–ADJs), where SFsPP are SFs perpendicular to the principal flow direction and APL–ADJ denotes the elements that are connected by the SF—in this case, the apical plasma membrane (AP) and the ADJs. Figure 4b demonstrates stresses for SFs which are located parallel to the principal FSS direction and attached to the apical layer to ADJs (SFsPL–APL–ADJs). Figure 4c shows stresses for SFs located perpendicular to the principal FSS direction and attached to the apical layer and FAs (SFsPP–APL–FAs). Figure 4d shows stresses for SFs located parallel to the principal FSS direction and attached to the apical layer and FAs (SFsPL–APL–FAs). Figure 4e shows stresses for SFs located perpendicular to the principal FSS direction and attached to FAs and the nucleus (SFsPP–FAs–NU). Figure 4f shows stresses for SFs located parallel to FSS and attached to FAs and the nucleus (SFsPL–FAs–NU). S represents the distance of SFs from the starting point of the EC edge. The maximal stresses of 5500 Pa are observed in SFs that are parallel to the long axis of the cell (SFsPL–APL–FAs) in ECs exposed to purely forward flow. In the cells exposed to steady flow, the maximal stresses of 5200 Pa are observed in SFsPL–APL–FAs. Significant differences due to flow regime are observed in stress magnitudes over SFsPL–APL–FAs, while SFsPP–APL–ADJs and SFsPL–APL–ADJs experience small differences. Note that, SFs attached to the nucleus experience high magnitudes of stress (with a maximum of 4500 Pa), independent of the alignment of SFs to the shear direction applied over cell surface. The multi-directional and pulsatile flow regimes significantly reduce stresses in the highest SFs (figure 4c–f).

Figure 4.

The time-averaged von Mises stress magnitude over the SFs in ECs. (a) SFs are located perpendicular to FSS and attached to the apical layer and ADJs (SFsPP–APL–ADJ), (b) SFs are parallel to FSS and attached to the apical layer to ADJs (SFsPL–APL–ADJs), (c) SFs are perpendicular to FSS and attached to the apical layer and FAs (SFsPP–APL–FAs), (d) SFs are parallel to FSS and attached to the apical layer and FAs (SFsPL–APL–FAs), (e) SFs are perpendicular to FSS and attached to FAs and the nucleus (SFsPP–FA–NU), (f) SFs are parallel to FSS and attached to FAs and the nucleus (SFsPL–FAs–NU). S represents the distances of SFs from the starting point of the EC edge that SFs are located along it. Note that t* is the relaxation time. The same legends and directions (X and Y) shown in the inset of a apply to all other parts. (Online version in colour.)

Time constants of mechanical stimulus transmission have been shown to play an important role in determining the dynamics of cellular responsiveness to mechanical stimulation [37–40]. The present model tested and quantified this role. Results for a purely elastic model (where the relaxation time of all subcellular structures is assumed 0) are also shown in figure 4a–f for multi-directional flow and pulsatile flow with reversal. Results of the time-averaged von Mises stress magnitude on SFs for purely forward flow are not affected by assigning the time constant values to 0. Note that there is a significant rise in stresses on SFs when either the multi-directional flow or pulsatile flow with reversal is applied over the surface of ECs without viscoelastic elements.

Figure 5 shows the time-averaged bending strain along the SFs in the EC monolayer exposed to four different shear flows. The bending strain of any SF is calculated using equation (2.6). The coordinates and displacements of endpoints of the SFs are used to calculate the strain magnitude. The maximal values of strain magnitude for all SFs are observed in EC monolayers exposed to steady flow. Multi-directional flow and pulsatile flow with reversal impose greatly reduced strains compared with steady flow. Note that strains of SFs are dramatically increased by removing the role of viscoelasticity in cells exposed to purely forward flow, pulsatile flow with reversal and multi-directional flow.

Figure 5.

The bending strain along the SFs in ECs exposed to shear stress. (a) SFsPP–APL–ADJs, (b) SFsPL–APL–ADJs, (c) SFsPP–APL–FAs, (d) SFsPL–APL–FAs, (e) SFsPP–FAs–NU, (f) SFsPL–FAs–NU. Note the same directions (X and Y) shown in the inset of a applies to all other parts. Note that t* is the relaxation time. (Online version in colour.)

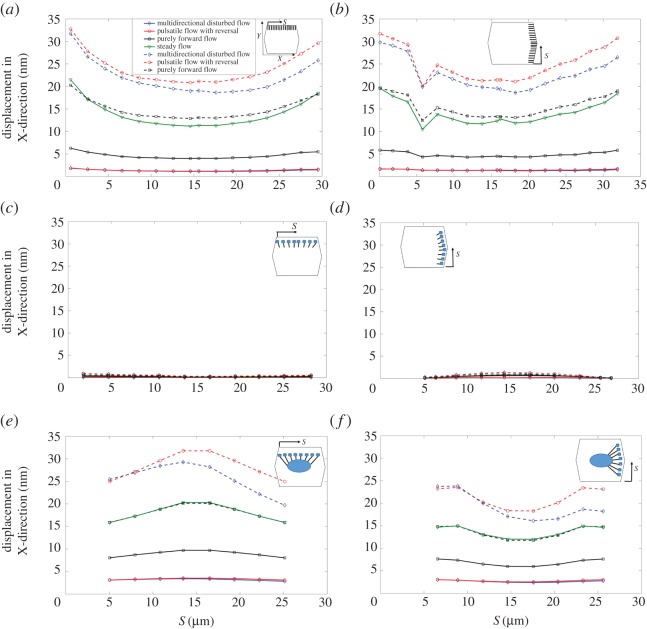
Figure 6 demonstrates the time-averaged displacement of SFs due to flow exposure. Maximum magnitudes of displacement occur in SFs perpendicular to the flow direction and attached to the apical layer and ADJ (figure 6a). SFs attached to the apical layer and FAs experience almost no displacement (figure 6c,d). The lowest mean displacement is for the multi-directional and pulsatile flow cases. Note that the displacement is calculated from the upper edge of SFs that are attached to the apical layer or nucleus. Moreover, figure 6 shows that the displacements of SFs are significantly affected by assigning the relaxation time to 0 in ECs exposed to purely forward flow, pulsatile flow with reversal and multi-directional flow.

Figure 6.

Displacement of SFs in ECs exposed to shear stress. (a) SFsPP–APL–ADJs, (b) SFsPL–APL–ADJs, (c) SFsPP–APL–FAs, (d) SFsPL–APL–FAs, (e) SFsPP–FAs–NU, (f) SFsPL–FAs–NU. Note the same directions (X and Y) shown in the inset of a applies to all other parts. Note that t* is the relaxation time. (Online version in colour.)

3.3. Influence of shear flow regime on stress transmission from the cell surface to focal adhesions and adherens junctions

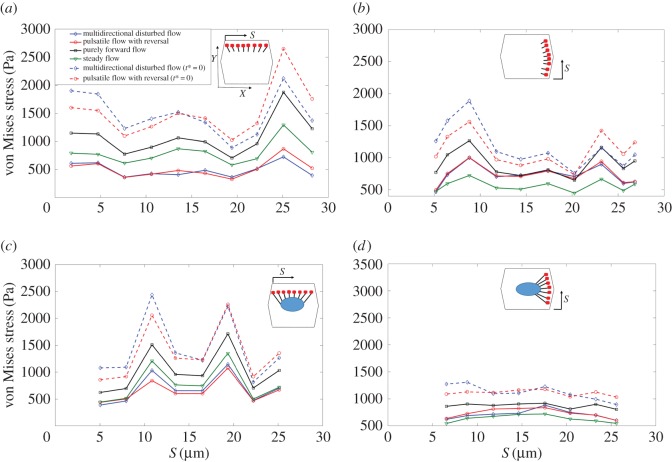
Figure 7 displays the time-averaged von Mises stress distributions over the FAs. Figure 7a shows stresses over FAs which are located perpendicular to the flow direction and are connected to the apical layer by SFs. Figure 7b shows stresses over FAs which are located parallel to the flow direction and are connected to the apical layer by SFs. Figure 7c displays stresses over FAs which are located perpendicular to the flow direction and are connected to the nucleus by SFs. Figure 7d displays stresses over FAs located parallel to the flow direction and connected to the nucleus by SFs. The maximum values of stress are observed, in figure 7a for FAs perpendicular to the axial flow direction when ECs are exposed to purely forward flow. However, the maximum values of stress in cells exposed to pulsatile flow with reversal and multi-directional flow appear in FAs attached to the nucleus by SFs and oriented perpendicular to long axis of the cell (figure 7c). Note that the von Mises stresses on FAs are not affected by assigning the time constant values to 0 in cells exposed to purely forward flow. However, there is a significant rise in stresses on FAs for multi-directional flow or pulsatile flow with reversal.

Figure 7.

The average von Mises stress magnitude over the FAs. (a) FAs located perpendicular to the flow direction and connected to the apical layer through SFs, (b) FAs located parallel to the flow direction and connected to the apical layer through SFs, (c) FAs located perpendicular to the flow direction and connected to the nucleus through SFs, (d) FAs located parallel to the flow direction and connected to the nucleus through SFs. Note that the same directions (X and Y) shown in inset of a applies to all other parts. Note that t* is the relaxation time. (Online version in colour.)

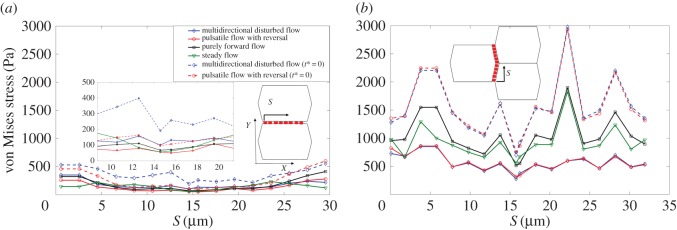
Figure 8 displays the time-averaged von Mises stress magnitude over ADJs. Figure 8a shows stresses over ADJs which are oriented perpendicular to FSS. The region of figure 8a displaying large differences among flow conditions is enlarged in the inset. Figure 8b shows stresses over ADJs which are oriented parallel to FSS. Junctions oriented parallel to FSS experience higher values of stresses in all shear conditions imposed. The highest values are observed over ADJs in cells exposed to purely forward flow. Note that ADJs which are located perpendicular to FSS experience relatively higher stresses when cells are exposed to the multi-directional flow. The von Mises stresses over ADJs significantly rise when either multi-directional flow or pulsatile flow with reversal are applied over the surface of ECs, under relaxation time equal to 0. Stresses on ADJs in cells exposed to steady flow and purely forward flow (data not shown) show no difference by assigning the time constant values to 0. But there are significant differences for multi-directional and reversing flows.

Figure 8.

The average von Mises stress magnitude over ADJs. (a) Along the upper edge (perpendicular to FSS) of the middle EC. Inset zooms at areas of high discrepancy between different flow conditions in (a) and (b) along the right-upper and right-lower edges (parallel to FSS) of the middle EC. Note that t* is the relaxation time. (Online version in colour.)

In order to understand the potential significance of the computed stresses over the SFs, FAs, ADJs and nucleus for mechanotransduction, the corresponding traction forces were determined. The traction forces are based on the integral over the contact surface area of the surface traction force magnitude 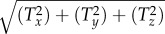, where T_x, T_y and T_z are the Cartesian components of traction force. Table 3 reports the range of time-averaged traction forces acting on the SFs, FAs, ADJs and nucleus due to exposure of ECs to four different flow regimes. In the last four rows, the relaxation times of all subcellular structures are taken as 0. Table 4 presents the range of force per integrin molecule on FAs and free filaments of ADJs due to exposure of ECs to four different flow regimes. In the last two rows, the relaxation time of all subcellular structures is set to 0. The forces calculated in table 4 are based on the assumption of 1000 integrins in a single FA [12,26,55] and 5–100 free filaments at the tip of each finger in the ADJ [12,34–36].

Table 3.

The magnitude of traction forces acting on the glycocalyx, apical layer, SFs, FAs, ADJs and nucleus. In last six rows, the relaxation time of all subcellular structures are assumed to be 0.

	cellular structure
traction force	multi-directional disturbed flow	pulsatile flow with reversal	purely forward flow	steady flow
glycocalyx	3.07 nN	2.94 nN	2.80 nN	2.03 nN
apical layer	19.22 nN	18.66 nN	11.86 nN	10.96 nN
SFs	0.53–6.6 pN	0.37–7.8 pN	0.74–25.3 pN	0.7–24.4 pN
FAs	0.7–1.35 pN	0.8–1.35 pN	0.95–2.2 pN	0.8–1.5 pN
ADJs	1.62–9.66 pN	0.48–9.10 pN	0.42–14.17 pN	0.32–14.09 pN
nucleus	25 nN	23 nN	68 nN	62 nN
glycocalyx (relaxation time = 0)	3.40 nN	3.29 nN	3.07 nN	2.22 nN
apical layer (relaxation time = 0)	13.73 nN	13.17 nN	12.19 nN	8.86 nN
SFs (relaxation time = 0)	1.9–48 pN	1.1–39 pN	0.7–25.5 pN	0.7–24.4 pN
FAs (relaxation time = 0)	1–2.4 pN	1.1–2.4 pN	1–2.8 pN	0.6–1.9 pN
ADJs (relaxation time = 0)	3.2–20 pN	0.5–19.3 pN	0.45–17.5 pN	0.3–14 pN
nucleus (relaxation time = 0)	124 nN	105 nN	97 nN	65 nN

Table 4.

The range of force per integrin molecule over FAs and filaments over ADJs depending on the location of FAs and ADJs. In last two rows, the relaxation time of all subcellular structures are assumed to be 0.

	cellular structure
traction force	multi-directional disturbed flow	pulsatile flow with reversal	purely forward flow	steady flow
per integrin molecule over FAs	0.14–0.27 pN	0.16–0.27 pN	0.19–0.42 pN	0.16–0.3 pN
per filament over ADJs	0.32–1.93 pN	0.096–1.8 pN	0.084–2.83 pN	0.064–2.83 pN
per integrin molecule over FAs (relaxation time = 0)	0.22–0.54 pN	0.20–0.54 pN	0.19–0.51 pN	0.12–0.38 pN
per filament over ADJs (relaxation time = 0)	0.64–4.0 pN	0.1–3.86 pN	0.09–3.50 pN	0.060–2.80 pN

3.4. The sensitivity of the model to the key mechanical parameters

In our previous study of steady shear on an EC monolayer [12], we performed simulations with wide variations in the Young's modulus of SFs, ADJs and glycocalyx. These parameter variations had small effects on displacement but larger effects on the von Mises stresses of certain SF connections. In this study, we have further considered the sensitivity of our results, when the cells are exposed to multi-directional flow, to the choice of viscoelastic model by comparing the displacement and von Mises stresses of SFs, ADJs, FAs and the nucleus for the Kelvin–Voigt and standard linear solid models (shown in electronic supplementary material, table B.1). Note that the same time constant is taken for both models [56]. Table B.1 in the electronic supplementary material shows that the magnitude of displacement and time-averaged von Mises stresses over SFs, FAs, ADJs and the nucleus are not significantly affected by the chosen model. Additional details about the standard linear solid model are presented in electronic supplementary material, appendix B.

4. Discussion

This study investigated mechanotransmission in ECs exposed to pro-atherogenic fluid mechanical forces using a multi-scale, multi-structural model. The role of multi-directional flow in force transmission was considered and cellular viscoelasticity effects were explored. Our study reveals that flows with the same TAWSS but different dynamic characteristics can display a wide range of time-averaged stresses, strains and displacements leading to a broad distribution of local forces on mechanotransduction elements.

The influence of blood flow regimes on mechanotransmission in ECs was investigated by exposing cells to steady flow, purely forward flow with no reversal, pulsatile flow with reversal and multi-directional. Figures 3, 4, 7 and 8 demonstrate that the amplitudes of stresses transmitted to subcellular structures are highly dependent on the nature of shear flows applied on the cell surface. In addition, the multi-structural component model of ECs allowed us to show that the viscoelastic time constants of cellular structures have a significant effect on mechanotransmission forces. Assigning time constants to zero results in large increases in the stresses transmitted to subcellular structures in comparison to viscoelastic cells in the cases of pulsatile flow with reversal parallel to the long axis of the cells and multi-directional flow with a transverse component. However, the mechanotransmission in cells exposed to purely forward flow with no reversal is not dependent on the viscoelastic time constants. A similar influence was observed in the strain and displacement magnitudes of SFs (figures 5 and 6), but purely forward flow cases also experienced increases in the strain and displacement magnitudes of SFs when time constants were set to zero.

The findings of the study reveal that the highest stresses over junctions perpendicular to the principal FSS direction occur in EC monolayers exposed to multi-directional, disturbed flow (figures 4b and 8a). These higher stresses may contribute to the findings of Yumnah et al. [9], who mapped lesion prevalence around aortic branch ostia in mature and immature rabbits. They found the best correlation between lesion location and fluid mechanics to be associated with the transWSS parameter which accounts for multi-directional flow. These stresses, however, are much lower than those induced over the junctions parallel to the principal FSS direction (compare figures 3a,b and 8a,b).

There are several very consistent and significant trends that emerge from the simulations. First, except for the junctions perpendicular to the principal FSS direction (figure 8a), there appear to be no significant differences between the pulsatile flow with reversal case and the multi-directional, disturbed flow case in any of the stresses, strains and displacements determined at any location around the cell. This finding suggests that ‘reversing’ flows and ‘disturbed’ flows, terms that are often used interchangeably, are very similar in the sense that the stresses and strains they impose on most of the cellular structural elements are similar. The second trend is that the pulsatile flow with reversal and multi-directional disturbed flow cases always result in lower stresses, strains and displacements compared with the pulsatile flow without reversal and steady flow cases even though the TAWSS is the same for all cases. The third trend is that when the viscoelastic time constants are set to zero so that all structures behave in a purely elastic manner, the pulsatile flow with reversal and multi-directional disturbed flow cases produce higher stresses, strains and displacements compared with pulsatile flow without reversal and steady flow. These three trends taken together suggest that reversing flow is the main source of low stresses, strains and displacements because viscoelastic response times dampen the development of larger stresses and strains.

Mechanotransducers in ECs respond to forces of order 1 to several of piconewton [22,27,30,34,35,41,57]. Tables 3 and 4 demonstrate that the force values over several potential mechanotransducers fall in this range. Table 4 demonstrates that a maximum force per integrin molecule of 0.27 pN and per ADJ filament of 1.93 pN are estimated by the present model. Note that integrins over FAs which are located parallel to the long axis of ECs experience the maximum forces, whereas the filaments over ADJs which are located near to the joint points of three ECs experience the maximum forces. It has been suggested that the integrin linker protein talin is the likely force sensing protein in the FA complex, and at 0–5 pN of force, rapid impact assessment matrix binding to talin R2R3 would predominate, supporting integrin activation and the assembly of nascent adhesions [58,59]. Thus, the force on integrin that the present model estimates (0.27 pN) is close to the range that is predicted to activate intracellular signalling in FAs. PECAM-1 has also been identified as a mechanosensor in cell–cell junctions [49,52,60]. It has been shown that shear stress triggers association of PECAM-1 with vimentin, which transmits myosin-generated forces to PECAM-1 [52,60]. The magnitude of the force produced by a single myosin molecule falls in the range of 0.4–4 pN [49,57]. Thus, our estimated junctional forces (1.93 pN) appear to be in the range that can activate PECAM-1. Forces in the range of 0.1–0.5 pN are reported to deform the boundaries of the microdomains of the cortical actin cytoskeleton. Our computed junctional forces (1.93 pN) are therefore in a range that can deform the actin cytoskeleton.

The role of the cytoskeleton in mechanotransduction has been suggested to extend beyond rapid force transmission to direct mechanochemical conversion [37,61]. Gouget et al. [37] indicated that mechanochemical conversion may also occur along the length of SFs. Na et al. [29] and Han et al. [62] showed that applying a stress of 20 Pa by magnetic tweezers on the apical cell surface could activate Src along SFs through binding to the mechanosensitive protein AFAP. In addition, the extent of zyxin binding to SFs is directly related to the force-induced strain in the SFs [37]. The magnitudes of stresses and the mechanical strain over SFs calculated in this study (figures 3a–e and 4a–e and table 3) are in good agreement with data reported by Weinbaum et al. [18] and sufficient to stimulate the biological activity of these proteins. Thus, our model confirms that SFs may be directly activated by FSS acting on the cell surface.

There are limitations to our study. Although we have given the detailed distribution of surface stresses imposed on the apical endothelial surface—the glycocalyx (equations (2.7a), (2.7b)), we have treated the glycocalyx as a solid layer, not considering in detail how the glycocalyx transmits force to the cell through its transmembrane syndecan components and membrane-anchored glypican components [63]. We have not considered the distribution of forces on mechanosensors in the plasma membrane [42], but rather have lumped the plasma membrane into the surface cortical layer. These assumptions were made to allow us to more easily focus on the basal and intercellular forces. We have also assumed that the FAs are bound to a rigid substrate and have not considered the influence of substrate stiffness on force distribution [64]. And, of course, our model is strictly a passive mechanical model with no active stress elements. Nonetheless, we have been able to gain important insights into mechanical force distribution and mechanosensing in ECs.

In conclusion, we have shown the distinct effects of atherogenic flow profiles (reversing unidirectional flow and reversing multi-directional flow) on subcellular structures relative to non-atherogenic flow profiles (non-reversing flow). Reversing flow lowers stresses and strains due to viscoelastic effects and multi-directional flow alters stress on the ADJs perpendicular to the axial flow direction. We estimated that these stresses produce forces on integrins, ADJ filaments and other substructures in the range that activate mechanotransduction. In addition, taking into account that activation of certain mechanotransduction molecules leads to atheroprotective phenotypes in cells [54], if reversing flow over viscoelastic cells leads to forces below the threshold for mechanoactivation of atheroprotective molecules and unidirectional flow over ECs leads to forces above the threshold, then this might in part explain why reversing flows are atherogenic and unidirectional forces are atheroprotective. Future work should consider how the forces would be altered when ECs are elongated in the direction of flow as they are in atheroprotected regions of the circulation.

Data accessibility

All data are available at: http://personal.lut.fi/users/payman.jalali/BlankPage8.htm.

Authors' contributions

M.D. led the project, developed the model, run the simulations and directed writing of the manuscript and rebuttal. P.J. contributed in model development and post-processing. P.J.B. contributed in model planning and linking to proper literature. A.R. contributed in finalizing the initial draft by giving comments on the text. J.M.T. contributed in co-leading the project in the whole process of preparing the manuscript and results, and preparing the rebuttal. All the authors contributed to discussions and commented on the manuscript.

Competing interests

We declare we have no competing interests.

Funding

No funding has been received for this article.