Modelling human skull growth: a validated computational model

Abstract

During the first year of life, the brain grows rapidly and the neurocranium increases to about 65% of its adult size. Our understanding of the relationship between the biomechanical forces, especially from the growing brain, the craniofacial soft tissue structures and the individual bone plates of the skull vault is still limited. This basic knowledge could help in the future planning of craniofacial surgical operations. The aim of this study was to develop a validated computational model of skull growth, based on the finite-element (FE) method, to help understand the biomechanics of skull growth. To do this, a two-step validation study was carried out. First, an in vitro physical three-dimensional printed model and an in silico FE model were created from the same micro-CT scan of an infant skull and loaded with forces from the growing brain from zero to two months of age. The results from the in vitro model validated the FE model before it was further developed to expand from 0 to 12 months of age. This second FE model was compared directly with in vivo clinical CT scans of infants without craniofacial conditions (n = 56). The various models were compared in terms of predicted skull width, length and circumference, while the overall shape was quantified using three-dimensional distance plots. Statistical analysis yielded no significant differences between the male skull models. All size measurements from the FE model versus the in vitro physical model were within 5%, with one exception showing a 7.6% difference. The FE model and in vivo data also correlated well, with the largest percentage difference in size being 8.3%. Overall, the FE model results matched well with both the in vitro and in vivo data. With further development and model refinement, this modelling method could be used to assist in preoperative planning of craniofacial surgery procedures and could help to reduce reoperation rates.

1. Introduction

The cranium consists of many bones that are connected together around their periphery by soft tissue structures known as sutures, which are important new bone deposition sites during skull growth and development [1,2]. It is widely accepted that various genetic and epigenetic factors regulate bone formation at the sutures [3–5], with one of the key driving factors for skull growth being provided by the rapidly expanding brain [6–8].

During the early years of life, human brain volume increases rapidly and the cranium undergoes rapid morphological changes in both size and shape, with the neurocranium in particular required to expand to provide protection for the brain [9]. The neurocranium is normally 25% of its adult size by birth, 50% by six months and 65% by 1 year, with minimal further growth after 10 years [10,11]. Developmental and growth disorders, as well as some infections, can lead to the occurrence of abnormal skull shapes such as those observed in microcephaly, hydrocephalus and craniosynostosis [12–14].

Understanding the relationship between the biomechanical forces, especially from the growing brain, the soft tissue structures and individual bone plates, and their influence on the growth and shaping of the skulls of infants is clearly important. It would not only help our basic understanding of the biomechanics of normal skull growth, but also be useful in the management of pathological conditions such as craniosynostosis, and in craniofacial reconstruction procedures.

The finite-element (FE) method is a powerful numerical technique used to analyse a wide variety of engineering problems [15] and is now becoming increasingly applied in the life sciences to reveal the biomechanical performance of skeletal elements. In brief, this method works by dividing the geometry of the problem under investigation (e.g. a skull) into a finite number of subregions, called elements. The elements are connected together at their corners and sometimes along their mid-sides, called nodes. For stress analysis, a variation in displacement (e.g. linear or quadratic) is then assumed through each element, and equations describing the behaviour of each element are derived in terms of the (initially unknown) nodal displacements. These element equations are then combined to generate a set of system equations that describe the behaviour of the whole problem. After modifying the equations to account for the boundary conditions applied to the problem, these system equations are solved. The output is a list of all the nodal displacements. The element strains can then be calculated from the displacements, and the stresses from the strains.

The FE method has the potential to predict the morphological changes during skull growth. Here, the brain or intracranial volume (ICV) can be modelled and used to load the overlying cranial bones and joints, to predict overall skull shape. However, FE models need to be validated against laboratory and in vivo data to build confidence in their results [16–20]. While there are several studies using FE analysis to model the human infant skull [20–24], to the best of our knowledge no one has attempted to use it to model normal human skull growth.

The overall aim of this study was to understand the biomechanics of skull growth. The specific aim of the study was to develop a validated computational model of skull growth during the early postnatal period (0–12 months) based on the FE method. This was undertaken in two steps (figure 1). The first involved a three-dimensional printed physical experimental model (in vitro) and matching FE model (in silico (A)), both of which were based on the same micro-CT scan of an infant's skull. This set-up was used to test whether the in silico (A) model could correctly predict the size and shape changes of the in vitro physical model under the same loading conditions. In the second step, the FE model was further developed (in silico (B)) and compared against a series of patient-specific CT (in vivo) data (n = 56) to predict the change in cranial size but more importantly overall cranial shape during growth in the age range of 0–12 months.

Figure 1.

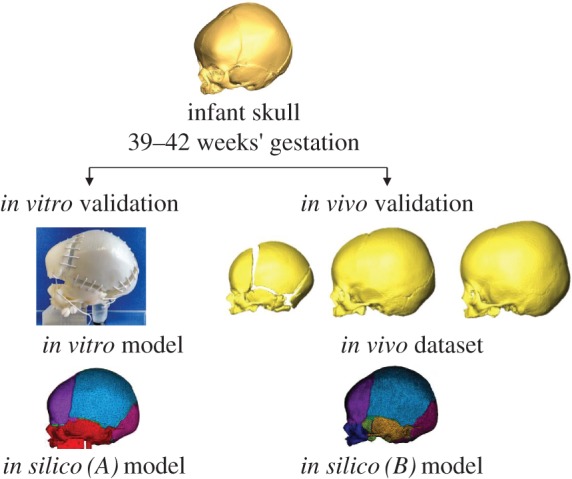
Workflow of the study: two in silico FE models were created with the same micro-CT scan. The left branch shows the validation with a three-dimensional printed in vitro model and the right branch shows some of the in vivo CT skulls used to validate a second FE model.

2. Material and methods

2.1. Image processing

An infant skull with an estimated age of 39–42 weeks’ gestation and unknown sex was scanned in an X-Tek HMX160 micro-CT scanner (XTek Systems Ltd, Tring, UK) at the University of Hull, UK, at a resolution of 0.132 mm. The resultant stack of two-dimensional images was imported into the image-processing software Avizo (FEI Ltd, Hillsboro, OR, USA) to develop the three-dimensional models. The specimen used to develop the models was loaned from the University of Dundee, UK, and was from an archaeological source (skull ID: SC-108). Ethical consent was therefore not required.

The skull was divided into four sections: skull vault bones, cranial sutures, skull base and ICV. The first section consisted of five cranial bones: two frontal, two parietal and the occipital bone, which were segmented separately. The frontal bones were separated by the metopic (or frontal) suture, which can fuse between three and nine months of age [25]. The sutures and fontanelle were segmented as individual materials to allow for them to be manipulated separately. The skull base consisted of the rest of the occipital bone, both temporal bones, the sphenoid and the ‘face’ with the respective connecting sutures also segmented individually. The ‘face’ included the maxillofacial bones (lacrimal, ethmoid, vomer, nasal bones, palatine bones, maxilla and zygomas) and connecting sutures which were all segmented as a single piece due to the study's focus on neurocranial growth. Finally, the ICV was defined as a single material to allow it to be expanded to simulate the brain growth. The resultant skull dataset was used to develop both the in silico and in vitro physical models described in the following sections.

2.2. In vitro three-dimensional printed physical model

For the first validation phase of the study (in silico (A) model versus in vitro physical model), the individual bones and sutures of the skull base were combined into a single structure and a solid block was further segmented onto the palate to allow the model to be mounted securely during experimentation.

The segmented skull vault and skull base bone sections were then three-dimensionally printed (Stratasys Objet 500; Stratasys Ltd, Edina Prairie, MN, USA). The material chosen to represent the bone was VeroWhitePlus RGD835 (Stratasys Ltd, Edina Prairie, MN, USA), which has a Young's modulus of 3000 MPa, similar to that of infant cranial bone [26]. The cranial sutures were simulated with 1 mm thick elastic thread, a 5 mm length of which was found to have a Young's modulus of 10.38 MPa (measured on a TA Instruments Q800 Dynamic Mechanical Analyser; TA Instruments, DE, New Castle). This allowed the in vitro physical model to expand (figure 1). Before closure of the skull, a custom-made silicone brain-shaped balloon (manufactured from a clay mould of the endocranium) was inserted under the cranial vault. Water was injected into the balloon via a syringe to increase its volume to the ICV values of infants aged zero, one and two months (using data reported by [27]). These values were 408, 507 and 581 ml for females, and 476, 569 and 651 ml for males [27]. Before water was added, the system was primed to remove the air. Sensitivity tests regarding the repeatability of the model found a standard deviation of ±1.9% in the measurements recorded. At the end of each volume expansion, the in vitro physical model was scanned by micro-CT, so that the geometries could be compared with the in silico (A) predictions.

2.3. In vivo CT skull dataset

For the second part, anonymous clinical CT data from 56 infants (see electronic supplementary material, appendix tables 1 and 2) were obtained from Necker—Enfants—Malades University Hospital in Paris (Assistance Publique—Hôpitaux de Paris, Université Paris Descartes). This observational study was approved by a local ethical committee (CPP ‘Ile-de-France VIII’, Hôpital Ambroise Paré, Boulogne-Billancourt, France). The population was aged from less than 1 day old to 11 months and 27 days old, with 27 males and 29 females. The most common reasons for the head CT scan were minor trauma (n = 11 males, n = 12 females), followed by epilepsy (n = 4 males, n = 2 females) and nausea (n = 2 males, n = 4 females). In all cases, the brain and skull were judged to be normal. Skulls in this dataset were similarly reconstructed using Avizo. ‘Average’ skulls were found (based on length, width and circumference measurements) for each month of age for use as a direct comparison with the in silico (B) model. There were, however, no male skulls that came within the 10-month-old and 12-month-old age category, and no seven-month-old female skulls.

2.4. In silico finite-element models

Two FE models were developed in this study based on the infant skull described in §2.1. The first (in silico (A)) was used for comparison with the in vitro physical model (§2.2) and the second (in silico (B)) for comparison with the in vivo data (§2.3). In both cases, the three-dimensional geometries were converted into a tetrahedral mesh using Avizo, for input into ANSYS FE software (ANSYS 17 Mechanical; ANSYS, Inc., Canonsburg, PA, USA) as quadratic tetrahedral elements. Mesh convergence was performed by increasing the number of elements and observing the convergence of the results in the normal way. The final models had over 1 040 000 elements. All sections in this model were assigned isotropic material properties.

In the first FE model (in silico (A)), a value of 3000 MPa was specified for Young's modulus of the VeroWhitePlus RGD835 ‘bone’ material, with 100 MPa specified for the ICV, modelled as a brain/dura mater composite, found through sensitivity tests. With the in vitro physical model, elastic thread was used to simulate the cranial sutures, which had a Young's modulus of 10.38 MPa (see §2.2). The individual threads were originally modelled using LINK (spring) elements; however, after conducting sensitivity tests, this modelling approach was found to have little effect on the predictions of skull expansion when compared with equivalent SOLID elements. Therefore, the SOLID elements which were already in place from the imported tetrahedral mesh were used to model the sutures. Where multiple thread strands were used in the physical model, the modulus of the equivalent area of suture in the in silico (A) model was calculated accordingly. A Poisson's ratio of 0.3 was used for bone [28] and 0.48 for the elastic thread material and the ICV. The ICV was prevented from expanding through the foramen magnum and airways by constraining the material in the perpendicular direction at these points, with the skull being constrained in all directions at the block on the cranial base and loaded via an equivalent thermal expansion of the ICV material (initial volume = 358 ml). To simulate brain growth, increasing thermal expansion was specified for the ICV material in the in silico models to increase its volume. An isotropic linear expansion was assumed to generate the expansion of the brain material using the following standard equation:

2.1

where α is the expansion coefficient and ΔV is the change in volume, equal to the target volume of the next age V2 minus the current volume V1. The change in temperature ΔT was set at an arbitrary constant value of 100°C, and α was then calculated to give the necessary volume change. The target volumes were determined from values in the literature [27] for the in silico (A) versus in vitro physical model, with actual ICV values determined from the patient CT scans for the in silico (B) versus in vivo skulls. In this way, the ICV material was expanded at each age simulating the growth of the brain. To facilitate comparison between the in vitro physical and in silico (A) models, both were aligned using the fixed block on the skull base.

In the second FE model (in silico (B)), used for validation with the in vivo CT data, the material properties for cranial sutures were updated and the cranial base was modelled as individual bones and sutures (these were all assumed as one piece in the in silico (A) model— figure 1). The same material properties as those of the in silico (A) model were used for the bone and ICV, with a Young's modulus of 30 MPa and Poisson's ratio of 0.3 specified for the sutures [29,30]. The ICV was expanded in the same way with similar constraints at the foramen magnum and airways, while the skull was constrained at the basilar part of the occipital bone. The model was loaded via thermal expansion of the ICV at intervals of 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11 months of age for males and 0, 1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 12 months for females with the target expansion values taken from the average skulls of the clinical CT dataset (§2.3). The average skulls for each group had ICVs of 395, 521, 608, 801, 840, 769, 878, 925, 920, 912 and 1017 ml for male skulls, and 399, 635, 692, 702, 772, 790, 818, 899, 915, 956, 945 and 1030 ml for female skulls corresponding to each age interval. Unlike the previous validation study, there was no common alignment point for the in silico (B) models and in vivo data. Cephalometric analysis involves using anatomical landmarks that are mostly located on the face of the patient. One of the most frequently used reference planes is the Frankfort horizontal plane, which is taken from the most inferior point on the lower part of the orbit to the most superior point of the external auditory meatus [31]. The face of the in silico (B) model, however, does not increase in size. Thus, to take the position from the lower orbits would not be an accurate measure of where they should be. Therefore, the in silico (B) model and the in vivo skulls were orientated along the nasion (figure 2), the most anterior point of the frontonasal suture, and the subspinale, which is the deepest point on the concave outline of the upper labial alveolar process [31]. Once the skulls had been orientated in the correct planes, they were then aligned with one another using the centroids of the basilar part of the occipital bone on the skull base (figure 2). This bone was chosen as it does not change its relative position in the skull during the first few years of growth [9].

Figure 2.

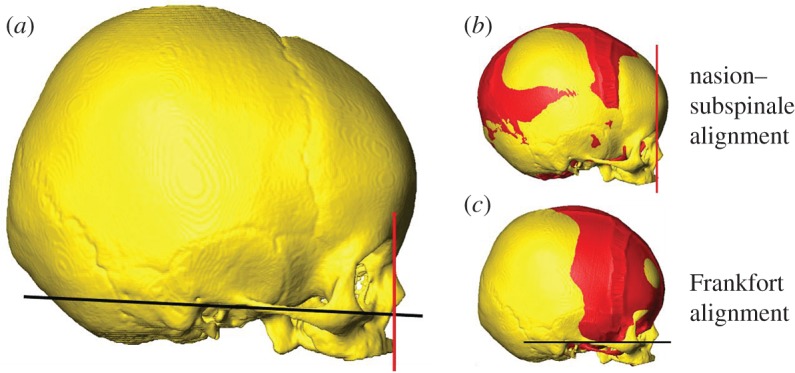
Orientation of the in silico (B) and in vivo skulls. The red line passes through the nasion and the subspinale and defines the orientation of the skulls in this study. The Frankfort plane is shown in black and should be parallel to the ground for a normal head position. (b) and (c) show the in silico (B) model (seen in red) and the in vivo skull aligned with each other using the two orientations described.

2.5. Analysis of size and shape changes

For every skull model (in silico (A and B), in vitro physical model and the in vivo CT scans), the size and shape of the cranial vault was recorded. For size measurements, the maximum length, width and circumference of the skulls were taken and used for comparison with their corresponding skull as mentioned in the previous sections. For the in silico (B) versus in vivo study, we conducted additional statistical analysis via a non-parametric pairwise test (Wilcoxon signed-ranks test) to test for differences between the paired data (e.g. in vivo width versus in silico (B) width etc.). A Bonferroni correction was applied to avoid the accumulation of statistical error. All of the statistical analysis was done in R (R Development Core Team, 2012). We did not conduct any statistical test on the in silico (A) versus in vitro physical model as the amount of data we had collected was too small for any meaningful statistical result to be found. Therefore, the percentage differences in the widths, lengths and circumferences at each age were calculated. The percentage differences were also calculated for the in silico (B) versus in vivo data.

Three-dimensional distance plots were created using Avizo to quantify the change in shape and to visualize the differences between the skulls. Models were aligned with one another and the points on the first surface mesh were measured to the closest point on the second surface. The areas at which the two surfaces differed (both positively and negatively) could be clearly seen and used to show where the in silico models over- or under-predicted skull growth. The maximum differences (mm) in both the positive and negative directions were calculated and used on the colour map scale.

3. Results

3.1. In silico (A) versus in vitro physical model (first validation study)

3.1.1. Size analysis

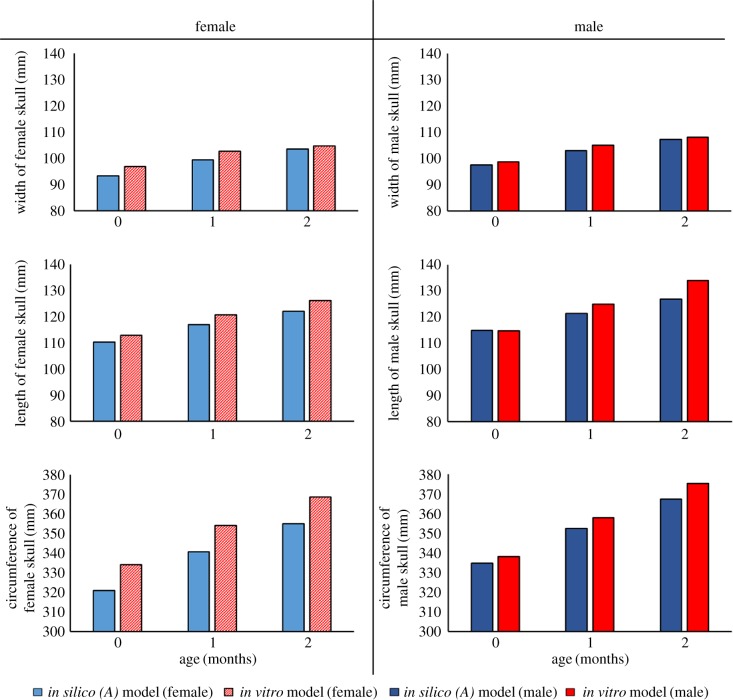
When comparing the predicted widths of the skulls (figure 3), the largest percentage difference between the in silico (A) model and in vitro models was 3.7% and 4.9% for male and female models, respectively. Overall, the male in vitro physical model increased in width by 6% compared with 8.9% for the male in silico (A) model. The female in vitro physical model increased in width by 7.7%, while the female in silico (A) model increased by 10%. Finally, the smallest percentage difference with regard to the prediction in width was observed at the ages of two months for females, being 2.5%, and one month for males, at 0.6%.

Figure 3.

In silico (A) versus in vitro physical model bar plots: the width, length and circumference parameters are recorded in the rows, while the female and male results are shown in the columns. Note the y-axis does not start at 0 mm.

The largest overall difference between the in silico (A) and in vitro physical models was found when observing the length. The zero-month-old male in silico model had a difference of only 1.3% compared with 7.6% for the two-month-old male. The largest female difference was less than half of that of the male model, being 3.3%, while the smallest difference was 2%. The in vitro physical model recorded a change in length of 15.2% and 10.9%, with the in silico (A) model increasing by 9.5% and 9.6% for males and females, respectively.

All of the in silico (A) circumference measurements were within 5% of the measurements recorded by the in vitro physical model. The largest difference for the male model comparisons was 4.8%, while the smallest was 4.3%; the female model comparisons had a largest difference of 4.9% and the smallest was 4.6%. Despite the female in silico (A) model producing slightly higher percentage differences, it produced the closest comparable percentage increase for the circumference. The in vitro physical model increased by 9.4% for the ages of zero to two months, while the female in silico (A) model increased by 9.6%.

3.1.2. Shape analysis

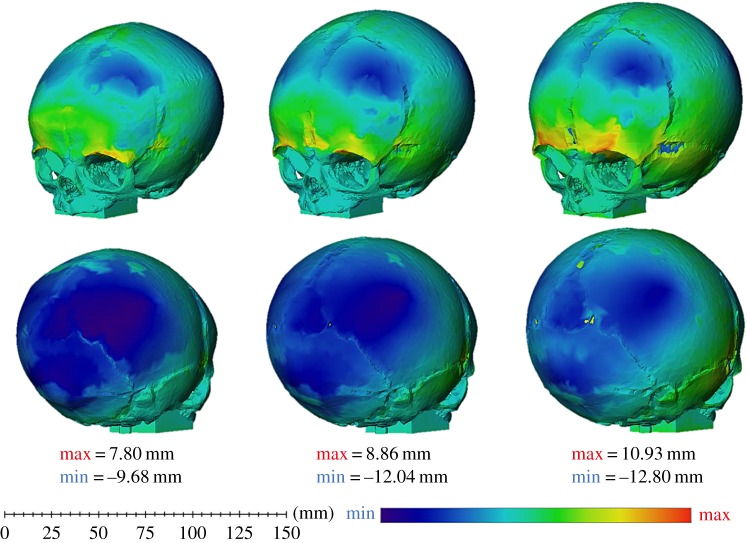
Only the three-dimensional distance plots (figure 4) of the female skulls are presented due to the male skulls producing similar results. Here, the blue areas highlight where the in silico (A) model under-predicts the in vitro physical model shape after expansion. The red areas show where the in silico (A) model over-predicted the shape, and the green areas display where there is little to no difference between the two models. It is important to note that the colour scale is set individually for each age. While it may appear that the zero-month-old in silico (A) skull under-predicted the in vitro physical skull more than the two-month-old in silico (A) skull due to the larger blue patch on the parietal and occipital bones, this is not the case as shown by the maximum and minimum values for the colour scale.

Figure 4.

In silico (A) versus in vitro physical model: three-dimensional distance plots. The red sections highlight where the in silico (A) model over-predicted the shape of the in vitro physical model, while the blue areas indicate where the in silico (A) model under-predicted how the in vitro physical model expanded. Each skull has been scaled individually with the maximum and minimum scores for the colour chart given under each age.

The blue areas located on the posterior part of the parietal bone and the occipital bone, for all ages, correlate to the size measurements taken showing that the in silico (A) skull does not grow as much as the in vitro physical model at the posterior part of the skull. The in silico (A) model over-predicted the in vitro physical model towards the anterior part of the skull with the maximum over-prediction located above the orbits. Interestingly, the in silico (A) skull also over-predicted the expansion of the width of the skull in the medial–lateral direction. This is most clearly seen when viewing the temporal region on the one-month-old and two-month-old skulls.

3.2. In silico (B) versus in vivo (second validation study)

3.2.1. Size analysis

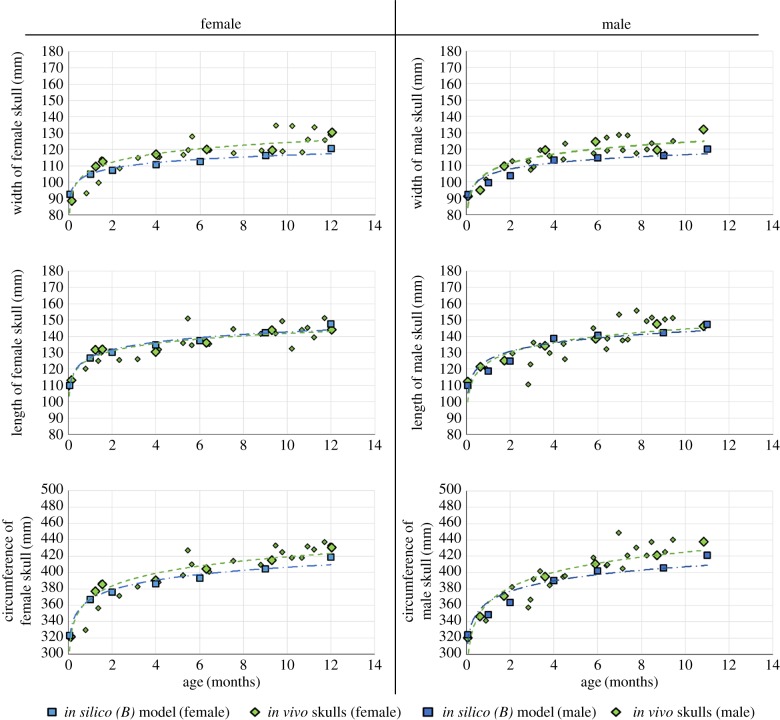
A comparison of the results of the in silico (B) model growth predictions at each of the seven average ages (0, 1, 2, 4, 6, 9 and 12 months) is presented in figure 5. Values of skull width, length and circumference are shown, for males and females, and compared with the CT data. The large green rhomboid shapes indicate the most ‘average’ skulls against which the in silico (B) models were compared. For the width measurement, the largest percentage difference between the average in vivo CT skull data and in silico (B) models was 6.7% for males and 5.1% for females, at the oldest ages. The smallest differences were only 1.6% for male models located at zero months of age and 0.2% for female models at nine months of age. When comparing the length of the skulls, the largest difference was observed at nine months of age for the in silico (B) male model, being 5.4%, and the female models had a maximum difference in length of 4.8% recorded at one month of age. The smallest difference in the prediction of the length of the skull was 0.2% for the male in silico (B) models, located at six months of age; and for the female in silico (B) models, a difference of 0.4% was recorded at six months of age. Finally, the circumference was compared. Out of the male in silico (B) models, the largest difference in circumference when compared with the in vivo models was 4.2% when comparing the models at the oldest age of 11 months. The predicted greatest circumference difference for the female models was 2.5%, found when comparing the in silico (B) and in vivo skull at six months of age. The smallest differences in circumference between the in silico (B) models and in vivo scans were both 0.5% at four months of age (male models) and zero months of age (female models).

Figure 5.

In silico (B) versus in vivo: width, length and circumference are shown in the rows, while the columns show the female and male results for each parameter. The larger green rhomboid shapes are the in vivo ‘average’ skulls with which the in silico (B) model was compared. Green, in vivo data; light blue, female in silico (B) models; dark blue, male in silico (B) models. Note that the y-axis does not start at 0 mm.

3.2.2. Statistical comparison

The results (table 1) from the Wilcoxon signed-ranks test gave p-values of 0.21, 0.37, 0.10 and 0.21 when testing the male widths, lengths, circumferences and ICV values, respectively, across all 11 ages. For the females, the p-values were 0.22, 0.21, 0.008 and 0.13 for the width, length, circumference and ICV comparisons, respectively, across the 12 monthly ages. Thus, out of the eight tests conducted, only the female circumference comparison showed a significantly different (p < 0.05) result between the in silico (B) versus in vivo results.

Table 1.

Statistical analysis in silico (B) versus in vivo. The results from the Wilcoxon signed-ranks test with Bonferroni corrections are given.

comparison	median (mm)	CI (95%)	p-valuea
male
width	4.3	−1.4 to 8.8	0.21
length	1.4	−2.3 to 8.0	0.37
circumference	8.6	−2.0 to 14.6	0.10
ICV	0.6	−0.1 to 0.7	0.21
female
width	0.5	−2.0 to 0.5	0.22
length	2.9	−0.6 to 5.2	0.21
circumference	7.4	4.4 to 9.4	0.008
ICV	0.3	0.1 to 0.5	0.13

^aAfter Bonferroni correction.

3.2.3. Shape analysis

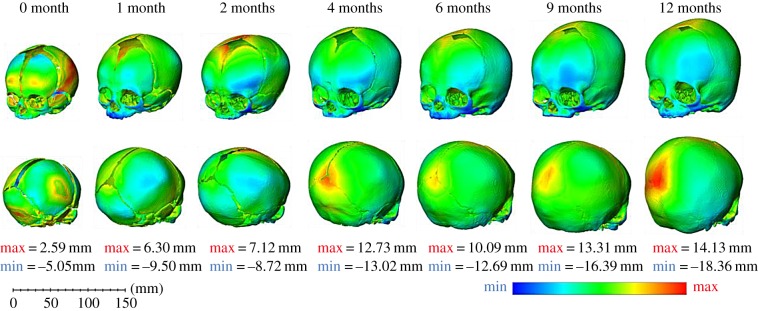
The differences in shape between the in silico (B) and in vivo datasets are shown by three-dimensional distance plots (figure 6). The differences produced by the male models were not dissimilar from those produced by the female results, and hence only the female skulls are shown. The red areas show where the in silico (B) skull over-predicted the in vivo skull shape, whereas the blue areas show where it under-predicted the in vivo skull shape. The area at which in silico (B) is most likely to under-predict the in vivo skull is the face. This is not surprising as the face of the in silico (B) model did not grow. Disregarding the face, the areas of under-prediction differ with age. At zero months of age, the height of the frontal bones near the anterior fontanelle are taller in the in vivo skull. As the age increases, the area of under-prediction tends to move down the frontal bones to just above the orbits, indicating that the front of the in silico (B) model does not flatten as much as the in vivo skulls do. Towards the posterior part of the skull, the areas of under-prediction again change with age. From zero to four months, the bony eminences of the parietal bone protrude more than for the in silico (B) skulls. As the age of the skulls increases, the eminences become flatter, which reduces the blue areas around this part. It is interesting to note that, like the in silico (A) model previously, the width of the base of the skull, especially at the temporal bones, is tending towards over-prediction. After two months, however, the in vivo skull base starts to outgrow the in silico (B) model at these areas. While the maximum under-prediction distances appear larger than the maximum over-prediction, it should be noted that the colour scales are set individually to each age.

Figure 6.

In silico (B) versus in vivo—three-dimensional distance plots: the blue areas on the plots highlight where the in silico (B) model under-predicted the in vivo CT data and the red areas indicate where the in silico (B) skull over-predicted the geometry of the in vivo CT data. Each skull has been scaled individually with the maximum and minimum values for the colour chart displayed below each age.

The areas of over-prediction also vary with age. On the zero-month-old skull, the maximum area of over-prediction is on the left parietal bone, followed by that on the occipital bone. For the one-month model, these areas move more towards the posterior and anterior fontanelles. At two months, the anterior fontanelle is the location of the largest over-prediction between the models. For the 4-month to 12-month-old models, the areas stay mostly in the same positions with the main difference being located at the posterior fontanelle, while the second highest area remains at the anterior fontanelle.

4. Discussion

A series of FE models were developed to model the rapid skull growth that occurs during the first year of life due in part to the biomechanical forces created by the expanding brain. An FE model (in silico (A)) was validated against an in vitro physical model, which simulated early skull growth. The model was then developed further (in silico (B)) to predict growth from 0 to 12 months, and compared with in vivo clinical CT data. Both models were validated by comparing both size and shape, with the change in shape being the main focus of the study.

The congruence between the in silico (A) and in vitro physical models gives us confidence in the FE modelling approach, with the measurements predicted at each age being less than 5% of the in vitro physical model measurements, with one exception of 7.6%. The lowest difference was only 0.6% smaller than the result given by the in vitro physical model. Both models had similar shapes when considering the three-dimensional distance plots. The differences between the two models may have been caused by the weight of the water used to expand the skull coupled with a lack of support at the posterior section of the skull in the in vitro physical model.

The in vivo CT dataset was also compared with the literature regarding normal skull growth. However, very few studies have been conducted in this area. Dekaban [11] carried out one such study, although there were some inconsistencies in the results, such as the one-month-old female skull, which was smaller than expected. The reasons for this reduction in size were unclear but both the clinical in vivo data and the results from another study [32] suggest that the skull continually increases in size during the first year. Disregarding this anomaly, the highest percentage difference was 8.9% observed in the male micro-CT scan at six months of age. The largest difference in the female micro-CT scan was 7.9%; however, the disparities between the in vivo and literature data are most likely to be caused by the unequal values given for the ICV. Also, the results from Dekaban [11] were physical clinical measurements which would have increased the results slightly with the inclusion of hair, skin, muscle tissue etc. This would therefore explain some of the discrepancies with our data.

The comparison between the in silico (B) and in vivo models, investigated in the second phase of the study, was used to validate the prediction of skull growth up to 12 months of age. The smallest differences were 0.3% for the male and 0.8% for the female in silico (B) model comparison. The largest percentage difference was 8.3% for the male and 5.1% for the female in silico (B) model. This is likely to be due to the isometric modelling of brain growth in this study, using the thermal expansion method, whereas in reality it is an anisotropic phenomenon caused by different regions of the brain developing at different rates along with restriction of the growth caused by the fusing sutures [33,34]. This growth of the brain can be seen in the three-dimensional distance plots (figure 6). As the skull age increases, the lambdoid sutures at the posterior part of the skull begin to close in response to the forces rising from the growing brain on the dura mater and the sutures [35]. This gradual bone formation at the sutures restricts the growth in this direction, causing the brain to grow perpendicular to the fusing suture.

The positive median differences (table 1) indicate that, on average, all of the in silico (B) skulls were smaller than the in vivo CT scans although this difference is not significant with the exception of the female circumferences. Despite a finding of a significant difference (p = 0.008) when comparing the female in vivo circumferences against those predicted by the female in silico (B) models, the largest percentage difference between the measurements taken was 3% (12.9 mm). Therefore, the difference (albeit statistically significant) between the female in vivo and in silico (B) models is very small. The shape analysis carried out on the skulls also produced small differences. The largest difference recorded was an under-prediction of 18.4 mm. This, however, was located on the face of the skull, so it is most probably smaller than this because of the study's focus on cranial vault expansion.

In the current model, the growth of the skull was achieved by expanding the ICV material to the volume of the next age in monthly stages so that there could be a direct comparison between the models and in vivo data. Clinically, growth happens as a continual process for normal skulls [10,11,32]. Using a rate of expansion, instead of specific target volumes, could be more appropriate for future models as it would allow for the prediction of the skull growth without knowing the final ICV. Another consideration for future models is brain and ICV volumes in patients with craniosynostosis and the rate at which the brain grows. From the literature, the volume of the brain and the ICV of a patient with craniosynostosis depend on the severity and type of fusion. For example, non-syndromic isolated sagittal suture fusion causes larger than average ICVs [36], whereas unilateral coronal synostosis shows no significant difference compared with normal ICVs and brain volumes [37]. Therefore, when trying to model the growth of a synostotic skull such considerations must be taken into account.

One additional approach to quantifying the change in shape would be to use geometric morphometrics (GM). GM is primarily used in the biological sciences and is the quantitative analysis of biological forms [38]. The process involves placing landmarks (two dimensional or three dimensional) at specific anatomical points located on the biological form. The problem with using this method to measure the changes in infant cranial vault shape is the lack of anatomical points available. Many of the landmarks found on the human skull are located on the face and cranial base. There are a few exceptions to this: the Bregma and Lambda locations [39–41]; however, these are located at the points where the coronal and sagittal sutures intersect (Bregma) and the midline point where the sagittal and lambdoid suture (Lambda) intersect [41] and, therefore, will not be in the same position on each infant skull. Li et al. [42] did landmark the infant calvaria without using the landmarks on the cranial face or base, but the method described is very subjective as to the placement of the landmarks along the suture and difficult to replicate. One reason for this is suture fusion rates are different for each person and the interdigitated patterns vary from person to person. The method used by Li et al. [42] offers a clever and simple solution to the suture fusion problem by taking landmarks on either side of the suture and calculating the midpoint. As the sutures fuse on the older skulls, there would remain a landmark in the centre of the suture. The question still arises, however, as to where precisely to place the landmarks along the suture. A more appropriate method to use was presented by Loyd [43], as it is an automated process and removes user error.

Even with the close comparisons between these results, there were several limitations to our modelling approach:

1. Alignment of the skulls. As mentioned previously in §2.6, cephalometric analysis involves using anatomical landmarks that are mostly located on the face of the patient with the Frankfort horizontal reference plane commonly used [31]. The face of the in silico (B) model does not increase in size, however. Thus, to use the position of the lower orbits would lead to the two datasets being orientated in different directions and therefore very few meaningful comparisons could be made. For completion and due to it being a well-regarded anatomical plane, three-dimensional distance plots for the in silico (B) models and the in vivo skulls aligned in the Frankfort plane can be seen in the electronic supplementary material, appendix 2.

2. Isotropic expansion of the ICV material. While different sections of the brain are known to grow at different rates [33,34], it would be extremely difficult to incorporate this differential expansion into the model due to the quality of our original CT being unable to detect the soft tissue of the brain, so an accurate representation of the morphology of the ex vivo skull's brain is not possible.

3. The model itself consisted of only bone, suture and an ICV material, while no soft tissues (e.g. skin, muscles or dura mater) were considered.

4. Only the ICV grew. The cranial bones did not increase in thickness and their shape remained roughly the same during the 12-month expansion. There was also no gradual fusion of the suture material.

The results of this study suggest that further development and application of suitably constructed patient-specific models might be useful with pre-surgical planning for craniofacial surgery procedures, such as in craniosynostosis surgery. Despite the simplifications and limitations of the model, the results are reasonable, and show a good prediction of actual cranial vault growth in both size and shape. Model development and incorporation of more tissue structures can be expected to increase the model's accuracy further. With the approach used here, prediction of the severity of the deformity could be used to aid surgeons with their treatment plans. One consideration when planning for craniofacial surgery is to obtain an age-matched normal skull adapted to the skull dimension of the patient to offer a visual guide as to how best to correct the cranial bones to produce a normal-shaped skull [44]. This approach would be of great help in clinical practice by solving the issue of the expected result when preparing for skull vault surgery for craniosynostosis, and, with future development, could be used to predict the growth of the skull post surgery.

Data accessibility

The datasets supporting this article have been uploaded as part of the electronic supplementary material, appendix 1.

Authors' contributions

J.L., M.M., M.J.F., D.J. and R.H.K. designed the study. J.L. performed the study. J.L. and A.M. performed the analysis. J.L., M.M., M.J.F., D.J. and R.H.K. wrote the paper. All authors gave their final approval for publication.

Competing interests

The authors have no competing interests.

Funding

This work was supported by the Royal Academy of Engineering (grant no. 10216/119 to M.M.) and the University of Hull (to J.L.).