Conformational model of the Holliday junction transition deduced from molecular dynamics simulations

Abstract

Homologous recombination plays a key role in the restart of stalled replication forks and in the generation of genetic diversity. During this process, two homologous DNA molecules undergo strand exchange to form a four-way DNA (Holliday) junction. In the presence of metal ions, the Holliday junction folds into the stacked-X structure that has two alternative conformers. Experiments have revealed the spontaneous transitions between these conformers, but their detailed pathways are not known. Here, we report a series of molecular dynamics simulations of the Holliday junction at physiological and elevated (400 K) temperatures. The simulations reveal new tetrahedral intermediates and suggest a schematic framework for conformer transitions. The tetrahedral intermediates bear resemblance to the junction conformation in complex with a junction-resolving enzyme, T7 endonuclease I, and indeed, one intermediate forms a stable complex with the enzyme as demonstrated in one simulation. We also describe free energy minima for various states of the Holliday junction system, which arise during conformer transitions. The results show that magnesium ions stabilize the stacked-X form and destabilize the open and tetrahedral intermediates. Overall, our study provides a detailed dynamic model of the Holliday junction undergoing a conformer transition.

INTRODUCTION

Homologous recombination is an essential process in maintaining genomic stability and its defects can lead to serious human diseases including cancer. To cope with DNA damage encountered during genome duplication, a four-way (Holliday) junction is formed between two nearly identical DNA molecules. Homologous recombination is also an important means for generating genetic diversity to provide raw material for evolution (1,2). The Holliday junction can undergo spontaneous branch migration in which the branch point can hop forward or backward in a stochastic way (3). Extensive branch migration over long stretches of DNA requires branch migration enzymes that provide a direction in an otherwise random walk. The Holliday junction is resolved into two duplex DNA molecules via the action of junction resolving enzymes (4), and the extent of genetic information exchange depends on the orientation of resolution.

In order to understand how proteins process Holliday junctions, one needs to know the physical and geometrical properties of the junctions themselves. The Holliday junction free in solution adopts multiple conformations [see (5) and references therein]. Under low salt conditions and in the absence of multivalent ions, the junction extends to an open form, minimizing the repulsion between the negatively charged phosphates concentrated at the junction (6,7). In the presence of multivalent cations or in high concentration of monovalent cations, the junction overcomes the electrostatic repulsion and folds into the stacked-X structure (6,8–10). By symmetry, two folded conformers are possible as illustrated in Figure 1. The two conformers interconvert (11–14) and their relative population depends on the DNA sequence near the junction (6,14,15). Single-molecule measurements have shown that the rate of conformational transitions decreases at high-Mg²⁺ concentrations (14), indicating that the junction has to unfold first, hence achieving an intermediate that resembles the Mg²⁺ free open form, before making the conformer transition (Figure 1). Spontaneous branch migration was slowed by Mg²⁺ ions, also implicating an open intermediate form (16). Furthermore, the junction unfolds to various degrees upon binding to branch migration enzymes or junction resolving enzymes (5). Therefore, unfolded open forms of the junction appear to be involved in almost every aspect of junction processing despite being minority species under physiological conditions.

Figure 1.

Schematic view of the Holliday junction conformer transition. The stacked conformer I (left), the open form (middle) and the stacked conformer II (right) are shown. The four DNA strands are labeled as a, b, c and d.

In spite of their potential biological significance, the precise nature of the open form intermediates is presently unknown. Gel electrophoresis and FRET measurements suggested that the four arms of the junction point to four corners of a square in the absence of multivalent ions, but it is not known if minority species different from the square planar structure exist and how far such structures are transiently populated under physiological conditions (6,7). Under physiological conditions, the open forms are too short-lived to be detected directly even in single-molecule measurements (17). Crystal structures exist for the stacked-X structure, but not for an open form of a free junction [see (18) and references therein]. Owing to the lack of information, the detailed pathways of conformer transitions are still unknown and it is highly desirable to remedy this situation through the use of proven modeling methodologies such as molecular dynamics (MD). Numerous MD simulations have been carried out previously on simple forms of DNA as well as DNA–protein complexes; representative publications are (19–24) and (25–29). The Holliday junction had been modeled as well (30–33); however, these studies did not investigate conformational transitions.

The conformer transition occurs on a time scale of hundreds of microseconds to hundreds of milliseconds (12,14,17). This time scale is a thousand to a million times longer than that covered presently by MD simulations (34). However, it is known that MD simulations at an elevated temperature accelerate conformational changes of macromolecules drastically, for example, protein unfolding (35). Thus, an elevated temperature may induce the conformational transitions of the Holliday junction on a time scale tractable by MD simulations. Once one has identified a small number of coordinates that characterize the transition, one can also systematically sample the respective conformational surface through room-temperature simulations and identify reaction intermediates.

In this paper, we explore the global conformations involved in the conformer transitions of the Holliday junction. Based on available solution structure data, crystal structures, and the principal symmetry of the conformations, a schematic framework of the conformational changes is constructed. Transition steps within that framework are explored computationally by means of elevated temperature MD simulations. The resulting intermediate conformations are analyzed and principal pathways for conformer transitions are proposed. A key intermediate suggested for these pathways is corroborated by its formation of a stable complex with T7 endonuclease I in a separate MD simulation. Finally, free energy minima and the local free energies of reactant and intermediate states arising in the suggested framework are explored by hundreds of short MD simulations at room temperature.

MATERIALS AND METHODS

In this paper, a simplified model of the Holliday junction is introduced and protocols of all MD simulations are outlined. Then, we explain how the Holliday junction is prepared in various conformations, for performing MD simulations at an elevated temperature. We describe a separate MD simulation of a complex between the junction and a junction resolving enzyme. A method for exploring the local free energy surface of the junction system is introduced at the end.

Simplified model of Holliday junction in two geometric coordinates

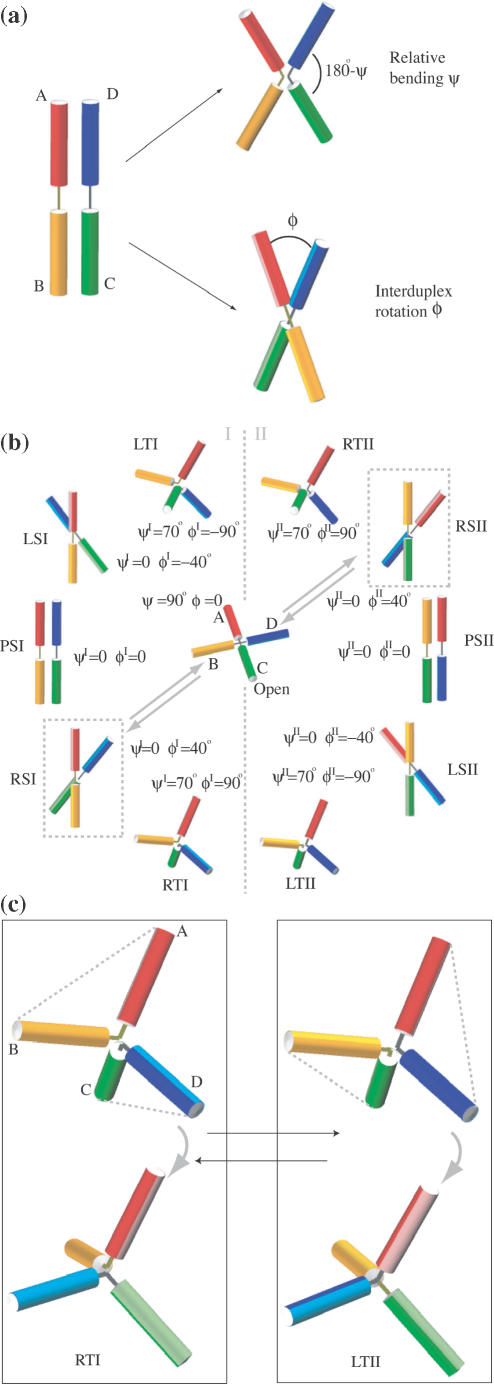
We use cylinders to represent the DNA arms of the Holliday junction, as shown in Figure 2a. The arms are labeled A, B, C and D and colored in red, orange, green and blue, respectively. Each cylinder is colored darker on one side and lighter on the opposite side, which will help to illustrate the relative rolling between arms discussed further on. In the stacked-X or open form, the darker-colored side corresponds to the major groove side of the junction while the lighter-colored side corresponds to the minor groove side (5,30). A pair of arms stacked on one another, termed stacking partners, has their darker/lighter-colored sides facing the same direction.

Figure 2.

Simplified model describing the Holliday junction. (a) The geometries of the Holliday junction conformations are defined through two coordinates, the relative bending angle between the two arms in a DNA duplex AB or CD, and the angle between duplexes AB and CD. Arms A, B, C and D are represented by cylinders and colored in red, orange, green and blue, respectively. Each cylinder is colored heavier on one side and lighter on the opposite side. (b) The participating conformations of the junction involved in the conformer transition are shown. To name each conformation, the first letter R/L/P denotes right-handed/left-handed/planar forms; the second letter S/T denotes stacked/tetrahedral forms; the third letter I/II denotes conformer group I/II. The arrows shown link RSI to RSII via the open form, corresponding to the scheme in Figure 1. (c) Tetrahedral forms, namely, RTI, the right-handed tetrahedral conformer I (left), and LTII, the left-handed tetrahedral conformer II (right) are shown. In RTI, A and B (C and D) are stacking partners while in LTII, A and D (C and B) are stacking partners. The two forms shown at top and bottom are viewed from two different perspectives related by a rotation.

In order to describe the global conformation of the Holliday junction in a simple manner, we define two geometric coordinates. Starting from the planar stacked form, arms A/C stacked on B/D as shown in Figure 2a, one geometric coordinate ψ is the bending angle between arms A and B, or C and D. In the planar stacked form, ψ is zero. As the junction opens, ψ increases to 90°. Duplexes AB and CD are treated symmetrically in their bending angles. The other geometrical coordinate ϕ, the interduplex angle, is the angle between the duplex AB and CD. From the view in Figure 2a, if duplex AB rotates in the counterclockwise direction relative to duplex CD, ϕ is defined as positive, and this conformation is called ‘right-handed’; if duplex AB rotates in the other direction, ϕ is negative and the conformation is called ‘left-handed’. We note that ϕ is equivalent to J_twist in a recent report that analyzed the geometry of the Holliday junction with more degrees of freedom (36).

A series of conformations that are likely to be involved in the conformer transitions are shown in Figure 2b, denoted by the corresponding values of ψ and ϕ. Following the same convention as used in Figure 1, arrows link one stacked-X conformer (RSI) to the other (RSII) via an open form in Figure 2b. These conformations are classified into two groups, I and II. In group I, arms A and B (C and D) are stacking partners while arms A and D (C and B) are stacking partners in group II. The following notations are defined to label these conformations. For both groups I and II, RS is the right-handed stacked form with ψ = 0, ϕ = 40°; LS is the left-handed stacked form with ψ = 0, ϕ = −40°; PS denotes the planar stacked form with ψ = 0, ϕ = 0; RT, the right-handed tetrahedral form with ψ = 70°, ϕ = 90°; LT, the left-handed tetrahedral form with ψ = 70°, ϕ = −90°. The ideal open form corresponds to ψ = 90°, ϕ = 0. These coordinates do not necessarily describe the exact geometry arising in the real junction system; rather, they describe idealized forms. The experimentally detected DNA-only structures of the Holliday junction are all in the RS form, with the interduplex angle ϕ ranging from 36° to 42° (18). The crystal structure we used is in the RSI form with an interduplex angle ϕ of 41.4° (37). The left-handed structure [one of the DNA–RNA junction crystal structures adopts the LS form (38)] is assumed to be symmetrical to the corresponding right-handed form with the same magnitude of interduplex angle but opposite sign; however, the interduplex angles do not necessarily have to be of the same magnitude since the junction has two inequivalent sides. Furthermore, the interduplex angle may depend on a variety of factors such as ionic conditions and DNA sequence (5,18). Therefore, the RS or LS forms may accommodate a range of interduplex angles. The open form of the Holliday junction is a loosely defined entity as well. Generally speaking, an open form is in an extended square conformation; it is not clear if it is planar or not (for instance, taking a pyramidal shape). The ideal open form defined above is a planar square.

The two tetrahedral forms shown enlarged in Figure 2c are RTI and left-handed tetrahedral conformer II (LTII). RTI belongs to conformer group I, with arm A partnering with B (C partnering with D). The angle between A and B (C and D) is ∼110°, thus ψ is ∼70°. The interduplex angle between AB and CD is 90°. This perpendicular orientation is a clear feature of the tetrahedral form, which is observed in MD simulations. LTII belongs to conformer group II since arm A switches stacking partner from B to D (C switches from D to B). If we do not consider the stacking pattern and relative rolling between arms, RTI and LTII would look exactly the same. However, a closer look at the RTI and LTII conformations in Figure 2c reveals subtle differences between these two forms. In RTI, arms A and B are stacking partners; and thus, they have their darker/lighter colored sides facing the same direction, while in LTII arms A and B roll away from each other as they are not stacking partners anymore. The close similarity of the global shape shared by RTI and LTII makes the stacking partner exchange between them easy, involving only relative rolling of arms, but no large-scale spatial rearrangements. Conformations other than the tetrahedral forms, sharing certain symmetries, may also facilitate the stacking partner exchange in the same way. This will be illustrated in Discussion.

Molecular dynamics simulation protocols

All simulations were performed using the program NAMD2 (39), the CHARMM27 force field (40), the TIP3P (41) water model, with integration time step of 1 fs and periodic boundary conditions. Van der Waals energies were calculated using a smooth (10–12 Å) cutoff. The Particle Mesh Ewald (PME) method (42) was employed for full electrostatics, with the density of grid points at least 1/Å in all cases. The PME electrostatic forces were computed every four time steps. The simulations were performed in the NpT ensemble, using the Nose–Hoover Langevin piston method (43,44) for pressure control (1 atm), with an oscillation period of 100 fs and a damping time of 50 fs; we applied Langevin forces (45) to all heavy atoms for temperature control (300 or 400 K) with coupling coefficient of 5/ps. The system was always solvated in a box of explicit water molecules. Cations (e.g. sodium and magnesium) and anions (chloride) were added to control the ionic strength of the solvated system, and to neutralize the negative charges of DNA and protein. The program Delphi (46), a finite difference Poisson–Boltzman equation (non-linear form) solver, was used to locate the positions with minimal electrostatic energies, where the water molecules were then replaced by the ions.

Preparation of an initial structure and other constructed structures of the Holliday junction

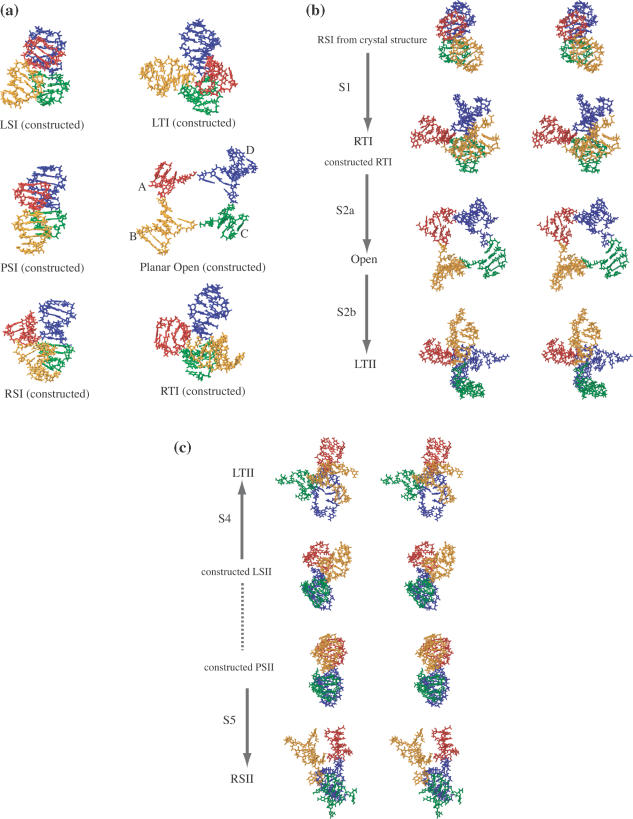
We started from a crystal structure of the Holliday junction solved at 2.1 Å resolution (37) [PDB code: 1DCW, d(CCGGTACCGG)]. The junction was solvated in a water box (∼70 × 70 × 70 ų) with sodium and chloride ions. The resulting system, ∼34 000 atoms in total, was energy minimized for 5000 steps and pre-equilibrated for 100 ps at room temperature. The coordinates of the initial junction structure were extracted from the final frame of the pre-equilibration trajectories. This initial structure adopts the RSI form (right-handed stacked conformer I, see Figure 2). Geometric operations, e.g. spatial rotations according to the two rotational coordinates (see Figure 2a), were applied to this initial structure using the VMD program (47) to construct structures in various global conformations that were used as starting structures in the following simulations. Some of these structures are shown in Figure 4a.

Figure 4.

Structures of the Holliday junction arising in elevated temperature simulations. The junction is shown in licorice representation and colored in red, orange, green and blue for arms A, B, C and D, respectively. (a) Exemplary constructed structures used to start some of the simulations are shown. The RSI form was obtained directly from the X-ray structure. Other structures were obtained through geometric operations to the RSI form structure. (b) Represented in stereo view are structures arising in simulations 1 and 2 (S1/S2). S1 started from the RSI form and evolved into the RTI form; S2 started from a constructed RTI form, evolved into an open form during the first stage (S2a), switched stacking partners thereafter, and evolved to the LTII form. (c) Shown in stereo view are structures in simulations 4 and 5 (S4/S5). S4 started from a constructed LSII form and evolved into the LTII form. S5 started from a constructed PSII form and evolved into the RSII form. There was no transition observed between LSII and PSII. The dotted linkage between the two conformations indicates that the transition is possible in principle (see text). Therefore, the whole conformer transition process from RSI to RSII is visualized in steps shown in (b) and (c).

Simulations at an elevated temperature and a schematic framework of the conformer transition

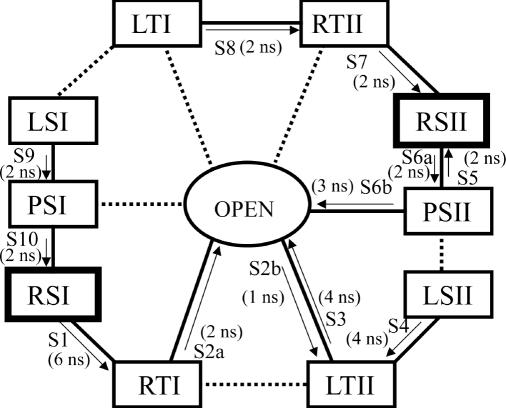
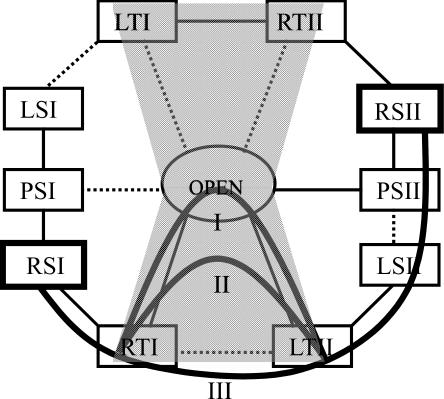
With the participating conformations of the model junction defined in Figure 2b, a schematic framework based on the conformational symmetries and simulation results (discussed later) can be constructed as shown in Figure 3. A line between two conformations denotes a possible transition step. MD simulations from 1 to 10 (labeled S1–S10 in Figure 3) were performed to test if these steps can take place.

Figure 3.

Schematic framework proposed for the conformer transition. A line between two conformations denotes a possible transition step. A solid line is used when the step has been directly observed in our MD simulations, S1–S10. The arrow indicates the direction of the step. A dotted line is used when the step was not observed in the simulation, but can be deduced by symmetry from an analogous step observed in our MD simulations. The approximate time each transition step lasted in a simulation is indicated in ns. S3 and the other simulation from the open form (data not shown) were performed in the presence of magnesium ions (0.2 M ionic strength of sodium, chloride and magnesium ions together); further simulations were performed in the absence of magnesium ions (0.1 M ionic strength of sodium and chloride ions).

An elevated temperature of 400 K was used to accelerate the conformational changes of the Holliday junction. If a simulation ended up in a product form similar to one of the conformations shown in Figure 2b, we constructed a junction in that conformation as the starting structure for a subsequent simulation. Since it has been shown that magnesium ions destabilize the extended intermediates (open form, and probably tetrahedral forms), stabilize the stacked forms (RS, and probably LS and PS), and inhibit the conformer transition (5,14), simulation 3 from LTII and a simulation from the open form (see below) were performed in the presence of magnesium ions (0.2 M ionic strength of sodium, chloride and magnesium ions together); other simulations were performed in the absence of magnesium ions (0.1 M ionic strength of sodium and chloride ions).

Simulation 1 started from the initial structure, the RSI form of the junction. After ∼6 ns, a significant number of hydrogen bonds between DNA base pairs were broken, the two strands of the helix were separated, and the simulation was stopped. Since the junction adopted a conformation very similar to the RTI form at the late stage of simulation 1, we adopted the RTI form as the starting structure in simulation 2. This structure was solvated in the water box with sodium and chloride ions, and energy minimized for 5000 steps before simulation 2 started. This simulation was stopped at ∼6 ns for the same reason as simulation 1. In the second stage of simulation 2, the junction changed from an open form to a form similar to LTII. Simulation 3 was then started from a constructed LTII form; monitoring simulation 3 revealed formation of an open form. A simulation was then started from the open form, but no global conformational changes were observed before the DNA started melting.

Without further conformational forms derived from the above four simulations, we explored additional possible conformations that may be involved in the conformer transition, e.g. the LSII and PSII forms, as shown in Figure 2. Accordingly, simulation 4 was started from a constructed structure in the LSII form, which evolved to a structure similar to LTII after ∼4 ns. Simulation 5 started from a constructed structure in the PSII form, which evolved to an RSII form after ∼2 ns.

Simulation 6 was then started from a constructed RSII structure, resulted in the PSII form after ∼2 ns, and opened to some extent in another 3 ns. Simulation 7 was started from a constructed RTII structure, which resulted in the RSII form after ∼2 ns. Simulation 8 was started from a constructed LTI structure and changed to the RTII form in ∼2 ns. Simulation 9 was started from a constructed LSI structure that resulted in a PSI form after ∼2 ns. Simulation 10 was started from a constructed PSI structure and found to result in the RSI form after ∼2 ns. The conformational transitions described are available as movies in Supplementary Material.

A feasible complex between T7 endonuclease I and the tetrahedral form of the Holliday junction

The RTI form Holliday junction was constructed by geometric operations to the initial RSI structure and used to investigate a possible complex with junction resolving enzyme bacteriophage T7 endonuclease I. A crystal structure of the enzyme without DNA was solved at 2.1 Å resolution (48) (PDB code: 1M0D). A complex of the protein and RTI was built according to the 2-fold symmetry of protein and DNA junction, taking into account a previous molecular model of the complex (49). The complex was solvated in a water box (95 × 85 × 125 ų), neutralized by sodium, chloride and magnesium ions, and energy minimized for 5000 steps before equilibration. The whole system contained ∼97 000 atoms. About 1.4 ns of equilibration at room temperature was performed to test if a possible stable complex could be formed between the RTI form of the junction and the T7 endonuclease I.

Exploring the free energy surface of the junction system

In order to investigate the conformations that may be involved in conformer transitions of the Holliday junction, we explored the free energy surface for conformer group I states (see Figure 3). We confined our exploration to the ψ, ϕ degrees of freedom defined above. Even with this reduction in dimensionality, it is impossible at present to construct an accurate free energy surface due to limited computational resources. Therefore, we employed a coarse discretization of the coordinate space, a two-dimensional (2D) grid with 10° intervals along each direction. In a study with magnesium ions, the whole conformation space (ψ from 0 to 90° and ϕ from −180° to 180°) was explored; in the study without magnesium ions, only half of the conformation space (with positive interduplex angle ϕ) was explored. For altogether over 400 grid points, the force F_i = −∂A/∂s_i acting along ψ, ϕ was calculated; here A is the free energy and s_i (where i = 1, 2) denotes the two coordinates ψ, ϕ.

In order to calculate F_i (where i = 1, 2), one needs to average over the remaining degrees of freedom. This was accomplished through a restrained dynamics approach to determine the force over the course of a 50 ps MD simulation. For this purpose we adopted the following scheme: let us assume a system moving along coordinate x confined in a chosen (i.e. k is known) harmonic potential V(x) = ½k(x − x_o)² and subject to an indigenous force f corresponding to a potential . The minimum of the combined potential is located at x_o + f/k. Observation of the system's average position (the minimum) will permit one to determine f, as long as k is known. Following this strategy, the system was initiated with the ψ, ϕ degrees of freedom chosen at the grid points using the construction method outlined earlier. The constructed structure was solvated with ions and energy minimized for 5000 steps. Two independent 50 ps MD simulations were started with room temperature initial velocities and restrained through a harmonic potential. The first 20 ps of the dynamics were considered an equilibration period and not used for further analysis. During the simulations, one dihedral and two symmetrical angles which changed in proportion to the interduplex angle ϕ and the relative bending angle ψ, were restrained by stiff harmonic springs (k_ψ = 1000 kcal/mol · rad²; k_ϕ = 2000 kcal/mol · rad²) to specified values, in a fashion that reproduced closely ψ, ϕ-restraints, but was computationally simpler to handle. The forces F_i (where i = 1, 2) were calculated through the deviations from the specified values of the average values of the dihedral/angles sampled every 50 fs. Altogether, >400 trajectories, each 2 × 50 ps long, were accumulated, corresponding to an overall simulation time for the 34 000 atom system of >40 ns. The long duration explains why a finer grid and further sampling was not feasible.

In order to visualize the minima on the resulting surface we utilized the history-dependent Gaussian potential algorithm suggested in (50). According to this algorithm, one calculates the trajectory s_i^t for coordinates i = 1, 2 at time t, which is discretized into constant steps. s_i^t follows the dynamics

where we define s₁^t = ψ(t), s₂^t = ϕ(t) and the corresponding forces F₁^t, F₂^t [the forces are inertia weighted, i.e. divided by inertia corresponding to ψ and ϕ, respectively, ]. The forces are adjusted by adding a term due to the assumed history-dependent Gaussian potentials with height W and width δ (we chose W = 0.1 kal/mol and δ = 5°) according to the rule

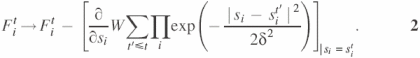
The history-dependent potential is designed to repel the system from positions s_i^t′ visited before (t′ ≤ t). Therefore, if the iterative dynamics reaches a local minimum, the [ψ(t), ϕ(t)] trajectory will oscillate there for a while, and thus one can locate local minima by viewing the trajectory behavior. Eventually, owing to the additional history-dependent term in Equation 2, the trajectories jump out of the minimum and search for another minimum. The history-dependent potential given by u_t(s₁,s₂) = W∑_t′≤t∏_iexp(−|s_i − s_i^t′|²/2δ²) permits escape of the trajectory when the energy minimum is compensated (‘filled’) by the history-dependent potential u_t(s₁, s₂). At the moment t^* when the trajectory leaves the minimum, −u_t^*(s₁,s₂) provides an estimate of the depth of the local minimum (50).

Two ionic conditions of the solvated system were investigated, one at 0.1 M ionic strength of sodium and chloride ions, in the absence of magnesium; the other at 0.2 M ionic strength of sodium, chloride and magnesium ions together. The adoption of a very high-ionic strength condition in the simulation, compared with those adopted in experiments, was due to the limited size of the small water box used (with periodic boundary condition). In order to neutralize the −40e negative charges of the DNA junction in a water box of ∼70 × 70 × 70 ų in volume, tens of ions had to be added. Comparing the local depth of the minima at the two ionic conditions, one can estimate the effect of magnesium ions on the stability of RSI, RTI and the open form, which are directly involved in the conformer transition (see Discussion).

Geometry of perpendicular forms

For the purpose of discussing below the geometry of conformer transitions, we provide here a brief mathematical analysis for the case that the Holliday junction assumes a perpendicular form, which will facilitate stacking partner exchange (see Discussion and Figure 9). This form is characterized through the unit vectors and that point along arms A, B, C and D, respectively, together with the associated unit vectors and . The perpendicular form is assumed when the vectors and are orthogonal. In this case, angles ψ, ϕ defined in Figure 2a are determined through

Figure 9.

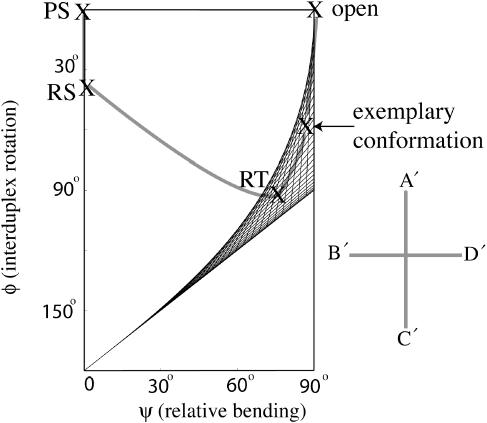
Coordinate space governing the stacking partner exchange. The half space with positive interduplex angle is shown. The positions of typical conformations, denoted by ‘X’, correspond to conformations PS, RS, RT, the open form and an exemplary conformation in the exchange area (the shaded region). The exchange area is composed of conformations facilitating the stacking partner exchange. These conformations are defined by Equations 3 and 4 in Materials and Methods, with alpha and beta assuming permitted values. The grey lines denote possible pathways linking different conformations of the junction, as observed in the elevated temperature MD simulations. These pathways represent schematically trajectories from PS to RS, from RS to RT, and from the open form to RT, as shown in Figure 7.

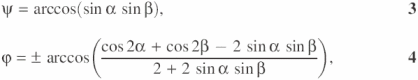
where and . The angles α and β can assume values in the interval [0, π/2).

RESULTS

In the following paragraphs, a series of global conformational changes observed in elevated temperature MD simulations are described; based on these results, a schematic framework of the conformer transition is constructed. A complex between the tetrahedral form of the junction and an endonuclease is simulated. Finally, local energy minima corresponding to conformations of the reactant and intermediate states of Holliday junction conformer transitions are identified.

Schematic framework of global conformational changes

A schematic framework for Holliday junction transitions based on simulation results and the conformational symmetries can be constructed as shown in Figure 3. Solid lines between states represent steps directly observed in our MD simulations, arrows indicating observed transfer directions. Dotted lines indicate transitions that were not observed directly in simulations, but are possible in principle, since analogous, symmetry-related steps were actually observed.

The MD simulations were performed at 400 K as described in Materials and Methods. Each simulation started from a distinct conformation. The RSI form was obtained from the crystal structure while others were constructed by geometric operations to the RSI form. Typical constructed structures are shown in Figure 4a. The major goal of the simulations was to test if a pathway could be stitched together, beginning from the RSI form and ultimately reaching the other stable conformer, the RSII form.

Simulation 1 started from the RSI form. During the simulation, the interduplex angle increased gradually. After ∼6 ns the junction adopted a conformation with a perpendicular (right-handed) crossing between duplex AB and CD, with some extent of bending arms A and B (C and D) relative to each other. This conformation is similar to the RTI form.

Simulation 2 started from a constructed RTI form. During the first stage, the RTI form extended to a non-planar square open form, consistent with the early experimental measurements (6,7). During the second stage, in ∼1 ns, the arms of the open form began switching partners, and then the junction evolved to a more compact form with duplex AD and BC perpendicular to each other, similar to the LTII form.

Simulations 1 and 2 may have revealed the most critical steps in the conformer transition, since the junction started from RSI in conformer group I and changed into a conformation in conformer group II. The two simulations are summarized in Figure 4b, with S2a and S2b indicating the first and the second stage of simulation 2, respectively. Simulation 3 started from the LTII form, with the expectation that it might go to the LSII form. However, during the simulation, LTII changed to an open form.

From the simulations above, it is not clear what conformational changes could bring LTII to the ‘destination’ form RSII. The symmetry, as reflected in the schematic framework in Figure 3, suggests that LSII and PSII might jointly bridge the transition from LTII to RSII. In simulation 4, which started from a constructed LSII form, the interduplex angle between AD and BC changed to nearly −90°; this was accompanied by a change of the angle ψ between arms A and B (C and D) and resulted in a form similar to LTII. The occurrence of the transition from LSII to LTII suggests that the inverse transition is also possible. Simulation 5 started from a constructed planar PSII form, and in 2 ns a right-handed interduplex angle appeared, showing that PSII transformed into RSII. The mentioned conformational changes are summarized in Figure 4c.

In simulation 6, the constructed RSII form changed to the planar PSII form within 2 ns. Further simulation saw the PSII form expanded to a seemingly planar ‘open’ form. However, the form was not yet square, nor did it open at the center. The shape did not look similar to the open form that appeared in the RTI to LTII transition. Thus, it is not certain if the transition from PSII to a real open form happens or not.

In simulation 7, the constructed RTII form evolved to the RSII form in ∼2 ns. In simulation 8, the stacking partner exchange was directly observed as a constructed LTI in conformer group I subtly changed to RTII in conformer group II, in ∼2 ns. The global conformation of the tetrahedral form remained almost unchanged. However, the rolling of arms was obvious, e.g. arm A rolled in a way that it broke the original stacking between A and B, and at the same time, a new stacking between A and D formed. This suggests that the stacking partner exchange, the critical step in the conformer transition, does not necessarily involve an open form. In principle, the stacking partner exchange could happen through any conformation satisfying certain symmetry requirements (see the analysis of Figure 9 in Discussion).

In simulations 9 and 10, it was observed that the LSI form changed to the planar PSI form within 2 ns and PSI changed to the RSI form in ∼2 ns. The transition between LSII and PSII was not observed. However, the analogous (symmetry-related) transition from LSI to PSI, suggests that the transition between LSII and PSII would be possible. Similarly, the LTI to LSI transition may be possible because a LSII to LTII transition was observed; LTI/RTII to the open form is possible since RTI/LTII was observed to transit to the open form; RTI may change to LTII directly because the symmetry-related transition LTI to RTII was observed. The deduced steps mentioned are shown as dotted lines in Figure 3. In principle, any of the transitions may happen in either direction. (Movies illustrating the simulations described above are provided in Supplementary Material.)

Feasible structure of the complex between T7 endonuclease I and RTI

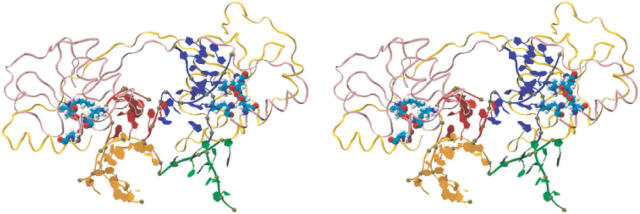
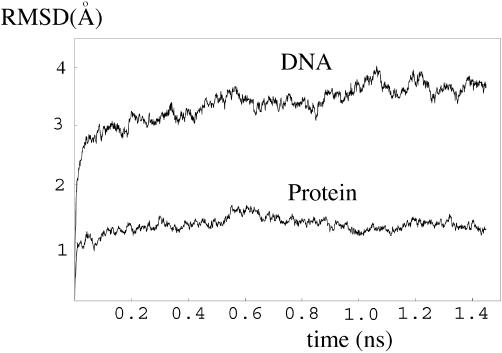
From our MD simulations, the RTI form of the Holliday junction emerges as a key bridging element in conformer transitions. The perpendicular orientation of the duplex AB and CD, with A partially stacking on B (C on D), is reminiscent of the global conformation of the junction in complex with T7 endonuclease, deduced from biochemical studies (49). The crystal structure is available for the protein only, but not for a complex with a junction. In order to test if the RTI form can indeed form a stable complex with the enzyme, the complex between the protein and the RTI form junction was constructed and equilibrated at room temperature for ∼1.4 ns. The shape of the RTI form junction matched well with that of the protein, forming a stable complex in the simulation. The complex at the end of the simulation is shown in Figure 5. The RMSD value in Figure 6 suggests that the protein maintained its structure well during the simulation. Since the RTI junction was modeled from the RSI form crystal structure, it adjusted its structure more than the protein, settling down to a stable form as well. The final junction structure still maintained the tetrahedral conformation. (The coordinate file for the complex at the end of the simulation is provided in Supplementary Material.)

Figure 5.

A feasible structure of the complex between T7 endonuclease I and the RTI form Holliday junction. Shown is a stereo view of the complex after equilibration for ∼1.4 ns. The protein is represented in ribbon representation, colored in pink and yellow for two different polypeptides. The active site residues, Glu20, Asp55, Glu65 and Lys67, involved in DNA binding are shown in VDW representation, colored in red for oxygen, blue for nitrogen, cyan for carbon and white for hydrogen. The magnesium ions binding to the active site are shown in purple VDW representation. The RTI form of the Holliday junction is represented in ribbon representation, colored the same way as in the previous figures. The phosphorous atom is shown as a small dark sphere.

Figure 6.

RMSD values for the protein T7 endonuclease I and the tetrahedral form DNA junction (RTI) in a MD simulation.

Exploration of energy minima characterizing the Holliday junction

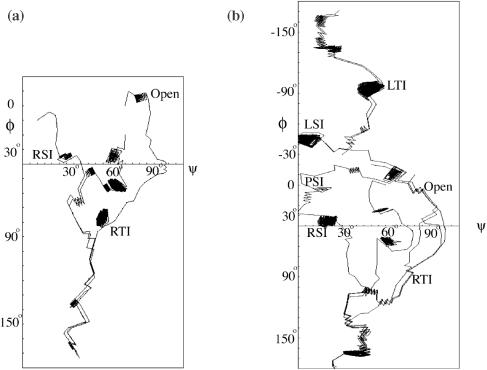
Employing the algorithm adopted from (50) and described in Materials and Methods, we explored the energy surface of the Holliday junction system along the ψ, ϕ coordinates. ψ and ϕ were chosen as the relevant collective coordinates, since they differentiate the global conformations involved in conformer transitions. At every ψ, ϕ conformation, selected by the discretization scheme, the ‘force’ due to the local energy changes along each direction of the two coordinates was estimated from short MD simulations at room temperature. Energy minima of the system were then located, as described in Materials and Methods, from [ψ(t), ϕ(t)] trajectories as shown in Figure 7.

Figure 7.

Exploration of the free energy surface of the Holliday junction system. Free energy minima correspond to the ‘spots’, around which the iterative dynamics oscillates; the steepest descent pathways are shown as piecewise linear trajectories. The cases without magnesium ions (a) and with magnesium ions (b) are shown.

An energy minimum near the RSI form can clearly be identified in Figure 7. For the 0.1 M ionic strength condition in the absence of magnesium ions, the minimum is calculated to be about −2 kcal/mol locally; adding the magnesium ions and increasing the ionic strength to 0.2 M, the local energy minimum is found to become much deeper, decreasing to about −20 kcal/mol. It was observed that 5 out of 10 magnesium ions aggregated around the center of the junction where negatively charged phosphate groups are densely packed; the five magnesium ions remained there in a 1 ns test simulation of RSI, as well. The screening from magnesium ions weakens the electrostatic repulsion at the center and therefore stabilizes the stacked-X form of the junction. A shallow energy minimum of about −2 kcal/mol was also found near the ideal open form in simulations without magnesium ions. The minimum disappeared after adding magnesium ions. These magnesium ions were distributed almost equally around each arm of the open form, but were diffusing rapidly. Without magnesium ions, there was a deep local minimum near the RTI form of about −30 kcal/mol; after adding magnesium ions, no minimum could be located and one magnesium ion was bound at the point of exchange of the junction. Qualitatively, the disappearance of a local minimum suggests that magnesium ions destabilize the tetrahedral form, which is a possible intermediate in the conformer transition. We emphasize that all energies quoted here are relative local values; they can be understood as activation free energies for escape from the local minimum, but they do not reflect the relative stability between separate minima. In the presence of magnesium ions, the whole conformational space was searched, and other local minima near PSI, LSI and LTI forms were located (only conformer group I being investigated).

The minima described can be recognized in Figure 7 through dense meanderings of the ψ(t), ϕ(t) trajectory shown. Approximate positions of the minima mentioned above are indicated by their names. It is noted that the RSI form has a minimum located at ψ ∼ 20° rather than 0°; it is not clear if this deviation is due to a non-coaxial stacking optimal conformation of RSI, or due to inaccuracies in the calculation. In fact, the rather coarse discretization of the conformational space into the 2D grid with 10° intervals (see Materials and Methods) may be a direct cause of the deviation. Besides the minima mentioned above, there are some further uncharacterized minima shown in Figure 7, e.g. those close to ψ ∼ 60°.

Combing explorations in both ionic conditions, with and without magnesium ions, all the conformations in conformer group I proposed in the schematic framework of the conformer transition were thus identified as local energy minima in this approach, the details depending on the presence/absence of magnesium ions in solution. In both ionic conditions, the calculated [ψ(t), ϕ(t)] trajectories (see Equations 1 and 2 in Materials and Methods) reveal an escape out of the local RSI energy minimum and a transit to the RTI form; the trajectories also went from PSI to RSI as well as from the nearly planar open form to the RTI form, consistent with transition steps observed in the high-temperature simulations. The pathways identified in Figure 7 are also represented schematically by the grey line pathway in Figure 9.

DISCUSSION

In the following, we discuss the pathways for the conformer transitions of the Holliday junction as revealed by our MD simulations.

High-temperature acceleration of large conformational changes

At room temperature, the time scale for the conformer transition ranges from hundreds of microseconds to hundreds of milliseconds (12,14), which is far beyond the time scale of tens of nanoseconds that can be reached in MD simulation nowadays (34). Since the log value of the rate constant of a transition decreases approximately in a linear manner with ΔH/k_BT (temperature T, activation enthalpy ΔH, Boltzmann constant k_B), one can conclude that with a value of ΔH in the range 20–40 kcal/mol (14), increasing T from 300 to 400 K should increase the transition rate by up to six orders of magnitude, i.e. into the nanosecond range accessible to MD simulation. This acceleration is not likely to change the reaction pathway, except possibly shifting the balance between slower and faster processes.

However, increase in temperature alters the balance between internal energy and entropy contributions to the free energy of the Holliday junction, which could systematically favor intermediates when a transition is accompanied by a significant change in entropy, but such change is not expected. Previous MD studies of protein unfolding employed temperatures of up to 500 K and suggest that the pathway of unfolding was unaltered (35). We also note that the simulations were stopped within 10 ns, before the double strands of the DNA helix separated. Water evaporation at the high temperature can be ignored because of the short simulation period.

Nevertheless, it appears prudent to compare the results from high-temperature dynamics with room temperature simulations. For this purpose, we have also explored the free energy surface along the two relevant collective coordinates, ψ and ϕ, using room temperature simulations. The two approaches showed qualitatively consistent results: (1) all of the conformations observed in the high-temperature simulations were identified as local minima of free energy in the room temperature simulations and (2) pathways identified in Figure 7 (RSI to RTI, PSI to RSI and the open form to RTI) match transitions observed in the high-temperature simulations. Further mathematical analysis, discussed below, shows that the tetrahedral conformation is possibly a key intermediate bridging the overall conformer transition of the Holliday junction.

The simulations at the elevated temperature were performed only once each due to present limitation in computer power. The simulations reveal a detailed scheme for the conformer transition of the Holliday junction, for the first time. All events observed occurred spontaneously in the simulations, some as quickly as 1–2 ns, some as slowly as 6 ns. In reality, transitions do not proceed unidirectionally, but rather exhibit back-and-forth transitions, as seen in simulations 2 and 3 (from the open form to LTII, and from LTII back to the open form). The back and forth trajectories may arise, however, on a time scale longer than that of our MD simulations, which accordingly caught only steps in one direction.

Open and tetrahedral intermediates in the conformer transition

Early considerations of the Holliday junction conformation evoked both the planar open form and the tetrahedral form as possible structures (51,52). Experiments later found that under low-salt conditions and in the absence of multivalent ions, an extended square, i.e. open form, rather than the tetrahedral form, is stable (6,7). The open form was proposed as the common intermediate for both conformer transition and branch migration (5,14). The exact conformation of this open form, whether it is planar or not, was not specified. It is more likely to be non-planar since the two sides of the junction (major or minor groove side) are not equivalent. However, it is not clear whether this non-planar open form should be more tetrahedral or pyramidal (structure with four corners in a plane plus an apex).

Both open and tetrahedral intermediates were observed in our simulations. In simulation 2, the open form appeared as a non-planar square, with some tetrahedral character; there were transitions between the tetrahedral (right- or left-handed) form and the open form (shown in Figure 4b), suggesting that the tetrahedral structure is an additional intermediate besides the open form. Indeed, we observed stacking partner exchange through tetrahedral forms without involving the open form, as seen in simulation 8 (see Results).

T7 endonuclease I, a junction-resolving enzyme, binds to the Holliday junction with high specificity and makes two cuts diagonally across the junction. In comparative gel electrophoresis experiments (49), the enzyme-bound junction was seen to adopt two alternative conformations, which share as a common feature a perpendicular ‘cross’ shape while differing in the stacking partners. The orientation of junction resolution was shown to be directly determined by the stacking conformation of the complex. It was also pointed out by Declais et al. (49) that the stacking was not perfect because of localized structural perturbations around the point of exchange. Both the perpendicular ‘cross’ and imperfect stacking characteristics suggest that the two equivalent forms most likely correspond to the tetrahedral form RTI and LTII, which are the bridge conformations between groups I and II. Indeed, our simulations show that the tetrahedral form can engage in a stable complex with the enzyme. We note that another endonuclease, Escherichia coli RusA, has been proposed to bind a Holliday junction in a pseudo-tetrahedral form (53). There now arises the interesting possibility that the enzyme recognizes the tetrahedral form populated in a free junction and stabilizes it via binding. In this case, the relative populations of the tetrahedral forms in groups I and II may determine the orientation of junction resolution and, hence, the outcome of recombination.

Most probable pathway in the conformer transition

Based on the observations made in our simulations and based on consideration of symmetry, we propose the pathways summarized in Figure 8 as the most probable pathways for the conformer transition of the Holliday junction. Starting from the crystal structure in the RSI form, the conformation evolves into the RTI form at first. Although it was observed in a high-temperature simulation that RSI transited directly to RTI, an alternative pathway from RSI through PSI, the open form, and PSII to RSII is also possible. We like to argue now that a tetrahedral conformation is in fact more likely to bridge the conformer transition.

Figure 8.

Probable pathways of the conformer transition between RSI and RSII. All pathways start from the RSI form of the junction and proceed to the RTI form first. Pathway I involves an open form in the stacking partner exchange between RTI and LTII, pathway III goes directly from RTI to LTII. Pathway II passes through some other intermediate in the exchange area, corresponding to the shaded region in Figure 9.

Suppose the junction initially has arms A and B (C and D) as stacking partners (as is the case in conformer group I). In order to facilitate the stacking partner exchange, e.g. arm A switching partnership from B to D, with the least rearrangement of the arms, a conformation may be required in which arms B and D are symmetric relative to A (or C) in space, so that the transition from A–B to A–D partners involves only relative rolling of the arms (see Figure 2c). Similarly, A and C should be symmetric relative to B (or D). A conformation satisfying these requirements should have a 2D projection A′B′C′D′, in which A′C′ is perpendicular to B′D′ (see Figure 9), which is defined as a perpendicular form in Materials and Methods (see Equations 3 and 4). The mathematical analysis identifies an area in the coordinate plane (ψ, ϕ) composed of such conformations. This area is shown as a shaded region in Figure 9. We suggest that the stacking partner exchange (from conformer group I to conformer group II) happens in this area rather than through other regions of the conformational space. Both the tetrahedral and the ideal open form belong to the area indicated. An exemplary conformation other than the tetrahedral or ideal open form is presented in Figure 9. It is important to realize that the exchange area is widened in the region around the tetrahedral form, i.e. there are more conformations near the tetrahedral form, which can facilitate the stacking partner exchange. Therefore, once the conformation of the junction evolves to the tetrahedral region, e.g. as a pseudo-tetrahedral form, the junction is more likely to undergo the stacking partner exchange, which links the conformations in conformer groups I and II.

In summary, we propose the pathways shown in Figure 8 as the most probable pathways. The shaded area corresponds to the exchange area in Figure 9. Pathway I involves an open form in the stacking partner exchange, pathway III realizes the stacking partner exchange directly from RTI to LTII (see also Figure 2c). Pathway II passes through some other form in the exchange area.

Exploration of the free energy surface

The free energy surface governing the Holliday junction solvated in solution should be understood as being constructed in the 2D (ψ, ϕ) manifold of the high-dimensional conformational space of the Holliday junction system. Previous studies (5,14) suggested that the stacked-X form (RSI) transforms into the extended open form before making a transition to the other stacked conformer (RSII). In fact, there exist many ways to achieve this conformational transition, which makes it difficult to identify a single reaction coordinate. Accordingly, a set of relevant collective coordinates describing the slow motions (54) is better suited to describe the conformational transition of the junction. The existence of a 40° interduplex angle with a zero bending angle in the RSI form, and zero interduplex angle with 90° bending angle in the open form, suggest that at least two global degrees of freedom are involved in the conformational change, namely ϕ and ψ. The elevated temperature MD simulations showed that the two coordinates clearly differentiate global conformations involved in the conformer transition.

However, it is most likely that there exist other important degrees of freedom facilitating the transitions, such as the bending of arms orthogonal to the bending angle ψ, relative rolling of the arms, relative rolling and sliding between the two duplexes (36,55), and possibly small unwinding of the helix during the transitions (56). In principle, if these other degrees of freedom are less essential than ψ and ϕ, and if they relax sufficiently quickly during the data collection time, the free energy profile on (ψ, ϕ) reflects the averaged effects of all these degrees of freedom.

Our calculation located energy minima for all conformations proposed in the schematic framework in Figure 3: RS and LS form, RT and LT form, PS as well as open form. The presence of the conformations as stable or intermediate states is qualitatively confirmed through room temperature simulation. The intermediates, even if only marginally stable, may be important for protein recognition and binding as long as they are populated frequently enough. Experiments have shown that stacking conformer transitions occur hundreds of times a second in physiologically relevant conditions, presumably visiting these intermediates as frequently. Recognition of such intermediates by proteins may be facilitated via such dynamic characteristics of the junction.

For the RSI form, the estimated depths of the respective energy minimum (about −20 kcal/mol in the presence of magnesium ions and −2 kcal/mol without magnesium ions) clearly show the stabilization effect of magnesium ions on the stacked form. In contrast, the magnesium ions are found in our calculations to destabilize RTI, the tetrahedral form. This is consistent with the proposal that tetrahedral forms provide the gateway for the stacking partner exchange; destabilization of RTI may make the tetrahedral local minimum disappear, thus blocking the gateway. This is also consistent with the experimental fact that the conformer transition is inhibited by magnesium ions (14).

In principle, the calculation carried out here could provide the free energy landscape of the system in the long iteration-time limit after exploring the whole coordinates space, and yield the relative free energy differences between any two free energy minima located. However, owing to insufficient sampling in our MD simulation and resulting inaccurate local free energy data, a free energy surface linking local minima and yielding accurate relative energy of the minima could not be ‘stitched together’. Therefore, although the calculations locate the free energy minima of the junction system, they are still unable to determine the free energy landscape quantitatively.

CONCLUSIONS

The Holliday junction is a highly polymorphic molecule. While it folds into one of the two stacked conformations under physiological conditions, it could also undergo spontaneous conformer transitions and branch migration. Both these processes are accelerated upon lowering divalent ion concentrations, suggesting common intermediate conformations that are unfolded. Since these intermediate conformations are too transiently populated to be crystallized or to be detected even in single-molecule measurements, we carried out molecular dynamics simulations to probe them. In addition to the expected open form, we observed tetrahedral intermediates, which may facilitate exchange of stacking partners without global rearrangements. Despite being minority species, these transient intermediates may be recognized by junction-specific proteins and stabilized via protein binding, hence playing important roles in the processing of the Holliday junction during recombination.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR online.