Effect of Arrangement of Stick Figures on Estimates of Proportion in Risk Graphics

Abstract

Background

Health risks are sometimes illustrated with stick figures, with a certain proportion colored to indicate they are affected by the disease. Perception of these graphics may be affected by whether the affected stick figures are scattered randomly throughout the group or arranged in a block.

Objective

To assess the effects of stick-figure arrangement on first impressions of estimates of proportion, under a 10-s deadline.

Design

Questionnaire.

Participants and Setting

Respondents recruited online (n = 100) or in waiting rooms at an urban hospital (n = 65).

Intervention

Participants were asked to estimate the proportion represented in 6 unlabeled graphics, half randomly arranged and half sequentially arranged.

Measurements

Estimated proportions.

Results

Although average estimates were fairly good, the variability of estimates was high. Overestimates of random graphics were larger than overestimates of sequential ones, except when the proportion was near 50%; variability was also higher with random graphics. Although the average inaccuracy was modest, it was large enough that more than one quarter of respondents confused 2 graphics depicting proportions that differed by 11 percentage points. Low numeracy and educational level were associated with inaccuracy.

Limitations

Participants estimated proportions but did not report perceived risk.

Conclusions

Randomly arranged arrays of stick figures should be used with care because viewers’ ability to estimate the proportion in these graphics is so poor that moderate differences between risks may not be visible. In addition, random arrangements may create an initial impression that proportions, especially large ones, are larger than they are.

Stick-figure graphics are frequently used to illustrate health risks in educational and decision support materials for patients and consumers.^1,2 These graphics (sometimes called pictographs or icon graphics) are often considered appropriate for patients with lower education or numeracy because they require no familiarity with scientific graphic conventions such as axes and because qualitative studies find that they are relatively well liked by consumers.^3–5 Stick-figure graphics can effectively draw people’s attention to statistical information, reduce the influence of vivid text anecdotes on decision making,⁶ and help explain risk-reduction information.⁷

These graphics are most likely to be useful if viewers correctly interpret the proportions they depict. Previous studies have used a variety of designs for these graphics, making it difficult to draw firm conclusions about the best design formats. Some graphics have used a random arrangement, in which the stick figures affected by the health hazard are scattered randomly throughout a larger group of unaffected figures.⁸ Others have used a sequential arrangement in which the affected stick figures are lined up in blocks along an edge or at a corner of the rectangular field.^6,7 In a previous qualitative study,⁵ we found that sequential arrangements were generally perceived as easier to understand and estimate, which appears consistent with psychophysical research showing that estimation tasks that require mentally summing noncontiguous areas (as in the random graphic) are less accurate than estimating proportions in lines or blocks as in the sequential one.^9–11 However, in our qualitative study, many people also considered random arrangements more realistic. “The chance is random, it’s not everybody bunched in one area,” one focus group participant told us.⁵ This appears consistent with the findings of others that random graphics are perceived as more “true.”¹² The findings might indicate that randomly arranged figures would be more useful for expressing the concept of unpredictability. However, it also appeared that randomly arranged graphics might be less successful at conveying proportion. A quantitative study was indicated, as viewers’ opinions about which graphic format they prefer do not strongly predict accuracy in judgment.^13,14

Graph comprehension appears to take place in multiple steps: the initial rapid perception of visual elements such as line and area, followed by more cognitively effortful integration and interpretation steps that are influenced by the viewer’s goals and background knowledge.^10,15–17 Depending on the design of the graph, proportion may be immediately visible through a part-whole relationship, or it may require more cognitive steps such as mentally summing noncontiguous areas.¹⁰ Thus, if random and sequential designs had different effects on risk perception or decision making, this could be attributable to difficulties in ascertaining the proportion or effects on subsequent interpretation steps, or both.

The current study was designed to examine the initial visual perception step only. Participants were asked to estimate proportions depicted in a rectangular array of randomly or sequentially arranged stick-figure graphics under a 10-s time limit. We hypothesized that estimates of proportion would be different within person and across people when the graphic was in a random arrangement than when it was in a sequential arrangement. We also hypothesized that random arrangements would be estimated with less accuracy. Finally, we hypothesized that poor numerical skills would be associated with inaccuracy in estimating proportions.

METHODS

We sought to recruit participants with a range of educational levels to expand generalizability beyond the Internet population and to ensure sufficient low-numeracy respondents to examine the numeracy hypothesis. One sample (n = 65) was recruited from waiting rooms at New York-Presbyterian Hospital, a teaching hospital in a largely Hispanic neighborhood in northern Manhattan. These participants completed the questionnaire on a laptop computer. An additional 100 participants were recruited through the Virtual Laboratory of Columbia University’s Center for the Decision Sciences (https://vlab2.gsb.columbia.edu/decisionsciences.columbia.edu/). The laboratory’s participant pool is diverse in age, education level, and geographic location, and all participants register with a PayPal account linked to a credit card, which helps prevent repeat participation. These participants completed the questionnaire on a secure Web site.

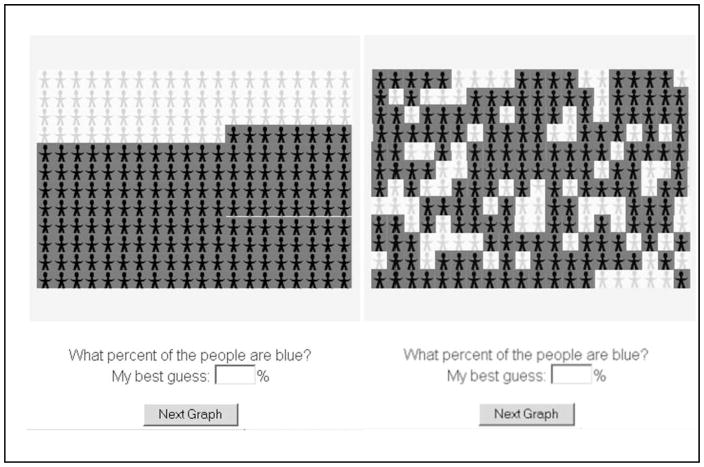
Participants viewed a sequence of 6 unlabeled graphics, each showing a grid of yellow and blue stick figures, and were asked to estimate the percentage of blue figures by providing a number between 0 and 100 (Figure 1). Each graphic faded to gray after 10 s to ensure a uniform deadline and to discourage counting. The graphics were not described as depicting a risk or a chance. The instructions read, “In this section, we will show you pictures of groups of people, and ask you to guess what percentage of the people are blue. You will have 10 seconds to see each picture before it disappears. Don’t worry about being accurate. Don’t count the people. Just take a guess!”

Figure 1.

(A) Sequential display with 70% of figures colored dark blue. In the original computer display, the dark figures were dark blue and the lighter ones were bright yellow. Participants were asked to guess what proportion were colored blue; the screen faded to gray after 10 s. (B) Random arrangement of same quantity.

Each participant was shown 6 graphics: (A) 6% random; (B) 6% sequential; (C) 29% random; (D) 29% sequential; and then (E) the random version of either 40%, 50%, 60%, or 70%; and (F) the sequential version of the same graphic as E (Table 1). Thus, all 165 respondents saw the 6% and 29% graphics, but one quarter saw the 40%, one quarter saw the 50%, one quarter saw the 60%, and one quarter saw the 70% graph. The order of presentation was A, F, C, B, D, and E.

Table 1.

Average Inaccuracy in Estimates of Unlabeled Graphics

	Random Arrangement			Sequential Arrangement
Percentage Depicted and Sample Size	Mean Estimate	Mean Inaccuracy (95% CI)	Pa	Mean Estimate	Mean Inaccuracy (95% CI)	Pa
6 (n = 165)	8.7	2.7 (1.4 to 4.1)	<0.001	6.5	0.5 (−0.7 to 1.7)	0.43
29 (n = 165)	33.7	4.7 (2.6 to 6.8)	<0.001	27.7	−1.3 (−3.2 to 0.6)	0.19
40 (n = 43)	41.6	1.6 (−3.1 to 6.2)	0.50	43.2	3.2 (−1.7 to 8.1)	0.20
50 (n = 39)	53.3	3.3 (−1.2 to 7.8)	0.15	50.5	0.5 (−2.3 to 3.4)	0.72
60 (n = 44)	66.0	6.0 (0.5 to 11.5)	0.03	62.6	2.6 (−0.5 to 5.6)	0.10
70 (n = 39)	81.0	11.0 (5.0 to 17.1)	<0.001	76.5	6.5 (3.4 to 9.7)	<0.001

^aSignificance of difference from 0.

The graphics were developed in Adobe Flash CS Professional, version 9.0, using ActionScript 2.0 (Adobe Systems Inc., San Jose, CA) and embedded in an html/php questionnaire. The graphic showed 20 ×12 stick figures; the large array size was chosen to carry the implication of a large sample, as other researchers have found that small stick-figure groups can be interpreted as indicating small (and therefore less reliable) sample sizes.³ We also intentionally avoided 100 to discourage people from counting individual stick figures and to encourage a gestalt interpretation.

After completing this unlabeled graphics study, participants proceeded to a 2nd study of hypothetical health decisions in which the decision scenarios were illustrated with interactive graphics. Results of this 2nd study are reported elsewhere.¹⁸

Sociodemographic information was collected, and all participants took an 8-item numeracy scale modified from that of Lipkus and others.¹⁹ The scale assesses applied numerical skills such as the ability to convert between percentage and proportion (modification described by Ancker and others¹⁸). The study was approved by the Columbia University Institutional Review Board. All participants granted informed consent in an online form and were provided with a small incentive upon completion (movie ticket voucher for clinic participants, equivalent dollar amount through PayPal for lab participants).

Statistical Analysis

Chi-square and 2-sample t tests were used to examine demographic differences between the 2 samples. We defined inaccuracy as the difference within person between the estimated proportion and the true proportion (so that positive differences indicate that the estimated one is higher). We reported mean inaccuracy for each graph with confidence intervals, using 1-sample t tests to supplement the confidence intervals with P values. In addition, we computed mean paired differences between estimates of sequential and random graphics for within-person comparisons, accompanied by confidence intervals and paired t tests to supplement the confidence intervals with P values. To express the relationship between the magnitude of the inaccuracy and the true proportion depicted in the graphic, we computed relative inaccuracy (inaccuracy divided by the true proportion). To explore the other factors affecting inaccuracy, we conducted univariate analyses with Pearson correlations for continuous variables (numeracy, education, and age) and analysis of variance for categorical variables (clinic status v. online, sex, and race). The variables were combined in a linear mixed model, with the 6 relative inaccuracies treated as repeated measures within person, true proportion and arrangement as fixed-effects variables, and respondent characteristics as random-effects variables. Predictors were retained at the 0.05 level, and, in addition, likelihood ratio tests were conducted to assess the effect of dropping factors in nested models. Analyses were conducted in SPSS version 16 (SPSS Inc., Chicago, IL) and R version 2.9.2 (R Foundation for Statistical Computing, www.r-project.org).

RESULTS

The sample (Table 2) had a mean age of 32.0 y (range, 18–72 y), and was 64% female.

Table 2.

Characteristics of Online and Clinic Study Samples

Characteristic	Online (n = 100)	Clinic (n = 65)	P	Total Sample (N = 165)
Mean age, y (range)	32.8 (19–61)	30.7 (18–72)	0.90	32.0 (18–72)
Women, n (%)	64 (64.0)	41 (63.1)	>0.99	105 (63.6)
Educational level, n (%)			<0.001
No bachelor’s degree	19 (19.0)	28 (45.0)		47 (28.5)
Some college	37 (37.0)	23 (35.4)		60 (36.4)
Bachelor’s or graduate degree	44 (44.0)	14 (21.5)		58 (35.2)
Race and ethnicity, n (%)			<0.001
African American	10 (10.0)	10 (15.4)		20 (12.1)
Asian	20 (20.0)	0		20 (12.1)
White	60 (60.0)	6 (9.2)		66 (40.0)
Hispanic	2 (2.0)	43 (66.2)		45 (27.3)
Other	3 (3.0)	3 (4.5)		6 (3.6)
Mixed race	5 (5.0)	3 (4.5)		8 (4.8)
Numeracy category, n (%)			<0.001
Poor ( ≤5 out of 8)	16 (16.0)	32 (53.3)a		48 (29.6)a
Adequate (>5 out of 8)	84 (84.0)	30 (46.7)		114 (70.4)

^aThree numeracy scores missing due to interruptions in the computerized assessment.

The 1st hypothesis was that estimates would differ, within person and across person, according to the stick-figure arrangement. For both arrangements, mean estimates were in general somewhat larger than but fairly close to the true proportions (Table 1); that is, all mean estimates except 1 were within 6 percentage points of the true proportion. Nevertheless, across person, most of the mean estimates and mean inaccuracies (Table 1) and mean relative inaccuracies (Figure 2) were higher for random graphs than for sequential graphs. Within-person estimates for random versus sequential graphics were significantly different from zero for the 6% and 29% graphics, and very few participants gave precisely the same estimate when viewing the same graphic in the different arrangements (Table 3). Thus, arrangement could make the same proportion appear to be of different magnitudes.

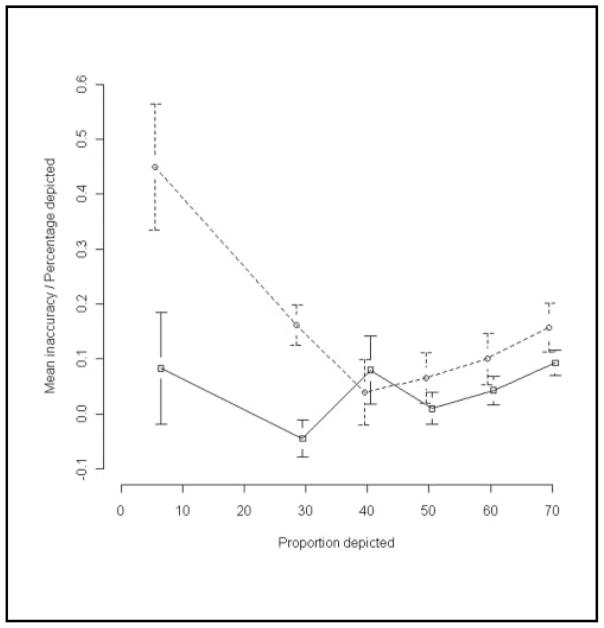
Figure 2.

Relative inaccuracy (inaccuracy as a proportion of the percentage depicted) was higher for random graphics (dotted line) than for sequential graphics (solid line), except at 40%. Differences were statistically significant at 6% and 29%. Error bars depict standard errors, and lines have been slightly jittered to avoid overlap.

Table 3.

Differences between Estimates of Percentages Depicted by Random and Sequential Graphics

Percentage Depicted and Sample Size	Mean Paired Difference (95% CI)	P	Random Estimate Higher	Estimates Exactly Equal	Sequential Estimate Higher
6 (n = 165)	2.2 (1.3 to 3.2)	<0.001	101 (61.2%)	33 (20.0%)	31 (18.8%)
29 (n = 165)	6.0 (3.8 to 8.1)	<0.001	98 (59.4%)	14 (8.5%)	53 (32.1%)
40 (n = 43)	−1.6 (−3.8 to 7.1)	0.55	21 (48.8%)	2 (4.7%)	20 (46.5%)
50 (n = 39)	2.7 (−1.1 to 6.7)	0.16	15 (38.5%)	16 (41.0%)	8 (20.5%)
60 (n = 44)	3.4 (−2.3 to 9.2)	0.24	24 (54.5%)	2 (4.5%)	18 (40.9%)
70 (n = 39)	4.5 (−2.8 to 11.8)	0.22	32 (82.1%)	2 (5.1%)	5 (12.8%)

The 2nd hypothesis was that random graphs would be estimated with less accuracy. Mean inaccuracy was significantly larger than zero for 4 of the 6 random graphs but only for 1 of the 6 sequential graphs (Table 1). In addition, confidence intervals for inaccuracy with the random arrangements were wider than the corresponding intervals for the sequential ones, except at 40% (Table 1). Relative inaccuracy was larger for random graphs than for sequential ones, except at 40% (Figure 2). The strongly U-shaped curve for random graphics indicates that relative inaccuracy was higher when the graphic depicted low or high percentages. By contrast, for sequential graphics, relative inaccuracy was much smaller, never rising above 0.09. Also, the curve was roughly flat or slightly increasing, suggesting that inaccuracy in estimating sequential graphs was less strongly affected by the percentage depicted.

All of the respondents saw the 29% graphic, and about one quarter (n = 43) also saw the 40% graphs. For these respondents, we ascertained whether they correctly ranked the 29% and 40% random graphs, that is, whether they assigned the 29% graphic a lower estimate than the 40% one. Of the 43 subjects, 31 (72%) correctly ranked the 2 random graphs, 11 (26%) estimated the 29% proportion to be larger than the 40% one, and 1 person assigned them exactly the same estimate. This suggests that the inaccuracy induced by the random arrangement was sometimes large enough to cause confusion between proportions differing by as many as 11 percentage points. By contrast, with sequential graphics, only 4 people (9%) wrongly assigned the sequential 29% graph a larger estimate than the sequential 40% one. However, respondents’ estimates of the same quantity in different arrangements were correlated (all r’s greater than 0.43), suggesting that the inaccuracy associated with the random graphic did not eliminate all sense of the size of the proportion.

For the random 6% graph, 22 people (13.3% of all respondents) gave “14” as the answer, raising the possibility that they had counted the 14 blue figures (which represented 6% of the 240 figures in the graph). (Nine of these respondents also gave “14” as the answer for the sequential 6% graph.) No similar pattern was evident for the other graphs. We repeated the analysis of mean inaccuracy and relative inaccuracy omitting these respondents. For the 6% random graph, mean inaccuracy decreased from 2.7 percentage points to 1.9 percentage points but remained statistically significantly different from 0 (P = 0.01); relative inaccuracy decreased from 0.46 to 0.32. For the 6% sequential, mean inaccuracy decreased from 0.5 to 0.03 percentage points, which remained not statistically different from 0 (P = 0.96); relative inaccuracy decreased from 0.03 to 0.005. The proportion whose random estimates were higher than their sequential estimates changed only slightly from 61.2% to 64.3%. Thus, omitting these responses reduced the mean overestimation but did not change conclusions about statistical significance.

Our 3rd hypothesis was that numeracy would be associated with accuracy in estimation. Better numeracy was correlated with decreasing inaccuracy for 29% random and sequential (r = −0.26, P = 0.001 for random; r = −0.16, P = 0.04 for sequential) and 6% random (r = −0.17, P = 0.03), but not for the 6% sequential or for 40%, 50%, 60%, or 70% graphics in either arrangement (all r < |0.15|, all P > 0.10). Low-numeracy respondents gave higher mean estimates for all graphics than high-numeracy ones, and the differences were statistically significant for 6% random (7.7 v. 11.6, P = 0.01), 29% random (38.7 v. 31.5, P = 0.002), and 29% sequential (31.7 v. 25.8, P = 0.005) but not for the 6% sequential or for the 40%, 50%, 60%, or 70% graphics in either arrangement. Low numeracy was not associated with the tendency to answer 50% for any graphic. Inaccuracy was not associated with sex or age but was higher among lower educational levels, clinic respondents, and Hispanic respondents.

In linear mixed models of relative inaccuracy, effects of clinic status and Hispanic ethnicity became nonsignificant when we controlled for numeracy, although education remained marginally significant. Overall, mean relative inaccuracy was 41%, and Table 4 shows that relative inaccuracy was 10% higher for random arrangements, decreased by 3% with each increment of the 8-item numeracy scale, and decreased by 2% for each additional level of education. (Although the P value for education was 0.08, it was retained because the effect size appeared meaningful and because a likelihood ratio test showed that dropping it would result in a significant loss of information: difference in −2LL: 6.0, P = 0.001.)

Table 4.

Parameter Estimates for Linear Mixed Model of Relative Inaccuracy

Parameter	Estimate	SE	df	t	P	95% CI
						Lower Bound	Upper Bound
Intercept	0.35	0.04	403.8	8.07	<0.001	0.26	0.44
Proportion depicted
0.70	Reference
0.60	0.02	0.03	365.9	0.59	0.55	−0.05	0.09
0.50	−0.07	0.04	355.5	−1.88	0.06	−0.14	0.003
0.40	0.09	0.03	362.6	2.59	0.01	0.02	0.16
0.29	0.16	0.03	586.8	5.72	<0.001	0.11	−0.22
0.06	0.50	0.07	389.1	7.00	<0.001	0.36	0.64
Random arrangement (v. sequential)	0.10	0.02	369.6	6.21	<0.001	0.07	0.14
Numeracy score	−0.03	0.006	214.9	−4.04	<0.001	−0.04	−0.01
Education	−0.02	0.01	154.5	−1.75	0.08	−0.04	0.002

DISCUSSION

This heterogeneous group of health consumers was able to estimate proportions depicted by stick-figure graphics under a time limit with fair accuracy, on average. However, individual estimates varied widely. As we had hypothesized, randomly arranged stick-figure graphics elicited different (somewhat higher) mean estimates than sequential ones for almost all the graphs; randomly arranged graphics were estimated with less accuracy for almost all proportions; and the viewer’s numeracy level correlated with accuracy. The only other respondent characteristic that was a meaningful predictor was educational level, although the effect size for education was somewhat smaller than the effect size for numeracy.

Schapira and others¹² have also recently found that randomly arranged graphics elicited higher probability estimates. Random arrangements in health promotion or medical decision-making materials for the public may make proportions appear larger than they truly are, at least at first glance.

We had hypothesized that estimates of random arrangements would be more inaccurate than estimates of sequential ones. This was confirmed for high proportions and low ones, although not for the proportions of 40% and 50%. In general, this seems consistent with other research suggesting that mentally summing noncontiguous areas is more effortful and less accurate than estimating proportions in lines or blocks,^9–11 although these studies did not use time limits. In our study, the inaccuracy induced by the random arrangement was large enough that more than one fourth of respondents confused 2 graphics depicting proportions that differed by 11 percentage points.

An implication of these findings is that when graphics are to be placed side by side (as in illustrations of risks before and after some behavior change), random arrangements are probably suboptimal. In particular, small to moderate differences in the risks may not be immediately discernible with the random arrangement, although they might be detectable after a longer examination period. However, this inflation in perceived proportion associated with random arrangement may not necessarily lead directly to inflation in perceived risk when the graphic is viewed for a longer time, labeled with the percentage, and accompanied by a verbal scenario, according to a companion study.¹⁸

Our results also support the hypothesis that performance on a numeracy assessment¹⁹ was associated with accuracy in estimating the proportions for many of the proportions we tested, especially for random arrangements. The skills assessed in the numeracy scale may be related either to the interpretation of the visual information or to the ability to report it in numerical form. The less numerate respondents gave higher estimates for almost all graphs. Although this particular study did not tell the respondents that the graphics portrayed risks, the results nevertheless seem compatible with others’ findings that low numeracy is linked with overestimates of personal risk of disease.^20,21

It was interesting that low numeracy was not associated with the likelihood of answering “50%,” as others have suggested that a response of 50% may be in part an expression of uncertainty or confusion, and thus low-numeracy respondents might be expected to use it more often.^21,22 Others have shown that icon graphics produced better understanding of risk reduction information than numbers alone, for high- and low-numeracy respondents.⁷

Because 29% is approximately equal to 100% −70%, and 40% = 100% – 60%, we might anticipate that the inaccuracies would be symmetrical for the 29%/70% pairs and the 40%/60% pairs. Relative inaccuracy did appear somewhat symmetrical for random graphics but not for sequential ones (Figure 2). Further study would be needed to determine how symmetry might be affected by manipulations such as asking for estimates of the proportion in yellow instead of the proportion in blue or by changing the colors to alter figure/ground perception.

Estimates were more likely to end with the digit 5 (30.2% of all estimates) or 0 (36.2% of estimates) than any other digit. For example, the 2 modal responses for the 6% random graph were 10 (18.2% of responses) and 5 (15.2% of responses), and for the 6% sequential graph the modal response was 5 (26.1% of responses). This may have slightly increased the mean estimates for both 6% graphs (as 10 is further from 6 than 5 is) and slightly decreased them for 29% graphs (25 is further from 29 than 30 is). However, this bias would not be expected to affect the proportion who gave larger estimates for the random version (Table 3).

Limitations

We chose 2 common types of stick-figure arrangements to compare, the random and the sequential, but did not explore other possible variants such as placing the block of stick figures in other areas of the rectangular array, nor did we explore different graphic sizes. We also did not address the problem of explaining extremely small probabilities.²³ The instruction encouraging participants to “take a guess” at the correct proportion were intended to discourage counting and alleviate anxiety about the 10-s time limit, but we cannot rule out the possibility that it may have encouraged careless responses (thereby increasing the variance in the estimates) or induced some systematic bias (increasing or decreasing the average estimate). The inclusion of 2 samples, one representing urban outpatients and their families and another representing an Internet population, broadened the range of education and numeracy levels in our study. As sample origin (clinic v. online) was not statistically significant in the regression models, it appears that this factor did not otherwise affect the results. The samples nevertheless were relatively young and had high average health literacy and relatively good self-rated health, so generalizability to other patient groups may be limited.

CONCLUSIONS

Health risks are often depicted with groups of stick figures, with a certain proportion of figures in a different color to indicate that they suffer from the disease. Such graphics will be most successful at conveying information about risks if viewers can accurately interpret the proportion they depict. We showed unlabeled graphics to a heterogeneous group of health consumers and patients to determine if they could do so, imposing a time limit to elicit first impressions. Although average estimates of the proportions were fairly good, variation from person to person was quite high, and accuracy was impaired by low numeracy and by random arrangement of stick figures.

We conclude that although stick-figure graphics may help illustrate risks to consumers, graphics that are not labeled with the numerical probability may be misinterpreted. With randomly arranged graphics, visual estimates are inaccurate enough that small to moderate differences between risks are unlikely to be visible at first glance. Random arrangements may also create an initial impression that large risks are larger than they are. Although these misleading impressions may disappear when the viewer examines the graph more carefully, the findings nevertheless suggest that random arrangement places an additional cognitive burden on the patient who is interpreting medical information.